Математическая модель процесса хаотизации сигнала в цепочке нелинейных усилителей приемного устройства

Математическая модель процесса хаотизации сигнала в цепочке нелинейных усилителей приемного устройства

Математическая модель процесса хаотизации сигнала в цепочке нелинейных усилителей приемного устройства

Разработана математическая модель процесса хаотизации входного квазипериодического сигнала при прохождении в приемно-усилительном тракте цепочки нелинейных усилителей с квадратичной характеристикой.

Постановка проблемы.

Одним из самых важных и естественных вопросов, которые надо решить при исследовании, такого достаточно сложного устройства, состоящего из многих блоков, как приемно-усилительный тракт (ПУТ), является вопрос о вкладе разных блоков в общий эффект хаотизации ПУТ под воздействием внешних импульсных сигналов[1,3]. Такие вопросы должны быть решены как при экспериментальных исследованиях, так и при теоретических. При этом, чаще всего исследователей интересуют слабые по мощности воздействия, находящиеся существенно ниже порога разрушения полупроводниковых устройств входящих в состав ПУТ. Высокая чувствительность ПУТ и малые амплитуды воздействующих сигналов приводит к тому, что хотя исследуемые устройства и содержат средства контроля за прохождением сигнала по ПУТ, но их использование затруднительно. Это связано с тем, что либо необходима очень чувствительная регистрирующая аппаратура, либо измерительная аппаратура будет искажать измеряемую информацию.

Эти обстоятельства делают очень существенным построение адекватной эксперименту математической модели и проведении предварительных численных экспериментов для выяснения механизмов возникновения хаоса и вклада различных блоков ПУТ в процессы его хаотизации.

Анализ последних достижений и публикаций.

Математическая модель динамической системы считается заданной, если введены координаты системы, определяющие однозначно ее состояние и указан эволюционный оператор, позволяющий решать задачу определения изменения состояния системы во времени. В зависимости от степени приближения одной и той же реальной системе могут быть поставлены в соответствие принципиально различные математические модели. Более того, эти математические модели не должны выходить за рамки корректно поставленных задач [1-3].

Для системы, обладающей хаотическим характером поведения траекторий, естественным путем получения информации о ее поведении является изучение эволюции средних значений физических величин. Самым распространенным методом описания средних характеристик системы, является статистический метод с использованием функции распределения. Функция распределения определяется в результат решение кинетического уравнения, а средние величины находятся путем усреднения функцией распределения. Однако, существует другой подход к системам обладающим динамическим хаосом. Хаотической динамической системе ставится в соответствие не система обыкновенных дифференциальных уравнений, определяющая ее состояния в фазовом пространстве, а система уравнений, в основе получения которых лежит фундаментальное понятие регуляризующего оператора [3]. То есть, обыкновенная производная заменена дробной производной, порядок которой связан с показателем Ляпунова[3,6]. Этот математический аппарат, позволяет описать возникновение хаоса при прохождении сигнала через ПУТ.

Целью статьи является разработка математической модели процесса преобразования входного сигнала в хаотический при прохождении цепочки нелинейных усилителей в приемно-усилительном тракте.

Основной материал.

Рассмотрим цепочку усилителей, каждый из которых состоит из соединенных последовательно безынерционного усилителя и фильтра. Обозначим сигнал на выходе n-го звена через 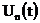. Будем предполагать, что усилитель безинерционный, т.е. сигнал на его выходе 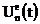 записывается через сигнал на входе 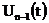 алгебраически:

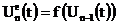. (1)

Линейный фильтр описывается оператором :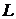

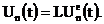 (2)

Комбинируя (1), (2), получаем соотношение, связывающее на выходе (n-1) и n-го элементов

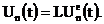, (3)

при этом входной сигнал 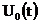 должен быть задан.

Рассмотрим систему, в которой усилитель описывается квадратичной функцией:

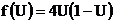, (4)

а линейный фильтр есть фильтр низких частот с частотной характеристикой

В качестве единицы времени принята постоянная времени фильтра. Систему (3) можно записать как систему обыкновенных дифференциальных уравнений [1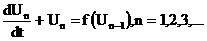-6]

. (6)

Рассмотрим преобразование периодического входного сигнала 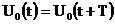. Тогда, как следует из однородности во времени уравнений (3), при любом значении n сигнал 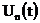 также имеет период T: 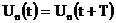. Таким образом, хаотизации сигнала во времени не происходит. Однако возможен механизм пространственной стохастизации[6], когда сигнал, оставаясь периодическим во времени, хаотически меняется по переменной n. Механизм возникновения хаоса можно понять, если рассмотреть систему без фильтра. Используя, с учетом (4), получаем:

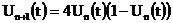 (7)

Отображение (7), как хорошо известно[1,6], приводит к хаотическому по n изменению величины 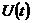. Значения  и 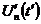 при любых  и 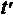 преобразуются независимо. Сигнал  искажается, обогащаясь гармониками, но остается периодическим. Линейный фильтр сглаживает сигнал, его влияние тем сильнее, чем меньше период сигнала. При 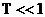 все гармоники входного сигнала, кроме нулевой, затухают по n и устанавливается режим хаотического по n изменения постоянного сигнала.

При изменении периода T динамика режимов следующая [1,3]. При  наблюдается хаотический по n режим, при  - регулярный (периодический или квазипериодический), а при 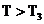 - хаотический.

Рассмотрим теперь устойчивость преобразования в цепочке усилителей квазипериодического по t сигнала. Пусть входной сигнал имеет вид:

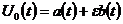, (8)

где 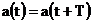 - периодический сигнал,  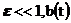- возмущение, имеющее в общем случае несоизмеримые с 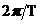 спектральные компоненты. Это могут быть последовательности СВЧ или ЭМИ импульсов. Линеаризуя уравнение (3) на фоне решения 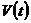, соответствующего  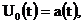получим

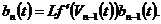 (9)

Уравнение (9) задает периодически зависящее от t линейное отображение в пространстве функций. Будем искать его решения в виде:

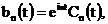 (10)

где 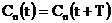. Это представление аналогично представлению Блоха[1,3], используемому при решении линейных дифференциальных уравнений с периодическими коэффициентами. С учетом (10) уравнение (9) можно записать в виде

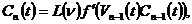 (11)

Отображение (11) в отличие от (9) действует уже на классе периодических по t функций. В общем случае при больших значениях n решение (11) ведет себя асимптотически[1] как

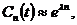 (12)

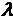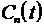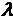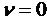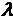где  - показатель устойчивости, который будем называть квазиляпуновским. Соотношение (12) следует понимать в статистическом смысле: в среднем сигнал  возрастает от усилителя к усилителю с показателем . При  уравнение (11) описывает эволюцию возмущений с тем же периодом, что и основной сигнал. В этом случае  есть обычный ляпуновский показатель ( по дискретному времени ), который определяет, есть хаос или нет. В общем случае 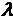 зависит от частоты  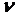и определяет устойчивость периодического сигнала: 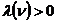 означает, что возмущение вида (10) нарастает с n.

Описанная выше неустойчивость образования периодического сигнала позволяет дать качественную картину хаотизации сигнала в цепочке усилителей. Пусть сигнал на входе имеет вид

математический усилитель сигнал хаотизация

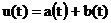 (13)

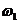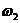Рассмотрим подробнее случай, когда входной сигнал квазипериодический, т.е. частоты  и  компонент a и b несоизмеримы. При нелинейном преобразовании возникают спектральные компоненты на разностных и суммарных частотах, которые возрастают в силу описанной неустойчивости; появляются новые спектральные компоненты и т.д. В результате спектр становится неотличимым от сплошного и сигнал можно считать случайным.

Результаты численных расчетов преобразования (3), в которых максимальный период сигнала 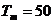 и учитывая что на фоне сигнала с 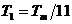 добавляли компоненту с 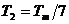 на уровне 60дБ показывают, что рост комбинационных частот происходит весьма быстро и практически заканчивается к .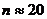

Остановимся на математической природе описанного выше хаоса, возникающего при двухчастотном входном сигнале. Цепочка из n усилителей описывается системой из n обыкновенных дифференциальных уравнений (6). Для этой системы можно найти ляпуновские показатели[3], описывающие устойчивость движений по t. Из системы (6) следует, что два показателя равны нулю, а остальные отрицательные и равны - 1. Таким образом, с математической точки зрения при любом n аттрактор представляет собой двумерный тор. Это противоречит наблюдаемому хаотическому характеру сигнала. Парадокс объясняется тем, что с ростом n тор становится все более изрезанным и в пределе 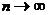 фрактальным. На спектральном языке существование тора означает, что в спектре присутствуют только частоты вида . 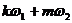Фрактализация же тора связана с том, что комбинационные гармоники с большими значениями k и m по величине имеют тот же порядок, что и гармоники с малыми k и m.

Выводы и направления дальнейших исследований.

Разработанная математическим модель процесса возникновения хаоса в цепочке усилителей при двухчастотном воздействии входного сигнала подтвердила результаты экспериментов [4-6]. Динамика системы при этом определяется "квазиаттрактором" в фазовом пространстве системы.

В дальнейшем представляет интерес не только разработать модели работы существующих систем защиты РЕА систем связи от электромагнитного поражения, а и наметить пути их усовершенствования.

Литература

1.          Электромагнитная совместимость радиоэлектронных средств и систем./В.И.Владимиров, А.Л.Докторов, Ф.В.Елизаров и др. Под ред. Н.М.Царькова. - М.: Радио и связь, 1985. - 272 с.

2.        Кравченко В.И., Болотов Е.А., Летунов Н.И., Радиоэлектронные средства и мощные электромагнитные помехи, Москва: Радио и связь, 1987. -361 с.

3.       Анищенко В.С., Стохастические колебания в радиофизических системах, Ч.1, Саратов: 1985. -253 с.

.         Афраймович В.С., Некоркин В.И., Осипов Г.В., Шалфеев В.Д., Устойчивость, структуры и хаос в нелинейных сетях синхронизации/ Под ред. Гапонова-Грехова Ф.В., Рабиновича М.И., Горький, 1989. -230 с.

.         Кальянов Э.В. , Дистанционная синхронизация генератора релаксационных колебаний последовательностью импульсов для кардиостимуляции, Радиотехника и электроника, 1991. Т. 36, С.617--619.

.         Неймарк Ю.И., Ланда П.С., Стохастические и хаотические колебания. М.:Наука.1987, -271с.