Безынерционные адаптивные алгоритмы для управления техническими объектами с ограниченной неопределенностью

Безынерционные адаптивные алгоритмы для управления техническими объектами с ограниченной неопределенностью

Санкт-Петербургский государственный электротехнический

университет «ЛЭТИ» им. В.И.Ульянова (Ленина)

Безынерционные адаптивные алгоритмы для управления техническими объектами с ограниченной неопределенностью

Н.Д. ПОЛЯХОВ, И.А. ПРИХОДЬКО, ХА АНЬ ТУАН

Аннотация. Методом функций Ляпунова синтезированы безынерционные адаптивные алгоритмы сигнального и параметрического типа для управления техническими объектами с ограниченной неопределенностью по схеме с настраиваемой моделью. Целесообразными с точки зрения реализации Эти алгоритмы не изменяют параметры и структуры регуляторов систем, а подключатся прямо ко входу штатных регуляторов, что немаловажно при их реализации. Кроме того, такие алгоритмы остаются грубыми (нечувствительными) к влияниям внешних возмущений, которые трудно измерить или учесть в модели технического объекта. Исследование моделированием в среде MatLab/Simulink выполнено на примере управления динамикой синхронного генератора.

The keywords: Adaptive control, inertia-free signal and parametric adaptation, synchronous generator.

Реальные процессы в динамических системах обладают разнообразными по физической природе источниками не­определенности. Характер (параметры) этих неопределенностей почти всегда точно неиз­вестны. Последнее обстоятельство приводит к необходимости адаптивного подхода в построении законов управления такими объектами. Именно адаптивное управление позволяет эффективно управлять и повышать каче­ство функционирования объектами с неопределенностью. К настоящему времени имеется определенный задел в разработке адаптивных систем раз­личного назначения [1-3]. Однако адаптивные разработки не приспособ­лены к реальным объектам, где практически отсутст­вует возможность в изменении структуры регулятора и остается только вари­ант введения дополнительных сигналов управления. Разработке адаптивных стратегий, как правило, сопутствует проблема получения полного вектора со­стояния управляемого объекта. В адаптивной постановке указанная проблема и построение законов управления возможно решать совместно, что и принято в работе.

Построение адаптивного управления техническими системами, как правило, основано на двух главных подходах: адаптивное управление по схеме с эталонной моделью (АСЭМ) и по схеме с настраиваемой (идентификационной) моделью (АСНМ). Однако, преимуществами по стабильности функционирования и реализации обладает адаптивная система типа АСНМ [1] со структурой на рис. 1.

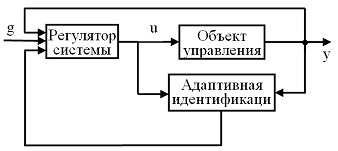
Рис. 1

Алгоритм безынерционной сигнальной адаптации

Управляемый объект задается в виде

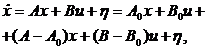  (1)

где 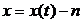-мерный вектор состояния; 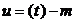-мерный вектор управления,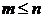; 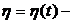ограниченная функция возмущений; 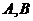 - матрицы с ограниченными элементами и в общем случае, зависящие от 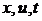;  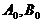является результатом линеаризации матриц 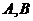 в режимной точке. Все размерности согласованы.

Из уравнения (1) получаем уравнение  (2)

где .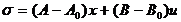

При управлении объектом (1) принят идентификационный подход в синтезе закона адаптивного управления на основе схемы с настраиваемой моделью. Уравнение настраиваемой модели имеет вид

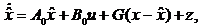 (3)

где 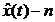-мерный вектор состояния настраиваемой модели, матрица 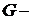выбирается из условия гурвицевости матрицы 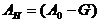, поскольку может содержать собственные значения с положительной вещественной частью, 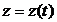- адаптивный сигнал.

Введем ошибку 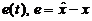 (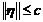), тогда из выражений (2) и (3) получим дифференциальнное уравнение вида

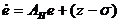  (4)

Выберем квадратичную функцию Ляпунова в виде 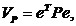 где постоянная матрица 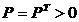и является решением матричного уравнения Ляпунова: 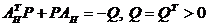является заданной. Тогда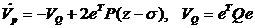. (5)

Закон управления 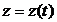выбирается из условия максимальной скорости убывания функции Ляпунова в виде .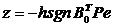

В правой части дифференциального уравнения (5) для асимптотической устойчивости должно быть выполнено условие 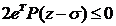, которое обеспечивается при 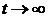, если  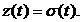Однако это невозможно, так как функция 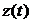 имеет разрывный характер и для использования адаптивного закона в построении следует применить малоинерционный фильтр с описанием

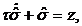 (6)

где 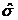 - непрерывная функция, являющаяся оценкой для 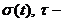 достаточная малая величина.

Пусть 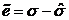. Из выражения (6) получаем:

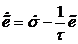. (7)

Примем 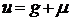, где 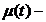адаптивный закон управления, 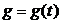- внешнее воздействие. Тогда уравнение системы (1) примет вид

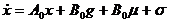
При выполнении условия согласованности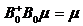, имеем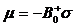. Оценим влияние введенного фильтра на устойчивость адаптивной системы. Введем функцию Ляпунова 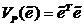, полная производная по времени которой в силу (7) равна

.

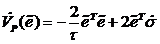Используя известную подстановку 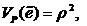получаем

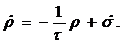 (8)

Решение уравнения (8) имеет вид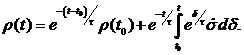  

Переходя к оценке 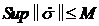, 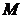= const, получаем, при 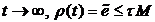.Полученная оценка по влиянию малоинерционного фильтра, указывает на диссипативную (экспоненциального типа) устойчивость, причем размер предельного множества регламентируется выбором значения самого параметра τ .

Теорема 1. Пусть существуют параметры 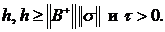 Тогда алгоритм 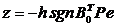 с фильтром  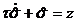обеспечивает адаптивность системы (2) при ограниченной неопределенности и регламентируемую параметром 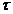 диссипативность процессов адаптации.

Из результатов моделирования процессов управления синхронного генератора [4] с адаптивным регулятором следует, что адаптивный регулятор хорошо группирует формы процессов («близко к одному процессу») при изменении режимов работы сети с разными нагрузками и сопротивлениями линии электропередачи.

Алгоритм безынерционной параметрической адаптации. Объект управления задан в виде

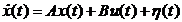, (9)

где все обозначения такие же, как в уравнении (1); у матрицы 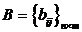 все элементы точно известны, а элементы матрицы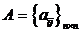имеют параметрическую (интервальную) неопределенность в области 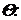 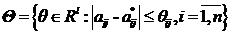, 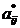- номинальные значения, .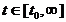

Уравнение настраиваемой модели аналогично (3) и имеет вид

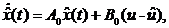 (10)

где 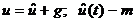-мерный вектор сигналов адаптации модели, со стационарной правой частью, соответствующей желаемой динамике.

Введем ошибку , .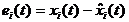

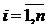Из уравнений (9), (10) после несложных преобразований получаем дифференциальное уравнение ошибки

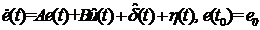, (11)

где 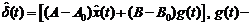входной сигнал.

Здесь 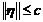. Из уравнения (11) следует уравнение адаптивного регулятора

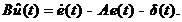 (12)

Уравнение (9) представим в виде 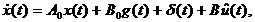 (13)

где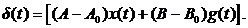

На основе уравнений (12), (13), а также с учетом того, что при t→∞, получаем уравнение (9) в виде

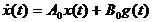
как результат действия адаптивного регулятора (12).

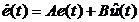 (14)

Закон адаптации 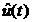ищется таким, чтобы обеспечить асимптотическую устойчивость решения уравнения (14).

Пусть структура регулятора задается в форме линейной обратной связи

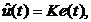 (15)

где 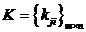 - матрица настраиваемых параметров.

Уравнение ошибки (14) тогда примет вид

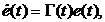 (16)

где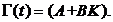  

Закон настройки элементов матрицы настраиваемых параметров 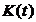 должен обеспечивать асимптотическую устойчивость решения уравнения (14) с интервально неопределенной матрицей A.

Пусть функция Ляпунова выбрана как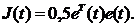

Ее полная производная по времени имеет вид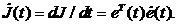  

Для обеспечения асимптотической устойчивости системы (14) достаточно, чтобы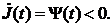  

С учетом уравнения (16) имеет место

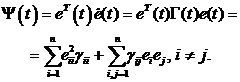
Обозначим: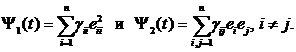

 Лемма. Существуют постоянные параметры 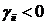 и функции 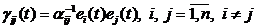, при которых условие 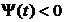 выполняется.

Действительно, примем диагональные элементы матрицы 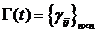 постоянными и отрицательными, т. е. 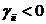, тогда  .

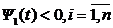Теперь, найдем условия для выполнения неравенства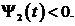  

Используем подстановку [5]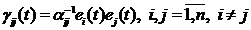. Тогда  (17)

При выборе , .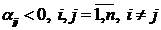

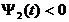Из выражения 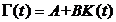 получаем матрицу настраиваемых параметров 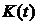, которая, в случае  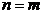и неособенности матрицы 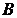, имеет вид 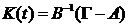, а при  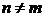- в виде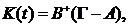

Так как матрица 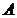 в уравнении (9) имеет параметрическую неопределенность, для вычисления матрицы 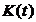 используются “номинальные” значения .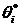

Теорема 2. Система (9) обладает асимптотической устойчивостью с законом безынерционной параметрической адаптаци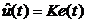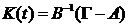и ,  или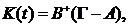  

Результаты моделирования переходных процессов синхронного генератора с адаптивным регулятором и с тремя наборами элементов матриц 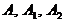(с номинальными значениями и уменьшением/ увеличением в 5 раз) в среде MATLAB/Simulink представлены на рис. 2., 3, где на рис. 2 - переходные процессы синхронного генератора без адаптации, на рис. 3 - переходные процессы синхронного генератора с адаптацией.

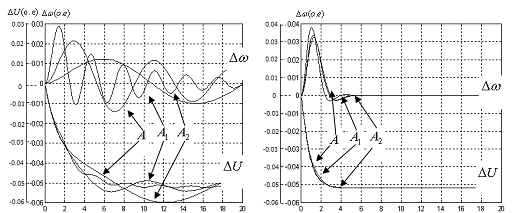
Рис. 2 -

Рис. 3 -

Из результатов моделирования следует, что переходные характеристики адаптивного синхронного генератора на рис. 3 локализованы в достаточно узкой окрестности кривых, (почти совпадение) при значительных вариациях его параметров, что можно обобщить как «адаптивное управление СГ с усиленной грубостью».

Литература

безынерционный адаптивный алгоритм

1. Борцов Ю.А., Поляхов Н.Д., Путов В.В. Электромеханические системы с адаптивным и модальным управлением. Л: Энергоатомиздат, 1984 - 216 с.

2.      Александров А.Г. Оптимальные и адаптивные системы, 2003 - 279 с.

3. Кунцевич В. М., Лычак М. М. Синтез систем автоматического управления с помощью функций Ляпунова. М.: Наука. 1977 - 400с.

4. Андерсон П., Фуад А. Управление энергосистемами и устойчивость. - М: Энергия, 1980 - 568 с.

5.      Кожекова Г. А. Расчет адаптивной системы управления для синхронного генератора. Известия КГТУ им. И. Раззакова. 2010,- № 21- С. 158-162.