Створення глобальних мереж методами супутникової геодезії

Міністерство освіти та науки, молоді та спорту України

Київський національний університет будівництва і архітектури

Кафедра геоінформатики та фотограмметрії

Курсова робота

Створення глобальних мереж методами супутникової геодезії

Виконав: ст. гр. ГД-41

Мачуха С.О.

Перевірив:

доц. Єгоров О.І.

Київ 2012

План

 

1. Вступ

1.1 Сучасний стан української мережі станцій супутникової геодезії

2. Системи координат та системи виміру часу

2.1 Системи координат та їх перетворення

2.2 Системи відліку часу

2.3 Визначення координат пункту та ШСЗ в геоцентричній системі координат за результатами спостережень

3. Незбурений рух ШСЗ

3.1 Визначення елементів орбіти із спостережень

3.2 Визначення ефемериди ШСЗ

4. Методи спостережень ШСЗ

3.3 Радіотехнічний метод: допплерівський і радіоінтерферометри з наддовгою базою

5. Геометричні методи побудови мереж

5.1 Тріангуляційні побудови

5.2 Лінійно-кутові побудови

5.3 Врівноваження супутникових мереж

Висновок

Список літератури

1. Вступ

За допомогою штучних супутників Землі супутникова геодезія вирішила ряд важливих питань, а саме: однозначне визначення положення будь-яких точок земної поверхні у загальноземній системі координат, визначення і постійне уточнення фігури і гравітаційного поля Землі та ін.

Наприкінці сімдесятих років пріоритетним напрямом у розвитку космічної геодезії став динамічний метод, при реалізації якого супутник розглядається не тільки як висока візирна ціль, але і як носій координат.

Кінець XX століття ознаменований широким впровадженням в геодезію глобальних супутникових радіонавігаційних систем. Ці системи увібрали в себе, по суті, досягнення космічної геодезії та радіоелектроніки.

Тепер вже актуальним завданням стає не тільки визначення положення пунктів і параметрів гравітаційного поля Землі, але і їх зміни з часом.

Метою даної курсової роботи є ознайомлення з основними етапами створення глобальних мереж, методами супутникової геодезії.

 

.1 Сучасний стан української мережі станцій супутникової геодезії

Цілеспрямоване створення мереж станцій супутникової геодезії розпочалося в 1992 р.

березня 1992 р. Міністерство освіти і науки України видало наказ № 68, в якому був сформульований комплексний міжвузівський проект "Створення і забезпечення постійної експлуатації мережі ЛЛС-спостережень ШСЗ на території України для розв'язання задач екології, ресурсозберігання, геодезії, картографії, навігації та метеорології", розрахований на 1992-1996 рр.

Подальший розвиток українська мережа станцій космічної геодезії та геодинаміки отримала завдяки Державній програмі "Створення та розвиток Державної служби єдиного часу і еталонних частот", яка була затверджена Постановою Кабінету Міністрів України від 16 червня 1995 р. № 434, та Постанові Кабінету Міністрів України від 18 липня 1998 р. № 1121 "Про затвердження Положення про Державну службу єдиного часу і еталонних частот", а саме проекту "Створення та розвиток системи визначення параметрів обертання Землі та шкали всесвітнього часу" (шифр "Орієнтація"). За підтримки Державної програми була модернізована та вступила в експлуатацію перша черга станцій Української ЛЛС-мережі: станції "Голосіїв-Київ", "Сімеїз", "Кацівелі" та "Львів".

Сучасний стан Укргеокосмомережі закріплено Постановою Кабінету Міністрів України № 486 від 7 квітня 2003 "Про утворення державної мережі моніторингу глобальних навігаційних супутникових систем". Відповідальність за координацію роботи, пов'язаної із забезпеченням функціонування та розвитку державної мережі моніторингу глобальних навігаційних супутникових систем, покладено на Національне космічне агентство України (НКАУ, м. Київ). У програмі приймають участь 11 організацій, підпорядкованих МОН України, НАН України, Держспоживстандарту, Національному космічному агентству України. Одним з головних виконавців програми є НДІГК. [11. с.10]

супутникова геодезія штучний земля

2. Системи координат та системи виміру часу

Для вирішення завдань супутникової геодезії застосовуються різні системи координат.

Вони відрізняються за формою їх задання:

         прямокутні (плоскі або просторові);

-       

         криволінійні (сферичні і еліпсоїдальної).

За розташуванням початку відліку:

геоцентричні, з початком відліку у центрі мас Землі;

референцної (квазігеоцентричні), з початком в центрі прийнятого референц-еліпсоїда;

топоцентричні, з початком відліку на поверхні Землі в точці спостереження.

За вибору основної (фундаментальної) координатної площини:

         екваторіальні - в площині екватора на певну епоху;

-        горизонтальні - у площині місцевого горизонту;

         орбітальні - у площині орбіти.

За орієнтування площині ХО2:

         інерціальні (рівноденні), вісь OX спрямована в точку весняного рівнодення, а вісь OZ співпадає з віссю обертання Землі.

-        Грінвіцький, площина XOZ збігається або паралельна площині Гринвіцького меридіану. [12. с.13-17]

Одиниці відліку часу, що застосовуються при супутникових вимірах, можна розділити на дві групи - астрономічні та неастрономічні. Повний оборот Землі навколо своєї осі ставить одиницю часу, звану добами (приблизно 86 400 сек) - основну астрономічну одиницю часу. Оберти Землі фіксуються щодо напрямку на будь-яку зірку або направлення на центр Сонця. [12. с.22]

2.1 Системи координат та їх перетворення

 

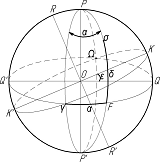
Друга екваторіальна система

В другій екваторіальній системі координат, так само як і в першій, основним колом служить небесний екватор QΩQ’γ.

Перша координата - схиляння δ (або полярна відстань Δ). Це дуга кола схилення відлічена від площини екватора до світила. Ця координата не залежить від часу.

Для визначення другої координати потрібно вибрати на сфері початкове коло і початкову точку. Для того щоб друга координата не залежала від часу і місця спостереження, потрібно, щоб початкова точка. Знаходилася на екваторі і була незмінно пов'язана зі сферою.

Через вісь світу РР' і точки весняного γ і осіннього Ω рівнодення проведемо коло схилення рівноденних точок РσР'. Це велике коло називається колюром рівнодення.

Другою координатою буде дуга екватора γF від точки весняного рівнодення до основи кола схилення даного світила. Вона називається прямим сходженням і позначається буквою α.

Пряме сходження може бути виміряне також двогранний кутом γPP’σ між площиною колюра рівнодення і площиною кола схилення даного світила, або сферичним кутом γPσ при північному полюсі світу між колюром рівнодення і кругом схилення.

Прямі сходження виражаються в годинній мірі і відраховуються від точки весняного рівнодення проти годинникової стрілки, тобто в напрямку, протилежному видимому добового руху світил, від 0 до 24^h. Пряме сходження відраховується від точки весняного рівнодення, яка бере участь у добовому обертанні, як і всі світила небесного зводу. Положення світил відносно точки весняного рівнодення не змінюється і, отже, пряме сходження, як і схилення, не залежить від добового обертання небесної сфери.

Оскільки розглянута система координат не пов'язана з горизонтом і меридіаном, екваторіальні координати α і δ від географічного положення місця спостереження також не залежать.

Екваторіальні координати α і δ визначаються зі спеціальних спостережень на обсерваторіях і публікуються в астрономічних щорічниках і зоряних каталогах. При виконанні астрономо-геодезичних робіт екваторіальні координати вважаються відомими. [1. с.28-29]

Перетворення координат

Основне завдання: перетворити вихідні координати пунктів і спостережені координати ШСЗ в одну і ту ж систему, інерційну або Грінвіцьку.

Перетворення геодезичних координат в прямукутні

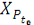
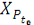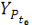
Спочатку розглянемо перетворення вихідних геодезичних координат станцій спостережень В, L, Н у Грінвіцькі прямокутні координати , ,  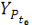пов'язані з референц-еліпсоїдом. Для цього застосовуються формули сфероїдичної геодезії.

;

;

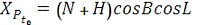
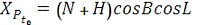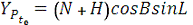
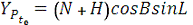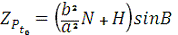
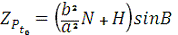
де а - велика піввісь референц-еліпсоїда, 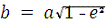 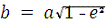- його мала піввісь, N - радіус кривизни першого вертикала, який обчислюється за формулою:

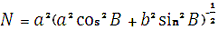
e - ексцентриситет меридіанного еліпса.

Зворотний перехід проводиться методом послідовних наближень. Спочатку з перших двох формул знаходимо:

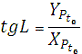
Розділивши третю формулу на корінь квадратний із суми квадратів двох перших формул, отримаємо:

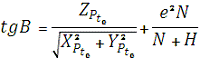
В першому наближення другий член в цьому рівнянні відкидається і знаходимо перше наближення В ^(1). З цим значенням знаходимо перше наближення Н ⁽¹⁾ по формулі:

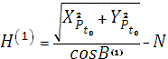
Знаючи Н ⁽¹⁾ за попередньою формулою знаходимо друге наближення В ^(2), далі за останньою формулою - друге наближення Н ⁽²⁾ зі значенням В ⁽²⁾ і т.д. Процес наближення закінчується коли різниця між останнім і передостаннім наближенням стаю менше заданої величини. Якщо задана похибка має порядок 0,01". то достатньо трьох-чотирьох наближень. [4. с.22-23]

Перетворення з референцних координат в геоцентричні

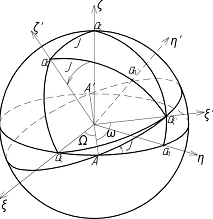
Всі подальші перетворення полягають у паралельних перенесеннях і поворотах координатних осей. Нагадаємо спочатку загальне правило повороту системи координат. Нехай потрібно перейти від деякої системи координат ξ, η, ζ до системи ξ’, η’, ζ’. Основою перетворення служать кути Ейлерa: кут прецесії Ω - кут між віссю ξ і лінією перетину АA' площин ξη і ξ’η’; кут нутації І - кут між площинами ξη і ξ’η’ або, що те ж саме, між напрямками осей ζ і ζ’; кут чистого повороту ω - кут в площині ξ’η’ між АА’ і напрямком осі ξ’.

Кути Ейлера дозволяють обчислити косинуси кутів між осями "старої" системи ξηζ і осями "нової" системи ξ’η’ζ’ - так звані напрямні косинуси. Наприклад, направляючий косинус осі ξ’ відносно осі ξ знайдеться по теоремі косинусів з сферичного трикутника а_ξа_ξ’А (див. рис.)

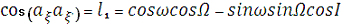
Направляючий косинус осі ξ’ відносно осі η - з трикутника Aa_ξ’a_η:

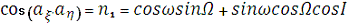
Направляючий косинус ξ’ відносно ζ - з трикутника Аа_ξ’а_ζ

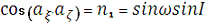
Аналогічним чином знаходять напрямні косинуси l₂, m₂, n₂ осі η’ відносно осей ξ, η, ζ напрямні косинуси l₃, m₃, n₃ осі ζ’, відносно осей ξ, η, ζ відповідно:

 

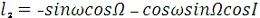
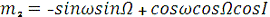
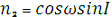
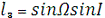
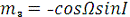
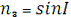
Як відомо з аналітичної геометрії, пряме і зворотне перетворення можна записати так:

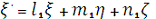
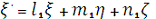
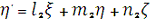
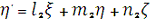
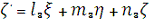
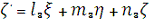
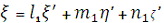
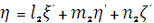
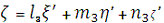 [4. с.24-25]

Зв’язок між прямокутними і сферичними координатами α, δ

 

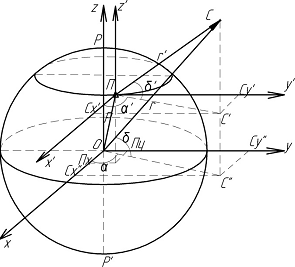
З трикутника ОСС”, ОС”С_x’, ОС”С_y’ для геоцентричних координат отримаємо:

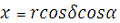
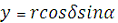
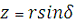
Те ж ля топоцентричних координат:

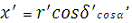
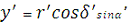
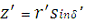
Зворотне перетворення:

; ; ;

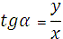
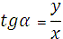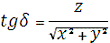
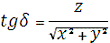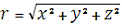
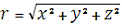топоцентричні координати:

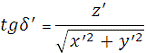
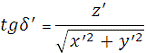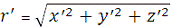
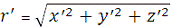; ; . [4. с.29]

2.2 Системи відліку часу

Вихідною системою вимірювання часу, яка застосовується в космічній геодезії, є система всесвітнього часу - система середнього сонячного часу на Грінвічському меридіані. Найбільш вживані позначення:

(Universal Time) або TU (Temps Universel).

Зі спостережень зірок у пункті з відомою астрономічної довготою λ визначають місцевий зоряний час s, тобто часовий кут точки весни відносно місцевого астрономічного меридіана в момент спостережень. Грінвічський зоряний час в цей момент рівний:

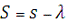
а всесвітній:

 

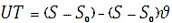
де S₀ - зоряний час в Грінвічську північ, a ν - коефіцієнт переходу від зоряного часу до середнього. Таким чином, всесвітній час, по суті, теж визначається зі спостережень зірок. Це час, віднесений до положення миттєвого полюса і миттєвого екватора, а значить, і до миттєвого положенню точки весни, позначається UT0. Всесвітній час в системі UT0 є нерівномірним через нерівномірності добового обертання Землі. Ці нерівномірності обумовлені рухом земних полюсів, сезонними змінами кутової швидкості обертання Землі під дією геофізичних і метеорологічних факторів, віковим уповільненням обертання Землі через приливне тертя в системі Земля-Місяць, неперіодичними змінами кутової швидкості обертання Землі, зумовленими, більш за все, сонячною активністю.

Дані станцій спостережень Міжнародної служби руху полюсів дозволяють визначити поправку Δλ до системи UT0, що враховує рух миттєвого полюса відносно до середнього. За допомогою цієї поправки утворюється система UT1:

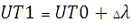
Служби часу дають поправки ΔUT за сезонні варіації кутової швидкості обертання Землі. За допомогою цих поправок утворюється система квазірівномірного всесвітнього часу UT2:

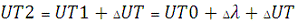
Міжнародне бюро часу регулярно публікує поправки Δλ і ΔUT для редукції моментів подачі радіосигналів часу до системи UT2 у виданнях "Circulaires du Bureau de l'Heure" і "Bulletin Horaire". [4. c. 19-20]

 

.3 Визначення координат пункту та ШСЗ в геоцентричній системі координат за результатами спостережень

Вихідною системою координат, в якій задається положення станції спостереження ШСЗ, є геодезична, що визначається прийнятим на даній території референц-еліпсоїдом. В цій системі координати точок земної поверхні задаються геодезичною широтою В, геодезичною довготою L і висотою Н над еліпсоїдом.

Рішення задач супутникової геодезії засновано на реалізації певних математичних залежностей між координатами ШСЗ і координатами станцій спостереження. Найбільш простий вигляд ці залежності мають, якщо вони задані в прямокутних координатах. Тому виникає необхідність переходу від геодезичних координат B, L, H до гринвіцьких прямокутних координат X, У, Z, пов’язаних з референц-еліпсоїдом. Для цього застосовують відомі формули сфероїдальної геодезії, наведені в пункті 2.1 [3. c.7]

Теорія руху ШСЗ завжди будується в геоцентричній інерціальній системі координат, в цій же системі попередньо обчислюють теоретичні координати супутників.

Подальший перехід від гринвіцьких прямокутних координат пов’язаних з референц-еліпсоїдом до інерціальної геоцентричної системи координат здійснюється на основі відомого співвідношення паралельного переносу і повороту системи, оскільки початки не співпадають і відповідні осі не паралельні (див. пункт 2.1). В цих формулах лише три кута з дев’яти є незалежними, а тому шість кутів, що залишились можна виразити через відомі три. Для цієї цілі більш за все підходять так звані кути Ейлера. [3. c.8]

Ці формули дають можливість здійснювати перехід від прямокутних гринвіцьких координат до геоцентричних, якщо відомі кути Ейлера і взаємне положення початку координат двох систем.

Спостереження ШСЗ проводяться з поверхні Землі, тому спостережені координати супутників отримуються в так званій топоцентричній системі координат, початок якої знаходиться на поверхні Землі в пункті спостережень. В якості координат, які спостерігаються найчастіше виступають сферичні координати r, α, δ. Зв’язок між прямокутними і сферичними координатами виражаються залежністю, яка приведена в пункті 2.1.

Обов’язковою умовою спостереження ШСЗ є фіксування моменту спостереження, тобто вимірювання часу. Вихідною системою вимірювання часу, що застосовується в супутниковій геодезії, є системі всесвітнього часу - система середнього сонячного часу на гринвіцькому меридіані UТ0. [3. c.10-11]

Приклад визначення координат ШСЗ в геоцентричній системі координат за результатами спостережень

Обчислення прямокутних координат пункту

B	46	58	28,17	L	41	54	56,22
B°	46,97449167			L°	41,91561667
радианы	0,819859544			Lrad	0,731565519
sin B	0,73105			sin L	0,668035402
cos B	0,682323894			cos L	0,744129493
cos B cos L	0,507737333			cos B sin L	0,455816517
sin2 B	0,534434103			1-e2 sin2 B	0,996422807
e2 sin2 B	0,003577193			(1-e2 sin2 B) - 1/2	1,001793409
a	6378245			1-e2	0,993306578
N	6389683,804			N (1-e2)	6346914,957
H	213			N (1-e2) +H	6347127,957
N+H	6389896,804
				X=	3244389,164
				Y=	2912620,505
				Z=	4640067,896

Обчислення координат пункту в геоцентричній системі

ε"	2,2	ψ"	1,91	ω"	1,49
εrad	0,038397	ψrad	0,033336	ωrad	0,026005
ψY	97094,5	-ψX	-108154	ωX	84371,66
-ωZ	-120667	εZ	178165,8	-εY	-111837
Xn	3220817	Yn	2982632	Zn	4612603

Обчислення топоцентричних прямокутних координат ШСЗ

UTO	20	39	58,73	r'	812013
UTO°	309,9947083			α'	18	46	37,27
UTO° " '	309	59	40,95	α'°	281,6552917
S	16	37	2,13	α'° ' "	281	39	19,05
S° " '	249	15	31,95	α'rad	4,915812195
S°	249,258875			δ'° ' "	38	6	37,24
So	199,2535833			δ'°	38,11034444
(α'-S)	1,43818112			δ'rad	0,66515099
sin (α'-S)	0,991219483			sinδ'	0,617177942
cos (α'-S)	0,132226836			cosδ'	0,786823607
cosδ'cos (α'-S)	0,104039196			cosδ'sin (α'-S)	0,779914889
x'c=	84481,17971			Srad=	3,477631076
y'c=	633301,0285
z'c=	501156,5122

Обчислення геоцентричних прямокутних та сферичних координат ШСЗ

Xc	3305297,996			Yc	3615933,079
Xc10^-13	3,3053E-07			Yc10^-13	3,61593E-07
tg (α-S)	1,093980961			(Xc^2+Yc^2) 10^-13	2,399996688
(α-S)°	47,56979473			(Xc^2+Yc^2) ^1/2	4898976,105
So	199,2535833			δ°	46,22886428
Sh	13,28357222			δ° ' "	46	13	43,91141
Shms	13	17	0,86	r^2*10^-13
α°	246,8233781			tgδ	1,0438425
αh	16,45489187			r
αhms	16	27
Zc	5113759,466			Zc10^-13

3. Незбурений рух ШСЗ

Незбурений рух супутників називається ще кеплерівським рухом, так як він підкоряється трьом законам, які були відкриті 1609-1618 роках німецьким астрономом Іоганом Кеплером. Стосовно руху супутників закони Кеплера можна сформулювати наступним чином:

)        Кожен супутник рухається по еліпсу навколо Землі, яка знаходиться в одному з його фокусів;

2)      Площа, яку проходить геоцентричний радіус-вектор супутника, пропорційна часу;

)        Відношення квадратів періодів обертання навколо Землі пропорційне до відношення кубів їх великих півосей. [5. с.28]

Незбурений рух ШСЗ по орбіті характеризується такими її елементами:

         великою піввіссю а (визначає розмір орбіти);

-        її ексцентриситет е (визначає форму орбіти);

         кутом нахилу і площини орбіти до площини земного екватора;

         довготою висхідного вузла Ω (останні визначають орієнтацію площини орбіти в просторі);

         аргументом перицентра ω;

         часом проходження ШСЗ через перицентр τ;

         істинною аномалією ν (останні визначають положення ШСЗ на орбіті).

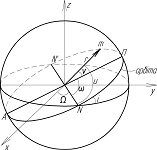
Найближча до Землі точка орбіти ШСЗ називається перицентром П, найбільш віддалена - апоцентром А.

Обидві точки - перицентр і апоцентр називаються апсидами, а лінія, що їх з’єднує, називається лінією апсид.

Точка N, в якій орбіта ШСЗ перетинає площину екватор при переході ШСЗ з південної півсфери в північну, називається висхідним вузлом орбіти. Точка N’ в якій орбіта ШСЗ перетинає площину екватора при переході з північної півсфери в південну, називається спадним вузлом орбіти. Лінія, що з’єднує обидва вузла називається лінією вузлів. [3. с.22-23]

3.1 Визначення елементів орбіти із спостережень

Будь яка з виміряних координат q_j супутника є функцією шести шуканих елементів орбіти і часу t.

Тоді для визначення елементів орбіти потрібно знайти із спостережень принаймні шість різних значень координат q_j, де j = 1, 2, 3, 4, 5, 6, щоб рівняння, які випливають із формул незбуреного руху могли в принципі бути вирішеними.

При спостереженнях ШСЗ можуть вимірюватися:

а) топоцентричні напрямки на супутник (тобто α’, δ’);

б) топоцентричні відстані до супутника (тобто r');

в) напрямки і відстані до ШСЗ;

г) швидкості або прискорення ШСЗ в заданому напрямку

Зазвичай для визначення орбіти з одного або декількох пунктів виконують як можна більше число спостережень супутника. Визначення орбіти розбивають на два етапи:

) з усіх спостережень вибирають мінімально необхідну кількість вимірювань та визначають так звану попередню орбіту,

) використовуючи всі виміри, уточнюють елементи попередньої орбіти - це операція уточнення орбіти, що дає елементи остаточної орбіти. [4. с.49-50]

Тоді з вирішення прямокутного сферичного трикутника "вузол орбіти - ШСЗ - проекція ШСЗ на екватор" знаходять всі елементи орбіти. [3. с.26]

 

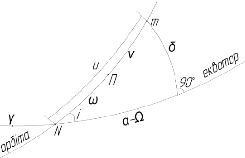
Приклад обчислення елементів незбуреної орбіти ШСЗ

	1	2
ri =	7 077 226,960	7 290 226,960
ai =	246,0621402	286,1163069
di =	46,5891952	56,80586187
Si =	199,2535833	201,0035833

μ = 3,98603E+14 м³/с²

.        Довгота висхідного вузла:

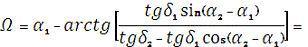
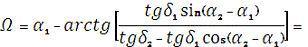3,537156316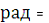 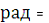202?39'50,86"

2.      Нахил орбіти:

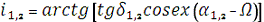
i₁ = 0,994443608 рад = 56?58'38,72", i₂ = 0,994443608 рад = 56?58'38,72"

.        Аргумент широти:

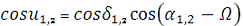
u₁ = 1,047963744 рад = 60?2'38,04"

u₂ = 1,508325487 рад = 86?25'14,46"

Фокальний параметр:

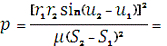
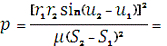7 472 527,362

4.      Істинна аномалія:

, .

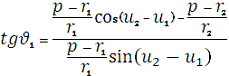
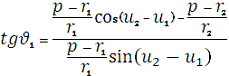ν₁ = 0,789795395 рад = 45?15'6,99"

ν₂ = 1,250157138 рад = 71?37'43,42"

5.      Велика піввісь, ексцентриситет і середній рух:

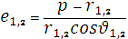
e₁ = 0,079340923

e₂ = 0,079340923

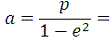
 7519864,776 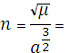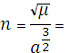0,00097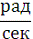

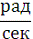
6.      Аргумент перицентра:

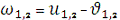
ω₁ = 0,258168349 рад = 14?47'31,04"

ω₂ = 0,258168349 рад = 14?47'31,04"

.        Ексцентрична аномалія:

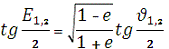
E₁ = 0,734907265 рад = 42?6'25,5"= 2h48m25,7s

E₂ = 1,175708166 рад = 67?21'47,22"= 4^h29^m27,14^s

8.      Момент проходження через перицентр:

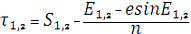
τ₁ = 3,426426461 рад = 196?19'11, 19"= 13h5m16,75^s

τ₂ = 3,425364602 рад = 196?15'32,17"= 13^h5^m2,14^s

3.2 Визначення ефемериди ШСЗ

Під ефемеридою в астрономії розуміється таблиця значень "видимих координат небесного тіла на задані моменти часі. Вихідні дані для обчислення ефемериди ШСЗ:

) елементи орбіти Ω, і, ω, а, е, τ;

) координати ξ, η, ζ деякого пункту на земній поверхні в геоцентричної інерціальній системі;

) момент часу t=UT1 в системі всесвітнього часу.

Потрібно: для даного пункту на заданий момент часу обчислити топоцентричне пряме сходження α’, топоцентричне схилення δ’ і топоцентричний радіус-вектор r’ ШСЗ.

На практиці необхідно, щоб у обчислених координатах ШСЗ були враховані збурення.

Тому:

) для системи елементів орбіти зазвичай зазначається епоха t₀=UT1 ^(0), до якої вони віднесені;

) у формлам теорії збурень обчислюються величини збурень в кожному елементі орбіти за інтервал часу t-t₀;

) утвориться система збурених елементів шляхом додавання до заданих елементів величин їх збурень. Теорія збурень заздалегідь побудована так, що обчислення реальної, тобто, збуреної ефемериди ШСЗ проводиться по тим же формулам, що і обчислення незбуреної. Одночасно з обчисленням ефемериди розраховують умови видимості ШСЗ для даного пункту. [4. с.48-49] Порядок обчислення ефемериди:

Вихідні дані

xn =	3244382,621
yn =	2912639,957
zn =	4640060,246
Ω рад =	3,537156316
i рад	0,994443608
ω	0,258168349
a, м	7519864,776
e	0,079340923
n	0,00097
n рад	13,31340394
t =	28h25m29,73s
=21h7m19,82s

.        Середня аномалія:

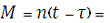
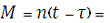1,696887919 97?13'28,26"

2.      Ексцентрична аномалія:

Вирішується методом послідовних наближень. Припускаємо, що

E0, рад	1,696887919
E1, рад	1,774813595
M1, рад	1,697118159
DE1, рад	-0,0002266
E2, рад	1,774586999
M2, рад	1,696887921
DE2, рад	-1,9632E-09
E3, рад	1,774586997

Контроль:

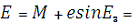
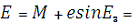1,774586997

Е = 1,774586997 рад = 101?40'34,84"

3.      Істинна аномалія:

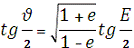, ν = 1,851749634 рад = 106?5'50,78"

Геоцентричний радіус-вектор:

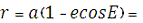
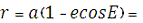7 640 613,156 м

4.      Аргумент широти:

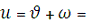
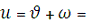2,109917983120?53'21,82"

Геодезичні прямокутні координати ШСЗ:

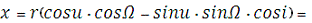
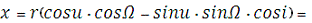4 996 546,075

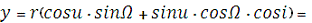
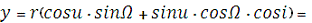-1 785 889,233

5 497 644,620 м

5.      Топоцентричні прямокутні координати:

1 752 163,455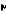

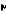
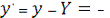
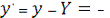4 698 529, 191м

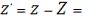
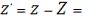857 584,374м

6.      Топоцентричні сферичні координати:

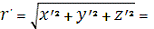
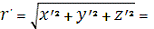5 087 406,440 м

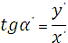
α’ = 1,927739938 рад = 110?27'4,9"= 7h21m48,327^s

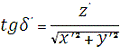
δ’ = 0,169378782 рад = 9?42'16,88"

4. Методи спостережень ШСЗ

В даний час методи спостереження прийнято ділити на оптичні і радіотехнічні - залежно від діапазону електромагнітних коливань, в якому виконуються вимірювання. Оптичним методом визначається напрям на супутник шляхом фотографування супутника на тлі зірок. До оптичних методів відноситься також метод виміру дальності супутника лазерними далекомірами.

З радіотехнічних методів найбільшого поширення при вирішенні геодезичних завдань отримали так звані диференціальні і інтегральні доплерівські методи і фазові методи вимірювання дальності. Цікаво, що доплерівські методи, спочатку використовувалися для порівняно неточного стеження за ШСЗ при визначенні їх орбіт, у міру вдосконалення та підвищення точності вимірювань стали використовуватися для вирішення навігаційних і геодезичних завдань.

Кожен з методів спостереження ШСЗ має свої переваги і недоліки. Важливими достоїнствами всіх радіотехнічних методів є їх всепогодність і можливість проводити спостереження в будь-який час доби. Оптичні методи залежать від погодних умов, і спостерігати ШСЗ в оптичному діапазоні можна тільки в ранкові або вечірні години, коли поверхня Землі занурена у темряву, а сам ШСЗ, перебуваючи на великій висоті над горизонтом, вже (чи ще) освітлений Сонцем.

З точки зору збільшення точності всі можливості фотографічних методів значною мірою вже вичерпані, і доплерівські методи спостережень супутників в деякій мірі навіть перевершують фотографічні. Але найбільш перспективними з усіх методів спостереження ШСЗ із Землі вважаються лазерні спостереження (завдяки їх надзвичайної точності). Взагалі ж в даний час всі методи спостережень не виключають, а взаємно доповнюють один одного. Крім того, як ми вже відзначали, при вирішенні геодезичних задач використовуються спостереження та інших космічних об'єктів, штучних і природних, як радіотехнічними, так і лазерними засобами. Розглянемо ж докладніше основні методи спостереження ШСЗ та інших космічних об'єктів для цілей космічної геодезії. [8. с.15-16]

 

4.1 Класифікація ШСЗ

 

Класифікувати штучні супутники Землі можна за різними ознаками. Основний же принцип класифікації - по цілям запуску і завдань, що вирішуються за допомогою штучних супутників Землі. Крім того, штучні супутники Землі розрізняються по орбітах, на які вони виводяться, типами деякого бортового устаткування і так далі.

По цілям і завданням штучні супутники Землі поділяються на дві великі групи - науково-дослідні та прикладні. Науково-дослідні супутники призначені для отримання нової наукової інформації про Землю і навколоземному космічному просторі. Прикладні супутники призначені для задоволення практичних потреб людини, отримання інформації.

По орбітах, на які штучні супутники Землі виводяться, супутники Землі діляться на кругові, еліптичні, екваторіальні, полярні, стаціонарні.

Обладнання штучних супутників Землі дуже різноманітно. Це, по-перше, апаратура, за допомогою якої забезпечується виконання поставлених перед супутником завдань, - науково-дослідна, навігаційна, метеорологічна і тому подібна. По-друге, так зване службове обладнання, покликане забезпечити необхідні умови для роботи основної апаратури і зв'язок між штучним супутником Землі і наземним пунктом. До службової устаткування відносяться системи енергоживлення (сонячні батареї, електрохімічні джерела струму, радіоізотопні електрогенератори), радіотелеметрична система для передачі на Землю інформації та прийняття на супутнику командних сигналів, система терморегулювання для створення і підтримки необхідного теплового режиму роботи апаратури. Службові системи обов'язкові для переважної більшості штучних супутників Землі. Крім того, як правило, штучний супутник Землі забезпечується системою орієнтації в просторі, тип якої залежить від призначення супутника (орієнтація по небесних тіл, по магнітному полю Землі тощо), і бортовий електронної обчислювальної машиною для керування роботою приладів і службових систем. [2]

 

.2 Оптичні методи спостережень: фотографічні спостереження і лазерні

 

Візуальні методи спостережень супутників для геодезичних цілей не досить точні. Особливе значення мають фотографічні спостереження супутників. Вони дозволяють визначити з більш високою точністю (± 0,5 - ± 2 ") напрямок одиничного топоцентричного вектора від станції спостережень до миттєвого положення супутника, якщо застосовується хороша камера і якщо час фіксується з точністю близько однієї мілісекунди. [6. с.73]

Головною метою візуальних методів є отримання наближених даних про супутники для негеодезичних цілей або попередніх даних про нові супутниках для продовження їх спостережень. Роль цих спостережень особливо важлива для так званих пасивних супутників, тобто супутників, що не мають радіопередавачів, або мають передавачі, що вийшли з ладу з яких-небудь причин. [7. с.221]

Фотографічні методи спостережень. Для визначення напрямку на ШСЗ використовується його зображення на тлі так званих опорних зірок, небесні координати яких відомі. Основна особливість і разом з тим основна складність спостереження ШСЗ, пов'язані з великими кутовими швидкостями ШСЗ. Через це виникає необхідність, крім направлення на об'єкт, отримувати з дуже високою точністю і момент часу, що відповідає зафіксованому на знімку положенню ШСЗ.

Жорсткі вимоги до точності реєстрації часу (точніше, 0,0005 с) викликають відповідно особливі вимоги до фотографічної апаратури і методів зберігання і реєстрації часу на станціях спостереження за ШСЗ. Основними особливостями фотографічних супутникових камер є обтюраторний затвор безперервної дії та система, що дозволяє відстежувати фотоплівці слабкі ШСЗ. Обтюраторний затвор дозволяє отримувати зображення ШСЗ або у вигляді ряду майже точкових зображень, або у вигляді коротких розривів в слід ШСЗ.

Рух слабкого ШСЗ відстежується поворотом камери або фотоплівки щодо орбітальної осі, тобто по руху ШСЗ (при фотографуванні яскравих об'єктів камера зазвичай залишається нерухомою або відстежує рух зірок).

У результаті тривалої дослідницької роботи над фотографічними камерами найвища точність визначення напряму на яскравий ШСЗ складає в даний час 0,5 "по одному знімку (для більшості камер ця точність знаходиться в межах 1 - 2"). При спостереженні за слабким ШСЗ ця точність коливається в межах 2 - 3".

Точність реєстрації моментів часу залежить від багатьох технічних причин і для більшості камер характеризується помилками 0,1 - 0,5 мс. Але є одна причина помилки, а саме - синхронізація годин камери з еталонною системою часу, і вона може вносити додаткові помилки близько 1 мс.

Такі помилки у вихідному наглядовій матеріалі призводять до помилок у визначеному положенні ШСЗ на орбіті близько декількох метрів, що за сучасних геодезичних вимогах ще терпимо, але для більш серйозних геодезичних робіт майбутнього - неприйнятно.

Тому фотографічні методи супутникової геодезії стали ніби класичними і використовуються в основному для вирішення геометричних завдань, таких, як побудова мереж супутникового тріангуляції. [8.16-17]

Приклад обробки фотографічних спостережень

№	Сферичні координати
	А				D
1	10	58	37,7	10,97714	40	30	37,94	40,51054
2	10	6	32,847	10,10912	35	19	5,84	35,31829
3	10	16	11,715	10,26992	42	59	22,76	42,98966

Результати вимірювань
	X'	Y'
1	132,98	118,22
2	53,34	67,47
3	59,08	118,77
ШСЗ	91,11	105,78
МО	90,13	100,12

Прямокутні координати
	Х	У
1	42,85	18,1
2	-36,79	-32,65
3	-31,05	18,65
ШСЗ	0,98	5,66

Xc-X1	-41,87	Xc-X2	37,77	Xc-X3	32,03
(Xc-X1) 2	1753,097	(Xc-X2) 2	1426,573	(Xc-X3) 2	1025,921
Yc-Y1	-12,44	Yc-Y2	38,31	Yc-Y3	-12,99
(Yc-Y1) 2	154,7536	(Yc-Y2) 2	1467,656	(Yc-Y3) 2	168,7401
D2c1	1907,851	D2c2	2894,229	D2c3	1194,661
Dc1	43,67895	Dc2	53,79804	Dc3	34,56387

Спосіб Тернера

Вихідні дані
NN	α				δ				x'	y'	x-x0	y-y0
1	14	22	26,9	14,37414	41	2	22,14	41,03948	60,621	45,901	-5,666	0,922
2	14	17	13,09	14,28697	38	57	42,56	38,96182	69,632	54,054	3,345	9,075
3	14	12	42,72	14,21187	41	43	1,87	41,71719	67,674	38,480	1,387	-6,500
4	14	8	17,26	14,13813	40	58	38,43	40,97734	73,475	40,188	7,188	-4,792
5	21	49,95	14,36388	39	31	17,43	39,52151	63,954	53,231	-2,333	8,252
6	14	17	17,42	14,28817	42	12	1,97	42, 20055	62,366	38,023	-3,921	-6,957
Серед.	14	16	37,89	14,27719	40	44	10,73333	40,73631	66,287	44,980
ШСЗ									68,608	48,607	2,321	3,628

NN		α		α0		α радіани		δ	δ радіани
1		14,37414		215,6121		3,763141		41,03948	0,716274
2		14,28697		214,3045		3,74032		38,96182	0,680012
3		14,21187		213,178		3,720658		41,71719	0,728102
4		14,13813		212,0719		3,701353		40,97734	0,71519
5		14,36388		215,4581		3,760454		39,52151	0,68978
6		14,28817		214,3226		3,740635		42, 20055	0,736538
Ідеальні координати опорних зірок
	NN		ζ		η
	1		5,966834		1,698819
	2		0,620634		-9,65493
	3		-3,97925		5,358611
	4		-8,56773		1,413358
	5		5,45736		-6,56951
	6		0,663921		7,967058

f=

311,66

Координати початку ідеальної системи
A0	D	A радіани	Dрадіани
214,1579	40,73631	3,73776	0,710983

ζ0=	0,026961
η0=	0,035569

Лазерні спостереження. Світловий імпульс, отриманий за допомогою лазера, посилають до супутника (поверхня якого обладнана уголковими відбивачами), після чого імпульс відбивається від супутника до тієї ж наземної станції. Помноживши час Δt проходження імпульсу на швидкість світла, отримують подвійну відстань до супутника:

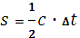
При цьому необхідно дуже ретельно відстежувати рух супутника, що здійснювалося за допомогою візуальних спостережень в зорову трубу. Потрапляючи на супутник, промінь відбивався уголковими відбивачами у зворотному напрямку. Зорова труба, змонтована паралельно лазеру, приймала відображені до Землі імпульси і направляла їх на вторинний електронний помножувач

При перших експериментах за допомогою лазера визначили відстань до супутника з точністю до декількох метрів. У 1967 р. вже досягли точності ± 2 м.

Такою помилкою характеризується внутрішня збіжність результатів. Вплив клімату вимагає більш ретельного розгляду, однак можна очікувати, що реальна точність буде не гірше, ніж ± 3 м. У майбутньому сподіваються збільшити точність до ± 1 м. Зараз застосовуються лазерні імпульси тривалістю 15 мсек і потужністю 500 Мвт.

В інших варіантах спостережень за допомогою лазера отримують не відстань за часом проходження лазерного імпульсу, а фотографують відображений лазерний імпульс на тлі зірок. При фотографічних спостереженнях за допомогою лазера застосовують лазерні імпульси тривалістю 2,7*10^-3 сек. Пучок лазерних променів має тут кут розходження 15'.

Комбінуючи обидва варіанти, вимір відстаней і вимірювання напрямків, повністю визначають топоцентричний вектор положення супутника.

У порівнянні з фотографічним методом спостережень супутників лазерний метод дозволяє спостерігати супутник і тоді, коли він не освітлений Сонцем, а знаходиться в тіні Землі. З іншого боку, в розпорядженні є тільки лише кілька супутників з уголковими відбивачами. [6. с.81-82]

 

.3 Радіотехнічний метод: допплерівський і радіоінтерферометри з наддовгою базою

Допплерівський метод. Ефект Допплера, як відомо, полягає в тому, що частота сигналу змінюється при русі джерела випромінювання сигналу щодо спостерігача. Ця зміна (воно називається допплерівським зсувом частоти, а іноді допплерівською частотою) прямо пропорційно частоті передавача і швидкості руху передавача щодо приймача. Відносну швидкість часто називають променевою швидкістю (оскільки вона спрямована по променю зору спостерігача), або радіальної швидкістю, так як цей промінь є радіус-вектор рухомого об'єкту.

Таким чином, допплерівські вимірювання дають нам дуже інформативну величину: маючи графік безперервного запису променевої швидкості для деякого інтервалу часу, ми можемо отримати і дальність до об'єкта, і прискорення об'єкта в певній точці його орбіти.

Існують три варіанти допплерівських систем. Це насамперед беззапитні системи, які в основному і застосовуються у космічній геодезії. На борту космічного апарата перебуває передавач радіосигналів, що виробляються високостабільним генератором частоти. На наземній приймальні станції також є генератор опорних сигналів. Порівняння частот приймається і опорного сигналів дозволяє виділити вимірювану частоту, яка дорівнює різниці частоти підставки і допплерівської частоти (частотою підставки називається різниця частот генераторів - наземного і супутникового). Спеціальний пристрій перетворює вимірювану частоту в число періодів (циклів) допплерівського сигналу (і тому воно є безпосередньо вимірюваною величиною) за певний проміжок часу (він зазвичай складає величину від 0,5 до кількох секунд).

На відміну від беззапитних систем в системах із запитом використовується лише один - наземний - генератор частоти, а на борту космічного об'єкта поміщають прийомовідповідач, що ретранслює прийняті зі станції сигнали назад на Землю. Наземна станція порівнює частоти запитального і відповідного сигналів і вимірює зрушення частоти.

Координати пунктів радіотехнічними методами виходять точніше, ніж фотографічними. Середня точність визначення радіальної швидкості складає зараз кілька сантиметрів на секунду. Це дає можливість визначати положення ШСЗ на орбіті або положення наземної станції (залежно від того, яка ставиться завдання: уточнення орбіти ШСЗ або визначення координат на поверхні Землі) з високою точністю. Головними джерелами помилок тут є неточність в синхронізації системи допплерівських станцій і шуми вимірювальної апаратури.

Радіоінтерферометри з наддовгою базою. У 1967 р. був розроблений новий інтерферометричний метод з прийомними елементами, рознесеними на великі відстані один від одного, з незалежної реєстрацією сигналів без передачі даних в реальному часі. При цьому результати вимірювань записуються на магнітні стрічки для подальшої крос-кореляційної обробки на спеціалізованому обчислювальному центрі. Цей метод назвали радіоінтерферометрія з наддовгими базами (РНДБ). [10. с.276]

Перші РНДБ-вимірювання дали результати в трьох напрямках:

) прості розподіли яскравості, отримані порівнянням виміряних функцій видимості з моделями джерел;

) карти лазерів в порівнянні частот інтерференції для різних спектральних деталей;

) координати джерел виміряні з точністю порядку ~ 1", а довжини баз - з точністю до кількох метрів. [10. с.278]

Метод РСДБ - локації (1998) являє собою об'єднання двох методів:

метод радіоінтерферометрії з наддовгою базою (РНДБ), що дозволяє виконувати вимірювання кутових координат і кутових швидкостей,

далекомірного-допплерівського локаційного методу для вимірювання дальності і радіальної швидкості.

Основне завдання експериментів

Отримання інформації про становище космічного об'єкта (КО) з вимірів різниці часів приходу сигналів в пункти інтерферометра і допплерівського зсуву частот сигналів.

Навігаційне завдання полягає в знаходженні 6 параметрів із затримки частоти інтерференції:

ρ₀ (ρ_X, ρ_Y, ρ_Z) - геоцентричний вектор положення КО

w (w_α, w_δ) - кутова швидкість КО

V_{ρ0 -} радіальна швидкість [9. с.1-7]

У РСДБ, щоб знайти правильне співвідношення часу і отримати максимальний коефіцієнт кореляції, необхідно провести пошук в деякому інтервалі значень затримок. Зазвичай коефіцієнти кореляції для низки зрушень по затримці розраховуються одночасно, так що РСДБ-корелятор має близьку схожість з цифровим спектральним корелятором, хоча кількість спектральних каналів може бути менше зазвичай використовується в спектральних спостереженнях. Відхилення частоти стандартів від номіналу, що викликають плавне зміна апаратурною затримки з часом, також призводять до зміщення зсуву частоти інтерференції. Тому РНДБ-експеримент починають з двовимірного пошуку по затримці і за частотою інтерференції (швидкості зміни затримки), щоб знайти максимум кореляційної функції. Цей процес називається пошуком інтерференційних пелюсток.

Час когерентності в РСДБ - один з головних чинників обмеження чутливості. При усередненні сигналу за час більше часу когерентності усереднюється амплітуда інтерференційних пелюсток. У цьому випадку чутливість поліпшується лише як корінь четвертого ступеня з часу накопичення.

При визначенні координат в якості вимірюваних величин корисні частота інтерференції і групова затримка.

5. Геометричні методи побудови мереж

При створенні і реконструкції геодезичних мереж із застосуванням супутникової технології геометрична форма мережі не впливає на точність визначення координат. У разі використання результатів супутникових вимірювань для визначення геометричних елементів (довжин ліній і кутів) у традиційних побудовах (тріангуляція, трилатерація, полігонометрія), необхідно дотримувати встановлені відповідними інструкціями вимоги до форми мережі. Зрівняльні обчислення в таких мережах виконуються за звичайними програмами, що застосовуються в традиційних геодезичних методів. При використанні супутникової технології рекомендується дві основні схеми побудови мереж:

замкнутих геометричних фігур (полігонів);

радіальна. [12. с.51]

5.1 Тріангуляційні побудови

Найпростішим геометричним побудовою, отриманим за допомогою ШСЗ, є трикутник, який утворюється в результаті одночасного (синхронного) спостереження ШСЗ з двох станцій, Це трикутник А (станція-1) С (супутник) В (станція-2) є основним елементом всіх супутникових геометричних побудов. Це, по суті справи, трикутник класичної тріангуляції, одна з вершин якого піднята в космічний простір. Способи вирішення такого трикутника значно полегшені тим, що він завжди плоский. Правда, таке "полегшення" зводиться нанівець величезною кількістю матеріалу спостережень: супутників багато, і спостерігаються вони регулярно. Залишається у супутниковій тріангуляції проблема, яка була основною і в наземній тріангуляції, - вимірювання базису. Але додається проблема, специфічна для космічних методів: синхронізація спостережень супутника з різних станцій. [8. с.148]

Є такі тріангуляційні побудови:

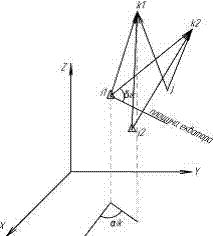
Просторова кутова засічка: для визначення координат супутника необхідно спостерігати синхронно з двох вихідних і одного визначуваного пункту.

В ідеальному напрямки в точках k₁, k₂ будуть перетинатися, що рівносильне дотриманню умови компланарності.

Для даного випадку визначення координат пункту j може відбуватися в наступній послідовності.

Запишемо такий вираз: D_i1i2+r_i11-r_1-i2=0

Переходимо до проекцій на координатні осі, це дозволяє не тільки обчислити невідомі відстані r_1-i2 і r_i11, а й зробити контроль обчислень.

Далі обчислюють координати супутника в точці k₁, за відомими формулами.

Аналогічно можна обчислити координати супутника в положенні k₂, а потім, використовуючи ці обчислені координати отримати координати пункту спостережень j. [8. с.148-149]

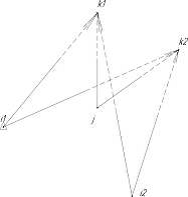
Кутова засічка хорд: вимагає спостереження двох положень супутника одночасно з визначуваного і одного з вихідних пунктів

Знаходимо напрямки i1j і i2j та напрямні косинуси з пунктів на супутники. Потім обчислюють функції напрямних косинусів. За ними обчислюють напрямні косинуси для напрямку між пунктами. Обчислюємо орієнтуючі кути за відомими формулами. А потім координати шуканого пункту. [8. с.149-150]

5.2 Лінійно-кутові побудови

Лінійно-кутові (комбіновані) супутникові геодезичні мережі будуються на основі виміряних сферичних координат напрямків з наземних пунктів на супутник і виміряних відстаней за допомогою лазерних спостережень або різниць відстаней, отриманих за допомогою допплерівських систем спостережень. В лінійних мережах (трилатерації) використовують лише лінійні вимірювання.

Розглянемо елементарні фігури побудов комбінованих і лінійних мереж.

Якщо на наземному пункті і виміряні сферичні координати αік і δік на супутник в положенні k і відповідно відстань r.

Аналогічно обчислюють координати наземного пункту, якщо відоме положення ШСЗ.

На першій схемі показано засічку, де виміряні сферичні координати пункту спостереження і відстань.

На другій - з одного пункту виміряний напрямок, з іншого - відстань.

На останній - лише відстані. [8. с.152-153]

5.3 Врівноваження супутникових мереж

Геодезичні мережі обов'язково повинні містити збиткові вимірювання. Вони потрібні для своєчасного виявлення і виправлення не якісних величин і для оцінки точності вимірювань.

Однак при неминучості похибок надлишкові величини ведуть до неоднозначних значень визначуваних пapaмeтpів - висот і координат. Урівнювання виконується для того, щоб отримати однозначні результати шляхом виправлення вимірювань поправками такими, щоб точність всіх величин не знизилася, а стала вище. Ця задача вирішується за методом найменших квадратів.

Основними елементами космічних геодезичних побудов є компоненти векторів: пункт-супутник (топоцентричний вектор супутника), пункт-пункт (земна хорда), компоненти геоцентричного вектора пункту. Ці елементи при зрівнянні використовуються як виміряні величини.

Компоненти вектора пункт-супутник, які називають безпосередньо виміряними величинами, пов'язані з грінвічськими координатами пункту і супутника формулами, які приведені в пункті 2.1.

Як виміряних величин в космічному геодезичному побудові можна використовувати також різниці відстаней з пункту до двох положень супутника і топоцентричну радіальну швидкість супутника. Ці виміряні величини пов'язані з координатами пункту, супутника і складовими швидкості супутника співвідношеннями:

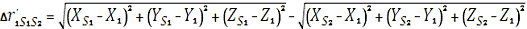
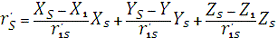
Орієнтують кути і довжина земного хорди, а також геоцентричні довгота, широта і модуль геоцентричного радіус-вектора пункту, звані в цьому випадку штучно виміряними величинами, пов'язані з прямокутними координатами співвідношеннями, які вже неодноразово згадувалися (п.2.1). [5. с.121-122]

Висновок

З усього вище сказаного можна зробити висновок, що супутникова геодезія - це наука, яка розвивається і, до того ж, на теперішньому етапі дуже швидко і динамічно. З’являється все біліше і більше нових можливостей реалізовувати старі способи супутникових спостережень, їх обробки і побудов.

Навіть Україна, з допомогою міжнародних наукових організацій, тепер приймає активну участь у виконанні багатьох наукових програм і досліджень в різних галузях. Що сприяє, звісно ж і розвитку геодезії зокрема. Що в свою чергу дозволяє розв’язувати головні задачі супутникової геодезії.

В даній курсовій роботі ми ознайомилися з основними методами спостережень в супутниковій геодезії, а також розглянули головні способи побудови супутникових геодезичних мереж.

Список літератури

1.      Белова Н.А. Курс сферической астрономи. - Москва: НЕДРА, 1971. - 182 с.

2.      Энциклопедический словарь юного астронома. - Москва: "Педагогика", 1980. - 320 с.

3.      Єгоров О.І. Супутникова геодезія/ Методичні вказівки. - Київ: 2006. - 32 с.

.        Краснорилов И.И., Плахов Ю.В. Основы космической геодезии. - Москва: НЕДРА, 1976. - 216 с.

.        Крылов В.И. Космическая геодезия. - Москва: МИИГАиК, 2002. - 162 c.

.        Курт Арнольд Методы спутниковой геодезии. - Москва: НЕДРА, 1973. - 224 с.

7.      Меллер И. Введение в супутниковою геодезію. - Москва: Мир, 1967. - 368 с.

.        Микиша А.М. Космические методы в геодезии. - Москва: Знание, 1983. - 64 с.

.        Нечаева М., Дугин Н. Шмелд И. Метод РСДБ в приложении к задаче радиолокации объектов в околоземном космическом пространстве. - 1 Вентспилсский международный радиоастрономический центр (Латвия), ФГБНУ"Научно-исследовательский радиофизический институт" (Россия), 2009. - 20 с.

.        Томпсон А.Р., Моран Д.М., Свенсон Д.У. Интерферометрия и синтез в радиоастрономии. - Москва: ФИЗМАТЛИТ, 2003. - 624с.

.        Українська мережа станцій космічної геодезії та геодинаміки (Укргеокосмомережа). - Київ: Компанія BAITE, 2005. - 62 с.

.        Шумаков Ф.Т. Супутникова геодезія. - Харків: ХНАМГ, 2009. - 88 с.