Расчет системы водопроводов
К КУРСОВОЙ
РАБОТЕ
по
Гидрогазодинамике
На тему:
«Расчет системы водопроводов»
Исходные данные для проектирования
ЭСКИЗ ВОДОПРОВОДА

Введение
Трубопроводы являются неотъемлемой частью всех
тепловых установок и обеспечивают возможность их бесперебойной работы. В более
широком смысле трубопроводы - это транспортные магистрали для движения
различных жидкостей, газов, суспензии, продуктов сгорания, теплоносителей и
т.д. Трубопроводы могут иметь самую различную форму и протяженность, а по
конфигурации классифицируются на простые и сложные.
Простыми трубопроводами называют трубопроводы
без ответвлений с постоянным расходом движущейся среды на всех участках. Сеть
трубопроводов, имеющие различные отводы и параллельные участки движения,
относятся к классу сложных.
Гидравлический расчет является одним из
важнейших разделов проектирования и эксплуатации трубопроводов.
Системы водоснабжения представляют собой сложные
гидравлические системы, в которых работа отдельных звеньев находятся во
взаимной зависимости.
Для правильного регулирования системы необходимо
знать гидравлическую характеристику сети. Гидравлическая характеристика сети -
это зависимость потери напора от расхода жидкости.
Основными задачами гидравлического расчета
являются определение диаметров трубопроводов и потерь давления при заданных
расходах воды. По результатам расчета строится гидравлическая характеристика
сети и отдельных ее участков.
1. Гидравлический расчет линии
нагнетания водопровода
Целью расчета является определение диаметров
участков водопровода и потерь давления при заданных расходах теплоносителя.
Расчет участка 7.
Расчетные данные участка представлены в задании
на проектирование.
Задаемся скоростью Uзад =1 м/с.
Определяем площадь поперечного сечения
трубопровода по формуле:

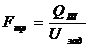 ,
,
где Q - заданный расход жидкости на
заданном участке, м/с3;зад - заданная скорость, м/с.
Отсюда: Fтр = 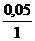 = 0,05 (м2).
= 0,05 (м2).
Определяем диаметр трубопровода на
данном участке по формуле:
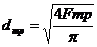 , м; (из формулы
, м; (из формулы 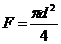 ) (1.1), где
) (1.1), где
тр - площадь поперечного сечения
трубопровода, м.
Таким образом: 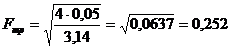 (м)
(м)
По ГОСТ 8732-70 (таб. 4) принимаем
трубу бесшовную, горячекатанную из стали 10 диаметром 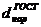 =245 мм, б =
30 мм.
=245 мм, б =
30 мм.
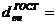
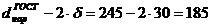 мм = 0,185 м;
мм = 0,185 м;
Уточняем значение скорости на данном
участке по формуле:
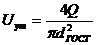 , м/с;
, м/с;
следовательно 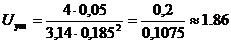 (м/с).
(м/с).
Полученное значение скорости воды
удовлетворяет условию U = 1÷3 м/с.
Определяем критерий Рейнольдса по
формуле:
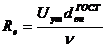 (1.2), где
(1.2), где
ν - коэффициент кинематической
вязкости, м/с2.
Принимаем ν = 0,3905∙10-6
м2/с при температуре t = 75ºC` (из т.2, интерполяцией.)
Следовательно, 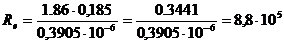 ;
;
В зависимости от числа Рейнольдса по
табл.11 выбираем формулу для расчета коэффициента жидкосного трения λ.
Если Re >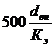 , то λ вычислим по
формуле Шифринсона:
, то λ вычислим по
формуле Шифринсона:
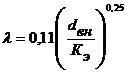 (1.3), где
(1.3), где
Кэ - коэффициент шероховатости, м,
Эквивалентная шероховатость Кэ для
бесшовных стальных труб (старых) находим по таблице 8:
Кэ=1 мм =1·10-3 м;
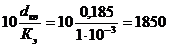 ;
;
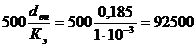 , и тогда=8,8·105 >9,25·104
, и тогда=8,8·105 >9,25·104
Значение числа Рейнольдса входит в
данные пределы и поэтому величину λ вычислим по формуле (1.3)
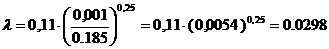
определяем потери напора на данном
участке по формуле:
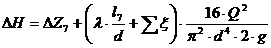 , м;
, м;
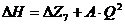 , где
, где
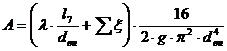 ;
;
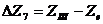 , где
, где
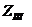 и
и 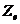 - геометрические отметки начала и
конца трубопровода, м;- геометрическая длина, м;- ускорение свободного падения,
м/с2;
- геометрические отметки начала и
конца трубопровода, м;- геометрическая длина, м;- ускорение свободного падения,
м/с2;
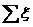 - сумма коэффициентов местного
сопротивления.
- сумма коэффициентов местного
сопротивления.
Вычисляем сумму коэффициентов
местного сопротивления для данного участка по формуле:
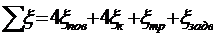 , где
, где
ξпов, ξк, ξтр, ξ задв
коэффициент местного сопротивления,
где ξ пов, -
коэффициент местного сопротивления при входе в трубу без закруглений входных
кромок. По табл. 12 ξпов=0,5.
ξтр - коэффициент местного
сопротивления тройника. Значение ξтр при разделении потоков
относящиеся к части общего расхода, движущейся параллельно направлению скорости
суммарного потока. Для выбора ξтр находим соотношение:
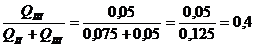
По табл. 16 принимаем ξтр =1,2;
ξзадв - коэффициент местного
сопротивления при входе в трубу при хорошо закругленных кромках. По табл. 12 ξпов=0,1.
ξк,=2,5.
При длине участка l7 =380 м
принимаем 4 поворотов и 4 компенсаторов. Отсюда:
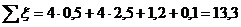 ;
;
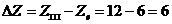 м;
м;
Находим А по формуле:
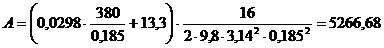
Подставив в формулу значения А и ΔZ получим:
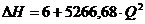 (1.4).
(1.4).
По формуле (1.4) определим потери
напора при различных значениях расхода жидкости, и результаты расчета сводим в
таб.1.1.
Задаемся значениями расхода Q в
интервале [0÷0,075]
Таблица 1.1 - Зависимость ΔH=f(Q) для
участка 7
|
Q,
м3/с
|
0
|
0,01
|
0,02
|
0,03
|
0,04
|
0,05
|
0,06
|
0,07
|
0,075
|
|
ΔH,
м/с
|
6
|
6,53
|
8,11
|
10,74
|
14,43
|
19,17
|
24,96
|
31,81
|
34,97
|
По данным таблицы 1.1 строим график зависимости ΔH
= f(Q).
Расчет участка 6.
Целью данного расчета является определение
зависимости падения давления на участке 6 от расхода.
Расчетные данные участка представлены в задании
на проектирование.=0,075 м3/с
Задаемся скоростью U =1 м/с.
Определяем площадь поперечного сечения
трубопровода по формуле:
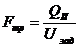 , м2, где
, м2, где
- заданный расход жидкости на
заданном участке, м/с3.зад - заданная скорость, м/с.
Отсюда: Fтр = 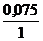 = 0,075
(м2).
= 0,075
(м2).
Определяем диаметр трубопровода на
данном участке по формуле (1.1):
Таким образом: 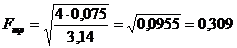 (м).
(м).
По ГОСТ 8732-70 (таб. 4) принимаем
трубу бесшовную, горячекатанную из стали 10 диаметром 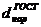 =299 мм, б =
40 мм.
=299 мм, б =
40 мм.
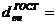
 мм = 0,219 м;
мм = 0,219 м;
Уточняем значение скорости на данном
участке по формуле:
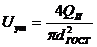 , м/с,
, м/с,
следовательно 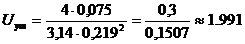 (м/с).
(м/с).
Полученное значение скорости воды
удовлетворяет условию U = 1÷3 м/с.
Определяем критерий Рейнольдса по
формуле (1.2):
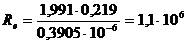 ;
;
Принимаем ν = 0,3905·10
-6 м2/с при температуре t
= 75 ºC
по табл. 2.
В зависимости от числа Рейнольда по
табл. 11. выбираем формулу для расчета коэффициента жидкостного трения λ.
Если Re >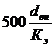 , то λ вычислим по
формуле Шифринсона (1.3):
, то λ вычислим по
формуле Шифринсона (1.3):
Кэ=1 мм =1·10-3 м;
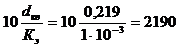 ;
;
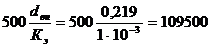 , и тогда=1,1·106 >1,095·105
, и тогда=1,1·106 >1,095·105
Значение числа Рейнольдса входит в
данные пределы и поэтому величину λ вычислим по формуле (1.3):
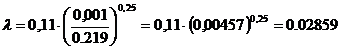 ;
;
Вычисляем сумму коэффициентов
местных сопротивлений для данного участка по формуле:
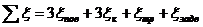 , где
, где
ξпов;ξк; ξтр; ξ задв -
коэффициенты местного сопротивления, где
ξпов - коэффициент местного
сопротивления при входе в трубу без закруглений входных кромок. По табл. 12 ξпов, =0,5.
ξтр - коэффициент местного
сопротивления тройника. Значение ξтр при разделении потоков,
учитывающего потери напора частичного расхода, движущегося под углом 90 оС к
суммарному потоку. Для выбора ξтр находим соотношение:
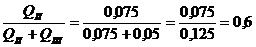
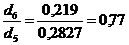 ;
;
где 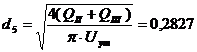 ;
;
По табл. 17 принимаем ξтр =1,2;
ξ задв - коэффициент местного
сопротивления при входе в трубу при хорошо закругленных кромках. По табл. 12 ξзад =0,1.
ξк,=2,5.
При длине участка l6 =160 м
принимаем 3 шт. поворотов и 3 шт. компенсаторов. Отсюда:
 ;
;
Подставляем известные величины в
формулу и получаем зависимость потери напора на данном участке от расхода
жидкости:
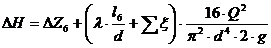 , м;
, м;
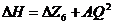 , где
, где
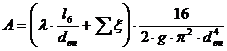 ;
;
ΔZ6 = ZII -Zе =11-6 =5 м;
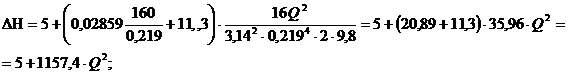
ΔH = 5+1157,4·Q2 (1.5).
По формуле (1.5) определяем потери
напора при различных значениях расхода жидкости и результаты расчета сводим в
таблицу 1.3. Задаемся значениями расхода Q в интервале: [0 ÷
0,16].
Таблица 1.2 - Зависимость ΔH = f(Q) для участка
6
|
Q,
м3/с
|
0
|
0,015
|
0,03
|
0,045
|
0,06
|
0,075
|
0,09
|
0,105
|
0,12
|
0,14
|
0,16
|
|
ΔH,
м/с
|
5
|
5,26
|
6,04
|
7,34
|
9,17
|
11,51
|
14,38
|
17,76
|
21,67
|
27,68
|
34,63
|
По данным таблицы 1.2 строим график зависимости ΔH
= f(Q).
Расчет участка 5
Целью данного расчета является определение
зависимости падения давления на участке 5 от расхода.
Расчетные данные участка приведены в задании на
проектирование.
Задаемся U = 1 м/с
Определяем площадь поперечного сечения
трубопровода по формуле:
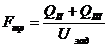 ;
;
где Q - заданный расход жидкости на
заданном участке, м/с3.зад - заданная скорость, м/с.
Отсюда: 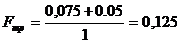 (м2).
(м2).
Определим диаметр трубопровода на
данном участке по формуле (1.1):
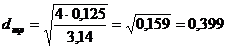 (м);
(м);
По ГОСТ 8732-70 (таб. 4) принимаем
трубу бесшовную, горячекатанную из стали 10 диаметром 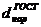 = 402 мм, б
= 40 мм.
= 402 мм, б
= 40 мм.
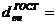
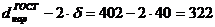 мм = 0,322 м;
мм = 0,322 м;
Уточняем значение скорости на данном
участке по формуле:
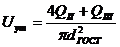 ;
;
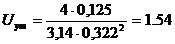 (м/с);
(м/с);
Полученное значение скорости воды
удовлетворяет условию U
=1÷3 м/с.
Определяем критерий Рейнольдса по
формуле (1.2):
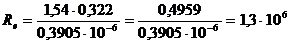 ;
;
Принимаем ν =
0,3905·10-6 м2/с, при t = 75ºC по табл. 2. интерполяцией.
В зависимости от числа Рейнольда по
табл. 11. выбираем формулу для расчета коэффициента жидкостного трения λ.
Если Re >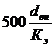 , то λ вычислим по
формуле Шифринсона (1.3):
, то λ вычислим по
формуле Шифринсона (1.3):
Кэ=1 мм =1·10-3 м;
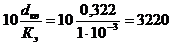 ;
;
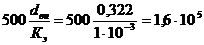 , и тогда=1,3·106 >1,6·105;
, и тогда=1,3·106 >1,6·105;
Значение числа Рейнольдса входит в
данные пределы и поэтому величину λ вычислим по формуле (1.3):
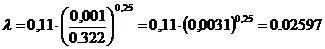
Вычисляем суммарный коэффициент местного
сопротивления на участке:
Σξ =3ξпов+3ξк
(1.14), где
ξ пов, - коэффициент
местного сопротивления при входе в трубу без закруглений входных кромок. По
табл. 12 ξпов, =0,5.
ξк,=2,5.
При длине участка 300 м, принимаем
количество поворотов из соотношения 1000 м -10 отводов. Количество поворотов: 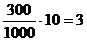 шт.
шт.
Количество компенсаторов из
соотношения 1000 м - 10 компенсаторов примем равное:
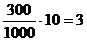 шт.
шт.
Умножив это число на количество компенсаторов
на участке, получим:
Σξ =
3.0,5+3.2,5 =9.
Подставим известные величины в
формулу и получаем зависимость потери напора на данном участке от расхода
жидкости:
 , м;
, м;
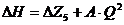 , где
, где
 ;
;
ΔZ5 = Zе -Zс =6 - 4 =2 м;
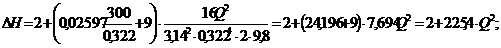
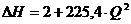 (1.6);
(1.6);
По формуле (1.6) определяем потери
напора при различных значениях расхода жидкости и результаты расчета сводим в
таблицу 1.4. Задаемся значениями расхода Q в интервале [0 ÷ 0,26].
Таблица 1.3 - Зависимость ΔH=f(Q) для участка
5.
|
Q,
м3/с
|
0
|
0,025
|
0,05
|
0,075
|
0,1
|
0,125
|
0,15
|
0,175
|
0,2
|
0,22
|
0,24
|
0,26
|
|
ΔH,
м
|
2
|
2,14
|
2,56
|
3,27
|
4,25
|
5,52
|
7,07
|
8,9
|
11,01
|
12,91
|
14,98
|
17,37
|
Затем по данным табл. 1.4. стоим графики
зависимости ΔH=f(Q) на участке 5.
Расчет участка 4.
Целью данного расчета является определение
зависимости падения давления на участке 4 от расхода.
Расчетные данные участка представлены в задании
на проектирование.
Задаемся скоростью U = 1 м/с.
Определяем площадь поперечного сечения
трубопровода по формуле:
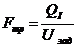 ;
;
где Q - заданный расход жидкости на
заданном участке, м/с3.зад - заданная скорость, м/с.
Отсюда: 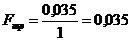 (м2).
(м2).
Определяем диаметр трубопровода на
данном участке по формуле (1.1):
 (м).
(м).
По ГОСТ 8732-70 (таб. 4) принимаем
трубу бесшовную, горячекатанную из стали 10 диаметром 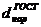 = 219 мм, б
= 30 мм.
= 219 мм, б
= 30 мм.
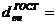
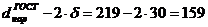 мм = 0,159 м;
мм = 0,159 м;
Уточняем значение скорости на данном
участке по формуле:
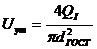 ;
;
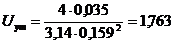 (м/с).
(м/с).
Полученное значение скорости воды
удовлетворяет условию U = 1÷3 м/с.
Определим критерий Рейнольдса по
формуле (1.2):
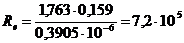 ;
;
ν =0,3905·10-6 м/с при t =
75°C по табл. 2 интерполяцией.
В зависимости от числа Рейнольдcа по
табл. 11 выбираем формулу для расчета коэффициента жидкостного трения λ.
Если Re >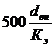 , то λ вычислим по
формуле Шифринсона (1.3):
, то λ вычислим по
формуле Шифринсона (1.3):
Кэ=1 мм =1·10-3 м;
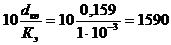 ;
;
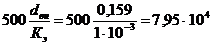 , и тогда=7,2·105 >7,95·104;
, и тогда=7,2·105 >7,95·104;
Значение числа Рейнольдса входит в
данные пределы и поэтому величину λ вычислим по формуле (1.4):
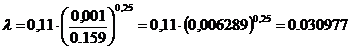 ;
;
Вычисляем сумму коэффициентов
местных сопротивлений для данного участка по формуле:
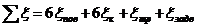 , где
, где
ξпов;ξк,;ξтр;ξ задв -
коэффициенты местного сопротивления, где
ξ пов - коэффициент местного
сопротивления при входе в трубу без закруглений входных кромок. По табл. 12 ξпов=0,5.
ξк,=2,5.
ξтр - коэффициент местного
сопротивления тройника. Значение ξтр при разделении потоков,
учитывающего потери напора частичного расхода, движущегося под углом 90 оС
к суммарному потоку. Для выбора ξтр находим
соотношение:
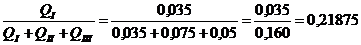
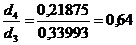 , где
, где 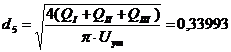
По табл. 17 принимаем ξтр =4,4;
ξ задв - коэффициент местного
сопротивления при входе в трубу при хорошо закругленных кромках. По табл. 12 ξзадв =0,1.
При длине участка 450 м принимаем 6
поворотов и 6 компенсаторов П.
Вычисляем сумму коэффициентов
местных сопротивлений для данного участка по формуле:
Отсюда: 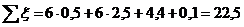 ;
;
Подставляем известные величины в
формулу и получаем зависимость потери напора на данном участке от расхода
жидкости:
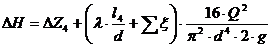 , м;
, м;
 , где
, где
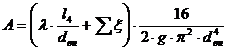 ;
;
ΔZ4 = ZI -Zс =5 - 4 =1 м;
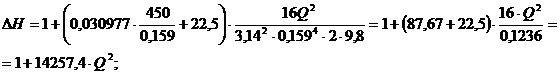
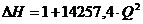 (1.7).
(1.7).
По формуле (1.7) определяем потери
напора при различных значениях расхода жидкости и результаты сводим в табл.
1.4. Задаемся значениями расходов в интервале [0 ÷ 0,05].
Таблица 1.4 - Зависимость ΔH=f(Q) для участка
4
|
Q,
м3/с
|
0
|
0.05
|
0.01
|
0.015
|
0.02
|
0.025
|
0.03
|
0.035
|
0.04
|
0.045
|
0.05
|
|
ΔH,
м
|
1
|
1,36
|
2,43
|
4,21
|
6,7
|
9,91
|
13,8
|
18,47
|
23,81
|
29,87
|
36,6
|
По данным таблицы 1.5 строим графики зависимости
ΔH=f(Q).
Расчет участка 3
Целью данного расчета являются определение
зависимости падения давления от расхода на участке 3.
Расчетные данные участка приведены в задании на
проектирование.
Задаемся скоростью U= 1 м/с.
Определяем площадь поперечного сечения
трубопровода:
 ;
;
где Q - заданный расход жидкости на заданном
участке, м/с3.зад - заданная скорость, м/с.
Отсюда: 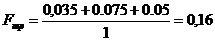 (м2).
(м2).
Определяем диаметр трубопровода на
данном участке по формуле (1.1):
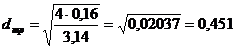 (м).
(м).
По ГОСТ 8732-70 (таб. 4) принимаем
трубу бесшовную, горячекатанную из стали 10 диаметром 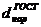 =450 мм, б =
40 мм.
=450 мм, б =
40 мм.
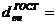
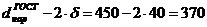 мм = 0,370 м;
мм = 0,370 м;
Уточняем значение скорости на данном
участке по формуле:
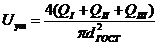 , м/с;
, м/с;
следовательно 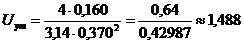 (м/с).
(м/с).
Полученное значение скорости воды
удовлетворяет условию U = 1÷3 м/с.
Определим критерий Рейнольдса по
формуле (1.2):
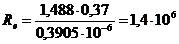 ;
;
ν =0,3905·10-6 м/с при t =
75°C по табл. 2 интерполяцией.
В зависимости от числа Рейнольдcа по
табл. 11 выбираем формулу для расчета коэффициента жидкостного трения λ.
Если Re >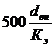 , то λ вычислим по
формуле Шифринсона (1.3):
, то λ вычислим по
формуле Шифринсона (1.3):
Кэ=1 мм =1·10-3 м;
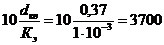 ;
;
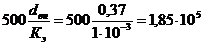 , и тогда=1,4·106 >1,85·105;
, и тогда=1,4·106 >1,85·105;
Значение числа Рейнольдса входит в
данные пределы и поэтому величину λ вычислим по формуле (1.3):
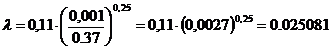 ;
;
Вычисляем суммарный коэффициент
местного сопротивления на участке:
нагнетательный
водопровод давление напор
Σξ =ξпов+ξк, где
ξпов - коэффициент местного
сопротивления при входе в трубу без закруглений входных кромок . По табл. 12 ξпов =0,5.
ξк,=2,5.
При длине участка 100 м, принимаем
количество поворотов из соотношения 1000 м -10 отводов. Количество поворотов: 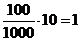 шт;
шт;
Количество компенсаторов из
соотношения 1000 м -10 компенсаторов примем равное:
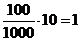 шт;
шт;
Умножив это число на количество
компенсаторов на участке, получим:
Σξ =
1.0,5+1.2,5 =3.
Подставляем известные величины в
формулу и получаем зависимость потери напора на данном участке от расхода
жидкости:
 , м, (1.6),
, м, (1.6),
 ;
;
ΔZ3 = Zс -Zб =4 - 7 = - 3 м;
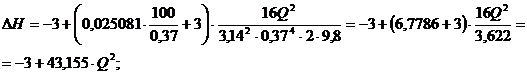
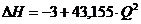 , (1.8).
, (1.8).
По формуле (1.8) определяем потери
напора при различных значениях расхода жидкости и результаты расчета сводим в
табл. 1.6. Задаемся значение расхода в интервале [0÷0,26].
Таблица 1.5 - Зависимость ΔH = f(Q) для участка
3
|
Q,
м3/с
|
0
|
0,04
|
0,08
|
0,12
|
0,160
|
0,2
|
0,24
|
0,26
|
|
DH,
м
|
-3
|
-2,93
|
-2,75
|
-2,38
|
-1,89
|
-1,27
|
-0,51
|
-0,01
|
По данным таблицы 1.6. строим график зависимости
ΔH
= f(Q).
Расчет подогревателя «П».
Целью данного расчета является определение
зависимости падения давления (потери напора) на участке «П» от расхода.
Расчетные данные участка представлены в задании
на проектирование.= QI +QII+ QIII =35+50+75 =0,16 м3/с;
Δh = 7 м - потеря
напора в подогревателе (из задания);
Зависимость потери напора от расхода жидкости
для подогревателя определяем по формуле:
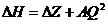 ;
;
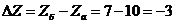 .
.
По заданному значению потери напора
в подогревателе и при известном расходе находим А:
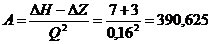
Полученное значение А подставляем в
формулу и получаем:
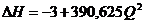 , (1.9).
, (1.9).
По формуле (1.9) определяем потери
напора при различных значениях расхода жидкости, и результаты расчета сводим в
таблицу 1.2. Задаемся значениями расхода Q в интервале [0÷0,26]
Таблица 1.6 - Зависимость ΔH=f(Q) для
подогревателя
|
Q,
м3/с
|
0
|
0,02
|
0,04
|
0,06
|
0,1
|
0,14
|
0,16
|
0,18
|
0,22
|
0,26
|
|
ΔH,
м
|
-3
|
-2,84
|
-2,38
|
-1,59
|
0,91
|
4,66
|
7
|
9,66
|
15,91
|
23,41
|
Расчет участка 2.
Целью данного расчета является определение
зависимости падения давления на участке 2 от расхода.
Расчетные данные участка представлены в задании
на проектирование.
Задаемся скоростью U = 1 м/с.
Определяем площадь поперечного сечения
трубопровода по формуле:
 ;
;
где Q - заданный расход жидкости на
заданном участке, м/с3.зад - заданная скорость, м/с.
Отсюда: 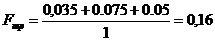 (м2).
(м2).
Определяем диаметр трубопровода на
данном участке по формуле (1.1):
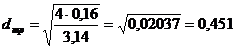 (м).
(м).
По ГОСТ 8732-70 (таб. 4) принимаем
трубу бесшовную, горячекатанную из стали 10 диаметром 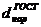 =450 мм, б =
40 мм.
=450 мм, б =
40 мм.
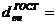
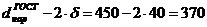 мм = 0,370 м;
мм = 0,370 м;
Уточняем значение скорости на данном
участке по формуле:
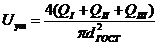 , м/с.
, м/с.
следовательно 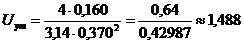 (м/с).
(м/с).
Полученное значение скорости воды
удовлетворяет условию U = 1÷3 м/с.
Определим критерий Рейнольдса по
формуле (1.2):
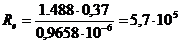 ;
;
где ν =
0,9658·10-6 м2/с при t
= 22ºC по
табл. 2 интерполяцией.
В зависимости от числа Рейнольдcа по
табл. 11 выбираем формулу для расчета коэффициента жидкостного трения λ.
Если Re >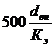 , то λ вычислим по
формуле Шифринсона (1.3):
, то λ вычислим по
формуле Шифринсона (1.3):
Кэ=1 мм =1·10-3 м;
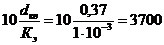 ;
;
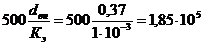 , и тогда=5,7·105 >1,85·105;
, и тогда=5,7·105 >1,85·105;
Значение числа Рейнольдса входит в
данные пределы и поэтому величину λ вычислим по формуле (1.3):
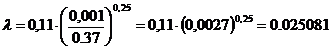 ;
;
Вычисляем сумму коэффициентов
местных сопротивлений для данного участка по формуле:
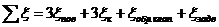 ;
;
где ξпов;ξк,;ξобр.клап,;ξ задв
коэффициенты местного сопротивления, где
ξпов - коэффициент местного
сопротивления при входе в трубу без закруглений входных кромок. По табл. 12 ξпов =0,5.
ξобр.клап. - коэффициент
местного сопротивления обратного клапана определяется по табл. 15.
интрополяцией;
ξобр.клап. =2,24;
ξзадв - коэффициент местного
сопротивления при входе в трубу при хорошо закругленных кромках. По табл. 12 ξзадв, =0,1.
ξк,=2,5.
При длине участка 150 м принимаем 1
поворот и 1 компенсатор.
Вычисляем сумму коэффициентов
местных сопротивлений для данного участка по формуле:
Отсюда: 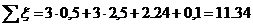 ;
;
Подставляем известные величины в
формулу и получаем зависимость потери напора на данном участке от расхода
жидкости:
 , м (1.6)
, м (1.6)
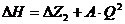 , где
, где
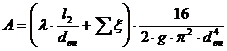 ;
;
ΔZ3 = Zа -Zн =10 - 4 = 6 м;

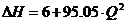 , (1.10).
, (1.10).
По формуле (1.10) определяем потери
напора при различных значениях расхода жидкости и результаты расчета сводим в
табл. 1.7. Задаемся значениями расхода Q в интервале [0÷0,26].
Таблица 1.7 - Зависимость ΔH = f(Q) для участка
2
|
Q,
м3/с
|
0
|
0,04
|
0,06
|
0,08
|
0,12
|
0,14
|
0,16
|
0,2
|
0,22
|
0,26
|
|
ΔH,
м
|
6
|
6,15
|
6,34
|
6,61
|
7,37
|
7,86
|
8,43
|
9,8
|
10,6
|
12,43
|
По данным таблицы 1.7 строим график зависимости ΔH
= f(Q).
В результате данного расчета определены диаметры
участков водопровода и потери давления при заданных расходах жидкости.
Результаты расчетов занесены в таблицы: 1.1;
1.2; 1.3; 1.4; 1.5; 1.6; 1.7.
2. Гидравлический расчет линии
всасывания водопровода
Целью данного расчета является определение
давления всасывания Pвс. Найденное давление сравнивается с давлением насыщения
PН. Это обусловлено тем, что всасывающий трубопровод насоса работает под
разрежением, что может привести к возникновению кавитации, т.е. вскипанию
жидкости с последующей конденсацией. Для предотвращения этого нежелательного
явления должно выполняться условие: Pвс >PН.
Расчетные данные участка представлены в задании
на проектирование.
Задаемся скоростью Uвс = 0,5 м/с.
Расход равен Q = ΣQ
= 0,160 м3/с.
Определяем площадь поперечного сечения
трубопровода по формуле по формуле:
 ;
;
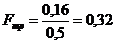 (м2);
(м2);
Определяем диаметр трубопровода на
линии всасывания по формуле (1.1):
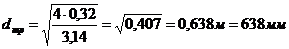 .
.
По ГОСТ 5525-61 принимаем стальную
бесшовную горячекатаную трубу 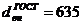 мм и толщиной стенки б = 19 мм.
мм и толщиной стенки б = 19 мм.
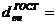
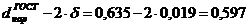 м;
м;
Уточняем значение скорости во
всасывающем трубопроводе по формуле (1.2):
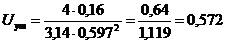 (м/с);
(м/с);
Полученное значение скорости воды удовлетворяет
условию U = 0,4 ÷ 0,8 м/с.
Определим критерий Rе по формуле (1.3):
 ;
;
где ν =
0,9658·10-6 м2/с при t
= 22ºC по
табл. 2 интерполяцией.
В зависимости от числа Рейнольдcа по
табл. 11 выбираем формулу для расчета коэффициента жидкостного трения λ.
Если Re >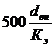 , то λ вычислим по
формуле Шифринсона (1.4):
, то λ вычислим по
формуле Шифринсона (1.4):
Кэ=1 мм =1·10-3 м;
 ;
;
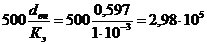 , и тогда=0,35·106 >2,98·105;
, и тогда=0,35·106 >2,98·105;
Значение числа Рейнольдса входит в
данные пределы и поэтому величину λ вычислим по формуле (1.3):
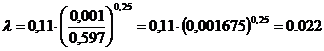 ;
;
Вычислим сумму коэффициентов местных
сопротивлений для данного участка по формуле: Σξ = ξвсас.клап. + ξпов., где
ξвсас.клап. - коэффициент
местного сопротивления всасывающего клапана с сеткой, принимаем ξвсас.клап. =
2,15 по табл. 15. инторополяцией.
ξпов. - коэффициент местного
сопротивления при колене на трубе с углом поворота 90 оС по табл. 12;
ξпов. = 0,5,
и тогда Σξ = 2,15+0,5
= 2,65.
Подставляем известные величины в
формулу, в результате получаем зависимость потери напора на данном участке от
расхода жидкости:
ΔZ = Zвс - Zо = 4,5-0 =
4,5 (м);
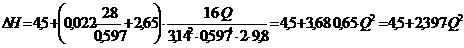 , (2.1)
, (2.1)
По формуле (2.1) определяем потери
напора при различных значениях расхода жидкости, и результаты расчета сводим в
табл. 2.1. Задаемся значениями расхода в интервале [0÷0,26].
Таблица 2.1 - Зависимость ΔH = f(Q) для участка
1
|
Q,
м3/с
|
0
|
0,04
|
0,08
|
0,12
|
0,16
|
0,2
|
0,24
|
0,26
|
|
ΔH,
м
|
4,5
|
4,504
|
4,515
|
4,535
|
4,561
|
4,596
|
4,638
|
4,662
|
По данным таблицы 2.1. строим график зависимости
ΔH
= f(Q).
По уравнению Бернулли определяем давление во
всасывающем патрубке насоса (по формуле):
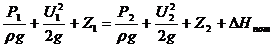
сечение 1-1 (0-0) сечение 2-2= 0 U2
= 0,572 м/с= 0 Z2 = Zвс
РI = Pатм (атмосф. давл.) P2 = Pвс
Рати = 105 Па; 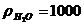 кг/м3 ; Zвс
= 4,5 м
кг/м3 ; Zвс
= 4,5 м
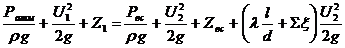 ;
;
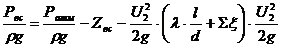
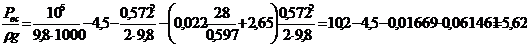
и тогда Рвс = ρg·5,62 =
1000·9,8·5,62 = 55094 (Па) ≈ 55 (кПа).
При t = 22 ºC;
Рн = 2,7 кПа (давление насыщения).
Сравниваем Рн и Рвс и видим, что Рвс > Рн .
Делаем вывод: при данной температуре и давлении
вскипания жидкости не произойдет. В результате данного расчета определены
диаметр участка 1 водопровода и потери давления при различных значениях расхода
жидкости. Результаты расчета занесены в таблицу 2.1.
Заключение
По результатам проведенных расчетов строятся
графики зависимости потерь напора от расхода жидкости и для каждого участка
заданного трубопровода. При этом данные для построения кривой ΔH
= f(Q)
участка 7 берутся из табл. 1.1., для участка 6 из табл. 1.2., для участка 5 из
табл. 1.3, для участка 4 из табл. 1.4., для участка 3 из табл. 1.5., для
участка 2 из табл. 1.7, и для участка 1 из табл. 2.1. Данные для построения
зависимости потери напора от расхода жидкости для подогревателя берутся из
табл. 1.6.
Построение суммарной кривой последовательно
соединенных участков проводится путем сложения потерь напора при одних и тех же
расходах. Для параллельно соединенных участков построение суммарной характеристики
проводится путем сложения расходов при постоянном значении величины потери
напора.
Для построения суммарной кривой следует,
графически начиная с последнего участка (7) прибавлять предыдущие, т.е. участок
6, а затем к суммарному графику зависимости ΔH = f(Q)
7+6 прибавлять участок 5 и так далее. В результате получим суммарный график
2+П+3+4+5+6+7 (П-подогреватель). График складывается с учетом того, как
соединены между собой участки. Участок 7-6 соединены параллельно: Q6+7 = Q7+Q6,
перепад давлений ΔH6+7
= ΔH7 + ΔH6.
Участок 5 и участок 7+6 соединены
последовательно, т.е. Q5+6+7=Q5=Q6+7, а падение давления: ΔH5+6+7
= ΔH5 + ΔH6+7,
т.е. сложение кривых участков 5 и 6+7 идет по вертикали, а суммирование кривых
участка 7,6 идет по горизонтали.
Участок 4 и 5+6+7 соединены параллельно;
суммирование кривых горизонтали:+5+6+7 = Q4 + Q5+6+П+7;
ΔH4+5+6+7
= ΔH4 = ΔH5+6+7.
Участок 3 и 4+5+6+7 и П соединены
последовательно и суммирование кривых по вертикали: Q П+3+4+5+6+7=
Q3=QП+4+5+6+7;
ΔHП+3+4+5+6+7
=ΔH3
+ΔHП++4+5+6+7.
Участок 2 и П+3+4+5+6+7 соединены
последовательно, т.е. суммирование по вертикали: Q2+П+3+4+5+6+7= Q2 =
QП+3+4+5+6+П+7
ΔH2+П+3+4+5+6+7=ΔH2
+
ΔHП+3+4+5+6+П+7.
В результате получаем график зависимости ΔH
= f(Q)
для всей системы водопроводов на линии нагнетания, кривая 2+П +3+4+5+6 +7.
Литература
1. Дейч
М.Е., Заряпкин А.Е. Гидрогазодинамика,М.:Энергоиздат, 2014.-384 с.
. Альтшуль
А.Д., Киселев П.Т. Гидравлика и аэродинамика 2011.
. Кумагин
Ю.М., Капустина Т.И. Расчет водопроводов ИЭИ, 2009.