Геодезическая подготовка перенесения проекта планировки поселения в натуру
Федеральное государственное бюджетное
образовательное учреждение высшего образования
"Омский государственный аграрный
университет им. П.А. Столыпина"
Землеустроительный факультет
Кафедра геодезии и дистанционного
зондирования
Направление 21.03.03 - Геодезия и
дистанционное зондирование
КУРСОВОЙ ПРОЕКТ
на тему:
ГЕОДЕЗИЧЕСКАЯ ПОДГОТОВКА ПЕРЕНЕСЕНИЯ
ПРОЕКТА ПЛАНИРОВКИ ПОСЕЛЕНИЯ В НАТУРУ
Выполнил: ст. 42 группы Сохторов В.И,
Руководитель: к.т.н., доцент Уваров А.И.
Омск 2015
Содержание
Реферат
Введение
. Аналитический расчет проекта
.1 Определение проектных координат точек пересечения осей
улиц
.2 Вычисление проектных координат углов квартала
. Проектирование плановой и высотной разбивочной сети
.1 Проектирование плановой сети
.1.1 Вычисление веса по способу Попова
.1.2 Вычисление веса по способу Юршанского
.2 Проектирование высотной сети
. Перенесение в натуру проектных точек углов квартала
.1 Перенесение точки на местность способом полярных координат
.2 Вынесение точки на местность способом прямоугольных
координат
.3 Перенесение на местность проектной точки способом линейной
засечки
.4 Вынесение в натуру проектной точки способом прямой угловой
засечки
Заключение
Библиографический список
Реферат
Данный курсовой проект содержит: 37 формул, 11 таблиц, 7 рисунков, 3
приложения и 3 литературных источника.
Целью выполнения курсового проекта является подготовка студента к решению
следующих профессиональных задач:
· разработки технологий инженерно-геодезических работ и
инженерно-технических изысканий для проектирования, строительства и монтажа
инженерных сооружений;
· выполнения специализированных инженерно-геодезических работ
при изысканиях, проектировании, сооружении и эксплуатации инженерных объектов;
· инженерно-геодезическое обеспечение городского хозяйства.
Вынесением проекта в натуру называют геодезические работы, выполняемые на
местности для определения планового и высотного положения характерных точек и
плоскостей строящегося сооружения согласно рабочим чертежам проекта.
Введение
Как научная дисциплина, прикладная геодезия занимается изучением методов
проектирования разбивочных сетей и выноса элементов сооружений и зданий в
натуру, используемых в производстве с учетом требуемой точности.
В настоящее время, из всего разнообразия геодезических работ, широкое
применение занимают работы в строительстве и в эксплуатации различных
сооружений, которые включают в себя: проектирование разбивочных сетей;
разбивочные работы; сопровождение строительства; контроль за деформациями
сооружений и зданий.
Целью выполнения данной работы является аналитический расчет проекта
населенного пункта, проектирование планово-высотной геодезической сети и
подготовка геодезической разбивочной сети, и подготовка геодезических данных
для выноса в натуру главных точек проекта.
В данном курсовом проекте мы используем традиционные методы
проектирования, а так же рассматриваем основные геодезические методы для выноса
положения точек кварталов и подготовку геодезических данных для выноса
проектных точек квартала в натуру.
1. Аналитический
расчет проекта
Аналитический расчет проекта предполагает определение координат основных
точек проекта. Для аналитического расчета необходимо:
. Созданный генеральный план (Приложение А)
2. Дирекционные углы основных планировочных направлений.
. Размеры проектируемых кварталов и ширина улиц.
На фрагменте генерального плана восстанавливаем координатную сетку. За
основу для определения координат были взяты дирекционные углы основных
планировочных направлений, которые располагаются вдоль центральных улиц.
Условно проводим направления через точки А, С, и D, E, которые в свою
очередь пересекаются в точке В, схематическое изображение представлено на
Рисунке 1.
Рисунок 1. Схематическое изображение генерального плана.
Далее графически сняли координаты этих точек, и после решения обратных
геодезических задач были получены дирекционные углы линий АВ и BC, а также DB и ЕВ. Расчет дирекционных углов представлен в Таблице 1.
Таблица 1. Расчет дирекционных углов основных направлений.
|
обозн.
|
направления
|
|
AB
|
BC
|
DB
|
BE
|
|
∆x
|
100
|
276
|
142
|
154
|
|
∆y
|
-160
|
-440
|
92
|
103
|
|
tg r
|
-1,6
|
-1,5942029
|
0,64788732
|
0,66883117
|
|
r
|
-57,9946168
|
-57,9010727
|
32,9386905
|
33,7758396
|
|
б, ˚
|
302,005383
|
302,098927
|
32,9386905
|
33,7758396
|
|
S, м
|
188,679623
|
519,399653
|
169,198109
|
185,270073
|
|
|
|
|
|
|
Исходные данные
|
точка
|
x
|
y
|
|
A
|
2200
|
5800
|
|
B
|
2300
|
5640
|
|
C
|
2576
|
5200
|
|
D
|
2158
|
5548
|
|
E
|
2454
|
5743
|
|
a
|
2293
|
5652
|
|
b
|
2309
|
5625
|
Так как координаты точек снимались графически, расхождение дирекционных
углов отрезков направлений АС и DE не
должно превышать величины, определяемой по формуле:
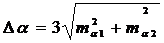 , (1)
, (1)
где
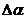 - средняя квадратическая погрешность дирекционного
угла отрезка оси улицы.б1,2 - ошибки в определении расхождения
дирекционных углов отрезков оси каждой улицы.
- средняя квадратическая погрешность дирекционного
угла отрезка оси улицы.б1,2 - ошибки в определении расхождения
дирекционных углов отрезков оси каждой улицы.
Ошибки
в определении расхождения дирекционных углов отрезков оси каждой улицы в свою
очередь вычисляют по формуле:
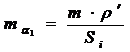 , (2)
, (2)
где m - средняя квадратическая погрешность графического определения
координат,i - длина отрезка, дирекционный угол которого
определяется.
Средняя квадратическая погрешность графического определения координат
составляет 18 мм в масштабе плана, то есть 0,36 метров. В данной работе:
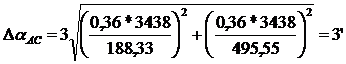
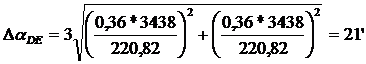
Из
Таблицы 1 видно, что расхождения дирекционных углов отрезков улиц допустимы:
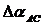 = 42’
= 42’
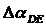 = 0’
= 0’
Далее
были рассчитаны средние дирекционные углы:
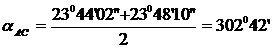
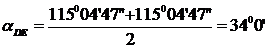
В
данном проекте прямоугольная планировка кварталов, следовательно направления
улиц при пересечении должны образовывать угол 90 градусов (прямой).
Рассчитывается он как разность дирекционных углов АС и DE (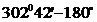 -
-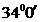 =
=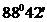 ), данная величина отличается от прямого угла на 1018'41.
Необходимо увязать значения дирекционных углов так, что бы их разность была
равна 90 градусам. В результате получили следующие дирекционные углы:
), данная величина отличается от прямого угла на 1018'41.
Необходимо увязать значения дирекционных углов так, что бы их разность была
равна 90 градусам. В результате получили следующие дирекционные углы:
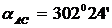
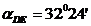
.1
Определение проектных координат точек пересечения осей улиц
По значениям полученных дирекционных углов основных планировочных
направлений и размерам квартала, улиц и используя графические координаты точки
В, взятую за исходную, вычисляем координаты точек. Для этого от точки В
проложили теодолитный ход, углы поворота в котором кратны 90 градусам, а длины
линий графически сняты с плана. Схема проложенного теодолитного хода
представлена на Рисунке 2, а расчет координат представлен в Таблице 2.
Рисунок 2. Схематическое изображение теодолитного хода.
Таблица 2.Ведомость вычисления проектных координат точек пересечения осей
улиц.
|
точки
|
в
|
б
|
S
|
Дx
|
Дy
|
x
|
y
|
|
В
|
270
|
|
|
|
|
2300
|
5640
|
|
|
|
33,7758
|
190
|
157,932
|
105,63
|
|
|
|
1
|
90
|
|
|
|
|
2457,932
|
5745,6296
|
|
|
|
123,776
|
190
|
-105,63
|
157,932
|
|
|
|
2
|
90
|
|
|
|
|
2352,302
|
5903,5612
|
|
|
|
-146,22
|
190
|
-157,93
|
-105,63
|
|
|
|
3
|
180
|
|
|
|
|
2194,37
|
5797,9316
|
|
|
|
-146,22
|
170
|
-141,31
|
-94,511
|
|
|
|
4
|
90
|
|
|
|
|
2053,063
|
5703,4209
|
|
|
|
-56,224
|
190
|
105,63
|
-157,93
|
|
|
|
5
|
180
|
|
|
|
|
2158,693
|
5545,4893
|
|
|
|
-56,224
|
245
|
136,207
|
-203,65
|
|
|
|
6
|
180
|
|
|
|
|
2294,899
|
5341,8407
|
|
|
|
-56,224
|
200
|
111,189
|
-166,24
|
|
|
|
7
|
90
|
|
|
|
|
2406,088
|
5175,5969
|
|
|
|
33,7758
|
170
|
141,307
|
94,5107
|
|
|
|
8
|
180
|
|
|
|
|
2547,396
|
5270,1076
|
|
|
|
33,7758
|
190
|
157,932
|
105,63
|
|
|
|
9
|
90
|
|
|
|
|
2705,327
|
5375,7371
|
|
|
|
123,776
|
200
|
-111,19
|
166,244
|
|
|
|
10
|
90
|
|
|
|
|
2594,138
|
5541,9809
|
|
|
|
-146,22
|
190
|
-157,93
|
-105,63
|
|
|
|
11
|
270
|
|
|
|
|
2436,207
|
5436,3514
|
|
|
|
123,776
|
245
|
-136,21
|
203,649
|
|
|
|
|
|
|
|
|
2300
|
5640
|
1.2
Вычисление проектных координат углов квартала
координата квартал местность засечка
Вычисление проектных координат углов квартала так же было произведено на
основе известных дирекционных углов и длин сторон кварталов, а так же вспомогательных
точек "a" и "b", лежащие на пересечении
наиболее длинной улицы. Начиная от исходного пункта В, проложили замкнутый
теодолитный ход с прямыми углами поворота и получили координаты углов
кварталов. Схема теодолитного хода по углам квартала представлена на Рисунке 3,
а вычисления представлены в Таблице 3.
Рисунок 3. Схематическое изображение теодолитного хода по углам квартала.
Таблица 3.Ведомость вычисления проектных координат углов квартала.
|
точки
|
в
|
б
|
S
|
Дx
|
Дy
|
x
|
y
|
|
b
|
|
|
|
|
2309
|
5625
|
|
|
|
122,702
|
30
|
-16,208
|
25,2447
|
|
|
|
a
|
270
|
|
|
|
|
2292,792
|
5650,2447
|
|
|
|
32,7022
|
15
|
12,6224
|
8,10408
|
|
|
|
VI 2
|
180
|
|
|
|
|
2305,414
|
5658,3488
|
|
|
|
32,7022
|
160
|
134,638
|
86,4435
|
|
|
|
4
|
90
|
|
|
|
|
2440,053
|
5744,7923
|
|
|
|
122,702
|
160
|
-86,444
|
134,638
|
|
|
|
3
|
90
|
|
|
|
|
2353,609
|
5879,4308
|
|
|
|
212,702
|
160
|
-134,64
|
-86,444
|
|
|
|
1
|
180
|
|
|
|
|
2218,971
|
5792,9873
|
|
|
|
212,702
|
30
|
-25,245
|
-16,208
|
|
|
|
I 3
|
180
|
|
|
|
|
2193,726
|
5776,7791
|
|
|
|
212,702
|
140
|
-117,81
|
-75,638
|
|
|
|
1
|
90
|
|
|
|
|
2075,917
|
5701,141
|
|
|
|
302,702
|
160
|
86,4435
|
-134,64
|
|
|
|
2
|
90
|
|
|
|
|
2162,361
|
5566,5026
|
|
|
|
392,702
|
140
|
117,809
|
75,6381
|
|
|
|
4
|
270
|
|
|
|
|
2280,169
|
5642,1406
|
|
|
|
302,702
|
30
|
16,2082
|
-25,245
|
|
|
|
II 3
|
270
|
|
|
|
|
2296,378
|
5616,8959
|
|
|
|
212,702
|
140
|
-117,81
|
-75,638
|
|
|
|
1
|
90
|
|
|
|
|
2178,569
|
5541,2578
|
|
|
|
302,702
|
220
|
118,86
|
-185,13
|
|
|
|
2
|
90
|
|
|
|
|
2297,429
|
5356,1299
|
|
|
|
392,702
|
140
|
117,809
|
75,6381
|
|
|
|
4
|
270
|
|
|
|
|
2415,237
|
5431,768
|
|
|
|
302,702
|
20
|
10,8054
|
-16,83
|
|
|
|
III 3
|
270
|
|
|
|
|
2426,043
|
5414,9382
|
|
|
|
212,702
|
140
|
-117,81
|
-75,638
|
|
|
|
1
|
90
|
|
|
|
|
2308,234
|
5339,3001
|
|
|
|
302,702
|
180
|
97,249
|
-151,47
|
|
|
|
2
|
90
|
|
|
|
|
2405,483
|
5187,8319
|
|
|
|
392,702
|
140
|
117,809
|
75,6381
|
|
|
|
4
|
180
|
|
|
|
|
2523,292
|
5263,4699
|
|
|
|
392,702
|
30
|
25,2447
|
16,2082
|
|
|
|
IV 2
|
180
|
|
|
|
|
2548,537
|
5279,6781
|
|
|
|
392,702
|
160
|
134,638
|
86,4435
|
|
|
|
4
|
90
|
|
|
|
|
2683,175
|
5366,1216
|
|
|
|
482,702
|
180
|
-97,249
|
151,468
|
|
|
|
3
|
90
|
|
|
|
|
2585,926
|
5517,5899
|
|
|
|
572,702
|
160
|
-134,64
|
-86,444
|
|
|
|
1
|
270
|
|
|
|
|
2451,288
|
5431,1464
|
|
|
|
482,702
|
20
|
-10,805
|
16,8298
|
|
|
|
V 2
|
|
|
|
|
2440,482
|
5447,9762
|
|
|
|
392,702
|
160
|
134,638
|
86,4435
|
|
|
|
4
|
90
|
|
|
|
|
2575,121
|
5534,4197
|
|
|
|
482,702
|
220
|
-118,86
|
185,128
|
|
|
|
3
|
90
|
|
|
|
|
2456,261
|
5719,5476
|
|
|
|
572,702
|
160
|
-134,64
|
-86,444
|
|
|
|
1
|
180
|
|
|
|
|
2321,622
|
5633,1041
|
|
|
|
572,702
|
15
|
-12,622
|
-8,1041
|
|
|
|
b
|
270
|
|
|
|
|
2309
|
5625
|
|
|
|
482,702
|
30
|
-16,208
|
25,2447
|
|
|
|
a
|
270
|
|
|
|
|
2292,792
|
5650,2447
|
|
|
|
392,702
|
|
|
|
|
|
2.
Проектирование плановой и высотной разбивочной сети
Построение разбивочной сети как плановой, так и высотной, производится
когда геодезическая сеть имеет недостаточную точность или густоту, для выноса в
натуру. Полигонометрические сети или строительная геодезическая сетка -
наиболее распространенные методы построения плановой сети на застроенной
территории. В данном курсовом проекте имеется всего два опорных пункта: один
находится на пересечении главных улиц, в точке В, а второй располагается за
пределами населенного пункта, но имеется видимость с пункта В.
.1
Проектирование плановой сети
Проектирование плановой сети было произведено в виде полигонометрической
сети, с учетом того, что при определении их координат должна быть обеспечена
видимость между всеми пунктами сети, а также возможность выноса всех точек
проекта в натуру. Так же необходимо обеспечить сохранность пунктов,
расположение по возможности как можно дальше от проезжей части, вблизи лини
застройки.
Для определения необходимой точности измерений в запроектированной сети
был определен вес уравненного положения точки, расположенной в наиболее слабом
месте сети, по способу Попова, а так же по способу Юршанского.
.1.1
Вычисление веса по способу Попова
1. Выбор наиболее слабого места сети, точки максимально удаленной от
исходного пункта В.
. Выбор ходовой линии
. Расчет невязок в полигонах, как длин ходовой линии в полигоне, со
знаком "+/-", в зависимости от расположения полигона относительно
ходовой линии.
. Расчет красных чисел пропорционально длинам линий.
. Уравнивание и получение поправок полигона.
Метод уравнивания по способу профессора Попова представлен в Приложении
Б.
Вес уравненного положения точки в слабом месте сети был вычислен по
формуле:
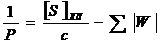 , (3)
, (3)
где [S]хл - длина ходовой линии в км,
с - постоянная, равная 1,- поправки в длины линий, полученные из
уравнивания.
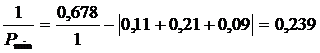
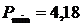
После
установления обратного веса были рассчитаны показатели необходимой точности по
приближенным формулам. Средняя длина стороны в запроектированных ходах
рассчитана по формуле:
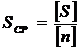 , (4)
, (4)
где
[S] - сумма длин всех ходов,- число запроектированных ходов.

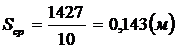
Эквивалентный
вес рассчитан по формуле:
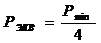 (5)
(5)
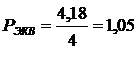
Длина
эквивалентного хода, заменяющего запроектированную систему ходов, была
рассчитана следующим образом:
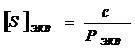 , (6)
, (6)
где
с - постоянная, равная 1000
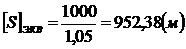
Число
сторон в эквивалентном ходе определено как:
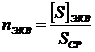 ,
(7)
,
(7)
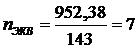
Допустимая
средняя квадратическая невязка хода была рассчитана по формуле:
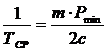 , (8)
, (8)
где
m - заданная ошибка положения точки в слабом месте сети, равная 0,1 м.
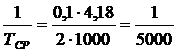
Допустимая
предельная невязка хода принимается в 2 раза большей, чем предыдущая невязка.
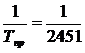
Допустимая
относительная средняя квадратическая погрешность измерений сторон определена по
формуле:
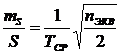 , (9)
, (9)
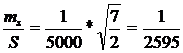
Допустимая
средняя квадратическая погрешность измерений углов определена по формуле:
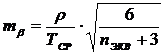 , (10)
, (10)
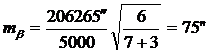
Далее
согласно полученным значениям допустимых ошибок было установлено, что для
определения координат разбивочной сети необходимо производить измерения по
программе полигонометрии второго разряда, так как относительная ошибка
определения стороны, полученная из вычислений, не превышает 1:2000.
После
выбора подходящего вида построения необходимо убедиться в правильности выбора.
Для этого величина допустимой среднеквадратической невязки хода была вычислена
по характеристикам полигонометрии 2-го разряда по формуле:
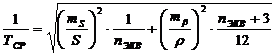 , (11)
, (11)
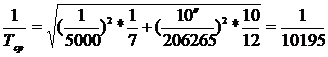
Следовательно
выбранные параметры сети удовлетворяют необходимым.
.1.2
Вычисление веса по способу Юршанского
Вычисление обратного веса точки, расположенной в слабом месте сети по способу
Юршанского, называемого иначе способом эквивалентной замены производилось на
основе замещения частей сети эквивалентным ходом. Схема сети представлена в
Приложении В.
Ходы 1, 4 и 7 были заменены на эквивалентный полигон из 2-х ходов по
формуле:
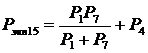 , (12)
, (12)
Ходы
2,3 и 15 были заменены на эквивалентный полигон из 3-х ходов по формуле:
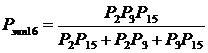 , (13)
, (13)
Далее
ходы 8, 9, 12, образующие были заменены на эквивалентный ход 17, 18 и 19 по
формуле:
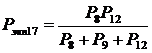 , (14)
, (14)
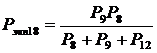 , (15)
, (15)
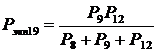 , (16)
, (16)
Ходы
11, 14 и 17 заменены на ход 20 с весом, который был вычислен по формуле:
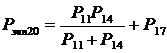 , (17)
, (17)
Ходы
13,14,18 и 20 заменены на ход 21 с весом, который был вычислен по формуле:
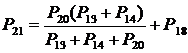 , (18)
, (18)
Проложить
ходовую линию к точке К, расположенной в слабом месте сети, можно по ходам 21 и
6, либо по ходу 16, поэтому вес точки К был определен по формуле:
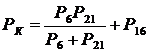 , (19)
, (19)
В
Таблице 4 представлены расчеты весов ходов. При этом веса одиночных ходов сети
вычислялись как величина, обратно пропорциональная длине хода.
Таблица 4.Расчет весов эквивалентных ходов.
|
№ хода
|
S, км
|
Pхода.
|
|
1
|
0,162
|
6,17
|
|
2
|
0,221
|
4,52
|
|
3
|
0,177
|
5,65
|
|
4
|
0,176
|
5,68
|
|
5
|
0,188
|
5,31
|
|
6
|
0,239
|
4,18
|
|
7
|
0,232
|
4,31
|
|
8
|
0,190
|
5,26
|
|
9
|
0,178
|
5,62
|
|
10
|
0,168
|
5,95
|
|
11
|
0,148
|
6,76
|
|
12
|
0,172
|
5,81
|
|
13
|
0,239
|
4,18
|
|
14
|
0,195
|
5,13
|
|
15
|
|
8,21
|
|
16
|
|
1,92
|
|
17
|
|
1,77
|
|
18
|
|
1,96
|
|
19
|
|
1,83
|
|
20
|
|
4,75
|
|
21
|
|
6,14
|
|
22
|
|
4,45
|
|
К
|
|
2,16
|
Вывод: способ эквивалентной замены также как и способ полигонов
профессора В.В. Попова является строгим. Вычислив вес точки К двумя этими
способами мы не получили одинаковые значения. Это объясняется тем, что при
вычислении веса способом эквивалентной замены мы отбросили два хода, таким
образом, уменьшили жесткость сети.
Рп=4,18
Далее
проверяется правильность выбранной точности измерений путём просчёта моделей
сети на ЭВМ. Для этого по программе ПУКС-96, задаваясь вычисленной необходимой
точностью измерений углов и линий, устанавливаются ожидаемые ошибки в положении
всех пунктов запроектированной сети.
Таблица 5. Координаты пунктов разбивочной сети
|
Обозначение
|
X
|
Y
|
|
1
|
2422
|
5142,9
|
|
2
|
2570
|
5238
|
|
3
|
2702
|
5334,2
|
|
4
|
2572,1
|
5540,5
|
|
5
|
2454,3
|
5728
|
|
В
|
2354,5
|
5888
|
|
7
|
2218,5
|
5792,5
|
|
8
|
2070
|
5704,2
|
|
9
|
2172,6
|
5538,1
|
|
10
|
2300
|
5330,5
|
|
11
|
2434
|
5432,9
|
|
12
|
2300
|
5670
|
Ожидаемая точность измерений в запроектированной сети была рассчитана по
формуле:
.
(21)
Таким
образом:
Мs=75м.;
Мn=23’’
.
Необходимая
точность измерений в запроектированной сети, рассчитанная в соответствии с
выбранным видом построений:
Таблица
6. Результаты вычислений на ЭВМ
|
№ пункта
|
ошибка пункта для
необходимой точности измерений
|
ошибка пункта для
полигонометрии второго разряда
|
|
1
|
6,39
|
2,40
|
|
2
|
47,3
|
17,6
|
|
3
|
63,4
|
23,8
|
|
4
|
40,5
|
15,2
|
|
5
|
62,5
|
23,63
|
|
6
|
89,1
|
32,4
|
|
7
|
78,2
|
28,3
|
|
8
|
92,2
|
33,6
|
|
9
|
65
|
24,1
|
|
10
|
43,1
|
16,1
|
|
11
|
0
|
0
|
|
12
|
53,4
|
19,7
|
Вывод: Выбранный вид
построения разбивочной сети удовлетворяет необходимой точности, в связи с тем,
что ошибка в наиболее слабом месте сети мм не превышает допустимой ( < 110
мм). Программа показала 2 слабые точки сети с приближенно равными значениями
СКО положения пункта. Одна из этих точек совпадает с выбранным ранее слабым
местом сети.
.2
Проектирование высотной сети
При проектировании разбивочной сети необходимо учесть, что для всех
пунктов плановой сети будут определены высоты. Схема высотной сети совпадает со
схемой плановой сети. Имеет те же исходные пункты. Необходимая точность
высотной разбивочной сети характеризуется средней квадратической погрешностью
определения высот пунктов разбивочной сети относительно исходных, которая
составляет величину 0,01 м.
Для обеспечения заданной точности определения высот разбивочной сети
следовало:
. Установить необходимую точность нивелирования, применяя формулу:
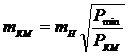 (22)
(22)
где 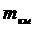 - допустимая средняя квадратическая погрешность нивелирования
на один километр хода;
- допустимая средняя квадратическая погрешность нивелирования
на один километр хода;
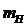 - допустимая средняя квадратическая погрешность определения
высот пунктов разбивочной сети относительно исходных данных;
- допустимая средняя квадратическая погрешность определения
высот пунктов разбивочной сети относительно исходных данных;
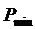 - вес уравненной высоты пункта, расположенного в наиболее
слабом месте разбивочной сети;
- вес уравненной высоты пункта, расположенного в наиболее
слабом месте разбивочной сети;
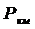 - ход длиной в один километр.
- ход длиной в один километр.
. Согласно полученному значению 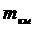 был установлен необходимый вид
нивелирования по классификации высотных геодезических сетей, характеристики
точности некоторых из них представлены в таблице 7, и даны рекомендации о
необходимых приборах и методике измерений.
был установлен необходимый вид
нивелирования по классификации высотных геодезических сетей, характеристики
точности некоторых из них представлены в таблице 7, и даны рекомендации о
необходимых приборах и методике измерений.
Таблица 7. Классификация геодезических сетей.
|
Класс (вид) нивелирования
|
Допустимая невязка хода, мм
|
Допустимая средняя
квадратическая погрешность нивелирования на один километр хода 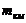 , мм , мм
|
|
III класс
|
10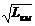
|
5
|
|
IV класс
|
20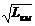
|
10
|
|
Техническое
|
50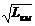
|
25
|
|
Геометрическое
(горизонтальным лучом теодолита, тахеометра)
|
100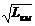
|
50
|
|
Тригонометрическое
|
200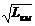
|
100
|
Так как в данном курсовом проекте, следовательно, необходимый вид
нивелирования - IV класс.
Затем была вычислена ожидаемая ошибка определения высот пунктов
разбивочной сети при выбранной методике нивелирования по следующей формуле:
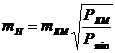 , (23)
, (23)
где
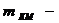 величина, взятая из таблицы 9 для выбранного вида
нивелирования.
величина, взятая из таблицы 9 для выбранного вида
нивелирования.
Вычисленное
значение 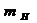 по формуле (23) не должно превышать ранее
установленную допустимую величину
по формуле (23) не должно превышать ранее
установленную допустимую величину
В
данном курсовом проекте:
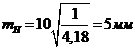
Вывод: так как ,
следовательно, вид построений установлен правильно.
3.
Перенесение в натуру проектных точек углов квартала
В данном курсовом проекте были вынесены на местность углы кварталов
населенного пункта четырьмя наиболее часто применяемыми способами:
. Способ полярных координат
. Способ линейной засечки
. Способ прямой угловой засечки
Так же была вычислена необходимая точность измерений для каждого способа
и подобраны соответствующие приборы для выноса точек в натуру.
.1
Перенесение точки на местность способом полярных координат
Способ полярных координат заключается в том, что положение проектной
точки на местности находится путем откладывания от исходного направления
проектного угла, после чего в этом направлении откладывается проектное
расстояние.
В данной работе этим способом была вынесена точка I.1. Чертеж представлен на Рисунке 4.
Исходное направление - линия разбивочной сети 4-5. Необходимо найти
дирекционные углы линий, образующие проектный угол в, для его последующего
определения. Вследствие чего решаем обратные геодезические задачи. Решение
приведено в Таблице 8.
Рисунок 4. Схема выноса угла квартала способом полярных координат.
Таблица 8. Решение обратных геодезических задач для выноса точки I.1.
|
обозн
|
8-I.1
|
8-9
|
|
yк
|
5701,141
|
5538,1
|
|
ун
|
5704,2
|
5704,2
|
|
∆y
|
-3,0589687
|
-166,1
|
|
хк
|
2075,9173
|
2172,6
|
|
хн
|
2070
|
2070
|
|
∆х
|
5,9173036
|
102,6
|
|
r
|
-27,336845
|
-58,296367
|
|
б
|
332,66316
|
301,703633
|
|
S
|
6,661214
|
|
|
впр
|
30,959522
|
57
|
Проектный угол в рассчитывается как разность дирекционных углов и равен
в= 30˚57ґ34ґґ
Рассчитываем необходимую точность измерений при выносе, ошибка выноса
точки mС должна составлять не более 0,1м. Эта ошибка определяется по
формуле:
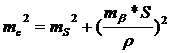 , (24)
, (24)
где
ms - средняя квадратическая ошибка выноса линии,в -
средняя квадратическая ошибка выноса проектного угла.
На
ошибку выноса точки влияют ошибки выноса угла и линии. Применяя принцип равных
влияний, получим формулу для вычисления необходимой точности выноса линии:
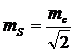 , (25)
, (25)
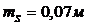
Относительная
ошибка линии вычисляется по формуле 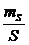 и в
данном проекте равна:
и в
данном проекте равна:
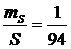
Из
этого следует, что проектное расстояние можно вынести рулеткой.
Формула
для вычисления необходимой точности выноса проектного угла:
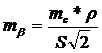 , (26)
, (26)
где
S - проектное расстояние.
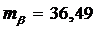 ґ
ґ
Для
выноса углов можно использовать теодолит Т30. Далее были произведены расчеты по
проверке правильности выбранных приборов. Для этого в формулу (22) были
подставлены принятые значения точности: 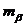 = 30ґ и
= 30ґ и 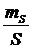 =
=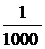 , в результате чего получена ожидаемая mc=6мм,
и означает, что выбранные средства удовлетворяют необходимой точности.
, в результате чего получена ожидаемая mc=6мм,
и означает, что выбранные средства удовлетворяют необходимой точности.
3.2
Вынесение точки на местность способом прямоугольных координат
Способ заключается в вычислении приращения координат, расстояние от
ближайшего пункта разбивочной сетки до выносимой точки, затем по одной из
сторон откладываем соответственное приращение, затем в полученной точке на
стороне откладываем перпендикуляр. После чего откладываем второе приращение
координат по перпендикуляру.
В данной работе способ применялся к точке 3-IV.4. Рабочий чертеж
представлен на Рисунке 5. Были решены обратные геодезические задачи для
определения дирекционных углов линий 3-IV.4 и 3-4, и расстояния 3-IV.4.
Вычисления приведены в Таблице 9.
Рисунок 5. Схема выноса угла квартала способом прямоугольных координат.
Таблица 9.Решение обратных геодезических задач для выноса точки II.3.
|
обозн
|
3-4
|
3-IV.4
|
|
yк
|
5540,5
|
5334
|
|
ун
|
5334,2
|
5334,2
|
|
∆y
|
206,3
|
-0,2
|
|
хк
|
2572,1
|
2696
|
|
хн
|
2702
|
2702
|
|
∆х
|
-129,9
|
-6
|
|
r
|
-57,80279
|
1,909152433
|
|
б
|
122,19721
|
181,9091524
|
|
S3-I.1
|
|
6,003332408
|
|
ϕ
|
59,711945
|
42
|
|
S1
|
3,0277663
|
1
|
|
S2
|
5,1838818
|
11
|
Угол в рассчитывается как разность дирекционных углов и равен 59˚42ґ43ґґ,
и необходим для нахождения приращений координат.
Из свойств прямоугольного треугольника получим формулы для нахождения
приращений S2 и S1:
S2=S3-IV.4.*sin в, (27)1= S3-IV.4.*cos
в, (28)
S1=1,00 (м)
S2=10,00 (м)
На ошибку выноса точки повлияли ошибки выноса двух расстояний и ошибка
построения перпендикуляра, что следует из формулы среднеквадратической ошибки
определения положения точки:
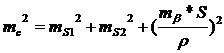 , (29)
, (29)
где
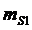 и
и 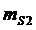 - средние
квадратические ошибкти построения линий,в - средняя квадратическая
погрешность вынесения перпендикуляра.
- средние
квадратические ошибкти построения линий,в - средняя квадратическая
погрешность вынесения перпендикуляра.
Формула
для вычисления необходимой точности выноса линий S1 и S2:
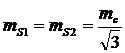 , (30)
, (30)
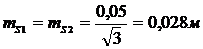
Относительная
ошибка линии вычисляется по формуле 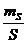 и в
данном проекте равна:
и в
данном проекте равна:
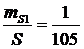 ;
;
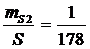
Следовательно
проектное расстояние можно вынести рулеткой.
Формула
для вычисления необходимой точности выноса проектного угла:
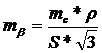 (31)
(31)
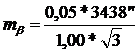 =19,14ґ
=19,14ґ
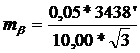 =9,92ґ
=9,92ґ
Для
построения прямых углов можно использовать экер. Далее были произведены расчеты
по проверке правильности выбранных приборов. Для этого в формулу (29) были
подставлены принятые значения точности: 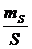 =
=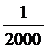 , в результате чего получена ожидаемая mc =
0.028м, которая меньше чем 0,05м. Это означает, что выбранные средства
удовлетворяют необходимой точности.
, в результате чего получена ожидаемая mc =
0.028м, которая меньше чем 0,05м. Это означает, что выбранные средства
удовлетворяют необходимой точности.
3.3
Перенесение на местность проектной точки способом линейной засечки
Способ выполняется с учетом того, что все стороны должны находится в
пределах длины одного мерного прибора, в нашем случае мы отложим расстояние в
20 метров по линии 1-10 и получим вспомогательную точку А, а угол г должен
находится в пределах 90˚. После чего с полученной вспомогательной точки
делают засечку, откладывая расстояние S2, так же от точки 1
откладываем расстояние S1. В результате на пересечении засечек и
будет находиться искомая точка. Рабочий чертеж представлен на Рисунке 6. Для
нахождения сторон треугольника были решены обратные задачи, представленные в
Таблице 10.
Рисунок 6. Схема выноса точки квартала способом линейной засечки.
Таблица 10 Решение обратных геодезических задач для выноса точки V.4.
|
обозн.
|
направления
|
|
|
10-1
|
III.1-10
|
III.1-A
|
|
∆x
|
122
|
-8,2342526
|
2,648890735
|
|
∆y
|
-188,1
|
-1,5
|
-18,27966602
|
|
tg r
|
-1,5418033
|
0,1821659
|
-6,900875819
|
|
r
|
-57,032914
|
10,3241303
|
-81,75471137
|
|
б
|
302,96709
|
190,32413
|
278,2452886
|
|
S
|
224,19993
|
8,36976196
|
18,47059317
|
|
|
19
|
14
|
|
ϒ
|
87,9211583
|
55
|
|
|
|
|
|
|
A
|
10
|
III.1
|
|
x
|
2310,8831
|
2300
|
2308,234253
|
|
y
|
5313,7203
|
5330,5
|
5332
|
|
d
|
20
|
|
|
Угол г находим как разность дирекционных углов и равен 87˚55ґ16ґґ
На ошибку выноса точки повлияли ошибки выноса двух расстояний:
Рассчитаем ошибку выноса:
;
(33)
где
равна 0,05м
;
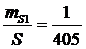
Исходя
из полученной точности для выноса точки способом линейной засечки можно
применить мерную ленту. Далее были произведены расчеты по проверке правильности
выбранных приборов. Для этого в формулу (32) были подставлены принятые значения
точности: 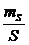 =
=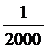 , в результате чего получена ожидаемая = 0.014м,
которая меньше чем 0,05м. Это означает, что выбранные средства удовлетворяют
необходимой точности.
, в результате чего получена ожидаемая = 0.014м,
которая меньше чем 0,05м. Это означает, что выбранные средства удовлетворяют
необходимой точности.
.4 Вынесение
в натуру проектной точки способом прямой угловой засечки
Способ заключается в том, чтобы, отложив от двух пунктов сети и исходного
направления два проектных угла, получить на пересечении створов искомую точку
квартала.
В данной работе способ применялся к точке VI.2. Рабочий чертеж представлен на Рисунке 7. Были решены
обратные геодезические задачи, вычисления которых приведены в Таблице 11.
Рисунок 7. Схема выноса точки квартала способом прямой угловой засечки.
Таблица 11.Решение обратных геодезических задач для выноса точки 5-VI.3
|
обозн.
|
направления
|
|
5-VI.3
|
5-6
|
6-5
|
6-VI.3
|
|
∆x
|
-100,6908
|
-99,8
|
99,8
|
-0,890844658
|
|
∆y
|
156
|
160
|
-160
|
-4
|
|
tg r
|
-1,549297
|
-1,603206413
|
-1,603206413
|
4,490120657
|
|
r
|
-57,15961
|
-58,04614755
|
-58,04614755
|
77,44449905
|
|
б
|
122,84039
|
121,9538524
|
301,9538524
|
257,4444991
|
|
S
|
185,67349
|
188,5736991
|
188,5736991
|
4,098000025
|
|
|
|
|
|
|
в1
|
0,8865351
|
53
|
|
|
|
в2
|
44,509353
|
30
|
|
|
|
ϒ
|
134,60411
|
36
|
|
|
|
|
|
|
|
|
50
|
57
|
57
|
26
|
Проектные углы в1 и в2 были определены как разности соответствующих
дирекционных углов и получили:
в1= 0˚53ґ12ґґ
в2= 44˚30ґ34ґґ
Вспомогательный угол г, необходимый для расчета необходимой точности, был
найден как дополнение суммы углов в1 и в2 до 180 градусов и равен 134˚36ґ14ґґ
Рассчитаем необходимую точность измерений. Ошибку выноса точки в данном
случае можно вычислить по формуле:
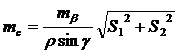 , (36)
, (36)
Что
ошибка выноса угла будет вычисляться по формуле:
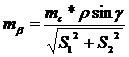 , (37)
, (37)
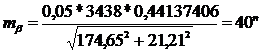
После
вычислений были сделаны выводы от том, что выносить проектные углы возможно с
применением теодолита 2Т 5К. Произведены расчеты по проверке правильности
выбранных приборов, для этого в формулу (36) было подставлено принятое значение
точности, в результате чего получена ожидаемая mC=0,05мм.
Это означает, что выбранные средства удовлетворяют необходимой точности.
Итак,
в результате проделанных работ были вынесены 4 точки квартала различными
способами.
Заключение
В результате проделанной работы проанализируем точность и
целесообразность методов проектирования разбивочной сети и результаты расчета
точности выноса точек в натуру различными методами.
Метод проектируемой сети профессора В.В. Попова является более строгим,
так как при вычислениях методом Юршанского жесткость сети была уменьшена. Судя
по сложности выполнения способ Юршанского более сложен.
Исходя из результатов расчета точности выноса точек в натуру различными
методами, можно сказать, что каждый метод выноса имеет свои преимущества и
недостатки в зависимости от используемых приборов, местности и требуемой
точности выноса.
Библиографический
список
1. СНиП 11-02-96. Инженерные изыскания для строительства.
Основные положения. - М.: МИНСТРОЙ РОССИИ, 1997. - 44 с.
2. Пархоменко Н.А., Прикладная геодезия. Часть 1.
Геодезические разбивочные работы: учебное пособие / Н.А. Пархоменко, А.И.
Уваров, - Омск: Издательство ФГОУ ВПО ОмГАУ, 2010. - 69с.
. Михелёв, Д.Ш. Прикладная (инженерная) геодезия
(маленький рассказ о большой профессии/ Д.Ш. Михелёв// Геопрофи.- М., 2003