Прогнозирование цен на акции на примере ПАО 'Газпром'

Прогнозирование цен на акции на примере ПАО 'Газпром'

Введение

Прогнозирование будущих цен на акции широко изучается во многих областях знаний, в том числе трейдинге, финансах, статистике и информатике. Основной целью прогнозирования будущих цен на акции является получение спекулятивной прибыли. Предсказания цен на финансовые инструменты используются для снижения рыночного риска и увеличения доходности, и производятся на основе рыночной информации. С момента начала торговли на фондовом рынке до текущего момента объём и характер информации существенно изменились: сегодня любой человек с доступом в сеть Интернет может получить терабайты данных, так или иначе связанных с фондовым рынком. Из-за увеличения информационного потока и его скорости методы, изначально использовавшиеся для торговли, претерпели значительные преобразования.

Динамика рынков капитала изучается уже более 100 лет, анализ и прогнозирование цен на финансовые инструменты описаны в большом количестве исследований, основными из которых являются работы Дж. Литнера, Г. Марковица, Ж. Моссина, Дж. Тобина, У. Шарпа, Э. Элтона. В области финансов большинство традиционных моделей прогнозирования цен акций используют статистические модели и модели нейронных сетей, обученных на исторических данных о ценах (Park, Irwin, 2007).

Выделяют два основных подхода к прогнозированию курсов акций: традиционные методы, применяемые инвесторами на фондовом рынке, и математические модели. Традиционный подход включает в себя фундаментальный и технический анализ. Математический подход к прогнозированию представлен статистическими методами, моделями на основе нейронных сетей, генетическими алгоритмами, моделями системной динамики и многими другими.

Проблема состоит в том, что оба подхода не гарантируют абсолютную точность: по неофициальной статистике, процент успешных трейдеров весьма мал, а трейдер, закрывающий хотя бы 50% сделок с прибылью, считается достаточно успешным. Математические модели чаще всего критикуют за сложность и структуру, тяжело адаптирующуюся под процессы на фондовом рынке, а также за нереалистичные предпосылки. Например, главная предпосылка в теории детерминированного хаоса - случайность колебаний цен на финансовые инструменты (Робертс, 1959), ставится под сомнение после наблюдения за падением котировок компаний, опубликовавших финансовый отчёт ниже ожиданий рынка.

Таким образом, очевидно, что на данный момент не существует универсального метода прогнозирования цены на финансовый инструмент: для каждого инструмента необходимо проводить отдельный анализ.

Объектом исследования в представленной работе являются цены на обыкновенные акции ПАО «Газпром» (тикер GAZP), котирующиеся на Московской Бирже.

Предметом исследования являются методы описания и прогнозирования цены на акции на вторичном фондовом рынке.

Актуальность исследования состоит в привлекательности данной акции для инвесторов в силу её популярности: частотность поискового запроса, содержащего слова «купить акции Газпром», составляет 5575 показов ежемесячно. Для сравнения, аналогичные запросы для акций компаний Apple и Tesla имеют частотность 410 и 425 запросов соответственно. Таким образом, данная акция считается одной из самых привлекательных на российском фондовом рынке, однако её цена при детальном рассмотрении противоречит общепринятому восприятию выгодности покупки. Для того, чтобы установить, стоит ли инвестировать в акции GAZP, необходимо проанализировать и предсказать будущее движение цен.

Цель данной работы: исследовать эффективность основных существующих методов прогнозирования цен на акции, предложить подход, позволяющий эффективно их прогнозировать. На основе полученных результатов оценить привлекательность инвестирования в акции ПАО «Газпром».

Задачи, которые необходимо решить для достижения цели:

Обобщить основные положения современных подходов к прогнозированию цен акций и оценить возможность их использования для прогнозирования акций ОАО «Газпром».

Оценить трудоемкость, эффективность, достоинства и недостатки существующих методов, а также определить основные критерии для их использования.

Произвести оценку различных методов для прогнозирования цены на акции ПАО «Газпром» и провести их эмпирическую апробацию на реальных данных.

Построить ретроспективный прогноз и проанализировать полученные результаты.

В данной работе использованы методы научного синтеза, анализа, математического моделирования и сравнения полученных результатов.

Новизна данного исследования состоит в сочетании традиционных и статистических методов прогнозирования, позволяющих одновременно с прогнозом цены на акции получать оценку риска. Также в ходе работы получены выводы, углубляющие знания о прогнозировании цен акций.

Практическая значимость. В исследовании разработан подход к прогнозированию цены акций ПАО «Газпром», который позволяет с высокой долей вероятности получать спекулятивный доход выше нулевого.

Первая глава диссертации описывает предметную область. Вторая глава содержит описание методов прогнозирования цен финансовых инструментов, а также необходимую методологическую базу для выполнения практической части работы. В третьей главе представлена апробация подхода к прогнозированию цен на обыкновенные акции компании ПАО «Газпром». В заключении подведены итоги выполненной работы и даны практические рекомендации по использованию результатов.

1. Описание предметной области

Данная глава даёт основную информацию относительно предметной области исследования: представлены основные понятия и термины, необходимые и достаточные для понимания темы работы. Также, описаны традиционные методы прогнозирования на фондовом рынке, их достоинства и недостатки, а также их применимость к объекту исследования.

В первом разделе главы дано описание фондового рынка и принципов его функционирования. Второй раздел представляет собой описание компании ПАО «Газпром». В третьем разделе изложены основные принципы прогнозирования цен на финансовые инструменты на вторичном рынке методами фундаментального анализа. Четвёртый раздел описывает основные предпосылки и инструменты технического анализа. В последнем разделе главы сделаны выводы по применимости, эффективности и трудоемкости представленных ранее методов.

1.1 Фондовый рынок

Фондовый рынок - это рынок, на котором акции публичных компаний выпускаются и торгуются либо на бирже, либо путём обмена между двумя сторонами напрямую (over-the-counter, OTC). Фондовый рынок также называют рынком ценных бумаг.

Фондовый рынок является одним из наиболее важных компонентов свободной рыночной экономики, поскольку предоставляет компаниям доступ к капиталу в обмен на предоставление инвесторам доли собственности в компании. Это позволяет инвесторам получать прибыль за счёт финансовых достижений компаний, чьи акции они держат. Когда компания развивается, инвесторы получают доход в качестве дивидендов, а также за счет продажи акций по цене, превышающей цену покупки. Недостатком является то, что инвесторы могут потерять деньги, если компания терпит убытки.

Фондовый рынок можно разделить на две основные части: первичный и вторичный. На первичном рынке компании продают акции посредством первичного публичного размещения акций (IPO), при котором цена акций устанавливается на основании оценки перспектив развития бизнеса и количество выпускаемых акций. Институциональные инвесторы чаще всего приобретают большую часть этих акций у инвестиционных банков. Все последующие торги происходят на вторичном рынке, где участники включают в себя как институциональных, так и индивидуальных инвесторов.

Вторичные торги акциями осуществляются на биржах. Биржа - это организованный рынок, на котором осуществляется перераспределение свободных денежных средств и прав на собственность. Основная функция биржи состоит в обеспечении ликвидности. Ликвидностью называется способность актива быть быстро проданным по цене, близкой к рыночной (Азрилян, 2007). Высокая ликвидность активов обеспечивается за счёт объёма торгов (количество сделок) и влияет на привлекательность финансового инструмента.

Крупнейшей фондовой биржей в России является Московская Межбанковская Валютная Биржа и Российская Торговая Система (ММВБ-РТС), основанная в 2011 году путем слияния Московской Межбанковской Валютной Биржи (ММВБ) и Российской Торговой Системы. На ММВБ-РТС ведётся торговля акциями, облигациями, депозитарными расписками (ДР), деривативами, валютой и металлами. Также, биржа имеет два собственных индекса: индекс РТС и индекс ММВБ, которые рассчитываются на основе пятидесяти наиболее ликвидных акций крупнейших эмитентов.

1.2 Описание компании

ПАО «Газпром» является одной из крупнейших газовых компаний мира. Основная деятельность «Газпрома»: добыча природного газа, газового конденсата, нефти, их транспортировка, переработка и реализация как в России, так и за рубежом. Доля «Газпром» в мировых запасах газа составляет порядка 17%, в российских - более 60%. Данная компания является крупнейшим акционерным обществом в России. Количество счетов, на которых учитывается 23 673 512 900 акций «Газпрома», составляет более 470 тысяч. Государство контролирует более 50% акций компании (точное соотношение изменяется с течением времени).

Акции «Газпрома» считаются одними из наиболее ликвидных финансовых инструментов на фондовом рынке России. В 2014 году среднедневной объем торгов акциями Общества составил порядка 17% от среднедневного объема торгов акциями, АДР и паями на Московской Бирже. Со второго полугодия 2014 года по настоящий момент акции компании занимают второе место по ликвидности на Московской бирже. Обыкновенные акции «Газпром» имеют наибольший удельный вес в индексах РТС и ММВБ и включены в первый уровень листинга на российских фондовых биржах ЗАО «ФБ ММВБ» и ПАО «Санкт-Петербургская биржа».

Компании-аналоги для ПАО «Газпром» представлены компаниями с развитых рынков, так как только в этом случае достигается адекватность сравнения. Из аналогичных компаний на мировом рынке можно назвать следующие: ChevronTexaco, Conoco Philips, Eni, EXXON MOBIL, TNK-BP, Лукойл, Новатек, Роснефть, Сургутнефтегаз.

Далее необходимо рассмотреть наиболее значимые показатели деятельности компании. В первом полугодии наблюдалось снижение экспорта за границу на 6,2%, однако «Газпром» повысил оценку экспорта с 155 до 160 млрд. куб. м. вследствие повышения спроса. Таким образом, экспорт газа за рубеж вырос на 23% (14,29 млрд куб. м) по сравнению с 11,66 млрд куб. м в аналогичном периоде прошлого года. Также, увеличился объем поставок в европейские страны из-за отложенного спроса в начале года. Так как цены по контрактам ПАО «Газпром» имеют лаг порядка 6-9 месяцев при реакции на падение цены на нефть, потребители отложили закупки на вторую половину 2015 года.

На фоне роста спроса со стороны европейских стран, спрос в России сократился, что привело к уменьшению планируемой добычи на 6%. Вследствие разности цен в России и за рубежом, рост рентабельности «Газпром» должен увеличиться, так как в России цены ниже в среднем в 4 раза. По итогам 2015 года снижение экспортных цен составило 32% с 345,9 долл. за тыс. куб. м в 2014 г. до 235 долл. в 2015 г., что означает фактический рост цен в рублевом выражении примерно на 5,5% (Велес Капитал, 2015).

Данная информация представляет собой описание перспектив развития ПАО «Газпром», которая необходима для изучения предметной области и для оценки общего состояния компании.

1.3 Фундаментальный анализ

Фундаментальный анализ зародился в начале 20 века и основан на работе «Анализ ценных бумаг» (Грэхем, Додд, 1934). Фундаментальный анализ представляет собой способ прогнозирования количественных показателей развития компании, финансовых инструментов или экономических условий и представляет собой рассмотрение всех значимых фундаментальных факторов экономики, которые могут повлиять на цену финансового инструмента.

1.3.1 Принципы фундаментального анализа

Основные принципы фундаментального анализа (Грэхем, Додд, 1934) могут быть представлены в качестве следующих утверждений:

главный тренд движения цены акций на развитом рынке определяется чувствительностью к фундаментальным факторам;

текущие колебания цен - это естественный фон, который можно не принимать в расчет с точки зрения общего перспективного движения стоимости ценных бумаг;

рыночные котировки акции представляют собой пассивное отражение истинной ценности акции, лежащей в их основе;

каждая акция имеет свою внутреннюю стоимость, и рыночная цена акции всегда стремится к ее внутренней стоимости;

если рыночная цена акции превышает её справедливую стоимость, акция полагается переоцененной рынком, в противном случае акция недооценена.

1.3.2 Этапы фундаментального анализа

В исследованной литературе авторы чаще всего выделяют следующие уровни фундаментального анализа: макроэкономический, отраслевой, микроэкономический и моделирование цены. В данном случае, так как речь идёт о прогнозировании цены акций компании, наиболее полно этапы фундаментального анализа определяются схемой, представленной на рис. 1.

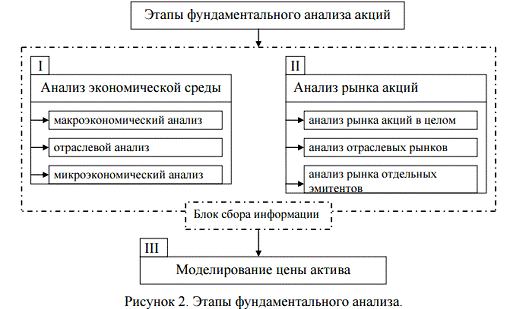
Рис. 1 - Основные этапы фундаментального анализы

Первые два этапа представляют собой сбор информации. На первом этапе рассматривается экономическая среда, которая включает в себя три пункта: макроэкономический анализ, анализ отрасли и микроэкономический анализ. Второй этап описывает состояние фондового рынка и также включает в себя три уровня: анализ рынка акций, анализ рынка акций отрасли, анализ акции. На этапе моделирования цены актива формируется эконометрическая модель для расчета цены на акции компании на основе информации, собранной на предыдущих двух этапах.

Рассмотрим данные этапы более подробно. Макроэкономический анализ рассматривает макроэкономические индикаторы, описывающие экономику страны и учитывающие следующие факторы: внешний национальный продукт (ВНП), занятость населения, инфляция, валютный курс и т.п., с целью определения привлекательности инвестиционной деятельности. Анализ отрасли предполагает изучение индексов деловой активности, а также включает в себя качественный анализ развития рассматриваемого сегмента рынка. Анализ предприятия представляет собой оценку фирмы, а именно перспектив её развития и финансового состояния на основе финансовой отчётности.

Анализ рынка акций. При анализе финансового рынка выделяют две основные его характеристики: ликвидность и волатильность. Ликвидность рынка - это способность рынка амортизировать изменения в спросе и предложении без значительных колебаний цен на рынке (Азилян, 2007). Волатильность представляет собой риск инвестиций в финансовый инструмент. Анализ финансового рынка позволяет оценить внутреннюю стоимость акции и описать корреляцию между различными финансовыми инструментами.

Моделирование цены. На данном этапе производится оценка прибыльности компании в будущем и рассчитывается риск инвестирования, описываемый эконометрической моделью. Эконометрическая модель - это экономико-статистическая модель, параметры которой оцениваются с помощью методов математической статистики на основе статистической информации. После определения потенциального дохода от инвестирования и уровня риска, определяется справедливая цена актива. Наиболее распространёнными методами для расчёта справедливой цены акции являются метод дисконтирования будущих денежных потоков и метод экономической добавленной стоимости.

1.3.3 Расчёт справедливой цены акции

Расчёт справедливой цены акции по методу дисконтирования будущих денежных потоков использует следующую формулу:

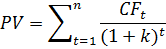
где PV - внутренняя стоимость актива; CFt - ожидаемое поступление денежных средств (денежный поток), связанных с данным активом, в момент времени t, k - ставка дисконтирования для денежных потоков данной степени риска (Невейкин, 2008). Методы, основанные на дисконтировании денежных потоков широко распространены, но, тем не менее, не достаточно точны, так как некоторые показатели, используемые в данном методе (например, ставка дисконтирования), чаще всего субъективны.

Метод экономической добавленной стоимости (EVA) основан на определении разницы между операционной прибылью компании и фактической стоимостью капитала, рассчитываемой в общем случае по следующей формуле:

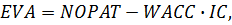
Где NOPAT - чистая операционная прибыль после уплаты налогов, WACC - средневзвешенная стоимость капитала, IC - инвестированный капитал.

Таким образом, фундаментальный анализ представляет собой полное исследование организации и окружения, в котором она функционирует, на основе чего выводится справедливая цена актива. Недостатком фундаментального анализа является его трудоёмкость, большие временные затраты, необходимость наличия большого количества компетенций и субъективность аналитика. Также, критике подвергается и временной фактор фундаментального анализа: если акция переоценена, то возможно она в итоге и приблизится к своей справедливой цене, но время наступления данного события не определяется.

1.4 Технический анализ

Основные работы, положившие начало техническому анализу, датируются концом 19 века. Среди них указываются работы Ч. Доу, У. Ганна, Р. Эллиотта, Дж. Мерфи и Р. Прихтера.

Технический анализ представляет собой анализ динамики движения рынка с целью прогнозирования направления изменения цен (Мэрфи, 1996). В его основе лежит анализ временных рядов цен, объемов торгов и других статистических данных.

1.4.1 Принципы технического анализа

В отличие от фундаментального анализа, технический анализ полагает, что макро- и микроэкономические факторы уже отражены в цене и объёме финансового инструмента (принцип «рынок учитывает всё», (Мэрфи, 2011). Таким образом, данный тип анализа не предполагает поиска ответа на вопрос, почему изменился тренд движения цены инструмента, а руководствуется лишь тем фактом, что он уже изменился.

Второй принцип технического анализа предполагает, что исторические тенденции на рынке повторяются снова (принцип «история повторяется»). Данный принцип связан с неизменностью информации, на основе которой большинство инвесторов принимают решение, а также паттерны в поведении индивидов на фондовом рынке.

Третий принцип предполагает, что движение цен на различных рынках подчинено тенденциям. Данный принцип базируется на работах Дж. Мерфи (Мэрфи, 2012) и описывает взаимосвязь между различными финансовыми инструментами.

Технический анализ также не даёт точного прогноза. В большинстве случаев, технический анализ - лишь способ описать текущую динамику рынка и распознать текущий тренд.

В результате развития интернет-трейдинга на рынке появилось большое количество игроков, не обладающих достаточной квалификацией и следующих индикаторам технического анализа, что стимулирует движение тренда в описанном индикаторами направлении.

1.4.2 Инструменты технического анализа

Инструменты технического анализа классифицируются следующим образом:

Графический анализ, выявляющий на графиках цен повторяющиеся паттерны, которые позволяют определить дальнейшее движение тренда. К графическим моделям относят трендовые линии, уровни поддержек и такие графические фигуры, как треугольники, флаги, «голова и плечи» и прочие.

Компьютерный анализ, определяющий тенденции движения рынка с помощью индикаторов и осцилляторов. Индикатор технического анализа представляет собой функцию, построенную на статистических показателях торгов на рынке (например, на основании цен или объемов торгов).

В свою очередь, индикаторы тренда классифицируются следующим образом:

Группа индикаторов «простые средние».

Простые скользящие средние. Данный индикатор представляет собой среднее арифметическое цен за последние t дней.

Взвешенные скользящие средние. Данный индикатор присваивает вес каждому значению цены. При этом чем ближе значение индекса дня к окончанию рассматриваемого периода, тем больше значение весового коэффициента.

Экспоненциальные скользящие средние. Данный метод сходен с методом взвешенных скользящих средних, но веса присваиваются всем значениям цены, а не только заданному интервалу.

Группа индикаторов «сложные средние». Данная группа представляет собой некоторые комбинации скользящих средних, использующие разные периоды.

Метод схождения/расхождения скользящего среднего (MACD). Представляет собой разность двух экспоненциальных скользящих средних с периодами в 12 и 26 дней. Среди индикаторов MACD выделяют линейный MACD (для анализа трендов) и гистограмма MACD.

Огибающие линии. Представляет собой пару параллельных скользящих средних, расположенных на определённом расстоянии от основной скользящей средней.

Полосы Боллинджера. Данный индикатор представляет собой огибающие линии, которые строятся на расстояниях, равных определённому числу стандартных отклонений.

Канал цен (PCU). Канал цен строится на основе простого скользящего среднего и представляет собой коридор вокруг него.

Осцилляторы (или контртрендовые индикаторы) показывают хорошие результаты при использовании на рынке без выраженного тренда. Данные индикаторы обычно дают сигналы нескольких типов и показывают, что рынок перекуплен и перепродан, а также указывают на расхождение между ценой актива и показанием индикатора.

Индикатор Момент (Momentum). Данный индикатор представляет собой отношение цены закрытия за текущий период к цене t периодов назад.

Индекс Торгового Канала (CCI). Представляет собой нормализованный график индикатора Момент.

Индекс относительной силы (RSI). Данный индикатор представляет собой следующий за ценой осциллятор.

Индекс Денежных Потоков (MFI). Данный индикатор схож с индексом относительной силы, но с учётом объёмов торгов. Индикатор определяет интенсивность денежных потоков.

Окончательный осциллятор (Ultimate Oscillator). Данный осциллятор представляет собой взвешенную сумму трёх осцилляторов за разные временные периоды.

Процент сопротивления (РСR). Данный индикатор рассчитывается на основе расстояния от экстремума цены за рассматриваемый период.

Индекс силы (FI). Данный осциллятор вычисляется как произведение объёма торгов за текущий торговый день и разности цен закрытия текущего и предыдущего дня.

При ближайшем рассмотрении, технический анализ представляет собой усечённые методы статистического анализа, что совсем не способствует их эффективности. Графический технический анализ ещё более неопределённый, так как фигуры, образуемые котировками акций можно трактовать двояко.

Таким образом, с помощью методов технического анализа можно распознавать тенденцию и её разворот, однако, вероятность адекватного результата не гарантирована.

Конечная цель покупки акций состоит в получении дохода от изменения её цены. Формирование цены на акции зависит от баланса между спросом и предложением на рынке. При росте спроса цена акции растёт, в противном случае - падает. При падении цены держатели акций более агрессивны, так как они готовы продавать активы по цене ниже рыночной. Покупатели же в свою очередь готовы покупать по более низким ценам. Цена будет продолжать падать, пока не достигнет точки, где покупатели будут готовы покупать по более высоким ценам, сообщая рынку восходящую тенденцию.

Среди факторов, которые могут влиять на цену акции, можно выделить следующие: состояние мировой экономики (мировые фондовые индексы), государственная политика, цены на нефть (для российского фондового рынка), поведение игроков на рынке, публикации и новости, искусственные манипуляции крупных игроков. В силу сложности фондового рынка, большого количества участников на нём и высоких объёмов информации, прогнозирование движения цен на акции весьма затруднено.

2. Методы прогнозирования курсов акций

В настоящее время компьютерная обработка данных занимает в разы меньше времени, чем в начале развития теорий прогнозирования цен акций, что привело к относительной доступности методов математического моделирования для решения текущих задач. При прогнозировании цен акций начали набирать популярность статистические методы, в том числе и временные ряды. Основные статистические методы прогнозирования описаны далее.

Перед тем, как перейти к методам, следует указать определения ключевых терминов.

Метод прогнозирования - последовательность действий, необходимых для получения модели прогнозирования. Понятие «метод прогнозирования» шире, чем «модель прогнозирования».

Модель прогнозирования - функциональное представление, адекватно описывающее временные ряды, и служит в качестве основы для получения будущих значений процесса (Парзен, 2004).

2.1 Обзор основных статистических методов

Чаще всего на входе процесса прогнозирования находятся исторические данные об исследуемом объекте и делаются предположения о его развитии. Далее происходит преобразование данных в модель. Выходом процесса является прогноз.

На основе исторических данных подбирается модель, которая наиболее полно описывает закономерности в известных наблюдениях. Далее, производится экстраполяция модели. Стоит учитывать, что данная экстраполяция исходит из предположения, что в будущих периодах природа и характер закономерностей в наблюдениях не изменятся. Ошибка прогнозирования используются для оценки степени неопределенности в будущих периодах.Прогнозирование во многом основано на статистических понятиях. Данный обзор рассматривает базовые понятия, необходимые для выполенния задачи прогнозирования. Большинство статистических процедур направлено на получение информации об исследуемых объектах, множество которых называется генеральной совокупностью. Исследуемая часть генеральной совокупности, у которой известны интересующие нас характеристики, называется выборкой. Именно на основе выборки делается заключение о всей генеральной совокупности.

Основными статистическими характеристиками описываемого объекта являются математическое ожидание и дисперсия. Говоря о выборке, используют понятия выборочного среднего и среднеквадратичного отклонения.

Математическое ожидание E(t) - среднее значение случайной величины.

Выборочное среднее - это приближение среднего распределения, основанное на его выборке. Рассчитывается по формуле:

.

Дисперсия - мера разброса случайной величины, то есть отклонение от математического ожидания. Дисперсия рассчитывается по следующей формуле:

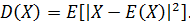
Выборочная дисперсия - оценка теоретической дисперсии распределения на основе выборки. Формула расчёта:

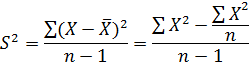
Среднеквадратичное отклонение - показатель рассеивания значений случайной величины относительно её математического ожидания. Рассчитывается по формуле:

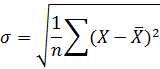
Также используется понятие стандартного отклонения, которое использует оценку отклонения случайной величины относительно её математического ожидания на основе несмещённой оценки дисперсии случайной величины. Рассчитывается по формуле:

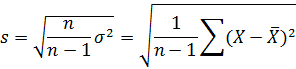
Далее стоит ввести понятие регрессии. Регрессия - это зависимость среднего значения некоторой величины от других - одной или нескольких - величин. Регрессионный анализ - это статистический метод, используемый в исследовании влияния зависимой переменной от независимых регрессоров (предикторов).

Метод наименьших квадратов (МНК). Метод наименьших квадратов очень часто используется при прогнозировании, так как позволяет оптимально оценить предикторы по данным выборки таким образом, что сумма квадратов остатков является минимальной. Например, для парной линейной регрессии  составляется функционал F:

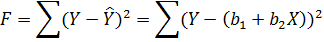
Следующий этап предполагает минимизацию функционала F. Необходимые условия минимизации:

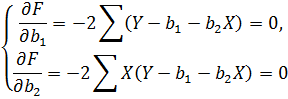
Решение данной системы имеет вид

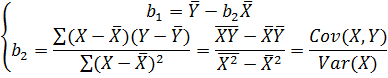
Автокорелляционный анализ. Применяется, в основном, при анализе данных за некоторый период времени (временные ряды). Автокорреляция - корреляция данных между текущим значением и лагом в один и более шагов. Коэффициент автокорреляции вычисляется по следующей формуле:

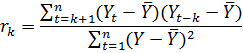
где  - коэффициент автокорреляции для запаздывания на k периодов (Айвазян, 2010).

Точность предсказания является наиболее важной характеристикой прогноза. Есть несколько основных аспектов, влияющих на точность прогнозирования. Первая группа включает в себя первоначальное качество данных. Вторая группа включает в себя технические ресурсы прогнозирования: программное и аппаратное обеспечение для реализации модели, качество алгоритмов и квалификацию специалиста. Также крайне важным аспектом является выбор модели прогнозирования. Кроме того, увеличение точности прогнозирования представляет собой уникальный процесс для каждой модели (Hank, 2003).

Обычная практика заключается в оценке ошибки предсказания, а не точности прогноза. Значение ошибки прогноза противоположно точности прогнозирования. Среди всех оценок ошибки прогнозирования, стоит отметить две наиболее популярные: MAE и MAPE. Пусть ошибка прогноза - это разница  где  - фактическое значение,  прогнозируемое значение. Тогда формулы оценки ошибок прогнозирования временных рядов для N могут быть записаны в следующих формах.(средняя абсолютная относительная ошибка):

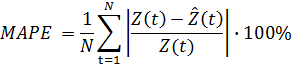
МАE (средняя абсолютная ошибка):

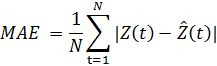
Оценка MAPE используется для моделей, чьи фактические значения значительно больше единицы. Если фактические значения близки к нулю, то знаменатель будет очень мал, что приводит к значению MAPE, близкому к бесконечности. В таких случаях, использование МАE гораздо больше подходит для оценок ошибок прогнозирования.

В дополнение к этому используются и другие оценки ошибок. Они менее популярны, но также применимы.(среднеквадратичная ошибка):

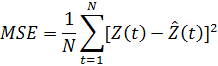
(корень из среднеквадратичной ошибки):

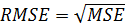
(средняя ошибка):

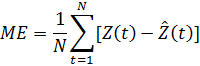
(стандартное отклонение):

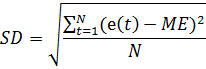
Таким образом, для определения точности прогнозирования, производится расчёт ошибки прогноза, то есть значения MAPE и/или МАE. Соотношение между точностью прогнозирования и ошибкой предсказания заключается в следующем: 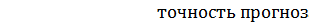 Таким образом, если MAPE = 5%, точность предсказания составляет 95%.

Стоит отметить, что точность прогнозирования не указана для любой из групп моделей (и методов), рассмотренных в данном исследовании. Это связано с тем, что точность прогнозирования процесса зависит от всех вышеуказанных факторов и определяется только после построения модели.

2.2 Классификация методов и моделей прогнозирования

Прогнозирование понимается как предсказание будущего с помощью научных методов. В настоящее время, количество методов и моделей прогнозирования стало значительно шире и нуждается, по крайней мере, в основной классификации. Чтобы дать необходимую теоретическую основу для исследования, составлена классификация методов прогнозирования и основных моделей прогнозирования, которая представлена на рис. 2.

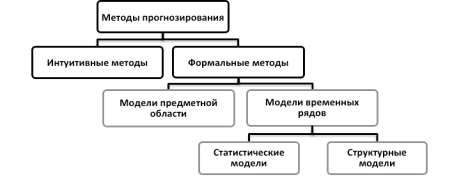
Рис. 2 - Классификация моделей прогнозирования

В представленной классификации методы разделены на две группы: интуитивные и формальные (Тихонов, 2006).

Интуитивные методы прогнозирования также называют качественными методами, так как они имеют дело с суждениями и оценками экспертов. В настоящее время, они часто используются в прогнозировании развития экономики и политики, когда система либо слишком сложна и не может быть описана формально, либо слишком проста и не требует математического описания. Данные методы включают в себя методы экспертной оценки, исторические аналогии, метод Дельфи, метод консенсуса, морфологический анализ и другие (Муратова, 2009). Кроме того, последнее время среди экспертных систем получили большое распространение экспертные системы, использующие нечеткую логику (Леоненков, 2005).

Формальные методы - методы, которые обеспечивают построение модели прогнозирования, то есть определяют математическую зависимость для получения будущих значений процесса.

Представленная классификация далее продолжается моделями прогнозирования. На первом шаге классификации формальных методов, модели могут быть разделены на две группы: модели предметной области и модели временных рядов.

Модели предметной области являются математическими моделями прогнозирования, которые используются для построения законов предметной области. Наиболее часто приводимым примером моделей предметной области является физика: модели прогнозирования погодных условий базируются на законах гидродинамики. Также, часто приводятся примеры прогнозирования уровня населения и уровня сахара в теле человека: первый прогноз использует дифференциальное уравнение, а вторая модель - систему дифференциальных уравнений. Данные модели применимы и к фондовому рынку.

Модели временных рядов - математические модели прогнозирования, которые производят поиск зависимости между прошлыми значениями внутри самого процесса для прогнозирования будущих значений. Эти модели являются универсальными для различных сфер, так как их общий вид не меняется в зависимости от природы серий.

Следует подчеркнуть, что невозможно получить полную классификацию моделей предметной области, так как их количество невероятно велико. Тем не менее, модели временных рядов всё ещё поддаются классификации на следующем шаге, и можно выделить две группы моделей: статистические и структурные.

В статистических моделях зависимость между будущими значениями и прошлым дается в виде уравнения. Этот тип моделей включает в себя модели регрессии (линейной и нелинейной), авторегрессионные модели (ARIMA, ARIMAX, GARCH, ARDLM), модели с экспоненциальным сглаживанием, модели максимального правдоподобия.

В структурных моделях зависимость будущего от прошлых значений задается в виде структуры. То есть чаще всего это подразумевает наличие неких правил переходов. Этот термин обычно включает в себя модели нейронных сетей, модели, использующие цепи Маркова, модели, основанные на классификационных и регрессионных деревьях.

Рассмотрим подробнее класс структурных моделей, так как практическая часть работы частично основана на них.

Модели и методы нейронных сетей. Главным преимуществом нейросетевых моделей является нелинейность, то есть умение устанавливать нелинейную зависимость между будущими и прошлыми значениями. Другие важные преимущества - адаптивность, масштабируемость (параллельная структура искусственной нейронной сети ускоряет вычисления) и равномерность их анализа и проектирования. В то же время есть и недостатки: отсутствие прозрачности моделирования, сложность выбора архитектуры сети, высокие требования к согласованности обучающей выборки, сложность выбора алгоритма обучения и ресурсоемкость обучения.

Модели и методы, основанные на цепях Маркова. Достоинствами этих моделей являются простота и однородность их анализа и проектирования. Недостатком является невозможность моделировать процессы с долгой памятью.

Основными преимуществами моделей на основе классификационных и регрессионных деревьев являются скорость и однородность процесса обучения, масштабируемость. Кроме того, есть возможность использовать категориальные внешние факторы. Всё это позволяет быстро обрабатывать большие объемы данных. К недостаткам этих моделей можно отнести неоднозначность алгоритма построения дерева, сложность останова, отсутствие единообразия анализа и моделирования (Чжу, 2002).

Рассмотрим основные виды статистических моделей.

Модели и методы регрессии. Преимущества этих моделей прогнозирования заключаются в простоте, гибкости и согласованности их анализа и проектирования. При использовании модели линейной регрессии результат может быть получен быстрее, чем с использованием других моделей. Кроме того, возможность проанализировать все промежуточные вычисления также является преимуществом. Основным недостатком нелинейных моделей регрессии является трудность определения формы функциональной зависимости, а также сложность определения параметров. Также, недостатки линейной регрессионной модели включают низкую адаптивность и невозможно моделировать нелинейные процессы (Draper, 1981).

Авторегрессионные модели и методы. Преимущества этого класса моделей - простота и прозрачность моделирования. В настоящее время этот класс моделей является одним из самых популярных. Недостатками данного класса моделей являются: большое количество параметров модели, не всегда однозначно определяемых, низкий уровень адаптивности, а также линейность, что ведёт к неспособности моделировать нелинейные процессы, которые часто встречаются на практике (Хэнк, 2003).

Модели экспоненциального сглаживания. Преимуществом данного класса моделей являются простота и однородность их анализа и проектирования. Этот класс моделей чаще всего используется для долгосрочного прогнозирования. Недостатком этого класса моделей является отсутствие гибкости (Prajacta, 2003).

Данная классификация представляет основные и часто используемые модели прогнозирования. Тем не менее, в настоящее время моделей прогнозирования насчитывается гораздо больше: например, существует большое количество моделей временных рядов; есть множество моделей, использующих методы опорных векторов и генетического алгоритма. Они тоже получили широко распространение. Основные характеристики методов и моделей представлены в Приложении 1.

2.3 Временные ряды

Процесс прогнозирования представляет собой исследование конкретных перспектив развития предсказываемого процесса. Временной ряд - это последовательность значений, полученных в определенные моменты времени. Временной ряд включает в себя два обязательных элемента - метку времени и соответствующее ей значение ряда (Бокс и Дженкинс, 1974). Основной принцип, предполагающий возможность использования временных рядов заключается в предположении, что факторы, влияющие на объект исследования в прошлом, влияют на него и в будущем.

При прогнозировании временных рядов выделяют следующие этапы:

построение и описание графика временного ряда;

выбор и анализ модели, характеризующей данные;

декомпозиция временного ряда на трендовую, сезонную и циклическую компоненты;

фильтрация и удаление высоко- и низкочастотных составляющих временного ряда;

анализ остатков, полученных после декомпозиции временного ряда;

прогнозирование значений временного ряда (Грешилов, Стакун, 2000).

Так как при анализе временных рядов поиск зависимостей производится в самом ряде, то и факторы, влияющие на значения ряда, обнаруживаются внутри ряда. Для обнаружения данных факторов применяют метод декомпозиции временного ряда на компоненты. Основными компонентами ряда являются тренд, цикл, сезонная и случайная компоненты.

Выделяют четыре основных типа моделей исследуемых данных: горизонтальная, тренд, сезонная и циклическая. Горизонтальная модель поведения данных предполагает флуктуацию наблюдений относительно некоторого постоянного уровня. Трендом называют модель поведения, при которой наблюдения возрастают или убывают в течение большого временного периода. Соответственно, трендом называют компоненту временного ряда, отражающую длительную возрастающую или убывающую тенденцию. Циклическая компонента представляет собой флуктуации наблюдений вокруг тренда. О наличии циклического поведения в данных говорит наличие подъёмов и спадов с нефиксированным интервалом времени. Циклическую компоненту и тренд называют тенденцией. О сезонности свидетельствуют единообразные изменения в данных с фиксированным периодом. Выбросы, не обусловленые сезонностью, цикличностью или трендом, называют случайными компонентами.

Существуют два типа моделей временного ряда: аддитивная и мультипликативная. Аддитивная модель предполагает значение ряда суммой его компонент. Мультипликативная модель динамического ряда, признанная классической в силу более широкого применения, полагает любое значение ряда произведением его компонентов: для i-ого годового наблюдения:

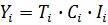
где Ti - тренд, Ci - циклический компонент для i-ого наблюдения, Ii - значение случайного компонента в i-ом году. Для значений ряда за период, не превышающий год, уравнение для i-ого периода принимает следующий вид:

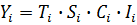
где Ti - значение тренда, Si - значение сезонного компонента в i-ом периоде, Ci - значение циклического компонента в i-ом периоде, Ii - значение случайного компонента в i-ом периоде.

Мультипликативная модель легко сводится к аддитивной модели временного ряда логарифмированием. После декомпозиции временного ряда, производится экстраполяция на заданное количество шагов.

В настоящее время выделяют три основных класса статистических методов прогнозирования временных рядов: эконометрические, регрессионные и Бокса-Дженкинса (краткие характеристики были представлены в предыдущей главе).

Рассмотрим эконометрические методы прогнозирования: наивные методы прогнозирования временных рядов, методы средних и скользящих средних, методы Хольта, Винтерса и Брауна.

При наивном прогнозировании предполагается, что последний период описывает будущее значение наилучшим образом. Именно поэтому в данном типе моделей прогнозное значение задаётся простой зависимостью от значений временного ряда в недалеком прошлом. Самая простая функция наивного прогноза полагает, что будущее будет неизменно, и задаётся функцией следующего вида:

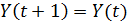
Такой подход немного примитивен, особенно для описания сложных процессов. Поэтому, выделяют другой вид наивных моделей, задающийся формулой

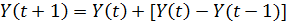
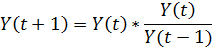
То есть, такой вид наивного прогнозирования пытается учесть сезонную компоненту и тренд временного ряда.

Метод средних. Относительно простыми моделями являются модели, основанные на усреднении. Одной из таких моделей является модель, описываемая уравнением

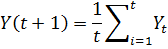
Данная модель предполагает некоторую зависимость от предыдущих периодов, в данном случае, от среднего значения временного ряда. Таким образом, данная модель может описать сложный процесс адекватно, но высокого соответствия процессу добиться сложно.

Метод скользящих средних не совсем объективен, так как для вычисления средних значений выбирается некоторый период L, но, по крайней мере, он более адекватен относительно рассмотренных ранее методов. Основная проблема прогнозирования процесса состоит в следующем: модель предполагает, что будущие значения с большей вероятностью будут похожи на последние значения временного ряда. С целью исключить циклические колебания, длина выбранного периода должна быть кратна средней длине цикла. Скользящие средние для выбранного периода, имеющего длину L, образуют последовательность средних значений, вычисленных для последовательностей длины L. Скользящие средние обозначаются символами MA(L).

Также часто используется метод экспоненциальных средних: он постоянно адаптируется за счёт использования новых значений временного ряда. Его формула выглядит следующим образом:

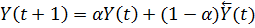
где  - предыдущий прогноз на период t, а  - постоянная сглаживания. Данная постоянная определяет взаимосвязь прогнозного значения текущего периода от прогнозных значений предыдущих периодов, причём данная взаимосвязь становиться слабее с течением времени. Чаще всего, параметр  тестируется итеративно, и в модель выбирается тот показатель, при котором точность прогноза наибольшая.

Данные классы моделей, несмотря на иногда предельное несоответствие исследуемым процессам всё же используют при прогнозировании, благодаря их простоте в качестве вспомогательных или трансформирующих. Для обеспечения большей точности рекомендуется использовать другие классы моделей.

Метод экспоненциального сглаживания является последовательностью экспоненциально взвешенных скользящих средних. При использовании данного метода некоторые данные не отбрасываются, а берутся с весами: часто встречаемые величины получают большие веса, чем более редко встречаемые. Сглаживание производится на основе уравнения, содержащего три компонента: текущее значение ряда, значение ряда, предшествующее текущему значению, и присвоенный вес .

Метод Хольта - это метод, представляющий собой усовершенствование метода экспоненциального сглаживания: сглаживаются тренд и уровень с разными параметрами, то есть получают двухпараметрическое экспоненциальное сглаживание:

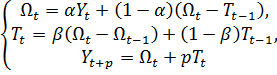
Первое уравнение данной системы сглаживает общий уровень ряда, второе - оценивает тренд, а третье уравнение задаёт прогноз на p шагов вперед.

Веса, с которыми берутся переменные в данной системе уравнений, определяются так же итеративно, как и в методе экспоненциального сглаживания. При  данный метод называется методом Брауна. Данный метод не описывает сезонные колебания.

Метод Винтерса - это трёхпараметрическое экспоненциальное сглаживание, которое старается учесть динамику сезонной компоненты временного ряда и задаётся следующей системой:

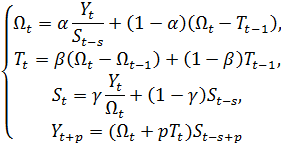
Первое уравнение данной системы исключает сезонную компоненту и учитывает её только в прогнозном уравнении.

Далее рассмотрим регрессионные методы прогнозирования. Дадим определение множественной регрессии. В общем случае, она задаётся уравнением вида

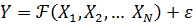
Множественная линейная регрессия задаётся уравнением вида

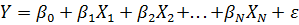
где  - коэффициенты регрессии, а  - независимая и нормально распределённая компонента ошибки.

Данные модели чаще всего решают методом наименьших квадратов, который был рассмотрен в разделе 2.1, либо методом наибольшего правдоподобия.

Отдельного внимания требуют модели Бокса-Дженкинса: AR(p), MA(q), ARMA(p,q), ARIMA (p,r,q), ARIMA (p,r,q)(P,R,Q), ARIMAX. Предполагается, что данные модели не имеют независимых переменных, то есть ищут взаимосвязи внутри самого временного ряда. Также есть расширения, которые позволяют включать независимые переменные.

Методы Бокса-Дженкинса задают только класс моделей, а не их чёткое построение, что делает данный метод гибким. После определения класса моделей, подгоняются параметры модели в зависимости от природы временного ряда, и на выходе получается оптимальная модель. Связь моделей в методе Бокса-Дженкинса можно определить следующим образом:

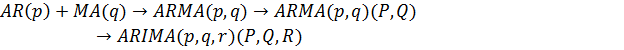
Рассмотрим авторегрессионную модель порядка p AR(p). Данная модель задаётся следующим уравнением:

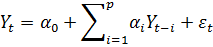
где  - зависимая переменная в момент времени t.  - оцениваемые параметры авторегрессии,  - ошибка модели. Чаще всего, поиск параметров авторегрессии производят с помощью системы уравнений Юла-Уолкера, основанной на автокорреляционной функции либо с помощью метода наименьших квадратов.

Модель со скользящим средним порядка q MA(q) в общем виде представлена уравнением:

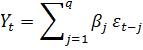
Белый шум считается моделью порядка - MA(0). Чаще всего, используют процесс скользящего среднего первого порядка MA(1).

Модель ARMA (p,q) объединяет модели авторегрессии порядка p и скользящего среднего порядка q. Уравнение модели имеет вид

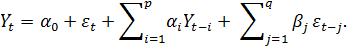
Данная модель иногда интерпретируется как модель множественной линейной регрессии, в которой предикторами являются значения временного ряда предыдущих периодов, а регрессионный остаток дан в виде скользящих средних белого шума. Данная модель имеет меньшее количество параметров по сравнению с составляющими его AR(p) и MA(q) процессами.

Модель ARIMA (p, d, q) - это интегрированная модель авторегрессии - скользящего среднего. Является расширением модели ARMA (p, q) для нестационарных рядов. Полагается, что нестационарный ряд можно привести к стационарному временному ряду путём взятия разности порядка d от исходного ряда динамики. Задаётся уравнением вида

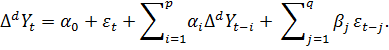
Простейшим примером данной модели является модель случайного блуждания. При  наблюдается модель ARMA(p, q).

Обобщённая модель авторегрессионной условной гетероскедастичности (GARCH) - семейство моделей, предназначенных для анализа финансовых временных рядов. Основной особенностью данного класса моделей является то, что условная дисперсия ряда зависит от предшествующих значений и их дисперсий. Процесс GARCH чаще всего используется для профессионального финансового моделирования, так как предпосылки, заложенные в модели, обеспечивают более реальные условия при прогнозировании цен и доходностей, чем другие формы. Используется как при инвестировании, так и при торговле финансовыми инструментами и хеджировании. Качество результатов, полученных с помощью данных моделей чаще всего оказывается выше из-за учёта кластеров волатильности временного ряда.

Рассмотрев основные принципы и понятия прогнозирования, его методы и модели, а также современные средства для выполнения данной работы, можно сделать промежуточное заключение.

Фундаментальный анализ с теоретической точки зрения основывается на гипотезе эффективности рынка, что не совсем соответствует реальности, так как в противном случае на рынке не существовало бы недооценённых или переоценённых активов. Применение фундаментального анализа на практике требует наличия доступа к информации, высокой квалификации и больших затрат времени, но при этом всё равно основывается на субъективной оценке аналитика. Из-за недостатков фундаментальный анализ чаще всего применяется для принятия решений с целью долгосрочного инвестирования. Эффективность применения фундаментального анализа отражена в ряде работ, например, «Оценка активов с использованием мультипликаторов» (Шрайнер, 2007). Его неэффективность также описана в большом списке работ, одна из которых, например, «Прогнозирование доходности на фондовом рынке» (Hjalmarsson, 2008).

Технический анализ, как и фундаментальный, имеет свои преимущества и недостатки, приведённые в различных работах. Например, среди трудов, рассматривающих технический анализ как эффективный, можно назвать «Profitable Technical Trading Rules for the Italian Stock market» (Metaghachi, 2003), «Эффективность использования технического анализа: доказательства, полученные на российском фондовом рынке» (Щербаков, 2010). Негативные отзывы о результатах применения данного типа анализа можно найти в работе «Применение технического анализа на современном российском фондовом рынке» (Бучко, 2011), «Энциклопедия торговых стратегий» (Кац, МакКормик, 2000) и многих других. Среди недостатков технического анализа можно назвать следующие: ограниченность используемой информации (цены и объёмы), вследствие чего не учитывается влияние связанных параметров, излишнее упрощение зависимостей динамики цен, низкий уровень адаптивности к влиянию рыночных факторов. Среди преимуществ использования технического анализа можно назвать его эффективность в краткосрочном и среднесрочном прогнозировании.

Чаще всего, для принятия решения используются и фундаментальный, и технический анализ.

Статистические методы представляются наилучшим вариантом для прогнозирования цен на акции, так как с помощью адекватной модели можно прогнозировать как на краткосрочный, так и на долгосрочный период. Также, при использовании статистических методов, одновременно применяются как принципы фундаментального анализа (при изучении достаточного количества данных акция должна стремиться к своей справедливой цене), так и, как было отмечено ранее, принципы технического анализа в более расширенном варианте.

3. Прогнозирование цен на акции на примере ОАО «Газпром»

В данной главе представлены результаты исследования по прогнозированию цен на обыкновенные акции ОАО «Газпром». Исследование представляет собой комплексный подход к моделированию и включает в себя как прогнозирование традиционными, так и математическими методами.

В основе данного исследования были использованы работы авторов из России и зарубежных стран в области финансов, анализа и прогнозирования на фондовом рынке, а также материалы статей периодических зданий, таких как «Finаnсiаl One», «Jоurnаl оf Finаnсiаl Есоnоmiсs», «РБК Dаily» и других, а также обзоры и прогнозы инвестиционных компаний. Кроме того, активно использовались ресурсы сети Интернет, такие как официальные сайты российских эмитентов и фондовых бирж, информационных агентств РБК, БКС, Сbоnds.ru и другие.

Данные. Основные данные для исследования представляют собой информацию о компании ОАО «Газпром». В ходе работы использовались данные финансовых отчётов компании, представленные на официальном сайте эмитента. Графики и котировки акций эмитента были собраны с официального сайта Московской Биржи (ММВБ). Данные консенсус-прогнозов предоставлены ООО «РосБизнесКонсалтинг». Также были использованы статистические данные ЦБ РФ.

В данной работе описаны основные методы прогнозирования цен на акции, их применимость и эффективность. Приведён практический результат использования некоторых моделей для оценки, анализа и прогнозирования курса акций ОАО «Газпром».

3.1 Оценка справедливой стоимости акций «Газпром»

Для оценки справедливой стоимости акций «Газпрома» используется фундаментальный анализ на основе DFC-модели (см. раздел 1.1). В ходе анализа эмитента была определена справедливая стоимость акций ПАО «Газпром» за период 2007-2020 гг.

Для расчета чаще всего применяется модель дисконтированных денежных потоков на основе двухпериодной DCF-модели свободных денежных потоков:

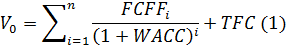
где FCFF - свободный денежный поток фирмы.

Рассмотрим основные предпосылки данной модели:

Прогнозный период имеет единую ставку дисконтирования. В пост-прогнозном периоде компания имеет устойчивый темп роста, сопоставимый с темпами роста экономики. В пост-прогнозном периоде ставка дисконтирования полагается равной целевому значению и предполагает оптимальность структуры капитала. Остаточная стоимость эмитента производится по модели Гордона, с приведением к моменту времени оценки стоимости компании. В данной работе для расчёта остаточного денежного потока (TCF, Terminal Cash Flow) формула (1) преобразуется следующим образом:

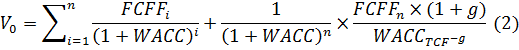
где  - справедливая стоимость компании,  - свободный денежный поток компании в i-ом периоде,  - свободный денежный поток компании в последнем периоде,  и  - ставки дисконтирования в прогнозном и постпрогнозном периодах, g - темпы роста свободных денежных потоков в постпрогнозном периоде, n - количество периодов наблюдения.

 Поскольку при расчете фактической справедливой стоимости компании за 2007-2015 гг. используется фактическая отчетность компании, а при оценке справедливой стоимости на 2016-2020 гг. - планируемые показатели ее деятельности, следует пересмотреть решение о постоянной ставке дисконтирования на всём периоде. Ставку дисконтирования WACC может быть получена на основе исторических данных для периода с 2006 по 2015 годы. Формула (1) модифицируется до следующего вида:

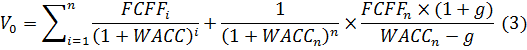
где  - ставка дисконтирования в i-ом периоде наблюдения,  - ставка дисконтирования в последнем периоде наблюдения.

Построение графика фактической справедливой цены предполагает ежеквартальный пересчет на основе полученных данных финансовой отчетности, а также аналитических прогнозов по компании и рынку в целом. Метод позволяет фиксировать значение WACC для каждого периода в прошлом. Исследование основывается на исторических данных за период с 31 декабря 2006 г. по 31 декабря 2015 г., в результате чего получается 37 точек наблюдения. В таблице 1 приведены основные этапы расчета с указанием необходимой для него информации.

Таблица 1 - Расчет справедливой стоимости акций Газпром, основные источники

Свободный денежный поток компании рассчитывается по формуле

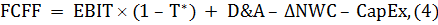
где EBIT -прибыль до выплаты процентов и налога на прибыль; T* - эффективная ставка налога на прибыль; D&A - износ и амортизация; ΔNWC - изменение оборотного капитала; CapEx - капитальные затраты.

При определении исходных данных для расчета свободного денежного потока на основе финансовой отчетности следует учесть три основных момента: стандарт финансовой отчетности, ее периодичность и валюту. Газпром предоставляет финансовую отчётность по стандарту РСБУ раз в квартал, валютой отчётности является рубль (RUB).

Эффективная ставка налога на прибыль (Т*) рассчитывается как отношение фактически выплаченных денежных средств в виде налога на прибыль (Tax) к операционной прибыли. Изменение чистого оборотного капитала (ΔNWC) рассчитывается как разность чистого оборотного капитала (NWC) текущего и предыдущего периода. Показатель NWCi за i-тый период наблюдения рассчитывается по формуле (2) как сумма по трем статьям:

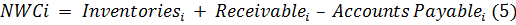
Другими словами, увеличение запасов и дебиторской задолженности уменьшает денежный поток, а увеличение кредиторской задолженности, наоборот, увеличивает.

3.1.1 Расчёт коэффициентов модели

Дисконт-фактор. Риски учитываются посредством ставки дисконтирования WACC по формуле:

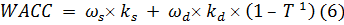
где  - стоимость собственного капитала, %;  - доля собственного капитала, %;  - стоимость заемного капитала, %;  - доля заемного капитала, %; T - ставка налога на прибыль, %.

Расчет WACC определяется горизонтом оценки. Учитывая специфику данной конкретной задачи, его следует производить ежегодно для каждой точки наблюдения, поэтому все элементы WACC будут рассчитываться в соответствии с рассматриваемым периодом. В этом случае в качестве ставки налога может быть применена эффективная ставка.

Расчет стоимости собственного капитала. Оценка требуемой доходности инвестирования в акционерный капитал компаний производится с использованием модели ценообразования финансовых активов (CAPM). Расчет безрисковой ставки осуществлён на основании данных о среднесрочных ставках доходностей по рынку со сроком обращения до пяти лет и представляет собой медианное значение доходностей за период. Бета-коэффициент представляет собой отношение ковариации доходности акций и рынка к дисперсии доходности рынка. В данной работе бета-коэффициент рассчитан на основе исторических данных при оценке следующей регрессионной модели:

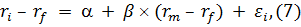
где - вектор доходностей i-го актива; - безрисковая ставка; - рыночная доходность; β - бета-коэффициент; a - вектор свободных членов регрессионной модели; ε - вектор ошибок регрессионной модели.

При оценке стоимости акционерного капитала в качестве бета-коэффициента были использованы значения отраслевых бета-коэффициентов (РБК). Произведена корректировка отраслевого бета-коэффициента на значение финансового рычага для нивелирования расхождений с отраслью.

Рычаговый бета-коэффициент определяется по формуле Хамады (Хамада, 1972):

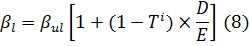
где  - рыночный риск предприятия; - производственный риск предприятия; Т - ставка налога на прибыль; D / E - уровень финансового рычага, измеряемого отношением рыночной стоимости заемного капитала D к рыночной стоимости акционерного капитала E.

Рыночная премия за риск (Market Risk Premium, MRP) представляет собой ожидаемую доходность без учёта безрисковых финансовых инструментов. MRP необходима инвесторам для принятия решения об инвестировании, что иллюстрируется на диаграмме ниже (рис. 3).

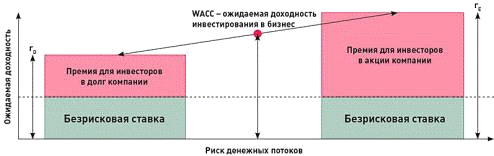
Рис. 3 - Риск денежный потоков

В зависимости от конкретной задачи MRP рассчитывается исходя из разных предпосылок. При рассмотрении разных временных интервалов рыночная премия за риск будет различной, поскольку фактически требуемая премия за риск отражает ожидания инвесторов относительно перспектив деятельности компании. Как следствие MRP является прогнозным значением, зависящим от макроэкономических факторов, горизонта инвестирования, типа ценных бумаг и других параметров.

Значение MRP по рынку варьируется от 3,3% до 6,5%. В данной работе требуемая рыночная премия за риск при инвестировании в акции российских компаний принята равной 5,4% на основании субъективной оценки автора работы. Безрычаговый бета-коэффициент для нефте- и газодобывающей отрасли равен 0,71 (Дармодан, 2016).

Расчет стоимости заемного капитала. В связи с отсутствием единого подхода к оценке стоимости заемного капитала, необходимо рассмотреть два типа: кредитование и облигационный заем.

Самый простой метод оценки стоимости заемного капитала основан на использовании доходности к погашению облигаций, если облигационный выпуск торгуется на организованном фондовом рынке. В данной работе в качестве стоимости заемного капитала было принято медианное значение YTM.

Стоит отметить, что данный способ оценки не универсален, так как цели выпуска облигаций могут быть нерегулярными, например, при выпуске облигаций для финансирования инвестиционного проекта.

Кредитование является второй формой привлечения финансирования в долгосрочном периоде. Для анализа финансирования компании используется отчетность, которая, однако, не всегда отражает реальную структуру капитала. В качестве альтернативы можно использовать рейтинги компаний-заемщиков. С каждым значением рейтинга соотносится соответствующая премия к бенчмарку, в качестве которого может выступать ставка доходности по безрисковым инструментам.

Расчет весов элементов капитала. В работе был использован комбинированный подход, в котором стоимость акционерного капитала оценена как рыночная капитализация компании, а стоимость заемных средств - по балансовым статьям. Расчет рыночной капитализации осуществляется по следующей формуле:

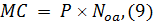
где MC - рыночная капитализация компании (Market Capitalization); P - расчетная рыночная цена одной обыкновенной акции компании;  - количество обыкновенных акций компании. Расчетная рыночная цена P определяется как медианное значение ряда цен акции за анализируемый период (год), а количество обыкновенных акций - согласно открытой информации, опубликованной на сайте эмитента.

Расчет балансовой стоимости долга компании. Долг компании представляет собой сумму краткосрочных и долгосрочных заимствований. При оценке стоимости долга часто используется понятие «чистый долг». Предполагается, что часть задолженности может быть погашена с помощью денежных средств, поэтому величина чистого долга является более наглядным показателем по сравнению с общим долгом компании. Чистый долг рассчитывается по формуле:

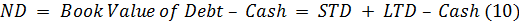
Результаты расчета средневзвешенной стоимости капитала (WACC). Расчет значений WACC осуществляется по формуле согласно вычисленным составляющим конструкции по каждому периоду

. Ввиду того что в работе оценка стоимости компании осуществляется на ежеквартальной основе, возникает необходимость пересчета годовой ставки дисконтирования в квартальную ставку. Он осуществляется на основе формулы сложных процентов:

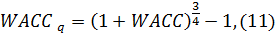
Пересчет годовой ставки дисконтирования в квартальную ставку предполагает допущение о том, что средневзвешенная стоимость капитала меняется дискретно от года к году и остается постоянной в рамках календарного года.

Прогнозирование денежных потоков. В рамках данной работы прогнозные значения свободных денежных потоков рассчитаны на основании данных, опубликованных в информационно-аналитической базе (Thomson One). Формула расчета прогнозных значений FCFF аналогична формуле для вычисления фактических значений FCFF, поскольку их расчетная база полностью совпадает. Как отмечалось выше, в рамках настоящего исследования использован также пятилетний временной горизонт.

3.1.2 Расчет справедливой стоимости акции

Определение справедливой стоимости одной обыкновенной акции компании является завершающим этапом расчета. Он производится по формуле:

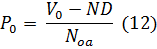
где - справедливая стоимость акции;  - стоимость фирмы; ND - чистый долг; - количество обыкновенных акций.

Консенсус-прогноз - один из приемов прогнозирования, основанный на усреднении прогнозов различных аналитических агентств. Усреднение осуществляется с учетом весовых коэффициентов в зависимости от точности прогноза. Консенсус-прогноз меняется во времени в зависимости от макроэкономической ситуации и новостного фона. Ниже приведён график зависимости рыночной цены акций ПАО «Газпром» от времени и соответствующие консенсус-прогнозы (рис. 4).

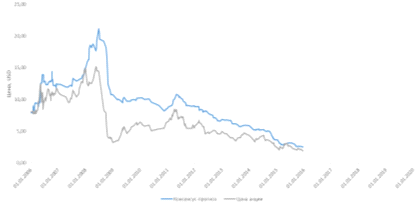
Рис. 4 - Консенсус-прогноз и цена акций «Газпрома»

Консенсус-прогноз сигнализирует о недооценке компании на протяжении продолжительного периода, на основании чего инвестор может принять решение о покупке акций компании. Также стоит отметить, что с течением времени цена акций и консенсус-прогнозы стремятся друг к другу. Далее представлены тот же график с наложением кривых справедливых цен акций компаний (рис. 5).

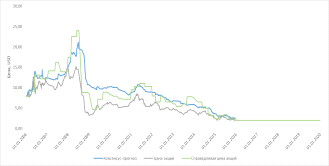
Рис. 5 - Справедливая цена акций и консенсус-прогноз для ПАО «Газпром»

На графике (рис. 5) видно, что кривая справедливых цен ПАО «Газпром», рыночные цены и консенсус-прогноз почти сходятся к концу периода. Графический анализ динамики справедливых цен данных акций позволяет классифицировать анализируемую компанию как справедливо оценённую, и представляющую интерес для получения спекулятивной прибыли, но не для долгосрочного инвестирования.

3.2 Прогнозирование курса акций с помощью временных рядов

Данная глава описывает прогнозирование курса акций ПАО «Газпром» как временного ряда.

В общем виде, процесс прогнозирования временного ряда представляет собой следующую последовательность:

Визуализация ряда и его паттернов с акцентирование внимания на наблюдениях, необычных или экстремальных для данного ряда.

Проведение теста на стационарность ряда, при необходимости преобразование ряда к стационарному.

Построение графиков автокорреляционных функций ACF/PACF и определение подходящих моделей.

Применение модели к тестовой и тренировочной выборкам, оптимизация параметров модели с помощью информационного критерия Акаике, определение средних абсолютных ошибок моделей (MAPE).

В данной работе помимо анализа динамики курса финансового инструмента также представлено исследование риска инвестирования в выбранный актив.

3.2.1 Визуализация данных

Перед построением модели, необходимо проанализировать тенденции временного ряда, так как данные могут содержать тенденции, сезонность или случайное поведение. Исследование данных выполнено в RStudio. На рис. 6 представлена визуализация данных, представляющая собой график акций компании ПАО «Газпром», построенный по всем доступным данным (2006-2016 годы).

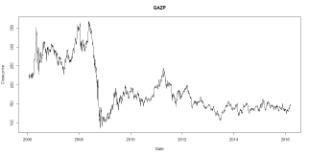
Рис. 6 - Визуализация графика ряда за период 2006-2016 гг.

На графике видны основные тенденции, отразившиеся на курсе акций за представленный период: кризисы 2008 и 2010 года, а также то, как новости и отчёты компаний-эмитентов влияют на курс их акций.

Приведена декомпозиция временного ряда, результат представлен на графике (рис. 7). Выделен тренд, сезонная и случайная компоненты.

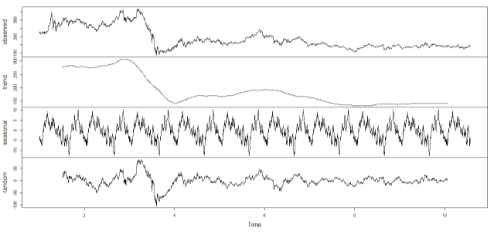
Рис. 7 - Декомпозиция временного ряда

Очевидно, что данные имеют сезонность, причём эта сезонность годовая и имеет четыре основных периода: в начале календарного года до конца марта, в период с марта по август, сентябрь и октябрь, и оставшийся период - ноябрь-декабрь. Такая закономерность была вполне предсказуема, так как помимо того, что нефтяная и газовая промышленности имеют сезонность, так и отчётность эмитентов предоставляется в один и тот же срок. Случайная компонента достаточно стабильна после кризиса 2008 года. Стоит отметить, что при прогнозировании котировок случайная компонента в большей мере обуславливается внешними факторами, которые при достаточном объёме информации также могут быть введены в модель. К сожалению, набор данных, способный описать все изменения ряда слишком велик.

.2.2 Стационарность ряда

После определения закономерностей, тенденций, циклов и сезонных колебаний, производится проверка на стационарность ряда. Чаще всего, для этого используется тест Дики - Фуллера. Стационарность временного ряда является необходимым условием для построения его модели. Если предпосылки стационарности нарушаются, то в первую очередь производится его приведение к стационарному временному ряду, и только затем производится его прогнозирование с использованием стохастических моделей. Есть несколько способов приведения ряда к стационарности, например, вычитание тренда, дифференцирование и другие. Данная работа в большей мере опиралась на дифференцирование временного ряда.

Нулевой гипотезой в тесте считается существование единичного корня. Единичным корнем принимается один из корней характеристического полинома, находящийся внутри окружности с радиусом, равным единице. В качестве альтернативной гипотезы предполагается стационарность ряда. В рассматриваемом случае, значимость составляет 0.21 и тест Дики-Фуллера показывает нестационарность ряда.

Для исследователя прогнозирование курса акций может представлять интерес скорее теоретический и не имеющий ничего общего с практикой. Со стороны инвестора, наоборот, есть исключительно практический интерес. Однако, для трейдинга существует единственный важный параметр: доходность акции. Таким образом, для практической реализации необходимо предсказывать, куда пойдёт цена акции относительно момента покупки.

Помимо практической значимости, обоснованием использования именно ряда доходностей акции является то, что он чаще всего стационарен и автокорреляция слабая или отсутствует. Также, данный ряд чаще всего обладает более стабильным средним и дисперсией. Иногда используется логарифм доходностей. В работе был произведён расчёт значений ряда доходностей (первые разности ряда цен). Результаты отражены на графике (рис. 8).

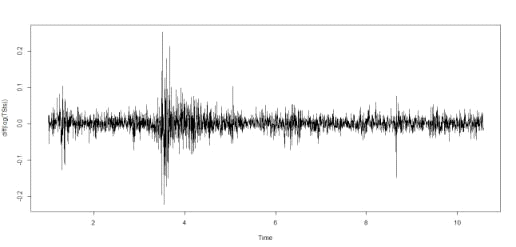
Рис. 8 - Стационарный ряд доходностей акций ПАО «Газпром»

Тест Дики-Фуллера и тест Филлипса-Перрона для ряда доходностей отвергает нулевую гипотезу на уровне 99%. Таким образом, ряд доходностей является стационарным. Ту же гипотезу подтверждает тест KPSS. Это можно интерпретировать как то, что курс акций ПАО «Газпром» является интегрированным первого порядка. Были построены графики автокорреляционных функции ACF и PACF (рис. 9).

Рис. 9 - График автокорреляционной и частной автокорреляционной функций

С помощью графиков было установлено, что ряд дневных доходностей не автокоррелирован, то есть параметры p и q в модели скорее всего равны нулю. Оценив параметры, действительно получаем результат, что лучше всего данные котировок акции GAZP описываются с помощью модели ARIMA (0,1,0), так как критерий Акаике является для этой модели наилучшим.

3.2.3 Описание моделей

Далее представлены модели, тестируемые в данной работе. Модели, выбранные для сравнения, имеют структуру от самой примитивной до более сложных. Иногда один из самых простых методов может оказаться лучшим доступным методом прогнозирования. Но во многих случаях, эти методы будут служить в качестве ориентиров, а не в качестве модели. То есть, независимо от разрабатываемых методов прогнозирования, сравнение будет происходить с данными методами для гарантии того, что новый метод лучше, чем эти простые альтернативы.

Модель среднего. В данной модели прогнозы всех будущих значений равны среднему значению исторических данных. Уравнение данной модели описывается следующими формулами:

Для периода 60 дней: ;

Для периода 120 дней: ;

Для периода 240 дней: .

Наивный метод прогнозирования. Этот метод подходит только для временных рядов. Все прогнозные значения устанавливаются как значение последнего наблюдения. При всех недостатках, этот метод хорошо работает для многих экономических и финансовых временных рядов.

Уравнение данной модели описывается следующими формулами:

Для периода 60 дней: ;

Для периода 120 дней: ;

Для периода 240 дней:

Наивный метод прогнозирования с сезонной компонентой. Подобный метод полезен для сезонных данных c выраженными флуктуациями. В этом случае каждое прогнозное значение равно последнему наблюдаемому значению из того же сезона года.

Экспоненциальное сглаживание (ETS). Нелинейные модели экспоненциального сглаживания не имеют эквивалентных аналогов в модели ARIMA. В то же время линейные модели экспоненциального сглаживания являются частными случаями моделей ARIMA. Также, большое количество моделей ARIMA не имеют аналогов в моделях экспоненциального сглаживания. В частности, каждая модель ETS является нестационарной, тогда как модели ARIMA могут быть стационарными.

Модели ETS с сезонностью или без затухающего тренда имеют два единичных корня (то есть они нуждаются в двойном дифференцировании, чтобы сделать их стационарными). Все остальные модели ETS имеют один единичный корень (они нуждаются во взятии первых разностей).

Метод Хольта. Модель Хольта была описана ранее в разделе 2.3. Стоит отметить, что в случае, когда временные ряды могут быть описаны с использованием аддитивной модели с монотонным трендом и без сезонности, экспоненциальное сглаживание Хольта применяется для краткосрочных прогнозов.

Экспоненциальное сглаживание Хольта оценивает уровень и наклон в текущий момент времени. Сглаживание управляется двумя параметрами: альфа, для оценки уровня в текущий момент времени, а также бета для оценки наклона тренда на текущий момент времени. Как и в случае простого экспоненциального сглаживания, параметры модели имеют значения между 0 и 1, а значения, близкие к 0 означают, что последние значения ряда имеют меньший вес. Уравнение данной модели описывается следующими параметрами:

Для периода 60 дней: ;

Для периода 120 дней: ;

Для периода 240 дней: .

Метод Хольта-Винтерса. Используется для временных рядов, которые могут быть описаны с использованием аддитивной модели с увеличением или уменьшением тренда и сезонностью. Применим для краткосрочных прогнозов.

Экспоненциальное сглаживание Хольта-Винтерса оценивает уровень, наклон и сезонную компоненту в текущий момент времени. Сглаживание управляется тремя параметрами: альфа, бета и гамма, для оценки уровня наклона, компонент тренда и сезонной составляющей. Параметры альфа, бета и гамма все имеют значения между 0 и 1, а значения, близкие к 0 означает, что относительно небольшой вес имеют последние наблюдения. Уравнение данной модели описывается следующими параметрами:

Для периода 60 дней: ;

Для периода 120 дней: ;

Для периода 240 дней: .. В данной работе представлена модель ARIMA, имеющая лучшее значение информационного критерия Акаике. Остальные модели не представлены, так как сравнение моделей производилось в программном циклическом режиме. В итоге, лучшей моделью по итогам сравнения оказалась модель ARIMA(0,1,0) с блужданием. Следует отметить, что данные параметры модели предполагают, что в долгосрочной перспективе данная модель сходится к прямой линии.

Нейронная сеть. Нейронную сеть можно рассматривать как сеть "нейронов", организованных в слоях. Входы образуют нижний слой, а выходы сети формируют верхний слой. Также существуют скрытые слои, содержащие "скрытые нейроны".

Самые простые сети не содержат скрытых слоев и эквивалентны линейной регрессии. После добавления промежуточного слоя со скрытыми нейронами, нейронная сеть становится нелинейной. Это также известно, как многослойная однонаправленная сеть, где каждый слой сети принимает входные сигналы от предыдущих слоев. Входы каждого узла объединяются с использованием взвешенной линейной комбинации. Конечный результат модифицируется нелинейной функцией.

Количество скрытых слоев, а также количество узлов в каждом скрытом слое, должны быть определены заранее с помощью перекрестной проверки. В данной работе представлена лучшая модель, описываемая следующими параметрами:

Для периода 60 дней: ;

Для периода 120 дней: ;

Для периода 240 дней: ;

где p - количество лагов, использованных в качестве входов модели, k - количество узлов в скрытом слое.

Тригонометрическое экспоненциальное сглаживание пространства состояний модели с преобразованием Бокса-Кокса, ARMA ошибок, тренда и сезонности (TBATS). Эти модели требуют оценки сезонных значений, что, как ожидается, должно значительно уменьшать число параметров, требуемых по сравнению с данным типом моделей. Применение тригонометрических функций также позволяет моделировать нецелые сезонные колебания. Модель описывается следующими параметрами:

Для периода 60 дней: ;

Для периода 120 дней: ;

Для периода 240 дней: ;

где L - коэффициент трансформации Бокса-Кокса.

3.3 Сравнение моделей

В данном разделе описывается сравнение моделей при прогнозировании в краткосрочном периоде. Шаг прогнозирования выбран как один день. Для прогнозирования были выбраны три периода прогнозирования - 60, 120 и 240 торговых дней.

В таблице 2 представлены результаты сравнения ошибки моделей MAPE для каждого из периодов прогнозирования.

Таблица 2 - Результаты сравнения моделей

Таким образом, на тестируемых данных наименьшую ошибку MAPE в краткосрочном периоде даёт модель ARIMA, наивный метод с сезонной компонентой показывает лучший результат в среднесрочной перспективе, а нейронная сеть в долгосрочном периоде. Это объяснимо тем, что в обучающей выборке присутствуют стрессовые значения, что искажает значения сложных моделей, но при этом не влияет на более простые модели.

Далее проведено равнение данных моделей на более коротком историческом интервале для валидации полученных результатов. По последовательной выборке произведём построение моделей. Результаты представлены в таблице 3.

акция анализ газпром прогнозирование

Таблица 3 - Результаты сравнения моделей на интервале без стрессовых значений

Таким образом, на данных без стрессовых значений нейронная сеть лучше по всем показателям. Графики, представленные на рис. 10 отражают адекватность модели, построенной с помощью нейронной сети.

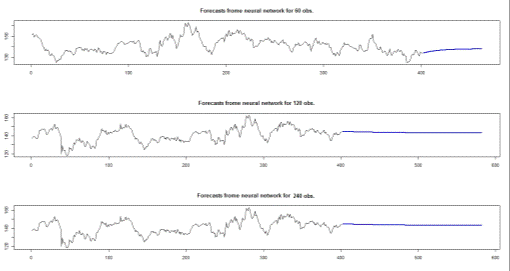
Рис. 10 - Прогноз модели, построенной с помощью нейронной сети

Таким образом, были протестированы модели временных рядов и было получено относительно небольшое значение MAPE как для краткосрочного, так и для долгосрочного периода. Также, очевидно, что имеется выраженная тенденция к снижению цены и её дальнейшей стабилизации на уровне около 140 рублей в долгосрочной перспективе, 153 рубля в краткосрочной перспективе.

3.4 Оценка рисков

Риск является неотъемлемой частью инвестиций в финансовые инструменты, что делает его важным критерием при прогнозировании. Статистически риск акции измеряется как отклонение доходности акций от её среднего значения или от рынка.

Для количественной оценки риска существуют различные концепции, разработанные в течение последних 50 лет. В целом существуют две точки зрения на риск. Первая подчёркивает важность фундаментальных показателей компании и её менеджмента. Второй подход в большей мере используется в научных кругах и измеряет риск следующими показателями:

Оценка риска, основанная на измерении колебаний доходности акций от его среднего значения. Чем выше дисперсия, тем рискованнее акция.

Коэффициент бета измеряет рискованность акций по сравнению с рынком или индексом. Акции, имеющие коэффициент бета больше единицы являются более рискованным, чем индекс.

Значение риска (Value-at-Risk, VAR), основанное на распределении доходностей и использующее вероятностный подход к оценке риска.

Оценка риска, основанная на дисперсии. Впервые Г. Марковиц (Markowitz, 1952) ввел понятие дисперсии в качестве меры риска. Риск определяется как вероятность того, что фактическая доходность может отличаться от ожидаемой доходности. Это означает, что акции, имеющие более высокую дисперсию несут более высокий риск. Дисперсия в качестве меры риска отражает общее отношение рынка к неопределенности. Более высокая флуктуация делает прогноз цен на акции более трудным, увеличивая неопределенность и, следовательно, риск.

Бета или CAPM Бета как мера риска была введена Уильямом Шарпом, который получил Нобелевскую премию за разработку САРМ-модели определения стоимости финансовых активов. По существу, Шарп привёл аргументы Марковица к логическому завершению. В своих работах он утверждает, что только те риски, которые не могут быть диверсифицированы, должны быть вознаграждены. В то время как дисперсия измеряет отклонение доходности от среднего значения, бета измеряет совместное движение ценной бумаги по отношению к рынку, что в целом является индексом, как индекс РТС или S&P500. Акция, которая движется в тандеме с рынком имеет бета 1. Акция, которая имеет большее отклонение, чем в среднем по рынку имеет бета больше единицы и наоборот. Акция будет иметь более высокий коэффициент бета только если она несёт дополнительный риск для рыночного портфеля. Коэффициент бета рассчитывается как ковариация акции с рынком в отношении к дисперсии рынка:

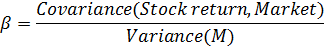
Где Stock return является доходностью акции, а Market представляет собой доходность рынка (в данном случае можно использовать индекс РТС).

Бета на сегодняшний день является наиболее широко используемым показателем риска, связанного с акциями. Однако недавние исследования показывают, что бета не может объяснить все риски, связанные с финансовым инструментом. На самом деле, иногда бета слабо коррелирована с риском (Fama, French, 1992). Эти исследования также показывают, что САРМ, который использует бета как меру риска, занижает показатели доходности акции компаний с низким бета и завышает доходности акций с высокими бета. Расчёт коэффициента бета был приведён ранее в разделе 3.2.

Значение риска (VAR) представляет собой последнюю тенденцию при измерении риска. VAR квантифицирует наихудший сценарий на данный период времени и уровень доверия. Основное различие между дисперсией и VAR является то, что в то время как дисперсия не делает различий между увеличением или снижением в цене, VAR оценивает только снижение цены. Для VAR существуют три ключевых элемента: максимальный уровень потерь, временной горизонт и уровень доверия.

Существуют три различных метода расчета VAR.

Исторический метод моделирования. В этом методе доходности ценной бумаги располагаются в порядке возрастания, и VAR на 95% уровне достоверности будет значение доходности на пятом процентиле.

Метод ковариации. Этот метод предполагает нормальное распределение доходности акций и вычисляет VAR на основе среднего значения и стандартного отклонения. Такой подход становится сложным, если количество активов в портфеле возрастает, поскольку данный метод также учитывает ковариации между динамикой цен различных активов.

Метод Монте-Карло. Отличие от исторического метода состоит в том, что данные доходностей генерируются случайным образом.

Рассмотрим оценку риска VAR для доходностей акций компании Газпром. Воспользуемся историческим методом оценки на 95% уровне доверия (рис. 11).

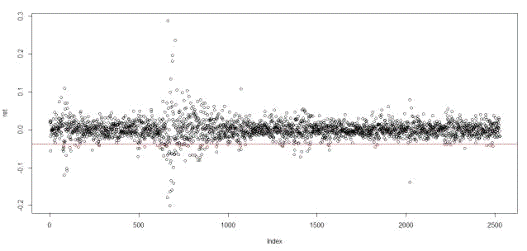
Рис. 11 - Исторический метод расчёта VAR

Проведя тест Кулика, получаем, что реальное количество пробитий пятипроцентного квантиля составляет 6,31%. Опыт показывает, что вероятность возникновения ситуации, приводящей к большим потерям на сравнительно устойчивом рынке, довольно мала. Ориентация на такие ситуации при текущем управлении рисками приведет к неоправданному сокращению объемов операций. Поэтому при решении задач текущего управления рисками следует ориентироваться на нестрессовые динамические потери. Крупные катастрофические потери при этом целесообразно рассматривать отдельно в рамках стресс-тестинга.

Для получения нестрессовой оценки рыночного риска, имеющей практическую ценность, из рассмотрения имеет смысл исключить небольшую долю (обычно 5% или 1%) самых неблагоприятных случаев, то есть сузить интервал возможных значений случайной величины. Тогда оценкой риска будут убытки, которые возникнут в самом неблагоприятном из оставшихся 95% или 99% случаев. Воспользуемся динамической переоценкой VAR на 95% уровне доверия (рис. 12). В данной работе представлен лучший из полученных вариантов, основанный на моделях ARMA(1,1) и GARCH(1,1). Тест Кулика показывает реальную долю пробитий, равную 2,5%.

Рис. 12 - Кривая VAR при моделировании ~ARMA(1,1) + GARCH(1,1) с динамическим пересчётом (шаг прогноза 1 день)

Данная модель показала самые точные и адекватные варианты оценки риска в силу того, что распределение ряда доходностей имеет тонкие хвосты по сравнению с нормальным распределением. В финансах толстые хвосты распределения подразумевают дополнительный риск. При оценке VAR очень важно рассматривать график распределения ряда доходностей. При нормальном распределении вероятность получения отрицательной доходности меньше, чем 0,0001%, но практика показывает, что обычно это число гораздо больше. События, негативно влияющие на цены акций (например, нефтяной шок, банкротство корпорации, резкое изменение политической ситуации) математически не стабильны. Примеры включают в себя события чёрного понедельника в 1987, пузырь дот-комов, кризис 2000-х годов.

Заключение

В данной работе были рассмотрены основные подходы к оценке стоимости акций на фондовом рынке и методы их прогнозирования. На основе полученных данных, был представлен прогноз цены на акции ПАО «Газпром», описываемый наиболее эффективной моделью. Также было определено, что привлекательность этого финансового инструмента является низкой и не соответствует общественному восприятию.

Для решения поставленной цели, а именно предсказания будущих цен на акции ПАО «Газпром», были выполнены следующие задачи:

рассмотрены основные подходы к оценке и прогнозированию цен финансовых инструментов, как традиционные, включающие в себя фундаментальный и технический анализ, так и математические методы моделирования цен, представленные статистическими и эконометрическими моделями, моделями временных рядов и нейросетевым моделированием;

оценена трудоемкость, эффективность, достоинства и недостатки исследуемых методов, а также их применимость к акциям ПАО «Газпром»;

произведена оценка методов для прогнозирования цены финансового инструмента и проведена эмпирическая апробация;

построен ретроспективный прогноз и проанализированы полученные результаты.

Результатом работы стал вывод о том, что в данный момент компания ПАО «Газпром» оценена справедливо, откуда следует подтверждённое статистическими моделями заключение о том, что её акции не представляют интереса для долгосрочного инвестирования. Также был сделан вывод о том, что и в краткосрочной перспективе акции компании будут демонстрировать достаточно низкую доходность.

На практике оказалось, что ни один метод не гарантирует абсолютной точности прогноза вследствие сложности системы: на цены акций влияют макроэкономические и отраслевые факторы, основные показатели финансового состояния компании, ожидания инвесторов, структура капитала, количество и качество игроков на рынке.

Применение фундаментального анализа на практике требует наличия доступа к информации, высокой квалификации и больших затрат времени, но при этом всё равно основывается на субъективной оценке аналитика.

Технический анализ, как и фундаментальный, имеет свои преимущества и недостатки. Среди недостатков технического анализа можно назвать следующие: ограниченность используемой информации (цены и объёмы, усечённые исторические данные), вследствие чего не учитывается влияние связанных параметров; излишнее упрощение зависимостей динамики цен; низкую адаптивность к влиянию рыночных факторов. Среди преимуществ использования технического анализа можно назвать его эффективность при краткосрочном и среднесрочном прогнозировании.

Эффективность применения математических и нейросетевых моделей также имеет свои ограничения. Математические модели сложны для расчётов, но при наличии навыков программирования это не представляет проблемы. Статистические методы показывают лучшие результаты при прогнозировании цен на акции ПАО «Газпром» (в частности, модель нейронных сетей).

Для дальнейшего исследования рекомендуется рассмотреть акции компании в более краткосрочной перспективе (торговля intra-day) для получения спекулятивного дохода. Также следует рассмотреть акции компании ПАО «Газпром» для диверсификации портфеля акций.

Литература

1.      Айвазян С.А. Эконометрика. М.: Маркет ДС, 2010.

.        Бокс Дж., Дженкинс Г.М. Анализ временных рядов, прогноз и управление. М.: Мир, 1974.

.        Бучко Ю.В. Оптимизация алгоритмических торговых систем фондового рынка. М.: Бизнес Элайнмент, 2011.

.        Леоненков А. Нечеткое моделирование в среде MATLAB и fuzzyTECH. СПб: БХВ-Петербург, 2005.

.        Тихонов Э.Е. Прогнозирование в условиях рынка. Невинномысск, 2006.

.        Большой экономический словарь / под ред. А. Н. Азриляна. - 7-е изд., доп. - М. : Инт новой экономики, 2007.

.        Грешилов А. А., Стакун В. А., Стакун А. А. Математические методы построения прогнозов. М., 2000.

8.      Московская межбанковская валютная биржа ММВБ. [Электронный ресурс]; - Режим доступа: <http://moex.ru/> (Дата обращения: 12.04.2016)

.        Мерфи Джон Дж. Межрыночный анализ. Принципы взаимодействия финансовых рынков. М.: «Альпина Паблишер», 2012.

.        Мэрфи Джон Дж. Технический анализ фьючерсных рынков. Теория и практика - М.: «Альпина Паблишер», 2011.

.        Невейкин, В.П. Скрытые проблемы методологии фундаментального анализа для оценки истинной стоимости акций / В.П. Невейкин // Финансы и кредит. - 2008. - № 41.

.        Нормативные системы в прогнозировании развития предпринимательского сектора экономики / Л.И. Муратова [и др.] // Управление экономическими системами. 2009, №20.

.        Официальный сайт Газпром. [Электронный ресурс]; - Режим доступа: <http://www.gazprom.ru/> (Дата обращения: 12.04.2016)

.        РБК. [Электронный ресурс]; - Режим доступа: <http://www.rbc.ru/> (Дата обращения: 12.04.2016)

.        РБК Quotes. [Электронный ресурс]; - Режим доступа: <http://www.quote.rbc.ru/> (Дата обращения: 12.04.2016)

.        Центробанк РФ. [Электронный ресурс]; - Режим доступа: <http://cbr.ru/> (Дата обращения: 12.04.2016)

.        Щербаков В. Эффективность использования технического анализа: доказательства на российском фондовом рынке // Экономика и менеджмент. 2010. № 4.

.        Cbonds. [Электронный ресурс]; - Режим доступа: <http://cbonds.ru/> (Дата обращения: 12.04.2016)

19.    Draper N., Smith H. Applied regression analysis. New York: Wiley In Press. 1981

.        Graham B., Dodd D. Security Analysis. The Classic 1934 Edition. McGraw-Hill Companies, 1996

.        Fama E., French K. The Cross-Section of Expected Stock Returns. The Journal of Finance, Volume 47, Issue 2 (Jun., 1992).

.        Hamada R.S. «The effect of the firm’s capital structure on the systematic risk of common stocks». The Journal of Finance, 1972. Vol. 27, No. 2, pp. 435-452.

.        Hank J., Reitsch A. Business Forecasting. Boston: Prentice Hall Press. 2003

.        Hjalmarsson E. Predicting Global Stock Returns // Board of Governors of the Federal Reserve System. International Finance Discussion Papers. 2008.

.        Katz J.O. Encyclopedia of trading strategies. - M: Alpina publisher, 2000

.        Markowitz H. Portfolio Selection. The Journal of Finance, Vol. 7, No. 1. (Mar., 1952), p. 77-91.

.        Metaghachi D., Chang C. Profitable Technical Trading Rules for the Italian Stock market. 2003;

.        Murphy, John J. Technical analysis of the futures markets. 1999.

.        Park C., Irwin S. The Profitability of Technical Analysis [Электронный ресурс]; Режим доступа: <http://citeseerx.ist.psu.edu> (Дата обращения: 12.04.2016)

.        Prajakta S.K. Time series Forecasting using Holt-Winters Exponential Smoothing. Kanwal Rekhi. School of Information Technology Journal. No 13. 2004.

.        Roberts, H.V. (1959) ‘Stock-market “patterns” and financial analysis: Methodological suggestions’, The Journal of Finance, 14(1), p. 1. doi: 10.2307/2976094.

.        Schreiner A. Equity Valuation Using Multiples: An Empirical Investigation. 2007.

.        Thomson One. [Электронный ресурс]; - Режим доступа: <http://thompsonone.com/> (Дата обращения: 12.04.2016)

34.    Turner T. A Beginner’s Guide to Day Trading Online. Adams Media, 2nd edition, 2007.

.        Zhu J., Hong J., Hughes J.G. Using Markov Chains for Link Prediction in Adaptive Web Sites. UK, London: 1st International Conference on Computing in an Imperfect World. 2002.

Приложение 1

Основные характеристики моделей