Прогноз неравномерности вращения Земли для спутниковых навигационных систем
Содержание
Аннотация
Введение
I. Литературный обзор
1.1 Неравномерность вращения Земли
1.1.1 Астрономические данные
1.1.2 Оптические наблюдения XYII-XX веков
1.1.3 Античные наблюдения
1.1.4 Палеонтологические данные
1.1.5 Движение полюсов Земли
1.1.6 Природа периодических колебаний Земли
1.2 Методы спектрального анализа
1.2.1 Фурье-анализ
1.2.2 Метод сингулярного спектрального анализа
II. Обработка данных неравномерности вращения Земли
III. Выводы
Список литературы
Аннотация
В данной работе был проведен спектральный анализ и прогноз
данных неравномерности вращения Земли в период с января 2004 по декабрь 2007
г., с помощью компьютерной программы Caterpillars SSA 3.3 по обработке данных
методом сингулярного спектрального анализа. Работа состоит из введения, трех
разделов (литературного обзора на 18 страницах, практической части на 6
страницах). В написании работы было использовано 10 источников литературы.
В литературном обзоре рассмотрены вопросы, связанные с
неравномерностью вращения Земли, движению полюсов Земли, природе периодических
колебаний Земли, методами спектрального анализа.
В практической части разработана методика прогнозирования
данных неравномерности вращения Земли, сделаны прогнозы на 1, 11 и 21 числа
каждого месяца 2007 года. Полученные прогнозы лучше, чем прогнозы Международной
службы вращения Земли.
неравномерность вращение земля полюс
Введение
Вращение Земли вокруг своей оси испокон веков используется
человеком для измерения времени. В астрономии оно служит незаменимой основой
для введения различных систем координат. Однако Земля вращается не совсем
стабильно: меняется скорость ее вращения, движутся географические полюсы,
колеблется ось вращения в пространстве. Эти нестабильности доставляют много
хлопот астрономам, геодезистам и исследователям космоса, т.к. они искажают
координаты небесных и земных объектов. Неравномерность вращения Земли и
движение полюсов вызываются процессами, протекающими на нашей планете, и
зависят от особенностей строения и физических свойств земных недр. Являясь отражением
земных процессов, нестабильности вращения Земли содержат ценную информацию об
этих процессах, выдаваемую самой природой.
Таким образом, изучение неравномерности вращения планеты,
движения полюсов и нутаций земной оси имеет большое практическое и научное
значение. Оно позволяет исправлять искаженные координаты небесных и земных
объектов, способствует расширению и углублению наших знаний в различных
областях наук о Земле. Как же меняется суточное вращение Земли во времени? Чем
вызывается неравномерность вращения Земли, движение полюсов?
Целью моей работы является разработка методики
прогнозирования неравномерности вращения Земли.
Актуальность: Точное время необходимо знать астрономам,
геодезистам, морякам, связистам, исследователям космоса и т.д. Эта информация
важна также для пользователей глобальной навигационной спутниковой системы
ГЛОНАСС. Для пользователей навигационных спутниковых систем неучтенное
изменение длительности суток грозит неточностью в определении координат,
например, изменение длительности суток в течение 10 дней на 1 мс приведет к
погрешности в определении долготы на экваторе в 4,6 м. Начиная со второй
половины прошлого столетия, за неравномерностью вращения Земли ведутся
постоянные наблюдения. В России такого рода исследования проводит Институт
прикладной астрономии РАН. Текущие сведения, основанные на измерениях,
проведенных в различных странах, обрабатываются в Международной службе вращения
Земли IERS со штаб-квартирой в Париже. Необходимо не только контролировать
положение полюсов и длительность суток, но и уметь их предсказывать. Однако
точность прогноза, даваемого Обсерваторией ВМС США в рамках IERS и помещаемого в сети
Интернет, невелика.
I.
Литературный обзор
1.1
Неравномерность вращения Земли
1.1.1
Астрономические данные
В 123 г. до н.э. Гиппарх открыл явление предварения
равноденствий, или прецессию. В 1755 г. Джеймс Брадлей открыл явление нутации
оси вращения Земли. Сомнения в постоянстве скорости суточного вращения Земли
возникли после открытия Э. Галлеем в 1695 г. векового ускорения движения Луны.
Мысль о вековом замедлении вращения Земли под действием приливного трения была
впервые высказана И. Кантом в 1755 г. Во второй половине прошлого столетия
появились свидетельства нерегулярных флуктуаций скорости вращения Земли и движения
географических полюсов. С тех пор за неравномерностью вращения Земли и
движением полюсов ведутся регулярные наблюдения.
Скорость вращения Земли наиболее просто можно
охарактеризовать отклонением длительности земных суток от эталонных (86 400 с).
Чем короче земные сутки, тем быстрее вращается Земля.
Земля, вращающаяся вокруг своей оси, является своего рода
часами, а звезды и светила на небесной сфере - своего рода делениями
циферблата. Вращающиеся вместе с Землей телескопы, направленные на то или иное
светило, координаты которого можно найти в астрономическом ежегоднике,
позволяют "отсчитывать" по нему земное время.
Наряду с часами "Земля" астрономы использовали
сначала механические, потом кварцевые, а в последние десятилетия атомные часы.
Точность атомных часов столь высока, что с их помощью можно проверить ход часов
"Земля". Такая "проверка", ведущаяся в Международном бюро
времени с 1955 г., показывает, что часы "Земля" идут не лучшим
образом. Они иногда спешат, а иногда отстают. Плохой ход часов "Земля"
вызван непостоянством скорости вращения планеты.
До создания атомных часов ход часов "Земля"
контролировался лишь путем сравнения наблюденных и вычисленных (в соответствии
с небесно-механическими теориями) координат Луны, Солнца и планет. Таким путем удалось
получить представление об изменении скорости вращения Земли в течение последних
трех столетий - с конца XVII в., когда стали вестись первые инструментальные
наблюдения за движением Луны, Солнца и планет. Оказывается, что с начала XVIII
в. до середины XIX в. скорость вращения Земли менялась мало. Со второй же
половины XIX в. по настоящее время наблюдались значительные нерегулярные
флуктуации этой скорости с характерными временами порядка 60-70 лет. Наиболее
быстро Земля вращалась около 1870 г., когда длительность земных суток была на
0,003 с короче эталонных, а наиболее медленно - около 1903 г. (земные сутки
были длиннее эталонных на 0,004 с) (рис. 1). С 1903 по 1934 гг. происходило
ускорение вращения Земли, с конца 30-х гг. до 1972 г. наблюдалось замедление, а
с 1973 г. по настоящее время Земля ускоряет свое вращение. Колебание угловой
скорости вращения Земли, наблюдавшееся в ХХ в. (с 1903 г. по 1972 г.) часто
называют 60-70-летним. В XIX в. колебание примерно того же периода имело место
с 1845 г. по 1903 г. В более раннюю эпоху 60-70-летние колебания не
прослеживаются. К сожалению, данные XVII-XVIII вв. имеют низкую разрешающую
способность, т.к. тогда интервалы времени между наблюдениями достигали иногда
29 лет.
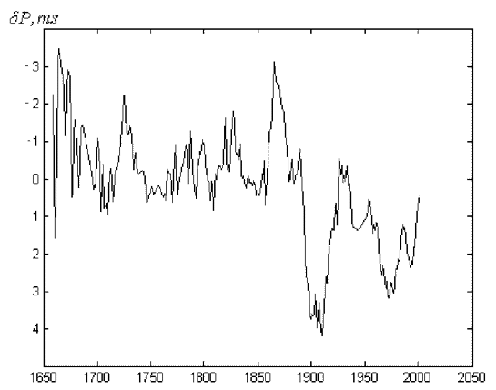
Рис. 1. Отклонения δP длительности суток от эталонных за последние 350 лет
Точность определения неравномерности вращения Земли
радикально улучшилась с 1955 г., после того как стали использоваться атомные
часы. С этого момента появилась возможность регистрировать все колебания
скорости вращения Земли периодом более одного месяца. Ход среднемесячных
величин отклонений δP (вследствие
неравномерности скорости вращения Земли) за период 1955-2000 гг. показан на
рис.2. Видно, что с 1956 г. по 1961 г. вращение Земли ускорялось, с 1962 г. по
1972 г. - замедлялось, а с 1973 г. по настоящее время - снова ускорялось.
Замедление вращения Земли, закончившееся в 1972 г., началось в 1935 г., т.е. за
пределами изображенного периода. Ускорение, возникшее в 1973 г., вероятно, еще
не закончилось и продлится до 2005-2010 гг. Ускорение вращения 1958-1961 гг. и
замедление 1989-1994 гг. являются кратковременными флуктуациями. На фоне
многолетних изменений хорошо видны сезонные колебания δP. Скорость вращения Земли бывает наименьшей в апреле и ноябре, а
наибольшей - в январе и июле. Январский максимум значительно меньше июльского.
Разность между минимальной величиной отклонения длительности земных суток от
эталонных в июле и максимальной в апреле или ноябре составляет 0,001 с.
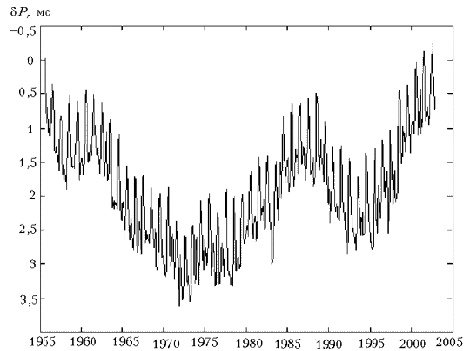
Рис. 2. Среднемесячные отклонения δP длительности земных суток от эталонных за последние 45 лет.
Формально сезонные колебания обычно описывают суммой годовой
и полугодовой гармоник. Амплитуды и фазы этих гармоник меняются от года к году,
обнаруживая интересные закономерности. Амплитуда годовой гармоники меняется с
характерным временем около шести лет, а полугодовой - около двух лет. Средняя
величина амплитуд годовой и полугодовой гармоник равна соответственно 0,000 35
и 0,000 32 с [1].
В 80-е гг. астрооптические наблюдения стали заменяться новыми
методами измерений: с помощью радиоинтерферометров со сверхдлинными базами
(РСДБ), лазерной локации спутников (ЛЛС) и Луны (ЛЛЛ), системы глобального
позиционирования (СГП/GPS) и т.д. Точность определения всемирного времени (UT)
увеличилась на два порядка. В итоге появилась возможность изучать
короткопериодные колебания скорости вращения Земли периодом до суток, а в
отдельные периоды специальных серий наблюдений до нескольких часов.
Известно, что спектральный анализ заключается, во-первых, в
представлении изучаемых колебаний в виде суммы элементарных гармоник, и
во-вторых, в выявлении зависимости средних квадратов амплитуд этих гармоник от
их частоты или периода, т.е. в нахождении спектральной функции или просто
спектра.
В спектре приливных колебаний скорости вращения Земли
выделяются составляющие периодами год, полгода, 13,7; 27,3; 9,1 сут.
Спектральный анализ всего 350-летнего ряда среднегодовых значений n дает
максимум спектральной плотности на периоде около 70 лет. Колебание с этим
периодом особенно заметно проявлялось в последние 150 лет. В начале ХХ в.
амплитуда 70-летнего колебания достигала 2 мс [1].
1.1.2
Оптические наблюдения XYII-XX веков
В силу особенностей определения скорости
осевого вращения Земли регулярные ее наблюдения до середины нынешнего столетия
были практически невозможны. Это связано, прежде всего, с тем, что для
определения скорости вращения Земли необходимо иметь высокоточную и стабильную,
опорную шкалу времени. Реализована же такая шкала была только после создания в
пятидесятых годах атомных стандартов частоты (шкала TAI). Определенную
возможность давали кварцевые часы, но в силу быстрого их старения получать
стабильные результаты на промежутках больше года не удавалось. Поэтому
единственной путем получать данные о режиме осевого вращения Земли до середины XX столетия был анализ и
обработка оптических наблюдений различных астрономических событий, таких как
покрытия звезд Луной, соединения планет, восходы и заходы Солнца и Луны и др.,
в которых опорная шкала определяется временем, являющимся аргументом в теории
движения небесных тел. Обработка таких наблюдений проводилась рядом
исследователей с начала этого столетия (В. Деситтер и Дж. Спенсер).
Среднегодовые значения продолжительности суток dP за период 1623-1955 гг.
получены в серии работ Л. Моррисона и Ф. Стефенсона (см., например, Stephenson and Morrison, 1984). В таблице 1
представлены стандартные отклонения (σΔT) для ΔT=TD-UT, где TD динамическое время (Stephenson and Morrison, 1983), и стандартное
отклонение σdP для продолжительности
суток dP. Величина σdP вычислена по формуле:
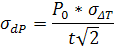 ,
,
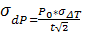
где Р0 = 86400 с - стандартные сутки,
t=365.25*P0 - интервал
времени между нормальными точками. Значения dP на полугодовых интервалах с 1656 по 1983 годы получены также в (McCarthy and Babcock,
1986).
Таблица 1
Стандартные отклонения отдельных измерений
ΔT и dP
|
Годы
|
σΔT, с
|
σdP, с
|
|
1620-1669
|
60
|
0.116
|
|
1670-1699
|
15
|
0.029
|
|
1700 - 1759
|
5
|
0.010
|
|
1760-1819
|
2
|
0.004
|
|
1820-1860
|
1.5
|
0.003
|
|
1861 - 1942
|
1.3
|
0.003
|
|
1943-1955
|
1.0
|
0.002
|
1.1.3
Античные наблюдения
Изучение лунных и солнечных затмений,
соединений светил с Луной, моментов равноденствий и солнцестояний дает
возможность получить данные об ускорении орбитального движения Луны и ускорении
вращения Земли. Древние рукописи и хроники, в которых встречаются упоминания об
этих явлениях, имеются примерно с 2500 г. до н.э. Сравнение теоретического (в
предположении равномерного вращения Земли) и наблюдаемого моментов событий
возможно даже в случае, если неопределенность в датировке документа достигает
десяти лет. Это связано с эффектом накапливания запаздывания вследствие
замедления вращения.
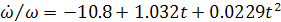
где t - в столетиях от эпохи 1790 г. н.э., а 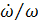 - в 10-9 рад/век. Приливная
компонента в замедлении вращения составляет (-32.6±0.8) *10-9 век-1.
Погрешность определения
- в 10-9 рад/век. Приливная
компонента в замедлении вращения составляет (-32.6±0.8) *10-9 век-1.
Погрешность определения 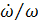
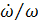 оценивается в 1*10-9 век-1. Полученные
данные дают изменение продолжительности суток в XYIII столетии около 0.9 мс/век и около 2 мс/век в начале нашей
эры. В работе (Stephenson and Morrison,
1984) средняя скорость увеличения продолжительности суток за последние 2500 лет
составляет 2.0 мс/век. Анализ античных наблюдений за 2700 лет, выполненный в (Stephenson et aL 1983),
дает 2.55 мс/век в период между 383 г. до н.э. и 948 г. н.э. и 1.25 мс/век -
между 948 и 1850 гг. Используя шестьдесят наблюдений солнечных и лунных
затмений за период с 829 по 1010 гг., в (Stephenson and Said, 1989) получено, что средние солнечные
сутки в эпоху 950 г. н.э. были на 11.6±0.6 мс короче современных, а средняя
скорость увеличения их продолжительности за последние 1000 лет оценивается в l.37±0.007 мс/век. A. D. Wittmann (1983)
по древним солнечным таблицам (1008-1895 гг.) получил замедление вращения Земли
оценивается в 1*10-9 век-1. Полученные
данные дают изменение продолжительности суток в XYIII столетии около 0.9 мс/век и около 2 мс/век в начале нашей
эры. В работе (Stephenson and Morrison,
1984) средняя скорость увеличения продолжительности суток за последние 2500 лет
составляет 2.0 мс/век. Анализ античных наблюдений за 2700 лет, выполненный в (Stephenson et aL 1983),
дает 2.55 мс/век в период между 383 г. до н.э. и 948 г. н.э. и 1.25 мс/век -
между 948 и 1850 гг. Используя шестьдесят наблюдений солнечных и лунных
затмений за период с 829 по 1010 гг., в (Stephenson and Said, 1989) получено, что средние солнечные
сутки в эпоху 950 г. н.э. были на 11.6±0.6 мс короче современных, а средняя
скорость увеличения их продолжительности за последние 1000 лет оценивается в l.37±0.007 мс/век. A. D. Wittmann (1983)
по древним солнечным таблицам (1008-1895 гг.) получил замедление вращения Земли
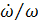
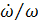 =-2.31*10-8 век-1, что соответствует
увеличению суток со скоростью 1.99 мс/век. Здесь же по наблюдениям моментов
равноденствий с 161г. до н.э. получено
=-2.31*10-8 век-1, что соответствует
увеличению суток со скоростью 1.99 мс/век. Здесь же по наблюдениям моментов
равноденствий с 161г. до н.э. получено 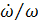
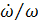 =-1.23*10-8 век-1 (dP/dt=1.06 мс/век). В последнее время появились
оценки вращения Земли по древним китайским летописям. Так, в работе (Pang, 1989) сутки в эпоху 1302 г. до н.э. были
короче на 47 мс, что дает среднюю скорость замедления вращения 1.4 мс/век.
=-1.23*10-8 век-1 (dP/dt=1.06 мс/век). В последнее время появились
оценки вращения Земли по древним китайским летописям. Так, в работе (Pang, 1989) сутки в эпоху 1302 г. до н.э. были
короче на 47 мс, что дает среднюю скорость замедления вращения 1.4 мс/век.
Т.о., античные и средневековые наблюдения
показывают, что среднее увеличение продолжительности суток за последние 2-3
тысячелетия существенно отличаются от оценки, полученной по приливным данным:
3.2 мс/век в работе (Парийский, 1972) и (3.7±0.5) мс/век в (Lambeck, 1975) и, Т.о.,
существует механизм неприливного ускорения вращения Земли.
1.1.4
Палеонтологические данные
Палеонтологический метод основан на том
факте, что скорость роста скелета простейших организмов (кораллов, моллюсков,
строматолитов и др.) существенно зависит от количества падающего света. Это
приводит к образованию суточных, месячных и годичных колец. Принимая
продолжительность года (период вращения вокруг Солнца) постоянной, можно
подсчитать количество суток в году в различные геологические эпохи. В табл. 2
представлены результаты палеонтологических оценок вращения Земли.
Таблица 2
Палеонтологические данные о продолжительности
суток в геологическом прошлом Земли
|
Эпоха
|
Шкала, млн. лет
|
Кол-во суток в
году
|
 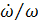 , 10 - 8 век - 1Продолжит, сут., час , 10 - 8 век - 1Продолжит, сут., час
|
|
|
Современ.
|
0
|
365.24
|
-3.80
|
24
|
|
Верх, меловой
|
-70
|
375
|
+0.61
|
23.38
|
|
Ср. триасовый
|
-220
|
371.6
|
-4.45
|
23.59
|
|
Верх, карбон
|
-290
|
383
|
-8.17
|
22.89
|
|
Ниж. карбон
|
-340
|
398
|
0.0
|
22.02
|
|
Ср. девонский
|
-360
|
398
|
-0.96
|
22.02
|
|
Ср. силурийский
|
-420
|
400
|
-13.11
|
21.91
|
К сожалению, достоверность данных,
получаемых по ископаемым, невысока из-за значительной доли субъективности при
подсчете количества колец. Видимо этим, по крайней мере, частично, объясняется
малое количество исследований в этом направлении. В последние предпринимались
попытки оценить палеовращение по толщине слоев донных отложений, подверженных
воздействию приливов. В ходе исследований получено, что продолжительность суток
позднем и раннем протерозое (около 680 млн. лет и около 2 млрд. назад)
составляла соответственно 21.9 и 19.7 час [2].
1.1.5
Движение полюсов Земли
Изменяется не только угловая скорость
Земли, наша планета совершает небольшие колебания относительно оси вращения.
Поэтому точки, в которых ось пересекает земную поверхность, - мгновенные полюсы
Земли - движутся. Они перемещаются по земной поверхности вокруг среднего полюса
в направлении вращения Земли, т.е. с запада на восток. Траектория движения
полюса имеет вид спирали, которая периодически то закручивается, то
раскручивается. Для примера на рис. 3 показана траектория движения мгновенного
Северного полюса за 1996-2000 гг. Максимальное удаление мгновенного полюса от
среднего отмечалось в мае-июле 1996 г. Затем полюс стал закручиваться, и это
продолжалось до 2000 г., когда полюс подошел на минимальное расстояние к центру
спирали. Сейчас полюс раскручивается и все далее удаляется от своего среднего
положения.
Самое большое удаление мгновенного полюса от среднего не
превышает 15 м. Закручивание и раскручивание траектории полюса объясняется тем,
что полюс совершает два периодических движения: свободное, или чандлеровское
(названо в честь открывшего его в 1891 г. Сэта Чандлера), периодом около 14
мес., и вынужденное - годовым периодом. Чандлеровское движение полюсов - это
движение, которое возникает, если ось вращения Земли каким-либо образом
отклонить от оси ее наибольшего момента инерции. Движение полюсов, вызванное
периодическим действием на Землю со стороны атмосферы и гидросферы, называется
вынужденным. Период свободного движения зависит не от периода возбуждающей
силы, как это характерно для вынужденного движения, а от динамического сжатия и
упругих свойств Земли. Сложение этих двух движений и дает наблюдаемую картину
биений [3]. Анализ координат полюса за последние 110 лет показывает, что
вынужденное движение происходит по эллипсу с запада на восток. Величины больших
полуосей эллипса колебались в пределах от 3,4 до 2,7 м, малых полуосей - от 2,5
до 1,8 м, эксцентриситетов - от 0,15 до 0,46, а восточные долготы большой
полуоси имели значения от 205° до 145° в. д.

Рис. 3. Траектория движения полюса в 1996-2000 гг. Сплошная
кривая - траектория среднего полюса с 1890 по 2000 гг. (IERS Annual Report,
2000)
Чандлеровское движение полюса, по тем же данным, имеет почти
круговую траекторию. Оно характеризуется еще большей изменчивостью своих
параметров. Радиус свободного движения имеет амплитудную модуляцию периодом
около 40 лет. Максимальные значения радиуса (9 м) наблюдались около 1915 и 1955
гг., а глубокий минимум (2 м) - около 1930 г. Из-за этого в спектрах координат
полюса возле основного пика на чандлеровской частоте 1/1,18 года имеется
боковой пик на частоте 1/1,24 года.
Из рис. 3 видно, что центр спирали находится в стороне от
начала координат - международного условного начала. Причина тому - так
называемое вековое движение полюса. Если из координат полюса отфильтровать
годовую и чандлеровскую составляющие, то останутся координаты среднего полюса.
Оказывается, он тоже смещается. Траектория среднего полюса за 1890-2000 гг.
изображена сплошной кривой. Видно, что в течение всего периода наблюдений
средний полюс смещался со скоростью около 10 см/год по сложной зигзагообразной
кривой с преобладающим направлением в сторону Северной Америки (меридиан 290°
в. д.).
1.1.6 Природа
периодических колебаний Земли
Фигура Земли близка к эллипсоиду вращения. Когда Луна и
Солнце не лежат в плоскости земного экватора, силы их притяжения стремятся
развернуть Землю так, чтобы экваториальные вздутия фигуры располагались по
линии, соединяющей центры масс Земли, Луны и Солнца. Но Земля не поворачивается
в этом направлении, а под действием момента пары сил прецессирует [4]. Ось
вращения Земли медленно описывает конус вокруг перпендикуляра к плоскости
эклиптики (рис.4). Вершина конуса совпадает с центром Земли. Точки
равноденствий и солнцестояний движутся по эклиптике навстречу Солнцу, совершая
один оборот за 26 тыс. лет (скорость движения 1° за 72 года).
Моменты сил притяжения, которые действуют на экваториальные
вздутия, меняются в зависимости от положений Луны и Солнца по отношению к
Земле. Когда Луна и Солнце находятся в плоскости земного экватора, моменты сил
исчезают, а когда склонения Луны и Солнца максимальны, то и величина момента
наибольшая. Вследствие таких колебаний моментов сил тяготения наблюдаются
нутации (от лат. nutatio - колебание) оси вращения Земли, складывающиеся из
ряда небольших периодических колебаний. Главнейшее из них имеет период 18,6
года - время обращения узлов орбиты Луны. Движение с этим периодом происходит
по эллипсу. Большая ось эллипса перпендикулярна направлению прецессионного
движения и равна 18,4''; малая параллельна ему и равна 13,7''. Таким образом,
ось вращения Земли описывает на небесной сфере волнообразную траекторию, точки
которой находятся на угловом расстоянии в среднем около 23° 27' от полюса
эклиптики.
Приливные выступы постоянно перемещаются по земной
поверхности вслед за Луной и Солнцем - с востока на запад, т.е. в направлении,
обратном суточному вращению Земли. Естественно, что при таком перемещении в
океанах и в Земле возникают силы трения, которые тормозят вращение планеты.
Благодаря этому и должно происходить вековое замедление вращения Земли. Оценки
показывают, что из-за этого сутки должны удлиняться на 0,003 с за 100 лет. Таким
образом, неравномерности вращения Земли, представленные на наших рисунках,
почти не связаны с влиянием приливного трения, а вызываются другими причинами.
Рис. 4. Схема движения оси вращения Земли в
пространстве для внеземного наблюдателя
Земные приливы играют заметную роль и в колебаниях скорости
вращения Земли с периодами менее одного месяца. Приливообразующая сила
растягивает Землю вдоль прямой, соединяющей ее центр с центром возмущающего
тела - Луны или Солнца. При этом сжатие Земли увеличивается, когда ось
растяжения совпадает с плоскостью экватора, и уменьшается, когда ось растяжения
отклоняется к тропикам. Момент инерции сжатой Земли больше, чем
недеформированной. А поскольку момент импульса Земли (т.е. произведение ее
момента инерции на угловую скорость) должен оставаться постоянным, то и
скорость вращения сжатой Земли меньше, чем недеформированной. При движении Луны
и системы Земля-Луна склонения Луны и Солнца и расстояния от Земли до Луны и
Солнца постоянно меняются. Поэтому приливообразующая сила колеблется во времени
соответствующим образом, что в конечном итоге и вызывает приливную
неравномерность вращения Земли. Наиболее значительными являются колебания с
полумесячным и месячным периодами.
Чем же обусловлена неприливная неравномерность вращения Земли
и движение полюсов? Имеется очень много процессов, которые в принципе могут
влиять на вращение Земли. Например, изменения в распределении воздушных масс в
атмосфере, снежного и ледяного покровов, осадков и растительности на земной
поверхности, вариации уровня Мирового океана, взаимодействие ядра и мантии
Земли, извержения вулканов, землетрясения, воздействия внешних сил и т.д.
Тщательные оценки вклада этих процессов позволили выявить наиболее существенные
из них.
В течение года массы воздуха и влаги (воды, снега и льда)
перераспределяются между материками и океанами, а также между Северным и Южным
полушариями. Так, в январе масса воздуха над континентом Евразия на 6*1015
кг больше, чем в июле. От января к июлю из Северного полушария в Южное
переносится 4*1015 кг воздуха. В течение всей зимы происходит
накопление снега в северных районах Евразии и Северной Америки. Весной же снег
тает, и влага возвращается в Мировой океан. Все это меняет момент инерции Земли
и в какой - то степени сказывается на ее вращении. Оценки показывают, что
сезонное перераспределение воздушных и водных масс мало влияет на сезонную
неравномерность вращения Земли, но почти полностью обусловливает вынужденное
движение полюсов.
Чандлеровское движение полюсов возникает, как мы уже
говорили, когда ось вращения Земли отклоняется от оси наибольшего момента
инерции Земли. Однако оно должно затухать со временем, т.к. энергия свободного
движения полюсов превращается в Земле в тепло. Отсутствие затухания свободного
движения полюсов указывает на то, что имеются какие-то процессы, непрерывно его
поддерживающие. К таким процессам относят землетрясения, электромагнитное
взаимодействие ядра и мантии Земли, лунно-солнечную прецессию и т.д. Наиболее
вероятно, что свободное движение полюсов поддерживается межгодовыми колебаниями
системы Земля-океан-атмосфера [4].
Исследования показали, что главной причиной сезонной
неравномерности вращения Земли является атмосферная циркуляция. Известно, что в
среднем атмосфера движется относительно земной поверхности в низких широтах с
востока на запад (дуют восточные ветры), а в умеренных и высоких - с запада на
восток (преобладают западные ветры). Момент импульса восточных ветров
отрицателен, а западных - положителен. Можно было бы думать, что эти моменты
компенсируют друг друга, и момент импульса ветров всей атмосферы всегда равен
нулю. Однако расчеты показывают, что момент импульса восточных ветров в
несколько раз меньше момента импульсов западных ветров. Поэтому момент импульса
ветров всей атмосферы не равен нулю, а составляет в среднем за год +14*1025
кг*м2/с. Его величина меняется в течение года от +16,1*1025
в апреле и ноябре до +10,9*1025 кг*м2/с в августе.
Момент импульса - это такая физическая величина, которая не
может возникать или уничтожаться. Она способна лишь перераспределяться. В
рассматриваемом случае перераспределение происходит между атмосферой и Землей.
Когда момент импульса атмосферы увеличивается, т.е. усиливаются западные ветры
или ослабевают восточные ветры, момент импульса Земли уменьшается, т.е.
замедляется ее вращение. Когда же момент импульса атмосферы уменьшается
(ослабевают западные или усиливаются восточные ветры), вращение Земли
ускоряется. Суммарный момент импульса Земли и атмосферы всегда остается неизменным.
Этот результат может служить хорошей иллюстрацией того, что закон сохранения
момента импульса справедлив не только в физических лабораторных экспериментах,
но и в глобальных масштабах в природе.
Факт, что момент импульса ветров всегда положителен, говорит
о том, что атмосфера в целом вращается вокруг оси быстрее Земли. Уподобляя
движение атмосферы в целом вращению твердого тела, можно сказать, что период
обращения атмосферы вокруг оси составляет в апреле и ноябре 23 ч 36 мин, а в
августе - 23 ч 45 мин. В среднем за год сутки для атмосферы длятся 23 ч 38 мин,
а не 23 ч 56 мин, как для Земли.
Иногда думают, что раз атмосфера обгоняет Землю в суточном
вращении, то она должна непрерывно его ускорять. Однако на неравномерность
вращения Земли влияют лишь изменения момента импульса ветров. Постоянная же
величина момента импульса ветров была заимствована атмосферой у Земли в момент
формирования атмосферной циркуляции. Тогда скорость вращения Земли немного
замедлилась, (длительность суток возросла на 0,0024 с) и остается таковой в
настоящее время. Если источник, поддерживающий ветры в атмосфере - Солнце, -
иссякнет, то атмосферная циркуляция прекратится, момент импульса ветров
"стечет" к Земле, и длительность суток примет свое первоначальное
значение (уменьшится на 0,0024 с).
Атмосферу, неравномерно разогретую по горизонтали солнечными
лучами, можно рассматривать как тепловую машину. Она превращает тепловую
энергию Солнца в кинетическую энергию ветров. Наиболее теплые части атмосферы в
этом случае играют роль нагревателя, а самые холодные - холодильника. Рабочим
телом служит сам воздух. В современной физике атмосферы известны несколько
тепловых машин. Важнейшими из них являются тепловые машины, порождаемые
контрастом температур между экватором и полюсами. Известный советский геофизик
В.В. Шулейкин назвал их тепловыми машинами первого рода [5]. Одна из них
работает в Северном полушарии, а другая - в Южном. Благодаря этим машинам
поддерживаются наблюдаемые восточные ветры в низких широтах и западные - в
умеренных и высоких. Чем больше контраст температур экватор-полюс, тем
интенсивнее атмосферная циркуляция в данном полушарии и тем больше величина
момента импульса ветров.
Контраст температур в каждом полушарии колеблется с годовым
периодом. Он бывает наибольшим зимой и наименьшим летом. Поэтому момент
импульса ветров Северного полушария, удерживаемый тепловой машиной первого
рода, совершает гармонические колебания с периодом один год от максимального
значения в январе до минимального в июле. В Южном полушарии годовое колебание
имеет противоположную фазу: момент импульса максимален в июле и минимален в
январе. Поэтому годовые колебания ветров Северного и Южного полушарий
компенсируют друг друга, и момент импульса ветров всей атмосферы должен
оставаться почти постоянным. Итак, тепловые машины первого рода обуславливают
появление в атмосфере положительной величины момента импульса ветров, но почти
не влияют на наблюдаемые сезонные колебания.
Долгое время оставалось неясным, почему момент импульса
ветров всей атмосферы испытывает наблюдаемые сезонные колебания. В 1975 г.Н.С.
Сидоренков открыл существование в атмосфере межполушарной тепловой машины. Было
обнаружено, что в верхних слоях атмосферы самой теплой областью является не
экватор и не параллель, на которой Солнце в полдень бывает в зените, а полярная
"шапка" летнего полушария (в июле - северная, в январе - южная).
Оказалось, что средняя температура воздуха непрерывно убывает от полюса летнего
полушария до полюса зимнего (в июле - от Северного полюса до Южного, в январе -
от Южного полюса до Северного). Стало ясно, что в атмосфере имеется
межполушарная тепловая машина, нагревателем которой является атмосфера летнего
полушария, а холодильником - атмосфера зимнего полушария. Межполушарная
тепловая машина препятствует работе тепловых машин первого рода. Она уменьшает
величину момента импульса ветров, удерживаемую в атмосфере тепловыми машинами
первого рода. Чем больше контраст температур между полушариями, тем
значительнее этот эффект. В январе и в июле, когда работа межполушарной
тепловой машины наиболее интенсивна, момент импульса ветров уменьшается до
минимальных значений, и скорость вращения Земли достигает максимума. В апреле и
в ноябре температурные различия между атмосферой Северного и Южного полушарий
выравнивается; межполушарная тепловая машина прекращает свою работу, поэтому в
атмосфере удерживается предельно большая величина момента импульса ветров, а
скорость вращения Земли становится минимальной.
Различие величин июльского и январского максимумов скорости
вращения Земли связано с тем, что атмосфера Северного полушария (в среднем за
год) теплее атмосферы Южного полушария. Поэтому контраст температур между
полюсами в июле значительно больше, чем в январе. Если бы подстилающие
поверхности в Северном и Южном полушариях были одинаковы, то величины
январского и июльского максимумов скорости вращения Земли не различались бы.
Интенсивность работы межполушарной тепловой машины меняется от года к году. В
соответствии с этим меняются и параметры сезонных колебаний скорости вращения
Земли [1].
1.2 Методы
спектрального анализа
1.2.1
Фурье-анализ
Одним из фундаментальных положений математики, нашедшим
широкое применение во многих прикладных задачах (процессы передачи информации,
в теории электротехники, в исследовании движения машин, в теории корабля и
др.), является возможность описания любой периодической функции f (t)
с периодом Т, удовлетворяющей условиям Дирихле (согласно теореме Дирихле
периодическая функция должна иметь конечное число разрывов и непрерывность
производных между ними.), с помощью тригонометрического ряда Фурье:
где ω1 = 2p /T - частота
повторения (или частота первой гармоники); k - номер гармоники. Этот ряд
содержит бесконечное число косинусных или синусных составляющих - гармоник,
причем амплитуды этих составляющих ak и bk
являются коэффициентами Фурье, определяемыми интегральными выражениями:
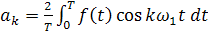
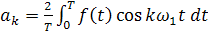 ,
,
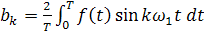
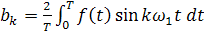 .
.
Помимо упомянутой формы ряд Фурье можно представить в виде
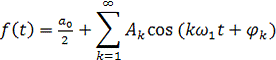
где амплитуда Аk и фаза φ k гармоник определяются
выражениями:
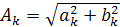
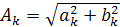 ,
,
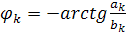
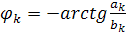 .
.
Гармоническим анализом называют разложение функции f (t),
заданной на отрезке [0, Т] в ряд Фурье или в вычислении коэффициентов Фурье
ak и bk.
Спектральный анализ периодических функций заключается в нахождении
амплитуды Аk и фазы φk гармоник (косинусоид) ряда Фурье:
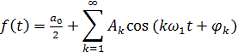
В результате исследования данных временного ряда Фурье-анализом не
удается отследить изменения амплитуды и фазы, но сделать это можно с помощью
сингулярного спектрального анализа [6].
1.2.2 Метод
сингулярного спектрального анализа
В настоящей работе применен аппарат сингулярного
спектрального анализа ("Гусеница"), разработанный и обоснованный
сотрудниками Санкт-Петербургского государственного университета.
Метод "Гусеница" основан на переходе от одномерного
временного ряда длиной n с равномерным шагом (x1, x2,
x3,… xn) к многомерным рядам,
построенным из исходного одномерного и на анализе главных компонентов.
Сингулярный спектральный анализ позволяет выделить интересующие компоненты
временных рядов, в частности, компоненты с заранее известным и заранее не
известным периодом, сгладить исходные данные, сделать прогноз ряда.
Из исходного ряда составляется матрица Х
x1 x2 x3 … xk … xm
x2 x3 x4 … xk+1 … xm+1
Х = x3 x4 x5 … xk+2 … xm+2
. …………………..….
xk xk+1 xk+2…. x2k-1 … xn.
Здесь m < n - длина гусеницы,
последней строкой с номером k = n - m+1 являются элементы (xk, xk+1,…,xn), причем xij = xi+1j-1. Эту матрицу можно
рассматривать как m-мерную выборку объема k или m-мерный временной ряд. В
некоторых приложениях могут быть вычислены средние значения mi и оценки стандартных
отклонений si по столбцам. Матрица Х может быть центрирована
по столбцами и нормирована на si; ниже использовано
центрирование. Далее вычисляется матрица R = 1/k X XT. Если матрица Х
центрирована, то R является выборочной корреляционной матрицей. Элементами матрицы R служат выражения.
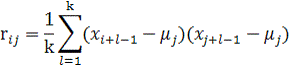
По обычной методике анализа главных компонентов вычисляются
собственные числа и собственные векторы матрицы R, т.е. проводится её
сингулярное разложение R = PLPT, L
- диагональная матрица упорядоченных по убыванию собственных чисел матрицы R:
l1 0 0 … 0
0 l2 0 … 0
L = ………
0 0 0 …lm,
P - ортогональная матрица собственных векторов матрицы R:
p11 p21 … pm1
p12 p22 … pm2=
…………
p1m p2m … pmm.
Выполняются следующие соотношения: PT = P-1, PPT = I, L
= PTRP, å li = m, I-единичная
матрица.
Из последнего выражения следует, что, при умножении собственных
чисел li на 1/m ×100%, получаются доли
дисперсий в процентах, которые можно рассматривать как доли общей информации,
содержащейся в каждом главном компоненте.
Матрицу P можно рассматривать как матрицу перехода к
ортогональным составляющим (главным компонентам) XP=Y= (y1,y2,.,ym). Преобразование yj
= Xpj является линейным преобразованием исходного процесса с
помощью дискретного оператора свертки:
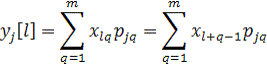
В этом случае собственные векторы pjq матрицы R играют роль передаточных
функций некоторых фильтров, настроенных на составляющие исходного процесса.
Ширина полосы пропускания фильтра зависит от формы передаточной функции фильтра
и определяется как видом собственного вектора, так и длиной интервала
усреднения, т.е. длиной "гусеницы" m. Чем больше m, тем уже полоса фильтра.
Максимальное значение m равно половине длины
ряда n, в этом случае при четном n матрица Х квадратная.
При выборе m, которое значительно меньше характерной
ритмичности ряда (в пределе при m = 2), происходит его
сглаживание.
Рассмотрение собственных векторов и главных компонентов,
полученных в результате линейной фильтрации, дает информацию о структуре
изучаемого процесса и свойствах его слагаемых.
В частности, среди главных компонентов можно выделить:
относящиеся к тренду (медленно меняющиеся), периодические, шумовые.
Ввиду ортогональности матрицы P можно восстановить
матрицу X=YPT, используя при этом
выбранные главные компоненты Yi.
Выбор нескольких главных компонентов эквивалентен
параллельному соединению соответствующих фильтров, что позволяет управлять
формой спектральной характеристики.
При выделении гармонических составляющих или близких к ним
"Гусеница" дает ортогональные пары собственных векторов, отличающихся
по фазе на p/2 (квадратурных компонентов) вида:
S1 = A (t)
cos [w0t + j (t)], S2 = A (t) sin [w0t + j (t)],
где A (t) и j (t) - медленно меняющиеся
амплитуда и фаза, w0 - фиксированная частота спектрального компонента.
Можно провести аналогии метода "Гусеница" с
Фурье-анализом (если ряд состоит из набора строго гармонических компонентов,
то, фактически, "Гусеница" осуществляет разложение в ряд Фурье).
Наиболее важные преимущества метода сингулярного спектрального анализа
"Гусеница" состоят в следующем: а) базовые функции метода порождаются
исследуемым рядом, так как являются собственными векторами R; б) выделенный тренд
правильно отображает поведение медленно меняющейся составляющей не только в
середине ряда, но и на его концах; в) возможна оценка частоты и амплитуды
периодических компонентов анализируемого ряда, но и мгновенной фазы; г)
возможно восстановления ряда по информативным компонентам с удалением шума [7].
II. Обработка
данных неравномерности вращения Земли
В качестве исходных данных использовались ряды ежедневных
величин ряда δP = (UT1 - TAI) отклонения длительности
земных суток от эталонных по данным Международной службы вращения Земли IERS [8] за три года.
Проведенный мной анализ показал, что при использовании меньшего периода времени
прогнозы не отслеживают общую динамику изменений данных, а при большем периоде
при составлении прогноза ошибка его первого значения может превысить 1 мс. На
рис.5 показан график ряда δP за 2004-2006 гг.; на
01.01.2004 взято δP =-32389.5814 мс. Ряд δP содержит тренд и периодические колебания с периодом в
несколько лет, один год, полгода и непериодические составляющие.
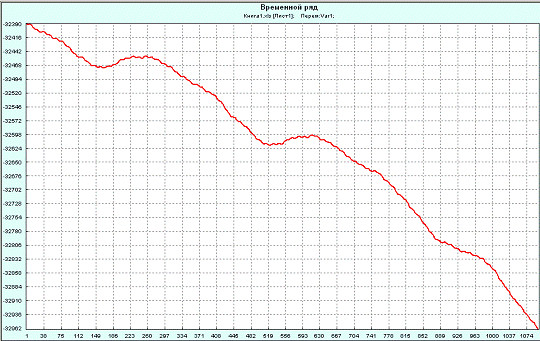
Рис 5. Файл "данные2004-2006. xls" открытый при
помощи программы Caterpillar SSA3.3.
Далее при помощи функции разложение вычисляются главные
компоненты.
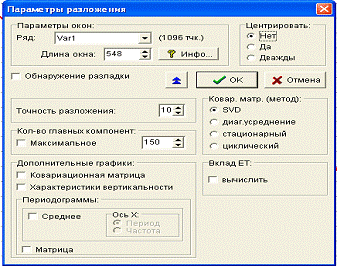
Рис. 6. Выбор параметров разложения.
Теперь группируем отобранные компоненты.
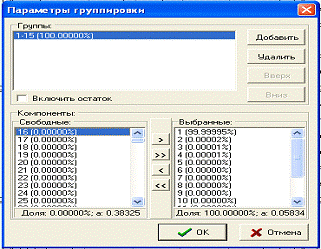
Рисунок 7. Группировка выбранных компонент
Далее восстанавливаем ряд содержащий сгруппированные
компоненты.
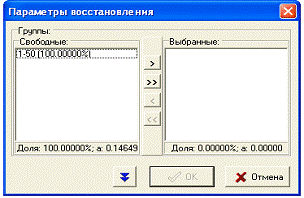
а)
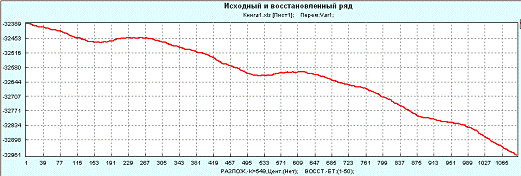
б)
Рисунок 8. Восстановление ряда:
а) параметры восстановления, б) восстановленный ряд.
Далее восстановленный ряд аппроксимируется.
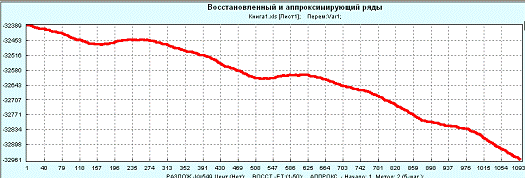
Рисунок 9. Аппроксимирующий ряд.
Также в ходе работы были сделан прогноз величины δP длительностью в 30 дней на январь 2007 г.
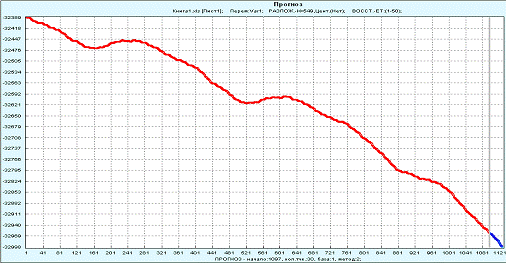
Рис 11. Прогноз на январь 2007 года.
Далее полученные данные прогноза сравниваются с исходными за
соответствующий период времени. Потом процесс повторяется с функции
группировки, но с другим количеством компонент. Прогноз, который дает наиболее
близкие значения к исходным данным, вносится в таблицу полученных значений.
Прогнозы составлены на весь период 2007 года с 1, 11 и 21 числа каждого месяца.
Кроме этого из исходных данных по методике IERS [9] были вычтены
приливные колебания и таким же способом были найдены прогнозы полученных
значений. К этим прогнозам обратно прибавлялись влияния приливных колебаний.
Полученные значения сравнивались с исходными данными. В сети Интернет были
найдены значения прогнозов величины P сделанные
Международной службы вращения Земли IERS [10] за соответствующие периоды времени, которые
также были сопоставлены с исходными данными.
На рис. 12 график (а) показывает ошибку прогноза данных IERS, график (б) ошибку
полученных значений методом сингулярного спектрального анализа. Другие графики
представляют ошибки прогнозов, не содержащих приливные колебания: (в) - период
которых не превышает 35 суток, (г) максимальный период колебаний составляет
6790,36 дней (примерно 18,6 года).
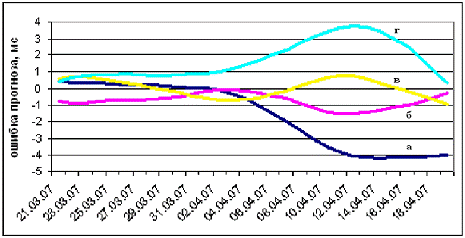
Рис 12. Ошибки прогнозов полученных при помощи сингулярного
спектрального анализа и прогноза IERS.
Как видно из рис. 12 наибольшую точность прогноза имеют
данные, из которых вычитались приливные колебания период, которых не превышает
35 суток. Для этих, а также прогнозов IERS составлена гистограмма заблаговременности
прогнозов, в которой показано, за какой период времени ошибка прогнозов не
превышает 1 мс.
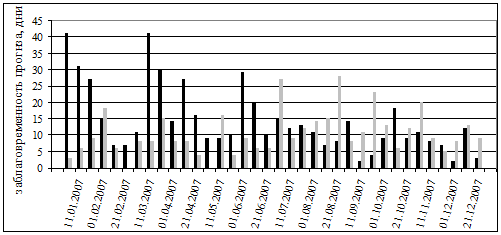
Рис 14. Заблаговременность прогнозов (черные - прогнозы
значений без приливных колебаний с периодом, не превышающим 35 суток, серые -
значения прогнозов IERS).
Точность прогнозов данных полученных при помощи вычитания приливных
колебаний с периодом T<35 суток превышает показания IERS прогнозов в 21 случае из
36, что составляет около 60%.
В табл. 3 для каждого месяца 2007 года показаны диапазоны
количества компонент обеспечивающую наибольшую точность прогноза для данного месяца.
Табл. 3
|
С приливными
колебаниями
|
Без приливных
колебаний с периодом менее 35 дней
|
Без приливных колебаний
|
|
Январь
|
15-30
|
25-45
|
45-60
|
|
Февраль
|
20-50
|
25-150
|
40-150
|
|
Март
|
50-80
|
40-100
|
70-80
|
|
Апрель
|
35-55
|
40-50
|
45-75
|
|
Май
|
20-35
|
70-80
|
7-20
|
|
Июнь
|
7-20
|
10-20
|
9-65
|
|
Июль
|
20-50
|
20-30
|
15-20
|
|
Август
|
90-150
|
140-170
|
90-150
|
|
Сентябрь
|
50-200
|
35-110
|
30-150
|
|
Октябрь
|
10-60
|
60-80
|
50-90
|
|
Ноябрь
|
50-90
|
65-80
|
25-55
|
|
Декабрь
|
80-150
|
100-200
|
25-160
|
|
|
|
|
|
Далее для проверки методики прогнозирования были вычислены
прогнозы величины δP на 2008 год с
количеством компонент за соответствующие день и месяц, которые обеспечили
наименьшую ошибку в 2007 году. В 50% случаев ошибка прогноза не превышала 1 мс
в течение 5 дней.
III. Выводы
1. Разработана методика прогнозирования данных неравномерности
вращения Земли, основанная на использовании метода сингулярного спектрального
анализа "Гусеница".
2. Получены прогнозы величины δP на 1, 11 и 21 число каждого месяца 2007 года с количеством
компонент обеспечивает меньшую ошибку прогноза.
. Также были спрогнозированы данные, не содержащие
приливных колебаний. Получено, что более точный прогноз значений получается
тогда, когда из исходных данных вычтены приливные колебания, период которых не
превышает 35 суток. Полученные значения сравнены с прогнозами, предоставленными
Международной службой вращения Земли. Примерно в 60% случаев полученные
прогнозы точнее данных IERS.
. Составлена таблица, в которой для каждого месяца
2007 года показаны диапазоны количества компонент обеспечивающую наибольшую точность
прогноза для данного месяца.
Список
литературы
1. Н.С. Сидоренков.
"Нестабильности вращения Земли”. http://elkin52. narod.ru/astro/sem/sem.
htm <http://elkin52.narod.ru/astro/sem/sem.htm>
2. Хомутов С.Ю. /
Взаимосвязь нерегулярных вариаций скорости вращения Земли и глобальных
геофизических параметров // Диссертация на соискание ученой степени кандидат ф.
- м. наук, Новосибирск, 1996 г.
. Сидоренков Н.С.
Межгодовые колебания системы атмосфера-океан-Земля. - Физика, № 25/98.
. Шулейкин В.В.
Взаимодействие звеньев в системе "Океан-Атмосфера-Материки". -
Природа, № 10/71.
6. Голяндина Н.Э. Метод
"Гусеница"-SSA: анализ временных рядов. С-П: Изд-во СПбГУ, 2003
. А.А. Баскова, В.Б.
Кашкин. /"Исследование неравномерности вращения земли с помощью
сингулярного спектрального анализа" // Вестник КрасГУ. Физ. - мат. Науки.
2006’7
8. Данные ежедневных
величин отклонения длительности земных суток от эталонных по данным
Международной службы вращения Земли IERS. http://hpiers. obspm.
fr/eop-pc/products/combined/C04.html
<http://hpiers.obspm.fr/eop-pc/products/combined/C04.html>
9. Изменение Земного
вращения из-за приливных колебаний. http://hpiers. obspm. fr/
. Данные прогнозов
величины dP сделанные
Международной службы вращения Земли IERS.
<http://www.iers.org/>