|
Рис.1.7.
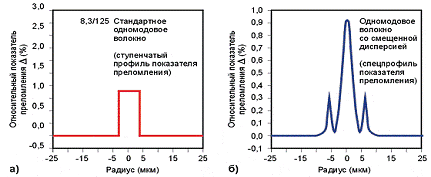
Профили показателей преломления стандартных одномодовых ОВ.
|
С целью оптимизации дисперсионных параметров
волокон на длине волны 1.55 мкм, на которой кварцевые ОВ имеют минимальное
затухание, были разработаны градиентные одномодовые ОВ.
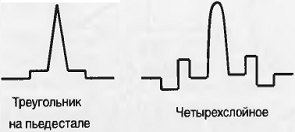
Усложняя профиль показателя преломления (рис.
1.8) и делая его форму близкой к треугольной, получили волокна, имеющие длину
волны нулевой дисперсии вблизи 1550 нм. Такие ОВ получили название ОВ со
смещенной дисперсией (Dispersion Shifted Fiber - DSF).
|
|
 а) а)
|
Рис.1.8. Профили показателей преломления ОВ со
смещенной дисперсией.
Эти ОВ имеют дисперсию на λ
= 1550 нм
менее 3.5 пс/(нм*км), а на λ = 1310 нм
до 18 пс/(нм*км).
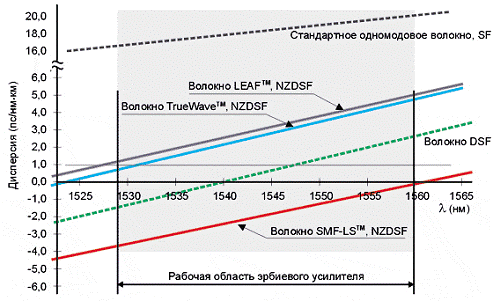
Рис. 1.9. Зависимость хроматической дисперсии в
одномодовых ОВ от длины волны.
Еще один
вид
одномодовых
ОВ
- ОВ
с
ненулевой
смещенной
дисперсией
(Non Zero Dispersion Shifted Fiber - NZDSF). Эти ОВ были
разработаны специально для систем спектрального уплотнения (DWDM).
Волокна NZDSF оптимизированы таким образом, что
длина волны нулевой дисперсии у них вынесена за пределы полосы пропускания
эрбиевого оптического усилителя (такие усилители могут использоваться только в
начале или в конце линии; выходная мощность составляет 10-500мВт (10-27дБм)).
Характеристики этих волокон приведены в таблице
1.2.
Таблица 1.2.
|
Характеристики
|
TrueWave™
|
SMF-LS™
|
LEAF™
|
|
Главное
рабочее окно (нм)
|
1550
|
1550
|
1550
|
|
Затухание
|
|
Макс.
затухание на длине волны 1550 нм (дБ/км)
|
0.22
- 0.25
|
>0.25
|
>0.25
|
|
Макс.
затухание в диап. 1525-1575 нм (дБ/км)
|
>0.30
|
>0.30
|
>0.30
|
|
Хроматическая
дисперсия в зоне ненулевой дисперсии
|
|
минимум
(пс/нм км)
|
0.8
(зона 1540-60 нм)
|
н/д
|
1.0
(1540-60 нм)
|
|
максимум
(пс/нм км)
|
4.6
(зона 1540-60 нм)
|
-3.5
(зона 1530-60 нм)
|
6.0
(1540-60 нм)
|
|
Наклон
нулевой дисперсии (пс/нм2 км))
|
н/д
|
>0.092
|
н/д
|
|
Длина
волны нулевой дисперсии (нм)
|
>1520
|
>1560
|
н/д
|
|
Диам.
модового поля при дл. волны 1550 нм (нм)
|
8.4
± 0.6
|
8.4
± 0.5
|
9.5
± 0.5 9.6 (типовое)
|
|
Кабельная
длина волны отсечки (нм)
|
>1260
|
>1260
|
н/д
|
|
|
|
|
|
В таблице 1.3. приведены рекомендации МСЭ по
параметрам волокон различных типов.
Таблица 1.3.
|
Параметры
ОВ
|
Рекомендации
МСЭ
|
|
G.652
|
G.653
|
G.654
|
G.655
|
|
Тип
волокна
|
SSF
|
DSF
|
CSF
|
+NZDSF
|
|
Окна
прозрачности, нм
|
1350/1550
|
1500-1600
|
1550
|
1530-1565
|
|
Коэффициент
затухания, дБ/км
|
1310
|
<
1.0 / < 0.34
|
<
1.0
|
не
норм.
|
не
норм.
|
|
1383
|
<
2.0
|
<
2.0
|
не
норм.
|
не
норм.
|
|
1550
|
<
0.22
|
<
0.22
|
<
0.22 / 0.15
|
<
0.22
|
|
Диаметр
поля моды, мкм
|
1310
|
9.3
- 9.8
|
не
норм.
|
не
норм.
|
не
норм.
|
|
1550
|
9.0
- 10.0
|
7.0
- 8.6
|
9.5
- 10.5
|
9.0
- 10.0
|
|
Максимальная
кабельная длина волны отсечки, нм
|
1260
|
1270
|
1530
|
1480
|
|
Длина
волны нулевой дисперсии, нм
|
1310
± 10
|
1550
± 25
|
1280
± 20
|
не
норм.
|
|
Наклон
нулевой дисперсии, пс/(нм2км)
|
0.093
|
0.085
|
0.095
|
<
0.169
|
В таблицах 1.2 и 1.3 присутствует параметр -
кабельная длина волны отсечки. Это длина волны отсечки волокна, уложенного в
кабель. Для волокна в кабеле длина волны отсечки меньше, чем для «прямого»
волокна, то есть одномодовый режим передачи наступает раньше.
Типы одномодовых волокон отличаются друг от
друга только формой профиля показателя преломления (рис. 1.10) и,
соответственно, дисперсионными характеристиками.
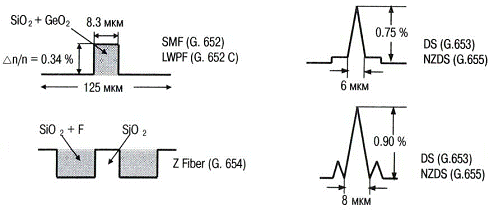
Рис.1.10. Профили показателя преломления в
одномодовых волокнах.
Основные типы одномодовых волокон, применяемых в
линиях связи, нормируются международными стандартами ITU-T Rec. G. 652-G. 655:
• G.652: волокна с несмещенной дисперсией (SM
волокна) с длиной волны нулевой дисперсии и длиной волны отсечки в районе 1310
нм.
• G.653: волокна со смещенной дисперсией (DS
волокна) с длиной волны нулевой дисперсии в районе 1550 нм и длиной волны
отсечки в районе 1310 нм.
• G.654: волокна с несмещенной дисперсией (SM
волокна) с длиной волны нулевой дисперсии в районе 1310 нм и длиной волны
отсечки в районе 1550 нм.
• G.655: волокна со смещенной ненулевой
дисперсией (NZDS волокна), обладающие малой дисперсией (0.1-6 пс/нм.км) в
диапазоне длин волн 1530-1565 нм.
• G.656: волокна с ненулевой дисперсией для
систем грубого уплотнения по длинам волн (CWDM - Coarse Wavelength Division
Multiplexing - большое расстояние между спектральными каналами - 20 нм).
Существует также несколько специальных типов
одномодовых волокон применяемых в волоконно-оптических устройствах:
• Волокна для компенсации дисперсии (DC -
Dispersion Compensating), применяемые в модулях компенсации дисперсии.
• Волокна с примесью редкоземельных элементов,
применяемые в оптических усилителях, например, в EDFA - Erbium Doped Fiber
Amplifier.
• Волокна, сохраняющие состояние поляризации
излучения (РМ - Polarization Maintaining), применяемые в гироскопах,
поляризационных делителях и смесителях.
• Дырчатые волокна (Holey Fiber), применяемые в
компенсаторах дисперсии, в оптических шнурах, в нелинейных элементах.
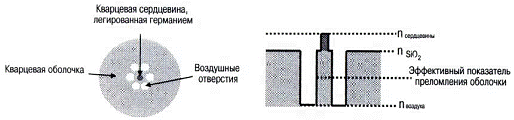
Рис. 1.11. Профиль показатель преломления
дырчатого волокна.
Помимо рассмотренных ОВ существуют также
одномодовые ОВ со сглаженной дисперсией Cutoff Shifted Fiber (CSF). В этих
волокнах используется четырехслойная оболочка, что позволяет добиться почти
плоской и близкой к нулевой дисперсионной характеристики (|Dх| = 1-6 пс/км/нм)
в диапазоне длин волн от 1300 до 1650 нм. При этом они имеют сниженный
коэффициент затухания благодаря чисто кварцевой сердцевине и увеличенного
диаметра модового поля.
Волокна со сглаженной дисперсией используются
только на длине волны 1550 нм для связи на большие расстояния без промежуточных
линейных усилителей и регенераторов, преимущественно в подводных магистралях.
Большой диаметр модового поля позволяет использовать большее усиление мощности
без увеличения нелинейных искажений сигнала.
оптическое волокно преломление
Глава 2. Параметры оптических волокон
2.1 Дисперсия в оптических волокнах
Информация по ОВ передается в виде коротких
оптических импульсов. Энергия импульса распределяется между всеми направляемыми
модами. Скорости всех мод вдоль их траектории в ступенчатом ОВ одинаковы.
Однако время, которое им понадобится для прохождения 1 км ОВ, будет различным.
На выходе ОВ импульсы отдельных мод, пришедшие в разное время, складываются,
образуя более широкий, по сравнению с входным, оптический импульс (рис. 2.1).
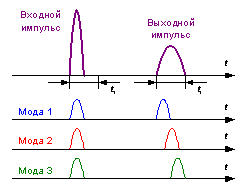
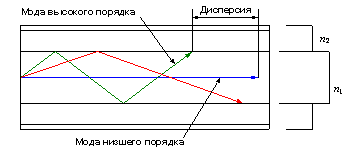
Рис. 2.1. Траектории меридиональных
лучей в ОВ со ступенчатым профилем показателя преломления.
Явление уширения импульса в
многомодовом ОВ называется межмодовой дисперсией, которая характеризуется
величиной Dm, измеряющейся в нс/км. Если величина дисперсии известна, то
уширение импульса Δt в ОВ
длиной L в первом приближении определится выражением:
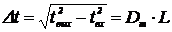 . (2.1)
. (2.1)
Верхняя оценка величины межмодовой
дисперсии: наименьшую траекторию и наименьшее время распространения tmin имеет
луч, распространяющийся вдоль оси ОВ.
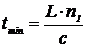 (2.2)
(2.2)
Наибольшую траекторию и наибольшее
время распространения tmax имеет луч, распространяющийся по ОВ, отражаясь от
границы раздела сердцевины и оболочки под углом полного внутреннего отражения.
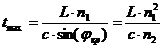 (2.3)
(2.3)
Тогда 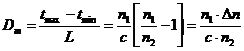 . (2.4)
. (2.4)
Дисперсия ограничивает скорость
передачи информации по ОВ.
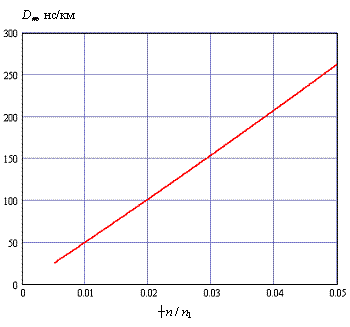
Рис. 2.2. Зависимость межмодовой
дисперсии от относительной разности показателей преломления сердцевины и
оболочки.
С величиной межмодовой дисперсии 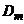 [нс/км]
связано понятие широкополосности волокна или удельной полосы пропускания B[МГц
км]
[нс/км]
связано понятие широкополосности волокна или удельной полосы пропускания B[МГц
км]
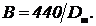 (2.5)
(2.5)
Величина широкополосности для
ступенчатых многомодовых кварцевых волокон ограничивается величиной 20-50 МГц
км.
Для градиентных многомодовых волокон
широкополосность лежит в пределах 200 - 2000 МГц км.
Радикальным способом уменьшения
дисперсии является переход от многомодовой передачи к одномодовой.
Впервые одномодовый режим передачи в
волокне со ступенчатым профилем показателя преломления был достигнут путем
уменьшения радиуса сердцевины до 5 мкм. Такие волокна называют стандартными
одномодовыми волокнами.
Важным нормируемым параметром у
одномодовых волокон является диаметр w или радиус rnм модового пятна (поля),
который характеризует потери при вводе света в волокно и используются для
расчетов вместо радиуса или диаметра сердцевины, его величина зависит от типа
волокна и рабочей длины волны и лежит в пределах 8..10 мкм (фактически он на
10-12% больше диаметра сердцевины).
Для одномодового ОВ распределение
интенсивности поля моды можно аппроксимировать гауссовской кривой:
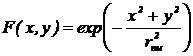 , (2.6)
, (2.6)
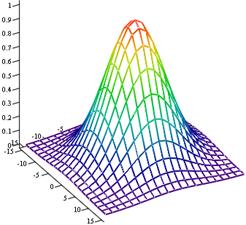
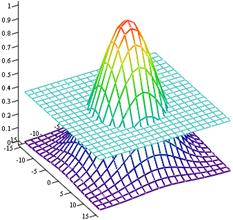
Рис. 2.3. Определение диаметра
модового поля.
На рис. 2.4. показаны рассчитанные
по выражениям распределения модового поля для стандартного волокна на длинах
волн, которые обычно используются для связи.
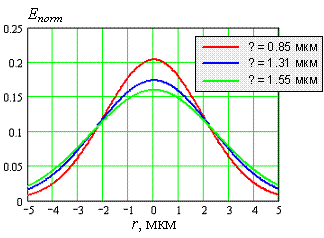
Рис. 2.4. Распределение модового
поля основной моды в стандартном волокне.
Поскольку скорость распространения
света в ОВ зависит от длины волны излучения λ, разные спектральные
составляющие сигнала распространяются с разной скоростью.
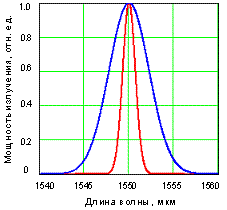
Рис. 2.5. Спектр излучения
источника.
Хроматическая дисперсия состоит из
двух составляющих: материальной и волноводной:
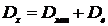 (2.7)
(2.7)
Как физическая величина измеряется в
пс / (нм·км) и означает уширение импульса в волокне длиной 1 км при ширине
спектра сигнала 1 нм (с учетом скорости передачи и ширины спектра источника
излучения).
Материальная дисперсия обусловлена
зависимостью показателя преломления кварца n (как фазового, так и группового)
или скорости распространения света в кварце 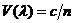 от длины волны (рис. 1.10) и
пропорциональна второй производной показателя преломления по длине волны:
от длины волны (рис. 1.10) и
пропорциональна второй производной показателя преломления по длине волны:
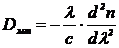 (2.8)
(2.8)
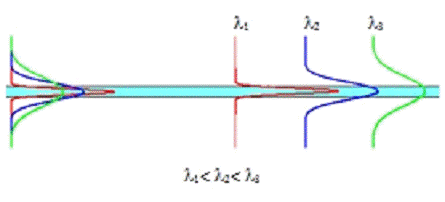
Рис. 2.6. Возникновение материальной
дисперсии.
На рис. 2.7 показана зависимость
материальной дисперсии от длины волны. Видно, что материальная дисперсия имеет
знак и при длине волны нулевой материальной дисперсии λ = λ0mat
проходит через 0.
Волноводная дисперсия Dв не связана
со свойствами материала, но зависит от конструкции и размеров волновода. Ее
появление связано с тем, что волна в одномодовом ОВ распространяется частично в
сердцевине, частично в оболочке и показатель преломления для нее принимает
среднее значение между показателями преломления сердцевины и оболочки. При
изменении длины волны глубина проникновения поля в кварцевую оболочку меняется
и, следовательно, меняется среднее значение показателя преломления.
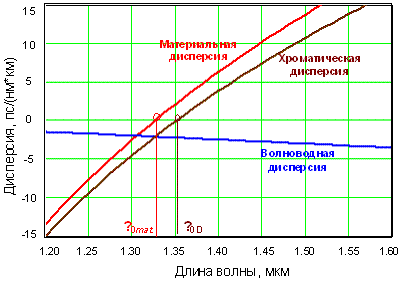
Рис. 2.7. Хроматическая дисперсия в
стандартном одномодовом
волокне.
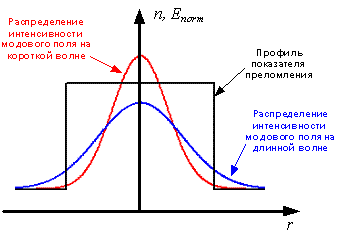
Рис. 2.8. Возникновение волноводной
дисперсии.
Волноводная дисперсия отрицательна и
с увеличением λ она уменьшается.
Это позволяет, изменяя размеры и конструкцию ОВ, управлять зависимостью Dв, а,
следовательно, и зависимостью Dхр от λ.
Существует такая длина волны, при
которой материальная и волноводная дисперсии равны по модулю и имеют
противоположные знаки, то есть хроматическая дисперсия равна нулю. Эту длину
волны называют длиной волны нулевой хроматической дисперсии или просто длиной
волны нулевой дисперсии λ0D.
В большинстве одномодовых ОВ
расположение осей наибольшей и наименьшей скорости является случайным и
расширение проходящего по ОВ импульса растет с увеличением длины L
пропорционально корню квадратному из длины ОВ:
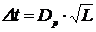 , (2.9)
, (2.9)
где Dp - поляризационно-модовая
дисперсия.
Для большинства одномодовых ОВ
величина поляризационно-модовой дисперсии лежит в пределах 0.02 - 0.2 пс/км0.5.
2.2 Затухание в оптическом волокне
По мере распространения света в
оптической среде, он, как известно, ослабевает, что носит название затухание a,
которое измеряется в децибелах или неперах. При оптических измерениях:
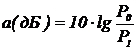
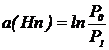 , (2.10)
, (2.10)
где P0, P1 - мощности сигнала на
входе и выходе ОВ, оптического кабеля (ОК) или любого компонента волоконного
тракта (ВТ).
Общее или вносимое затухание ОВ
можно разделить на собственное затухание и дополнительные потери.
Собственное затухание обусловлено
самим ОВ. Для однородного ОВ можно рассчитать коэффициент затухания -
величину затухания на единицу длины:
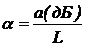 , дБ/км (2.11)
, дБ/км (2.11)
где L - длина ОВ, км.
Собственные потери в ОВ в основном
обусловлены двумя причинами: поглощением и рассеянием.
Рассеяние является фундаментальной
(технологически неустранимой) причиной затухания в ОВ и носит название рэлеевское
рассеяние. Его особенностью является сильная зависимость коэффициента рассеяния
αs от длины
волны λ проходящего
излучения:
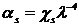 (2.12)
(2.12)
где χs -
коэффициент пропорциональности (0.7-0.9 дБмкм4/км). Зависит от
материала (вида и концентрации легирующих добавок и т.п.) и технологии
изготовления ОВ.
Поглощение обусловлено потерями в
основном материале ОВ - кварце и в примесях. Носит резонансный характер и дает
для кварца пики затухания в ультрафиолетовой и инфракрасной областях спектра. В
используемом диапазоне длин волн 0.8-1.6 мкм всплески поглощения у кварца
отсутствуют. Наибольший вклад в поглощение вносят гидроксильные группы OH.
Они дают мощный пик поглощения на длине волны 1.383 мкм.
К дополнительным потерям относятся
потери на вводе и выводе излучения; потери, связанные с нарушениями
геометрической формы ОВ и случайно расположенными структурными дефектами;
изгибные потери (особенно на микроизгибах); потери в соединениях (стыках)
строительных длин; потери, вызванные недостатками монтажа.
Затухание ограничивает максимальное
расстояние, на которое можно передать сигнал без регенерации. Затухание
ограничивает также минимальное расстояние, на которое можно передать сигнал без
принятия дополнительных мер по снижению его уровня. Максимально допустимое
затухание в линии определяется параметрами передающего и фотоприемного
устройства.
Как видно из рис. 2.9, для передачи
оптических сигналов может быть использован широкий участок спектра, где потери
в волокнах достаточно малы. Его принято разбивать на более узкие участки -
рабочие диапазоны, или окна прозрачности.
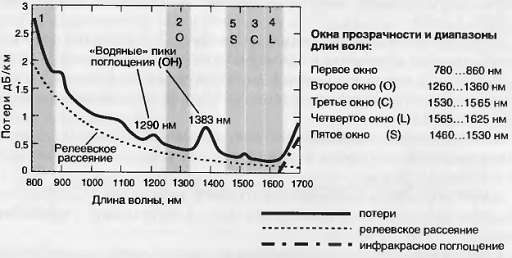
Рис. 2.9. Зависимость коэффициента
затухания от длины волны и положение окон прозрачности в кварцевых ОВ.
Первое окно прозрачности из-за
большой величины коэффициента затухания (2-2.5 дБ/км) используется в основном в
локальных вычислительных сетях.
Второе окно прозрачности (О -
Original, основной диапазон) используется преимущественно в городских и зоновых
линиях.
Третье окно прозрачности (C -
Conventional, стандартный диапазон) наиболее широко используется в
магистральных линиях.
Четвертое (L - Long wavelength,
длинноволновый диапазон) и пятое окно прозрачности (S - Short wavelength,
коротковолновый диапазон) вместе с третьим используются в системах
спектрального уплотнения.
2.3 Физические основы возникновения потерь в
изогнутых оптических волокнах
При прокладке и монтаже оптического кабеля
невозможно избежать изгибов ОВ. Радиус изгиба оптического кабеля при его стационарной
прокладке существенно влияет на его эксплуатационные характеристики. Изгиб
кабеля вызывает соответственно изгиб оптического волокна, которое при
определенных условиях может негативно отреагировать на данное механическое
воздействие, увеличив потери на прохождение сигнала, или, в крайнем случае,
разрушится. Изгибные деформации во многом определяют срок службы оптических
волокон.
Характерные места изгибов оптических кабелей во
внешней сети телекоммуникационных станций показаны на рис. 2.10. Кроме спиралеобразного
изгиба в самом кабеле, другие самые существенные изгибы волокон происходят в
многочисленных местах сращивания или разветвления кабелей и в различных
внутристанционных распределительных щитах. Технология, применяемая в точках
разветвления и распределения, идентична технологии, применяемой в
соединительных муфтах на самой трассе кабеля.
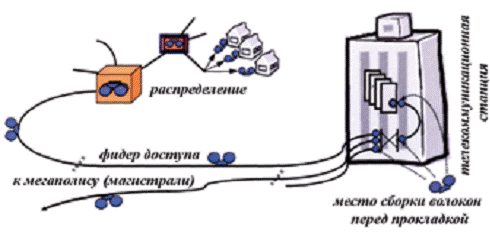
Рис. 2.10. Места изгибов оптических кабелей на
внестанционных участках оптических сетей.
В указанных на рис. 2.10 местах изгиба волокно
обычно прокладывается в соответствии со строгими предписаниями относительно
минимального радиуса изгиба. Однако правильность укладки волокна зависит от
умения исполнителя и тщательности выполнения операции. Из-за финансового
давления с точки зрения снижения стоимости трудовых затрат иногда возникают
случайные ошибки, в результате которых короткие длины волокон подвергаются
изгибам со значительно меньшим радиусом, чем предусмотрено. Это особенно
характерно для трудоемких участков абонентских линий, где требуются
многочисленные изменения из-за перехода абонентов к другому оператору, миграции
сети и ее реконструкции. Очень часто требуется выполнить разводку абонентских
линий в местах с ограниченным пространством, например в сетях внутри зданий. Поэтому
неудивительно, что в связи со все более широким применением одномодовых волокон
в абонентских линиях вновь возникает проблема, связанная с макроизгибами
волокон. При использовании оптических волокон, малочувствительных к изгибам,
характеристики сети в меньшей степени подвержены влиянию таких дефектов и в то
же время выявляются другие преимущества монтажа линий - уменьшение габаритов
устройств демонтажа ОВ (муфты, шкафы, монтажные платы и пр.).
Доминирующими внешними параметрами,
чувствительными к наличию макроизгибов, являются длина волны и радиус изгиба,
как показано на рис. 2.11, на котором представлена зависимость затухания
стандартного одномодового волокна, соответствующего рекомендации G.652 ITU-Т,
от длины волны и радиуса изгиба. Здесь отчетливо видно, что при больших длинах
волн, когда оптический сигнал в меньшей степени зависит от сердечника
одномодового волокна, потери на изгиб значительно возрастают. Они еще больше
увеличиваются, если радиус изгиба уменьшается, как это показано на рис.2.11 справа.
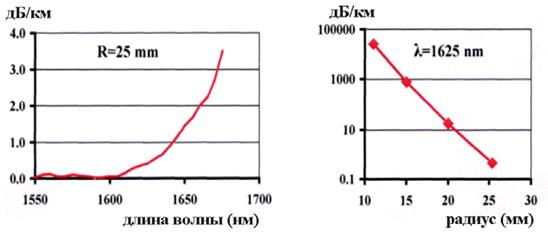
Рис. 2.11. Зависимость потерь, связанных с
макроизгибом.
В принципе это верно, так как уменьшение радиуса
изгиба приводит к появлению дополнительных напряжений в наружной части волокна
и силы сжатия на внутренней части волокна. Однако это дополнительное напряжение
обычно достаточно мало по сравнению с 1%-ным удлинением, которому волокно
подвергается в процессе производства. Кроме того, длина изогнутого волокна на
трассе невелика.
Таким образом, правильно спроектированные и
проложенные сети, магистральные или абонентские линии, явно не страдают от
эффектов макроизгибов. Этому способствует и заметное распространение оптических
волокон, менее чувствительных к изгибам.
Следующий вопрос - возникающие в результате
изгибов изменения характеристик волокна, выявление этих изменений и,
желательно, их предотвращение. Поскольку изгибы обычно вызывают дополнительные
потери, то этот эффект будет обнаружен только при вводе кабельной трассы в
эксплуатацию после прокладки или заполнения конфигурации линии связи. Если не
принимать в расчет возможность изгибов с малым радиусом в самом кабеле, то
изгиб, не соответствующий требованиям спецификации, всегда будет результатом
соединения волокон при сращивании.
При прокладке кабеля обычной практикой является
сращивание различных длин кабеля. Индивидуальный контроль мест сращивания
проводится локально после выполнения операции сращивания. Общие потери
проверяются при приемке всей трассы, когда каждая оптическая волоконная линия
испытывается с помощью оптического рефлектометра. Если обнаруживается дефектное
место сращивания, корпус соединительной муфты должен быть вскрыт и сращивание
должно быть выполнено заново. Повторный демонтаж одной-двух соединительных муфт
на канал связи - обычное дело при приемке на протяженных междугородных линиях
связи и городских сетях. Количество обнаруженных дефектов также зависит от
числа волокон в кабеле. Для кабеля со 192 волокнами вероятность одного дефекта
на соединительную муфту намного выше, чем для простого кабеля, состоящего из 6
волокон. Процесс повторного монтажа соединительной муфты достаточно
обременительный и дорогостоящий, так как необходимо дополнительное время для
того, чтобы команда испытателей и монтажников выкопала, демонтировала корпус
соединительного устройства и выполнила повторный монтаж. Особое значение при
этом имеет испытательная длина волны. Потери на сращивание сами по себе вряд ли
зависят от длины волны, в отличие от потерь, вызванных изгибами в месте
хранения волокна при прокладке. Т.к. при помощи обычного оптического
рефлектометра нельзя различить потери, возникающие из-за сращивания, петель,
образующихся в месте хранения при прокладке или случайных изгибах с малым
радиусом, то неудивительно, что расширенная проверка характеристик места сращивания
при длине волны 1625 нм на действующих кабелях, прошедших приемосдаточные
испытания при 1550 нм, выявила большое количество очень высоких потерь на
сращивание при 1625 нм.
Анализ показал, что эти дефекты были вызваны как
постоянной кривизной чувствительных к изгибам волокон в зоне места хранения,
так и случайными изгибами из-за неквалифицированного обращения с оптическими
волокнами.
Для случайных изгибов можно определить два
предельных значения: предельный срок службы и предельное значение потерь. Что
касается срока службы, то радиус единичного изгиба может быть очень малым, и
это не повлияет на срок службы. Доминирующее значение имеет предельная величина
потерь, установленная требованиями к потерям на сращивание. Потери вследствие
случайных изгибов ниже или сравнимы с потерями на сращивание. Это означает, что
можно избежать отбраковки волокна при приемосдаточных испытаниях. Величина
этого минимального радиуса определяется в зависимости от чувствительности
волокна к изгибам.
В главе 1 было описано, что при распространении
света в оптических волокнах используется принцип полного внутреннего отражения
лучей от границы раздела сердцевина/оболочка. Принцип соблюдается, если угол
падения луча достаточно велик, т.е. свет падает полого к плоскости отражения (рис.
1.3). При изгибе волокна с каким-то малым радиусом нарушается угловое условие,
и часть излучения уходит в оболочку, где потом и высвечивается.
С точки зрения электродинамики этот процесс
можно объяснить по-другому. Поле распространяемого излучения, концентрируясь в
сердцевине, частично выходит в оболочку (поэтому диаметр модового поля всегда
немного больше диаметра сердцевины), затухая по экспоненциальному закону.
Потери при изгибании волокна возникают по двум
причинам. Во-первых, потери возникают в месте соединения прямого и изогнутого
волокна и при переходе от изгиба к прямому волокну. Они обусловлены тем, что в
изогнутом волокне центр модового пятна смещен относительно оси волокна на
некоторую величину d, зависящую от радиуса изгиба волокна (рис. 2.12.а). В
результате модовые пятна прямого и изогнутого волокна в месте их соединения
оказываются смещенными также на величину d (рис. 2.12.б). Поэтому только часть
мощности моды прямого волокна (диаметром w) передается моде изогнутого волокна,
а остальная мощность преобразуется в моды оболочки и в конечном счете теряется.
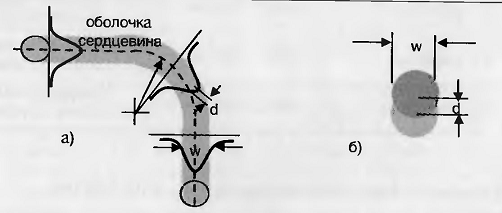
Рис. 2.12. Возникновение потерь.
Во-вторых, мощность теряется непосредственно в
самом изогнутом волокне. Это происходит из-за того, что в изогнутом волокне
периферийная часть моды распространяется со скоростью больше скорости света в
среде (в оболочке). Эта часть моды излучается в оболочку волокна и в итоге
теряется (рис. 2.13). Величина этих потерь тем больше, чем больше число витков
волокна и чем меньше радиус изгиба волокна.
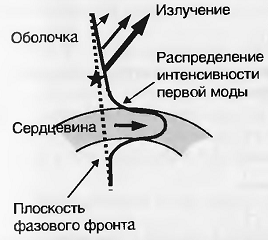
Рис. 2.13. Возникновение потерь в изогнутом
волокне ( - точка, где скорость распространения фазового фронта превысила скорость света
в среде).
- точка, где скорость распространения фазового фронта превысила скорость света
в среде).
Таким образом, потери в изогнутом волокне
возникают из-за двух различных механизмов. В первом случае потери зависят
только от радиуса изгиба волокна и не зависят от числа витков. А во втором -
они зависят и от радиуса изгиба, и от числа витков.
Фрагменты рефлектограмм SM волокна, два витка
которого намотаны на цилиндрическую оправку диаметром 23мм, представлены на
рисунке 2.14.
излучения (λ), но
и от радиуса сердцевина (а) и от разности показателей преломления между
сердцевиной и кварцевой оболочкой (n1-n2). Из этих параметров можно образовать
безразмерную комбинацию, часто используемую при расчетах и называемую
параметром волокна V:
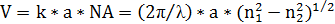 (2.12)
(2.12)
где k = 2π/λ - волновое
число (в вакууме), 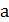 - радиус сердцевины,
NA=(n12 - n22)1/2- числовая апертура.
- радиус сердцевины,
NA=(n12 - n22)1/2- числовая апертура.
Параметр волокна V однозначно характеризует
относительные мощности, распространяющиеся в сердцевине и в оболочке волокна
(рис.2.15).
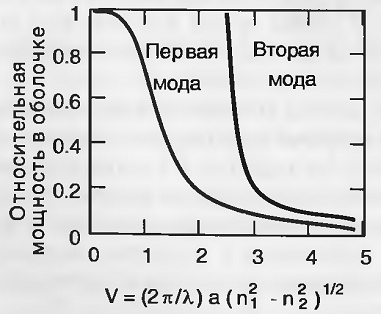
Из этого рисунка видно, что при V<1
практически вся мощность первой моды сосредоточена в оболочке и,
соответственно, при изгибе волокон с таким малым параметром V потери излучения
будут большими.
Характерно также, что кривая относительной
мощности для первой моды не обрывается при V→0. Это означает, что
теоретически в волокне может распространяться излучение со сколь угодно большой
длиной волны (т.е. основная мода волокна не имеет отсечки). Но при V→0
основная часть мощности распространяется вне сердцевины, то потери на изгибах в
таких волокнах велики.
При V>1 доля мощности основной моды,
распространяющейся в оболочке, быстро уменьшается с ростом V, соответственно
уменьшаются и потери при изгибе волокна. Дальнейшее увеличение параметра V
нецелесообразно, т.к. при V>2,4 в волокне уже может распространяться вторая
мода (рис.2.15).
Минимальная длина волны, при которой в волокне
распространяется только одна мода, называется длиной волны отсечки.
Следовательно, если волокно прямое, то в нем распространяются две моды. Но
вторую моду можно отсечь, изогнув волокно.
В отличие от теоретической длины волны отсечки,
которую можно рассчитать, эффективная длина волны отсечки, используемая на
практике (стандарт ITU-T,G.650), зависит от длины волокна и наличия в нем
изгибных деформаций. После укладки волокна в оптический кабель изгибных
деформаций в волокне становится больше. Поэтому максимально возможная длина
волны отсечки в кабеле всегда меньше максимально возможной длины волны отсечки
в волокне.
Известно, что в стандартных одномодовых волокнах
типа G.652 с ростом длины волны затухание на изгибах явственно увеличивается.
Это объясняется тем, что, чем дальше от длины волны отсечки (1260 нм)
проходящее излучение, тем больше оно выходит в оболочку, увеличивая диаметр
модового поля.
Чем ближе рабочая длина волны к длине волны
отсечки, тем лучше волокно «ведет» свет и тем меньше величина дополнительных
потерь, возникающих при изгибах такого волокна.
Итак, полное внутреннее отражение, которое имеет
место в прямолинейном волноводе, нарушается вследствие изгиба. При вычислении
потерь на излучение будем использовать геометрическую оптику для определения
траектории вытекающего луча внутри сердцевины изогнутого волновода и соответствующий
коэффициент прохождения мощности при определении потерь в точках поворота или
отражения. Полные потери на излучение равны сумме потерь вдоль всех траекторий
вытекающих лучей. Для многомодовых волокон потери на изгибе пренебрежимо малы,
т.к. радиус изгиба, как правило, чрезвычайно велик по сравнению с размерами
сердцевины.
На основании вышеизложенного можно сделать вывод
о том, что при изгибах волокна по-прежнему требуется некоторая осторожность, но
продолжающаяся оптимизация конструкций волокна обеспечивает его соответствие
все более жестким требованиям к монтажу и прокладке.
Каждому производителю волокна приходится идти на
компромисс при создании оптимальной конструкции оптического волокна.
Оптимизация собственных параметров волокна, определяющих стойкость к
макроизгибам, окажет влияние и на другие параметры волокна, такие как
дисперсия, собственные потери волокна, и последний, но не менее важный параметр
- производительность при изготовлении волокна. Кроме того, некоторые другие
параметры, такие как точный профиль показателя преломления сердечника волокна и
поперечное распределение механической нагрузки, также влияют на стойкость к
изгибам, хотя и в меньшей степени, чем значение отношения диаметра модового
пятна к длине волны отсечки.
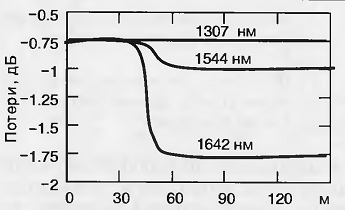
Рис. 2.14. Рефлектограммы потерь в SM волокне на
трех длинах волн.
Из рисунка видно, что в изогнутом волокне потери
увеличиваются с увеличением длины волны. Объясняется это тем, что при этом
увеличивается диаметр моды и все большая часть мощности моды излучается в
оболочку волокна. Этот факт используется в рефлектометрии для поиска мест
изгиба волокон.
Диаметр моды и, соответственно, относительные
мощности, распространяющиеся в сердцевине и оболочке волокна, зависят не только
от длины волны
Глава 3. Методика расчета потерь в изогнутых
стандартных оптических волокнах
.1 Расчет поля основной моды стандартного
волокна
На рисунке 3.1 представлено ОВ круглого
поперечного сечения и оси декартовых и цилиндрических координат, используемые
при описании полей мод.
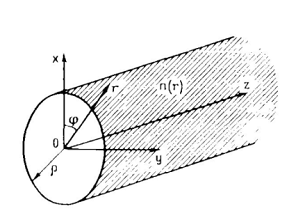
Рис. 3.1. ОВ с круглой симметрией и
неограниченными размерами вдоль осей r и z.
Радиус сердцевины волокна обозначим буквой a.
Вместо цилиндрической радиальной координаты r (расстояние от оптической оси
волокна до рассматриваемой точки) будем использовать ее нормированное значение
R=r/a.
Рассматриваемая в данной главе методика
применима к волокнам с осесимметричным профилем показателя преломления, который
можно представить в виде:
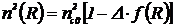 , (3.1)
, (3.1)
где nc0 - максимальное значение
показателя преломления сердцевины волокна, f(R) - функция изменения показателя
преломления (функция профиля), Δ - параметр высоты профиля или
относительная разность показателей преломления сердцевины и оболочки, которая
для ОВ с постоянным показателем преломления оболочки nс1 определяется
выражением:
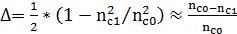
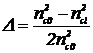 . (3.2)
. (3.2)
Пространственное распределение поля
основной моды F0(R) является решением скалярного волнового уравнения, которое
для слабонаправляющих ОВ круглого поперечного сечения имеет вид:
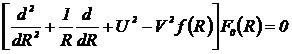 (3.3)
(3.3)
где 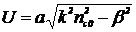 - параметр моды в сердцевине, k -
волновое число, V - нормированная частота, b
- постоянная распространения основной моды:
- параметр моды в сердцевине, k -
волновое число, V - нормированная частота, b
- постоянная распространения основной моды:
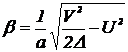 . (3.4)
. (3.4)
Уравнение (3.3) имеет точное
аналитическое решение для слабонаправляющих ОВ со ступенчатым профилем
показателя преломления, описываемым выражениями:
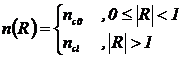 (3.5)
(3.5)
Функция профиля для такого волокна имеет вид:
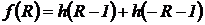 , (3.6)
, (3.6)
где h(x) - функция Хэвисайда.
Решение уравнения (3.3) для поля
основной моды F0(R) слабонаправляющего ОВ со ступенчатым профилем показателя
преломления с учетом нормировки (F0 = 1 при R=1) имеет вид:
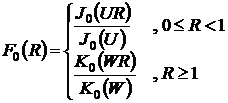 (3.7)
(3.7)
где J0 - функция Бесселя первого
рода; К0 - модифицированная функция Бесселя второго рода, 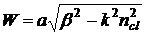 - параметр
моды в оболочке. W можно связать с U через нормированную частоту:
- параметр
моды в оболочке. W можно связать с U через нормированную частоту:
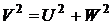
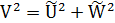 . (3.8)
. (3.8)
Рассчитать параметры моды в
сердцевине U и в оболочке W можно, решив характеристическое уравнение:
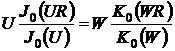 (3.9)
(3.9)
На рис. 3.2 представлены результаты
расчета зависимостей U и W от нормированной частоты.
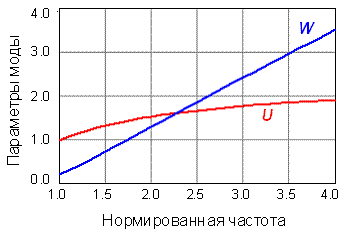
Рис. 3.2. Параметры основной моды в
сердцевине и оболочке
На рис. 3.3 представлены результаты
расчета нормированного распределения поля основной моды для различных значений
нормированной частоты V.
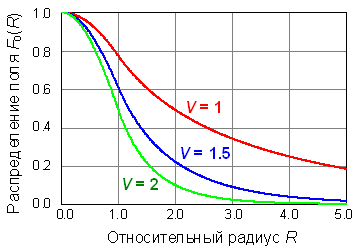
Рис. 3.3. Распределение поля
основной моды в поперечном сечении волокна
Полная мощность основной моды
определяется выражением:
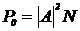 , (3.10)
, (3.10)
где A - амплитуда моды, N -
коэффициент нормировки:
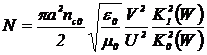 , (3.11)
, (3.11)
где e0 = 8.85×10-12 Ф/м - диэлектрическая проницаемость
свободного пространства; µ0 = 1.257×10-6 Гн/м - магнитная восприимчивость свободного
пространства.
3.2 Расчет коэффициента затухания
изогнутого участка стандартного волокна
Рассмотрим один из основных
механизмов потерь излучения в изогнутом участке ОВ. В прямом волокне с
произвольным профилем показателя преломления поле моды в каждой точке
поперечного сечения распространяется параллельно оси волокна с постоянной
фазовой скоростью, так что плоскость постоянной фазы ортогональна ей. Если
волокно изогнуто в плоскую дугу с постоянным радиусом Rс (рис. 3.4), то поля и
фазовые фронты вращаются вокруг центра кривизны изгиба с постоянной угловой
скоростью.
Таким образом, фазовая скорость,
параллельная оси волокна, должна линейно возрастать при увеличении расстояния
от центра кривизны С. Т.к. оболочка волокна имеет постоянный показатель
преломления, то фазовая скорость может превышать скорость света в данной среде.
Поэтому должен существовать некоторый радиус Rrad в плоскости изгиба, при
превышении которого поле уже не может направляться и должно становиться
излучающим, как это схематически изображено на рис. 3.4а.
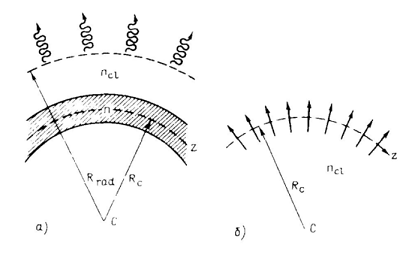
Рис. 3.4. Изогнутое ОВ (а) и
эквивалентное возмущение, аппроксимированное наведенным током с плотностью J
(стрелки), занимающим область сердцевины волокна (б).
Для расчета потерь мощности,
связанных с частичным излучением поля на изгибе, можно использовать
приближенную модель волокна, согласно которой изогнутое волокно представляется
токовой антенной бесконечно малой толщины, излучающей в неограниченную среду с
показателем преломления, равным показателю преломления оболочки.
В рамках приближения
слабонаправляющего волновода излученная мощность не зависит от состояния
поляризации волны, при условии Rс >> a. Для этого случая полная
излученная из изогнутого волокна мощность будет равна:
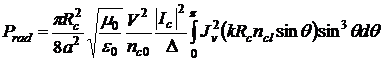 , (3.12)
, (3.12)
где 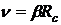 ; величина Ic задается выражением:
; величина Ic задается выражением:
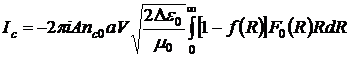 . (3.13)
. (3.13)
Доля мощности, излученная из петли
длиной 2πRc,
определяется отношением полной излученной мощности к начальной мощности моды:
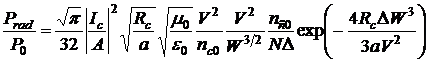 (3.14)
(3.14)
Из (3.13-3.14) следует, что часть
мощности, теряемая на единице длины, или коэффициент затухания мощности γ (Нп/м):
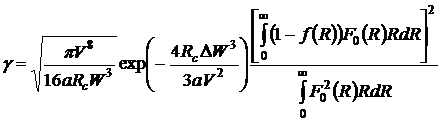 . (3.15)
. (3.15)
Доминирующей в этом выражении
является экспоненциальная зависимость коэффициента затухания от отношения
радиуса изгиба к радиусу сердцевины волокна, т.к. при Rc >> a коэффициент
затухания очень мал и относительно «нечувствителен» к остальным множителям
выражения (3.15).
Из (3.15) можно получить выражение
для коэффициента затухания мощности основной моды изогнутого слабонаправляющего
волокна со ступенчатым профилем показателя преломления:
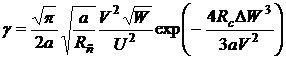 . (3.16)
. (3.16)
Полученное выражение для
коэффициента затухания мощности основной моды в изогнутом волокне со
ступенчатым профилем показателя преломления (3.12) не учитывает эффектов,
связанных с тем, что поперечные размеры сердцевины волокна конечны. Это можно
учесть, умножив коэффициент затухания, рассчитанный по выражению (3.15), на
масштабный множитель M:
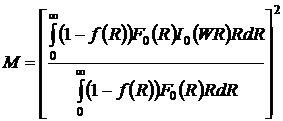 . (3.17)
. (3.17)
Для волокна со ступенчатым профилем
показателя преломления (3.17) примет вид:
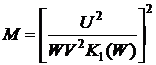 . (3.18)
. (3.18)
Отметим, что выражение (3.16) с
учетом (3.18) может быть представлено в виде:
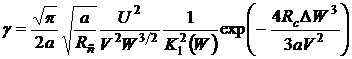 . (3.19)
. (3.19)
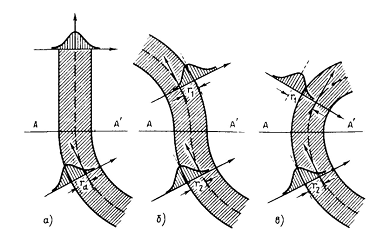
Рис. 3.5. Качественное представление
сдвигов поля основной моды, обусловленных одиночным изгибом (а); двумя изгибами
с противоположными радиусами кривизны (б) и различными радиусами изгиба (в).
Кроме потерь на излучение, связанных
с изгибом волокон, существуют переходные потери, обусловленные резким
изменением радиуса кривизны изгиба, как это показано на рисунке 3.5 в сечении
АА’.
Причиной потерь здесь является
рассогласование потерь, и поэтому падающее поле возбуждает не только локальные
моды, но и моды излучения, которые и определяют переходные потери.
Основное влияние изгиба на поле
основной моды проявляется в сдвиге распределения поля в плоскости изгиба в
радиальном направлении от центра кривизны на расстояние rd от оси волокна (рис.
3.5а). В случае ОВ с произвольным профилем в рамках гауссова приближения имеем:
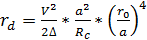 , (3.20)
, (3.20)
где r0 - размер пятна моды; Rc -
радиус изгиба (Rc >> a).
Если волокно одномодовое, то часть
мощности падающей моды, которая преобразуется в направляемую, определяется соотношением:
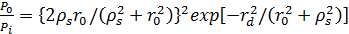 , (3.21)
, (3.21)
где 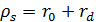 . (3.22)
. (3.22)
Тогда часть излученной мощности, или
переходные потери, при rd << r0 равны:
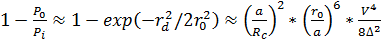 . (3.23)
. (3.23)
Этот результат справедлив при
падении волны на плоскость АА’ с любой стороны.
Если волокно имеет большое число
случайных изгибов с произвольным радиусом кривизны и длиной дуги, что
характерно для микроизгибов, то излучение на этих изгибах является
некоррелированным. Поэтому полные потери от изгибов и переходных участков могут
быть найдены простым суммированием. Поэтому полные потери на микроизгибах вдоль
волокна равны суммарной мощности, излученной на всех изгибах и переходных
участках.
Если отношение радиусов изгиба и
сердцевины велико, что, как правило, реализуется на практике, то для
определения потерь на микроизгибах могут быть использованы выше приведенные
формулы. Так, если радиус изгиба велик, то переходные потери доминируют над
потерями от чистого изгиба, т.к. последние имеют экспоненциальную зависимость
от радиуса кривизны изгиба (3.11).
3.3 Практический расчет изгибных
потерь
Расчет изгибных потерь будем
проводить для оптических волокон, параметры которых близки к параметрам волокон
известных производителей.
В табл. 3.1 приведены параметры
волокон со ступенчатым профилем показателя преломления, для которых проводились
расчеты.
Таблица 3.1
|
Параметр
|
Corning
SMF-28, SMF-28e (стандартное одномодовое волокно)
|
OFS
(бывшие подразд. Lucent Technologies) SM-332 (одномодовое ОВ с согласов.
оболочкой)
|
Samsung
Electronics SF-SMF-x (одномодовое ОВ со ступенч. проф. показ. преломл.)
|
|
Диаметр
мод. поля, мкм
|
λ0=1310нм
|
9,2±0,4
|
9,2±0,4
|
9,2±0,4
|
|
λ0=1550нм
|
10,4±0,8
|
10,5±1,0
|
10,4±0,8
|
|
Парам.
высоты профиля, %
|
0,36
|
0,33
|
0,34
|
Наиболее тщательно мы подошли к моделированию
волокна марки SMF-28, так как экспериментальные исследования проводились с
волокном именно этой марки.
Поскольку химический состав сердцевины и
оболочки данного волокна нам не был известен, мы предположили, что оболочка
изготовлена из чистого кварца, а сердцевина легирована примесями,
увеличивающими показатель преломления. Состав стекла оболочки выбирался, исходя
из известной высоты профиля.
Необходимый для проведения расчетов радиус
сердцевины волокна a оценивался с использованием приближенного выражения для
радиуса модового поля w:
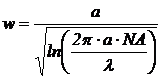 (3.24)
(3.24)
где NA - числовая апертура, определяемая
выражением (1.5). Поскольку диаметр модового поля w для каждого волокна
известен, уравнение (3.24) можно решить относительно a численным методом.
Полученные для каждого из указанных в табл. 3.1
параметры сведены в табл. 3.2.
Для расчета зависимостей показателей преломления
сердцевины и оболочки волокна от длины волны использовалось известное уравнение
Селлмейера:
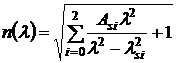 , (3.25)
, (3.25)
где Asi и λsi (i = 0,
1, 2) - коэффициенты Селлмейера, которые для различных стекол приведены в табл.
3.3.
Таблица 3.2
|
Параметр
|
Corning
SMF-28, SMF-28e (стандартное ОВ)
|
OFS
(бывшие подразд. Lucent Technologies) SM-332 (одномодовое ОВ с согласов.
оболочкой)
|
Samsung
Electronics SF-SMF-x (одномодовое ОВ со ступенч. проф. показ. преломл.)
|
|
Химический
состав оболочки волокна
|
100%
SiO2
|
100%
SiO2
|
1%
F, 99% SiO2
|
|
Химический
состав сердцевины волокна
|
3.5%
GeO2, 96.5% SiO2
|
3.1%
GeO2, 96.9% SiO2
|
100%
SiO2 (с добавками)
|
|
Радиус
сердцевины волокна, мкм
|
4.70
|
4.60
|
4.60
|
Таблица 3.3.
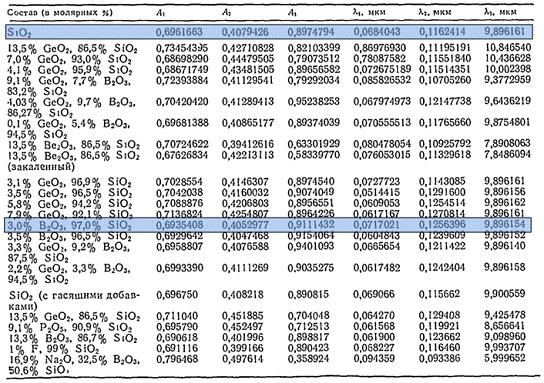
Графики зависимости показателей преломления
сердцевины и оболочки от длины волны для моделируемого волокна SMF-28,
рассчитанные по выражению (3.25), представлены на рис. 3.6.
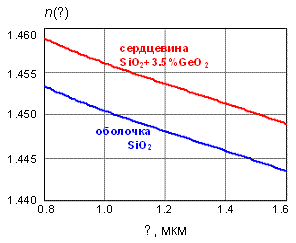
Рис. 3.6. Зависимости показателей
преломления сердцевины и оболочки от длины волны для волокна SMF-28 (Corning).
Нормированные функции распределения
поля основной моды для моделируемого волокна SMF-28 на разных длинах волн
представлены на рис. 3.7.
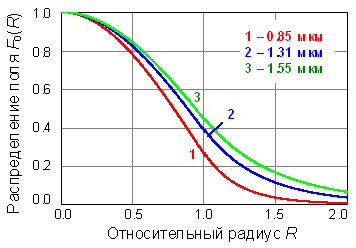
Рис. 3.7. Распределение поля
основной моды для волокна SMF-28 (Corning).
На рис. 3.8 представлены зависимости
коэффициента затухания изогнутого участка волокна SMF-28 от радиуса изгиба.
Расчеты проведены для длин волн двух основных окон прозрачности - 1310 и 1550
нм, а также для длины волны внеполосного контроля 1625 нм. Из рисунка видно,
что с уменьшением радиуса изгиба потери быстро возрастают. Кроме того, видно,
что потери растут с ростом длины волны.
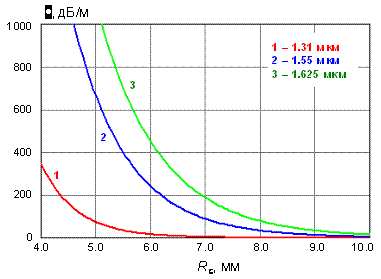
Рис. 3.8. Зависимость коэффициента
затухания изогнутого участка волокна SMF-28 (Corning) от радиуса изгиба на
разных длинах волн.
На рис. 3.9 представлены зависимости
коэффициента затухания изогнутого участка волокна SMF-28 от длины волны при
разных радиусах изгиба.
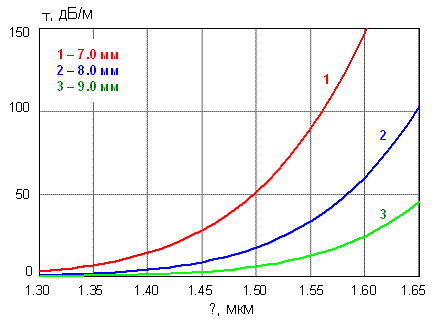
Рис. 3.8. Зависимость коэффициента
затухания изогнутого участка волокна SMF-28 (Corning) от длины волны при разных
радиусах изгиба.
Представленные результаты в главе 5 сопоставлены
с экспериментально измеренными величинами.
Ниже представлены результаты расчета
коэффицентов затухания изогнутых участков двух других волокон из табл. 3.1.
Параметры, которые использовались для моделирования этих волокон приведены в
табл. 3.2.
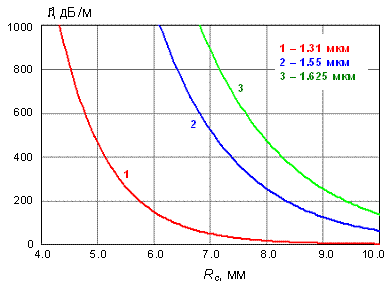
Рис. 3.9. Зависимость коэффициента
затухания изогнутого участка волокна SM-332 (OFS) от радиуса изгиба на разных
длинах волн.
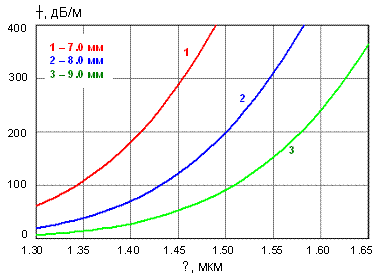
Рис. 3.10. Зависимость коэффициента
затухания изогнутого участка волокна SM-332 (OFS) от длины волны при разных
радиусах изгиба.
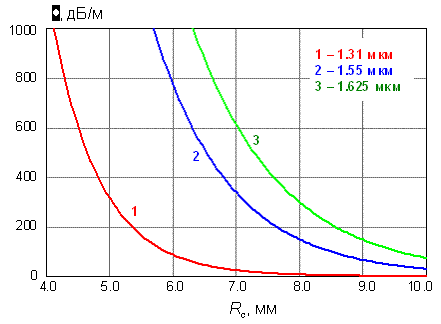
Рис. 3.11. Зависимость коэффициента
затухания изогнутого участка волокна SF-SMF-x (Samsung Electronics) от радиуса
изгиба на разных длинах волн.
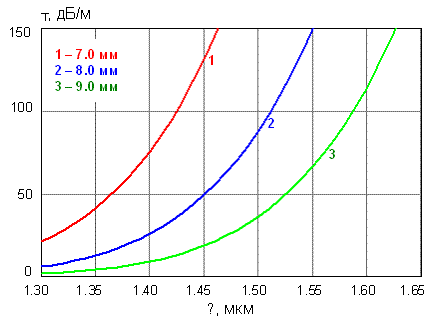
Рис. 3.12. Зависимость коэффициента
затухания изогнутого участка волокна SF-SMF-x (Samsung Electronics) от длины
волны при разных радиусах изгиба.
Проведенные расчеты показали, что потери в
изогнутом участке волокна существенно зависят от его конструкции. Например,
было замечено, что они уменьшаются при увеличении высоты профиля. В табл. 3.4
представлены результаты расчета коэффициента затухания изогнутого участка для
волокон с чисто кварцевой оболочкой, диаметром сердцевины 4.5 мкм и различной
величиной высоты профиля, которая достигалась использованием для сердцевины
германиево-силикатных стекол с различной концентрацией легирующей примеси
оксида германия.
Таблица 3.4
|
Концентр.
легир. примеси GeO2, %
|
3.1
|
3.5
|
4.1
|
5.8
|
7.0
|
7.9
|
13.5
|
|
Высота
профиля на длине волны 1.55 мкм
|
0.0032
|
0.0038
|
0.0043
|
0.0061
|
0.0078
|
0.0083
|
0.0149
|
|
Коэфф.
затух. изогн. участ. (дБ/м) на дл. волны 1.55 мкм с радиусом
|
3
мм
|
12593.1
|
6140.0
|
2500.2
|
48.4
|
0.31
|
0.044
|
7.6×10-15
|
|
4
мм
|
5539.6
|
1971.8
|
558.1
|
2.47
|
2.6×10-3
|
1.9×10-4
|
0.0
|
|
5
мм
|
2516.7
|
654.0
|
128.7
|
0.13
|
2.2×10-5
|
8.2×10-7
|
0.0
|
|
6
мм
|
1167.0
|
221.4
|
30.28
|
0.007
|
2.0×10-7
|
3.7×10-9
|
0.0
|
Из таблицы 3.4 видно, что изгибные потери быстро
убывают с ростом высоты профиля. Однако увеличение высоты профиля приводит к
ухудшению других параметров волокна, например, к уменьшению диаметра модового
поля.
Заключение
В диссертации в результате проведенных
теоретических и расчетных исследований, направленных на решение поднятой
проблемы:
рассмотрены конструкции и параметры различных
типов оптических волокон, применяемых в современных ВОЛС;
описаны причины появления изгибов оптических
волокон;
предложена методика расчета зависимостей
коэффициента затухания изогнутого участка волокна от радиуса изгиба и длины
волны;
выполнены практические расчеты изгибных потерь;
проведено исследование изгибных потерь в
одномодовых стандартных оптических волокнах и в волокнах с ненулевой смещенной
дисперсией в проходящем и рассеянном свете.
Литература
Былина
М.С., Глаголев С.Ф., Кочановский Л.Н., Пискунов В.В. Измерение параметров
волоконно-оптических линейных трактов: Учебное пособие/СПб ГУТ. - СПб, 2002.
Снайдер
А., Лав Д. Теория оптических волноводов - М.: Радио и связь, 1987.
Адамс
М. Введение в теорию оптических волноводов - М.: Мир, 1984.
Рекомендации
МСЭ-Т.
Ландсберг
Г. С. Оптика. Учеб. пособие: Для вузов. - 6-е изд., стереот. - М.: ФИЗМАТЛИТ,
2003.
Борн
М., Вольф Э. Основы оптики. Издание 2-е. Перевод с английского. Главная
редакция физико-математической литературы изд-ва «Наука», 1973.
Листвин
А. В., Листвин В. Н. Рефлектометрия оптических волокон - М.: ЛЕСАРарт, 2005.
Листвин
А. В., Листвин В. Н., Швырков Д. В. Оптические волокна для линий связи, М.:
ЛЕСАРарт, 2003.
Иванов
А.Б. Волоконная оптика. Компоненты, системы передачи, измерения, М.: Изд.
Syrus. Systems, 1999.
Наний
О.Е., Павлова Е.Г., МГУ им. М.В. Ломоносова, физический факультет. Материалы
статьи «Фотонно-кристаллические волокна» из журнала «LIGHTWAVE» российский
выпуск №3, 2004.
Боголюбов
А.Н., Буткарев И.А., Свешников А.Г. Синтез волоконных световодов.
Аксенов
В.А., Замятин А.А., Иванов Г.А., Исаев В.А., Маковецкий А.А.
Микроструктурированные кварцевые волоконные световоды, полученные методом
капиллярной сборки.
Яковлев
М.Я., Цуканов В.Н. Устройство диагностики волоконно-оптических трактов.
Слепов
Н.Н. Фотоника, 2007, № 4,6.
Слепов
Н.Н. Фотонно-кристаллическое волокно - уже реальность. - Электроника: НТБ,
2004, №5.
Развитие
технологий оптической связи и волокон: Материалы семинара Corning. - Москва, 28
ноября 2007.
Влияние
изгибов оптических волокон на их характеристики (по материалам технического
симпозиума общего собрания Ассоциации «Интеркабель») - Наука и техника №4(293),
2005.
Петренко
А., Никитченко Ю., Василенко Б., Беда А. (отдел волоконно-оптических технологий
и кабельных сетей, компания «Deps»). Волокно на карандаше или Волокно стремится
к дому, 16.12.2008.
Иванов
А.Б., Соколов И.В. Современные технологии OTDR. - Электросвязь, 11, 1998.
Гладышевский
М.А. и др. Оптическое волокно для систем передачи информации. - Волоконная
оптика, М.: ВиКо, 2002.
Гроднев
И.И., Мурадян А.Г., Шарафутдинов Р.М. и др. Волоконно-оптические системы
передачи и кабели. Справочник. - М.: Радио и связь, 1993.
Убайдуллаев
Р.Р. Волоконно-оптические сети. - Эко-Трендз, Москва, 2000.
Материалы
статьи
«Bend it like Corning» Stephanie N. Mehta из
журнала
«Fortune», 6 августа 2007.
Материалы
статьи «New technology provides breakthrough for MDU fiber
installation»
Bernhard Deutsch and David R. Velasquez из
журнала
«LIGHTWAVE», октябрь 2007.