Математическая модель когнитивной структуры обучающего пространства
Министерство образоваия и науки Российской
Федерции
Федеральное государственное бюджетное
образовательное учреждение
высшего профессионального образования
"Кубанский государственный
университет" (ФГБОУ ВПО "Кубу")
Кафедра теории функций
Выпускная
квалификационная работа бакалавра
Математическая
модель когнитивной структуры обучающего пространства
Работу выполнил
В.А. Бакуридзе
Научный руководитель
канд. физ.-мат. наук, доцент
Б.Е. Левицкий
Нормоконтролер,
ст. лаборант Н.С. Катачина
Краснодар
2015
Содержание
Введение
.
Основные обозначения и предварительные сведения
.
Навыки
.
Карты навыков: дизъюнктивная модель
.
Минимальная карта навыков
.
Карты навыков: конъюнктивная модель
.
Мультикарты навыков: модель компетентности
.
Маркировки и фильтры
.1
Примеры маркировки
.2
Отражение уровня знаний посредством оценки
Заключение
Список
используемых источников
Введение
Работа носит реферативный характер и посвящена
изучению одного из разделов монографии Ж-Кл. Фалмажа и Ж-П. Дуанона (см. [1]),
название которой переводится на русский язык, как
"Обучающиепространства". Монография посвящена построению абстрактной
математической теории, развивающей формальные методы для изучения взаимосвязей
и отношений состояний знаний субъектов в определенной предметной области.
В работе дан адаптированный перевод на русский
язык части одной из глав монографии, которая называется "Карты навыков,
метки и фильтры". В этой главе развивается формальный аппарат для
исследования отношений между состояниями знаний и тем, что принято называть
"навыками". Предполагается, что для достижения определенного
состояния знаний необходим некоторый объем навыков  .
.
Идея авторов заключается в том, чтобы с каждым
вопросом (проблемой) q из домена Q связать подмножество навыков из S, которые
можно использовать для ответа на вопрос q (решения проблемы q). Наряду с
поясняющими примерами, приведенными авторами в работе, приводятся аналогичные
примеры из курса "Комплексный анализ".
В первом разделе дипломной работы приведены
необходимые сведения из первых глав монографии [1], адаптированный перевод
которых был выполнен в дипломных работах Т.В. Алейниковой [2] и Н.А. Ралко [3].
Во втором разделе выполнен адаптированный
перевод соответствующего раздела монографии [1] с примером (см. п. 2.1), на
основе которого в третьем разделе вводится формализованное понятие "карты
навыков". По аналогии с этим примером самостоятельно построен пример из
курса "Комплексный анализ" (см. п. 2.2.).
В четвертом разделе рассматривается понятие
минимальной карты навыков. Конъюктивная модель карты навыков обсуждается в
разделе 5.
В разделе 6 дано формализованноеопределение
модели компетентности. Последний раздел дипломной работы посвящен проблеме
описания (маркировки) элементов и интеграции (фильтров) соответствующей
справочной информации, содержавшейся в состояниях знаний.
1. Основные обозначения и предварительные
сведения
Определение 1 (см. [1, п. 2.1.2]) .Структурой
знаний называется пара (Q, К), в которой Qявляется непустым множеством, а
К-семейство подмножеств Q, содержащее, по меньшей мере, Q и пустое множество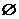 .
Множество Q называется доменом структуры знаний. Его элементы называются
вопросами или позициями, а подмножества семейства. К называются состояниями
знаний.
.
Множество Q называется доменом структуры знаний. Его элементы называются
вопросами или позициями, а подмножества семейства. К называются состояниями
знаний.
Определение 2 (см.[1, п. 2.2.1]).
Структура
знаний (Q,К) называется обучающим пространством, если выполняются два следующих
условия:
{L1} Гладкость обучения. Для любых двух
состояний K, L таких, что
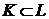 , существует
конечная цепь состояний
, существует
конечная цепь состояний
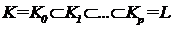 (2.2)
(2.2)
для которой |Ki\ Ki-1| = 1 для 1 ≤ i ≤
p и |L \ K| = р.
{L2} Согласованность обучения. Если K, L два
состояния знаний, такие что 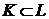 и
q
представляет собой вопрос (позицию), такую что K + {q}
и
q
представляет собой вопрос (позицию), такую что K + {q}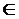 К,
то
К,
то 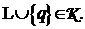
Определение 3 (см. [1, п. 2.2.2]).Семейство
множеств
К
называется замкнутым относительно объединения, если 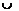 F
F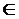 K
для любых F
K
для любых F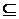 К. В частности,
К. В частности, 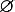
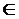 К, потому что
объединение пустых подсемейств является пустым множеством. Если семейство К
структуры знаний (Q, К) замкнуто относительно объединения, то пара (Q, К)
называется пространством знаний. Иногда в этом случае говорят, что К
пространство
знаний. Будем говорить, что К замкнуто
относительно конечного объединения, если для любых К и L из К
множество
K
К, потому что
объединение пустых подсемейств является пустым множеством. Если семейство К
структуры знаний (Q, К) замкнуто относительно объединения, то пара (Q, К)
называется пространством знаний. Иногда в этом случае говорят, что К
пространство
знаний. Будем говорить, что К замкнуто
относительно конечного объединения, если для любых К и L из К
множество
K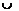 L
L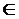 К.
К.
Отметим, что в этом случае пустое множество не
обязательно принадлежит семейству К.
Двойственной структурой знаний на Q по отношению
к структуре знаний К является структура знаний 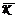 ,
содержащая все дополнения состояний К, то есть
,
содержащая все дополнения состояний К, то есть
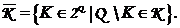
Таким образом, Ки 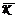 имеют
одинаковый домен. Очевидно, что если К
пространство знаний, то
имеют
одинаковый домен. Очевидно, что если К
пространство знаний, то 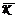 - структура
знаний, замкнутая относительно пересечения, то есть
- структура
знаний, замкнутая относительно пересечения, то есть 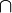 F
F
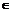
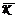 для любых F
для любых F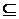
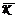 , причем
, причем 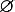 ,
Q
,
Q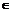
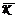 .
.
Определение 4 (см. [1, п. 3.3.1]).Под коллекцией
на множестве Q будем понимать семейство K подмножеств домена Q. Для обозначения
коллекции часто пишут (Q, K). Заметим, что коллекция может быть пустой.
Коллекция (Q, L) есть замкнутое пространство, когда семейство L содержит Q и
замкнуто относительно пересечения. Это замкнутое пространство называется
простым, если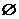 принадлежит
L.
Таким образом, коллекция K подмножеств домена Q является пространством знаний
на Q, тогда и только тогда, когда двойственная структура
принадлежит
L.
Таким образом, коллекция K подмножеств домена Q является пространством знаний
на Q, тогда и только тогда, когда двойственная структура 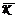 является
простым замкнутым пространством.
является
простым замкнутым пространством.
Определение 5 (см. [1, п. 1.6.10]).Цепью в
частично упорядоченном множестве (X, P) называется любое подмножество C
множества
X, такое что cPc′ или c′Pc для всех с, с’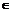 C
(другими словами, порядок, индуцируемый отношением P на
C,
является линейным порядком).
C
(другими словами, порядок, индуцируемый отношением P на
C,
является линейным порядком).
Определение 6 (см. [1, п. 4.1.1]).Обучающей
траекторией в структуре знаний (Q,K) (конечной или бесконечной) является
максимальная цепь Cв частично упорядоченном множестве (K,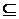 ).
Согласно определению цепи, имеем c
).
Согласно определению цепи, имеем c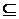 c’
или
c’
c’
или
c’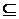 c
для
всех с, с’
c
для
всех с, с’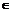 C. Цепь C
является
максимальной, если из условия C
C. Цепь C
является
максимальной, если из условия C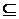 C‘
для
некоторой цепи состояний C‘ следует, что
С=C‘.
Таким образом, максимальная цепь обязательно содержит
C‘
для
некоторой цепи состояний C‘ следует, что
С=C‘.
Таким образом, максимальная цепь обязательно содержит 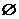 и
Q.
и
Q.
Определение 7 (см. [1, п. 3.4.1]).Охватом
семейства множеств G называется семейство G′, содержащее любое множество,
которое является объединением некоторого подсемейства из G. В этом случае пишут
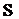 (G)=G′
и говорят, что G охватывается
G′.
По определению
(G)=G′
и говорят, что G охватывается
G′.
По определению 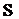 (G) замкнуто
относительно объединения. Базой замкнутого относительно объединения семейства F
называется
минимальное подсемейство B из F, охватывающее F(здесь "минимальность"
определяется по отношению к включению множеств: если
(G) замкнуто
относительно объединения. Базой замкнутого относительно объединения семейства F
называется
минимальное подсемейство B из F, охватывающее F(здесь "минимальность"
определяется по отношению к включению множеств: если 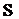 (H)=F
для
некоторого H
(H)=F
для
некоторого H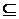 B, тогда H=B).
Принято считать, что пустое множество это объединение пустых подсемейств из B.
Таким образом, поскольку база - минимальное подсемейство, то пустое множество
не может принадлежать базе. Очевидно, что состояние K, принадлежащее некоторой
базе B из K не может быть объединением других элементов из B. Кроме того,
структура знаний имеет базу только, если она является пространством знаний.
B, тогда H=B).
Принято считать, что пустое множество это объединение пустых подсемейств из B.
Таким образом, поскольку база - минимальное подсемейство, то пустое множество
не может принадлежать базе. Очевидно, что состояние K, принадлежащее некоторой
базе B из K не может быть объединением других элементов из B. Кроме того,
структура знаний имеет базу только, если она является пространством знаний.
Теорема 1 ([1, теорема 3.4.2]). Пусть B является
базой для пространства знаний (Q, K). Тогда B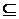 F
для некоторого подсемейства состояний F, охватывающего K. Следовательно,
пространство знаний допускает не более одной базы.
F
для некоторого подсемейства состояний F, охватывающего K. Следовательно,
пространство знаний допускает не более одной базы.
Определение 8 (см. [1, п. 1.6.12]).
Симметрично-разностным расстоянием или каноническим расстоянием на множестве
всех подмножеств множества конечного множества Е,
называется величина:
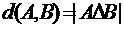 ,
,
определенная для любых
А,
В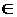 2E. Здесь,
2E. Здесь, 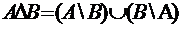 обозначает
симметрическую разность множеств
А
и В.
обозначает
симметрическую разность множеств
А
и В.
2. Навыки
Познавательные интерпретации приведенных выше
математических понятий ограничиваются использованием слов, вызывающих
ассоциации с процессом обучения, таких как "структура знаний",
"состояние знаний", или "обучающая траектория". Это связано
с тем, что многие результаты, полученные в [1] потенциально применимы к самым
различным научным областям. Можно заметить, что введенные фундаментальные
понятия согласуются с таким традиционным понятием психометрической теории, как
"навыки". В этой главе
исследуются некоторые возможные отношения между состояниями знаний, навыками и
другими особенностями элементов.
Для любой структуры знаний
(Q,
К)
предполагается существование некоторого основного набора "навыков"S.
Эти навыки могут состоять из методов, алгоритмов или приемов, которые в
принципе возможно идентифицировать. Идея состоит в том, чтобы связать с каждым
вопросом (задачей) q из домена Q навыки
из
S,
которые полезны или способствуют тому, чтобы ответить на этот вопрос (решить
задачу) и сделать вывод каково состояние знаний. В [1] приведен следующий
пример.
Пример 2.1 составления программы на языке UNIX.
Вопрос a): Сколько
строк файла "lilac" (сиреневый) содержит слово "purple"
(фиолетовый)? (Позволена только одна командная строка.)
Проверяемый объект соответствует вводимой
командной строке UNIX. Ответ на этот вопрос может быть получен множеством
методов, три из которых упомянуты ниже. Для каждого метода мы приводим
командную строку в печатной форме, следующую за знаком ">":
>greppurplelilac | wc
Система отвечает, приводя три числа; первое -
является ответом на вопрос. (Команда 'grep', сопровождаемая этими двумя
параметрами `purple' and `lilac', извлекает все строки, содержащие слово,
`purple' из файла `lilac'; команда '|' (разделитель) направляет этот вывод к
команде подсчета слов "wc", которая выводит число строк, слов и
символов в этом выводе).
>catlilac | greppurple | wc
Это менее эффективное решение, достигающее того
же результата. (Команда "cat" требует перечисления файла
"lilac", что не является необходимым.)
>morelilac | greppurple | wc;
Аналогично предыдущему решению.
Исследование этих трех методов предлагает
несколько возможных типов связей между навыками и вопросами и соответствующих
способов определить состояния знаний, соответствующие этим навыкам. Простая
идея состоит в том, чтобы рассматривать каждый из этих трех методов как навык.
Полный набор навыков S содержал бы эти три навыка и некоторые другие. Связь
между вопросами и навыками, таким образом, могла
бы быть формализована функцией: 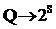 ,
сопоставляющей каждому вопросу q подмножество τ(q) множества
навыков
S.
В частности, мы получили бы:
,
сопоставляющей каждому вопросу q подмножество τ(q) множества
навыков
S.
В частности, мы получили бы:
Рассмотрим объект, включающий определенное
подмножество T навыков, содержащее некоторые навыки из τ(a)
плюс некоторые другие навыки, относящиеся к другим вопросам; например,
= {(1); (2); s; s’}.
Эта совокупность навыков обеспечивает решение
задачи а), поскольку T∩τ(a)
= {1; 2} ≠  . Фактически,
состояние знания K,соответствующее этой совокупности, включает все те задачи,
которые могут быть решены с использованием, по крайней мере, одного
из
навыков,
содержащихся в T; то есть
. Фактически,
состояние знания K,соответствующее этой совокупности, включает все те задачи,
которые могут быть решены с использованием, по крайней мере, одного
из
навыков,
содержащихся в T; то есть
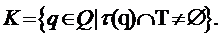
Эта связь между навыками и состояниями
исследована в следующем разделе, под названием "дизъюнктивная
модель". Мы увидим, что структура знаний, индуцированная дизъюнктивной
моделью, непременно является пространством знаний. Этот факт доказан в Теореме
3.3. Мы также кратко, для полноты картины, рассмотрим модель, которую назовем
"конъюнктивной" и которая является двойственной дизъюнктивной модели.
В дизъюнктивной модели только один из навыков, связанных с задачей
q
достаточен, чтобы решить эту задачу. В случае конъюнктивной модели требуются
все навыки, соответствующие данному элементу. Таким образом, K- состояние
знаний, если существует набор T навыков, таких, что для каждого элемента q,
имеем
q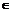 K
только,
еслиτ(q)
K
только,
еслиτ(q)
 (в
отличие от требования τ(q)
(в
отличие от требования τ(q) Т≠
Т≠
 для
дизъюнктивной модели). Конъюнктивная модель формализует ситуацию, в который для
любого вопроса q, есть уникальный метод решения, представленный множествомτ(q),
которое
включает все требуемые навыки. Получающаяся структура знаний замкнута
относительно
пересечения.
Будут
рассмотрены также различные типы связей между навыками и состояниями.
Дизъюнктивные и конъюнктивные модели были получены из элементарного анализа
Примера 2.1, в котором сами три метода рассматривались как навыки, несмотря на
то, что
в
каждом случае требовалось применение нескольких команд.
для
дизъюнктивной модели). Конъюнктивная модель формализует ситуацию, в который для
любого вопроса q, есть уникальный метод решения, представленный множествомτ(q),
которое
включает все требуемые навыки. Получающаяся структура знаний замкнута
относительно
пересечения.
Будут
рассмотрены также различные типы связей между навыками и состояниями.
Дизъюнктивные и конъюнктивные модели были получены из элементарного анализа
Примера 2.1, в котором сами три метода рассматривались как навыки, несмотря на
то, что
в
каждом случае требовалось применение нескольких команд.
Более тщательный анализ можно было бы получить,
рассматривая каждую команду как навык, включая команду '|'
("разделитель"). Полный набор навыков S имел бы вид
= {grep; wc; cat, |, more, s1, …,sk},
где, как и прежде, s1, …, sk
соответствуют
навыкам, относящимся к другим вопросам в рассматриваемом домене.
Чтобы
найти
ответ на
вопрос
a), может использоваться подходящее подмножество S. Например, объект,
соответствующий подмножеству навыков
R = {grep; wc; |; more; s1; s2}
мог бы стать решением вопроса а) при
использовании либо
Метода
1. Либо
Метода
3. В действительности, два релевантных набора команд включены в набор навыков
R; а именно, {grep; wc; |} ⊆R и {more,
grep, wc,|} ⊆R.
Этот пример наводит на размышления о более
сложной связи между вопросами и навыками.
Мы постулируем существование функции 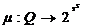 ,
связывающей каждый вопрос q с множеством всех подмножеств множества навыков,
соответствующих возможным решениям. В случае вопроса a), имеем
,
связывающей каждый вопрос q с множеством всех подмножеств множества навыков,
соответствующих возможным решениям. В случае вопроса a), имеем
μ (a) = {{grep; |; wc}; {cat; grep; |; wc};
{more; grep; |; wcg}}.
В целом объект,
включающий некоторый набор навыков R, способен к решению некоторого вопроса q,
если в μ(q)существует,
по крайней мере, один элемент C такой, что C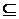 R. Каждое из подмножеств C в μ(q)
будет упоминаться как "компетентность для" q. Эта определенная связь
между навыками и состояниями будет рассмотрена под именем "модель
компетентности".
R. Каждое из подмножеств C в μ(q)
будет упоминаться как "компетентность для" q. Эта определенная связь
между навыками и состояниями будет рассмотрена под именем "модель
компетентности".
Пример 2.1 может привести к мысли, что навыки,
связанные с определенным доменом (определенным фрагментом области знаний),
могут быть легко идентифицированы. В действительности, далеко не очевидно, как
такая идентификация вообще возможна. Для большей части этой главы мы оставим
набор навыков не специфицированным и будем рассматривать S как абстрактное
множество. Наше внимание будет сосредоточено на формальном анализе некоторых
возможных связей между вопросами, навыками и состояниями знаний. Познавательные
или образовательные интерпретации этих навыков будут отложены до последнего
раздела этой главы, где мы обсуждаем возможную систематическую маркировку
элементов, которые могли привести к идентификации навыков, и более широко - к
описанию содержания самих состояний знаний.
Пример 2.2 из теории функции комплексного
переменного.
Рассмотрим задачу вычисления интеграла:
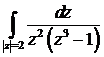 .
.
Существуют три способа решения задачи.
Первый способ (решение с использованием теоремы
Коши о вычетах):
Алгоритм вычисления контурных интегралов с
помощью вычетов:
. Найти особые точки функции
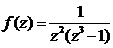 .
.
. Определить, какие из этих точек расположены в
области 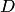 ,
ограниченной контуром
,
ограниченной контуром 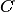 . Для этого
достаточно сделать чертеж: изобразить контур
. Для этого
достаточно сделать чертеж: изобразить контур 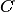 и
отметить особые точки.
и
отметить особые точки.
. Вычислить вычеты в тех особых точках, которые
расположены в области
Все особые точки подынтегральной функции
расположены в круге 
Находим корни уравнения 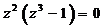 :
:
 - полюс кратности
2.
- полюс кратности
2.
Корни уравнения 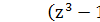 находятся
по формуле:
находятся
по формуле:
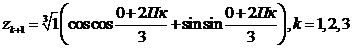 ;
;
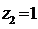 ,
,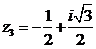 ,
,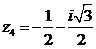
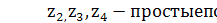 ..
..
Имеем 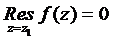 ,
,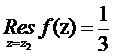 ,
,
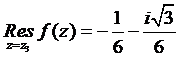 ,
,
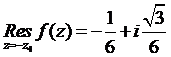 .
.
Следовательно, по теореме Коши о вычетах:
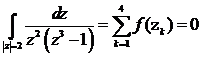
Используемые навыки:
1) Нахождение особых точек (А)
) Умение извлекать корень из комплексного числа
(B)
) Вычисление вычетов (С)
) Умение применять теорему Коши о вычетах (D)
Второй способ (решение с использованием интегральной
формулы Коши для производных):
Алгоритм вычисления контурных интегралов с
помощью интегральной формулы Коши для производных:
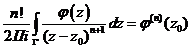 , n = 0,1,2,… .
, n = 0,1,2,… .
. Найти особые точки функции 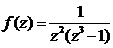 .
.
. Определить, какие из этих точек расположены в
области 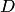 ,
ограниченной контуром
,
ограниченной контуром 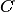 :
:  .
Для этого достаточно сделать чертеж: изобразить контур
.
Для этого достаточно сделать чертеж: изобразить контур 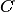 и
отметить особые точки (см. рис. 1).
и
отметить особые точки (см. рис. 1).
. Вычислить по интегральной формуле Коши для
производных следующие интегралы:
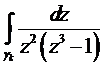 ,
,
где 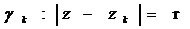 ,r>
0 - достаточно мало, zk (k = 1,2,3,4) - особые точки подынтегральной функции,
расположенные внутри круга
,r>
0 - достаточно мало, zk (k = 1,2,3,4) - особые точки подынтегральной функции,
расположенные внутри круга  :
:
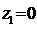 ,
,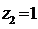 ,
,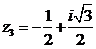 ,
,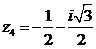 (смотреть рисунок 1).
(смотреть рисунок 1).
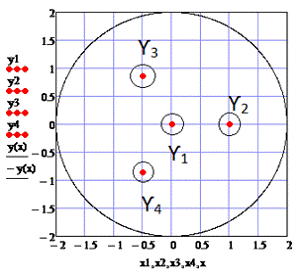
Рисунок 1 - Вычисление интеграла с помощью
интегральной формулы Коши
) Полагая 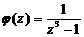 ,
находим:
,
находим:
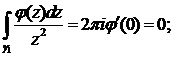
) Полагая 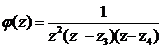 ,
находим:
,
находим:
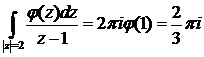
) Полагая,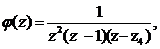 находим:
находим:
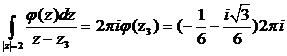
4) Полагая,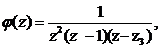 находим:
находим:
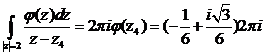
Используемые навыки:
) нахождение особых точек (А)
)умение извлекать корень из комплексного
числа(B)
) умение применять интегральную формулу Коши(E)
) умение применять интегральную формулу Коши для
производ. (F)
Третий способ:
По теореме о полной сумме вычетов:
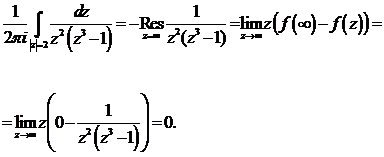
Используемые навыки:
) Умение находить особые точки (G)
) Нахождение вычета в бесконечно удаленной
точке(I)
) Умение применять теорему о полной сумме
вычетов (J)
Анализируя три решения интеграла 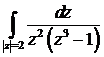 ,
приведенные выше, заметим, что самым эффективным решением является последнее,
так как мы не нуждаемся в вычислениях вычетов в конечных точках.
,
приведенные выше, заметим, что самым эффективным решением является последнее,
так как мы не нуждаемся в вычислениях вычетов в конечных точках.
3. Карты навыков: дизъюнктивная модель
Определение 3.1 Картой навыков называется тройка
(Q;S; ),
где Q-непустоемножество элементов, S- непустое множество навыков, и τ
- отображение
из
Q
в
2S \ {
),
где Q-непустоемножество элементов, S- непустое множество навыков, и τ
- отображение
из
Q
в
2S \ {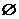 }.
В случае, если множества Q
и
S
понятны
из контекста, картой навыков называется функцияτ. Для
любого q из Qподмножествоτ(q) из S будет
рассматриваться как множество навыков, сопоставленных q (картойнавыковτ).
Пусть
(Q;
S;
τ)
- карта навыков и T- подмножество S.
Говорят,
что K
}.
В случае, если множества Q
и
S
понятны
из контекста, картой навыков называется функцияτ. Для
любого q из Qподмножествоτ(q) из S будет
рассматриваться как множество навыков, сопоставленных q (картойнавыковτ).
Пусть
(Q;
S;
τ)
- карта навыков и T- подмножество S.
Говорят,
что K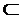 Q представляет состояние знаний, сформированное множеством
T
в рамках дизъюнктивной модели, если
Q представляет состояние знаний, сформированное множеством
T
в рамках дизъюнктивной модели, если
= {q 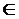 Q
| τ
(q)
Q
| τ
(q)
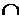 T
≠
T
≠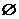 }.
}.
Заметим, что пустое подмножество навыков
формирует пустое
состояние
знаний (поскольку τ(q)≠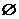 для каждого элемента q), и множество S
формирует
состояние
знаний Q. Семейство всех состояний знаний, сформированных
под
множествами
S,
является структурой знаний, сформированной картой навыков (Q;S;τ)
(дизъюнктивная
модель). Когда термин "сформировано" картой навыков
использован
без
ссылки на определенную модель, подразумевается, что рассматривается дизъюнктивная
модель. В случае, когда все неоднозначности устраняются содержанием контекста,
семейство всех состояний, сформированных подмножествами из
S,
называется сформированной структурой знаний.
для каждого элемента q), и множество S
формирует
состояние
знаний Q. Семейство всех состояний знаний, сформированных
под
множествами
S,
является структурой знаний, сформированной картой навыков (Q;S;τ)
(дизъюнктивная
модель). Когда термин "сформировано" картой навыков
использован
без
ссылки на определенную модель, подразумевается, что рассматривается дизъюнктивная
модель. В случае, когда все неоднозначности устраняются содержанием контекста,
семейство всех состояний, сформированных подмножествами из
S,
называется сформированной структурой знаний.
Пример3.2Пусть Q = {а, b, c, d, e} и S = {s, t,
u, v}. Определим
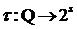 , полагая
, полагая
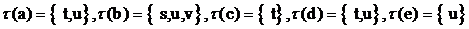
Таким образом (Q;S;τ)
является картой навыков. Состоянием знаний, сформированным множеством навыков
T
= {s, t} является {а, b, c, d}. С другой стороны, {а, b, c} не является
состоянием
знаний, так как не может быть сформировано никаким подмножеством R из S.
Действительно, такое подмножество R обязательно содержало бы t (поскольку
должно содержать ответ на вопрос); таким образом, состояние знаний,
сформированное R, также содержало
бы d. Сформированной структурой знаний является множество
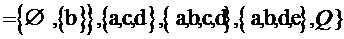
Заметим, что K - пространство знаний. Это не
случайность, поскольку имеет место следующий результат:
Теорема 3.3. Любая структура знаний,
сформированная
картой навыков, (в рамках дизъюнктивной модели) является пространством знаний.
Обратно, любое пространство знаний является сформированным, по крайней мере,
одной картой навыков.
Доказательство
Предположим, что (Q; S; Т) - карта навыков, и
пусть (Кi) iϵ I
некоторое
произвольное подмножество
сформированных
состояний. Если, для кого-либо iϵI,
состояние Кi сформировано
подмножеством Ti из
S,
то легко проверить, что 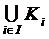 сформировано
сформировано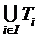 ;
то есть
;
то есть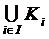 также
является состоянием знаний. Таким образом, структура знаний, сформированная
картой навыков, всегда является пространством знаний. Обратно,
пусть(Q;
K) пространство знаний. Мы построим карту навыков, выбрав
S
= Kи полагая τ(q) = Kq для любого q ϵ
Q. (Состояния знаний, содержащие q, определяются, таким
образом, навыками, соответствующими q; заметим, что τ(q)
≠ ᴓ следует из того, что q ϵ
Q ϵK).
Для T
также
является состоянием знаний. Таким образом, структура знаний, сформированная
картой навыков, всегда является пространством знаний. Обратно,
пусть(Q;
K) пространство знаний. Мы построим карту навыков, выбрав
S
= Kи полагая τ(q) = Kq для любого q ϵ
Q. (Состояния знаний, содержащие q, определяются, таким
образом, навыками, соответствующими q; заметим, что τ(q)
≠ ᴓ следует из того, что q ϵ
Q ϵK).
Для T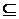 S
= K, проверим, что состояние K, сформированное
T
принадлежит
K.
Действительно, имеем
S
= K, проверим, что состояние K, сформированное
T
принадлежит
K.
Действительно, имеем
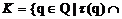 T
T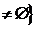
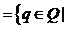 Kq
Kq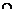 T
T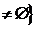
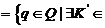 K,
K,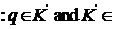 T
T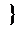
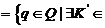 T
T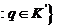
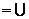 T
T
откуда следует, что Kϵ
K, поскольку K - пространство знаний. Наконец, мы покажем, что любое состояние
Kиз
K,
формируется некоторым подмножеством из S, а именно, подмножеством {K}.
Обозначая через L состояние, сформированное подмножеством {K}, получаем
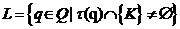
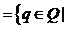 Kq
Kq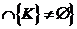
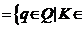 Kq
Kq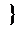
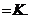
Откуда следует, что пространство K
сформировано
(Q; K; τ).
. Минимальная карта навыков
В последнем доказательстве мы построили для
произвольного пространства знаний специальную карту навыков, которая формирует
это пространство. Заманчиво расценить такое представление, как возможное
объяснение организации набора состояний, с помощью навыков, используемых, чтобы
освоить элементы этих состояний. В науке объяснения явлений обычно не
уникальны, и есть тенденция одобрить 'экономичные'. Материал в этом разделе
вдохновлен теми же соображениями.
Мы начнём с изучения ситуации, в которой два
отличных навыка различаются только простой перемаркировкой навыков. В таком
случае мы будем говорить об "изоморфных картах навыков, и будем иногда
говорить о таких картах навыков, что они являются
по
существу одинаковыми" по отношению к любому элементу q. Это понятие
изоморфизма дается в следующем определении.
Определение 4.1. Две карты навыка (Q; S; )
и (Q;
)
и (Q;  ;
; )
(с одинаковым набором Q элементов) изоморфны, если существует взаимно однозначное
отображение f множества S на
)
(с одинаковым набором Q элементов) изоморфны, если существует взаимно однозначное
отображение f множества S на  ,
котороедляпроизвольного
,
котороедляпроизвольного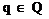 удовлетворяет
условию:
удовлетворяет
условию:
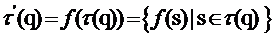
Функция f называется изоморфизмом между (Q; S; )и
(Q;
)и
(Q;  ;
; ).
).
Определение 4.1.
Определяет
изоморфизм карт навыков с одинаковым набором элементов. Более общая ситуация
рассматривается в Проблеме 2.
Пример 4.2 Пусть Q
= {а; b; c; d} и  = {1; 2; 3; 4}.
Определим карту навыков.
= {1; 2; 3; 4}.
Определим карту навыков.
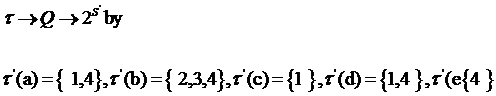
Карта навыков(Q;  ;
; )
изоморфна карте, приведённой в Примере 3.2: изоморфизм
)
изоморфна карте, приведённой в Примере 3.2: изоморфизм  задается
соотношениями:
задается
соотношениями:
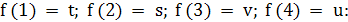
Следующий результат очевиден.
Теорема 4.3. Две изоморфных карты навыков (Q; S; )
и (Q;
)
и (Q;  ;
; )
формируют одинаковые пространства знаний на Q.
)
формируют одинаковые пространства знаний на Q.
Замечание 4.4. Две карты навыков могут
формировать одинаковые пространства знаний, не будучи изоморфными. В качестве
иллюстрации заметим, что, удаляя навык v из набора S в Примере 2.2 и
переопределяяτ, положив
τ(b)
= {с;
u}, приходим к тому же сформированному пространству K. Навык v, таким образом,
имеет первостепенное значение для формирования рисунка K. Как упомянуто во
введении в этот раздел, в науке общепринято искать экономные объяснения явлений
в ходе исследования. В нашем контексте это представлено предпочтением
небольших, возможно минимальных, наборов навыков. Точнее, мы назовем карту
навыков
"минимальной",
если удаление любого навыка изменяет сформированное
состояние
знаний.
Если это пространство знаний является конечным, минимальная карта навыков
существует
всегда и содержит наименьшее из возможных число навыков. (Это утверждение
следует из Теоремы 4.3.) В случае, если пространство знаний не является
конечным, ситуация несколько более сложная, потому что минимальная карта
навыков не обязательно существует. Однако карта навыков, формирующая
пространство знаний и имеющая минимальное кардинальное число существует всегда,
поскольку класс всех кардинальных чисел является вполне упорядоченным. Следует
отметить, что такая карта навыков с минимальным числом навыков не обязательно
определена единственным образом, даже с точностью до изоморфизма.
Пример 4.5. Рассмотрим семейство
O
всех
открытых подмножеств множества R вещественных
чисел и пусть J произвольное
семейство открытых интервалов из  ,
охватывающих O. Для
,
охватывающих O. Для , положим
, положим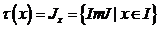 .
Тогда карта навыков(R;J;
.
Тогда карта навыков(R;J; ), формирует
пространство (R; O). Действительно, подмножество T
из J формирует состояние знаний
), формирует
пространство (R; O). Действительно, подмножество T
из J формирует состояние знаний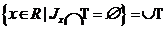 , и, кроме того,
открытое подмножество O формируется
семейством
тех интервалов из J, которые содержатся в O (
, и, кроме того,
открытое подмножество O формируется
семейством
тех интервалов из J, которые содержатся в O (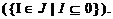 Известно,
что существует счетные семейства J, удовлетворяющие вышеупомянутым условиям.
Заметим, что такие счетные семейства порождают
карты навыков с минимальным числом навыков, то есть с множеством навыков
минимальной мощности (минимальным кардинальным числом). Тем не менее,
не
существует минимальной карты навыков. Это может быть доказано непосредственно
или выведено из Теоремы 4.8. Что касается единственности, то минимальные карты
навыков, формирующие данное пространство знаний, являются изоморфными. Это
будет показано в Теореме 4.8. Эта теорема также дает характеристику пространств
знаний, обладающих базой (в смысле
определения 5). Такие пространства знаний в точности совпадают с пространствами
знаний, которые могут быть сформированы какой-либо
минимальной картой навыков.
Известно,
что существует счетные семейства J, удовлетворяющие вышеупомянутым условиям.
Заметим, что такие счетные семейства порождают
карты навыков с минимальным числом навыков, то есть с множеством навыков
минимальной мощности (минимальным кардинальным числом). Тем не менее,
не
существует минимальной карты навыков. Это может быть доказано непосредственно
или выведено из Теоремы 4.8. Что касается единственности, то минимальные карты
навыков, формирующие данное пространство знаний, являются изоморфными. Это
будет показано в Теореме 4.8. Эта теорема также дает характеристику пространств
знаний, обладающих базой (в смысле
определения 5). Такие пространства знаний в точности совпадают с пространствами
знаний, которые могут быть сформированы какой-либо
минимальной картой навыков.
Определение 4.6 Карта навыков (Q’;
S’; τ’) продолжает (строго продолжает) карту навыков (Q;
S; τ), если выполняются следующие условия:
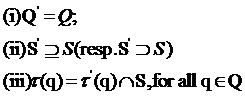
Карта навыков (Q; S’; τ’)
минимальна, если не существует карты навыков, формирующей то же пространство,
которая строго продолжается (Q; S’; τ’).
Пример 4.7. Удаляя навык v в карте навыков
Примера 3.2, получаем:
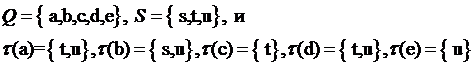
Можно проверить, что (Q; S; τ)является
минимальной картой навыков.
Теорема 4.8. Пространство знаний является
сформированным некоторой минимальной картой навыков, если и только если это
пространство имеет базу. В этом
случае мощность (кардинальное число) базы равна
мощности
множества
навыков.
Кроме того, любые две минимальных карты навыков, формирующих
одно
и то же пространство знаний, изоморфны. А также любая карта навыков (Q;
S;
τ),
формирующая пространство (Q;K), которое имеет
базу,
является продолжением минимальной карты навыков, формирующей то же
пространство.
Доказательство
Рассмотрим произвольную
(не обязательно минимальную) карту навыков (Q; S; τ), и
обозначим (Q; K)сформированное этой картой пространство навыков. Для любого s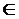 S
обозначим
через
K(s)
состояние знаний из K, сформированное{s}. Получаем, таким образом,
S
обозначим
через
K(s)
состояние знаний из K, сформированное{s}. Получаем, таким образом,
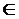 K (s)
K (s)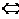 s
s
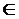 τ
(q).(1)
τ
(q).(1)
Возьмём любое состояние K 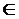 K
и
рассмотрим подмножество навыков Т, которое формирует это состояние. В силу (1)
для любого элемента q, имеем:
K
и
рассмотрим подмножество навыков Т, которое формирует это состояние. В силу (1)
для любого элемента q, имеем:
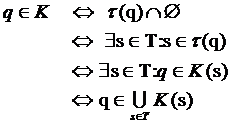
Откуда следует,
что 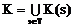 .
Следовательно,
.
Следовательно,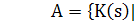 охватывает K. Если
предположить, что карта навыков(Q, S,
τ)
минимальна, то охватывающее семейство А
должно
быть базой. Действительно, если A не является базой, то некоторое K(s)
охватывает K. Если
предположить, что карта навыков(Q, S,
τ)
минимальна, то охватывающее семейство А
должно
быть базой. Действительно, если A не является базой, то некоторое K(s)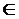 А
может быть представлено как объединение других элементов A. Удаление s из
S
привело бы к карте навыков, строго продолжающейся картой навыков
(Q,
S,
τ)
и
все еще формирующий (Q,
K),
что противоречит гипотезе о минимальности (Q, S, τ).
Мы
приходим к заключению, что любое пространства знаний, сформированное
минимальной картой навыков, имеет базу. Кроме того, мощность (кардинальное
число)
базы
равна
мощности
множества навыков. (Когда (Q, S,τ)
-
минимальна, имеем |A| = |S|).
А
может быть представлено как объединение других элементов A. Удаление s из
S
привело бы к карте навыков, строго продолжающейся картой навыков
(Q,
S,
τ)
и
все еще формирующий (Q,
K),
что противоречит гипотезе о минимальности (Q, S, τ).
Мы
приходим к заключению, что любое пространства знаний, сформированное
минимальной картой навыков, имеет базу. Кроме того, мощность (кардинальное
число)
базы
равна
мощности
множества навыков. (Когда (Q, S,τ)
-
минимальна, имеем |A| = |S|).
Предположим теперь, что пространство (Q,K)имеет
базу B. Из Теоремы 3.3 следует, что (Q,K)имеет, по крайней мере, одну карту
навыков, например,(Q,S,τ).Согласно
Теореме 1 ([1, теорема 3.4.2])база B. для (Q,K)должна содержаться в любом
охватывающем подмножестве из K. Мы имеем, таким образом,
B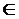 A=
A=
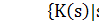 где
снова K(s) сформировано {s}. Полагая
где
снова K(s) сформировано {s}. Полагая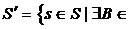 B:K(s)
= B}и
B:K(s)
= B}и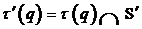 ,заключаем,
что (Q,
,заключаем,
что (Q, )
является минимальной картой навыков.
)
является минимальной картой навыков.
Заметим, что минимальная карта навыков(Q,S,τ)
для пространства знаний с базой B изоморфна
минимальной карте навыков (Q, B,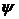 ), где
), где
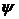 (q)=Bq.
Изоморфизм определяется соответствием s
(q)=Bq.
Изоморфизм определяется соответствием s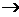 K
(s)
K
(s)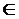 B,
где K (s) - состояние знаний сформированное s. Две минимальных карты навыков,
таким образом, всегда изоморфны друг другу.
B,
где K (s) - состояние знаний сформированное s. Две минимальных карты навыков,
таким образом, всегда изоморфны друг другу.
Наконец, пусть (Q, S,τ)
произвольная
карта навыков, формирующая пространство
знаний K, имеющее базу
B.
Определяя K(s), S’ и τ’, как прежде,
мы получаем минимальную карту навыков, продолжаемую(Q, S,τ).
. Карты навыков: конъюнктивная модель
В конъюнктивной модели структуры знаний, которые
сформированы картами навыков, являются простыми замкнутыми пространствами в
смысле Определения 3 (см. Теорему 5.3 ниже). Поскольку эти структуры знаний
являются двойственными пространствам знаний, сформированных в рамках
дизъюнктивной модели, нет необходимости в более глубокой детализации.
Определение 5.1. Пусть (Q,S, )
карта навыков и пусть T - подмножество S. Состояние знаний K, сформированное Tв
рамках конъюнктивной модели, определяется
правилом:
)
карта навыков и пусть T - подмножество S. Состояние знаний K, сформированное Tв
рамках конъюнктивной модели, определяется
правилом:
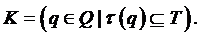
Полученное семейство всех таких состояний знаний
образует структуру знаний, сформированную в
рамках
конъюнктивной
модели картой навыков (Q,S, ).
).
Пример 5.2. Пусть, как в примере 3.2 Q = {а, b,
c, d, e} и S = {s, t, u, v}, где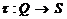 определено
соотношениями:
определено
соотношениями:
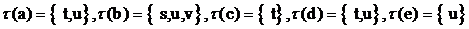
Тогда T ={t, u, v} формирует состояние знаний
{а,
c,
d,
e},в
рамках конъюнктивной модели. С другой стороны, {а,
b,
c}
не является состоянием знаний. Действительно, если бы {а, b, c}
было
состоянием знаний, сформированным некоторым подмножеством T
из
S,
то T включало бы 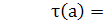 и
и
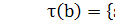 ;
таким образом, d и e также
принадлежали бы сформированному состоянию знаний. Структурой знаний,
сформированной данной картой навыков, является
;
таким образом, d и e также
принадлежали бы сформированному состоянию знаний. Структурой знаний,
сформированной данной картой навыков, является
L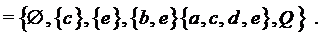
Заметим, что L- простое замкнутое пространство
(см. Определение 4). Двойственная структура знаний 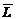 совпадает
с пространством знаний K, сформированным той же картой навыков
в
рамках дизъюнктивной модели; это пространство K было
получено в Примере 3.2.
совпадает
с пространством знаний K, сформированным той же картой навыков
в
рамках дизъюнктивной модели; это пространство K было
получено в Примере 3.2.
Теорема 5.3. Структуры знаний, сформированные в
рамках дизъюнктивной и конъюнктивной модели одной
и той же картой навыков, являются двойственными друг другу. Как следствие,
структуры знаний, сформированные в рамках конъюнктивной модели, являются
простыми замкнутыми пространствами.
Замечание 5.4. В конечном случае, Теоремы 3.3 и
5.3 являются простым перефразированием известного результата о "решетках
Галуа" отношений. Можно
переформулировать
карты навыков (Q, S,
T),
с конечными Q и S, как отношение R между множествами
Q
и S: для q 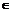 Q и s
Q и s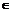 S,
определим
S,
определим
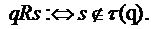
Тогда состояние знаний, сформированное
подмножеством T из S в
рамках
конъюнктивной модели, есть множество:
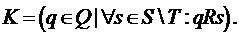
Хорошо известно, что любое конечное семейство
конечных множеств, замкнутое относительно пересечения, может быть получено, как
элементы "решетки Галуа" по
некоторому
отношению. Теоремы 3.3 и 5.3 обобщают этот результат на случай бесконечных
множеств. Конечно, существует прямой аналог Теоремы 4.8 для семейств
множеств,
замкнутых относительно
пересечения.
. Мультикарты навыков: модель компетентности
В двух последних разделах рассматривалось
формирование структур знаний, замкнутых относительно объединения или
пересечения. Однако не обсуждался общий случай.
Формирование произвольной структуры знаний
возможно с помощью обобщения понятия карты навыков. Интуитивно это обобщение
достаточно естественно. С каждым вопросом
q,
мы связываем коллекцию 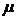 (q) подмножеств
навыков.
Любое
подмножество навыков C в
(q) подмножеств
навыков.
Любое
подмножество навыков C в 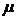 (q)
может
рассматриваться, как метод, называемый в следующем определении
"компетенцией" для решения вопроса q. Таким образом, наличие только
одной из этих компетенций является достаточным, чтобы решить вопрос q.
(q)
может
рассматриваться, как метод, называемый в следующем определении
"компетенцией" для решения вопроса q. Таким образом, наличие только
одной из этих компетенций является достаточным, чтобы решить вопрос q.
Определение 6.1. Мультикартой навыков
называется
тройка
(Q,
S, 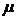 ),
где Q
-
непустое
множество
элементов (вопросов), S -
непустое
множество
навыков, а
),
где Q
-
непустое
множество
элементов (вопросов), S -
непустое
множество
навыков, а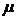 - отображение,
которое связывает с каждым
элементом
q
непустое семейство
- отображение,
которое связывает с каждым
элементом
q
непустое семейство 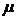 (q) непустых
подмножеств S. Таким образом,
(q) непустых
подмножеств S. Таким образом,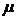 -
отображение множества Qво множество
-
отображение множества Qво множество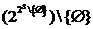 .
Любое множество, принадлежащее
.
Любое множество, принадлежащее 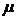 (q), называется
компетенцией
для
элемента
q. Подмножество K из
Q
называется
сформированным некоторым подмножеством навыков T, если K содержит все элементы,
имеющие, по крайней мере, одну компетенцию из T; формально:
(q), называется
компетенцией
для
элемента
q. Подмножество K из
Q
называется
сформированным некоторым подмножеством навыков T, если K содержит все элементы,
имеющие, по крайней мере, одну компетенцию из T; формально:
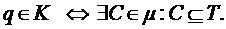
Полагая T =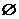 и T = S, видим, что
и T = S, видим, что 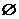 сформировано пустым
множеством навыков, а Q
сформировано
S.
Множество K всех подмножеств
Q, сформированных таким образом, образует
структуру знаний. В этом случае говорят, что структура знаний (Q,
K)
сформирована
мультикартой
навыков(Q, S,
сформировано пустым
множеством навыков, а Q
сформировано
S.
Множество K всех подмножеств
Q, сформированных таким образом, образует
структуру знаний. В этом случае говорят, что структура знаний (Q,
K)
сформирована
мультикартой
навыков(Q, S, 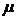 ). Эта модель
называется моделью компетентности.
). Эта модель
называется моделью компетентности.
Пример 6.2. Пусть Q = (а, b, c, d) и S = (с, t,
u). Определим отображение 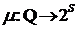 ,
перечисляя компетенции для каждого элемента из Q:
,
перечисляя компетенции для каждого элемента из Q:
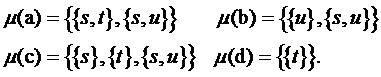
Применяя определение 6.1, видим, что эта
мультикарта навыков формирует структуру знаний:
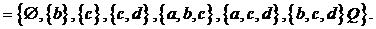
Заметим, что структура знаний K
не
является
замкнутой ни относительно объединения, ни относительно пересечения.
Теорема 6.3. Каждая структура знаний
сформирована, по крайней мере, одной мультикартой навыков.
Доказательство
Пусть (Q,K) - структура знаний. Мультикарту
навыков
определим,
полагая S = Kи 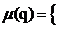 K
K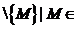 Kq}
для
Kq}
для
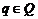 .
.
Таким образом, каждому
состоянию
знаний
M,
содержащему вопрос q соответствует
компетентность K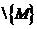 для q. Заметим, что
K
для q. Заметим, что
K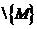 не
пусто, потому что оно содержит, как элемент, пустое подмножество из Q. Чтобы
показать, что(Q, S,
не
пусто, потому что оно содержит, как элемент, пустое подмножество из Q. Чтобы
показать, что(Q, S, 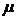 ), формирует
структуру знаний K, применим определение 6.1.
), формирует
структуру знаний K, применим определение 6.1.
Для любого 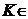 K
рассмотрим
подмножество K
K
рассмотрим
подмножество K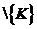 из
K
и
вычислим состояние L, которое его формирует:
из
K
и
вычислим состояние L, которое его формирует:
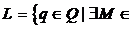 Kq: K\{M}
Kq: K\{M}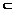 K
K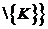
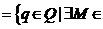 Kq
Kq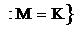
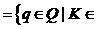 Kq
Kq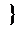
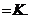
Таким образом, каждое состояние в K
сформировано
некоторым подмножеством из S. С другой стороны, если 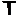
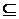 S = K, состояние L,
сформированное
S = K, состояние L,
сформированное 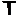 , определяется
правилом:
, определяется
правилом:
математический знание навык карта
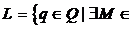 Kq:
K
Kq:
K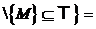
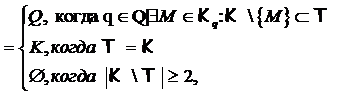
откуда следует, что L принадлежит K. Таким
образом,
K
действительно сформировано мультикартой навыков(Q,
S, 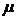 ).
).
Мы не будем продолжать исследование мультикарты
навыков, 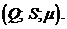 Как
и в случае, простой карты навыков, можно исследовать существование и
единственность минимальной мультикарты навыков для данной структуры знаний.
Возможны другие варианты формирования структур знаний. Например, можно
определить состояние знаний, как подмножество K из
Q,
состоящее из всех элементов q, компетенции для
которых принадлежат определенному подмножеству из S
(зависящему от K).
Как
и в случае, простой карты навыков, можно исследовать существование и
единственность минимальной мультикарты навыков для данной структуры знаний.
Возможны другие варианты формирования структур знаний. Например, можно
определить состояние знаний, как подмножество K из
Q,
состоящее из всех элементов q, компетенции для
которых принадлежат определенному подмножеству из S
(зависящему от K).
. Маркировки и фильтры
Для любого вопроса изестественной
области
знаний, таких как арифметика или грамматика, обычно есть богатые возможности
описания
соответствующих навыков и связанной с ними структуры знаний. Эти
возможности
могли бы использоваться, чтобы описать состояние знаний студента для родителей
или учителя.
Действительно, полный список элементов,
содержащихся в студенческом состоянии знаний, может иметь сотни элементов и
может быть трудным для
усвоения даже для эксперта. Может быть
составлен перечень значимой информации, отраженной в вопросах, формирующих
состояние знаний студента. Этот перечень может касаться намного большего, чем
навыки, которыми обладает или которых не хватает студенту и может включать
такие функции, как прогноз успеха в предстоящем тестировании, рекомендации по
направлению исследований или проведению работы над ошибками.
Этот раздел обрисовывает в общих чертах
программу описания (маркировки) элементов (вопросов) и интеграции (фильтра)
соответствующей справочной информации, содержавшейся в состояниях знаний.
Приведенные примеры
взяты из системы дистанционного обучения ALEKS (см.#"880039.files/image131.gif">n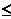 12),
фильтр вычисляет подмножество Gn из Q, содержащее все вопросы, изучающиеся на
этом уровне или ранее (маркировка 2. в приведенном выше списке). Если
образовательная система разумна, должно быть
12),
фильтр вычисляет подмножество Gn из Q, содержащее все вопросы, изучающиеся на
этом уровне или ранее (маркировка 2. в приведенном выше списке). Если
образовательная система разумна, должно быть
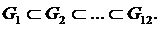
Таблица 1 - Два примера вопросов и связанный с
ними список маркировок.
|
Список
маркировок
|
Вопрос
|
|
(1)
Мера недостающего угла в треугольнике (2) 7 (3) Сумма углов плоского
треугольника (4) Геометрия треугольника (5) Элементарная Эвклидова геометрия
(6) Мера угла, сумма углов треугольника, сложение, деление, вычитание (7)
Вычисление (8) Числовая запись
|
В
треугольнике ABC угол А составляет Х градусов, угол В - Y градусов. Сколько
градусов составляет угол С?
|
|
(1)
Сложение и вычитание двухместных чисел с переносом (2) 5 (3) Сложение и
вычитание (4) Десятичные дроби (5) Арифметика (6) Сложение, вычитание,
десятичные дроби, перенос, валюта (7) Текстовая задача и вычисление (8)
Числовая запись
|
Мэри
купила две книги стоимостью Х долларов и Y долларов. Она дала Клерку Z долларов.
Сколько сдачи она получит?
|
Мы можем найти
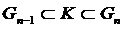
для некоторого n, откуда следует, что
учащийся
может
быть определён в класс n-1.
Однако это не является лучшим решением, если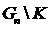 очень
мало. Необходима большая информация. Кроме того, мы должны предусмотреть
ситуации, в которых не существует ни одного такого n. Далее, фильтр вычисляет
стандартное расстояние
очень
мало. Необходима большая информация. Кроме того, мы должны предусмотреть
ситуации, в которых не существует ни одного такого n. Далее, фильтр вычисляет
стандартное расстояние 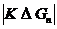 для каждого класса n и фиксирует
множество
для каждого класса n и фиксирует
множество
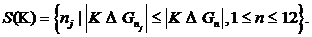
Таким образом, S(K) содержит все классы, которые
минимизируют расстояние до K. Предположим, что S(K) содержит единственный
элемент
nj,
и Gnj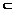 K.
Разумно
тогда
рекомендовать учащегося принять в класс no +
1, но S(K) может содержать больше, чем один элемент. Мы все еще нуждаемся в
большей информации. В частности, содержание K, с его достоинствами и
недостатками
относительно его близости к Gnj должно в итоге быть полезным. Не вдаваясь в
технические детали такого вывода, обрисуем, в общих чертах, пример отчета,
который система могла бы сделать в такой ситуации:
K.
Разумно
тогда
рекомендовать учащегося принять в класс no +
1, но S(K) может содержать больше, чем один элемент. Мы все еще нуждаемся в
большей информации. В частности, содержание K, с его достоинствами и
недостатками
относительно его близости к Gnj должно в итоге быть полезным. Не вдаваясь в
технические детали такого вывода, обрисуем, в общих чертах, пример отчета,
который система могла бы сделать в такой ситуации:
Ближе всего учащемуся X соответствует
5-й
класс.
Однако X был бы необычным учеником в этом
классе. Знание элементарной геометрии значительно превышает знание учащегося 5
- го класса. Например, X знает о Теореме Пифагора и способен к её
использованию. С другой стороны, X имеет удивительно слабые знания по арифметике.
Описания такого типа требуют разработки
различных наборов новых фильтров, кроме использованных
для
вычисления
S(K). Кроме того, у системы должна быть возможность преобразования через
генератор естественного языка и вывода фильтров в грамматически корректные
операторы на обыденном языке. Мы не будем обсуждать это здесь. Целью этого
раздела было проиллюстрировать, как маркировка элементов, значительно расширяя
понятие навыков, может привести к улучшению описания состояний знаний, которое
может
быть полезным в различных ситуациях.
Заключение
В работе дан адаптированный перевод на русский
язык части одной из глав монографии Ж-Кл.
Фалмажа и Ж-П. Дуанона [1], которая называется "Карты навыков, метки и
фильтры".
Приведены необходимые сведения из первых глав
монографии, перевод которых выполнен в дипломных работах [2] и [3]. Наряду с
поясняющими примерами, приведенными авторами в монографии, приводятся
аналогичные примеры из курса "Комплексный анализ".
Список используемых источников
1. J.-Cl.
Falmagneand, J.P. Doignon. Learning Spaces Berlin Heidelberg. 2011, 417 p.
2. Н.А.
Ралко.
Математические
модели пространств знаний. Дипломная работа,
КубГУ, 2013, 47 с.
3. Т.В.
Алейникова. Онтологический
инжиниринг в системах управления знаниями. Дипломная работа, Кубу, 2013, 66 с.