Анализ поведения финансовых индексов с помощью методов математической статистики на примере курса Центрального банка валютной пары евро/рубль
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное
образовательное учреждение высшего профессионального образования
«Ростовский государственный
строительный университет»
Институт информационных систем и
технологий
Кафедра прикладной математики и
вычислительной техники
КУРСОВАЯ РАБОТА
по дисциплине «Теория вероятностей и
математическая статистика»
на тему: «Анализ поведения финансовых
индексов с помощью методов математической статистики на примере курса Центрального
банка валютной пары евро/рубль»
Выполнила студентка группы ПИ-223 В.С. Самарина
Руководитель проекта
к.ф.-м.н., с.н.с., доцент В.В. Мисюра
Ростов-на Дону
г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
ГЛАВА 1.
ПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
1.1 Описание
входных данных. Получение ряда доходностей (случайной величины (СВ)Х).
Построение графика доходностей
1.2
Построение интервального статистического ряда и гистограммы
1.3
Выявление грубых ошибок в выборке. Исключение аномальных значений
1.4 Оценка
функции распределения и построение ее графика. Интерпретация полученных
результатов и предварительный закон распределения
ГЛАВА 2.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКИХ ДАННЫХ. ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ
РАСПРЕДЕЛЕНИЯ
2.1
Вычисление основных характеристик выборочных данных. Свойства полученных оценок
2.2 Точечные
оценки параметров предполагаемого закона распределения случайных величин
методом максимального правдоподобия
2.3
Восстановление теоретической функции распределения и плотности распределения СВ
2.4
Построение доверительных интервалов для математического ожидания и дисперсии с
надежностью 0,95
ГЛАВА 3.
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
3.1 Проверка
с помощью критерия согласия гипотезы о виде закона распределения СВ, уровень
значимости α=0,05
3.2
Построение графика функции плотности вероятности и сравнение его с гистограммой
ЗАКЛЮЧЕНИЕ
СПИСОК
ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
Статистический анализ выборочных данных является очень актуальной темой в
наше время. Очень часто невозможно провести анализ по всей совокупности данных
(любых данных) по причине их многочисленности. Либо анализ всей совокупности
может занимать много времени. Для получения данных проводится анализ выборочных
данных по этой совокупности.
В данной курсовой работе проводится анализ поведения финансовых индексов
с помощью методов математической статистики на примере ЦБ валютной пары
евро/рубль.
Целью данной работы является практическое закрепление теоретических
данных статистического анализа вариационных рядов.
Задачи курсовой работы:
. Произвести наблюдения над курсом ЦБ валютной пары евро/рубль;
. Вычислить логарифмы изменения цен;
. Выполнить первичный анализ данных;
. Вычислить основные характеристики выборки;
. Произвести проверки статистических гипотез;
. Интерпретировать полученные результаты.
ГЛАВА 1. ПЕРВИЧНЫЙ
АНАЛИЗ ДАННЫХ
.1 Описание
входных данных. Получение ряда доходностей (случайной величины (СВ)Х).
Построение графика доходностей
Исходные
данные к работе были взяты с официального сайта <#"879860.files/image001.gif">
Рисунок
1. Курс рубля
Получили
выборку, состоящую из 48 элементов. Для дальнейшей работы с данными преобразуем
их в доходности, то есть найдем функцию отражающую поведение изменения цен.
Значение натурального логарифма, при аргументе равным единице, равен нулю. Если
цены акций при закрытии равны, то доходность равна нулю, 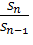
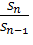 = 1, а
= 1, а 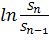
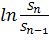 = 0, при
= 0, при
 ,
следовательно
,
следовательно 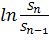
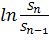 ,
является доходностью (См.[6]). Преобразуем цены акций в доходность.
,
является доходностью (См.[6]). Преобразуем цены акций в доходность.
Каждый
элемент выборки заменили на логарифм отношения текущего значения к предыдущему:
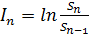
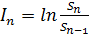 , где
(1.1.)
, где
(1.1.)
Sn-
цена рискового актива, n = 1,
2, 3,.., N.
Таким образом рассчитали финансовые индексы.
По полученным индексам курса рубля построили график доходностей, который
наглядно отражает динамику изменения валютной пары евро/рубль (Рисунок 2)
(См.[8]).
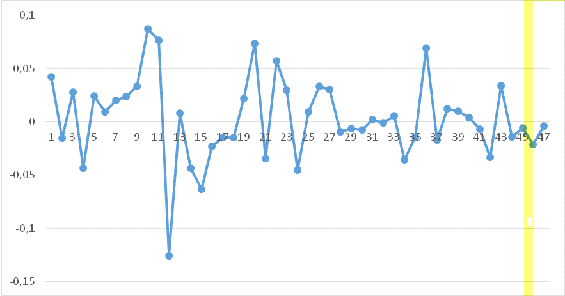
Рисунок
2. График доходностей
.2 Построение
интервального статистического ряда и гистограммы
Полученный первичный статистический материал подлежит дальнейшей
обработке, прежде всего упорядочению. Результаты наблюдений над случайной
величиной, необходимо расположить в порядке возрастания, т.е. проранжировать
выборку.
Интервальный статистический ряд - это таблица, в которой приведены
интервалы значений признака и относительные частоты попадания признака в эти
интервалы(См.[1]).
Интервальный статистический ряд строится для непрерывных случайных
величин и для дискретных случайных величин с большим числом вариант, в нем
определены границы для непрерывно варьируемого признака (См.[4]). Интервалы
будем брать с одинаковой длиной, число интервалов рассчитывается по формуле
Стерджеса:
= 1+1.4 ln (n) , (1.2)
где k - число интервалов, n - объем выборки.
Длина интервала определяется по формуле
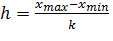
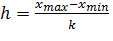 . (1.3)
. (1.3)
Находим
наименьшее и наибольшее значение в выборке, а также число интервалов и длину
интервалов (Рисунок 3). Отступаем на полшага h от наименьшего значения выборки.
Промежуточные интервалы получаем прибавляя к концу предыдущего интервала длину
частичного интервала h (в данном случае h=0,0304095) (См.[2]).
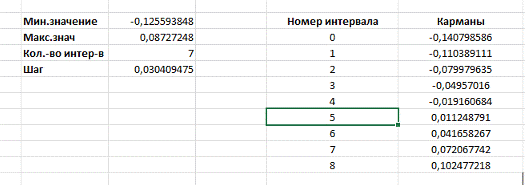
Рисунок
3. Интервалы карманов
Таблица частот при этом имеет вид (Рисунок 4):
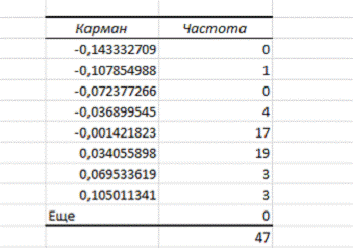
Рисунок
4. Интервальный статистический ряд
Первый столбец полученной таблицы - это квантиль данного для
распределения доходностей/убытков, второй- частота попадания доходностей в тот
или иной интервал.
Для наглядного изображения интервального ряда распределения построим
гистограмму доходностей, с помощью всторенного модуля Анализ данных/
Гистограмма (Рисунок 5). Гистограмма доходностей представлена на Рисунке 6
(См.[2]).
Рисунок
5. Модуль Анализ данных
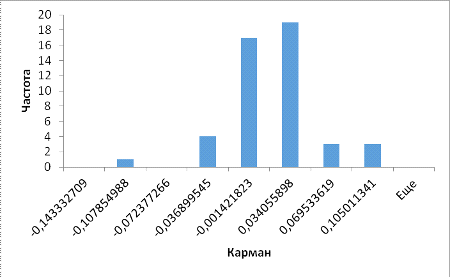
Рисунок
6. Гистограмма
Единицы статистической совокупности, у которых значения анализируемого
признака существенно отклоняются от основного массива, называются аномальными
явлениями, «грубыми ошибками» или выбросами.
При решении задач статистического анализа проблема наличия в выборке
аномальных измерений имеет чрезвычайно важное значение. Присутствие
единственного аномального наблюдения может приводить к оценкам, которые
совершенно не согласуются с выборочными данными.
Для данных индексов построим точечный график (Рисунок 7). В ходе
визуального анализа выявляем наличие в выборке аномальных значений (выбросов).
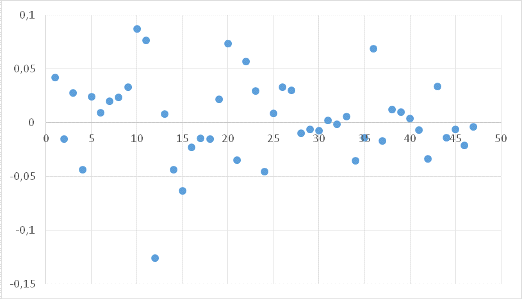
Рисунок
7. Точечный график
Самым простым методом обнаружения грубых ошибок считается метод, на
основании Т - Критерия Граббса:
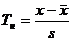 , где
(1.4)
, где
(1.4)
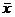 - среднее
значение, x - аномальное значение, s - выборочное
среднеквадратическое отклонение СВ.
- среднее
значение, x - аномальное значение, s - выборочное
среднеквадратическое отклонение СВ.
Данный
критерий можно использовать для выделения аномальных результатов измерений
только в случае нормального закона.
Так
как выборка распределена нормально, мы можем найти Тк, и проверить наличие
грубых ошибок в выборке.
Результаты расчетов по выборке представлены на Рисунке 8:
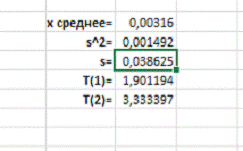
Рисунок
8.Результаты вычисления
Полученные
значения 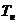 сравнивают с табличными значениями процентных точек
критерия Смирнова Граббса (Таблица 1). В том случае, если
сравнивают с табличными значениями процентных точек
критерия Смирнова Граббса (Таблица 1). В том случае, если 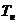 >
>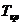 , мы
может утверждать, что проверяемое значение является грубой ошибкой и относится
к классу выбросов.
, мы
может утверждать, что проверяемое значение является грубой ошибкой и относится
к классу выбросов.
Таблица 1. Значения процентных точек критерия Смирнова Граббса
|
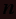
|
0.99
|
0.95
|
|
30
|
0.4257
|
0.4791
|
|
31
|
0.4376
|
0.4885
|
|
32
|
0.4477
|
0.4995
|
|
33
|
0.4558
|
0.5099
|
|
34
|
0.4688
|
0.5189
|
|
35
|
0.4779
|
0.5285
|
|
36
|
0.4874
|
0.5374
|
|
37
|
0.4970
|
0.5459
|
|
38
|
0.5048
|
0.5540
|
|
39
|
0.5145
|
0.5617
|
|
40
|
0.5211
|
0.5692
|
|
41
|
0.5307
|
0.5767
|
|
42
|
0.5385
|
0.5835
|
|
43
|
0.5450
|
0.5902
|
|
44
|
0.5522
|
0.5970
|
|
45
|
0.5599
|
0.6033
|
|
46
|
0.5675
|
0.6090
|
|
47
|
0.6154
|
|
48
|
0.5789
|
0.6211
|
|
49
|
0.5861
|
0.6270
|
|
50
|
0.5910
|
0.6324
|
Сравним полученные значения с табличным (при 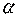 = 0,01) при числе наблюдений равном
48, а Ткр = 0,5789.
= 0,01) при числе наблюдений равном
48, а Ткр = 0,5789.
Так
как Тк(1) =1,9> 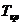 = 0,5789, то проверяемое значение является грубой
ошибкой и относится к классу выбросов.
= 0,5789, то проверяемое значение является грубой
ошибкой и относится к классу выбросов.
Аналогично
Тк(2) =3,33> 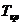 = 0,5789, что подтверждает, что рассматриваемое
значение является аномальным значением.
= 0,5789, что подтверждает, что рассматриваемое
значение является аномальным значением.
Критерий
Граббса имеет некоторые недостатки. Он не точен, и не чувствителен к
засорениям, когда ошибки группируются на расстоянии от общей совокупности.
Далее
подтвердим наличие грубых ошибок на основании L- критерия
Титьена-Мура (См.[9]).
Решающее
правило для исключения k наибольших членов вариационного ряда основано на
статистике:
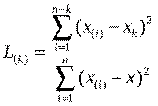 , где
, где 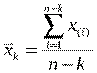 (1.5)
(1.5)
Воспользовавшись
формулами, было найдено значение L-критерия Титьена-Мура
для рассматриваемой выборки (Рисунок 9)

Рисунок
9. Значение L-критерия Титьена-Мура
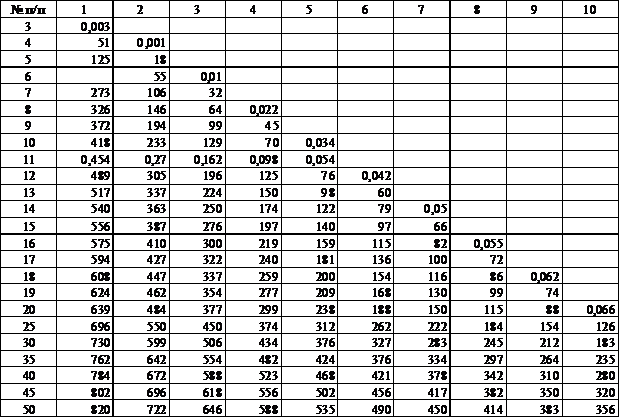
Сравниваем полученное значение с критическим пределом (Таблица 2). При
наличии выбросов статистика Lk
должна быть меньше критического предела. В данном случае Lk = 0,67887 <Cкр = 0,696, что подтверждает наличие
аномальных значений в выборке (См.[9]).
Таблица 2. Критические значения оценки для L - критерия Титьена и Мура (a=0,05)
Для избавления от выбросов изменим данные доходностей, исключим значение
0,076594461 и -0,125593848, что приведет к нормальному распределению.
Гистограмма при этом теперь имеет вид (Рисунок 10):
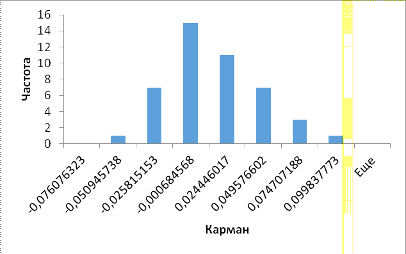
Рисунок
10.Гистограмма
.4. Оценка
функции распределения и построение ее графика. Интерпретация полученных
результатов и предварительный закон распределения
Каждая случайная величина полностью определяется своей функцией
распределения.
Если X - случайная величина, то функция
F(x) = FX (x) = P (X <x) называется
функцией распределения случайной величины X. Здесь P (X
<x) - вероятность того, что случайная величина X принимает значение, меньшее x.
Важно понимать, что функция распределения содержит всю информация о
случайной величине и поэтому изучение случайной величины заключается в
исследовании ее функции распределения, которую часто называют просто
распределением.
Функция распределения любой случайной величины обладает следующими
свойствами:
. F(x) определена на всей числовой прямой R;
. F(x) не убывает, т.е. если x1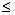 x2, то F(x1)
x2, то F(x1)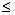 F(x2);
F(x2);
3. F(-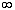 )=0,
F(+
)=0,
F(+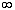 )=1, т.е.
)=1, т.е.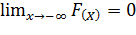
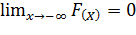 и
и 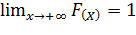
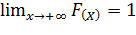 ;
;
. F(x)
непрерывна справа, т.е. 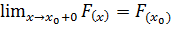
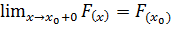
Для построения функции распределения необходимо взять накопленные
частоты. Они определяются путем последовательного суммирования частот
предшествующих интервалов (Рисунок 11).
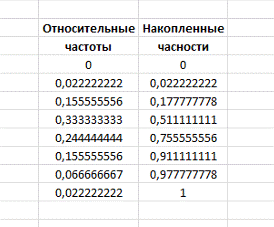
Рисунок
11. Накопленные частоты
Таким образом график оценки функции имеет вид (Рисунок 12):
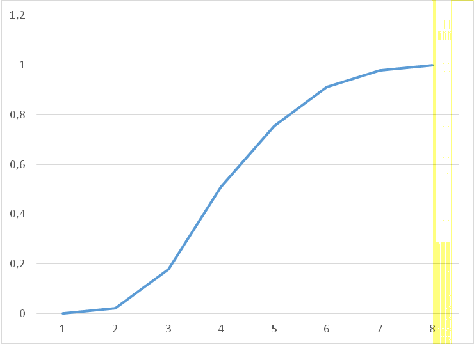
Рисунок
12. График оценки функции
Полученная функция распределения соответствует нормальному закону
распределения, поэтому логично предположить, что финансовые индексы валютной
пары евро/рубль распределены нормально.
ГЛАВА 2.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКИХ ДАННЫХ. ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ
РАСПРЕДЕЛЕНИЯ
.1 Вычисление
основных характеристик выборочных данных. Свойства полученных оценок
Основными характеристиками статистических данных являются среднее, мода,
медиана, размах, дисперсия, среднеквадратическое отклонение. Данные
характеристики можно получить с помощью инструмента «Описательная статистика»
(Рисунок 13).
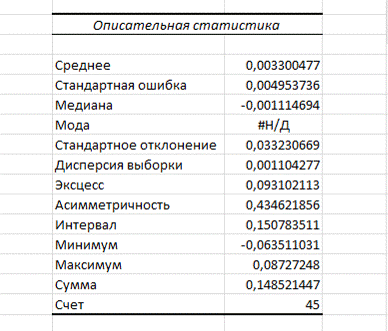
Рисунок
13. Описательная статистика
Математическое ожидание - это среднее значение СВ (центром распределения
СВ). Такое значение может быть использовано вместо случайной величины в приблизительных
расчетах или оценках. Математическое ожидание обозначается - М[Х] или mХ и
рассчитывается по формуле:
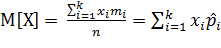
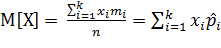 (2.1)
(2.1)
Стандартное
отклонение, среднеквадратичное отклонение - это очень распространенный
показатель рассеяния в описательной статистике. Данный показатель можно
использовать в техническом анализе для обнаружения степени рассеяния цены
анализируемого инструмента. Обозначается греческим символом Сигма «σ».
Алгоритм
вычисления стандартного отклонения:
1. Вычисляем среднее арифметическое выборки данных;
. Отнимаем это среднее от каждого элемента выборки;
. Все полученные разницы возводим в квадрат;
. Суммируем все полученные квадраты;
. Делим полученную сумму на количество элементов в выборке;
. Вычисляем квадратный корень из полученного частного (именуемого
дисперсией).
Общие формулы расчета выборочной дисперсии и выборочного среднего
квадратического отклонения (См.[2]):
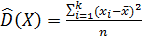
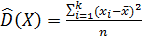 (2.2)
(2.2)
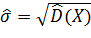
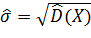 (2.3)
(2.3)
Если
количество элементов в выборке превышает 30, то необходимо рассчитывать
исправленную дисперсию, уменьшив объем выборки на 1:
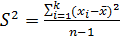
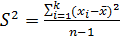 (2.4)
(2.4)
Соответственно
число 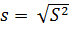
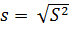 называется
исправленным выборочным средним квадратическим отклонением.
называется
исправленным выборочным средним квадратическим отклонением.
Результаты
расчетов представлены на Рисунке 14:

Рисунок
14.Расчет дисперсии и ср. квадрат-го отклонения
Чтобы судить о том, насколько точно проведенные измерения отражают состав
генеральной совокупности, необходимо вычислить стандартную ошибку средней
арифметической выборочной совокупности.
Стандартная ошибка средней арифметической характеризует степень
отклонения выборочной средней арифметической от средней арифметической
генеральной совокупности.
Стандартная ошибка средней арифметической вычисляется по формуле:
 , где (2.5)
, где (2.5)
s- стандартное отклонение результатов измерений, n - объем выборки.
В выборке отсутствует мода, так как значения не повторяются.
Асимметрия - это показатель симметричности / скошенности кривой
распределения, а эксцесс определяет ее островершинность(См.[5])..
При левосторонней асимметрии ее показатель является положительным и в
распределении преобладают более низкие значения признака. При правосторонней -
показатель положительный и преобладают более высокие значения. У всех
симметричных распределений (в том числе и у нормального распределения) величина
асимметрии равна (или близка) нулю. Формула показателя асимметрии является
следующей:
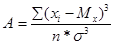 (2.6)
(2.6)
Если в распределении преобладают значения близкие к среднему арифметическому,
то формируется островершинное распределение. В этом случае показатель эксцесса
стремится к положительной величине. У нормального распределения эксцесс равен
(или близок) нулю. Если у распределения 2 вершины (бимодальное распределение),
то тогда эксцесс стремится к отрицательной величине. Показатель эксцесса
определяется по формуле(См.[9]):
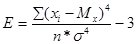 (2.7)
(2.7)
Таким образом, для нормального закона распределения, если эксцесс
положительный, то на графике функция распределения островершинная и для
отрицательных значений более пологая. Так можно установить отклонения заданного
закона от нормального.
2.2 Точечные
оценки параметров предполагаемого закона распределения случайных величин
методом максимального правдоподобия
В статистике существует два вида оценок: точечные и интервальные.
Точечная оценка представляет собой отдельную выборочную статистику, которая
используется для оценки параметра генеральной совокупности(См.[8]).
По гистограмме можно определить, что курс рубля имеет нормальное
распределение, поэтому описывается параметрами a и σ.
Популярным статистическим методом, который используется для создания
статистической модели на основе данных, и обеспечения оценки параметров модели,
является метод максимального правдоподобия. Метод максимального правдоподобия
точечной оценки неизвестных параметров заданного распределения сводится к
отысканию максимума функции одного или нескольких оцениваемых параметров. Метод
максимального правдоподобия применим для оценки параметров. Найдем параметры a
и σ
нормального
распределения:
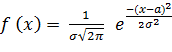
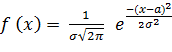 , (2.8)
, (2.8)
если
в результате n испытаний величина X приняла значения x1,x2,..,xn.
Составим
функцию правдоподобия, учитывая, что q1 = a, q2 = s:
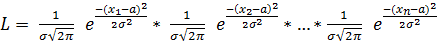
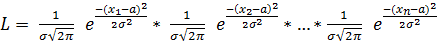 (2.9)
(2.9)
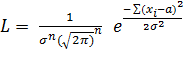
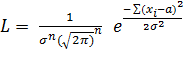 . (2.10)
. (2.10)
Найдем
логарифмическую функцию правдоподобия:
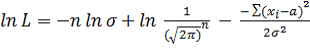
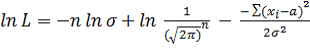 (2.11)
(2.11)
Найдем
частные производные по a и по σ:

 (2.12)
(2.12)
Приравняв
частные производные нулю и решив полученную систему двух уравнений относительно
a и 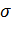
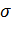 ,
получим:
,
получим:
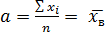
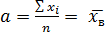 , a
, a 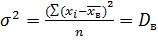
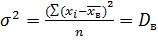 (2.13)
(2.13)
Итак,
с помощью метода максимального правдоподобия выяснили, что параметр 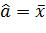
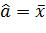 , а
параметр
, а
параметр 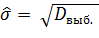
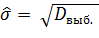 .
Заметим, что первая оценка несмещенная, а вторая смещенная.
.
Заметим, что первая оценка несмещенная, а вторая смещенная.
2.3
Восстановление теоретической функции распределения и плотности распределения СВ
Необходимо вычислить теоретическую вероятность и теоретическую частоту.
Для этого напротив каждого интервала запишем соответствующую ему частоту.
Воспользуемся функцией НОРМРАСП (х; среднее; стандартное_откл; интегральная). В
качестве значений х взяли левую границу интервала для вычисления F(x(i)) и
правую для F(x(i+1)); в качестве среднего берется выборочное среднее значение,
полученное в описательной статистике. Стандартное же отклонение - показатель
рассеивания значений случайной величины относительно ее математического
ожидания, интегральная функция показывает логическое значение.
Для нахождения теоретической вероятности для интервального
статистического ряда вычисляется вероятность попадания в интервал по формуле
P(a<X<b)=F(b)-F(a). А чтобы получить теоретические частоты, умножим
теоретическую вероятность на объем выборки. Для удобства округлим данные
значения (Рисунок 15).
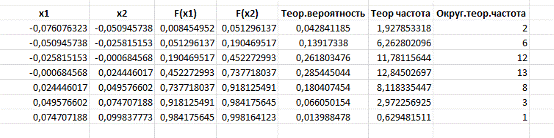
Рисунок
15. Восстановление теоритической функции
2.4
Построение доверительных интервалов для математического ожидания и дисперсии с
надежностью 0,95
Доверительный интервал - термин, используемый в математической статистике
при интервальной оценке статистических параметров, что предпочтительнее при небольшом
объеме выборки. Доверительным называют интервал, который покрывает неизвестный
параметр с заданной надежностью.
Интервальная
оценка, доверительный уровень которой равен 95%, интерпретируется следующим
образом: если из генеральной совокупности извлечь все выборки, имеющие объем n,
и вычислить их выборочные средние, то 95% доверительных интервалов, построенных
на их основе, будут содержать математическое ожидание генеральной совокупности,
а 5% - нет. На практике, как правило, из генеральной совокупности извлекается
только одна выборка, а математическое ожидание генеральной совокупности 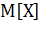
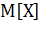 не
известно. По этой причине невозможно гарантировать, что некий конкретный
доверительный интервал содержит величину
не
известно. По этой причине невозможно гарантировать, что некий конкретный
доверительный интервал содержит величину 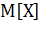
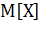 . Можно
лишь утверждать, что вероятность этого события равна 95%.
. Можно
лишь утверждать, что вероятность этого события равна 95%.
Найдем
доверительный интервал для среднего и среднеквадратического отклонения с
надежностью 0,95. Для начала посчитаем значение аргумента функции Лапласа - t (Рисунок
16).

Рисунок
16. Функция Лапласа
Данная оценка для курса рубля равна 0,057960064.
Затем находим точность интервальной оценки для среднего значения по формуле:

 (2.14)
(2.14)
Среднее
генеральной совокупности, имеющей нормальный закон распределения, с
доверительной вероятностью 1-a находится в доверительном
интервале:
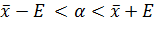
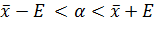 (2.15)
(2.15)
Таким
образом получен доверительный интервал для математического ожидания (Рисунок
17).

Рисунок
17. Границы доверительных интервалов
Это значит, что математическое ожидание может находиться в пределах
данного интервала при данном уровне надежности.
Построим доверительный интервал для неизвестной дисперсии нормально
распределенной генеральной совокупности (Рисунок 18). Оценкой для генеральной
дисперсии является выборочная дисперсия. Доверительный интервал находится по
следующей формуле:
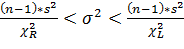
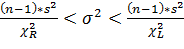 (2.16)
(2.16)
Значения
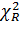
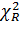 и
и 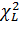
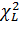 находятся
при помощи функции ХИ2ОБР(), исходя из следующих условий:
находятся
при помощи функции ХИ2ОБР(), исходя из следующих условий:
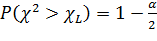
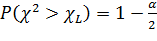 (2.17)
(2.17)
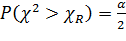
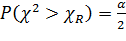 (2.18)
(2.18)
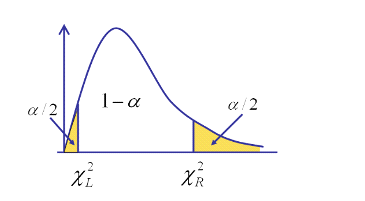
Рисунок
18. Нахождение левого и правого хи-квадрат значений
Таким образом получили доверительный интервал для дисперсии,
представленный на Рисунке 19.
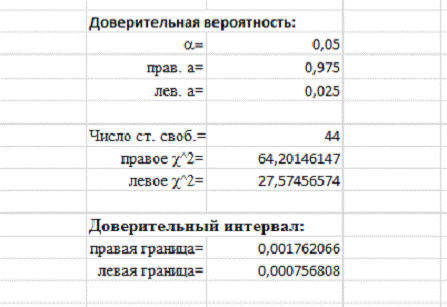
Рисунок
19. Доверительный интервал для дисперсии
Получили, что дисперсия выборки находится в интервале от 0,000756808 до
0,001762066.
Стоит вспомнить, что дисперсия отражает меру разброса данных вокруг
средней величины, поэтому доверительный интервал показывает, что данные могут
находиться в пределах найденного доверительного интервала.
ГЛАВА 3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
.1 Проверка с
помощью критерия согласия гипотезы о виде закона распределения СВ, уровень
значимости α=0,05
финансовый индекс
валютный статистика
Для оценки соответствия имеющихся экспериментальных данных нормальному
закону распределения выполним следующие действия:
. Выдвигаем основную гипотезу 𝐻0: случайная величина X подчиняется
нормальному закону распределения.
. Формулируем альтернативную гипотезу 𝐻1: случайная величина распределяется
не по нормальному закону.
. Имея частоты и теоритические частоты, укрупняем их так, чтоб они были
больше либо равны 5 и затем рассчитываем критерий по формуле:
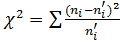
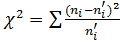 (3.1)
(3.1)
.
Выбирается правосторонняя критическая область, и граница ее при заданном уровне
значимости α и числом степеней свободы 𝑘 = 𝑣 −
1 − 𝑟, где v - число частичных интервалов выборки или
вариант, r - число параметров предполагаемого распределения находится по
таблице критических точек распределения 𝜒кр2 (𝛼,𝑘). Это
значит, что если 𝜒2 <𝜒кр2 (𝛼,𝑘), то
основная гипотеза принимается, в противном случае отвергается.
Произведя
все действия по данному алгоритму, получаем для выборки по курсу рубля значения
𝜒2 = 1,141 и 𝜒крит. (0,05;6) = 1,145 (Рисунок 20). Это говорит о том, что гипотеза о
нормальном распределении принимается с ошибкой 0,05.

Рисунок
20. Проверка гипотезы о нормальном законе распределения
.2 Построение
графика функции плотности вероятности и сравнение его с гистограммой
Для построения графика функции плотности вероятности необходимы
теоретические частоты, рассчитанные ранее. График плотности вероятности
показывает, сколько единиц доходности приходится на единицу интервала.
Построим данный график для курса ЦБ валютной пары евро/рубль и сравним
его с гистограммой (Рисунок 21).
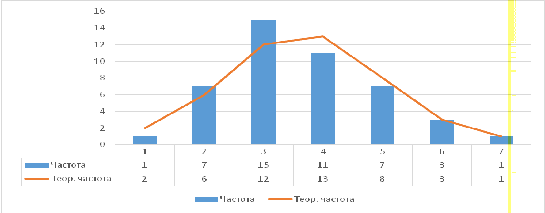
Рисунок
21.График функции плотности
Анализируя полученные графики, можно говорить о нормальном распределении
СВ, так как значения частот и теоретических частот практически повторяют друг
друга. Следовательно, нет причин утверждать обратное.
ЗАКЛЮЧЕНИЕ
В данной курсовой работе был проведен статистический анализ курса ЦБ
валютной пары евро/рубль. Были построены гистограммы, выполнена описательная
статистика выборочных данных, а так же проверены гипотезы о нормальном
распределении, равенстве средних и равенстве дисперсий.
В результате анализа посредством критерия согласия Пирсона было выявлено,
что финансовые индексы курса ЦБ валютной пары евро/рубль распределены по
нормальному закону распределения.
Также в работе были построены методами MS Excel график функции плотности
вероятности, функция распределения и гистограмма, что также подтверждает, что
закон распределения определен верно.
СПИСОК
ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. http://www.finam.ru/analysis/quotes/?0=&t=9281427
. Белявкий Г.И., Мисюра В.В. - Математическая статистика. -
Ростовна-Дону: Ростовский государственный строительный университет, 2010, - 71
с.
. Мисюра В.В. Компьютерные технологии анализа данных: учебное
пособие. - Ростов-на-Дону, Ростовский Государственный Строительный Университет,
2013. - 106 с.
. Кремер Н.Ш. Теория вероятностей и математическая
статистика. - М.: Юнити-Дана, 2006.-573 с.
. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы
эконометрики. Учебник для вузов. - М.: ЮНИТИ, 1998. -1022 с.
. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная
статистика: Основы моделирования и первичная обработка данных. Справочное
издание под ред. Айвазяна С.А. -М.: Финансы и статистика, 1983. - 471 с.
. Дэвид М. Левин, Дэвид Стефан, Тимоти С. Кребиль, Марк Л.
Беренсон. Статистика для менеджеров с использованием MicrosoftExcel. - М.:
Вильямс, 2005. -1312 с.
. Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные
статистические методы. Учебник. -М.: Финансы и статистика, 1998. -352 с.
. Эндрю Ф. Сигел. Практическая бизнес-статистика. - М.:
Вильямс, 2008. -1056 с.