Применение оператора Дынкина к оценке валютных опционов

Применение оператора Дынкина к оценке валютных опционов

Правительство Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

«Национальный исследовательский университет «Высшая школа экономики»

Факультет Мировой Экономики и Мировой Политики

Отделение Экономика

Кафедра Международных Валютно-Финансовых Отношений

ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА

на тему «Применение оператора Дынкина к оценке валютных опционов»

Студент группы № 463,

Попов Юрий Вадимович

Руководитель ВКР

Профессор, д.э.н.

Евстигнеев Владимир Рубенович

Москва, 2013

Оглавление

Введение

. Уравнение Дынкина

.1 Вид функций сноса и диффузии

.2 Метод разделения переменных

.3 Решение исходной задачи методом Фурье

.4 Решение задачи на собственные значения

.5 Весовая функция и ортонормированные полиномы

.6 Новое уравнение и итоговое общее решение

. Модель Блэка-Шоулза

. Сравнение результатов модели Блэка-Шоулза и уравнения Дынкина

.1 Опционы “при своих”

.2 Опционы “в деньгах” и “вне денег”

Заключение

Список использованных источников

Введение

На сегодняшний день валютный опцион является широко распространенным и быстро набирающим популярность производным финансовым инструментом. По данным Банка международных расчетов, ежедневный объем торговли валютными опционами на рынке Форекс вырос более чем в три раза за последние 10 лет и составил в 2010 году 207 млрд. долл. США при общем объеме рынка в 4 трлн. долларов.

Данный тип финансового контракта предоставляет покупателю опциона право в течение определенного срока (американский опцион) или на конкретную дату (европейский) обменять одну валюту на другую по заранее установленному курсу. Как правило, компании импортеры и экспортеры используют валютные опционы в качестве альтернативы форвардным контрактам для хеджирования своих валютных рисков. Валютный опцион ограничивает возможные потери от неблагоприятного изменения валютного курса ценой исполнения (страйком), при этом позволяя получить прибыль в противоположном случае.

Ввиду того, что опцион теоретически позволяет получить неограниченную прибыль при ограниченных потерях, весьма важным является процесс установления цены на данный производный контракт. Существует несколько моделей позволяющих оценить теоретическую стоимость (премию) опциона.

Наиболее известной и широко применяемой на практике является модель ценообразования опционов Блэка-Шоулза. Будучи несколько модифицированной, она также позволяет оценивать стоимость валютных опционов. В ее основе лежит дифференциальное уравнение Блэка-Шоулза, которое в финансовой литературе решается через замену переменных и приводит к знаменитой формуле Блэка-Шоулза . Данное уравнение является аналогичным обратному уравнению Колмогорова в конкретной спецификации, которое также называется уравнением Дынкина (по названию одноименного дифференциального оператора, входящего в это уравнение). Уравнение Дынкина для цены опциона можно решить другим способом - по методу Фурье. Полученное в итоге решение будет, скорее всего, отличаться от теоретической стоимости опциона, найденной с помощью формулы Блэка-Шоулза.

Цель настоящей работы заключается в том, чтобы оценить это различие - будет ли оно существенным и значимым, или, напротив, оценки стоимости опционов, полученные двумя разными методами, окажутся примерно одинаковыми.

Для достижения этой цели необходимо выполнить следующие задачи:

1.      Решить уравнение Дынкина методом Фурье, представить общее решение в виде разложения в ряд по базисным функциям.

2.      Используя исторические данные по процентным ставкам, валютному курсу и волатильности валютного курса, получить двумя способами оценки стоимости колл-опционов европейского типа на валютную пару евро доллар.

.        Сравнить полученные результаты с помощью методов статистического анализа.

.        Проанализировать итоговые результаты, сделать выводы.

В первой части данной работы будет приведен общий ход решения уравнения Дынкина. Во второй части - будут получены теоретические значения стоимости валютных опционов на основе и формулы Блэка-Шоулза. В третьей части будет проведено сравнение полученных оценок, а также будут проанализированы итоговые результаты и сделаны выводы.

.       
Уравнение Дынкина

В основе большинства моделей ценообразования производных финансовых инструментов лежат стохастические дифференциальные уравнения, прежде всего, уравнение геометрического броуновского движения:

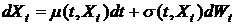 (1),

где 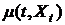- функция сноса равная 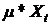, 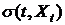- функция диффузии (волатильности) равная 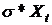, X - цена базового актива, t - время, µ - параметр сноса, σ - волатильность, W - винеровский процесс.

Уравнение (1) тесно связано c дифференциальным оператором A, который в одномерном случае равен:

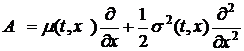
Этот инфинитезимальный оператор называется оператором Дынкина, или обратным оператором Колмогорова. Он происходит из дифференциального уравнения в частных производных второго порядка, которое называется обратным уравнением Колмогорова или уравнением Дынкина:

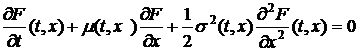 (2)

В данной работе мы будем рассматривать уравнение(2) в несколько иной спецификации, и искать такое его решение, которое удовлетворяло бы определенным условиям:

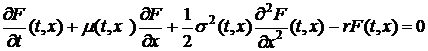 (3)

,

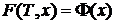где F(t,x) - это цена опциона, зависящая от времени и цены базового актива, t принадлежит интервалу (0;T), 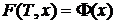- начальное (конечное) условие, 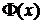- какая-то конкретная функция, которой равна функция F в момент времени Т, r - заданная константа.

Таким образом, мы получаем краевую задачу. Чтобы ее решить, необходимо определить вид функций сноса и диффузи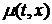и - и .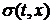

1.1    Вид функций сноса и диффузии

В основе ценового процесса производного финансового инструмента лежат изменения цены базового актива. Предположим, ценовой процесс базового актива (X) удовлетворяет следующему стохастическому дифференциальному уравнению:

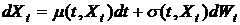
Параметризующая функция 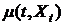 называется сносом процесса. Если 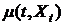>0, то траектория постепенно (в среднем) будет сдвигаться вверх (цена растет), иначе - вниз. Что касается функции 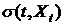, то она называется функцией волатильности, а ее квадрат - диффузией. Она показывает, насколько сильно ценовой процесс будет отклоняться от линии тренда, определяемой сносом.

Поскольку цена производного финансового инструмента зависит от цены базового актива, то функции сноса и волатильности входят в уравнение, описывающее динамику ценового процесса данного инструмента. В настоящей работе мы рассматриваем валютные опционы, поэтому базовым активом будет валюта, стоимость которой определяется валютным курсом. Следовательно, чтобы задать определенный вид функций сноса и волатильности, необходимо понять, чем определяется изменение валютного курса.

Для этого можно воспользоваться теорией паритета процентных ставок:

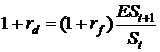 (4),

где 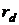, 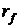внутренняя и внешняя безрисковые процентные ставки, 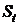- валютный курс в начальном периоде t, определяемый как отношение единиц отечественной валюты к единице иностранной, 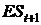 - ожидаемый валютный курс в следующем периоде.

Данная формула основывается на следующих предположениях: существует совершенная мобильность капитала, и выполняется условие отсутствия арбитража. Тогда можно реализовать две инвестиционные стратегии. Первая заключается в том, чтобы инвестировать сумму B под процент равный внутренней безрисковой ставке на период (T-t). Напротив, вторая стратегия предполагает, что деньги в отечественной валюте в количестве равном B будут обменяны на иностранную валюту по курсу 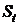 и после этого вложены под процент равный иностранной безрисковой ставке на тот же период. Тогда на момент времени T следует обменять полученную сумму в иностранной валюте по курсу 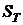 на отечественную валюту. В результате, если выполняются приведенные выше условия, доход от реализации первой и второй стратегий должен быть одинаковым.

Можно несколько преобразовать уравнение (4):

,

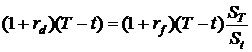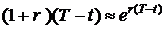 Þ .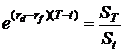

Устремляя t к T (следовательно 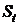®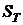) и принимая во внимание

,

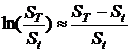
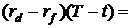
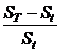или в форме дифференциала: 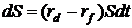 (5)

Таким образом, уравнение (5) это детерминированный процесс, определяющий динамику валютного курса. Если добавить в него 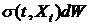 (часть, которая зависит от случайной величины), то мы получим уравнение (1), где функция сноса равняется 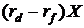, X - валютный курс.

Функцию волатильности - 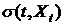принято задавать, как 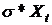, где σ - это волатильность базового актива. Ее можно рассчитать на основе стандартного отклонения по формуле:

, ,

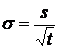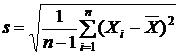где s- стандартное отклонение, t - длина временного интервала в годах, n - количество наблюдений, 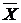 - среднее значение валютного курса за n наблюдений.

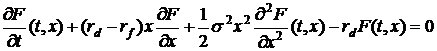 (6)

Если численно задать параметры (ставки, волатильность…) и решить уравнение (6) при условии 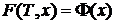, то мы получим выражение, позволяющее численно оценить теоретическую стоимость валютного опциона. Уравнение (6) является в точности дифференциальным уравнением Блэка-Шоулза в спецификации для валютных опционов. Следовательно, если решить его с помощью замены переменных можно получить модифицированную формулу Блэка-Шоулза. Однако цель данной работы заключается в том, чтобы решить это уравнение другим способом - методом Фурье. При этом, решая уравнение (3) мы не будем исключительно ограничиваться представленными выше спецификациями функций сноса и волатильности.

1.2    Метод разделения переменных

Метод Фурье, по-другому называемый методом разделения переменных, является одним из наиболее старых методов решений дифференциальных уравнений. Им можно решать задачи, описываемые линейными однородными дифференциальными уравнениями второго порядка. Уравнения (3) и, соответственно, (6) относятся именно к такому типу уравнений. Суть метода заключается в том, что мы ищем частное решение уравнения в виде произведения двух функций разных аргументов. Применительно к нашей задаче это означает, что одна часть искомого решения будет зависеть только от времени, а другая часть будет зависеть исключительно от финансовой переменной - валютного курса.

В книге Зайцева и Полянина приведена следующая схема решения дифференциального уравнения методом разделения переменных:

)        Дана исходная задача - уравнение с частными производными с начальными и граничными условиями.

2)      Ищем частное решение в виде произведения двух функций от разных аргументов, полагая, что .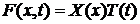

)        Приходим к уравнению: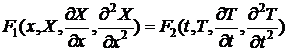

)        Обе части уравнения мы приравниваем к константе -l и получаем уравнения: , .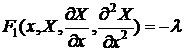

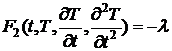)        Дальше мы ищем решение первого уравнения, удовлетворяющее граничным условиям. Мы имеем задачу на собственные значения (задача Штурма-Лиувилля). Находим собственные значения ln и собственные функции 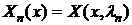, где n=1,2…

)        Решаем обыкновенное дифференциальное уравнение для T(t) и находим решения 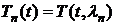, соответствующее собственным значениям l=ln.

)        Ищем общее решение в виде ряда 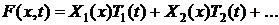 и, таким образом, мы получаем решение исходной задачи.

Особенность применения данной схемы к нашей задаче заключается в том, что мы имеем только начальное (конечное) условие -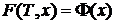, однако граничные условия не были заданы.

Граничные условия определяют поведение искомой функции на концах области определения аргумента. В нашем случае аргументом (x) является валютный курс. Теоретически он может принимать значения от 0 до +¥. Очевидно, что наша искомая функция (функция выплат или функция цены опциона), как и ее составляющая, зависящая только от x, будет равна 0 в том случае, если x=0.

Принимая во внимание такое явление как гиперинфляция, ситуация, когда валютный курс стремится к 0, выглядит достаточно правдоподобной, хотя в реальности он никогда не достигнет 0. Однако для того чтобы задать второе граничное условие, необходимо в качестве верней границы аргумента взять конкретное число.

Поэтому возникает проблема: как выбрать верхнюю границу области определения, а также как определить, чему равна искомая функция в данной точке?

Можно задать верхнюю границу и условие как x=l, F(l)=0, где l - некоторое число, но в настоящей работе мы не будем решать эту проблему и не станем задавать граничные условия. Постараемся решить исходную задачу без них, внося некоторые изменения в схему решения, изложенную выше.

1.3    Решение исходной задачи методом Фурье.

Будем решать уравнение (6) проведя в нем замену

,: .

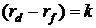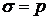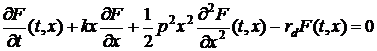Представив решение в виде 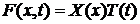, и разделяя переменные, получим:

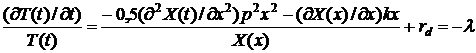 (7)

Сначала решим дифференциальное уравнение для T(t):

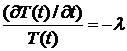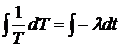ÞÞ,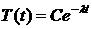

где С - константа, которую будем считать равной 1.

Таким образом, мы нашли вид функции, зависящей от времени, и теперь будем решать дифференциальное уравнение для X(x). Проведем замену 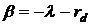, получая новый вид собственных значений, и перепишем уравнение (7):

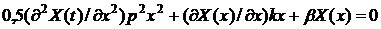 (8)

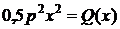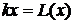Проводя замены - и , приведем уравнение (8) к операторной форме:

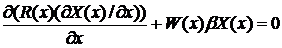 (9),

,

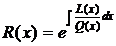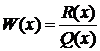
Если задать линейные однородные граничные условия в виде:

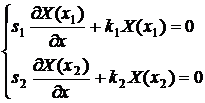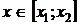 где  (10),

то уравнение (9) вместе с граничными условиями (10) представляет собой задачу на собственные значения. Чтобы ее решить необходимо найти собственные значения 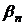и соответствующие им собственные функции 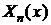, которые являются частными решениями исходного уравнения.

1.4    Решение задачи на собственные значения.

Пусть 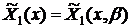и 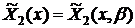- это линейно независимые частные решения уравнения (9). Тогда общим решением этого уравнения является линейная комбинация: 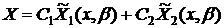(11), где C1 и C2 - это произвольные константы. ”Подставим решение в граничные условия. В результате для определения коэффициентов получим линейную однородную алгебраическую систему”:

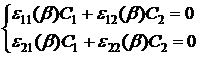 (12)

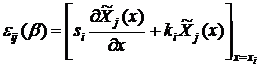
Чтобы полученная система имела нетривиальные решения, ее определитель должен быть равен 0. Решив ее, мы найдем собственные значения, а с помощью них - собственные функции.

Как правило, дискриминант характеристического уравнения меньше 0 и частные решения 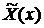в этом случае будут представлены в виде тригонометрических функций - косинусов и синусов. Следовательно, если решать исходное уравнение таким способом, то можно представить его общее решение в виде ряда тригонометрических функций.

Стоит также привести информацию, касающуюся свойств собственных значений:

-       Существует бесконечное счетное множество собственных значений.

-       Все собственные значения 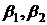… являются вещественными 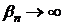и при .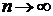

-       Каждое собственное значение единственно.

-       Каждому собственному значению соответствует с точностью до постоянного множителя лишь одна собственная функция.

-       Система собственных функций 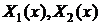… ортогональна на области определения x - 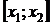с весовой функцией W(x) (их скалярное произведение равно 0):

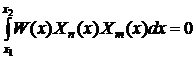 при n≠m.

Как уже было сказано выше, мы не будем задавать граничные условия. Поэтому нет смысла представлять общее решение в виде уравнения (11) и приходить к системе (12). Можно найти собственные функции в виде полиномов, причем условие ортогональности собственных функций с весовой функцией W(x) должно выполняться.

Уравнения (8) и (9) являются задачей Штурма-Лиувилля, кроме того, функции Q(x) и L(x) являются многочленами первого и второго порядка соответственно. Тогда частные решениями уравнения (9) можно получить в виде многочленов (полиномов) по формуле Родрига:

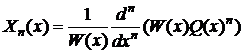 (13)

Для собственных значений 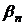 также существует формула:

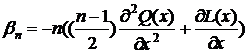
Тогда собственные значения 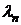получаем из уравнения: .

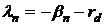Следовательно, мы можем представить общее решение уравнения (6) в виде суммы следующего ряда:

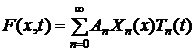 (14)

В данном уравнении вид функци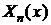й и 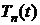 нам уже известен, n - это номер соответствующего многочлена и собственного значения. Так как существует бесконечное число собственных функций задачи (9), то мы можем разложить в ряд искомую функцию по любому, сколь угодно большому количеству полиномов, при этом данный ряд является абсолютно сходящимся. Как правило, чтобы с высокой точностью получить значение функции 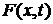, нам будет достаточно взять 10 первых многочленов (nmax=10) В формуле (14) присутствуют постоянные коэффициенты 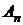, которые представляют собой веса в разложении искомой функции по собственным значениям.

Для того чтобы определить 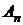мы воспользуемся начальным условием  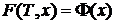и подставим в него ряд (14). В результате получим:

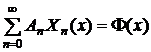
“Умножим обе части этого равенства на 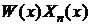 и проинтегрируем полученное выражение по x на отрезке 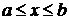. Учитывая свойство ортогональности собственных функций, находим коэффициенты”:

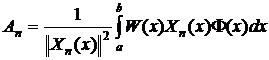, (15)

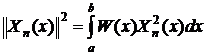
Таким образом, для того чтобы получить оценку опциона (подставив реальные данные по ставкам и т.д.) нам остается только задать область определения x и конкретный вид начального условия. Но прежде чем сделать это, необходимо проверить ортогональность собственных функций.

Мы хотим представить общее решение в виде разложения по базисным функциям. Для того чтобы оно было наиболее близким к искомой функции, базис должен быть ортогональным. Следовательно, собственные функции (полиномы) уравнения (13) должны быть ортогональны с весовой функцией W(x). Полиномы, получаемые по формуле Родрига, будут ортогональными, если выполняется следующее условие:

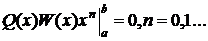 (16)

Весовая функция определяется следующим выражением:

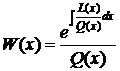
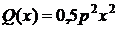 и 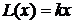, получим

.

.

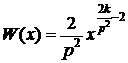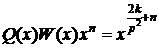Следовательно, мы приходим к уравнению:

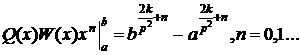 (17)

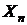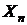Несмотря на то, что собственные функции  не являются ортогональными, они, тем не менее, представляют собой частное решение: подставляя полиноми соответствующее ему собственное значение  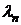в уравнение (8), мы получим тождественный 0. Это значит, что мы сможем представить общее решение в виде ряда, но, как уже было сказано выше, оно вряд ли нам подойдет.

Можно попытаться справиться с данной проблемой, если построить новые ортогональные полиномы (получить ортогональный базис) из старых, с помощью процесса Грама-Шмидта, или используя моменты весовой функции. Однако полученные новые многочлены уже не будут являться частными решениями исходной задачи, зато они могут оказаться решениями уравнения, похожего на уравнение (3), но уже с другими спецификациями функций сноса и волатильности (изменится вид 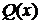и).

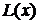Следовательно, можно получить это “новое” решение, считая его наилучшим приближением к решению нашей первоначальной задачи.

1.5    Весовая функция и ортонормированные полиномы

Чтобы получить ортогональные собственные функции, а также определить веса в разложении, необходимо задать область определения финансовой переменной. Как уже было сказано, теоретически валютный курс может принимать значения в интервале от 0 до +¥. Что касается весовой функции, то уравнение (9) останется неизменным по форме, если совершать с ней масштабные преобразования вида 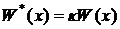, где k - ненулевая константа. Тогда представим ее в виде 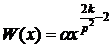. Учитывая, что k может быть меньше 0 (разность процентных ставок отрицательна), можно будет взять определенный интеграл вида 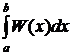 при любых значениях k, только если a и b - это определенные константы, причем a>0.

В настоящей работе будет оценена стоимость опционов для валютной пары евро доллар. Поэтому, чтобы задать конкретные значения a и b, посмотрим на график исторического курса евро к доллару:

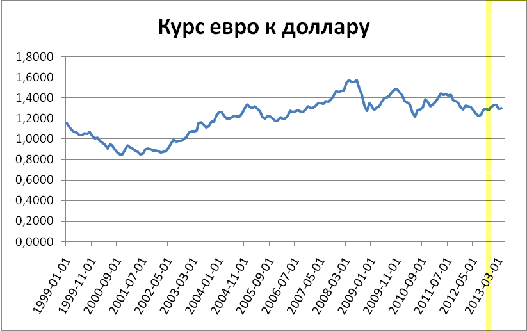
График 1

График, приведенный выше, построен на основе ежемесячных средневзвешенных данных. Он показывает, что минимальное значение котировки валютной пары было около 0.8, а максимальное - около 1.6. Тогда для удобства в качестве верхней границы валютного курса евро доллара возьмем значение равное 2, а в качестве нижней - значение равное 0.5. Следовательно, задав область определения подобным образом, можно без труда находить определенные интегралы от произведений весовой функции на полиномы.

Формула (16) для весов в разложении по собственным функциям представляет собой деление скалярного произведения полинома с весовой функцией и начального условия на квадрат нормы соответствующего полинома, которая определяется выражением

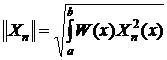
Можно упростить вычисления и избежать нормировки, если получить ортонормированные полиномы. Это можно сделать двумя способами: с помощью процесса Грама-Шмидта, и по моментам весовой функции. Оба данных метода будут изложены ниже.

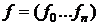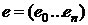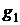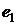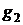Вначале рассмотрим процесс Грама-Шмидта. Пусть - некоторый базис в n-мерном евклидовом пространстве e. Модифицируя этот базис, построим новый базис , который будет ортонормированным. Последовательно вычисляем векторы  и,  и 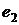 и т.д. по формулам”:

,

,

,

,

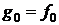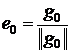
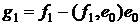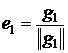
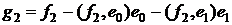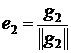
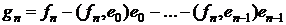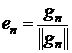
В нашем случае векторы 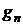,,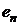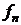являются функциями, где 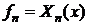- это старые полиномы, а 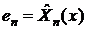- это искомые ортонормированные полиномы. Скалярное произведение 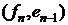 определяется следующей формулой:

.

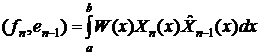Прежний полином нулевого порядка, получаемый по формуле Родрига, равняется единице. Следовательно, норма 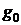 тоже равна 1. Так как

,

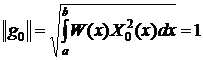определенный интеграл от весовой функции на заданной области определения должен равняться 1. Значит наша весовая функция, фактически, является функцией плотности вероятности с площадью под кривой равной единице на интервале [0.5;2]. Найдем ее конкретный вид:

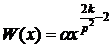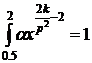
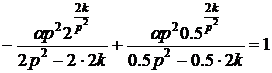, где a - это константа, Þ

Þ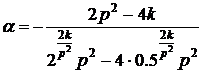ÞÞ

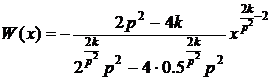
Таким образом, была получена весовая функция в конкретной спецификации, которая будет использован в дальнейшем. Теперь можно воспользоваться вторым способом - построить ортонормированные полиномы на ее моментах.

Весовая функция, заданная на интервале от a до b, однозначно определяет полином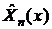 с точностью до нормировочного множителя. Тогда для этого полинома справедливо следующее явное выражение:

,

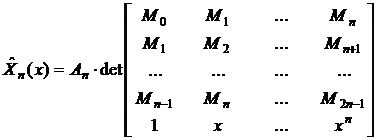где 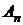- это нормировочный множитель,  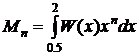- момент весовой функции W(x). Матрица моментов по-другому называется матрицей “Гамбургера”, что касается нормировочного множителя, то в него входят две матрицы Ганкеля:

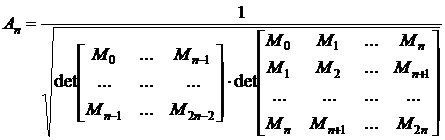
Процесс Грама-Шмидта и метод моментов приводят в точности к одному и тому же результату. Однако в данной работе ортонормированные полиномы будут найдены с помощью моментов весовой функции, поскольку данный способ является менее громоздким. Кроме того, процесс Грама-Шмидта относится к численно неустойчивым алгоритмам - ошибки округления и погрешности численного интегрирования накапливаются при увеличении номера многочлена.

1.6   
Новое уравнение и итоговое общее решение

Как уже было отмечено выше, ортонормированные полиномы не являются частным решением исходного уравнения вида:

,.

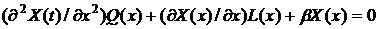
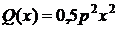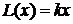Однако, возможно, существует такое дифференциальное уравнение второго порядка, решениями которого они бы являлись. Это уравнение обладало бы новыми спецификациями функций 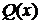, 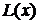и, следовательно, другими функциями сноса и волатильности. Тогда, имея новые ортонормированные полиномы, весовую функцию и старые собственные значения, можно попытаться найти уравнение, собственными функциями которого окажутся ортонормированные многочлены. Будет затруднительно сделать это в символьном виде, поскольку полученная весовая функция

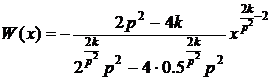
является довольно громоздкой. Тогда попробуем получить новое уравнение, задав конкретные значения параметров p и k.

Возьмем в качестве примера реальные данные по условно безрисковым процентным ставкам США и зоны евро и по волатильности курса евро к доллару на конец первого полугодия 2003 года. Волатильность была рассчитана по формуле

,

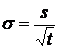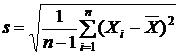
на основе ежемесячных средневзвешенных данных по валютному курсу за предшествовавшие полгода, и равнялась 0.1548. Ставка по десятилетним казначейским облигациям США была равна 0.0353, а по десятилетним европейским облигациям - 0.0372. Тогда 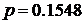, 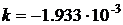. Теперь найдем конкретный вид уравнения (8) и весовой функции:

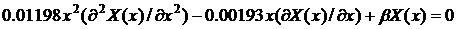
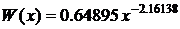
Тогда можно получить частные решения данного уравнения, а также ортонормированные полиномы по моментам весовой функции. Найдем собственные значения и первые десять многочленов, как старых, так и новых. Результаты приведены в таблице ниже:

Таблица 1

Как видно из таблицы, новые ортонормированные многочлены имеют более сложной вид, чем старые частные решения. Теперь с помощью ортонормированных полиномов и старых собственных значений можно получить уравнение вида:

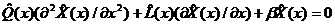или

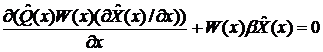 (18)

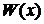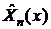Если подставить известную нам весовую функцию , а также полином и соответствующее ему собственное значение  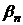в уравнение (18), то получим линейное дифференциальное уравнение первого порядка относительно переменной 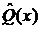вида:

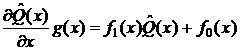, где

, ,

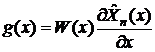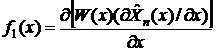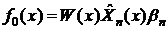
Тогда решение этого дифференциального уравнения находится по формуле:

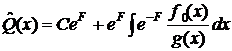, где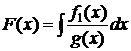

Подберем такую константу C, чтобы выполнялось условие ортогональности:

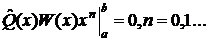 Þ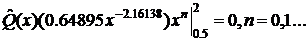

Это означает, что 2 и 0.5 должны являться корнями многочлена 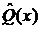, или должно выполняться равенство 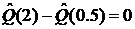. Тогда С= -0.0100396.

Учитывая константу C, подставляем в уравнение полученный ортонормированный полином первого порядка, соответствующее ему собственное значение и весовую функцию, получаем:

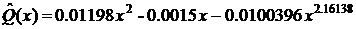
Тогда 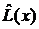найдем по формуле:

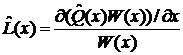
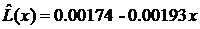
Получаем новое уравнение и сравниваем его со старым:

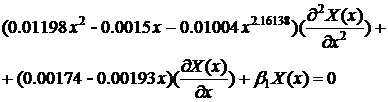
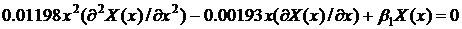
Как видно из уравнений приведенных выше, спецификации функци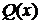й и 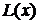, а значит и функций сноса и волатильности (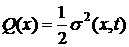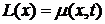) во многом похожи на первоначальную, но имеются серьезные отличия.

Однако ортонормированные полиномы старше первого порядка не являются решениями полученного выше уравнения при старых собственных значениях 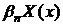. Также не получится найти соответствующие им новые собственные значения по формуле:

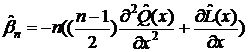
поскольку функция 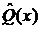больше не является многочленом второго порядка ( будет зависеть от x). Так оказалось потому что, чтобы выполнялось условие ортогональности, константа C должна иметь ненулевое значение. Данное условие будет выполняться и константа будет равна 0, тогда и только тогда, когда x будет определен на области от 0 до некоторого положительного числа (0 будет корнем многочлена 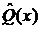, если C=0).

Значит, только на области определения [0;b] можно получить нужный нам вид функции 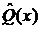, а также новое уравнения, частными решениями которого будут ортонормированные полиномы. Однако в данной работе используется область определения от 0.5 до 2, чтобы не возникало проблем с взятием определенного интеграла вида 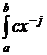,где j>0, j и с - константы. Следовательно, в сложившейся ситуации не удастся найти такое уравнение, для которого полученные ортонормированные полиномы будут являться частными решениями, хотя в принципе, если поменять область определения, это возможно.

Тем не менее, будем считать, что с помощью ортонормированных многочленов, можно получить оценку цены валютного опциона. Данное соображение имеет свою логику: ортонормированные полиномы мы находим по моментам весовой функции, которая, в свою очередь, зависит от исходных функци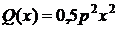й  и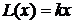

Получив ортонормированные полиномы, составим из них общее решение таким же способом, как это было сделано для старых неортогональных собственных функций:

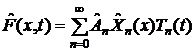, где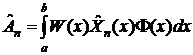

Также можно представить общее решение в виде ряда из десяти первых полиномов (как правило, этого достаточно, чтобы оно не менялось и оставалось устойчивым)

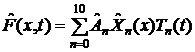
Из всех функций, составляющих общее решение, не было задано лишь начальное условие. Для того чтобы его определить, необходимо знать тип производного финансового инструмента (опциона). Опционы бывают двух видов: на покупку (колл) и на продажу (пут). Опцион колл (пут) предоставляет право его владельцу купить (продать) базовый актив по заранее оговоренной цене исполнения (страйк - K) в определенный момент времени в будущем. Следовательно, если в момент исполнения (T) спот цена базового актива окажется выше (ниже) страйка, то опцион колл (пут) принесет прибыль в размере x-K (K-x), в противном случае он не будет исполнен. Тогда стоимость опциона колл в этот момент будет равна либо 0, либо разнице между ценой базового актива и ценой исполнения:

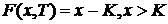
Начальное условие 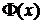для опциона колл зададим как

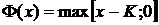
где K - страйк, или как

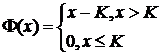
Тогда перепишем формулу для весов в разложении:

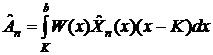
Аналогично для опциона пут:

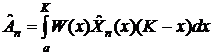
Подводя итоги данного раздела, еще раз перечислим основные моменты поиска общего решения, позволяющего оценить стоимость валютного опциона:

1)      Дана исходная задача - уравнение с частными производными второго порядка. Его параметризующие функции сноса и волатильности заданы как

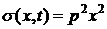 и ,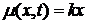

где x - валютный курс, k - разница безрисковых процентных ставок, а p - это волатильность.

2)      Ищем частное решение в виде произведения двух функций от разных аргументов, полагая, что

,

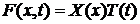где 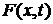 - это цена опциона.

3)      Разделяем переменные и находим, чему равняется часть искомой функции, зависящая от времени:

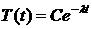
где t - время, измеряемое в годах, C - константа, l - собственное значение уравнения, зависящего от x.

4)      После разделения переменных получаем уравнение для x:

где 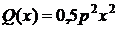, , 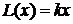,  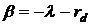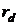- внутренняя безрисковая процентная ставка.

5)      Решаем данное уравнение (задачу Штурма-Лиувилля), получая полиномиальные частные решения по формуле Родрига:

.

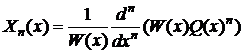6)      Представляем общее решение исходного дифференциального уравнения (уравнения Дынкина) в виде ряда:

,

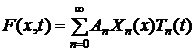где 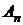- это веса в разложении.

7)      Проверяем частные решения на ортогональность и, в результате, приходим к выводу о том, что найденные полиномы не являются ортогональными. Следовательно, полученное общее решение, скорее всего, не позволит корректно оценивать теоретическую стоимость валютных опционов.

8)      С помощью найденной весовой функции находим ортонормированные полиномы 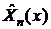и представляем общее решение в виде разложения в ряд, используя десять первых многочленов:

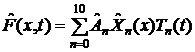
9)      Выбираем вид начального (конечного) условия в зависимости от типа производного финансового инструмента и получаем формулу для весов в разложении: для опциона колл -

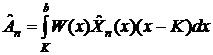, для пут - .

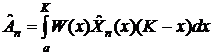10)    Подставляем исторические данные по валютному курсу, а также по процентным ставкам и волатильности в общее решение. Получаем оценку теоретической стоимости валютного опциона!

2.     
Модель Блэка-Шоулза

В начале 70-х годов 20 века Фишер Блэк и Майрон Шоулз разработали знаменитую модель, позволяющую оценивать теоретическую стоимость опционов европейского типа. В ее основе лежали следующие предположения:

·        Рынок является полным и эффективным.

·        Транзакционные издержки равны нулю.

·        Все доходы облагаются налогами по одной и той же схеме, следовательно, налогообложение не играет роли.

·        Все участники рынка могут занимать и давать в долг деньги по безрисковой ставке.

·        Отсутствует арбитраж.

·        Короткая продажа разрешается без ограничений.

·        По базовому активу не выплачиваются дивиденды.

·        Цена подлежащего актива имеет логнормальное распределение - подчиняется геометрическому броуновскому движению.

Тогда динамика цены опциона описывается следующим дифференциальным уравнением второго порядка:

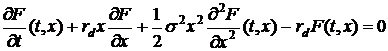
Решением данного уравнения является знаменитая формула Блэка-Шоулза для опциона колл:

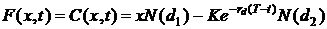
для опциона пут:

,

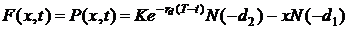где x - спот цена подлежащего актива, K - страйк, 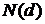 - это кумулятивная функция стандартного нормального распределения:

,

,

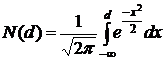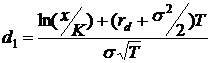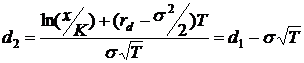
Другими словами, 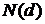- это вероятность, с которой случайная величина, подчиняющаяся стандартному нормальному распределению N(0,1), примет значение меньшее, чем d.

Приведем доказательство данной формулы, изложенное в книге Стохастический Мир. Решим уравнение Блека-Шоулза

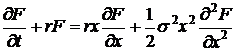
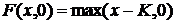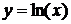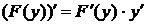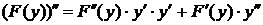с начальными условиями вида: . Сначала избавимся от множителей x при производных. Для этого перейдем к новой переменной . Учитывая и , получаем:

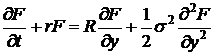, где .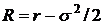

С помощью замены избавимся от члена с первой производной по y, где a и β - это некоторые константы:

.

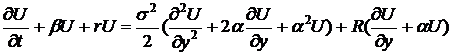Для того чтобы слагаемые, содержащие первую производную по y и члены, пропорциональные U, сократились, подберем нужные значения констант

,

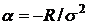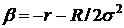
Тогда получим уравнение теплопроводности:

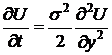
Оно решается с помощью преобразования Фурье. Частным решением такого уравнения является функция:

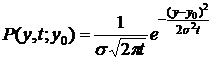
Поскольку уравнение линейное, его общее решение является суммой частных решений, соответствующих различным значениям :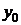

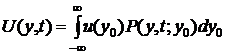
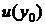имеет смысл начального значения функции 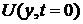. С учетом проделанной замены 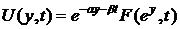начальное условие принимает следующий вид:

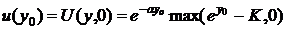
Тогда общее решение равно:

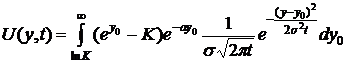
Нижний предел интегрирования дает функция max, которая отлична от 0 при 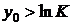. Теперь проведем замену :

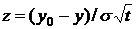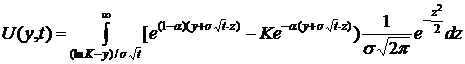
В показателе экспоненты появляются выражения вида 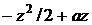. Преобразуем их к эквивалентному виду 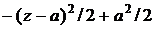. После замены 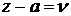общее решение становится равным:

,

, .

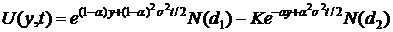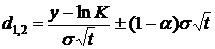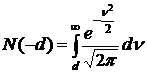Проводя обратные замены 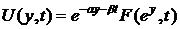, , 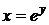получим формулу Блека-Шоулза для опциона колл.

Приведенное выше дифференциальное уравнение и его решение в виде формулы позволяет оценивать теоретическую стоимость опциона, в основе которого лежит актив, не приносящий доход (дивиденды) в течение всего срока до момента исполнения. Однако с помощью него нельзя оценить стоимость валютного опциона, поскольку базовый актив - это иностранная валюта. Данный актив будет приносить доход, если вложить сумму в иностранной валюте под процент равный безрисковой ставке в другой валютной юрисдикции. Тем не менее, валютный опцион можно оценить с помощью модели Блэка-Шоулза, если внести небольшие изменения. Тогда дифференциальное уравнение второго порядка будет выглядеть следующим образом:

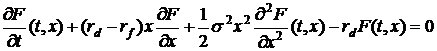
Это в точности то же самое уравнение - уравнение Дынкина в конкретной спецификации, которое было использовано в первом разделе данной работы. Его решение можно также представить в виде формулы Блека-Шоулза для валютных опционов:

,

,

,

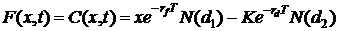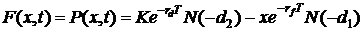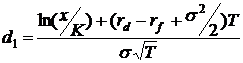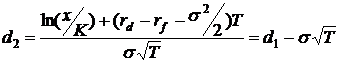
Следовательно, если подставить реальные данные в формулу, приведенную выше, можно получить оценку теоретической стоимости валютного опциона.

3.     
Сравнение результатов модели Блэка-Шоулза и уравнения Дынкина

В предыдущих разделах данной работы было приведено описание двух разных способов нахождения теоретической цены валютных опционов. В то же самое время, в основе обоих методов лежит одно и то же дифференциальное уравнение. Поэтому, скорее всего, результаты не должны сильно отличаться. Для того чтобы проверить это предположение, необходимо на основе реальных данных получить оценки стоимости валютных опционов, как с помощью формулы Блека-Щоулза, так и с помощью представления решения уравнения Дынкина в виде ряда полиномов, умноженных на соответствующие веса в разложении и функцию, зависящую от времени - T(t).

В настоящей работе будет оценена теоретическая стоимость европейских колл опционов для валютной пары евро доллар. Для того чтобы сделать это были использованы следующие данные:

-       данные по валютному курсу были получены из статистических источников Федерального резервного банка Сент-Луиса.

-       в качестве безрисковых процентных ставок были взяты доходности в годовом выражении по десятилетним казначейским облигациям ФРС США и по десятилетним европейским облигациям. Информация была получена из статистических источников Европейского центрального банка и Федерального резервного банка Сент-Луиса.

-       волатильность была рассчитана по формуле стандартного отклонения на основе месячных данных курса евро к доллару за полгода.

Как уже было сказано выше, решение уравнения Дынкина, позволяющее оценить стоимость опциона, можно получить с помощью неортогональных полиномов, которые являются его частными решениями. Используя выбранный массив данных, найдем теоретическую цену для опциона со сроком исполнения полгода и страйком, который равняется текущему валютному курсу. Представим полученный результат графически:

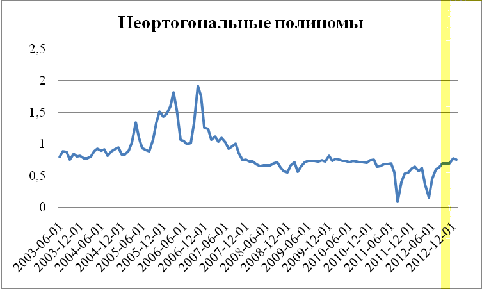
График 2

Как видно из графика, оценки стоимости валютного опциона, рассчитанные с помощью неортогональных полиномов, получились неоправданно высокими. Крайне маловероятной является ситуация когда, цена опциона может быть сравнимой и даже превышать цену базового актива. Однако на графике мы видим именно это: теоретическая стоимость опциона находится в диапазоне от 0 до 2 долларов за контракт на покупку одного евро, в то время как за рассматриваемый период валютный курс колебался в диапазоне от 1.1 до 1.6 долларов за евро. Следовательно, решение уравнения Дынкина, полученное на основе неортогональных полиномов, имеет мало общего с действительностью. Поэтому в настоящей работе будут рассмотрены только результаты, полученные с помощью ортонормированных многочленов, являющихся частными решениями дифференциального уравнения со спецификациями функций сноса и волатильности отличными от исходных.

Прежде чем сравнивать теоретические цены опционов, найденные с помощью разложения общего решения в ряд по ортонормированным многочленам и по формуле Блэка-Шоулза, стоит сказать о том, как влияет спот цена (текущее значение валютного курса), страйк и время до момента исполнения на стоимость опциона.

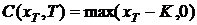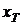Прибыль, которую приносит опцион колл, описывается выражением , где  - это цена базового актива в момент исполнения. Следовательно, доход от опциона, а значит и его цена формально не зависят от спот цены базового актива. Однако считается, что ценовой процесс является мартингалом, то есть предполагается, что в среднем цена не изменяется. Это значит, что лучшим прогнозом ее будущего значения будет ее текущее значение 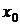. Тогда считаем, что 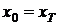. Поэтому в формулу Блэка-Шоулза и в ортонормированные полиномы подставляется значение именно спот цены. Принимая во внимание выражение 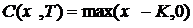, становится очевидным, что она положительно влияет на стоимость опциона, в то время как страйк влияет отрицательно.

Что касается времени, то оно также положительно влияет на стоимость опциона. Это объясняется простым соображением - чем ближе момент исполнения, тем меньше неопределенность относительно будущей цены актива. И наоборот - чем больше осталось времени, тем выше неопределенность, а значит и риск. Следовательно, цена за опцион будет выше.

Стоимость опциона определяется как сумма его внутренней стоимости и временной стоимости. Внутренняя стоимость является разницей между будущей ценой актива на момент исполнения и страйком: 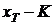. Если эта разница отрицательна, то внутренняя стоимость равна 0, поскольку опцион не будет исполнен. Временная стоимость, представляет собой надбавку к внутренней стоимости опциона за счет неопределенности значения цены актива в будущем. Она не может быть отрицательной и равняется 0 в момент исполнения. Кроме того, она стремится к 0 при увеличении цены актива или при снижении страйка. Когда цена подлежащего актива равняется цене исполнения, временная стоимость опциона принимает максимальное значение.

Что касается страйка, то с ним тесно связано такое понятие как денежность опциона. В зависимости от денежности возможны три ситуации:

)        опцион “в деньгах” (in the money) - цена спот выше, чем страйк -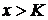

)        опцион “при своих” - цена равна страйку -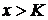

)        опцион “без денег” - цена актива меньше, чем страйк -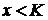

Рассмотренные выше ситуации показаны наглядно на рисунке:

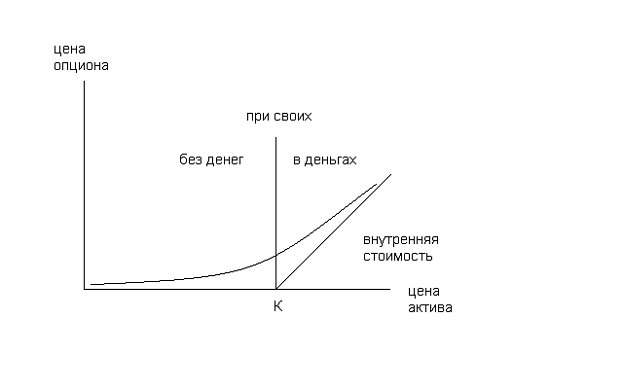
Рисунок 1

Поскольку в зависимости от соотношения страйка и текущей цены актива существуют три различные ситуации, будет целесообразно провести сравнение теоретических цен опционов, полученных с помощью разложения общего решения в ряд по ортонормированным полиномам и по формуле Блэка-Шоулза для трех различных случаев.

Тем не менее, можно показать, какой будет оценка теоретической стоимости опциона при любых значениях страйка. Для этого рассмотрим конкретное наблюдение, а не весь массив данных. Возьмем для примера процентные ставки и значение валютного курса (равняется 1.312) на конец 2012 года. Тогда представим графически зависимость оценок стоимости опционов, полученных по формуле Блэка-Шоулза и с помощью полиномов, от различных значений страйка:

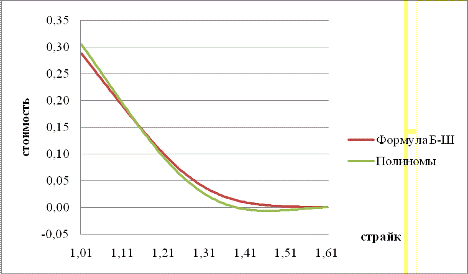
График 3

Как видно из графика, результаты получились очень близкими, практически одинаковыми. Однако оценки стоимости опциона по Блэку-Шоулзу, оказались меньше, чем рассчитанные с помощью полиномов в случае, когда спот курс (1.312 доллара за евро) существенно (20-30 центов) превышает страйк. Напротив, их значения получились большими в ситуации, когда страйк несильно отличается от текущего курса. Кроме того, любопытно то, что при высоких значениях страйка теоретическая стоимость опциона, полученная с помощью ортонормированных полиномов, оказалось отрицательной. Данный факт будет объяснен в дальнейшем.

3.2 Опционы “при своих”

Вначале рассмотрим результат, полученный с помощью ортонормированных полиномов по формуле 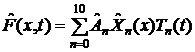, и покажем, что первых десяти многочленов вполне достаточно для представления общего решения.

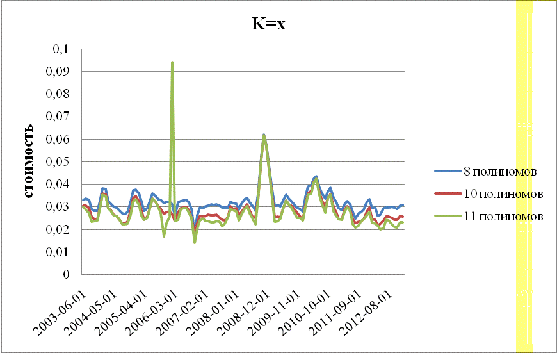
График 4

Как видно из графика, восемь, десять и одиннадцать первых многочленов практически одинаково представляют общее решение, однако в случае, когда были использованы 11 полиномов, в 2006 году наблюдается нехарактерный пик. Поэтому ограничимся только 10 первыми полиномами.

Теперь сравним теоретическую стоимость опционов, рассчитанную двумя разными способами. Представленные ниже результаты были получены для опционов со сроком исполнения полгода. Такой период времени был выбран потому, что волатильность была рассчитана за 6 месяцев. Дело в том, что существует общее правило, согласно которому целесообразно оценивать стоимость контракта с таким периодом исполнения, который равняется количеству времени, использованному для расчета волатильности.

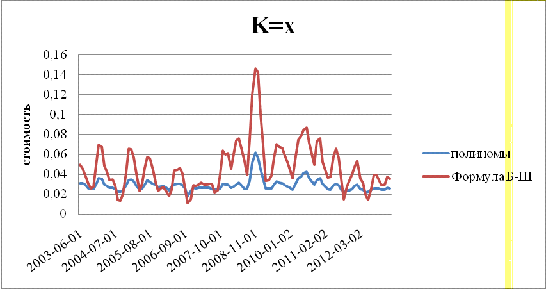
График 5

На графике 5 представлены две группы данных: оценки стоимости опционов, полученные с помощью ортонормированных полиномов; оценки, рассчитанные по формуле Блэка-Шоулза. В целом оба графика (процесса) довольно похожи - их тренды совпадают: большей теоретической стоимости опциона по Блэку-Шоулзу соответствует более высокое значение цены опциона, рассчитанной с использованием полиномов. Коэффициент корреляции между двумя группами данных составляет 93%, что свидетельствует о тесной положительной взаимосвязи.

Оценки стоимости опционов, найденные с помощью формулы Блэка-Шоулза, оказались существенно больше, чем полученные с помощью полиномов. Среднее значение для первых равняется 4.65 цента за контракт, в то время как для вторых - 2.9 цента. В целом данные результаты являются весьма правдоподобными. Так, например, цена валютных колл опционов на евро доллар со сроком исполнения полгода и страйком близким к спот курсу, торгуемых на Чикагской бирже опционов, лежит в диапазоне от 2 до 3 центов за один евро.

Таким образом, теоретическая премия по опциону, получаемая на основе модели Блека-Щоулза, оказалась в среднем на 1.75 цента больше, чем премия, найденная на основе ортонормированных многочленов.

Кроме того, из графика видно, что результаты, найденные с помощью модели Блэка-Шоулза, являются более “волатильными”, чем те, которые были получены с помощью полиномов. Чтобы проверить данный факт, воспользуемся коэффициентом вариации, поскольку, очевидно, что средние значения для двух групп полученных результатов не равны. Рассчитаем данный показатель по формуле: 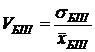, , 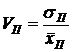где индексы БШ и П обозначают принадлежность к результатам, полученным на основе формулы Блэка-Шоулза и полиномов соответственно, σ - среднеквадратическое отклонение, 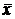- среднее значение. Тогда 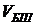=51%, 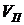=22%. Коэффициент вариации - это мера относительного разброса переменной, показывающая, какую долю среднего значения этой переменной составляет ее средний разброс. Следовательно, доля среднего разброса в среднем значении оценок, найденных по Блэку-Шоулзу, практически в 2,5 раза больше, чем аналогичный показатель для оценок стоимости опционов, полученных с помощью полиномов.

Приведенный выше результат относится только к ситуации “при своих”. Тот факт, что стоимость опциона, найденная с помощью формулы Блэка-Шоулза, оказалась систематически выше стоимости, оцененной на основе полиномов, требует дополнительной проверки. Дело в том, что, теоретически, не только процессы ценообразования опционов, полученные из модели Блэка-Шоулза и с помощью ортонормированных полиномов должны быть похожи, но и конкретные значения оценок теоретической стоимости опционов должны быть примерно равны. Данное предположение обуславливается тем, что в основе обоих методов лежит одно и то же дифференциальное уравнение.

В формуле оценки стоимости опционов, получаемой с помощью полиномов, присутствует константа, значение которой было принято равным единице:

,

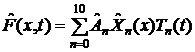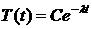
Тем не менее, ее значение можно выбрать произвольным. Тогда будет целесообразно задать константу таким образом, что оценки стоимости опционов, полученные с помощью полиномов, оказались максимально близки к оценкам, найденным по формуле Блэка-Шоулза.

Воспользуемся уравнением парной линейной регрессии вида:

,

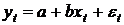где t - период, y - оценки по Блэку-Шоулзу, x - оценки на основе полиномов, b - искомый коэффициент регрессии, a - константа, чье значение примем равным 0, e - ошибка модели. Тогда с помощью метода наименьших квадратов найдем b. b=1.693, R^2=0.869. Теперь примем значение константы C равным значению b, и подставим в формулу

,

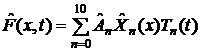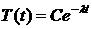
Следовательно, получим новый результат и представим его графически:

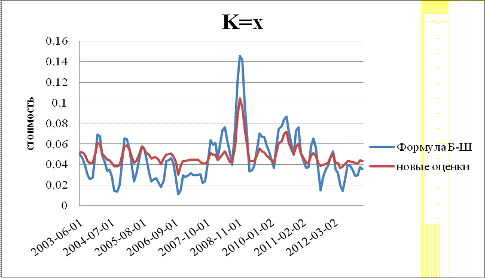
График 6

Как видно из графика 6, результаты, которые были найдены на основе двух разных способов, стали еще ближе. Оценки по Блэку-Шоулзу по-прежнему более волатильны: 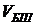=51%>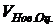=22% . Имеет смысл рассчитать разность между полученными результатами:

График 7

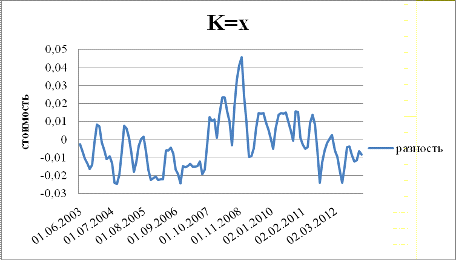
На графике 7 изображена выборка для разности между новыми оценками и результатами, найденными по формуле Блэка-Шоулза. Тогда можно проверить гипотезу о равенстве ее генеральной средней 0 при неизвестном значении генеральной дисперсии. Следовательно, имеем: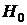(нулевая гипотеза): 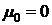, 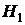(альтернативная гипотеза): 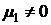. В основе проверки данной гипотезы лежит статистика

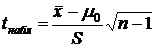
где S - стандартное отклонение, исследуемой выборки, 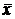- ее среднее значение, а n - это количество наблюдений равное 116. Данная статистика имеет распределение Стьюдента с n-1 степенями свободы. Проверим нулевую гипотезу на уровне значимости 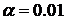Наблюдаемое значение статистики равно:

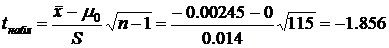
Рассчитаем критическое значение статистики:

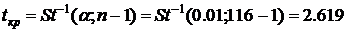
где St - распределение Стьюдента. Поскольку 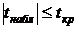, то можно сделать вывод что на уровне значимости 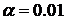гипотеза 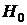:  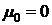не отвергается. Следовательно, есть основания утверждать, что в среднем теоретическая стоимость валютного опциона колл, оцененная по формуле Блэка-Шоулза, равняется теоретической стоимости, найденной с помощью ортонормированных полиномов, умноженной на отличную от 0 константу:

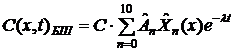
Данное утверждение справедливо только в том случае, если страйк равняется текущему валютному курсу.

В следующем подразделе, представленном ниже, мы рассмотрим случаи, когда опцион находится “в деньгах” “и вне денег”. Но поскольку таких ситуаций может быть бесконечно много, статистический анализ не будет проведен. Изложенная ниже информация всего лишь иллюстрирует некоторые возможные варианты.

3.2    Опционы “в деньгах” и “вне денег”

Покажем вначале какие значения будет принимать теоретическая стоимость опционов в случае, если страйк будет не намного меньше, чем текущий валютный курс. В качестве примера рассмотрим ситуацию, когда цена исполнения будет на 5 центов меньше, чем спот курс:

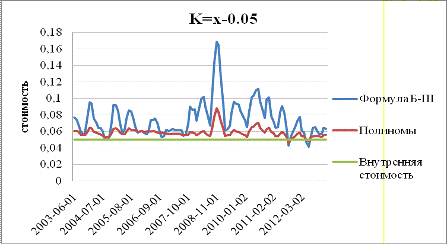
График 8

Из гравика видно, что оценки опционов, найденные по формуле Блэка-Шоулза, также значительно превышают оценки, которые были получены с помощью полиномов. Однако оба процесса ценообразования опционов по-прежнему имеют похожую динмаику. Это позволяет предположить, что результаты по Блэку-Шоулзу в среднем равняются оценкам теоретической стоимости опциона, найденным на основе ортонормированных многочленов, умноженным на некоторую константу.

Любопытным является то, что в конце рассматриваемого периода, как видно из графика 8, некоторые теоретические значения стоимости опционов оказались меньше, чем внутренняя стоимость - 5 центов. Приведенный выше факт, несомненно, требует логического объяснения, однако это не является целью настоящей работы - будем считать, что оба исследуемых метода - формула Блэка-Шоулза и полиномиально разложение в ряд иногда дают сбои. Ситуация, когда страйк существенно ниже спот курса (на 30 центов), является примером подобного сбоя:

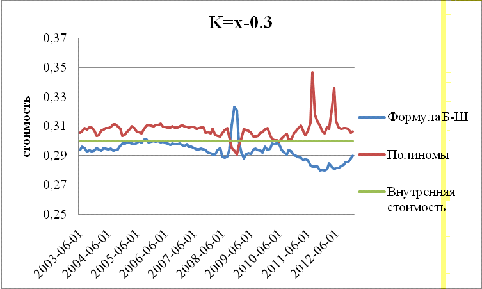
График 9

График 9 показывает, что практически все значения стоимости опционов, оцененные по формуле Блэка-Шоулза оказались меньше, чем внутренняя стоимость - 30 центов. Подобный результат не является правдоподобным, поскольку временная стоимость не может быть отрицательной, а значит цена опциона всегда больше, либо равна его внутренней стоимости.

Принимая во внимание факт, изложенный выше, результаты, полученные с помощью полиномов, оказались более правдоподобными. Однако это не свидетельствует о том, что данный способ получения теоретической цены опционов является лучшим по сравнению с моделью Блэка-Шоулза. Дело в том, что оценки стоимости опционов, найденные с помощью полиномов могут принимать отрицательные значения:

График 10

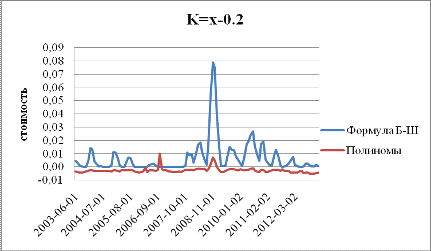
На графиках 10 и 11 показаны ситуации, когда опцион находится ”вне денег”: страйк превышает спот курс на 5 и 20 центов соответственно. С увеличением страйка, стоимость опциона колл достаточно быстро стремится к 0. Поэтому качество представленных выше результатов оставляет желать лучшего: оценки по Блэку-Щоулзу получились слишком большими (график 11), а оценки, найденные с помощью полиномов, оказались отрицательными, особенно это заметно на графике 11.

Неправдоподобно большие оценки стоимости опционов, найденные по формуле Блэка-Шоулза, по всей видимости, можно объяснить высокой волатильностью валютностью валютного курса, которая наблюдалась в некоторые моменты времени за рассматриваемый период. Что касается результатов, полученных с помощью полиномов, то некоторые из них оказались отрицательными (хотя и близкими к 0), скорее всего, потому, что взятых 10 полиномов было недостаточно в данной ситуации для корректного представления общего рещения. Одкако рассчет полиномов выше десятого порядка требует довольно много времени и существенной вычислительной мощности.

Исходя из информации, изложенной выше, оценки опционов по Блэку-Шоулзу и, полученные с помощью полиномов, оказались достаточно похожими друг на друга (в смысле совпадения трендов) только в случаях, когда страйк не намного (на 5 центов, например) отличается от спот курса - графики 8 и 10. Однако если цена исполнения существенно выше или ниже текущего валютного курса, различия могут оказаться значительными (график 9). Таким образом, с уверенностью можно утверждать только то, что лишь в ситуации “при своих” с учетом определенной константы оценки теоретической стоимости опционов, полученные двумя разными способами, в среднем окажутся равными.

Заключение

Итак, в настоящей работе были проанализированы два способа оценивания теоретической стоимости валютного опциона: по формуле Блэка-Шоулза и с помощью полиномов, полученных из уравнения Дынкина. Суть второго способа заключается в том, чтобы, разделив переменные, решить дифференциальное уравнение второго порядка, находя частные решения в виде многочленов.

Общее рещение уравнения Дынкина, позволяющее оценивать стоимость опционов, было представлено как с помощью неортогональных полиномов, являющихся частными решениями этого уравнения с заданными спецификациями функций сноса и воластильности, так и с помощью ортонормированных многочленов, которым соответствуют другие спецификации данных функций. Исходя из полученных результатов, можно сделать вывод о том, что теоретическая стоимость опционов, рассчитанная на основе неортогональных полиномов, имеет мало общего с действительностью - ее значения оказались неправдоподобно большими. Напротив, общее решение, найденное с помощью ортонормированных многочленов, достаточно хорошо соотносится как с реальностью, так и с оценками стоимости опционов, полученными с помощью формулы Блэка-Шоулза.

Проведенный сравнительный анализ позволяет утверждать, что в среднем теоретическая стоимость валютного опциона колл, оцененная по формуле Блэка-Шоулза, равняется теоретической стоимости, найденной с помощью ортонормированных полиномов, умноженной на отличную от 0 константу. Данный вывод является логичным, поскольку в основе обоих исследуемых способов нахождения теоретической цены опциона лежит одно и то же дифференциальное уравнение. Однако он однозначно справедлив только для ситуации, когда страйк равняется текущему валютному курсу. Что касается других случаев, то результаты могут существенно различаться. Причины этого, скорее всего, кроются в следующих проблемах:

)        Нахождение теоретической стоимости опционов с помощью ортонормированных полиномов - это не математически строгий способ, поскольку они не являются частными решениями исходного уравнения с конкретными спецификациями функций сноса и волатильности. Тем не менее, нельзя отрицать того факта, что ортонормированные многочлены были получены именно с помощью данных функций исходного вида. Следовательно, их можно использовать для получения общего решения.

)        Нахождение теоретической стоимости опционов с помощью ортонормированных полиномов - это весьма трудоемкий способ, требующий значительной вычислительной мощности и много времени. Поэтому очень проблематично находить большое число полиномов. Однако использованных 10 многочленов не всегда будет хватать - теоретическая стоимость опциона может оказаться отрицательной, если страйк существенно превышает спот курс.

)        По неизвестной причине значения оценок опционов, полученные как по формуле Блэка-Шоулза, так и с помощью полиномов, иногда оказываются ниже, чем внутренняя стоимость данных опционов.

Тем не менее, на основании изложенных выше проблем, нельзя сделать вывод, о том, что способ нахождения теоретической стоимости опциона с помощью ортонормированных полиномов является несостоятельным, поскольку полученные в настоящей работе результаты красноречиво свидетельствуют об обратном. Однако стоит попытаться решить данные проблемы в последующих исследованиях.

уравнение дынкин опцион шоулз

Список использованных источников

.     Балакин А. Б. Классически Ортогональные Полиномы. Казань: Казанский Государственный Университет, 2003.

.     Зайцев В.Ф., Полянин А.Д. Метод разделения переменных в математической физике. СПб.: Книжный Дом, 2009.

.     Канатников А. Н., Крищенко А. П. Линейная Алгебра. М.: МГТУ им. Баумана. 2002.

4.      Михатрян В. С. Теория вероятностей и математическая статистика: учеб. пособие. М.: Маркет ДС, 2010.

5.      Степанов С.С. Стохастический Мир. 2009. - http://synset.com/pdf/ito.pdf

.        Bjцrk <http://www.amazon.com/s/ref=ntt_athr_dp_sr_1?_encoding=UTF8&field-author=Tomas%20Bj%C3%B6rk&search-alias=books&sort=relevancerank> T. Arbitrage Theory in Continuous Time. Oxrord University Press, 2003.

7.   Coupeland L. Exchange rates and international finance. Pearson Education, 2008.

8.      Hull J. Options, futures, and other Derivatives. Pearson Education International, 2009.

9.      Triennial Central Bank Survey of Foreign Exchange and Derivatives Market Activity, 2010. - <http://www.bis.org/publ/rpfxf10t.htm>

10. Voit J. The Statistical Mechanics of Financial Markets. Berlin, Springer-Verlag, 2005.

11.    http://www.cmegroup.com/trading/fx/g10/euro-fx_quotes_globex.html

12.    <http://research.stlouisfed.org/fred2/series/EXUSEU/downloaddata?cid=95>

.        <http://sdw.ecb.europa.eu/home.do>