Омбилические поверхности второго порядка
МИНИСТЕРСТВО
ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН
САМАРКАНДСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ АЛИШЕРА НАВОИ
Механико-математический
факультет
-
математическое направление
омбилические поверхности второго порядка
(выпускная
квалификационная работа)
Ахророва
Гулноза
Разрешение
на защиту:
Декан
факультета: проф. А. Солеев
Зав.кафедрой:
доц.Х. Х. Рузимурадов
Научный
руководитель: проф. Артыков. А. Р.
Самарканд-2012
Введение
Подстановка задачи: Тема выпускной работы
посвящена изучению омбилических точек поверхностей второго порядка и
доказательству того факта, что в евклидовом пространстве Е3сфера
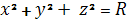
есть единственная поверхность второго порядка,
состоящая из омбилических точек (т. е. сфера S2
есть единственная омбилическая поверхность в Е3).
Актуальность темы: Поверхности второго порядка -
единственные поверхности, все плоские сечения которых являются линиями второго
порядка.
Цели и задачи. В работе изучаются следующие
задачи: Доказывается основная теорема: если поверхность второго порядка состоит
из одних лишь омбилических точек, то она может быть только сферой.
Отметим некоторые поверхности второго порядка,
которые имеют омбилические точки. Применяя растяжение к сжатому или вытянутому
эллипсоиду вращения, получим эллипсоид самого общего вида (трёхосный
эллипсоид). В то время как всякий эллипсоид вращения симметричен по отношению к
любой плоскости, проходящей через ось вращения, общего (трёхосный) имеет всего
три плоскости симметрии, которые расположены перпендикулярно друг к другу.
Отрезки трех линий пересечения этих плоскостей
имеют неравную длину (они называются «большой», «средней» и «малой» осями
эллипсоида).
Из трёхосного эллипсоида можно снова получить
сжатый или вытянутый эллипсоид вращения, если применив преобразование
растяжения, сделать равными друг другу большую и среднюю оси или среднюю и
малую оси.
Наиболее общими поверхностями, получающимися
путём растяжения гиперболоидов вращения и параболоида вращения, являются однополостный
и двуполостный гиперболоиды и эллиптический параболоид.
Оба гиперболоида имеют по три плоскости
симметрии, а эллиптический параболоид - две.
Три поверхности второго порядка - эллипсоид,
двуполостный гиперболоид и эллиптический параболоид не могут, содержат прямых
целиком, уже потому что они не простираются в бесконечность непрерывно в двух
противоположных направлениях. Некоторые поверхности второго порядка могут быть
присоединены бесчисленное множество окружностей.
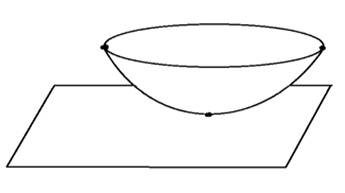
Для того, чтобы убедится в существовании
круговых сечений, рассмотрим трёхосный эллипсоид. Это поверхность в пересечении
со всеми плоскостями, проходящими через среднюю ос в, образует эллипсы, у
которых одна ось постоянна, а именно равна в.
Если мы возьмем плоскость, проходящую через ось
в и через малую ось с, и станем вращать ее вокруг оси в, до совпадения с
плоскостью проходящей через ось в и через большую ось а, то будем получать в
пересечении с поверхностью эллипсы, у которых вторая ось сначала будем меньше
оси в, а затем больше в. Значит, должен быть какое - то промежуточное положение
плоскости, при котором обе оси эллипса равны, и следовательно, кривая
получающаяся в сечение обращается окружность. Вследствие симметрии эллипсоида
мы получим путем зеркального
(отображения) отображения в плоскости,
проходящей через в и с, ещё одну плоскость проходящую через в и дающую в
пересечении с эллипсоидом окружность. Всякое сечение эллипсоида плоскостью,
параллельной плоскости одного из круговых сечений, также даёт окружность. Таким
образом, на всяком эллипсоиде имеется два семейства параллельных окружностей. В
случае эллипсоида вращения оба семейства круговых сечений совпадают.
Научно - исследовательские методы: Все сказанное
здесь в работе проводится аналитическим методом.
Центры круговых сечений эллипсоида лежат на его
двух диаметрах. Точки пересечения этих диаметров с эллипсоидом называется
точками округления (или омбилическими точками), так что эллипсоид имеет четыре
точки округления. Таким образом, четыре точки округления эллипсоида попарно диаметрально
расположены друг другу.
Поэтому двумя различными способами выбрать две
точки округления так чтобы они не будут противоположны.
Эллипсоид вращения
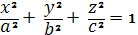
имеет две точки округления.
Содержание работы: Выпускная работа состоит из
пяти параграфов.
В§1 даётся классификация точек поверхности с
помощью понятия индикатрисы Дюпена.
Если индикатриса кривизны (Дюпена) является
кругом, то точка поверхности называется точкой округления или омбилической
точкой.
В §2 рассматривается вопрос об омбилических
точках поверхности в дифференциальной геометрии, в частности линии кривизны
поверхности в омбилических точках (точках округления).
Далее, двумя способами доказывается, что
поверхность, состоящая из точек округления, есть сфера.
Практическое значение работы: Здесь же
указывается геометрический способ построения омбилических точек поверхностей
вращения.
Приводится примеры нахождения омбилических точек
конкретных поверхностей
1)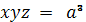
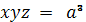
Омбилические точки определяются
равенствами
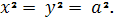
) эллиптический параболоид
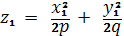
Омбилические точки
В случае параболоида вращения
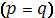
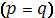 точка 0 (0 , 0 , 0).
точка 0 (0 , 0 , 0).
) омбилические точки синусоиды
вращения
Заполняют линию (параллельны,
описываемые вершинами синусоиды)
§3 являются основным, здесь
рассматриваются омбилические поверхности второго порядка, омбилические точки
поверхности связаны с круговыми сечениями поверхности второго порядка.
Даётся соответствующее определение
омбилической точки и доказывается, что поверхность второго порядка, состоящая
из точек округления, есть сфера.
Даётся способ нахождения омбилических
точек поверхности второго порядка, и используется этот способ для нахождения
точек округления эллипсоида, двуполостного гиперболоида и эллиптического
параболоида.
В §4 рассматриваются полу приводимые
риманова пространства, которые расслаиваются два семейства взаимно -
ортогональных поверхностей, одно из которых состоит из вполне геодезических
поверхностей, а другой - из омбилических поверхностей (базой служит само
риманово пространство 
 ).
).
Наконец, в §5 изучаются более общие
пространства - почти полу
приводимые римановы пространства как
расслоённые пространства (они также расслаиваются на два семейства взаимно -
ортогональных поверхностей , одно из которых состоит из вполне геодезических
поверхностей , а другое - из омбилических поверхностей ).
§1. Классификация точек поверхности
Известно, что каждой точке
поверхности соответствует индикатриса
кривизны (Индикатриса Дюпена), т. е.
некоторая кривая второго порядка
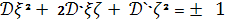
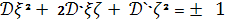 (1)
(1)
Как и всякая кривая второго порядка,
она может принадлежать к эллиптическому, гиперболическому или параболическому
типу.
В связи с этим точки поверхностей
распределяются на три класса и называются эллиптическими гиперболическими и
параболическими, в зависимости от того, к какому из этих трёх типов принадлежит
индикатриса Дюпена, соответствующая этим точкам. Чтобы определить, какому
классу принадлежит данная точка поверхности, достаточно вычислить коэффициенты
второй квадратичной формы в этой точке и составить дискриминант этой формы
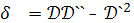
Очевидно, величина δ является
дискриминантом старших членов уравнения индикатрисы Дюпена, заданной уравнением
(1).
Если в данной точке δ > 0, то точка
эллиптическая, если δ
< 0, то
точка гиперболическая, если же δ = 0, то точка параболическая. Строго
говоря, кроме этих возможностей, существует ещё и четвертая. Может случиться,
что в данной точке все коэффициенты II формы
обращаются в нуль

 =0 (2)
=0 (2)
одновременно. В таком случае все
нормальные сечения имеют кривизну, равную нулю, и понятие индикатрисы Дюпена
теряет смысл. Такие точки поверхности называются точками уплощения.
Полная кривизна поверхности
определяется формулой
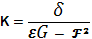
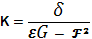 , (3)
, (3)
где дискриминант I формы
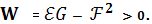
Поэтому точка поверхности будет
эллиптической, гиперболической или параболической, если полная кривизна K > 0, K < 0 или K = 0
(
 0).
0).
Полная кривизна в точке уплощения
равна нулю.
В евклидовом пространстве плоскость
является единственной поверхностью, состоящей только из точек уплощения. Это
следует из равенств:
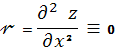
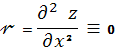 ,
,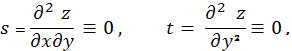
Строение поверхности вблизи эллиптической точки
Если индикатриса Дюпена эллиптическому типу, то
её уравнение в нормальной системе координат имеет вид:
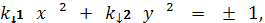
причем
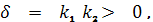
где k1,k2-главные
кривизны поверхности.
Итак, радиусы главной кривизны R1,
R2 имеют один знак,
можно считать всегда k1>0,
k2>0
Формула Эйлера:
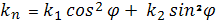
показывает, что в рассматриваемой точке
нормальные кривизны всех направлений положительны, т.е. все нормальные сечения
вогнуты.
Итак, вогнутость всех нормальных сечений,
проходящих через эллиптическую точку поверхности, направлена в одну сторону.
Отсюда следует, что все точки поверхности
достаточно близкие к эллиптической точке, расположены по одну сторону от
касательной плоскости в этой точке.
Уравнение индикатрисы будет иметь вид:
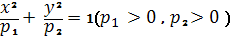
Итак, в эллиптической точке индикатриса будет
действительным
эллипсом.
В частности, если k1=
k2,то по формуле
Эйлера
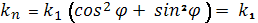
т.е. все нормальные кривизны равны между собой.
В этом случае индикатриса Дюпена имеет формулу
окружности. Точка поверхности, в которой индикатриса Дюпена является
окружностью, называется Омбилической.
Иногда в литературе омбилическая точка
называется также точкой округления.
В общей системе координат омбилическая точка
характеризуется пропорциональностью соответственных коэффициентов обеих
квадратичных форм:
или
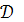
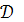 = λ
= λ 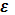
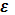 ,
,
 =
= 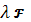
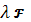 ,
, 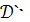
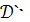 =λ G (λ≠ 0)
=λ G (λ≠ 0)
Примером омбилической точке может
служить всякая точка сферической поверхности.
Строение поверхности вблизи
гиперболической точки
Если точка гиперболическая, то в
нормальной схеме координат дискриминант её индикатрисы Дюпена
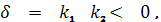
откуда следует, что главные
нормальные имеют разные знаки.
Выбрав направленного вектора
поверхности, мы можем написать

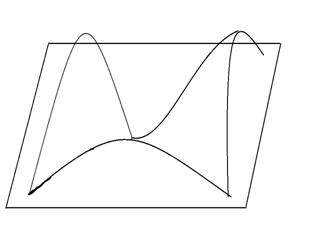
Поверхность вблизи гиперболической
точки располагается по обе стороны от касательной плоскости в этой точке.
Поэтому поверхность вблизи
гиперболической точки имеет седлообразную форму
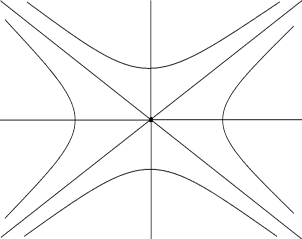
Индикатриса в гиперболической точке
имеет вид двух сопряженных гипербол
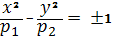
Строение поверхности вблизи
параболической точки
Параболическая точка характеризуется
условием
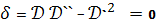
что равносильно условию
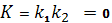
Предлагая, что нормальная кривизна 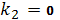
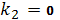 , выберем направление нормального
вектора поверхности так, чтобы
, выберем направление нормального
вектора поверхности так, чтобы
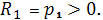
В таком случае уравнение индикатрисы
в нормальной системе координат примет вид:
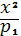
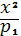 = 1
= 1
иона распадается на пару прямых,

Поверхность имеет вблизи
параболические точки полу седлообразное строение.


Можно непосредственно проверить что
поверхность,состоящая из уплощения, есть плоскость, а поверхность, составленная
из параболических точек - развертывающаяся.
Развертывающиеся поверхности это цилиндрические,
конические поверхности и поверхности касательных(поверхности нулевой кривизны)
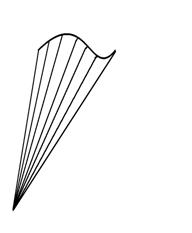

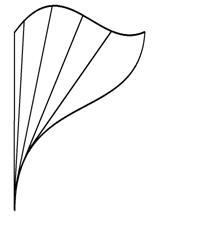
Эллипсоид, эллиптический параболоид состоят из
эллиптических точек. Гиперболический параболоид состоят из гиперболических
точек прямой
(геликоид). Винтовая поверхность
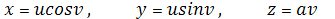
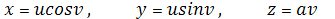
состоит из гиперболических, так как:
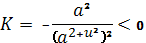
§2.Омбилические точки поверхности
Мы видели, что омбилические
поверхности характеризуются условиями
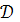
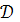 = λ
= λ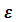
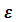 ,
,
 =
= 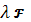
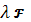 ,
, 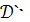
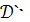 = λ G ( 1)
= λ G ( 1)
или равенствами
= k1
= k2,(2)
где k1,k2
- главные кривизны поверхности. Теперь покажем, что омбилическая точка
характеризуется равенством
(1) H²=K
Действительна по определению полная (гауссова)
кривизна, равна
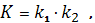
средняя кривизна
H=k1·
k2
Характеристическое уравнение поверхности есть:
kn - 2Hkn
+ K = 0,
дискриминант, которого равен
E = H²
-K (Эйлерова
разность)
Покажем, что корни характеристического уравнения
всегда действительны
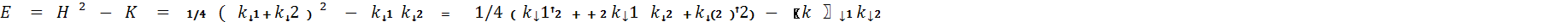
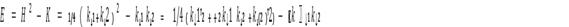
В омбилической точке 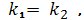
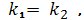 (Е = 0), поэтому
(Е = 0), поэтому
H ² ― K = 0, H ² = K
(2) Линии кривизны поверхности и
омбилические точки
Определение. Линия на поверхности,
во всех точках которой , нормальная кривизна равна нулю (kn= 0),
называется линией кривизны.
Направление касательной к линии
кривизны есть главное направление индикатрисы Дюпена.
Обратно: линия, касающаяся в каждой
своей точке главной оси индикатрисы кривизны (Дюпена), есть линия кривизны.
Например, всякая линия,
расположенная на поверхности шара (сфера),является линией кривизны. Это следует
из того что нормали поверхности, взятые вдоль этой линии всегда образуют
коническую поверхность с вершиной в центре сферы, если линия лежит на сфере. На
всякой поверхности существуют два семейства линий кривизны, которой образуют
ортогональную сеть.
Например, меридианы и параллели на
сфере образуют ортогональную сеть.
Дифференциальное уравнение линий
кривизны имеет вид:
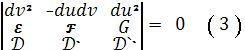
Решая это квадратное уравнение,
относительно 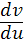
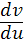 получим два
получим два
дифференциальных уравнений:

с действительным правыми частями.
Интегрируя эти дифференциальные уравнения, мы получим два семейства
взаимно-ортогональных линий кривизны (эти два семейства линий кривизны и
образуют ортогональную сеть).
Исключительное положение вещей будет
в области омбилических точек и в области точек уплощения.
Как мы знаем в этих областях или
или

и уравнение (3) обращается в
тождество и не определяет линий кривизны.
Таким образом, всякое направление в
области омбилических точек или в области точек уплощения будет главным, а
значит, и всякая линия будет линией кривизны.
Так, всякая линия сферы и плоскости
будет линией кривизны, так как сфера состоит из омбилических точек, а плоскость
- из точек уплощения.
Наконец, отметим, что если
координатная сеть совпадает с сетью линий кривизны, то выполняется условия
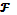
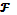 = 0 ,
= 0 , 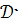
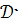 = 0 .
= 0 .
Рассмотрим пример: найти линии
кривизны прямого геликоида
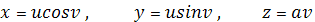
Находим коэффициенты I иII
квадратичных форм:
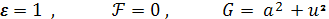
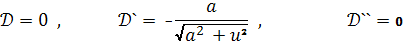
Дифференциальное уравнение линий
кривизны

 = 0
= 0
Отсюда
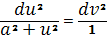
Или
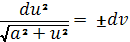
Интегрируем это уравнение
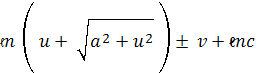
или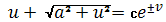
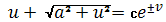
Это есть два семейства , два
семейства линий кривизны на геликоиде.
На плоскости
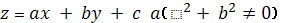
всякая линия будет линией кривизны,
так как
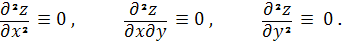
Поверхность, состоящая из
омбилических точек
Возьмём на поверхности, состоящей из
омбилических точек, некоторую точку A и проведём
через неё нормальное сечение. Как всякая линия на рассматриваемой поверхности,
полученная кривая будет линией кривизны, и нормали поверхности должны
образовать вдоль неё развертывающую поверхность.
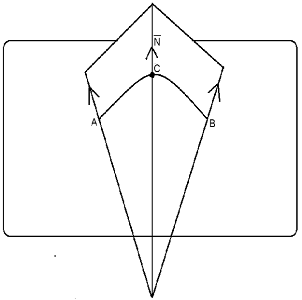
Но в таком случае угол наклона всех
этих нормалей к плоскости сечения должен быть постоянным и равен нулю, так как
нормаль в точке A заведомо лежит в этой плоскости.
Таким образом, плоское сечение
омбилической поверхности, нормальное в одной из своих точек, нормально и в
любой другой своей точке.
Проведём далее общее нормальное
сечение поверхности через две фиксированные точкиA и B и
рассмотрим произвольную точку C, не расположенную в плоскости этого
сечения. Нормальные сечения, соединяющие точки A и B с точкой C,
пересекаются по нормали в точке C. Если нормали в точках A и B
пересекаются, то нормаль в точке C, очевидно, пройдёт через точку их
пересечения. Если те нормали в точках A и B будут
параллельны, то им будет параллельно и нормаль в точке C.
Итак: все нормали омбилической
поверхности или пересекаются в одной точке или параллельны между собой. Однако
последний случай отпадает, потому что при его наличии вторая квадратичная форма
обращается в нуль, и мы имеем дело с плоскостью, которая состоит из не
омбилических точек, а из точек уплощения. Тогда остаётся рассмотреть первый
случай. Всякое нормальное сечение, проходящее через некоторую точку, есть
плоская кривая, нормали которой пересекаются в одной точке, т.е. окружность.
Все эти окружности имеют одну и ту же кривизну, так какточка омбилическая,
откуда мы видим, что омбилическая поверхность есть сфера.
Итак, мы доказали, что поверхность,
состоящая из омбилических точек, может быть только сферической поверхностью.
Мы сейчас дадим другое
доказательство этого основного предложения нашей работы.
Теорема. Единственной связной
поверхностью с ненулевой полной кривизной, состоящей целиком из точек
округления (омбилических точек), является сфера, или часть сферы.
Доказательство
Необходимость.
Если сфера определена
параметрическими уравнениями
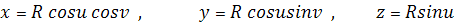
то
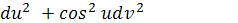
и
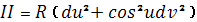
отсюда
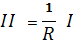
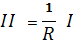
т. е. сфера состоит целиком из омбилических
точек.
Достаточность.
Пусть
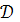
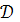 = λ
= λ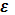
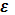 ,
,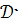
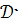 =
= 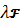
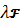 ,
, 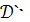
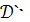 = λG
= λG
Если поверхность задано уравнением в
векторной форме
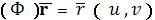
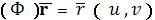 ,
,
то
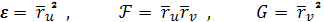

Подставляем значения квадратичных
форм:

или 
 ,
,
Присоединяя сюда равенство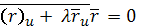
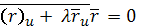 это следует из равенств
это следует из равенств
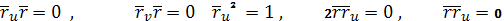
получаем
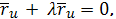
Аналогично
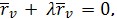
Дифференцируем первые равенство по 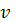
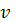 , второе - по
, второе - по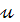
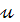 :
:
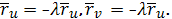
Тогда получим
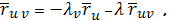
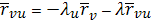
откуда
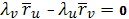
Отсюда видно, что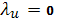
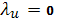 ,
, 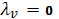
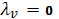 или
или 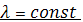
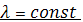 .
.
(иначе последнее равенство означала
бы, что векторы 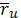
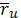 и
и 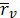
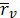 коллинеарными, что противоречит
регулярности поверхности
коллинеарными, что противоречит
регулярности поверхности

 ) .
) .
Таким образом, интегрируя последнее
равенство, имеем
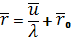
или
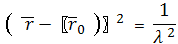
Это есть уравнения сферы с центром в
точке 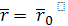
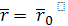 и радиусом
и радиусом 
Теорема полностью доказана.
Построение (геометрическое)
омбилических точек поверхности вращения
Для поверхности вращения можно
указать следующий геометрический способ построение точек округление.
Строим эволюту какого - либо
меридиана поверхности вращения и находим точки 
 встречи её с осью вращения.
встречи её с осью вращения.
Пусть 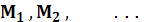
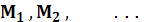 - соответствующие им точки
эвольвенты (меридиана).
- соответствующие им точки
эвольвенты (меридиана).
Тогда параллели поверхности,
проходящие через эти точки, состоят из точек округления (из омбилических
точек).
Приведём численные примеры.
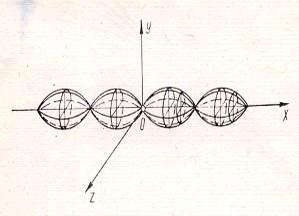
Пример 1. Синусоида

вращается вокруг оси (
Найдите на поверхности вращения
точки округления.
Решение. Уравнение поверхности
вращения, полученной вращением синусоиды вращениям вокруг оси ( 
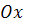 ) есть
) есть
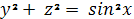
Ответ: параллели, описываемые
вершинами синусоиды и только они.
Точки округления можно построить
выше, указанным способом.
Пример 2 . Точки округления
поверхности
лежат на линиях
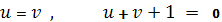
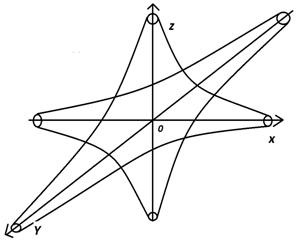
Пример 3. Найти омбилические точки
поверхности
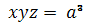
Омбилические точки определяются
равенствами
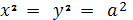
или
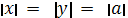
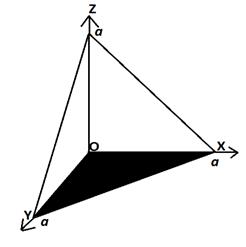
Например, в точке округления A1 (a, a , a)
касательная плоскость имеем уравнение:
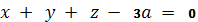
Эта плоскость с координатными
плоскостями образует тетраэдр объём, которого равен
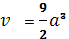
Пример 4.Найти омбилические точки
эллиптического параболоида
Решения. Для определенности будем
считать, что 0 <q ≤ p.
Омбилические точки поверхности
удовлетворяют условиям
или
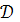
 = λ
= λ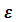
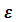 ,
,
 =
= 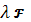
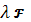 ,
, 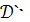
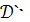 = λ G ( λ ≠ 0 )
= λ G ( λ ≠ 0 )
Из уравнения параболоида находим

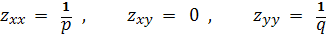
Теперь вычислим коэффициенты первой и второй
квадратичный формы поверхности
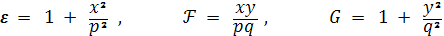

Тогда имеем систему уравнений
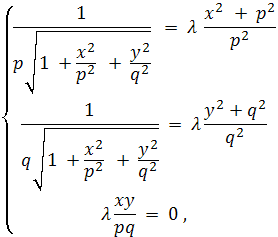
где λ - коэффициент
пропорциональности.
Из первого и второго уравнений системы получим:
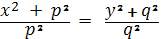
точка поверхность
кривизна омбилический
Из третьего уравнения имеем:
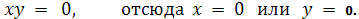
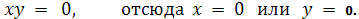
Пусть, например, х = 0 , у ≠
0,тогда:
у ² + q ² = p q , y ² = p q-q² , y ² = q (p - q)
Так как 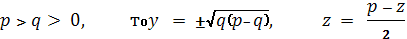
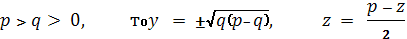
Таким образом, эллиптический
параболоид имеем две омбилические точки:
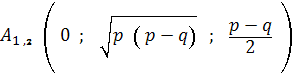
В частном случае, если p= q, то
получаем параболоид вращения

и точки 
 сливаются началом координат (0, 0,
0) - вершина параболоида.
сливаются началом координат (0, 0,
0) - вершина параболоида.
Задача полностью решена.
Пример 5. Тор.
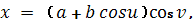
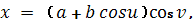
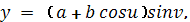
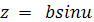
Квадратичные формы поверхности
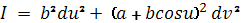
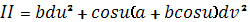
Если ось тора вертикальна то самая
верхняя и самая нижняя параллели тора состоят из параболических точек, эти параллели
отделяют внешнюю часть тора, состоящую из эллиптических точек, от внутренней
части с параболическими точками.
Дифференциальное уравнение
асимптотических линий
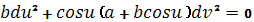
Линии 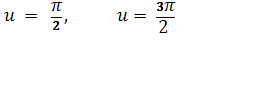
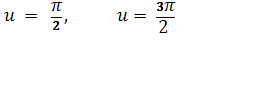 особые решения уравнения.
особые решения уравнения.
Омбилических точек на торе нет.
§ 3. Омбилические точки поверхностей
второго порядка
Классификация точек поверхностей
второго порядка
В качестве примера приложения
классификации точек поверхности (§1) различные типы поверхностей второго
порядка.
Сначала замечания общего характера.
Всякое плоское сечение поверхности
второго порядка есть кривая второго порядка.
Кривизна такой кривой может
обратиться в ноль, в какой - либо ее точке в том и только в том случае, если
эта кривая распадается на пару прямых (кривизна примой равна нулю).
Таким образом, кривизна нормального
сечения поверхности равна нулю в том и только в том случае, если его плоскость
содержит
прямолинейную образующую этой
поверхности.
Отсюда следует, что нормальная
кривизна поверхности второго порядка не обращается в ноль нелинейных
поверхностей и обращается в ноль для одного или двух сечений, если через точку
проходит одна или две прямолинейные образующие соответственно.
Если принять, с другой стороны, во
внимание, что в эллиптических точках нормальная кривизна не обращается в ноль,
а в параболических точках она обращается в ноль для сечения одного направления,
а для гиперболических точек для сечений двух направлений, то мы приходим к
следующим выводам:
. Эллипсоид, двуполостный
гиперболоид и эллиптический параболоид не имеют прямолинейных образующих и,
следовательно, состоят из эллиптических точек.
. Через каждую точку однополосного
гиперболоида и гиперболического параболоида проходят две прямолинейные
образующие, следовательно, они состоят из гиперболических точек.
. Через каждую точку цилиндра и
конуса второго порядка проходит одна прямолинейная образующая, вследствие чего
они состоят из параболических точек.
. Если поверхность распадается на
пару плоскостей, то она состоит из точек уплощения.
Отметим, что вершина конуса есть
особая точка. Через особую точку проходит бесконечно много касательных
плоскостей, содержащих прямолинейные образующие, проходящие через особую точку
(вершину) конуса.
Далее мы рассмотрим омбилические
точки поверхностей второго порядка эти точки, как правило, изолированы.
Круговые сечение поверхностей
второго порядка и их омбилические точки
Омбилические точки поверхностей
второго порядка связаны с круговыми сечениями этих поверхностей. Поэтому мы
сначала рассмотрим кратко вопрос о, круговых сечения поверхностей второго
порядка.
Эллипсоид. Каноническое уравнение
эллипсоида
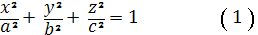
В дальнейшем будем считать, что а
>b>c (трёхосные
эллипсоид).
Оказываются, существуют плоскости,
которые пересекают по окружностям даже самого общего вида (трёхосные). Отметим,
что если такая плоскость существует, то и всякая параллельная плоскость
пересекает эллипсоид по окружности (так как сечения поверхности второго порядка
параллельными плоскостями подобны друг другу). Отсюда следует, что достаточно
найти такие круговые сечения эллипсоида, которые лежат в его диаметральных
плоскостях.
Допустим существование такой
диаметральной плоскости и обозначим через 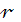
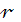 радиус соответствующего кругового
сечения. Проведем через последнее сферу с центром в начале координат
радиус соответствующего кругового
сечения. Проведем через последнее сферу с центром в начале координат
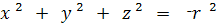
или
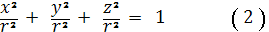
Ясно, что координаты точек кругового
сечения удовлетворяют уравнениям (1) и (2), поэтому они удовлетворяют
уравнению, которое получается из них вычитанием.
Это уравнение есть уравнение конуса
с вершиной в начале координат.
Покажем, что этот конус распадается
на две плоскости, и в которых одна есть плоскость ( 
 ), производящая круговое сечение.
), производящая круговое сечение.
Так как эти прямые принадлежат и
конусу второго порядка (3), то этот конус содержит плоскость в качестве
составной части; так что конус (3) распадается на две плоскости , поэтому
выполняется условия (дискриминант равен нулю).
Здесь только случай
нас интересует, тогда (3) принимает
вид:
или
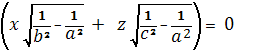
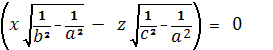
и, следовательно, представляет две
действительные плоскости,
пересекающиеся по оси (о у). Этими
плоскостями, а также и параллельными им и производится круговые сечения
эллипсоида. Центры круговых сечений эллипсоида лежат на его двух диаметрах.
Точки пересечения этих диаметров с
эллипсоидом называются его точками округления (или омбилическими точками); так
что трёхосный эллипсоид имеет четыре точки округления.
В частности, если a =b>c, то
уравнение имеет вид: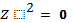
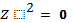 , т. е. обе плоскости, определяемые
этим уравнением, - совпадают с координатной плоскостью (xоy). Все
плоскости, параллельные ей также производят круговые сечения: так что в случае
сжатого эллипсоида вращения мы имеем семейство круговых сечений, ортогональных
по оси вращения (оси (оz)), вместе с тем будем иметь две
омбилические точки, совпадающие с концами этой оси.
, т. е. обе плоскости, определяемые
этим уравнением, - совпадают с координатной плоскостью (xоy). Все
плоскости, параллельные ей также производят круговые сечения: так что в случае
сжатого эллипсоида вращения мы имеем семейство круговых сечений, ортогональных
по оси вращения (оси (оz)), вместе с тем будем иметь две
омбилические точки, совпадающие с концами этой оси.
Если a = b<c , то есть
если эллипсоид вытянутый, то имеем совершенно аналогичное явление.
Наконец, в случае сферы, когда a = b =c, всякое
сечение - круговое, и потому все точки сферы - омбилические (сфера -
омбилическая поверхность второго порядка).
Двуполостный гиперболоид

Каноническое уравнение
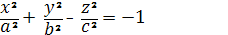
Уравнение конуса, проходящего через линию
пересечения двуполостного гиперболоида и сферы
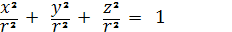
теперь будем
Этот конус будет распадаться на пару плоскостей
только, при
Так что плоскости, производящие круговые сечения
двуполостного гиперболоида (a>b),
представляются уравнениями:
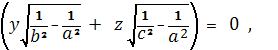
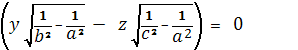
Здесь мы имеем два семейства круговых сечений с
центрами на двух диаметрах поверхности. Последние будут пересекать двуполостный
гиперболоид по четырём омбилическим точкам.
Лишь в случае двуполостного гиперболоида
вращения (a = b)
будем иметь одно семейство круговые сечений с центрами на оси (oz);
так что омбилические точки при этих условиях будут совпадать с его вершинами на
оси (oz).
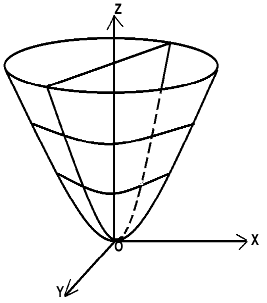
Эллиптический параболоид
Каноническое уравнение
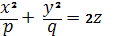
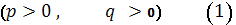
Эллиптический параболоид есть поверхность
переноса, т. е. эллиптический параболоид образуется поступательным движениям
параболы, вершина которой скользит по другой параболе, расположенной в
плоскости, перпендикулярной плоскости первой параболы, при этом оси обеих
парабол одинаково направленно.
Эллиптический параболоид не содержит никаких
прямых.
Теперь рассмотрим вопрос о круговые сечения
нашего параболоида.
В данном случае начало координат не является
центром, поэтому рассмотрим такое круговое сечение, плоскость которого проходит
через начало координат. Сфера задаётся теперь уравнением
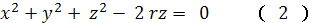
Как видно, это сфера проходит через начало
координат и расположена над плоскостью (x
o y)
и касается этой плоскости в начале координат.
Представим уравнение (2) сферы
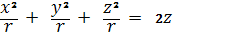
тогда уравнение конус с вершиной в начале
координат будет иметь вид:
Этот конус может распадаться на две плоскости
только при r =p(p>q).
Круговые сечения производятся плоскостями
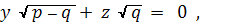
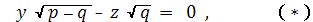
проходящими через начало координат и плоскостями
, им параллельными ;
так что на эллиптическом параболоиде мы имеем
два семейства круговых сечений, следовательно, две омбилические точки.
На примере эллиптического параболоида укажем
общий приём нахождения омбилических точек поверхностей второго порядка.
Воспользуемся известным утверждением:
касательная плоскость в омбилической точке параллельна плоскостям круговых
сечений. Обозначим координаты искомой омбилической точки через x1,
y1,z1.
Эти координаты должны удовлетворят уравнениям:
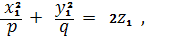
(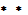
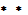 )
)
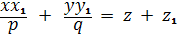
(это уравнение касательной плоскости
к эллиптическому параболоиду в точке (x1, y1 , z1)).
Так как коэффициенты уравнений (*) и
(* *) должны быт пропорциональны, то
откуда 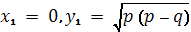
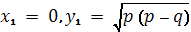
Подставляя эти значения в
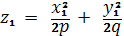
найдем
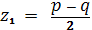
Таким образом, эллиптический
параболоид имеет две омбилические точки:
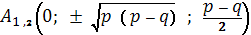
Еслиp = q мы имеем
поверхность - параболоид вращение

у которой омбилические точки 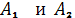
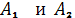 сливаются с началом координат
сливаются с началом координат
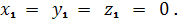
Эллипсоид
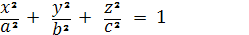
Координаты омбилических точек
удовлетворяют уравнениям
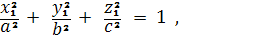
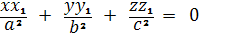
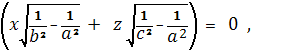
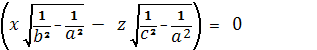
Из этих уравнений получаем:
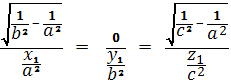
отсюда
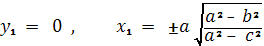
Подставляя, эти значения в
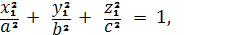
Найдем четыре точки округления
трёхосного эллипсоида
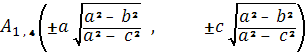
Если a = b,(эллипсоид
вращения ) имеем две омбилические точки
(0, 0, ± с).
Двуполостный гиперболоид
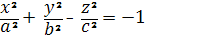
Координаты омбилических точек
удовлетворяют уравнениям
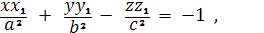
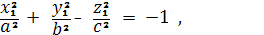
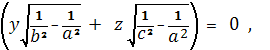
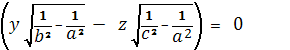
Решая эти уравнения относительно (x1, y1 , z1), находим
четыре точки округления
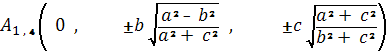
Если a = b
(гиперболоид вращения), как мы уже знаем, имеем две омбилические точки: (0; 0;
± c), которые
будут вершинами двуполостного гиперболоида на оси вращения (оси z).
§4. Полу приводимые римановы
пространства
Риманово пространство 
 называется полу приводимым, если
существует, такая система координат в которой его метрика
называется полу приводимым, если
существует, такая система координат в которой его метрика

представляется в виде:
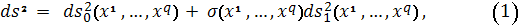
где,
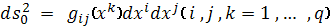
и
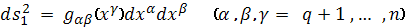
самостоятельные q- мерные и (n - q) - мерные
метрики, зависящие каждая от своих аргументов, а функция зависит только от
переменных из метрики 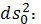
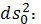
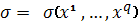
Представление метрики 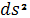
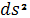 в виде (1) будем называть её полу
приводимым разложением.
в виде (1) будем называть её полу
приводимым разложением.
Полу приводимыми являются все
пространства постоянной ненулевой кривизны, которые, как известно, неприводимы.
Омбилические римановы пространства и
их геометрическая характеристика
Пусть в римановом пространстве 
 ,с метрическим тензорам
,с метрическим тензорам 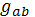
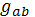
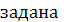
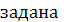 q-мерная, не изотропная поверхность
q-мерная, не изотропная поверхность 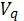
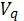 :
:
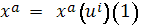

Обозначим 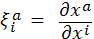
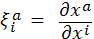 система q векторов
система q векторов 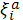
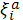 в каждой точке
в каждой точке
поверхности 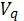
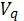 определяет в
определяет в 
 касательную к
касательную к 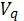
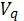 плоскость.
плоскость.
Метрика поверхности 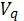
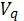 , индуцированная метрикой всего
пространства
, индуцированная метрикой всего
пространства 
 , задаётся тензором
, задаётся тензором
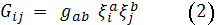
Как известно, характер вложения 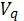
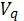 в
в
 определяется величинами
определяется величинами
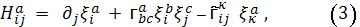
образующими так называемый аффинор
кривизны 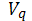
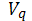 по отношению к
по отношению к 
 . Здесь
. Здесь 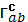
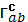 и
и 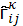
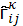 - символы Кристоффеля, вычисленные
в
- символы Кристоффеля, вычисленные
в 
 и
и 
 соответственно. По, индексу а
аффинор кривизны представляет вектор, нормальный к
соответственно. По, индексу а
аффинор кривизны представляет вектор, нормальный к 
 в
в 
 , а по индексам i, j является
симметрическим тензором в
, а по индексам i, j является
симметрическим тензором в 
 . Для того, чтобы поверхность
. Для того, чтобы поверхность
 была омбилической (т. е. имела
неопределенные линии кривизны), необходимо и достаточно, чтобы
была омбилической (т. е. имела
неопределенные линии кривизны), необходимо и достаточно, чтобы
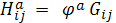
в каждой точке 
 .
.
В частности, равенство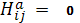
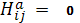 равносильно тому, что
равносильно тому, что 
 является
является
вполне геодезической поверхностью.
Предположим, что пространство
 расслаивается на два взаимно
ортогональных семейства не изотропных поверхностей
расслаивается на два взаимно
ортогональных семейства не изотропных поверхностей 
 и
и 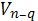
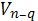 . Тогда, приняв их за координатные
поверхности
. Тогда, приняв их за координатные
поверхности 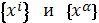
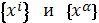 , получим
, получим
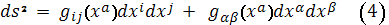
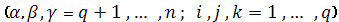
Так как за параметры на 
 выбраны координаты
выбраны координаты 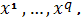
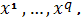 то
то
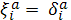
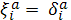 и
и 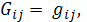
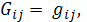
где

Подсчитаем аффинор кривизны для
поверхности 
 .
.
Теперь из (3) имеем:
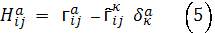
Но из вида метрики следует, что

учитывая эти равенства, из формул
(5) получим,
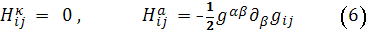
Аналогично для поверхностей 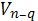
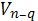

и
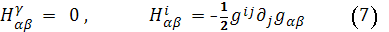
Из самой записи метрики (4) видно,
что полу приводимое пространство расслаивается на взаимно ортогональные
поверхности 

и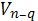
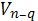 с метриками
с метриками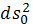
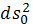 и
и 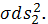
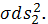 При этом в (4) надо положить
При этом в (4) надо положить
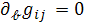
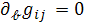 и
и 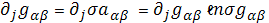
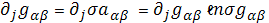
При этом из (6) получается,
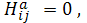
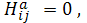 а из (7)
а из (7) 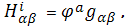
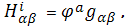
где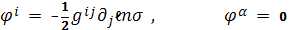
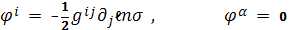
Это означает, что поверхности -
вполне геодезические, а поверхности
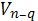
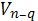 - омбилические.
- омбилические.
Кроме того поверхности 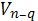
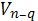 попарно подобные поверхности, так
как их метрики
попарно подобные поверхности, так
как их метрики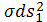
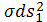 при двух наборах фиксированных
при двух наборах фиксированных 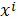
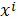 отличаются, друг от друга,
постоянным множителем.
отличаются, друг от друга,
постоянным множителем.
Обратно, пусть 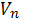
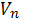 расслаивается на два взаимно
ортогональных семейство поверхностей, одна из которых состоит из вполне
геодезических, а другое - из омбилических и попарно подобных поверхностей.
Тогда в системе координат (4) должно быть
расслаивается на два взаимно
ортогональных семейство поверхностей, одна из которых состоит из вполне
геодезических, а другое - из омбилических и попарно подобных поверхностей.
Тогда в системе координат (4) должно быть
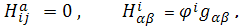
т. е. согласно (6) и (7)
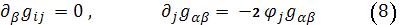
Здесь первые равенства означают, что
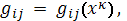
а вторые, что
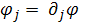
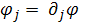 и
и 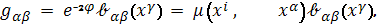
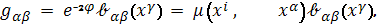
но вторые поверхности попарно
подобны, то отношение
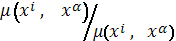
не зависит от переменных 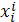
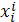 . Поэтому, фиксируя
. Поэтому, фиксируя 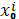
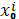 и меняя
и меняя 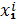
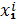 , получим:
, получим:
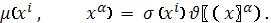
Наконец, обозначая
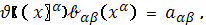
придем к полу приводимому разложению
метрики (1):
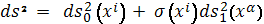
Таким образом, установлено следующее
предложение.
Теорема. Для того чтобы риманово
пространство 
 было полуприводимым, необходимо и
достаточно, оно расслаивалось на два семейства
было полуприводимым, необходимо и
достаточно, оно расслаивалось на два семейства 
 - мерных взаимно ортогональных
поверхностей, одно из которых состоит из вполне геодезических, а другое - из
омбилических и подобных друг другу поверхностей.
- мерных взаимно ортогональных
поверхностей, одно из которых состоит из вполне геодезических, а другое - из
омбилических и подобных друг другу поверхностей.
В частности, если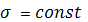
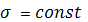 мы придем кприводимым римановым
пространством с метрикой
мы придем кприводимым римановым
пространством с метрикой
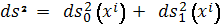
причем поверхности
 и
и 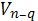
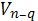 будут, вполне геодезическими.
будут, вполне геодезическими.
Можно указать тензорный признак полу
приводимых
 для того, чтобы риманово
пространство
для того, чтобы риманово
пространство
 было полуприводимым, необходимо и
достаточно, чтобы существовал симметрический тензор
было полуприводимым, необходимо и
достаточно, чтобы существовал симметрический тензор 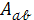
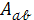 , не пропорциональный метрическому (
, не пропорциональный метрическому (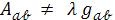
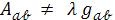 ), удовлетворяющий совместно с
некоторым градиентом уравнениям:
), удовлетворяющий совместно с
некоторым градиентом уравнениям:
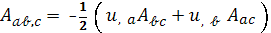
и алгебраическому условию
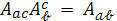
Условия интегрируемости этих
уравнений можно получить в виде:
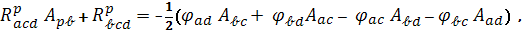
где 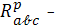
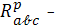 тензор кривизны
тензор кривизны
 ,
,
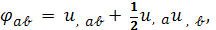
ясно, что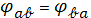
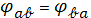 (
(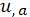
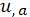 - градиент).
- градиент).
§ 5. Почти полу приводимые риманова
пространства как расслоённые пространства
В §4 мы изучали полу приводимые
риманова пространства как расслоенные пространства.
Теперь мы будем изучать почти полу
приводимые риманова пространства как расслоенные пространства.
Определение. Риманово пространство 
 с метрикой
с метрикой
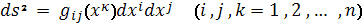
называется почти полу приводимым,
если в нем существует хотя бы одна система координат: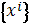
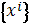 в которой метрика
в которой метрика 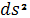
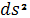 имеет следующий вид:
имеет следующий вид:
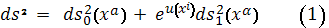
где 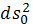
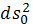 и
и 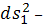
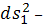 самостоятельные метрики, зависящие
каждая от своих переменных, а
самостоятельные метрики, зависящие
каждая от своих переменных, а 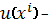
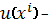 некоторая функция от всех координат
некоторая функция от всех координат 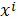
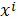 :
:
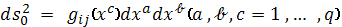
и
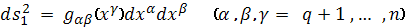
В частности, если
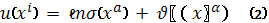
то, включая множитель 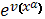
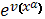 в метрику полу приводимого риманова
пространства
в метрику полу приводимого риманова
пространства 


 (3)
(3)
Таким образом, класс почти полу
приводимых римановых пространств, включает в себя все полу приводимые 
 , являясь их обобщением. Тем не
менее, оказывается, что почти полу приводимые пространства можно изучать как
расслоенные пространства.
, являясь их обобщением. Тем не
менее, оказывается, что почти полу приводимые пространства можно изучать как
расслоенные пространства.
Теорема 1. Для того чтобы риманово
пространство 
 было почти полу приводимым,
необходимо и достаточно, чтобы она расслаивалось на два взаимно ортогональных и
дополнительных по размерности семейства поверхностей
было почти полу приводимым,
необходимо и достаточно, чтобы она расслаивалось на два взаимно ортогональных и
дополнительных по размерности семейства поверхностей 
 и
и 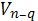
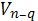 , одно из которых состоит из вполне
геодезических,а второе из омбилических поверхностей.
, одно из которых состоит из вполне
геодезических,а второе из омбилических поверхностей.
Доказательство. Если пространство 
 и
и 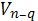
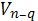 , то приняв их за координатные
поверхности
, то приняв их за координатные
поверхности 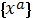
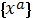 и
и 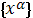
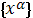 , получим в этой системе координат:
, получим в этой системе координат:
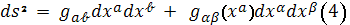
Аффинор кривизны, определяющий
характер вложения поверхности
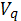
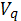 и
и 
 , имеет тогда компоненты:
, имеет тогда компоненты:
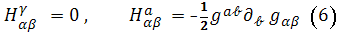
В почти полу приводимом пространстве
(1) компоненты 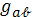
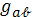 не зависят от координат
не зависят от координат 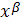
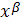 ,а
,а
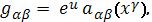
где 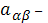
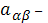 метрический тензор метрики
метрический тензор метрики 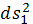
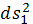 .
.
Поэтому из (5) и (6) получаем,
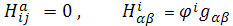
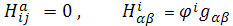 (7)
(7)
где вектор 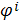
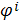 имеет компоненты
имеет компоненты
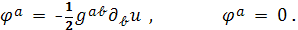
Условия (7) как раз и означают, что 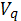
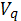 являются вполне геодезическими, а
являются вполне геодезическими, а 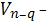
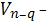 омбилическими поверхностями.
омбилическими поверхностями.
Обратно, если условия (7) выполнены,
то из (5) получим, что 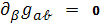
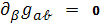 , т. е.
, т. е. 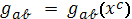
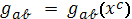 а из ( 6 ) последует
а из ( 6 ) последует
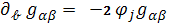
Отсюда видно , что при фиксированных
значениях 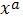
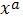 величины
величины 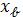
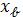
образуют градиент некоторой функции
и тогда
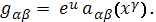
Подставляя полученные выражения 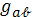
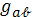 и
и 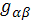
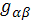 в (4).
в (4).
Мы приходим к почти полу приводимой
метрики.
Теорема полностью доказана.
Для нас в этой теореме главным
является то, что поверхности 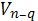
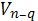 являются омбилическими, т. е.
поверхностями с неопределенными линиями кривизны.
являются омбилическими, т. е.
поверхностями с неопределенными линиями кривизны.
Заключение
Выпускная работа Ахроровой Г.
посвящена омбилическим поверхностям второго порядка. Главным в работе являются
следующие два вопроса:
) Всякая выпуклая замкнутая
поверхность должна иметь, по крайней мере, две омбилические точки;
) единственной поверхностью,
состоящей из одних лишь омбилических точек (омбилическая поверхность) является
сфера.
Первая задача проверена на примере
поверхностей второго порядка (эллипсоид имеет четыре омбилические точки,
эллиптический параболоид - две омбилические точки).
Вторая задача заключается в
следующем. Легко проверяется, что сфера состоит из одних лишь омбилических
точек, т. е. является омбилической поверхностью. Однако доказательство
утверждения, что сфера является единственной поверхностью, состоящей из одних
лишь омбилических точек (точек округления), совсем нетривиально.
В работе дается различные
доказательство этого утверждения.
Вообще омбилические точки
поверхности характеризуется следующими условиями:
) в омбилической точки все
нормальные сечения поверхности имеют одну и ту же кривизну
) индикатриса Дюпена в омбилической
точке есть окружность (круг), (отсюда название точке округления)
)нормальная кривизна не меняется от
направления касательных
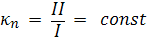
)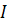
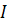 и
и 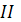
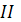 квадратичные формы поверхности
пропорциональны
квадратичные формы поверхности
пропорциональны
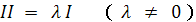
)или
или
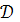
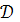 = λ
= λ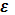
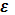 ,
,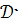
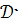 =
= 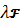
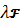 ,
, 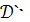
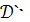 = λG(λ ≠ 0)
= λG(λ ≠ 0)
) Формула Родрига:
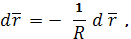
где R
- радиус нормальной кривизны
) H
²
= K ,
где K
- полная кривизна , H - средняя
кривизна поверхности
8) 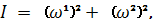
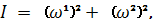
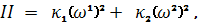
где 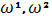
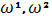 - инвариантные линейные формы, а
- инвариантные линейные формы, а 
 - главные кривизны поверхности.
- главные кривизны поверхности.
В омбилической точке
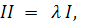
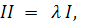 отсюда
отсюда

или
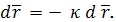
) В омбилической точке линии
кривизны поверхности не определены
) Омбилическая поверхность есть
сфера. Всякая линия, лежащая на сфере, есть линия кривизны.
(омбилическая поверхность - все
точки омбилические).
Все это показывает, задачи
поставленные в работе, решены полностью.
Список использованной литературы
1.
И.А.Каримов. Мировой кризис; пути и меры его преодоления в условиях
Узбекистана. Ташкент, 2009.
.
А.Нариманов.
Дифференциал геометрия курси. Учебное пособие. Ташкент «Ўқитувчи»,
2003.
.Норден
А. П. Краткий курс дифференциальной геометрии, Учебное пособие для
университетов и пединститутов Москва, Физ. Мат. Гиз. 1958
4.
Хатипов А.Э. - А. Курс аналитической геометрии, часть 2. Учебник для
университетов и пединститутов Издательство “ Учитель ” Ташкент 1967.
5.
Д. Гильберт, С. Кон - Фоссен, Наглядная геометрия Москва “Наука ” 1981.
6.
Сборник
задач по дифференциальной геометрии Учебное пособие для ВУЗ - ов Москва “Наука
” 1979. Под редакцией А.
С. Феденко.
7.Интернет-сайт: www.mathnet.ru
<http://www.mathnet.ru>
.Интернет-сайт: www.exponenta.ru
<http://www.exponenta.ru>