Определим далее вектор
угловой скорости 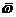 переднего
колеса. В соответствии с рис. 2. в первом приближении будем иметь
переднего
колеса. В соответствии с рис. 2. в первом приближении будем иметь 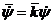 ,
,
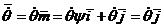
Вектор 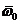 имеет
направления
имеет
направления 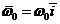 .
Следовательно, угловая скорость переднего колеса
.
Следовательно, угловая скорость переднего колеса 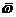 с точностью до малых
первого порядка определяется соотношением
с точностью до малых
первого порядка определяется соотношением
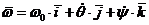 .
(2)
.
(2)
Модель движения
переднего и заднего колес. Динамические уравнения Эйлера. В
работе [5] рекомендуется составлять уравнения движения робота на основе
уравнений Лагранжа II - го рода для
неголономной системы. Однако, если строить приближенные модели, то
предпочтительней использовать динамические уравнения Эйлера, т.к. в этом случае
достаточно модели первого приближения. Если использовать уравнения Лагранжа II - го рода, то необходимо строить модель с точностью до малых
второго порядка [1].
Не разрывая велосипед на
части, (чтобы не возникли реакции связей), составим уравнения движения отдельно
для переднего колеса, для заднего и для рамы. Затем эти уравнения объединим.
Для получения уравнений
качения переднего колеса воспользуемся теоремой об изменении кинетического
момента относительно опорной точки переднего колеса 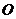 .
Пусть
.
Пусть 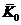 -
кинетический момент колеса относительно центра
-
кинетический момент колеса относительно центра 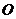 (рис. 2),
(рис. 2), 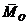 -
главный момент внешних сил относительно того же центра. Обозначим массу колеса
буквой
-
главный момент внешних сил относительно того же центра. Обозначим массу колеса
буквой 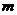 .
Тогда теорема моментов в неподвижной системе координат
.
Тогда теорема моментов в неподвижной системе координат 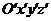 относительно
подвижного в этой системе центра
относительно
подвижного в этой системе центра 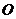 будет иметь вид
будет иметь вид
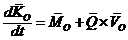 , (3)
, (3)
где 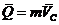 -
количество движения колеса,
-
количество движения колеса, 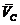 - скорость центра масс
колеса.
- скорость центра масс
колеса.
Определим кинетический
момент 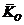 в
проекциях на оси системы координат
в
проекциях на оси системы координат 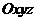 , которые параллельны
главным осям инерции колеса. Обозначим
, которые параллельны
главным осям инерции колеса. Обозначим 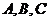 - моменты инерции колеса
относительно осей
- моменты инерции колеса
относительно осей 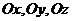 соответственно
соответственно
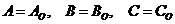 .
Тогда проекции кинетического момента на оси системы
.
Тогда проекции кинетического момента на оси системы 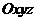 будут
иметь вид
будут
иметь вид
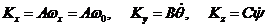 .
.
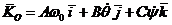 .
.
Выразим кинетический
момент 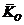 в
системе
в
системе 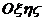 .
.
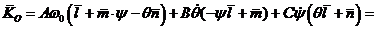
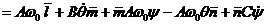 .
.
Проекции кинетического
момента на оси системы 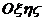 будут
будут
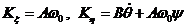 ,
,
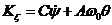 .
.
Тогда
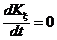 ,
,  ,
(4)
,
(4)
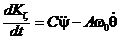 .
.
Пусть 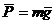 -
вес колеса, приложенный в центре масс колеса
-
вес колеса, приложенный в центре масс колеса 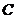 . Точка
. Точка 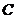 имеет
в системе
имеет
в системе 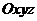 координаты
координаты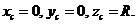 Тогда
Тогда
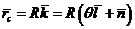 ,
, 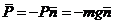 ,
,
где 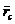 -
радиус-вектор центра масс переднего колеса относительно опорной точки О.
-
радиус-вектор центра масс переднего колеса относительно опорной точки О.
Главный момент внешних
сил относительно центра 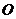 равен
равен
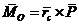 ,
,
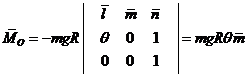 .
.
Следовательно,
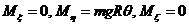 . (5)
. (5)
Далее получим выражение 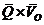 .
.
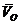 -
это скорость перемещения опорной точки
-
это скорость перемещения опорной точки 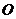 вместе с системой
вместе с системой 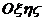 при
качении колеса по опорной плоскости,
при
качении колеса по опорной плоскости,
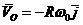 ,
, 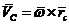 .
.
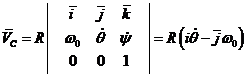 ,
,
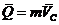 .
.
Следовательно,
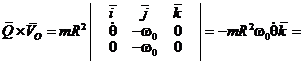
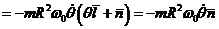 . (6)
. (6)
Поскольку оси системы 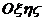 параллельны
соответствующим осям системы
параллельны
соответствующим осям системы 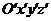 , то с учетом (4), (5),
(6) в системе координат
, то с учетом (4), (5),
(6) в системе координат 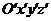 получаем
дифференциальные уравнения движения переднего колеса
получаем
дифференциальные уравнения движения переднего колеса
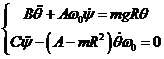 . (7)
. (7)
Это модель качения переднего колеса,
построенная на основе динамических уравнений Эйлера в проекциях на неподвижные
оси координат.
Кинематическая связь
между колесами
Для заднего колеса и для
рамы уравнения (3) составим относительно опорной точки заднего колеса 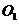 .
.
Модель движения заднего
колеса можно получить из модели (7), заменив угол 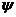 на
угол
на
угол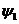 .
Угол наклона
.
Угол наклона 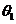 заднего
колеса с точностью до малых первого порядка равен углу наклона переднего колеса
[7]. Следовательно, модель движения заднего колеса в системе координат
заднего
колеса с точностью до малых первого порядка равен углу наклона переднего колеса
[7]. Следовательно, модель движения заднего колеса в системе координат 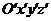 будет
иметь вид
будет
иметь вид
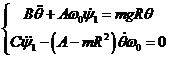 . (8)
. (8)
Получим соотношение
между углами 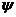 и
и
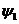 .
.

Рассмотрим траектории
движения переднего и заднего колес велосипеда на плоскости 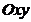 .
Пусть в некоторый момент времени переднее колесо соприкасается с опорной
плоскостью в точке
.
Пусть в некоторый момент времени переднее колесо соприкасается с опорной
плоскостью в точке 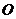 ,
(рис. 3), заднее в точке
,
(рис. 3), заднее в точке 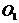 .
Векторы
.
Векторы 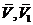 -
соответственно скорости точек соприкосновения переднего и заднего колес,
-
соответственно скорости точек соприкосновения переднего и заднего колес, 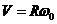 .
Звено
.
Звено 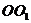 совершает
плоское движение вокруг мгновенного центра
совершает
плоское движение вокруг мгновенного центра  ,
, 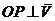 ,
,
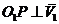 ,
,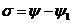 .
Угловая скорость
.
Угловая скорость 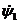 звена
звена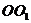 определяется соотношением
определяется соотношением
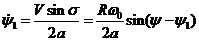 ,
,
где 2а - расстояние
между опорными точками переднего и заднего колес.
Обозначим
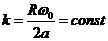 , тогда
, тогда

Это уравнение кинематической связи
переднего и заднего колес велосипеда.
Рассмотрим случай, когда
углы поворота переднего и заднего колес являются малыми. В этом случае 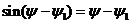 .
Определим угол поворота переднего колеса формулой
.
Определим угол поворота переднего колеса формулой  ,
где с,
,
где с,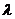 -
некоторые константы, [1]. В этом случае траектория движения переднего колеса
представляет собой синусоиду.
-
некоторые константы, [1]. В этом случае траектория движения переднего колеса
представляет собой синусоиду.
Тогда последнее
уравнение примет вид
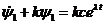 .
.
Решая это линейное
дифференциальное уравнение, получим
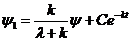
При 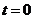 имеем
имеем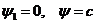 .
.
Тогда 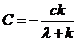 .
.
Таким образом, получим
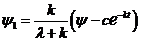 .
.
Это соотношение выражают
кинематическую зависимость движения переднего и заднего колес при малых
отклонениях велосипеда от прямолинейного движения, (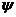 и
и 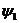 малые
углы), для случая, когда угол поворота переднего колеса определяется формулой
малые
углы), для случая, когда угол поворота переднего колеса определяется формулой  .
.
Обозначив
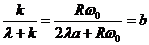 , (9)
, (9)
получим 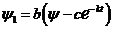 ,
,
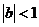 .
.
Для достаточно больших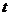 можно положить
можно положить 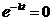 .
Тогда
.
Тогда 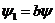 .
.
Уравнения движения рамы.
Уравнения движения рамы запишем в неподвижной системе координат 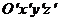 относительно
подвижного в этой систем центра О. Пусть
относительно
подвижного в этой систем центра О. Пусть 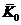 - кинетический момент
рамы относительно центра
- кинетический момент
рамы относительно центра 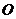 ,
,
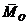 -
главный момент внешних сил относительно того же центра,
-
главный момент внешних сил относительно того же центра, 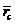 -
радиус вектор центра масс рамы. Обозначим массу рамы буквой
-
радиус вектор центра масс рамы. Обозначим массу рамы буквой 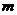 .
Тогда теорема моментов в неподвижной системе координат
.
Тогда теорема моментов в неподвижной системе координат 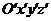 относительно
подвижного в этой системе центра
относительно
подвижного в этой системе центра 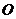 будет иметь вид
будет иметь вид
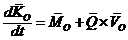 ,
,
где 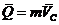 -
количество движения рамы,
-
количество движения рамы, 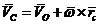 -
скорость центра масс рамы,
-
скорость центра масс рамы, 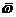 - угловая скорость
вращения рамы вокруг осей
- угловая скорость
вращения рамы вокруг осей 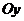 и
и
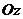 .
.
 .
.
Кинетический момент рамы
выражается соотношением
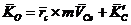 ,
,
где 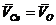 -
переносная скорость центра масс рамы,
-
переносная скорость центра масс рамы, 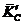 - кинетический момент
рамы относительно центра масс в ее движении по отношению к подвижной системе
- кинетический момент
рамы относительно центра масс в ее движении по отношению к подвижной системе 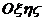 ,
перемещающейся вместе с центром масс рамы поступательно. Пусть
,
перемещающейся вместе с центром масс рамы поступательно. Пусть 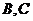 моменты
инерции рамы относительно осей
моменты
инерции рамы относительно осей 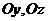 , а центр масс рамы в
системе
, а центр масс рамы в
системе 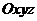 имеет
координаты
имеет
координаты 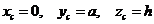 .
.
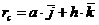
Тогда
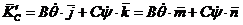 ,
,
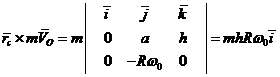 .
.
В системе  имеем
имеем
 ,
,
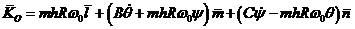 ,
,
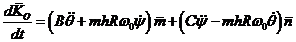 ,
,
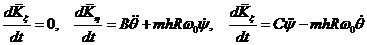 . (10)
. (10)
Пусть 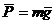 -
вес рамы, приложенный в центре масс рамы
-
вес рамы, приложенный в центре масс рамы 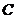 ,
,
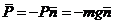 .
.
Точка 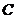 имеет
в системе
имеет
в системе 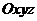 координаты
координаты
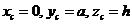 .
Тогда
.
Тогда
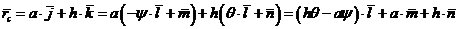 .
.
где 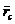 -
радиус-вектор центра масс рамы относительно опорной точкиОзаднего колеса.
Момент силы
-
радиус-вектор центра масс рамы относительно опорной точкиОзаднего колеса.
Момент силы 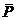 относительно
центра
относительно
центра 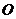 равен
равен
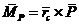 ,
,
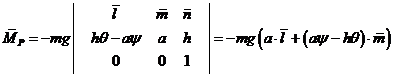 .
.
В точке соприкосновения
переднего колеса с опорной плоскостью приложена реакция опоры 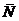 .
Полагая, что центр масс рамы находится в середине рамы, получим
.
Полагая, что центр масс рамы находится в середине рамы, получим 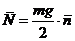 ,
,
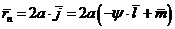 ,
,
Момент реакции опоры
равен
 .
.
Главный момент внешних
сил
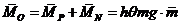 (11)
(11)
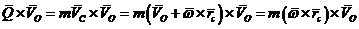
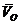 - это скорость
перемещения опорной точки
- это скорость
перемещения опорной точки 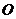 вместе
с системой
вместе
с системой 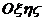 при
качении колеса по опорной плоскости,
при
качении колеса по опорной плоскости, 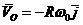 ,
,
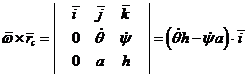
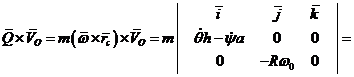
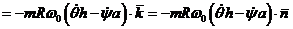 . (12)
. (12)
Поскольку оси системы  параллельны
соответствующим осям системы
параллельны
соответствующим осям системы  , то с учетом (10),
(11), (12) в системе координат
, то с учетом (10),
(11), (12) в системе координат 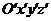 получаем
дифференциальные уравнения движения рамы
получаем
дифференциальные уравнения движения рамы
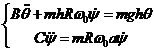
Уравнения движения
велосипеда. Перепишем последнюю систему, добавив в обозначения моментов
инерции рамы и ее массы индекс 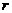 , а угол поворота рамы,
совпадающий с углом поворота заднего колеса, обозначим
, а угол поворота рамы,
совпадающий с углом поворота заднего колеса, обозначим 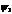 .
.
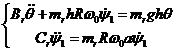 (13)
(13)
Добавим в уравнения
движения переднего колеса (7) уравнения движения заднего колеса (8) и уравнения
движения рамы (13). Учитывая соотношение 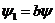 , получим полную
математическую модель движения велосипеда.
, получим полную
математическую модель движения велосипеда.
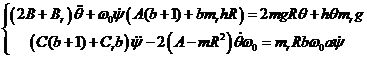 (14)
(14)
Исследование
устойчивости движения. Исследование
устойчивости движения, соответствующего модели (14) с помощью имитационной
модели.
Введем обозначения
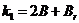 ,
, 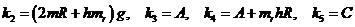 ,
,
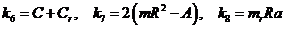 ,
, 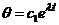 ,
,
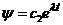 ,
,
тогда  ,
,
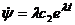 ,
,
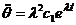 ,
,
 .
.
Перепишем уравнения (14) в новых
обозначениях
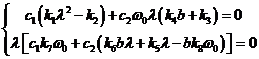 .
.
Получим первый корень 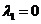 .
.
Для того, чтобы эта
система имела ненулевое решение 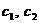 , необходимо, чтобы
имело место соотношение
, необходимо, чтобы
имело место соотношение
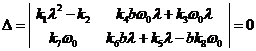 ,
,
или 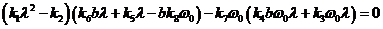 .
.
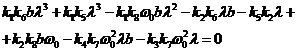 .
.
Введем еще обозначения
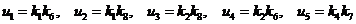 ,
,
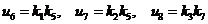
и подставим вместо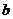 его
выражение (6), получим
его
выражение (6), получим
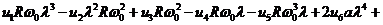

Сгруппируем по степеням 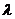
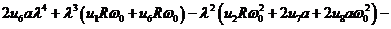
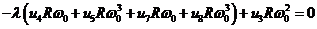 .
.
Далее обозначим
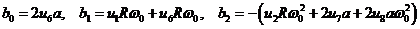
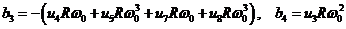 .
.
Теперь
характеристическое уравнение запишется в виде
 .
.
Для исследования
устойчивости соответствующего движения применим критерий Рауса-Гурвица [9].
Запишем матрицу 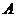 из
коэффициентов характеристического уравнения в виде
из
коэффициентов характеристического уравнения в виде
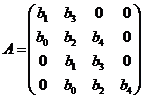
Условие устойчивости:
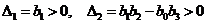 ,
,
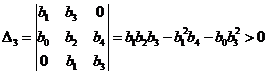

Значение 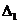 больше
нуля. Так как
больше
нуля. Так как 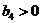 ,
то при
,
то при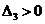 значение
значение 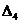 также
больше нуля. Следовательно, нужно определить значения
также
больше нуля. Следовательно, нужно определить значения 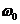 ,
при которых
,
при которых 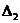 и
и
 имеют
положительные значения.
имеют
положительные значения.
Исследование значений 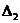 и
и
 проводились
численными методами. При этом были приняты следующие значения для величин,
входящих в
проводились
численными методами. При этом были приняты следующие значения для величин,
входящих в 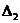 и
и
 .
.
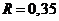 м.,
м.,
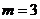 кг.,
2
кг.,
2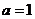 м.,
м., 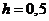 м.
Отношение массы рамы к массе колеса задавалось параметром
м.
Отношение массы рамы к массе колеса задавалось параметром 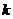 ,
,
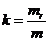 .
.
Предполагая, что масса
колеса сосредоточена по его ободу, получим моменты инерции колеса  .
Моменты инерции
.
Моменты инерции 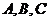 в
формулах (14) определены относительно осей
в
формулах (14) определены относительно осей 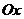 ,
, 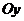 ,
,
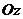 .
Тогда моменты инерции
.
Тогда моменты инерции 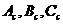 колеса
относительно осей, параллельных осям
колеса
относительно осей, параллельных осям 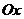 ,
, 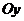 ,
,
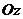 и
проходящим через центр масс колеса будут
и
проходящим через центр масс колеса будут
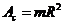 ,
, 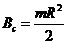 ,
,
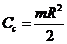 .
.
Моменты инерции 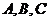 определяются
формулами
определяются
формулами
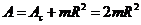 ,
, 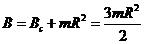 ,
,
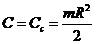 . Моменты инерции рамы
определялись по упрощенным формулам
. Моменты инерции рамы
определялись по упрощенным формулам 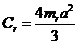 , (момент инерции
стержня относительно оси, проходящей через конец стержня),
, (момент инерции
стержня относительно оси, проходящей через конец стержня), 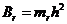 .
.
Численные расчеты
показали, что 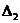 больше
нуля для любых значений
больше
нуля для любых значений 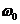 .
Это означает, что устойчивость движения велосипеда определяется только знаком
определителя
.
Это означает, что устойчивость движения велосипеда определяется только знаком
определителя 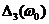
При 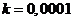 ,
когда масса рамы близка к нулю, устойчивое движение велосипеда начинается при
угловой скорости
,
когда масса рамы близка к нулю, устойчивое движение велосипеда начинается при
угловой скорости  рад/с.
Если радиус колеса
рад/с.
Если радиус колеса 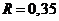 м.,
то это соответствует линейной скорости велосипеда равной 1 м/с. или 3,6 км/ч.
При
м.,
то это соответствует линейной скорости велосипеда равной 1 м/с. или 3,6 км/ч.
При 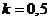 устойчивое
движение велосипеда начинается при угловой скорости
устойчивое
движение велосипеда начинается при угловой скорости 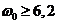 рад/с,
что соответствует линейной скорости велосипеда равной 2,17 м/с. или 7,8 км/ч.
Если
рад/с,
что соответствует линейной скорости велосипеда равной 2,17 м/с. или 7,8 км/ч.
Если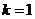 ,
т.е. масса рамы равна массе колеса, минимальная угловая скорость, при которой
возможно устойчивое движение велосипеда существенно увеличивается:
,
т.е. масса рамы равна массе колеса, минимальная угловая скорость, при которой
возможно устойчивое движение велосипеда существенно увеличивается: 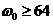 рад/с,
это соответствует линейной скорости велосипеда равной 22,4 м/с. или 80,6 км/ч,
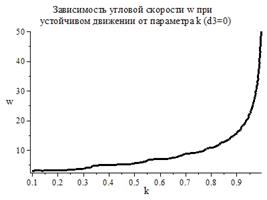
(рис. 4). На рис. 5 приведен график зависимости минимальной угловой скорости
рад/с,
это соответствует линейной скорости велосипеда равной 22,4 м/с. или 80,6 км/ч,
(рис. 4). На рис. 5 приведен график зависимости минимальной угловой скорости 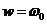 от
параметра
от
параметра 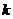 при
устойчивом движении велосипеда (
при
устойчивом движении велосипеда (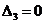 ).
).
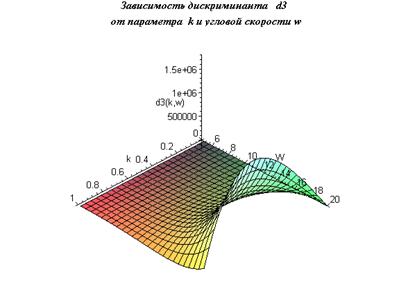
На рис. 6 изображена
поверхность, отображающая зависимость  от угловой скорости
от угловой скорости 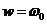 и
параметра
и
параметра 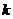 .
При приближении массы рамы к массе колеса устойчивость движения резко
снижается.
.
При приближении массы рамы к массе колеса устойчивость движения резко
снижается.
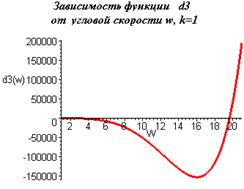
Аналитическое
исследование устойчивости движения велосипеда. Аналитическое исследование устойчивости полученной модели можно
провести для случая, когда масса рамы равна нулю. Применим метод исследования
устойчивости по корням характеристического уравнения.
Положим в уравнениях
(14) 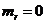 .
Тогда
.
Тогда 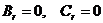 и
уравнения (14) примут вид
и
уравнения (14) примут вид
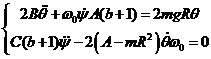 (15)
(15)
Обозначения 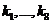 преобразуются
к виду
преобразуются
к виду
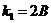 ,
, 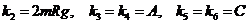 ,
,
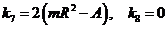 .
.
С учетом этих
обозначений уравнения (15) можно записать в виде
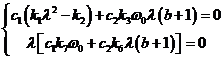 (16)
(16)
Получим первый корень 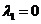 .
.
Для того, чтобы эта
система имела ненулевое решение 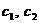 , необходимо, чтобы
имело место соотношение
, необходимо, чтобы
имело место соотношение
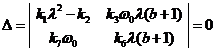 ,
,
или 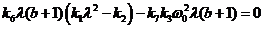 .
.
Далее имеем 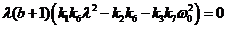
Получаем следующий
корень характеристического уравнения 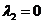 . Нулевые корни
характеристического уравнения свидетельствуют о том, что система (15) допускает
частное нулевое решение [7, с. 34].
. Нулевые корни
характеристического уравнения свидетельствуют о том, что система (15) допускает
частное нулевое решение [7, с. 34].
Подставим вместо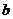 его
значение (9)
его
значение (9)
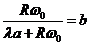 , получим
, получим
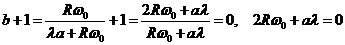 .
.
Откуда 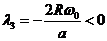 .
.
Остальные корни получим
из соотношения
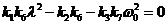 , (17)
, (17)
где  ,
,
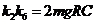 ,
,
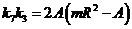
Поскольку 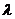 входит
в уравнение в четной степени, то вместе с корнем
входит
в уравнение в четной степени, то вместе с корнем 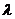 удовлетворять уравнению
будет и корень
удовлетворять уравнению
будет и корень 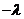 .
Следовательно, устойчивое движение возможно лишь при чисто мнимых значениях
.
Следовательно, устойчивое движение возможно лишь при чисто мнимых значениях 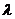 ,
т.е. необходимо, чтобы выполнялось неравенство
,
т.е. необходимо, чтобы выполнялось неравенство 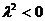 . Тогда условием
устойчивости движения велосипеда будет
. Тогда условием
устойчивости движения велосипеда будет 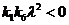 или
или
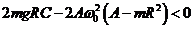 .
.
Следовательно, для
устойчивого движения велосипеда угловая скорость 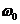 должна удовлетворять
условию
должна удовлетворять
условию
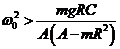 . (18)
. (18)
Тогда 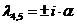 ,
где
,
где
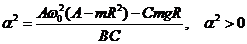 . (19)
. (19)
Для велосипеда с
приведенными выше параметрами формула (18) дает значение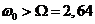 .
По критерию Рауса-Гурвица матрица из коэффициентов характеристического
уравнения (17) имеет лишь одну ненулевую строку. Все дискриминанты,
следовательно, будут нулевыми. При стремлении параметра k к нулю значение
.
По критерию Рауса-Гурвица матрица из коэффициентов характеристического
уравнения (17) имеет лишь одну ненулевую строку. Все дискриминанты,
следовательно, будут нулевыми. При стремлении параметра k к нулю значение 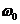 стремиться к числу 2,8,
что несколько выше значения
стремиться к числу 2,8,
что несколько выше значения 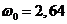 .
.
Малые колебания колес
велосипеда при его устойчивом движении. Решим систему
дифференциальных уравнений (16) и получим выражения, определяющие изменения
углов 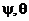 в
зависимости от времени
в
зависимости от времени 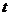 .
В системе двух уравнений (16) содержится три неизвестные
.
В системе двух уравнений (16) содержится три неизвестные 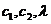 .
Значение
.
Значение 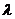 мы
уже определили, следовательно, одной из переменных
мы
уже определили, следовательно, одной из переменных 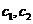 можно
придать произвольное значение, а значение другой вычислить по одной из формул
(16).
можно
придать произвольное значение, а значение другой вычислить по одной из формул
(16).
Пусть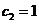 .
Перенумеруем
.
Перенумеруем 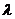 .
.
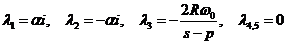 .
.
Подставив 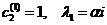 во
второе уравнение (16)
во
второе уравнение (16)
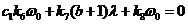 , получим
, получим
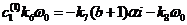 , где
, где
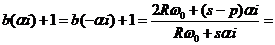
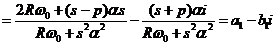 ,
,
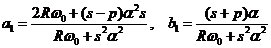 ,
,
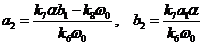 .
.
Для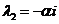 из уравнения
из уравнения 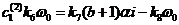 аналогично
получим
аналогично
получим 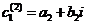 .
Значению
.
Значению 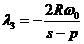 будет
соответствовать
будет
соответствовать 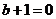 ,
следовательно,
,
следовательно,
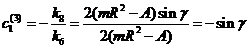 .
.
Частные решения системы
дифференциальных уравнений (16) будут
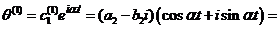
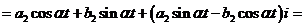
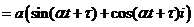 ,
,
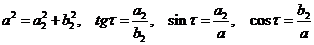 ,
,
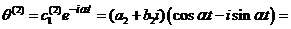
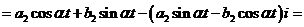
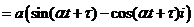 ,
,
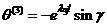 ,
, 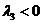 ,
,
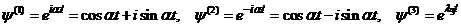 .
.
За системы частных
решений можно отдельно взять действительные и мнимые части.
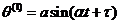 ,
, 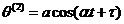 ,
,
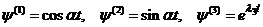
Общим решением будет
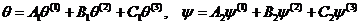 или
или
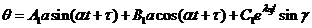 ,
,
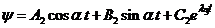 , (20)
, (20)
где 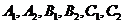 константы
интегрирования, которые находятся по начальным условиям. Пусть заданы начальные
условия: при
константы
интегрирования, которые находятся по начальным условиям. Пусть заданы начальные
условия: при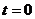 имеем
имеем 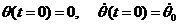 ,
,
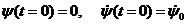 .
.
Определим производные
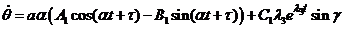 ,
,
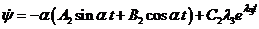 . (21)
. (21)
Поскольку у нас два
начальных условия, а констант три, то одной константе можно дать произвольное
значение. Пусть 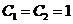 .
.
Подставляя в (20), (21)
начальные условия, получим
Для угла 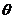 :
:
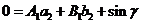 ,
,
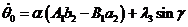 .
.
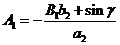 ,
, 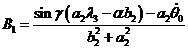 ,
(22)
,
(22)
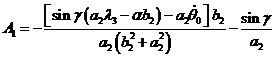 , (23)
, (23)
Для угла 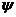 :
:
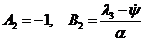 .
.
Тогда углы 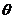 и
и
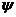 будут
меняться со временем согласно уравнениям
будут
меняться со временем согласно уравнениям
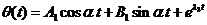 ,
,
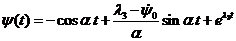
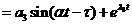 , (24)
, (24)
где 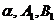 -
определены соответственно формулами (19), (22) и (23),
-
определены соответственно формулами (19), (22) и (23),
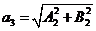 ,
, 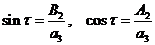 .
.
Гироскопическая
стабилизация. Как показывает рис. 5 минимальная скорость устойчивого движения
велосипеда резко возрастает при стремлении массы рамы к массе колеса. В данном
пункте работы исследована устойчивость движения велосипеда при наличии
гироскопической стабилизации. Впервые исследования движения твердых тел с
гироскопом начали проводиться в конце 19 века. В 1892 г. Бобылев [10] разрешил
в эллиптических функциях времени задачу о движении без скольжения по
горизонтальной плоскости шара с гироскопом внутри. В то же время эту задачу
исследовал Жуковский [11]. Известна классическая задача гироскопической
стабилизации однорельсового вагона [3]. В работе [6] рассматривается система
стабилизации вертикального положения двухколесного робота-велосипеда.
По теореме Томсона -
Тета - Четаева гироскопическую стабилизацию можно осуществить только при четном
числе неустойчивых координат. В нашей задаче имеется две неустойчивые
координаты: угол θ и угол  .
Следовательно, гироскопическую стабилизацию движения велосипеда можно
осуществить. Пусть в невозмущенном состоянии ось гироскопа, центр масс которого
совпадает с центром масс рамы, направлена вдоль оси, проходящей через центр
массС рамы параллельно оси
.
Следовательно, гироскопическую стабилизацию движения велосипеда можно
осуществить. Пусть в невозмущенном состоянии ось гироскопа, центр масс которого
совпадает с центром масс рамы, направлена вдоль оси, проходящей через центр
массС рамы параллельно оси  . Предположим, что рама
повернулась относительно оси
. Предположим, что рама
повернулась относительно оси  на малый угол
на малый угол 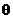 ,
а относительно оси
,
а относительно оси 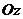 на
малый угол
на
малый угол 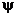 .
Пусть угловая скорость поворота будет
.
Пусть угловая скорость поворота будет 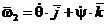 . Если гироскоп
вращается вокруг собственной оси с угловой скоростью
. Если гироскоп
вращается вокруг собственной оси с угловой скоростью 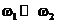 ,
,
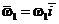 ,
то согласно правилу Жуковского со стороны гироскопа будет действовать пара сил
с гироскопическим моментом
,
то согласно правилу Жуковского со стороны гироскопа будет действовать пара сил
с гироскопическим моментом 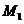 , поворачивающая ось
вращения гироскопа в сторону вектора
, поворачивающая ось
вращения гироскопа в сторону вектора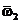 . При этом имеет место
соотношение
. При этом имеет место
соотношение
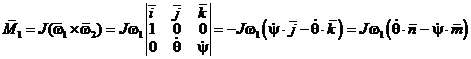 ,
,
где 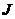 момент
инерции гироскопа.
момент
инерции гироскопа.
Добавим в систему
уравнений (14) гироскопический момент 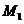 , получим
, получим
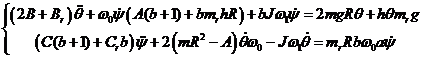 (25)
(25)
Ведя обозначения
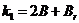 ,
, 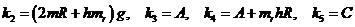 ,
,
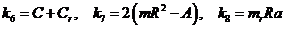 ,
, 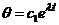 ,
,
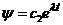 ,
,
где 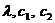 -
некоторые константы [1], будем иметь
-
некоторые константы [1], будем иметь
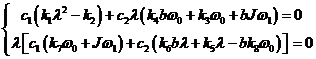 .
.
Получим первый корень 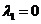 .
.
Для того, чтобы эта
система имела ненулевое решение 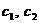 , необходимо, чтобы
имело место соотношение
, необходимо, чтобы
имело место соотношение
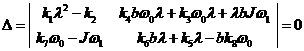 ,
,
или 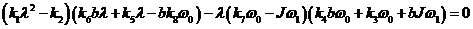 .
.
Подставим вместо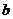 его
выражение (9), получим
его
выражение (9), получим
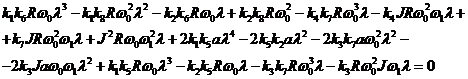
Сгруппируем по степеням 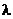 и
обозначим
и
обозначим 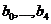 коэффициенты
соответственно при
коэффициенты
соответственно при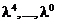
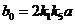 ,
, 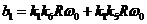 ,
,
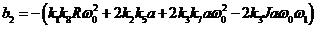 ,
,
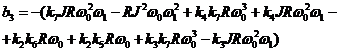
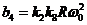 .
.
Теперь характеристическое уравнение
запишется в виде
 .
.
Для исследования
устойчивости соответствующего движения применим критерий Рауса-Гурвица. Матрица
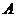 из
коэффициентов характеристического уравнения будет иметь вид
из
коэффициентов характеристического уравнения будет иметь вид
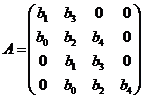
Условие устойчивости:
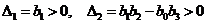 ,
,
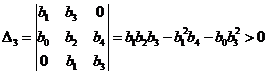

Значение 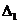 больше
нуля. Так как
больше
нуля. Так как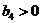 ,
то при
,
то при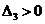 значение
значение 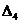 также
больше нуля. Следовательно, нужно определить значения
также
больше нуля. Следовательно, нужно определить значения 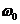 ,
при которых
,
при которых 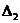 и
и
 имеют
положительные значения.
имеют
положительные значения.
Исследование значений 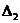 и
и
 проводились
численными методами.
проводились
численными методами.
Результаты приведены
ниже.
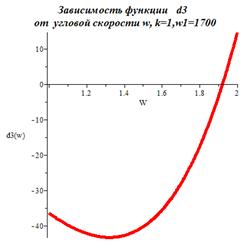
Если угловая скорость гироскопа w1=0, то устойчивое движение
велосипеда начинается при угловой скорости колесаw>64. При угловой скорости
гироскопа w1=1700 область устойчивого движения велосипеда начинается со
значения w>1.93
На рис. 8 приведен график
зависимости минимальной угловой скорости колеса при устойчивом движении
велосипеда с гиростабилизаторомот соотношения массы рамы к массе колеса,
угловая скорость вращения гироскопа 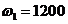 .
.
Имитационная модель. Ниже приведена имитационная модель, соответствующая движению
велосипеда с гироскопическим стабилизатором. Модель реализована в программной
среде MATLAB (программа m21).
Перепишем систему(25),
оставив в уравнениях угол поворота заднего колеса и рамы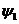
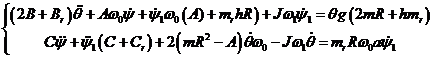
Введя обозначения
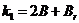 ,
, 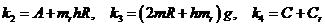 ,
,
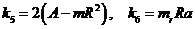 ,
,
перепишем последнюю
систему в виде
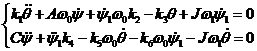
Выразим из первого
уравнения 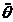 ,
а из второго уравнения
,
а из второго уравнения 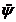
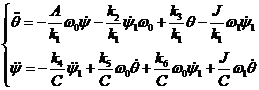
Обозначим
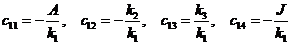
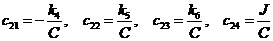 .
.
Получим
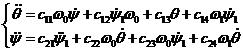
Массу рамы примем равной
массе колеса. Принимая параметры велосипеда из пункта 6, получим значения
констант 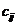 .
.
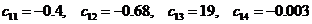
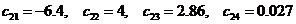
Структура модели
движения двухколесного велосипеда с гиростабилизатором будет иметь вид
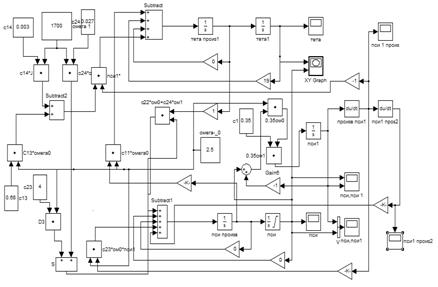
Приведенная модель соответствует
значению угловой скорости гироскопа w1=1700. Угловая скорость вращения колеса велосипеда w=2.5. Движение велосипеда
устойчивое.
График изменения угла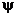 в
зависимости от времени
в
зависимости от времени 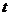

Графики изменения углов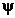 (желтый)
и
(желтый)
и 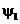 (красный)
в зависимости от времени
(красный)
в зависимости от времени 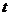
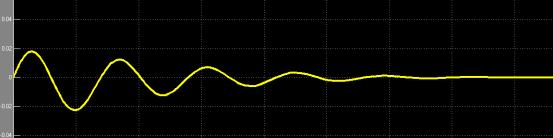
График изменения угла 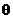 в
зависимости от времени
в
зависимости от времени 
Результаты исследования
1. Построена математическая модель
первого приближения для движения элементарного велосипеда с жесткими колесами
по горизонтальной плоскости.
. Проведено численное исследование
устойчивости движения велосипеда при разных соотношениях между массой рамы и
массой колеса велосипеда.
. Построены графики зависимости
угловой скорости устойчивого движения от параметра k, определяющего отношение массы рамы
к массе колеса велосипеда.
. Проведено аналитическое
исследование устойчивости движения велосипеда в частном случае при нулевой
массе рамы.
. Проведено исследование
устойчивости движения велосипеда с гироскопической стабилизацией.
Выводы
1. Устойчивое движение
велосипеда начинается с некоторого критического значения скорости движения
велосипеда. При увеличении скорости движения велосипеда устойчивость
прямолинейного движения повышается.
. Увеличение соотношения
массы рамы к массе колеса ведет к снижению устойчивости движения велосипеда и
повышает критическое значение скорости устойчивого движения.
. Устойчивость движения велосипеда
можно повысить с помощью гироскопической стабилизации.
Замечание.
В данной работе постановка задачи отличается от постановки задачи в работах [3,
4]. В данной работе сразу строится модель первого приближения, а в работах [3,
4] сначала строится точная модель, а затем она линеаризуется. В работах [3, 4]
рассматривается статическое положение велосипеда без учета собственного
вращения колес. Это приводит к тому, что отличие угла поворота заднего колеса
от угла поворота переднего колеса обуславливается наклоном рулевой оси, ее
смещением относительно центра масс переднего колеса и величиной так называемого
выноса. Это приводит к ошибочному результату. Действительно, если взять
элементарный велосипед, у которого рулевая вилка вертикальна, и проходит через центр
переднего колеса, то по формулам (6.70), Бутенин [3, с. 235], получается, что
угол поворота заднего колеса равен углу поворота переднего колеса. Очевидно,
что это не так. Для элементарного велосипеда угол поворота заднего колеса
меньше угла поворота переднего колеса [8]. При этом если велосипед не движется,
то при любом повороте переднего колеса, заднее колесо остается неподвижным.
Если при движении велосипеда угол поворота переднего колеса остается
постоянным, то угол поворота заднего колеса изменяется, постепенно приближаясь
к углу поворота переднего. Отметим также, что в работе [3] утверждается:
неуправляемый велосипед будет двигаться устойчиво в некотором интервале
скоростей 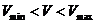 .
В данной работе условие устойчивости движения представлено односторонним
неравенством
.
В данной работе условие устойчивости движения представлено односторонним
неравенством 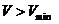 .
.
Основная литература
1. Бондарь А.И. Построение приближенной модели и исследование
устойчивости движения велосипеда. // Труды Новосибирского архитектурно -
строительного университета, Т.11, №1, Новосибирск, 2008, с. 78-105, (есть в
интернете)
2. Bourlet C. Traite des bicycles etbicyclettes // Paris:
Gauthier-Villars, 1898
3. Неймарк Ю.И. Динамика неголономных систем // Ю.И. Неймарк, Н.А.
Фуфаев.-М: Наука, 1967. - 519 с.
. Бутенин Н.В., Введение в аналитическую механику. // Н.В.
Бутенин, Н.А. Фуфаев. - М., «Наука», 1991, 255 с.
. Мартыненко Ю.Г. Управление движением мобильных роботов., //
Мартыненко Ю.Г. Фундаментальная и прикладная математика. - т. 11, вып. 8, 2005,
с. 29-80.
. Ленский А.В. Двухколесный робот-велосипед с гиростабилизатором.
// А.В. Ленский, А.М. Формальский. Изв. РАН. Теория и сист. управления. - 2003,
№3, с. 176-183
. Бондарь А.И. Построение приближенных моделей сферического
движения твердого тела // Бондарь И.М., Бондарь А.И - Вычислительные
технологии,
Т. 12, №4, 2007, с. 27-41 (есть в интернете)
. Бондарь И.М. Моделирование движения кинематически зависимых тел.
// Бондарь И.М., Бондарь А.И - Труды Новосибирского архитектурно -
строительного университета, Т.12, №2, Новосибирск, 2009, с. 84-97 (есть в
интернете)
. Алфутов Н.А. Устойчивость движения и равновесия // Н.А. Алфутов,
К.С. Колесников. - М: Из-во МГТУ им. Баумана, 2003. - 253 с.