Классические парадоксы теории вероятностей

Классические парадоксы теории вероятностей

Оглавление

Введение

Глава 1. Классические парадоксы теории вероятностей

.1 Парадоксы, разрешение которых способствовало возникновению и развитию теории вероятностей и ее приложений

2. Классические парадоксы теории вероятностей

2.1 Парадокс игры в кости, «азартные игры», в мире физических лиц

.2 Парадокс де Мере

.3 Парадокс раздела ставки

.4 Парадокс закона больших чисел Бернулли

.5 Парадокс дня рождения

.6 Парадокс Бертрана

2.7 Парадокс раздачи подарков

Заключение

Библиографический список

Введение

Открытия Кантора, относящиеся примерно к 1873 г. и постепенно оформившиеся в самостоятельную ветвь математики, вначале натолкнулись на недоверие, и даже прямой антагонизм многих математиков и безразличие со стороны подавляющего большинства философов. Только в начале девяностых годов теория множеств вошла в моду и стала, сверх всяких ожиданий, широко применяться в анализе и геометрии. Но в тот самый момент, когда смелое видение Кантора, казалось, с триумфом достигло кульминации, когда его результаты приняли окончательный систематизированный вид, он столкнулся с первым парадоксом.

Поэтому история математики, естественно, полна интересных парадоксов, и некоторые и служили отправной точкой больших изменений. Особенно богата парадоксами математика случайного. По мнения Карла Пирсона, в математике нет другого такого раздела, в котором столь же легко допустить ошибку, как в теории вероятностей.

Теория вероятностей - это раздел математики, в котором изучаются случайные явления (события) и выявляются закономерности при массовом их повторении. Математическая дисциплина, которая изучает объективные закономерности массовых случайных событий, является теоретической базой для математической статистики, занимающейся разработкой методов сбора, описания и обработки результатов наблюдений. Путем наблюдений (испытаний, экспериментов), т.е. опыта в широком смысле слова, происходит познание явлений действительного мира.

Важно различать парадоксы и софизмы. На уровне интуиции понятие «парадокс» является общепринятым. В широком смысле парадокс - это истинное высказывание, утверждение или суждение, кажущимися неверными, характеризующимися неожиданностью, непривычностью, противоречивостью себе, исходным посылкам, общепринятому, традиционному взгляду или здравому смыслу по содержанию и (или) по форме.

Кроме парадоксов существуют не менее удивительные утверждения - софизмы, в доказательствах которых, в отличие от доказательства парадоксов, кроются незаметные, а иногда довольно тонкие ошибки. Так, «софизм» - это рассуждение, формально кажущееся совершенно безупречным, но содержащее на самом деле ошибку, в результате чего конечный вывод оказывается абсурдом.

Таким образом, первые это справедливые, хотя и неожиданные утверждения, в то время как вторые - ложные результаты, полученные с помощью рассуждений, формально кажущихся правильными.

В данной работе мы рассмотрим классические парадоксы теории вероятностей.

Объект исследования - ознакомление с классическими парадоксами теории вероятностей.

Предмет исследования - парадоксы из книги Г. Секея (парадокс игры в кости парадокс де Мере, парадокс раздачи подарков, парадокс закона больших чисел Бернулли, парадокс Бертрана).

Цель исследования - разобрать историю возникновения и первых попыток разрешения парадоксов.

В соответствии с объектом, предметом и целью исследования были поставлены следующие задачи:

.        Рассмотреть понятие парадокса.

.        Изучить историю возникновения классических парадоксов.

.        Изучить парадоксы из книги Г. Секея.

Структура курсовой работы. Работа состоит из введения, одной главы, заключения, списка литературы.

Глава 1. Классические парадоксы теории вероятностей

.1 Парадоксы, разрешение которых способствовало возникновению и развитию теории вероятностей и ее приложений

вероятность парадокс бернулли бертран

Парадоксы, по определению, резко расходятся с общепринятым, традиционным мнением, но они всегда опираются на конкретную теорию и являются истинным.

Особой известностью пользуются парадоксы в логике. По сути, само определение парадокса позаимствовано из логики. Именно в ней и появились первые парадоксы. Рассмотрим некоторые из них.

Наиболее известным и, пожалуй, самым интересным из всех логических парадоксов является парадокс "Лжец", сформулированный греческим философом Эвбулидом из Милета в IV веке до н.э. (На самом деле этот парадокс еще древнее; он восходит к Эпимениду, жившему в VI веке до н.э. на острове Крит.)

Имеются различные варианты этого парадокса. В простейшем варианте "Лжеца" человек произносит всего одну фразу: "Я лгу", или говорит: "Высказывание, которое я сейчас произношу, является ложным". Традиционная лаконичная формулировка этого парадокса гласит: если лгущий говорит, что он лжет, то он одновременно лжет и говорит правду.

Данный парадокс можно переформулировать и так. Допустим, что на лицевой стороне карточки стоят слова: "На другой стороне этой карточки написано истинное высказывание" - и ничего более. Ясно, что эти слова представляют собой осмысленное утверждение. Перевернув карточку, мы находим на ее обороте слова: "На другой стороне этой карточки написано ложное высказывание" - и опять-таки ничего более. Предположим, что утверждение на лицевой стороне - истинно. Тогда утверждение на обороте должно быть истинным и, значит, утверждение на лицевой стороне должно быть ложным. Но если утверждение с лицевой стороны ложно, тогда утверждение на обороте также должно быть ложным и, следовательно, утверждение на лицевой стороне должно быть истинным. Выходит, что данное утверждение не может быть ни истинным, ни ложным. Но это противоречит принципу исключенного третьего. Парадокс ошеломляющий. Он произвел громадное впечатление на греков. Ходит даже легенда, что он привел к самоубийству некоего Филита Косского. Этот парадокс разбил Аристотель и многие другие логики, жившие позднее. Некоторые философы считали, что поскольку рассматриваемое утверждение содержит ссылку на самое себя, то оно просто не имеет смысла, а бессмысленные высказывания должны быть исключены из языка.

Самым известным, из уже открытых в нашем веке парадоксов, является парадокс Рассела, который формулируется следующим образом: ПустьK-множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит лиKсамо себя в качестве элемента? Если предположить, что содержит, то мы получаем противоречие с "Не содержат себя в качестве своего элемента". Если предположить, что K не содержит себя как элемент, то вновь возникает противоречие, ведь K - множество всех множеств, которые не содержат себя в качестве своего элемента, а значит должно содержать все возможные элементы, включая и себя.

Противоречие в парадоксе Рассела возникает из-за использования в рассуждении внутренне противоречивого понятия множества всех множеств и представления о возможности неограниченного применения законов классической логики при работе с множествами. Для преодоления этого парадокса было предложено несколько путей. Наиболее известный состоит в предъявлении для теории множеств непротиворечивой формализации М, по отношению к которой являлись бы допустимыми все «действительно нужные» (в некотором смысле) способы оперирования с множествами. В рамках такой формализации утверждение о существовании множества всех множеств было бы не выводимым.

Действительно, допустим, что множествоUвсех множеств существует. Тогда, согласно аксиоме выделения, должно существовать и множествоK, элементами которого являются те и только те множества, которые не содержат себя в качестве элемента. Однако предположение о существовании множестваKприводит к парадоксу Рассела. Следовательно, ввиду непротиворечивости теорииM, утверждение о существовании множества U не выводимо в этой теории, что и требовалось доказать.

В ходе реализации описанной программы «спасения» теории множеств было предложено несколько возможных её аксиоматизаций (теория Цермело - Френкеля, теория Неймана - Бернайса - Гёделя и т.д.), однако ни для одной из этих теорий до настоящего момента не найдено доказательства непротиворечивости. Более того, как показал Гёдель, разработав ряд теорем о неполноте, такого доказательства не может существовать (в некотором смысле).

Парадокс Рассела замечателен своей крайней общностью. Для его построения не нужны какие-либо сложные технические понятия, как в случае некоторых других парадоксов, достаточно понятия «множества» и «элемент множества». Но эта простота как раз и говорит о его фундаментальности: он затрагивает самые глубокие основания наших рассуждений о множествах, поскольку говорит не о каких-то специальных случаях, а о множествах вообще.

Рассел и Уайтхед разрешили данный парадокс введя требование: «То, что содержит все элементы множества, не должно быть элементом того же самого множества».

2. Классические парадоксы теории вероятностей

.1 Парадокс игры в кости, «азартные игры», в мире физических лиц

Правильная игральная кость при бросании с равными шансами падает на любую из граней 1, 2, 3, 4, 5 или 6. В случае бросания двух костей сумма выпавших чисел заключена между 2 и 12. Как 9, так и 10 из чисел 1, 2,..., 6 можно получить двумя разными способами: 9 = 3 + 6 = 4 + 5 и 10 = 4 + 6 = 5 + 5. В задаче с тремя костями и 9, и 10 получаются шестью способами. Почему тогда 9 появляется чаще, когда бросают две кости, а 10, когда бросают три?

.2 Парадокс де Мере

При четырех бросаниях одной игральной кости вероятность того, что, по крайней мере, один раз выпадет 1, больше 1/2. В то же время при 24 бросаниях двух костей вероятность выпадения двух 1 одновременно (по крайней мере однажды) меньше ½. Это кажется удивительным, так как шансы получить одну 1 в шесть раз больше, чем шансы выпадения двух 1, а 24 как раз в 6 раз больше 4.

.3 Парадокс раздела ставки

Два игрока играют в безобидную игру (т. е. у обоих шансы победить одинаковы), и они договорились, что тот, кто первым выиграет 6 партий, получит весь приз. Предположим, что на самом деле игра остановилась до того, как один из них выиграл приз (например, первый игрок выиграл 5 партий, а второй - 3). Как справедливо следует разделить призу. Хотя в действительности эта проблема не является парадоксом,

.4 Парадокс закона больших чисел Бернулли

Игроки часто уверены, что если правильная монета много раз падает гербом, то, согласно закону больших чисел, вероятность выпадения решки с необходимостью возрастает. В противном случае нарушалось бы то, что при очень большом числе бросаний выпадения герба и решки происходят приблизительно одинаково часто. С другой стороны, у монет, очевидно, нет памяти, поэтому они не знают, сколько раз они уже выпадали гербом или решкой. По этой причине шансы выпадения герба при каждом бросании равны 1/2, даже если монета уже выпала гербом тысячу раз подряд. Не противоречит ли это закону Бернулли?

.5 Парадокс дня рождения

Если собираются вместе не более чем 365 человек, возможно, что все они имеют различные дни рождения. Однако среди 366 человек наверняка найдутся, по крайней мере, два таких, у которых дни рождения приходятся на один и тот же день в году. (Предположим, что мы не рассматриваем високосные года). Однако если мы зададимся целью найти, сколько людей должно быть, чтобы с точностью до 99% два из них имели один и тот же день рождения, то обнаружим, что достаточно 55 человек. В то же время среди 68 человек с вероятностью 99,9%, по крайней мере, два имеют одинаковый день рождения.

.6 Парадокс Бертрана

Для некоторой окружности случайным образом выбирается хорда. Найти вероятность того, что эта хорда длиннее стороны правильного треугольника, вписанного в данную окружность. Парадокс Бертрана Парадокс утверждает, что эта вероятность определяется неоднозначно, т. е. различные методы приводят к разным результатам.

Первый метод: Случайным образом (равномерно) в данном круге выбирается точка. Эта случайная точка определяет единственную хорду, серединой которой она является. Эта хорда длиннее стороны нашего правильного треугольника тогда и только тогда, когда ее середина лежит внутри круга, вписанного в треугольник. Радиус этого круга равен половине радиуса исходного круга, следовательно, площадь вписанного круга составляет 1/4 площади исходного. Таким образом, вероятность того, что случайно выбранная точка лежит внутри вписанного круга, равна 1/4. Так что этот метод дает ответ 1/4.

Второй метод: Исходя из соображений симметрии, можем считать, что одним концом хорды является произвольная фиксированная точка на окружности. Пусть этой точкой является вершина вписанного.

Три способа выбора случайной хорды треугольника. Выберем другой конец случайно с равномерным распределением. Вершины треугольника делят окружность на три равные дуги, и случайная хорда длиннее стороны правильного треугольника, если она пересекает этот треугольник. Так что искомая вероятность теперь равна 1/3.

Третий метод: Выберем точку случайным образом равномерно на радиусе окружности и возьмем хорду, которая перпендикулярна этому радиусу и проходит через выбранную точку. Тогда случайная хорда длиннее стороны вписанного правильного треугольника, если случайная точка лежит на той половине радиуса, которая ближе к центру. Исходя из соображений симметрии, неважно какой радиус был выбран для построения, поэтому искомая вероятность равна 1/2.

.7 Парадокс раздачи подарков

Несколько человек решили сделать друг другу подарки следующим образом. Каждый приносит подарок. Подарки складываются вместе, перемешиваются и случайно распределяются среди участников. Этот справедливый способ раздачи подарков применяется часто, так как считают, что для больших групп людей вероятность совпадения, т. е. получения кем-то собственного подарка, очень мала. Парадоксально, но вероятность, по крайней мере, одного совпадения намного больше вероятности того, что совпадений нет (кроме случая, когда группа состоит из двух человек, тогда вероятность отсутствия совпадений равна 50%).

История возникновения и решение некоторых классических парадоксов

Парадокс игры в кости. «Азартные игры» в мире физических частиц

Игра в кости была самой популярной азартной игрой до конца средних веков. Само слово «азарт» также относится к игре в кости, так как оно происходит от арабского слова "азарт", переводимого как «игральная кость». Карточные игры стали популярны в Европе лишь в ХIV веке, в то время как игра в кости пользовалась успехом еще в Древнем Египте во времена 1-й династии и позднее в Греции, а также в Римской империи. (Согласно греческой легенде, игру в кости предложил Паламедей для развлечения греческих солдат, скучающих в ожидании битвы при Трое. Павсаний, писатель, живший во II веке, упоминает написанную в V веке до нашей эры картину Полигнота, на которой изображены Паламедей и Ферсит, играющие в кости.) Самой ранней книгой по теории вероятностей является «Книга об игре в кости» ("De Ludo Aleae") Джероламо Кардано (1501-1576 гг.), которая в основном посвящена игре в кости. Эта небольшая книжка была опубликована лишь в 1663 г., спустя почти 100 лет как была написана. Видимо, поэтому Галилей стал заниматься той же самой задачей о костях, хотя она была уже решена и работе Кардано. Галилей также написал трактат на эту тему где-то между 1613 и 1624 гг. Первоначально он назывался «Об открытиях, совершенных при игре в кости», но в собрании сочинений Галилея, изданном в 1718 г., название изменили на следующее: «О выходе очков при игре и кости».

Правильная игральная кость при бросании с равными шансами падает на любую из граней 1, 2, 3, 4, 5 или 6. В случае бросания двух костей сумма выпавших чисел заключена между 2 и 12. Как 9, так и 10 из чисел 1, 2,..., 6 можно получить двумя разными способами: 9 = 3+ 6=4+5 и 10 = 4+6 = 5+5. В задаче с тремя костями и 9, и 10 получаются шестью способами. Почему тогда 9 появляется чаще, когда бросают две кости, а 10, когда бросают три?

Задача настолько проста, что кажется странным, что в свое время ее считали страшно трудной. И Кардано, и Галилей отмечали необходимость учета порядка выпадения чисел. В противном случае не все исходы были бы равновозможными. В случае двух костей 9 и 10 могут получаться следующим образом: 9=3+6=6+3=4+5=5+4 и 10 =4+6=6+4=5+5. Это означает, что в задаче с двумя костями 9 можно «выбросить» четырьмя способами, а 10-тремя. Следовательно, шансы получить 9 предпочтительней. Поскольку две кости дают 6*6=36 различных равновозможных пар чисел, шансы получить 9 равны 4/36, а для 10-лишь 3/36. В случае трех костей ситуация меняется на противоположную: 9 можно «выбросить» 25 способами, а 10 - уже 26 способами. Так что 10 более вероятно, чем 9.

Парадокс Бертрана

Жорж Бюффон (1707-1788 гг.), знаменитый французский ученый, в работе, написанной в 1733 г. (но опубликованной в 1777 г.), положил начало новому направлению в теории вероятностей. Решение знаменитой «задачи об игле», обсуждаемое в этой статье, потребовало использования скорее геометрического (а не комбинаторного) метода. В задачах такого типа предполагается, что случайные точки равномерно распределены в некоторой области. (Например, попадания пуль в мишень.) Вероятность попадания в произвольную часть данной области пропорциональна ее площади (длине или объему). Таким образом, для вычисления вероятности нам лишь нужно найти отношение «благоприятной» площади ко «всей» площади (длине или объему). Вероятности такого типа приводят к ряду парадоксов. Например, шанс поразить центр (или любую другую заданную точку) мишени равен, очевидно, нулю. С другой стороны, попасть в эту точку можно и, следовательно, мы должны различать события. происходящие с вероятностью 0, и невозможные события (вероятность невозможного события равна 0, но обратное неверно). Довольно странно выглядит также следующий факт: события «поразить по крайней мере одну точку из конечного множества точек» и «поразить лишь одну точку» имеют одинаковые вероятности. (Обе вероятности равны 0. См. парадокс о нулевой вероятности.) Другая странность: взаимно однозначное преобразование может совершенно изменить шансы. Например, если мы случайным образом выбираем точку на интервале (0, 1), то шансы выбрать число, которое меньше 1/2, равны 50%. Однако если все числа из (0, 1) возвести в квадрат и равномерно выбирать из этих квадратов, то шансы увеличатся до 65,6%. Конечно, первый ответ, т.е. 50%, более естественен. Однако, в других задачах выбор между естественным и неестественным ответами может оказаться более сложным. Выше уже отмечалось (в последнем замечании к первому парадоксу), что такой выбор не всегда возможен на основе лишь логических рассуждений без учета данных практики. Именно в этом суть следующего парадокса, опубликованного в книге «Исчисление вероятностей» (1889 г.) Жозефа Луи Бертрана.

Первый метод: Случайным образом (равномерно) в данном круге выбирается точка. Эта случайная точка определяет единственную хорду, серединой которой она является. Эта хорда длиннее стороны нашего правильного треугольника тогда и только тогда, когда ее середина лежит внутри круга, вписанного в треугольник. Радиус этого круга равен половине радиуса исходного круга, следовательно, площадь вписанного круга составляет 1/4 площади исходного. Таким образом, вероятность того, что случайно выбранная точка лежит внутри вписанного круга, равна 1/4. Так что этот метод дает ответ 1/4.

Второй метод: Исходя из соображений симметрии, можем считать, что одним концом хорды является произвольная фиксированная точка на окружности. Пусть этой точкой является вершина вписанного.

Три способа выбора случайной хорды треугольника. Выберем другой конец случайно с равномерным распределением. Вершины треугольника делят окружность на три равные дуги, и случайная хорда длиннее стороны правильного треугольника, если она пересекает этот треугольник. Так что искомая вероятность теперь равна 1/3.

Третий метод: Выберем точку случайным образом равномерно на радиусе окружности и возьмем хорду, которая перпендикулярна этому радиусу и проходит через выбранную точку. Тогда случайная хорда длиннее стороны вписанного правильного треугольника, если случайная точка лежит на той половине радиуса, которая ближе к центру. Исходя из соображений симметрии, неважно какой радиус был выбран для построения, поэтому искомая вероятность равна 1/2.

Получение разных результатов кажется парадоксальным, так как было убеждение, что слова «равномерный случайный выбор» однозначно определяют искомую вероятность. Парадокс показывает, что возможны различные способы выбора равномерным образом, причем каждый способ выглядит по-своему «естественным». Каждый из трех указанных выше методов использует равномерное распределение (в круге, на окружности и радиусе круга). По мнению Пуанкаре («Исчисление вероятностей» Париж, 1912 г.), если у нас нет никакой дополнительной информации, то следует воспользоваться третьим методом (где ответ был 1/2), так как в этом случае имеем: если два множества хорд геометрически конгруэнтны, то с равными вероятностями случайно выбранная хорда будет принадлежать любому из этих множеств. Изучение инвариантности такого типа привело к очень интересному разделу математики, который называется интегральной геометрией. (Этот термин был введен Вильгельмом Бляшке в 1934 г.).

Как объяснить этот парадокс? Разные результаты мы получали потому, что по-разному конкретизировали понятие «случайно», фактически мы решали каждый раз новую задачу. Нам только казалось, что это прежняя задача.

Парадокс дня рождения

Если собираются вместе не более чем 365 человек, возможно, что все они имеют различные дни рождения. Однако среди 366 человек наверняка найдутся, по крайней мере, два таких, у которых дни рождения приходятся на один и тот же день в году. (Предположим, что мы не рассматриваем високосные года). Однако если мы зададимся целью найти, сколько людей должно быть, чтобы с точностью до 99% два из них имели один и тот же день рождения, то обнаружим, что достаточно 55 человек. В то же время среди 68 человек с вероятностью 99,9%, по крайней мере, два имеют одинаковый день рождения.

Утверждение, гласящее, что если дана группа из 23 или более человек, то вероятность того, что хотя бы у двух из них дни рождения (число и месяц) совпадут, превышает 50%. С практической точки зрения это означает, что если, например, в нашей группе 23 студента или более, то более вероятно, что у кого-то из одногруппников дни рождения придутся на один день, чем что у каждого будет свой собственный день рождения.

Для 60 и более человек вероятность такого совпадения превышает 99%, хотя 100% она достигает, только когда в группе не менее 367 человек (с учётом високосных лет).

Такое утверждение может показаться неочевидным, так как вероятность совпадения дней рождения двух человек в любой день года (1/365 = 0,27%), помноженная на число человек в группе из 23, даёт лишь 23/365 = 6,3%. Это рассуждение неверно, так как число возможных пар (253) значительно превышает число человек в группе. Таким образом, утверждение не является парадоксом в строгом научном смысле- логического противоречия в нём нет, а парадокс заключается лишь в различиях междуинтуитивным восприятием ситуации человеком и результатами математического расчёта.

Один из способов понять на интуитивном уровне, почему в группе из 23 человек вероятность совпадения дней рождения у двух человек столь высока, состоит в осознании следующего факта: поскольку рассматривается вероятность совпадения дней рождения у любых двух человек в группе, то эта вероятность определяется количеством пар людей, которые можно составить из 23 человек. Так как порядок людей в парах не имеет значения, то общее число таких пар равно числу сочетаний из 23 по 2, то есть (23×22)/2 = 253 пары.

Ключевым моментом здесь является то, что утверждение парадокса дней рождения говорит именно о совпадении дней рождения у каких-либо двух членов группы. Одно из распространённых заблуждений состоит в том, что этот случай путают с другим- похожим, на первый взгляд, - случаем, когда из группы выбирается один человек и оценивается вероятность того, что у кого-либо из других членов группы день рождения совпадёт с днем рождения выбранного человека. В последнем случае вероятность совпадения значительно ниже. Для адекватного интуитивного восприятия может оказаться полезным обратиться к самому понятию частотной вероятности. 50% означает, что из 1000 групп по 23 человека приблизительно в 500 группах окажется не меньше, чем по одному совпадению, с чем очень легко согласиться.

В данном примере для расчёта вероятности того, что в группе из n человек как минимум у двух дни рождения совпадут, примем, что дни рождения распределены равномерно, то есть нет високосных лет, близнецов, рождаемость не зависит от дня недели, времени года и других факторов. В действительности это не совсем так - обычно летом рождается больше детей; кроме того, в некоторых странах из-за особенностей работы больниц больше детей рождается в определённые дни недели. Однако неравномерность распределения может лишь увеличить вероятность совпадения дней рождения, но не уменьшить: если бы все люди рождались только в 3 дня из 365, то вероятность совпадения дней рождения была бы очень высокой.

Рассчитаем сначала, какова вероятность 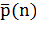 того, что в группе из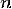человек дни рождения всех людей будут различными. Если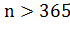, то в силу принципа Дирихле вероятность равна нулю. Если же 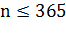, то будем рассуждать следующим образом. Возьмём наугад одного человека из группы и запомним его день рождения. Затем возьмём наугад второго человека, при этом вероятность того, что у него день рождения не совпадёт с днем рождения первого человека, равна 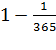. Далее возьмём третьего человека - при этом вероятность того, что его день рождения не совпадёт с днями рождения первых двух, равна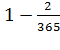. Рассуждая по аналогии, мы дойдём до последнего человека, для которого вероятность несовпадения его дня рождения со всеми предыдущими будет равна 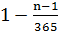. Перемножая все эти вероятности, получаем вероятность того, что все дни рождения в группе будут различными:

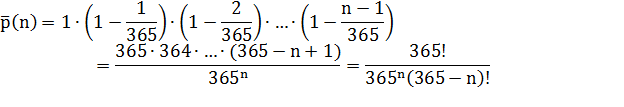
Тогда вероятность того, что хотя бы у двух человек из n дни рождения совпадут, равна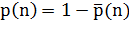

Значение этой функции превосходит 1/2 при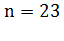(при этом вероятность совпадения равна примерно 50,7%). Вероятности для некоторых значенийиллюстрируются следующей таблицей:

Таблица 1

Данную задачу можно переформулировать в терминах классической «задачи о совпадениях». Пусть урна содержит 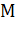 (в данном случае 365) шаров, занумерованных числами 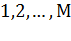. Производится выборка с возвращением объёма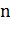(в данном случае количество человек в группе), при этом рассматриваемые выборки считаются упорядоченными (то есть выборк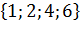и  и 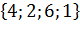 считаются различными). Требуется посчитать вероятность события, заключающегося в отсутствии повторений в выборке (все расчёты аналогичны приведённым выше).

Близкие дни рождения

Другое обобщение парадокса дней рождения состоит в постановке задачи о том, сколько человек нужно для того, чтобы вероятность наличия в группе людей, дни рождения которых различаются не более чем на один день (или на два, три дня и так далее), превысила 50%. Эта задача более сложная, при её решении используется принцип включения-исключения. Результат (опять-таки в предположении, что дни рождения распределены равномерно) получается следующим:

Таблица 2

Таким образом, вероятность того, что даже в группе из 7 людей дни рождения хотя бы у двух будут различаться не более чем на неделю, превышает 50%.

На этом примеры парадоксов в теории вероятностей не заканчиваются, но рассмотренными тремя, мы ограничимся.

Заключение

Как и большинство разделов науки, математика - это также и история парадоксов. Величайшие открытия, как правило, разрешали величайшие парадоксы, и в то же время они, в свою очередь, были источником новых парадоксов. Метод обучения Сократа, по которому о новых идеях надо узнавать через парадоксы, является самым фундаментальным, так как процесс научного познания сам опирается на парадоксы.

Парадоксы возникают в науке там, где теория не описывает процессы должным образом. Разрешение таких парадоксальных явлений ведет в свою очередь к возникновению новых теорий, даже новых наук.

Например, для развития дедуктивной математики огромную роль сыграл парадокс «несоизмеримости». Он привел к распаду пифагорейской школы, а также к созданию евклидовой геометрии (где роль чисел стали играть геометрические фигуры) и к «математическому идеализму» Платона (на практике «несоизмеримость» нельзя проверить непосредственно, поэтому, согласно Платону, опыт не может привести к истинному знанию).

Величайший парадокс математики средних веков состоял в том, что «ничто», т.е. нуль, следовало рассматривать как нечто и как-то его обозначать. В результате, благодаря индоарабскому способу записи чисел, вычисления в значительной степени облегчились. Позднее возникли парадоксы, связанные с отрицательными числами. Например, один из парадоксов утверждал, что равенство (-1): 1 = 1: (- 1) невозможно, так как отношение меньшего числа к большему не может равняться отношению большего числа к меньшему.

Проблемы, связанные с парадоксами, относятся к разным типам и затрагивают все основные разделы логики и математики. Требуется не просто разрешение парадоксов, необходимо их объяснение, углубляющее представления о логических закономерностях мышления.

Мы знаем, что парадокс в широком смысле - это утверждение, резко расходящееся с общепринятыми, устоявшимися мнениями, отрицание того, что представляется "безусловно правильным". В более современном значении - это два противоположных утверждения, для каждого из которых имеются представляющиеся убедительными аргументы.

Все парадоксы имеют одно общее свойство - самоприменимость или циркулярность.

Решение об отказе от каких-то логических средств, используемых при выводе парадоксального утверждения, должно быть связано с общими соображениями относительно природы логического доказательства и другими логическими интуициями.

Библиографический список

1.      Секей, Г. Парадоксы в теории вероятностей и математической статистике. [Текст] / Г. Секей; пер. с английского И.М. Яглома. - М.: Мир,1990. - 256с.

.        Соболь, И.М. Метод Монте-Карло. [Текст] / И.М. Соболь. - М.: Наука, 1972. -194с.

.        Феллер, В. Введение в теорию вероятностей и ее приложения. [Текст] / В. Феллер. - М.: Мир, 1972. -450с.