Иррациональные уравнения
Иррациональные уравнения
Аннотация
Актуальность: К решениям иррациональных уравнений приводят
многие задачи физики, химии, биологии, социологии и экологии. Поэтому важно
изучить различные методы решений иррациональных уравенний.
Цель: Изучение методов решений иррациональных уравнений.
Задачи:
1. Изучить теоретический материал, связанный
с равносильностью уравнений, равносильностью преобразований, методами решения
иррациональных уравнений;
2. Рассмотреть основные методы и приемы
решения различных иррациональных уравнений;
. Составить сборник задач с решениями
иррациональных уравнений, который может быть использован при изучении данной
темы.
Содержание
Введение
Решение иррациональных уравнений
Метод замены переменных
Линейные комбинации двух и более радикалов
Уравнения с одним радикалом вида 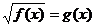
Умножение на сопряженное выражение
Метод решения уравнений путем нахождения и исследования ОДЗ
Метод решения уравнений путем выделения полных квадратов под знаком
радикала
Сборник задач
Заключение
Список использованной литературы
Введение
Материал, связанный с уравнениями, составляет значительную
часть школьного курса математики. Одним из сложных разделов алгебры, изучаемых
в школьной программе, являются иррациональные уравнения, так как в школе им
уделяют достаточно мало внимания.
Трудности при изучении данного вида уравнений связаны со
следующими их особенностями:
· в большинстве случаев отсутствие четкого
алгоритма решения иррациональных уравнений и неравенств;
· при решении уравнений и неравенств данного
вида приходится делать преобразования, приводящие к уравнениям, не равносильным
данному, вследствие чего чаще всего возникают ошибки, которые обычно связаны с
потерей или приобретением посторонних корней в процессе решения.
Опыт показывает, что учащиеся в недостаточной степени
овладевают умением решать иррациональные уравнения, часто допускают ошибки при
их решении. Однако задачи по теме "Иррациональные уравнения и встречаются
на вступительных экзаменах, и они довольно часто становятся "камнем
преткновения".
иррациональное уравнение радикал переменная
Решение
иррациональных уравнений
Иррациональным уравнением называют уравнение, в котором
неизвестная величина содержится под знаком радикала. Как правило, решение
иррациональных уравнений связано с возведением в степень обеих его частей. При
этом если обе части уравнения возвести в нечетную степень, то получим
уравнение, равносильное данному. Если же обе части возвести в четную степень,
то в общем случае получим уравнение, являющееся следствием исходного.
Уравнения, имеющие одни и те же корни, называют
равносильными.
В процессе решения заданное уравнение заменяют более простым,
при этом используют следующие правила преобразований уравнения в равносильное
ему:
а) перенос слагаемого из одной части уравнения в другую с
противоположным знаком;
б) обе части уравнения можно умножить или разделить на одно и
то же, отличное от 0 число;
в) уравнение 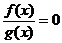 можно заменить равносильной системой
можно заменить равносильной системой 
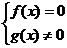

 или решить f (x) =0, а затем отбросить те корни, которые обращают в 0
знаменатель.
или решить f (x) =0, а затем отбросить те корни, которые обращают в 0
знаменатель.
Метод замены
переменных
Еще одним часто встречающимся методом преобразования уравнения
является метод замены переменных. Для уравнений этот метод состоит в следующем:
данное уравнение приводят к виду g (f (x)) =0, где z=g (f (x)) - сложная
функция, являющаяся композицией двух функций y=f (x) и z=g (y). Если y=y1; y=y2; …y=yn; все корни уравнения g (x) =0,f (x) =y1, f (x) =y2, то g (f (x)) =0 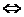 ……., f (x) =yn
……., f (x) =yn
Пример 1.
Решить уравнение:
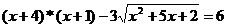 .
.
Решение:
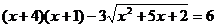
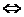
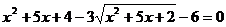
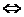
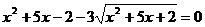 , применяя
замену
, применяя
замену 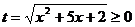 , уравнение можно переписать в виде равносильной системы:
, уравнение можно переписать в виде равносильной системы: 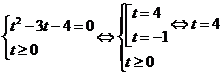
Обратная замена:
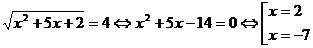
Ответ: - 7;
2
Линейные
комбинации двух и более радикалов
Если уравнение содержит два и более радикала, то необходимо
придерживаться следующих правил:
. указать область допустимых значений уравнения
2. распределить радикалы по обеим частям, чтобы обе
части уравнения стали неотрицательными
. только после этого возводить в квадрат левую и
правую части уравнения.
Пример 2.
Решить уравнение: 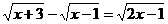 .
.
Решение:
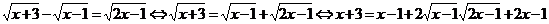
Еще одно правило равносильного перехода:
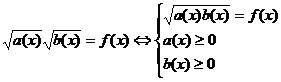
Вернемся к решению нашего уравнения с учетом рассмотренного
перехода:
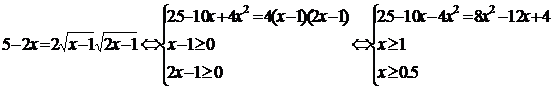
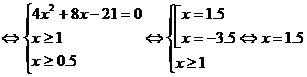
Ответ: 1,5
Пример 3.
Решить уравнение:
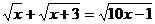 .
.
Решение:
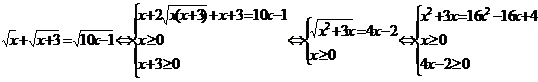
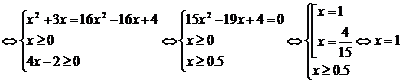
Заметим, что x=4/15
принадлежит ОДЗ уравнения, но не удовлетворяет условию 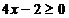 , возникшему при втором возведении в
квадрат. Таким образом, делая равносильные переходы на каждом этапе решения
уравнения, мы внимательно отслеживаем промежутки, в которых должны находиться
корни уравнения. Корни, которые не попадают в указанные промежутки, мы
отбрасываем, как посторонние.
, возникшему при втором возведении в
квадрат. Таким образом, делая равносильные переходы на каждом этапе решения
уравнения, мы внимательно отслеживаем промежутки, в которых должны находиться
корни уравнения. Корни, которые не попадают в указанные промежутки, мы
отбрасываем, как посторонние.
Ответ: 1
Уравнения
с одним радикалом вида 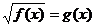
Здесь в правой части выражение g (x) может принимать как отрицательные, так и
положительные значения. Возведение в квадрат является равносильным
преобразованием, если g (x) 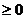 . Если g (x) <0, то уравнение решений не имеет.
. Если g (x) <0, то уравнение решений не имеет. 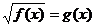
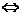
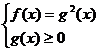 ; (условие f (x)
; (условие f (x) 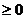 на область допустимых значений не
включается в систему, оно проверяется автоматически, так как правая часть
уравнения системы неотрицательна).
на область допустимых значений не
включается в систему, оно проверяется автоматически, так как правая часть
уравнения системы неотрицательна).
На что обратить внимание: часто учащиеся начинают решение с
определения области допустимых значений и записывают: ОДЗ:
 - это неправильная формулировка условий.
- это неправильная формулировка условий.
Пример 4.
Решить уравнение:
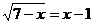 .
.
Решение:
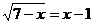
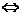
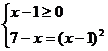
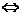
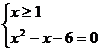
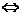
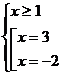
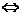 x=3.
x=3.
Ответ: 3
Пример 5.
Решить уравнение:
 .
.
Решение: 
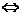 x
x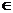 Ǿ, не имеет решения, так как по
определению арифметического квадратного корня:
Ǿ, не имеет решения, так как по
определению арифметического квадратного корня: 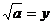
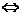
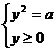 - это неотрицательное число, квадрат которого равен a, a-2<0.
- это неотрицательное число, квадрат которого равен a, a-2<0.
Ответ: решений
нет
Умножение на
сопряженное выражение
Умножением на сопряженное выражение часто пользуются, чтобы
избавиться от иррациональности в знаменателе. Для решения иррациональных
уравнений также можно использовать умножение на сопряженное выражение, но
обязательно нужно помнить о том, что мы получаем уравнение-следствие, поэтому
необходима проверка корней.
Пример 6.
Решить уравнение:
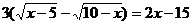 .
.
Решение:
Помножим исходное уравнение на сопряженное выражение
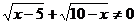
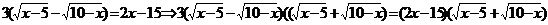
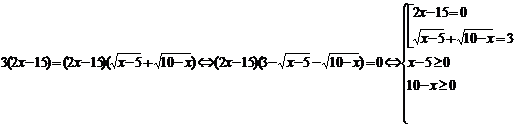
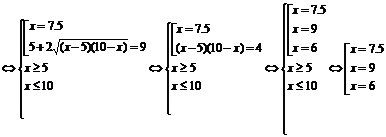
Проверка:
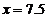
 .
.
x=9 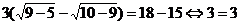 .
.
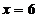
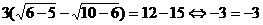 .
.
Проверка показала, что все решения являются корнями исходного
уравнения.
Ответ: 6; 7,5; 9
Метод решения
уравнений путем нахождения и исследования ОДЗ
Следует объяснить учащимся, что если уравнение кажется на
первый взгляд достаточно сложным, то следует начать его решения с нахождения
ОДЗ.
Пример 7.
Решить уравнение:
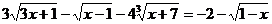 .
.
Решение:
ОДЗ: 
Область допустимых значений состоит из единственного значения.
Проверим, является ли это значение корнем уравнения.
 .
.
Следовательно, x=1 корень
нашего уравнения.
Ответ: 1
Метод решения
уравнений путем выделения полных квадратов под знаком радикала
Пример 8.
Решить уравнение:
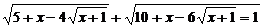 .
.
Решение:
Заметим, что подкоренные выражения представляют собой полные
квадраты. Действительно:
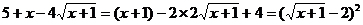
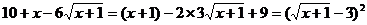
Напомним, что 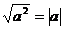 , пользуясь этим равенством, получим:
, пользуясь этим равенством, получим: 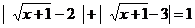 . Пусть
. Пусть  . Тогда уравнение примет вид:
. Тогда уравнение примет вид:
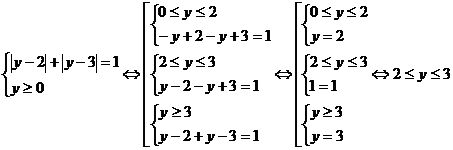
Вернемся к замене: 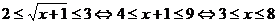
Ответ: 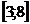 .
.
Сборник
задач
Пример 1.
Решить уравнение:
 .
.
Решение: 
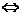 x
x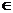 Ǿ, не имеет решения, так как по
определению арифметического квадратного корня:
Ǿ, не имеет решения, так как по
определению арифметического квадратного корня: 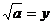
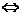
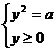 - это неотрицательное число, квадрат которого равен a, a-2<0.
- это неотрицательное число, квадрат которого равен a, a-2<0.
Ответ: решений
нет
Пример 2.
Решить уравнение:
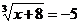
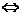 x+8= (-5)
3
x+8= (-5)
3 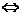 x+8= -
125
x+8= -
125 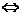 x= - 133.
x= - 133.
Ответ: - 133.
Пример 3.
Решить уравнение:
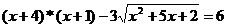 .
.
Решение: 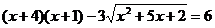
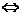
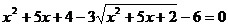
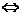
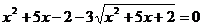 , применяя замену
, применяя замену 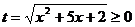 , уравнение
можно переписать в виде равносильной системы:
, уравнение
можно переписать в виде равносильной системы:
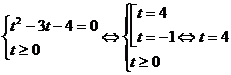
Обратная замена:
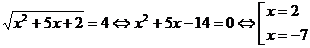
Ответ: - 7;
2
Пример 4.
Решить уравнение:
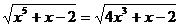 .
.
Решение:
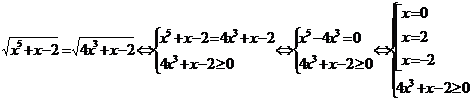
Подставляя их в неравенство, мы гораздо быстрее осуществим отбор,
чем, решая это неравенство, 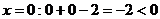 , следовательно, x=0 не
удовлетворяет нашему условию,
, следовательно, x=0 не
удовлетворяет нашему условию, 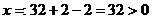 , следовательно, x=2
удовлетворяет нашему условию,
, следовательно, x=2
удовлетворяет нашему условию, 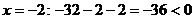 , следовательно, x=-2 не
удовлетворяет нашему условию.
, следовательно, x=-2 не
удовлетворяет нашему условию.
Ответ: 2
Пример 5.
Решить уравнение:
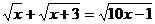 .
.
Решение:
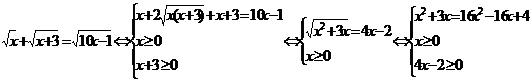
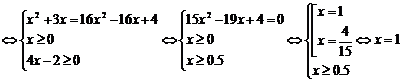
Заметим, что x=4/15
принадлежит ОДЗ уравнения, но не удовлетворяет условию 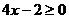 , возникшему при втором возведении в
квадрат. Таким образом, делая равносильные переходы на каждом этапе решения
уравнения, мы внимательно отслеживаем промежутки, в которых должны находиться
корни уравнения.
, возникшему при втором возведении в
квадрат. Таким образом, делая равносильные переходы на каждом этапе решения
уравнения, мы внимательно отслеживаем промежутки, в которых должны находиться
корни уравнения.
Корни, которые не попадают в указанные промежутки, мы отбрасываем,
как посторонние.
Ответ: 1
Пример 6.
Решить уравнение:
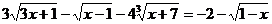 .
.
Решение:
ОДЗ: 
Область допустимых значений состоит из единственного значения.
Проверим, является ли это значение корнем уравнения.

Следовательно, x=1 корень
нашего уравнения.
Ответ: 1
Пример 7.
Решить уравнение:
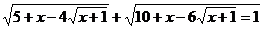 .
.
Решение:
Заметим, что подкоренные выражения представляют собой полные
квадраты. Действительно:
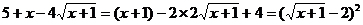
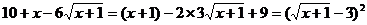
Напомним, что 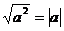 , пользуясь этим равенством, получим:
, пользуясь этим равенством, получим: 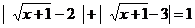 . Пусть
. Пусть  . Тогда уравнение примет вид:
. Тогда уравнение примет вид:
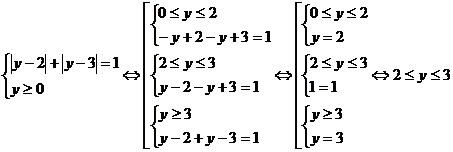
Вернемся к замене:
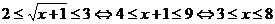
Ответ: 
Пример 8.
Решить уравнение:
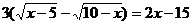 .
.
Решение:
Помножим исходное уравнение на сопряженное выражение
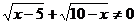
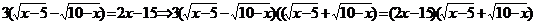
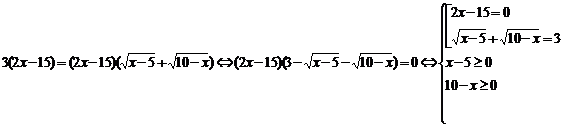
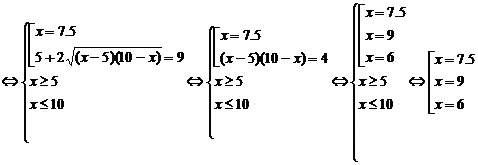
Проверка:
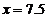
 .
.
x=9 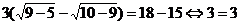 .
.
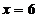
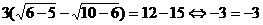 .
.
Проверка показала, что все решения являются корнями исходного
уравнения.
Ответ: 6; 7,5; 9
Пример 9.
Решить уравнение:
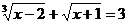 .
.
Решение:
Пусть 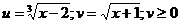 . Тогда
. Тогда 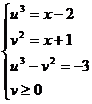 .
.
Наше исходное уравнение примет вид:
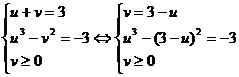
Решим второе уравнение системы:
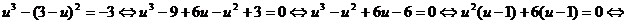
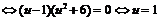
Итак, имеем: 
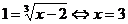 .
.
Ответ: 3
Пример 10.
Решить уравнение:
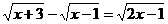 .
.
Решение:
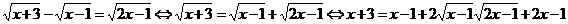
Еще одно правило равносильного перехода:
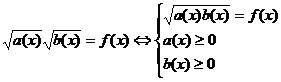
Вернемся к решению нашего уравнения с учетом рассмотренного
перехода:
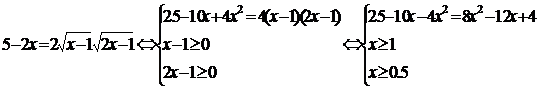
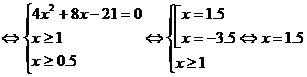
Ответ: 1,5
Решить уравнения:
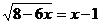 .
.
Решение:
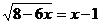
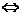
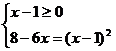
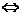

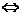
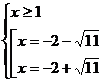
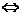
x=-2+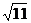 , Так как - 2-
, Так как - 2-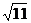 <1.
<1.
Ответ: - 2+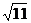
Заключение
В результате работы были решены следующие задачи:
1) Изучена учебно-методическая литература
по данной теме;
2) Рассмотрены основные методы и приемы
решения различных иррациональных уравнений;
3) Подобраны примеры решения
иррациональных уравнений для демонстрации излагаемого теоретического материала;
4) Составлен сборник иррациональных
уравнений с решениями, который может быть использован для изучений данной темы
другими учащимися.
Список
использованной литературы
1. Галицкий
М.Л. Сборник задач по алгебре для 8-9 классов [Текст]: учебное пособие для
учащихся школ и классов с углубленным изучением математики М.Л. Галицкий - М.:
Просвещение, 2009. - 271с.
2. Григорьев
А.М. Иррациональные уравнения [Текст] / А.М. Григорьев // Квант. - 1972. - №1.
- С.46-49.
. Егоров
А. Иррациональные неравенства [Текст] / А Егоров // Математика. Первое
сентября. - 2002. - №15. - С.13-14.
. Шарова
Л.И. Уравнения и неравенства [Текст]: пособие для подготовительных отделений /
Л.И. Шарова - Киев: Вища школа, 1981. - 280 с.
. Егоров
А. Иррациональные неравенства [Текст] / А Егоров // Математика. Первое
сентября. - 2012.
- №17. - С.13-14.
. Мордкович
А.Г. Алгебра. 8 класс [Текст]: В двух частях. Ч.1: учебник для
общеобразовательных учреждений / А.Г. Мордкович - М.: Мнемозина, 2014. - 315 с.
. Мордкович
А.Г. Алгебра. 8 класс [Текст]: В двух частях. Ч.2: задачник для
общеобразовательных учреждений / А.Г. Мордкович - М.: Мнемозина, 2010. - 239 с.