Застосування формули Тейлора
ЗМІСТ
ВСТУП
.
ЖИТТЯ ВЕЛИКОГО МАТЕМАТИКА
.
МНОГОЧЛЕН ТЕЙЛОРА
.
ФОРМУЛА ТЕЙЛОРА ДЛЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ
.1
Тейлорова формула із залишковим членом у формі Пеано
.2
Тейлорова формула із залишковим членом у Лагранжовій формі
.3
Тейлорова формула для многочлена
.4
Тейлорова формула в диференціальній формі
.5
Формула Тейлора із залишковим членом в інтегральній формі
.
РОЗВИНЕННЯ ДЕЯКИХ ЕЛЕМЕНТАРНИХ ФУНКЦІЙ ЗА ФОРМУЛОЮ ТЕЙЛОРА
.1
Формула f(x)
= ex
.2
Функція f(x)
= sin x
.3Функція
f(x)
= cos x
.4
Логарифмічна функція f(x)=ln(1+х)
.5
Степенева функція f(x)=(1+x)α
.
ЗАСТОСУВАННЯ ФОРМУЛИ ТЕЙЛОРА
ВИСНОВОК
СПИСОК
ВИКОРИСТАНИХ ДЖЕРЕЛ
ДОДАТКИ
ВСТУП
Математичний аналіз один з
найважливіших розділів математики, він включає дві основні частини:
диференціальне і інтегральне числення. Математичний аналіз виник приблизно в
XVIII столітті.
Розділ математичного аналізу, в
якому вивчається похідні і диференціали функції і і застосування до дослідження
функцій, називається диференціальним численням. Оформлення цього розділу в окрему
дисципліну пов'язаний з іменами І. Ньютона і Г. Лейбніца. Вони сформулювали
основні положення диференціального числення і чітко вказали на взаємно
обернений характер операції диференціювання і інтеграції. Створення цього
розділу відкрило нову епоху в розвитку математики.
Диференціальне числення відіграє
величезну роль в математичному аналізі. Тому так поважно вивчити формули
диференціального числення.
Метою даної роботи є вивчення
можливостей практичного вживання формули Тейлора.
Завдання: вивести Тейлорову
формулу-потужний математичний інструмент дослідження функцій, обчислення
границі і наближеного обчислення значень функцій,навчитися застосовувати на
практиці, а також розглянути приклади розкладання елементарних функцій по
формулі.
Об’єкт: дослідження функцій і кривих
ліній.
Предмет: застосування формули
Тейлора.
1. ЖИТТЯ ВЕЛИКОГО МАТЕМАТИКА
Брук Тейлор (англійський математик) народився
18 серпня 1685р. у селі Едмонтон в
графстві Мідлсекс, у восьми милях від Лондона. Його дід користувався увагою з
боку Кромвеля, батько був шталмейстером. Хлопчик отримав прекрасне виховання,
загальне, а також художнє і музичне .
У 1701 році, коли Тейлору виповнилося 15 років,
він поступив в Кембріджський університет, в коледж Сент-Джон. Якраз в цей час
Ньютон остаточно розлучився з Кембриджем, але, звичайно, залишався кумиром
молодих математиків. До них приєднався з самої своєї появи в Кембріджі і
молодій Брук Тейлор.
У 1709 році Тейлор отримав ступінь бакалавра, а
в 1714 році ступінь доктора права. Незалежно від цього він вивчав математику.
До 1712 року в його активі числиться вже два
мемуари: "Про центр коливань" і " Про підйом води між двома
площинами". Статті Тейлора були визнані настільки цінними, що в тому ж
році його обрали членом Королівського
суспільства.
У 1714р. Тейлор представив
cуспільству рукопис своєї книги "Метод приростів пряма і обернена". У
1716 р. Тейлор зробив поїздку до Парижа. Увага з боку вчених, знаки пошани,
цікаві знайомства в Парижі - все це справило гарне враження на Тейлора. Але
рокова "хвороба століття"-перехід від природних наук до теології і
містики оволоділа і Тейлором. У 1718 р. він йде з посади секретаря
Королівського суспільства, щоб звільнити час для філософської роботи.
У 1721р. Тейлор одружувався, що
викликало розрив з батьком. Щастя, куплене такою дорогою ціною, виявилося
неміцним. У 1723р. Тейлор втрачає дружину і дитину. У 1725р. він знову
одружується - вже при повному схваленні батька. Але щастя і цього разу не
прийшло до Тейлора: у 1730 р. дружина померла при пологах. Правда залишилася
дівчинка, але Тейлор був безутішний в своєму горі. Його здоров'я різко
погіршувалося і більше не відновлювалося.
29 грудня 1731р. він помер і був
похоронений в Лондоні.
Досягнення в математиці:
Відомий тим, що його ім'ям названа
загальна формула розкладання функції в степеневий ряд. Тейлор започаткував
математичне вивчення задачі про коливання струни. Йому належать заслуги в
розробці теорії кінцевих різниць. Тейлор також автор робіт про
перспективу, центр гойдання, взаємодію магнітів, капілярності, зчеплення між
рідинами і твердими тілами [посилання 1].
2. МНОГОЧЛЕН ТЕЙЛОРА
Відомо, що найбільш простими
функціями в сенсі обчислення є многочлени. Виникає питання про можливість
заміни функції f
в околі
точки x0
многочленом
певної міри.
З визначення диференціювання функції
f в точці x0
випливає, що якщо= f (x) диференційована в точці x
0, то її приріст можна представити у вигляді
∆f
( x 0 )= f
′(x
0 ) ∆x
+ о( x),
f(x)=f(x
0 )+f
′(x
0 )(x-
x 0 )+о(x-
x 0 ).
Іншими словами існує многочлен
першого ступеня
P1(x)=f(x0)+b1
(x-x0),
(1)
такий що при x
→
x0
f(x)=P1(x)+о(x-x0),
причому P1(x)
задовольняє такі умови: P1(x0)=f(x0),
P′(x0)=b1=f
′(x0).
Поставимо більш загальну задачу.
Нехай функція, визначена в деякій околі точки x0 має в цій точці n похідних f
′(x0),
f
′′ (x
0 ), f
′′′( x
0 )... f
(n)( x
0).
Потрібно з’ясувати, чи існує
многочлен Pn(x)
ступеня не вище n
такий, що
f
(x) = Pn
(x )+ o(
x - x0
)
Знайдемо многочлен ступеня не вище n
(запис якого аналогічна (1))
Pn
(x) = b0
+ b1 (x
- x 0) + b2
(x - x0)2
+ ... + bn(x
- x0)n,
(2)
за умови, що значення многочлена Pn
(x) і всіх його
похідних до n-го
порядку включно в точці x0
збігаються зі значеннями функції f
(x) та її відповідних
похідних в тій же точці:
f(x0)=Pn(x0),
f ′(x0)=Pn(x0),
…, f(n)(x0)=Pn(n)(x0).
(3)
Визначимо коефіцієнти b0,
b1, ..., bn
, так щоб вони задовольняли умови
(3). Для цього попередньо обчислимо похідні Pn(x):
Pn′(x)=b1+2b2(x-x0)+3b3(x-x0)2+…+nbn(x-x0)n-1n′′(x)=2∙1b2+3∙2b3(x-x0)2+…+n(n-1)bn
(x-x0)n-2 (4)‴(x)=3∙2b3+…+n(n-1)(n-2)bn
(x-x0)n-3
……………………………………………………(n)(x)=n(n-1)(n-2)
∙∙∙2∙1b
Підставляючи в ліві частини
рівностей (2) і (3) замість х значення x0
отримаємо значення всіх коефіцієнтів bi:
f(x0)=Pn(x0)=b0,
b0=f(x0)
f
′(x0)=Pn′(x0)=b1
, b1=f
′(x0)
f ″(x0)=Pn″(x0)=2∙1∙b2 , b2= 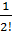
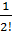 f″(x0)
(5)
f″(x0)
(5)
f‴(x0)=Pn‴(x0)=3∙2∙1∙b3 , b3=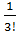
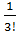 f‴(x0)
f‴(x0)
. . . . . . . . . . . . . . .
. . . . . . . . . . . .
f(n)(x0)=Pn(n)(x0)=n!bn , bn=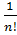
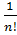 f(n)(x0)
f(n)(x0)
Факторіалом числа n
називається добуток послідовних натуральних чисел, починаючи з 1 до n
включно 1∙2∙3∙… ∙(n-1)n і
позначається
n!=1∙2∙3∙…
∙(n-1)n.
Зауваження! За домовленістю
0!=1.
Тепер можемо підставити отримані
значення коефіцієнтів у рівність (2), і отримаємо многочлен виду
Pn(x) =
f(x0) +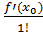
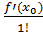 ( x-x0)+
( x-x0)+ 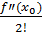
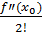 (x-x0)2
+…+
(x-x0)2
+…+ 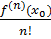
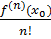 (x-x0)n,
(x-x0)n,
3. ФОРМУЛА ТЕЙЛОРА ДЛЯ ОДНІЄЇ
ЗМІННОЇ
Позначимо через Rn(x)
різницю значень даної функції f(x)
і побудованого многочлена Pn(x):
Rn(x)=f(x)-
Pn(x)
(додаток 1).
Звідси f(x)=
Rn(x)+Pn(x),
а в більш розгорнутій формі має вигляд:
Pn(x) = f(x0) +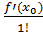
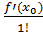 (x -x0)+
(x -x0)+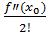
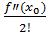 (x-x0)2
+…+
(x-x0)2
+…+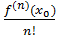
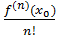 (x-x0)n + Rn(x) (6)
(x-x0)n + Rn(x) (6)
Функція (6) називається
формулою Тейлора, а Rn(x)
називається залишковим членом формули Тейлора [посилання 3].
Залишковий член формули
Тейлора Rn(x)
визначає похибку наближення функції f(x) її
многочленом Рп(х).
Якщо вважати, що залишок Rn(x)
малий, то його можна відкинути без великої погрішності; при цьому виходить
наближена формула
Pn(x) ≈
f(x0) +
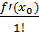
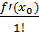 ( x-x0) +
( x-x0) +
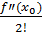
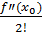 (x-x0)2
+…+
(x-x0)2
+…+ 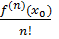
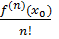 (x-x0)n,
(x-x0)n,
яка дає можливість для
наближеного знаходження значень функцій f(x).
.1 Тейлорова формула із
залишковим членом у формі Пеано
Доведемо, що
Rn(x)=o(x-x0)п ↔ 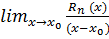
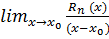 = 0.
= 0.
Згідно з визначенням многочлена
P n(x)
випливає, що
Rn (x0) =
Rn′ (x0) =
Rn″(x0) =…=
Rn(n)(x0) = 0.
Для обчислення границі 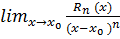
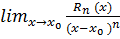 застосуємо правило Лопіталя n
разів і отримаємо:
застосуємо правило Лопіталя n
разів і отримаємо:
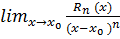
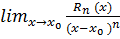 =
=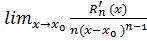
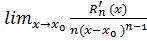 =…=
=…= 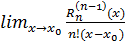
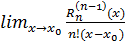 =
=
=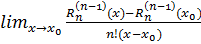
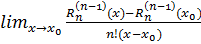 =
= 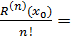
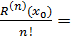 0
0
тобто Rn (x) = o(x-x0)n при
x→x0,
оскільки Rn (x) -
величина вищого порядку , чим (х - х0)п .■ Таким чином доведена теорема.
Теорема 1.
Якщо функція y=f(x)
означена на інтервалі
(a, b) і п
разів диференційована в околі точки х0, то правдива формула
f(x) = f(x0)
+ 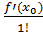
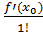 (x-x0) +
(x-x0) + 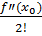
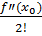 (x-x0)2
+…+
(x-x0)2
+…+ 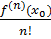
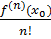 (x-x0) n +o(x-x0)n
(x-x0) n +o(x-x0)n
або можемо записати у
скороченій формі
f(x) = 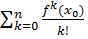
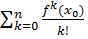 (x-x0)
k+
o(x-x0)n,
x→x0,
(7)
(x-x0)
k+
o(x-x0)n,
x→x0,
(7)
де Rn (x) = o(x-x0)n
-залишковий член у формулі Пеано [посилання 4].
Формула із залишковим членом
у формі Пеано носить локальний характер і тому її праву частину називають
асимптотичним представленням функції f в околі
точки
x0. Цю формулу
можна використовувати для наближених обчислень значень функції f в точках, наближених
до
точки
x0, оскільки
відомий порядок погрішності Rn(x) .
Відзначимо також, що формула
(7) вельми ефективна при відшуканні меж функцій.
Якщо в Тейлоровій формулі
покласти х0=0, дістанемо її окремий випадок - формулу Тейлора - Маклорена , яка
є асимптотичним представленням функції f в
околі 0.
f(x) = f(0)
+ 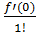
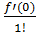 x +
x + 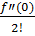
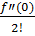 x 2
+…+
x 2
+…+ 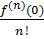
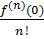 x n + o(x)n
x n + o(x)n
f(x) =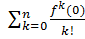
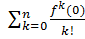 xk + o(xn). (8)
xk + o(xn). (8)
Ми отримали так звану формулу
Маклорена із залишковим членом у формі Лагранжа.
Слід зазначити, що при
розкладанні функції в ряд, вживання формули Маклорена переважає, чим вживання
безпосередньо формули Тейлора, оскільки обчислення значень похідних в нулі
простіше, ніж в якій-небудь іншій точці, звичайно, за умови, що ці похідні
існують.
.2.Тейлорова формула із
залишковим членом у Лагранжовій формі
Існують різні форми запису
залишкового члена Rn (x)
Тейлорової формули. У наближених обчисленнях зручною є Лагранжова форма
залишкового члену.
Теорема 2.
Якщо функція y = f(x)
означена й (n+1) разів
диференційована в околі точки х0, то виконується формула
f(x) = f(x0) + 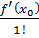
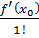 (
x-x0) +
(
x-x0) + 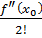
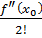 (x-x0)2
+…+
(x-x0)2
+…+ 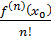
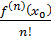 (x-x0) n+
Rn(x),
(x-x0) n+
Rn(x),
де Rn(x) =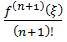
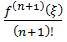 (x-x0)n+1-залишковий
член у Лагранжовій формі.
(x-x0)n+1-залишковий
член у Лагранжовій формі.
Доведення теореми 2 див.
(додаток 2).
.3 Тейлорова формула для
многочлена
Нехай задано многочлен
Pn(x)=b0+b1x+…+bnxn.
Для будь-якого х0 цей
многочлен можна зобразити як суму степенів різниці
х-х0 , узятих з деякими
коефіцієнтами. Покладемо
х=х0+t
Тоді Pn(x)=Pn(x 0+t)=b0+b1(x0+t)+…+bn(x0+t)n.
Розкриваючи у правій частині
дужки і групуючи подібні члени, одержимо
Pn(x)=A0+A1t+A2t2+…+Antn 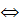
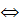
Pn(x)=A0+A1(x-x0)+A2(x-x0)2+…+An(x-x0)n.
Вираз справа - буде
Тейлоровим многочленом за степенями (х-х0) для многочлена Pn(x)
степеня п. Отже,
Ak = 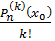
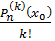 , k = 0, n; Rn(x) = 0;(x) = Pn (x0) +
, k = 0, n; Rn(x) = 0;(x) = Pn (x0) + 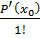
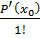 ( x-x0) +
( x-x0) + 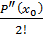
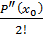 (x-x0)2
+…+
(x-x0)2
+…+ 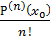
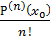 (x-x0)n.
(x-x0)n.
.4 Тейлорова формула в
диференціальній формі
Покладаючи х - х0 = ∆
х, х = х0 + ∆ х у Тейлоровій формулі
f(x) = f(x0) + 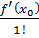
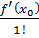 (
x-x0) +
(
x-x0) + 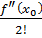
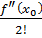 (x-x0)2
+…+
(x-x0)2
+…+ 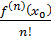
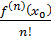 (x-x0) n+
Rn(x),(x0
+∆х)
=
f(x0) +
(x-x0) n+
Rn(x),(x0
+∆х)
=
f(x0) + 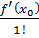
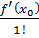 ∆х +
∆х + 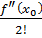
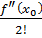 ∆х
2 +…+
∆х
2 +…+ 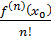
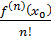 ∆х n+ Rn(x).
∆х n+ Rn(x).
Оскільки
f(x0 +∆х)
- f(x0)= ∆
f(x0),
f(n) (x0) ∆xn =dn f(x0),
то Тейлорову формулу п-го
порядку функції f можна записати у диференціальній
формі
∆f(x0)=df(x0) +
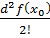
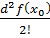 +
+ 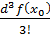
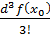 + . . .+
+ . . .+ 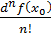
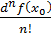 + Rn(x).
+ Rn(x).
.5 Формула Тейлора із
залишковим членом в інтегральній формі
Теорема 3.
Нехай функція f має
безперервну похідну (п+1)-го порядку в інтервалі
(х0-h, x0+h),
де h>0.
Тоді залишковий член Rn для x є (x0-h, x0+h)
може бути записаним в вигляді:
Rn (x )= 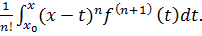
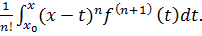 (9)
(9)
Формула (9)
називається залишковим членом формули Тейлора в інтегральній формі.
Доведення теореми 3 див.
(додаток 3).
4. РОЗВИНЕННЯ ДЕЯКИХ ЕЛЕМЕНТАРНИХ
ФУНКЦІЙ ЗА ФОРМУЛОЙ ТЕЙЛОРА
Вживання формули Тейлора для
розкладання функцій в степеневий ряд широко використовується і має величезне
значення при проведенні різних математичних розрахунків. Безпосереднє обчислення
інтегралів деяких функцій може бути зв'язане із значними труднощами, а заміна
функції степеневим рядом дозволяє значно спростити завдання. Знаходження
значень тригонометричних, зворотних тригонометричних, логарифмічних функцій
також може бути зведене до знаходження значень відповідних многочленів.
Якщо при розкладанні в ряд взяти
достатню кількість доданків, то значення функції може бути знайдене з будь-якою
наперед заданою точністю. Практично можна сказати, що для знаходження значення
будь-якої функції з розумною мірою точності (передбачається, що точність, яка
перевищує 10 - 20 знаків після десяткової коми, необхідна дуже рідко) достатньо
4-10 члени розкладання в ряд.
Знайдемо розклад за формулою Тейлора
при х0=0 (точніше за формулою Маклорена) функцій ех, sin
x, cos
x, ln(1+x),
(1+x)a
[посилання 5].
.1 Розвинення функції f(x)
= ex
f(x)
= eх, f(0)=1,
f′
′(x)
= eх f′
′(0) =1,
…………. ……………
f
(n)(x)
= eх f
(n)(0) =1,
f
(n+1)(x)
= eх f
(n+1)(Ѳx)
=eѲx,
Підставляючи одержані значення f(0),
f′ ′(0),…,
f (n)(0),
f (n+1)(Ѳx)у
формулу Тейлора-Маклорена із залишковим членом у Лагранжовій формі, дістаємо
ex=1+x+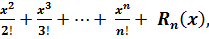
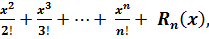
Rn(x)=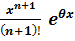
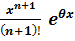
де 0<Ѳ<1.
Зауважимо, що для будь-якого
х:
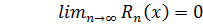
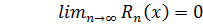 .
.
.2 Розвинення функції f(x) = sin x.
Функція f(x) = sin x
нескінченно диференційована на R. Знайдемо
послідовні похідні від f(x) = sin x:
а потім цикл знову
повторяється. Тому при підстановці х0 = 0 також виникає повторення:
f(x) = sin x, f(0)=0,
f′
′(x) = cos x=sin(x+
 ), f′
′(0) =1,
), f′
′(0) =1,
f ″
(x)= -sin x= sin(x+2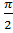
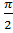 ), f ″
(x)=0,
), f ″
(x)=0,
f ‴(x)= -cos x=sin(x+3 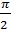
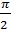 ), f ‴(x)=-1,
), f ‴(x)=-1,
…………… …………
f (n)(x) = sin (x+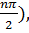
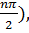 f (n)(0)
=sin
f (n)(0)
=sin 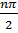
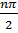 ,
,
f (n+1)(x) = sin(x+(n+1)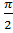
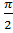 ), f (n+1)(Ѳx)=sin
(Ѳx+(n+1)
), f (n+1)(Ѳx)=sin
(Ѳx+(n+1)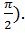
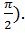 Отже,
Отже,
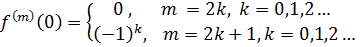
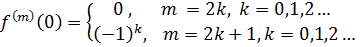
У Тейлоровому многочлені для sin x
рівні нулеві коефіцієнти при парних степенях х, так що многочлен степеня (2п+1)
та степеня (2п) збігаються.
Підставляючи знайдені
значення похідних у формулу Тейлора-Маклорена, дістаємо
sin x = x - 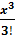
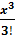 +
+ 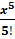
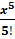 +
+ 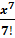
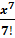 + …+ (-1)2 k-1
+ …+ (-1)2 k-1 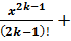
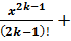 R2k-1 (x),
R2k-1 (x),
R2k+1(x)=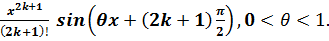
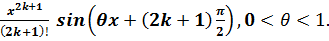
У цьому випадку, як і в
попередньому, при усіх значеннях х:
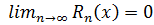
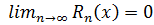 .
.
.3 Розвинення функції f(x) = cos x
Оскільки (cos x)(n) = cos (x+n 
 ), то
), то
f(m)(0)=cos 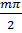
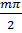 =
= 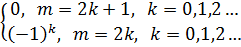
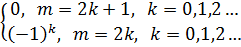
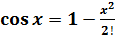
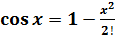 +
+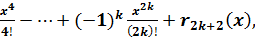
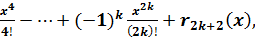
R2k+2= 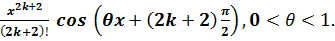
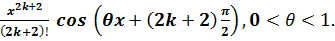
.4 Розвинення функції f(x)=ln(1+ x)
Функція f(x)=ln(1+x)
означена і нескінченно диференційована в інтервалі (-1;+∞). Знайдімо
послідовні похідні цієї функції
f(x)=ln(1+x), f(0)=0,
f ′(x) = 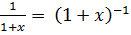
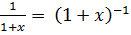 , f ′(0)=1,
, f ′(0)=1,
f ″(x) = 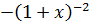
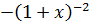 , f ″(0)=
-1,
, f ″(0)=
-1,
f ‴(x)=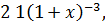
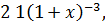 f ‴(0)=
2 1,
f ‴(0)=
2 1,
………………….. ………………
f (n)(x) =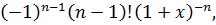
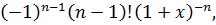 f (n)(0)
=
f (n)(0)
=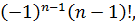
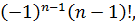
f (n+1)(x)=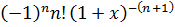
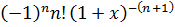 , f (n+1)(
, f (n+1)(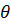
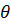 x)=
x)=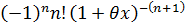
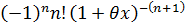 ,
,
Підставляючи обчислені
значення у формулі Тейлора-Маклорена, дістаємо розвинення ln(1+x)за
формулою Тейлора-Маклорена із залишковим членом у Лагранжовій формі:
ln(1+x) = x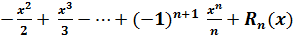
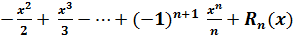 ,
,
Rn(x)=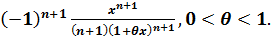
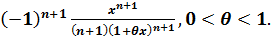
.5 Розвинення функції
f(x)=(1+x)α
Функція f(x)=(1+x)α ,αϵR,
означена і нескінченно диференційована в інтервалі (-1;1). Знайдемо послідовно
похідні від функції f(x)=(1+x)α.
(x)=(1+x)α,
f ′(x)=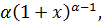
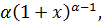
f ″(x)=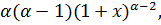
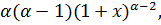
f ‴(x)=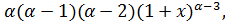
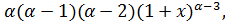
…………………………………
f(n)(x)=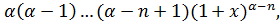
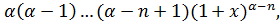
f(n+1)(x) =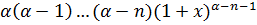
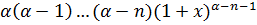 ,
,
f(0)=1,
f ′(0)=α ,
f ″(0)=α(α-1),
f ‴(0)=
α(α-1)(α-2),
…………………
f(n)(0)=
α(α-1)…(α-n+1),
f(n+1)(Ѳx)= α(α-1)…(α-n)(1+
Ѳx)α-n-1
Підставляючи знайдені
значення функції та її похідні у формулу Тейлора-Маклорена, дістаємо:
(1+x)a=1+αx + 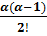
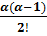 x2 +…+
x2 +…+ 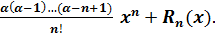
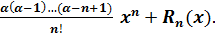
Rn(x)= 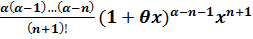
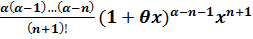
Якщо α=mϵN, то
всі члени формули Тейлора-Маклорена, починаючи з
(т+1)-го зникають, і формула
Тейлора-Маклорена перетворюється на відому формулу Ньютонового бінома.
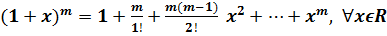
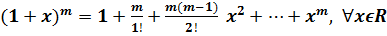
5.
ЗАСТОСУВАННЯ ФОРМУЛИ ТЕЙЛОРА
. Формули Тейлора-Маклорена
із залишковим членом у формі Пеано є джерелом асимптотичних формул.
Приміром, для функції f(x) = ex
маємо:
ex =
1+ 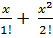
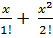 + o(x2),
+ o(x2),
ex =
1+ 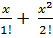
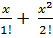 +
+ 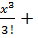
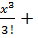 o(x3).
o(x3).
Використаємо ці формули до
обчислення границі:
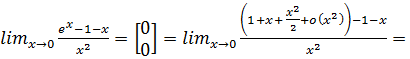
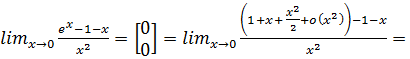
= 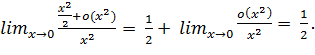
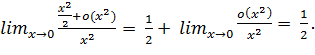
. Формулу
Тейлора за степенями (х - х0) із залишковим членом у формі Лагранжа застосовують
для обчислення наближених значень функції в
околі U (x0)х[посилання
6].
Значення f(x) в
околі U (x0)
обчислюють за формулою
f(x) ≈
f(x0) +
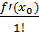
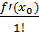 ( x-x0) +
( x-x0) +
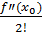
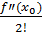 (x-x0)2
+…+
(x-x0)2
+…+ 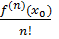
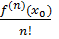 (x-x0)n
(x-x0)n
похибка наближення не
перевищує
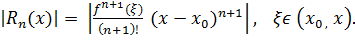
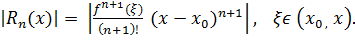
ВИСНОВОК
В даній роботі розглянуто формулу
Тейлора. Ми за допомогою різних функції вивели формулу Тейлора, як потужного
математичного інструменту дослідження функцій, обчислення границь і наближеного
значення функції. А також всі її залишкові члени, за допомогою яких можемо
розкладати елементарні функції , наприклад, ех, sin
x, cos
x, ln(1+x),
(1+x)a.
Для чого нам не потрібно знаходити 10-20 знаків після коми, а достатньо лише
4-10 членів розкладання в ряд. Також підтверджено, що такими формулами можливо
і зручно користуватися практично (для учнів шкіл та вищих навчальних закладів )
у розрахунках , що не вимагають дуже високої точності.
А також в цій роботі наведенні
приклади, які розв’язуються
за допомогою елементарних функцій.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
формула тейлор многочлен
1. Бугров
Я.
С. , Никольский С. М.;
Высшая математика: Учеб. для вузов: В 3 т. / под
ред. В. А. Садовничего. - 6-е изд., стереотип. - М.: Дрофа, 2004. - Т. 2:
Дифференциальное и интегральное исчисление. - 512 c.
2. Електронний ресурс: Біографія Тейлора:
<#"877849.files/image081.gif">х
Як видно з малюнка Rп
( x
) має погрішність, що виникає при заміні функції
у = f
( x
) многочленом Pп ( x
). Для
значень
х
з околу точки x0
,
для яких погрішність Rп
( x ) досить мала, многочлен Pп
(x) дає наближене
представлення функції.
ДОДАТОК 2.
Доведення теореми 2.
Вимагатимемо, щоб функція
f мала
похідну
(n+1)
-го порядку в околі точки x0.
Розгляньмо функцію g(x)=(x
- x0)n+1
. Очевидно, що
g(x0)
= g′(x0)
= …= g(n)(x0)
= 0,
g(n+1)(x0)
= (n+1)! ≠ 0.
Застосуймо до функції Rn(x)
та g(x)
= (x - x0)n+1
теорему Коші. Тоді на підставі умови
R′n(x0)
= R″n(x0)
= …= Rn(n)(x0)
= 0
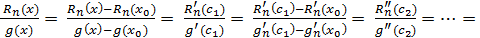
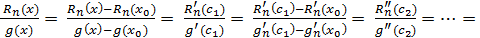
= 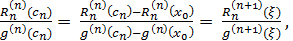
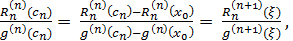
де c1 ϵ (x0 , x); c2 ϵ (x0 ,c1) ,
… , cn ϵ (x0, cn-1) ;
ξ ϵ (x0 , cn).
Отже, показано, що
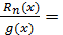
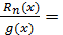
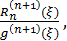
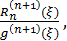 ξ ϵ (x0 ,
х).
ξ ϵ (x0 ,
х).
З урахуванням того, що
g(x) =
(x - x0)n+1 ,
g(n+1)
(ξ) =
(n+!)!,
Rn(n)(ξ)
= f (n+1)
(ξ),
дістаємо залишковий член у
Лагранжовій формі
Rn( x) = 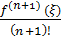
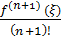 (x - x0)n+1 ,
ξ
ϵ (x0 ,
х).
(x - x0)n+1 ,
ξ
ϵ (x0 ,
х).
Оскілки ξ ϵ (x0 ,
х), то ξ
можна зобразити у вигляді
ξ = x0 + 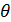
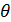 (x - x0) , 0<
(x - x0) , 0<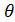
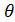 < 1,
< 1,
тобто залишковий член у
Лагранжовій формі можна записати у вигляді
Rn(x) = 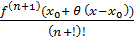
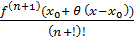 (x - x0)n+1.
(x - x0)n+1.
ДОДАТОК 3.
Доведення теореми 3.
Так як f(x) - f(x0) = 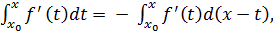
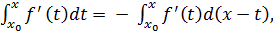
то, інтегруючи за частинами,
отримаємо
f(x) - f(x0) = --f 
 (t) (x-t)|xx0 +
(t) (x-t)|xx0 + 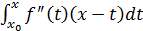
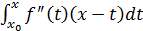 =
=
= f ′(x0)(x-x0) + 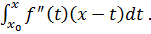
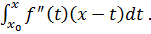
Нехай для деякого m ≤ n вже
доведено, що
f(x) - f(x0)= 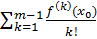
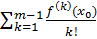 (x-x0)k +
(x-x0)k + 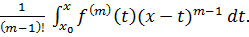
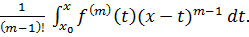 (9)
(9)
Інтегруючи за частинами
останній доданок, бачимо, що
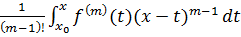
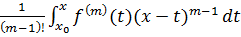 = -
= -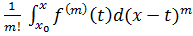
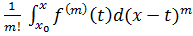 =
=
= - 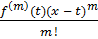
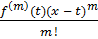 |xx0 +
|xx0 + 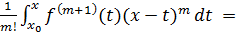
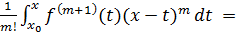
= 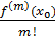
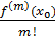 (x - x0)m +
(x - x0)m + 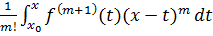
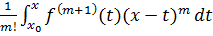 .
.
Підставляючи
цей вираз
в (9) ,
отримуємо ту ж саму формулу з заміною m на m+1 . Таким чином,
формула (9)
доведена
по індукції для всіх
m ≤ n. При
т=п вона приводиться до співвідношення (8).