Выпуклые множества и выпуклые функционалы. Функционал Минковского. Теорема Хана-Банаха
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ РФ (МИИТ)
Институт управления и информационных
технологий
Кафедра «Прикладная математика-1»
Курсовая работа по дисциплине
«Функциональному анализу»
на тему:
«Выпуклые множества и выпуклые функционалы.
Функционал Минковского. Теорема Хана-Банаха»
Выполнила:
студентка группы УПМ-311
Гафарова
Сабина
Проверил:
проф. Гапошкин В.Ф.
Москва 2015
СОДЕРЖАНИЕ
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.Выпуклые
множества
2.Выпуклый
функционал
3. Функционал
Минковского
4. Теорема
Хана-Банаха
2. ПРАКТИЧЕСКАЯ ЧАСТЬ
СПИСОК
ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. Выпуклые
множества
Пусть X-линейное вещественное пространство.
Определение 1.1. Множество C 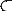 X называется выпуклым, если вместе с любыми двумя своими
точками x(1) и x(2) оно содержит и весь отрезок. (т.е. ρ(x(1), x(2)))
X называется выпуклым, если вместе с любыми двумя своими
точками x(1) и x(2) оно содержит и весь отрезок. (т.е. ρ(x(1), x(2)))
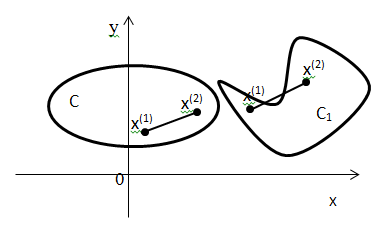
На рисунке изображены 2 множества на плоскости R2 C-выпуклое, а С1-нет.
Совокупность всех выпуклых множеств из линейного пространства X обозначается - CONV(X)
Рассмотрим множество С, такое, что С - множество точек, а x - любая фиксированная точка этого
пространства. Расстояние от x до С
обозначим ρ(x, С).
Тогда ρ(x, С)
- есть точная нижняя грань расстояний от х до всевозможных точек С. (если C  Еm, Еm
- m-мерное Евклидовое пространство).
Итак, получаем:
Еm, Еm
- m-мерное Евклидовое пространство).
Итак, получаем:
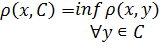
Множество ρ(x,y) всегда
ограничено снизу, для любого y∊С, ρ(x,y)=0.
Лемма: Пусть С - замкнутое множество из рефлексивного банахового пространства X
и пусть для любых x1, x2 ∈ C существует число α
= α(x1, x2) ∈[0, 1], вообще говоря, зависящее от x1
и x2, и такое, что:
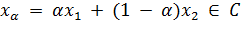
Тогда множество С - выпукло.
Доказательство: 1) Допустим, противное, т.е. множество C невыпукло. Тогда
найдутся точки x1, x2 ∈ C, x1 ≠ x2
и число α0 ∈[0, 1] такие, что:
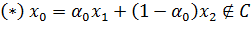
Положим
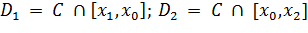
Эти множества замкнуты (т.к. пересечение замкнутых множеств), причем x0∉Di, i=1,2, поскольку x0∉C.
Кроме того, они очевидно ограничены.
) Далее, из свойств рефлексивного банахова пространства вытекает, что
существуют элементы z1 ∈ D1 и z2 ∈ D2 такие, что:
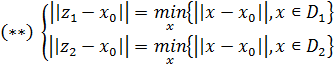
Из построения D1 и D2 следует, что, в частности, zi ∈ C, i = 1, 2.
) При этом на полуинтервалах (z1, x0] и [x0,
z2) нет точек из C (в соответствие с (**)). Так что: (z1,x0)∩C=ᴓ ; (x0,z2)∩C=ᴓ
Таким образом, z1, z2 ∈ C, но внутри отрезка [z1,
z2] нет ни одной точки из C, что противоречит условию (*). Следовательно, множество C
выпукло.
Определение 1.2. Пересечение всевозможных выпуклых множеств С, содержит данное
множество М, называется выпуклой оболочкой множества М и обозначается:
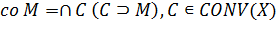
Определение 1.3. Пусть x1,…,xn - элементы пространства X. Тогда вектор  - называется линейной оболочкой или
выпуклой комбинацией x1,…,xn, если в (1.2) соответственно:
- называется линейной оболочкой или
выпуклой комбинацией x1,…,xn, если в (1.2) соответственно:
а) 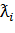 - любые действительные числа.
- любые действительные числа.
б) 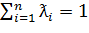
c)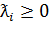
d)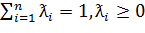
Другими словами, для выпуклого множества С, в частности, имеем:
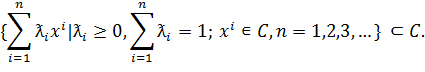
Где векторы x1,x2,…,xn∊X.
Рассмотрим теперь произвольное множество M ⊂ X.
Свойство 1.1. Выпуклая оболочка множества М состоит из всех выпуклых
комбинаций элементов из М.
Доказательство: Рассмотрим выпуклую оболочку М.
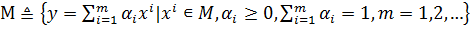 - множество всех выпуклых комбинаций точек из М. Покажем,
что М⊂М.
- множество всех выпуклых комбинаций точек из М. Покажем,
что М⊂М.
Пусть 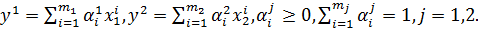 Тогда для ƛ∊[0;1] выпуклая комбинация точек y1 и y2
Тогда для ƛ∊[0;1] выпуклая комбинация точек y1 и y2
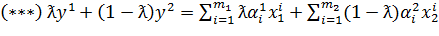 , а эта последняя сумма из (***) является выпуклой
комбинацией точек
, а эта последняя сумма из (***) является выпуклой
комбинацией точек 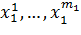 ;
; 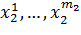 поскольку имеет место цепочка равенств:
поскольку имеет место цепочка равенств:
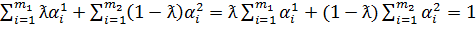 итак, М⊂М и М - выпукло. Следовательно, co M⊂ M.
итак, М⊂М и М - выпукло. Следовательно, co M⊂ M.
С другой стороны, если y⊂М, то y
является выпуклой комбинацией точек из М, и поэтому М=co M.
Свойство 1.1. Множество М выпукло тогда и только тогда, когда оно совпадает
со своей выпуклой оболочкой.
Значит, всякая точка из co М
может быть представлена в виде выпуклой комбинации некоторого конечного числа
точек (которое может быть достаточно большим).
2. Выпуклый
функционал
Определение 2.1. Выпуклым функционалом называется функционал, определенный на
векторном линейном пространстве и обладающий тем свойством, что его надграфик
является выпуклым множеством.
Функционал f, не принимающий
значений, равных -∞ на выпуклом множестве M, будет выпуклым на M тогда и только тогда, когда выполняется:
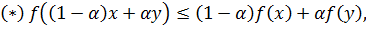

При обратном знаке неравенства функционал f называется вогнутым.
Примерами выпуклых функционалов является:
♦ норма;
♦ полунорма;
♦ линейный функционал;
♦ функционал Минковского выпуклого и симметричного множества;
Пусть функционалы f и g - определены на множестве М. f,g - выпуклые функционалы. Введем число α,
такое что α
> 0. Операции:
Сложение: 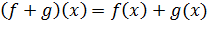
Умножение: 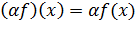
Взятие верхней грани: 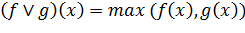
Инфимальная конволюция: 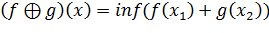
Выпуклый функционал, ограниченный сверху в окрестности некоторой точки х,
является непрерывным в этой точке. Если выпуклый функционал конечен в некоторой
точке х, то он имеет производную по любому направлению (конечную или
бесконечную) в этой точке. Замкнутые выпуклые функционалы (т. е. функционалы с
выпуклыми и замкнутыми надграфиками) в локально выпуклых линейных
топологических пространствах допускают двойственное описание: они являются
верхними гранями аффинных функций, их не превосходящих. Такая двойственность
позволяет связать с каждым выпуклым функционалом двойственный объект,
сопряженный функционал:
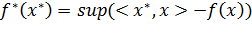
Функционал - f заданный на
выпуклом множестве М, называется строго выпуклым, если неравенство (*) перейдет
в строгий вид, при этом x ≠ y,
α∊(0;1).
Свойства строго выпуклых функционалов.
Строго выпуклый функционал имеет не более одной точки локального минимум
в М и ни одной точки локального максимума. Точки глобального максимума строго
выпуклого функционала, определенного на выпуклом компакте, лежат на границе
этого компакта. Глобальный минимум функционала f имеет в стационарной точке (если она существует).
3. Функционал Минковского
В функциональном анализе, функционал Минковского использует
линейную структуру пространства для введения топологии на нём.
Для любого векторного пространства X (вещественного
или комплексного) и его подмножества М определим функционал Минковского.
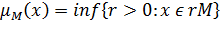
(предполагается, что 0∊M и множество {r>0|
x∊ rM} непустое).
• Если M - выпукло и симметрично, то:
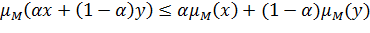
• Если M - сбалансированное множество, то
есть αM⊂M для ∀α,
|α|<1.
Свойство 3.1. Функционал Минковского неотрицателен и сублинейнен.
Свойство 3.2. Справедливы следующие включения:
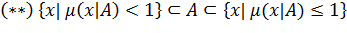
Свойство 3.3. Если X -
линейное топологическое пространство, то μ(x|A) - непрервна в точке 0 тогда и только тогда, когда 0∊inf A.
Доказательство:
.1.
Если μ(x|A) или μ(y|A) < +∞, по определению точной нижней грани ∀ε>0,∃t и ∃s такие, что:
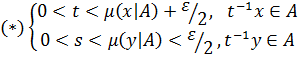
В силу выпуклости A:
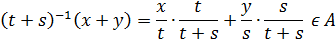
Поскольку  , то в силу (*):
, то в силу (*):
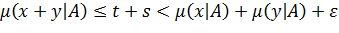
так как ε >0 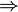
 и
и 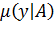 - суббадитивны.
- суббадитивны.
Для α >0, имеем:
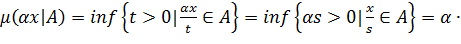
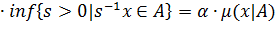
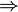
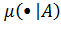 - положительно однородный.
- положительно однородный.
Таким образом 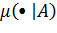 - является сублинейным. Не отрицательность функционала
Минковского следует из определения.
- является сублинейным. Не отрицательность функционала
Минковского следует из определения.
3.2. Если x ∊ A, то очевидно 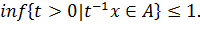 Поэтому включение очевидно. Пусть теперь x таково, что μ(x|A)<1. Тогда ∃t ∊ (0;1), такое, что
Поэтому включение очевидно. Пусть теперь x таково, что μ(x|A)<1. Тогда ∃t ∊ (0;1), такое, что 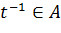 . Так как 0 ∊ A и A
выпукло, то
. Так как 0 ∊ A и A
выпукло, то
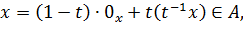
так что и первое включение в (**) также выполнено.
3.3. Пусть X - линейное топологическое
пространство. Тогда μ(x|A) непрерывен в 0
в том и только в том случае, когда:
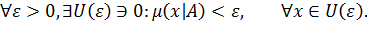
Рассмотрим окрестность U1:U(ε)=εU1. Тогда ввиду положительной однородности μ(x|A) из предыдущего
неравенства, будем иметь:
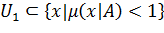 . Следовательно, из 3.2. будем иметь U1⊂ A, а U -
окрестность нуля.
. Следовательно, из 3.2. будем иметь U1⊂ A, а U -
окрестность нуля.
Свойство 3.4. пусть X*- множество линейных функционалов на X. Для того, чтобы функционал x*∊ X* на линейном топологическом пространстве X был непрерывен, необходимо и
достаточно, чтобы существовала сублинейная функция, непрерывная в нуле. p(x), мажорирующая x*:
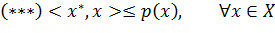
Доказательство:
1) Необходимость устанавливается непосредственно, если положить p(x)=|<x*,x>|.
) Достаточность. Пусть (***) - верна, где p(x) сублинейная и
непрерывная функция в нуле. Тогда ∀ε>0, ∃Uε 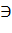 0 такая, что:
0 такая, что:
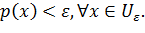
Поскольку 0∊Uε и 0=(-0)∊(-Uε), то ∃ окрестность нуля W такая, что 0 ∊W⊂ ⊂ Uε∩(-Uε). Если x ∊W, то x ∊ Uε и (-x) ∊W, т.е. функционал x*непрерывен
в нуле. Остается заметить, что линейный функционал, непрерывный в одной точке,
непрерывен на X.
4. Теорема Хана-Банаха
Теорема 4.1. Пусть L -
действительное линейное пространство и L0 - некоторое подпространство L. f0 - некоторый линейный функционал и
пусть он задан на L0. Линейный функционал f - определен на всем пространстве L. f - продолжение функционала, если f(x)=f0(x), ∀x ∊ L0.
Теорема 4.2. Пусть p -
однородный выпуклый функционал, определенный на действительном линейном
пространстве L, и пусть L0 - линейное пространство в L. Если f0 - линейный функционал на L0, подчиненный функционалу p(x) на L0 т.е. если на L0 f0(x)≤ p(x), то f0.может быть продолжен до линейного функционала f на L, подчиненного p(x) на всем L.
Доказательство: Покажем, что если L0≠ L, то функционал f0 можно продолжить с L0 на некоторое большое подпространство L’ с сохранением условия f0(x)≤
p(x). Действительно, пусть z - произвольный элемент из L, z ∉ L0 и L’ -
подпространство, порожденное L0
и z. Кждый элемент из L’ имеет вид: 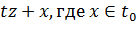 .
.
Если f’ - искомое продолжение функционала f0 на L’, то
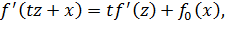 или, если положить
или, если положить 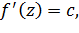
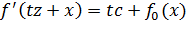 .
.
Теперь выбираем c так,
чтобы сохранить на L’ условие
подчинения f0(x)≤
p(x), т.е. ∀x ∊ L0 и ∀t (A -
действительное) выполнялось: f0(x)+tc≤ p(x+tz). При t > 0 оно равносильно: 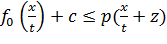 , или
, или 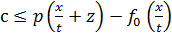 , а при t > 0:
, а при t > 0: 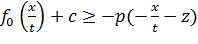 или
или 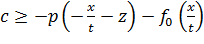 .
.
Покажем, что всегда ∃c, удовлетворяющее этим двум условиям. Пусть 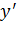 и
и 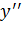 - произвольные элементы из L0, тогда:
- произвольные элементы из L0, тогда:
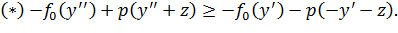
Это вытекает из неравенства:
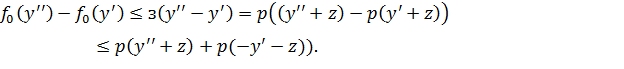
Положим 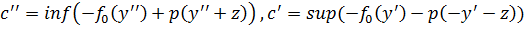 . Из (*)
. Из (*) 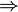
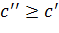 , т.к.
, т.к. 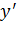 и
и 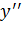 - произвольные. Выбрав c такое, что
- произвольные. Выбрав c такое, что 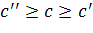 , определим
, определим 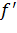 на
на 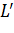 формулой
формулой 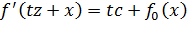 . Этот функционал удовлетворяет условиям
. Этот функционал удовлетворяет условиям 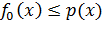 , ∀x ∊ L0.
, ∀x ∊ L0.
Итак, мы показали, что 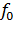 - определен на некотором подпространстве L0⊂ L и удовлетворяет на L0 условию
подчинения. Значит
- определен на некотором подпространстве L0⊂ L и удовлетворяет на L0 условию
подчинения. Значит 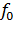 - можно продлить (с сохранением условия) на некоторое
большое подпространство
- можно продлить (с сохранением условия) на некоторое
большое подпространство  .
.
Если в L можно выбрать счетную систему
элементов x1,x2,…,xn,…, порождающую все L, то функционал на L строим по индукции, рассматривая
возрастающую цепочку подпространств:
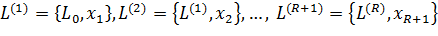 - минимальное линейное подпространство L, содержащие
- минимальное линейное подпространство L, содержащие 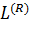 и
и 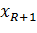 . Так как каждый элемент x ∊ L. В общем случае, когда счётного множества порождающего L не существует по Лемме Цорна.
. Так как каждый элемент x ∊ L. В общем случае, когда счётного множества порождающего L не существует по Лемме Цорна.
Теоремы отделимости.
Пусть X - линейное топологическое пространство, X* -
сопряженное к нему.
Определение 4.1. Говорят, что функционал x* ∈ X* разделяет множества A и B, A ⊂ X, B ⊂ X, если существует γ
∈ R, такое что
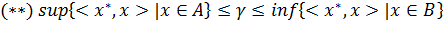
и строго разделяет A и B, если существует такое γ,
что:
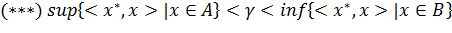
Геометрически неравенство (**)
означает, что гиперплоскость
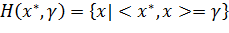
отделяет множества A и B друг от друга в том смысле, что A лежит в одном
полупространстве
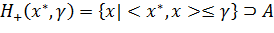
а B - в другом
Неравенство же (***) означает, что при этом γ
можно выбрать таким
образом, чтобы A и B лежали внутри соответствующих полупространств и не имели
общих точек с H(x*,
γ).
Теорема 4.3.( об отделимости)
Пусть A и B - выпуклые непустые подмножества пространства X, int A ≠
∅ и, кроме того,
(♦) int A ∩ B = ∅.
Тогда существует нетривиальный функционал x* ∈ X*, разделяющий A и B.
Доказательство:
а) Поскольку int A ≠ ∅ и B ≠ ∅ то существуют a0 ∈ int A и b0 ∈ B. Тогда множество
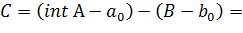
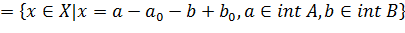
является непустым выпуклым множеством, содержащим 0.
Покажем, что это множество открыто. Действительно, пусть x ∈ C. Тогда x = a - a0 −
b + b0, a ∈ int A, b ∈ B. Поэтому существует окрестность U = U(a) точки a
такая, что U ⊂ int A. Тогда x ∈ V = U - a0 − b + b0 ⊂ C.) Кроме того, точка c = b0−a0
∉ C. Действительно, в противном случае
существовали бы точки a ∈ int A и b ∈ B, для которых b0 − a0= a
− a0− b + b0 ∈ C.
Отсюда a − b = 0 или a
= b ∈ (int A) ∩ B, что противоречит (♦).)
Обозначим через p(x) функцию Минковского множества C. Тогда p(x) - сублинейная
и непрерывная в точке 0 функция. Кроме того, p(x) ≤ 1 для любого x ∈ C.) На подпространстве
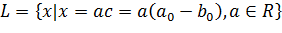
определим функционал l(·) по
правилу:
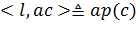
Покажем, что l(·) - линейный
функционал. Действительно,
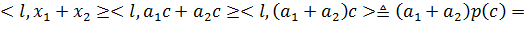
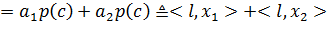
Покажем теперь, что
функционал l(·) мажорируется функцией Минковского p(·) множества C.
Если α > 0, то <l, αc> = αp(c) = p(αc). Если же α ≤
0, то, поскольку p(c) ≥ 0 <l, αc> = αp(c) ≤
0 ≤ p(αc).
Таким образом, <l, x> ≤
p(x) ∀x ∈ L. Тогда
по теореме Хана- Банаха l(·) можно продолжить до линейного функционала Λ ⊂ X:
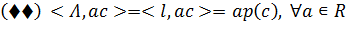 .
.
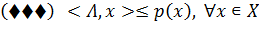 .
.
Поскольку p(·) непрерывна в
нуле, то из (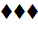 ) следует непрерывность функционала Λ (из <x*, x> ≤ p(x) ∀ x ∈ X.) и Λ ⊂ X*.) Для любого a ∈ int A и для любого b ∈ B имеем: <Λ, a - b> = <Λ, a - a0 −
b + b0>
+ <Λ, a0 - b0> (
) следует непрерывность функционала Λ (из <x*, x> ≤ p(x) ∀ x ∈ X.) и Λ ⊂ X*.) Для любого a ∈ int A и для любого b ∈ B имеем: <Λ, a - b> = <Λ, a - a0 −
b + b0>
+ <Λ, a0 - b0> ( ),(
),( ) ≤ ≤ p(a - a0 − b + b0)
− <l, a0 - b0> (
) ≤ ≤ p(a - a0 − b + b0)
− <l, a0 - b0> ( ) ≤ 1 − p(b0− a0),
поскольку (a - a0 − b + b0) ∈ C. Итак, для любого a ∈ int A и для любого b ∈ B.
) ≤ 1 − p(b0− a0),
поскольку (a - a0 − b + b0) ∈ C. Итак, для любого a ∈ int A и для любого b ∈ B.
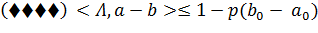
) Покажем теперь, что для
любого t из полуинтервала (0, 1] точка 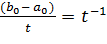 c не
может принадлежать C. В самом деле, если бы такое включение имело место, то,
поскольку 0 ∈ C и C выпукло, мы бы получили:
c не
может принадлежать C. В самом деле, если бы такое включение имело место, то,
поскольку 0 ∈ C и C выпукло, мы бы получили: 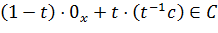 . Что невозможно, поэтому:
. Что невозможно, поэтому:
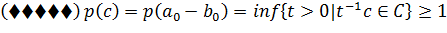
Тогда из (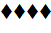 ) следует, что для любых a ∈ int A и b ∈
B <
Λ, a-b> ≤ 1- p(
) следует, что для любых a ∈ int A и b ∈
B <
Λ, a-b> ≤ 1- p(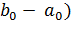 ≤ 0. Поскольку в полученном неравенстве:
≤ 0. Поскольку в полученном неравенстве: 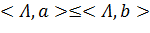 , a ∈ int A, b ∈ B переменные a и b независимы, то:
, a ∈ int A, b ∈ B переменные a и b независимы, то:
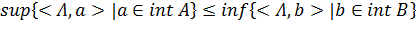 . Учитывая,
что:
. Учитывая,
что:
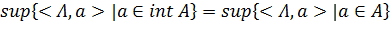 . получаем
требуемое.
. получаем
требуемое.
Кроме того, из ( ) и (
) и ( ):
):
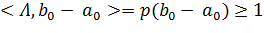 . так что Λ ≠ 0. Таким образом, Λ
нетривиален и разделяет
A и B.
. так что Λ ≠ 0. Таким образом, Λ
нетривиален и разделяет
A и B.
Теорема 4.4.( об отделимости)
Пусть X - локально выпуклое топологическое пространство, A - непустое
замкнутое выпуклое подмножество X, и существует точка z ∈ X, не принадлежащая A. Тогда
множество A и точка z строго разделимы.
Доказательство:
Поскольку z ∉ A и A замкнуто, то существует окрестность U = U(z) точки z
такая, что A ∩ U = ∅. Ввиду локальной выпуклости X эту окрестность можно считать
выпуклой. Тогда (по теореме 4.3) отделимости существует ненулевой функционал x*,
разделяющий A и U. Другими словами:
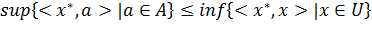
Остается заметить, что: 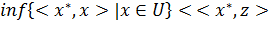 , поскольку нижняя грань ненулевого линейного функционала не
может достигаться во внутренней точке выпуклого множества.
, поскольку нижняя грань ненулевого линейного функционала не
может достигаться во внутренней точке выпуклого множества.
2. ПРАКТИЧЕСКАЯ ЧАСТЬ
Исходя из изложенного теоретического курса (в 1 части), мною были решены
следующие задачи:
Пример 1. В пространстве R2 с элементами 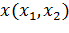 на подпространстве
на подпространстве
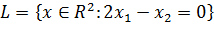 задан линейный функционал
задан линейный функционал  . Доказать, что существует
единственное продолжение f на
все R2 с сохранением нормы и найти это продолжение.
. Доказать, что существует
единственное продолжение f на
все R2 с сохранением нормы и найти это продолжение.
Решение:
По теореме Хана-Банаха для всякого ограниченного линейного функционала f, заданного на подпространстве L, существует его продолжение на все X с сохранением нормы. В пространстве R2
линейный ограниченный функционал имеет вид 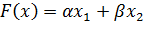 , тогда на подпространстве L, где
, тогда на подпространстве L, где 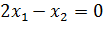 , имеем
, имеем 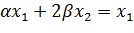 . Поскольку мы строим продолжение с
сохранением нормы, то
. Поскольку мы строим продолжение с
сохранением нормы, то
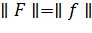 .
. 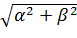 (по теореме Рисса). Вычислим
(по теореме Рисса). Вычислим 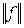 . Покажем, что в R2
задана, Евклидова норма, тогда на подпространстве L:
. Покажем, что в R2
задана, Евклидова норма, тогда на подпространстве L:
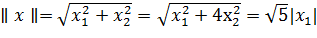 , а
, а 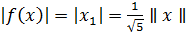
т.е. ; Итак
; Итак 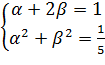 ; Систем имеет единственное решение:
; Систем имеет единственное решение:
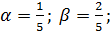 Значит и продолжение единственно:
Значит и продолжение единственно: 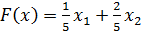 .
.
Пример 2. Доказать выпуклость множества 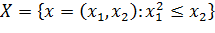
Решение:
Пусть 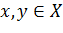 , то есть
, то есть 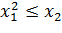 и
и 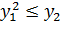 . Тогда
. Тогда 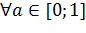 имеем:
имеем:
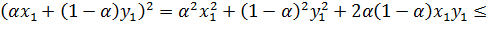
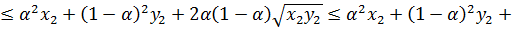
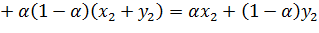 .
.
Значит 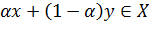 , т.е. множество выпукло.
, т.е. множество выпукло.
Пример 3. Записать уравнение гиперплоскости, к множеству 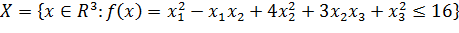 в точке
в точке 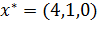 .
.
Решение:
Функция 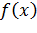 из
из 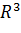 - строго выпукла, т.к.
- строго выпукла, т.к.  , а значит множество выпукло.
Следовательно опорной к плоскости является касательная плоскость
, а значит множество выпукло.
Следовательно опорной к плоскости является касательная плоскость 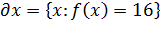 множества
множества 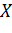 в точке
в точке 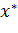
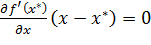 . →
. → 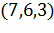 . По условию
. По условию 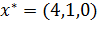 подставим и получим:
подставим и получим:
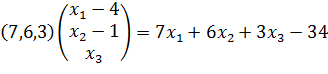 .
.
Пример 4. Определить, будет ли выпукла на множестве 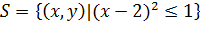 . Функция
. Функция 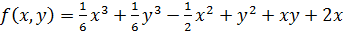 .
.
Решение:
Проверим выпуклость множества 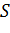 . Функция
. Функция 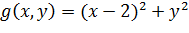 - выпукла на
- выпукла на  по свойству выпуклых функций
множество
по свойству выпуклых функций
множество  - выпукло.
- выпукло.
Составим матрицу 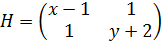 ;
; 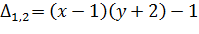 на подпространстве:
на подпространстве: 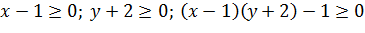 тогда функция будет выпуклой.
тогда функция будет выпуклой.
выпуклый множество функционал векторный
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. «Выпуклый
анализ» - 1973. В. М. Тихомиров.
. «Элементы
теории функций и функционального анализа» - А.Н. Колмогоров, С.В. Фомин
3. «Основы
функционального анализа. 3-е изд.» - 2000. Кутателадзе С.С.
. «Функциональный
анализ в упражнениях.» - Грибанов Ю.
. «Теоремы
и задачи функционального анализа.» - Кириллов, Гвишиани.
. «Функциональный
анализ.» - 2004. Л.В.Канторович, Г.П. Акилов