Аналитические свойства системы двух дифференциальных уравнений с рациональными правыми частями
Резюме
дифференциальный уравнение точка пенлеве
"Аналитические свойства системы двух дифференциальных уравнений с
рациональными правыми частями"
Работа содержит: 23 страницы, 2 использованных источника литературы.
Ключевые слова: подвижные критические особые точки.
Цель курсовой работы - исследовать систему двух дифференциальных
уравнений с рациональными правыми частями на отсутствие подвижных критических
особых точек.
Объектом исследования выступает система двух дифференциальных уравнений с
рациональными правыми частями.
Предметом исследования настоящей работы являются преобразования системы
двух дифференциальных уравнений с рациональными правыми частями.
В работе были использованы: метод малого параметра, линейные
преобразования и т.д.
Sumarry
"Analytical properties of the system of two differential
equations with rational right-hand sides"
The work includes: 23 pages, 2
references.: moving critical singularities.purpose of the job is to investigate
the system of two differential equations with rational right-hand sides in the
absence of moving parts critical singular points.object of research is a system
of two differential equations with rational right-hand sides.subject of
research is the conversion of this system of two differential equations with rational
right-hand sides.job were used: the method of small parameter, linear
transformations, etc.
Содержание
Введение
1. Некоторые
необходимые условия однозначности решений
2. Случай 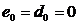
2.1 Случай 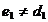
2.1.1 Случай 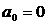
.1.2 Случай 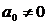
2.2 Случай 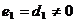
2.2.1 Случай 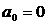
2.2.1.1 Случай 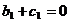
.2.1.2 Случай 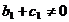
2.2.2 Случай 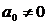
Заключение
Список литературы
Введение
Одной из важнейших задач аналитической теории дифференциальных уравнений
является задача выделения классов уравнений с систем, решения которых не имеют
подвижных критических особых точек. Уравнения и системы, для которых
выполняется это свойство, называются уравнениями и системами типа Пенлеве.
Объектом исследования в работе являются система двух дифференциальных
уравнений с рациональными правыми частями.
Целью исследования является нахождение необходимых и достаточных условий
отсутствия подвижны многозначных особых точек у решений заданной
дифференциальной системы.
Для достижения поставленной цели требуется решить следующие задачи:
последовательно находя необходимые условия, отсеять системы с подвижными
критическими особенностями; непосредственным интегрированием или путем
сравнения с классическими системами типа Пенлеве установить достаточность
найденных условий.
1. Некоторые
необходимые условия однозначности решений
Рассмотрим автономную систему дифференциальных уравнений
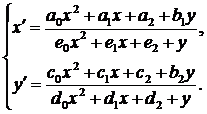 (1)
(1)
Найдем
условия, при которых (1) не имеет подвижных критических точек.
Введем
в систему (1) параметр 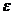 по формулам:
по формулам:
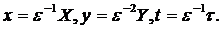
Получим
систему

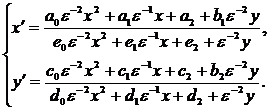
Отсюда
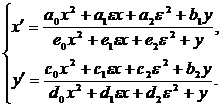
При
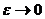 имеем для (1) упрощенную систему
имеем для (1) упрощенную систему
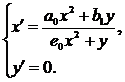 (2)
(2)
Из
системы (2) получаем:
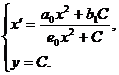 (3)
(3)
где
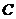 - произвольная постоянная.
- произвольная постоянная.
Для
отсутствия у решений системы (3) подвижных критических точек необходимо, чтобы 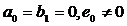 или
или 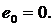
2.
Случай 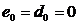
Имеем систему
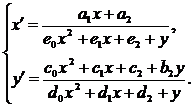 (4)
(4)
2.1
Случай 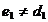
Пусть
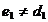 . (5)
. (5)
С
помощью линейного преобразования
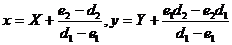
систему
(4) приводим к системе вида
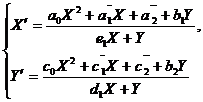
Где
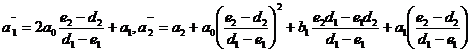

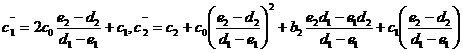
Поэтому
можем в (4), при 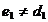 , считать
, считать 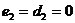 и
рассматривать систему вида
и
рассматривать систему вида
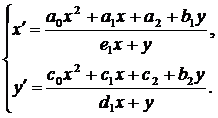 (6)
(6)
Найдем
необходимые и достаточные условия, при которых система (6) не имеет подвижных
критических точек. Введем в систему (6) параметр 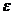 по
формулам:
по
формулам:
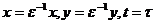 .
.
Получим
систему
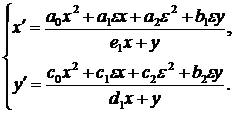
При
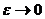 , имеем
, имеем
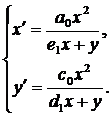 (7)
(7)
Получили
систему, упрощенную для системы (6).
2.1.1
Случай 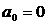
Пусть
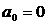 . (8)
. (8)
Тогда
из (7) имеем
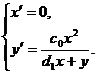
Откуда
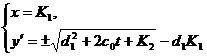
Для
однозначности компоненты 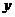 необходимо требовать
необходимо требовать
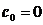 (9)
(9)
Учитывая
условия (8), (9), получаем систему
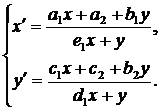 (10)
(10)
Из
системы (10) исключим 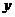 , получим дифференциальное уравнение вида
, получим дифференциальное уравнение вида
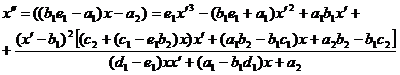 (11)
(11)
Для того, чтобы в решении уравнений (11) отсутствовали подвижные
критические особые точки необходимо, чтобы [1], [2]
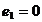 , (12)
, (12)
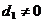 , т.к.
, т.к. 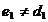 .
.
Учитывая
условие (12) уравнение (11) перепишется в виде
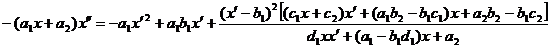 (13)
(13)
Уравнение
(13), для отсутствия подвижный критических особых точек, должно быть полиномом
по 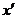 [1], [2].
[1], [2].
Если
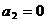 , то надо требовать
, то надо требовать
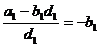
Откуда
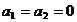 .
.
Тогда
(10) запишется в виде
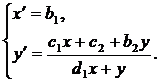 (14)
(14)
Из
второго уравнения следует, что (14) не имеет подвижных критических особых
точек, если только
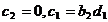 (15)
(15)
Пусть
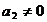 (16)
(16)
то
уравнение (13) перепишется в виде
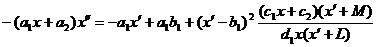 (17)
(17)
Где
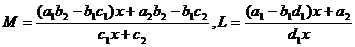 .
.
Для
отсутствия подвижных критических особых точек, в решении уравнения (17)
требуем, чтобы 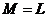 . Откуда необходимо
. Откуда необходимо
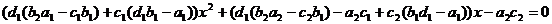 ,
,
что
имеет место, если
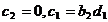 (18)
(18)
Уравнение
(17) примет вид
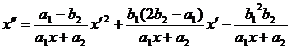 (19)
(19)
Если
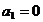 , то необходимо и достаточно, чтобы
, то необходимо и достаточно, чтобы 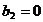 .
.
Пусть
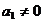 , тогда уравнение (19) перепишется в виде
, тогда уравнение (19) перепишется в виде
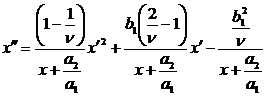 (20)
(20)
Где
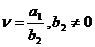 (21)
(21)
Если
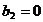 , (22)
, (22)
то
имеем уравнение
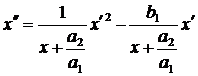 (23)
(23)
Уравнение
(20) не имеет подвижных критических особых точек, если 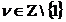 .
.
Уравнение
(23) также не имеет подвижных критических особых точек.
.1.2
Случай 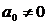
Пусть
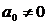 . Исключая из системы (7)
. Исключая из системы (7) 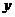 получаем уравнение
получаем уравнение
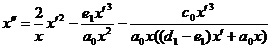 (24)
(24)
Выполнив
замену 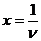 , получим
, получим
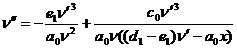 .
.
Так
как 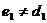 , то это уравнение не будет иметь подвижных
критических особых точек, когда
, то это уравнение не будет иметь подвижных
критических особых точек, когда
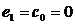 (25)
(25)
Пусть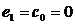 ,
, 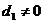 . Тогда с
помощью линейного преобразования
. Тогда с
помощью линейного преобразования 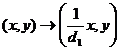 система
(6) приводится к системе, у которой
система
(6) приводится к системе, у которой 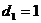 . Поэтому
будем рассматривать систему вида
. Поэтому
будем рассматривать систему вида
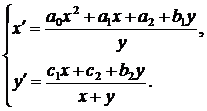 (26)
(26)
В
систему (26) введем параметр 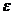 по
формулам
по
формулам
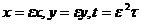
тогда
она примет вид
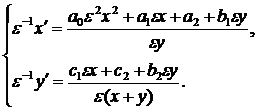
при
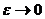 , имеем упрощенную систему
, имеем упрощенную систему
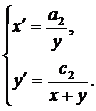 (27)
(27)
Если
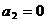 , то из (27) имеем
, то из (27) имеем
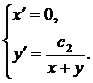
Или
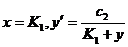 .
.
Решение
системы
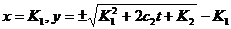 ,
,
где
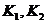 - произвольные постоянные.
- произвольные постоянные.
Для
однозначности решения необходимо требовать, чтобы 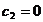 . Если
. Если 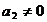 , то из
(27) имеем
, то из
(27) имеем
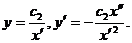
и
подставляем 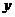 и
и 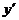 во второе
уравнение системы (27).
во второе
уравнение системы (27).
Получим
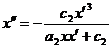
Для
отсутствия у этого уравнения критических особенностей необходимо, чтобы правая
часть уравнения была полиномом относительно 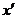 [1],[2],
что имеет место при
[1],[2],
что имеет место при 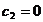 . Тогда система (26) примет вид
. Тогда система (26) примет вид
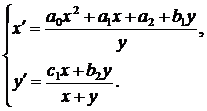 (28)
(28)
то
исключая из системы 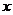 , получаем уравнение второго порядка для
, получаем уравнение второго порядка для 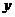
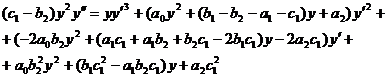 (30)
(30)
Уравнение
(30) не имеет подвижные критические особенности.
При
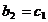 (31)
(31)
система
(28) перепишется в виде
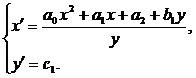 (32)
(32)
Исключаем
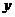 и получим для
и получим для 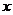 уравнение
второго порядка
уравнение
второго порядка
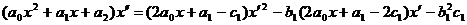 (33)
(33)
Для
отсутствия подвижных критических особых точек у этого уравнения требуем, чтобы 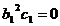 .
.
Если
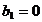 (34)
(34)
то
уравнение (33) имеет вид
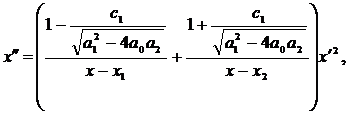
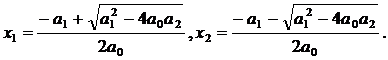
Это
уравнение не имеет подвижных критических особых точек только если
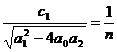 ,
,
где
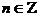 или
или 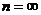 (35)
(35)
Если
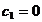 , (36)
, (36)
то
уравнение (33) имеет вид
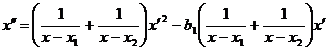 (37)
(37)
Выполнив
в (37) замену 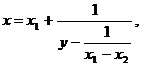 получим уравнение
получим уравнение
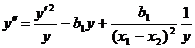 ,
,
имеющее
Пенлеве.
2.2
Случай 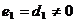
Система (4) примет вид
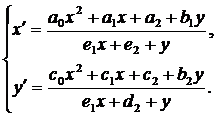 (38)
(38)
С
помощью линейного преобразования 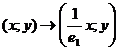 система
(38) приводится к системе, у которой
система
(38) приводится к системе, у которой 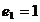 . Поэтому
будем рассматривать систему вида
. Поэтому
будем рассматривать систему вида
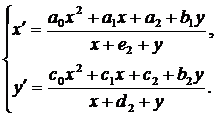 (39)
(39)
Исключая
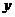 и
и 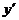 из
системы (39), получим уравнение
из
системы (39), получим уравнение
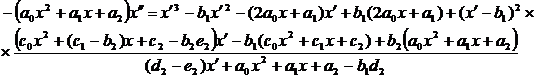 (40)
(40)
Уравнение
(40) не будет иметь подвижных критических особых точек, когда его правая часть
будет полиномом по 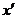 не выше второй степени [1],[2], поэтому надо
требовать
не выше второй степени [1],[2], поэтому надо
требовать
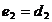 .
.
Учитывая
это условие, система (39) перепишется в виде
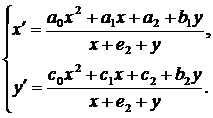 (41)
(41)
Линейным
преобразованием 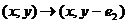 приводим систему (41) к виду
приводим систему (41) к виду
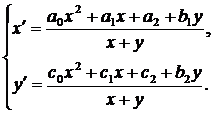 (42)
(42)
Найдем
необходимые и достаточные условия, при которых система (42) не имеет подвижных
критических точек. Введем в систему (42) параметр 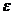 по формулам:
по формулам:
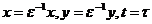 .
.
Получим
систему
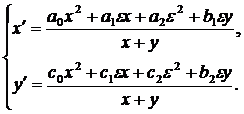
При
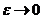 , имеем
, имеем
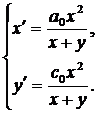 (43)
(43)
Получили
систему, упрощенную для системы (42).
2.2.1
Случай 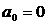
Пусть
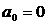 . Тогда из (43) имеем
. Тогда из (43) имеем
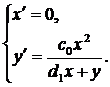
Откуда
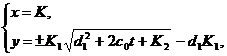
где
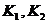 - произвольные постоянные.
- произвольные постоянные.
Для
однозначности компоненты 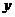 необходимо требовать
необходимо требовать 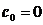 .
.
Рассмотрим
случай 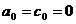 . (44)
. (44)
Получаем
систему:
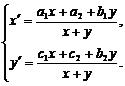 (45)
(45)
Исключая
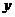 и
и 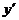 из
системы (45) для
из
системы (45) для 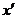 получим уравнение
получим уравнение
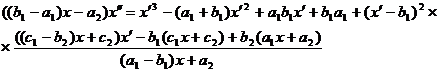 (46)
(46)
Для
однозначности решения уравнения (46) требуем
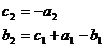 (47)
(47)
В
силу (47) уравнение (46) перепишется в виде
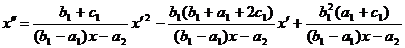 (48)
(48)
Рассмотрим
случаи
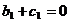 (49,а)
(49,а)
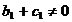 (49,б)
(49,б)
2.2.1.1
Случай 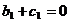
При условии (49,а) уравнение (48) перепишется в виде
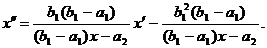
Для
отсутствия подвижных критических особых точек у решений этого уравнения надо
требовать, чтобы
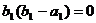 .
.
Это
условие выполняется, если 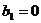 или
или 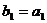 . Таким
образом имеем
. Таким
образом имеем
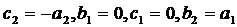 (50,а)
(50,а)
Или
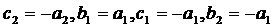 (50,б)
(50,б)
Пусть
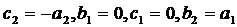 . Тогда система (45) примет вид
. Тогда система (45) примет вид
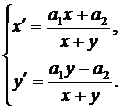 (51)
(51)
Из
системы (51) получаем, что компонента 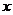 удовлетворяет
уравнению
удовлетворяет
уравнению
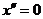
Откуда
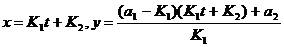 ,
,
где
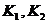 - произвольные постоянные. Таким образом, система
(51) не имеет подвижных критических особых точек.
- произвольные постоянные. Таким образом, система
(51) не имеет подвижных критических особых точек.
Пусть
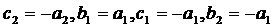 . Тогда система (45) примет вид
. Тогда система (45) примет вид
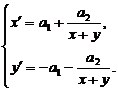 (52)
(52)
Компоненты
удовлетворяет уравнению
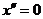 .
.
Получаем
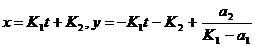 ,
,
где
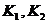 - произвольные постоянные. В данном случае система
(52) также не будет иметь подвижных критических особых точек.
- произвольные постоянные. В данном случае система
(52) также не будет иметь подвижных критических особых точек.
2.2.1.2
Случай 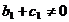
Если
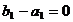 , то уравнение (48) имеет подвижные критические особые
точки.
, то уравнение (48) имеет подвижные критические особые
точки.
Если
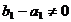 , то уравнение (48) перепишется в виде
, то уравнение (48) перепишется в виде
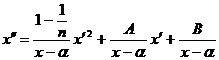 (53)
(53)
Где
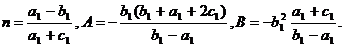
Так
как 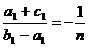 , то
, то 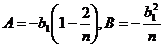 .
.
Таким
образом, уравнение (53) перепишется в виде
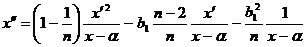 (54)
(54)
Полагая
в (54) 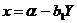 , получим уравнение
, получим уравнение
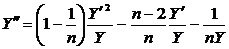 (55)
(55)
Уравнение
(55), а значит и система (45) не имеет подвижных критических особых точек,
только при условии
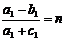 ,
, 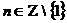 (56)
(56)
2.2.2
Случай 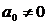
Из
системы (43) исключаем 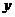 и получаем уравнение для
и получаем уравнение для 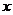
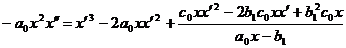
Уравнение
имеет подвижные критические особые точки, так как 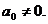
Заключение
В итоге мы можем сформулировать теорему.
Теорема.
Для того чтобы система (4) имела однозначные решения необходимо и достаточно,
чтобы она принимала один из видов: (14) при условии (15); (10) при условиях 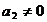 , (12), (18) и одном их условий: 1)
, (12), (18) и одном их условий: 1) 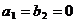 , 2)
, 2) 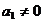 , (21),
3)
, (21),
3) 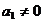 ,
, 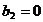 ; (26)
при условии
; (26)
при условии 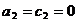 ; (32) при одном из условий: 1) (34), (35), 2) (36);
(45) при одном из условий: 1) (49,а), (50,а), 2) (49,а), (50,б), 3) (47),
(49,б),
; (32) при одном из условий: 1) (34), (35), 2) (36);
(45) при одном из условий: 1) (49,а), (50,а), 2) (49,а), (50,б), 3) (47),
(49,б), 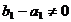 , (56).
, (56).
Список
литературы
1. Айнс Э.Л.
Обыкновенные дифференциальные уравнения / Э.Л. Айнс. - Харьков: ГНТИУ, 1939. -
719 с.
. Мартынов
И.П. Системы типа Пенлеве / И.П. Мартынов, Н.С. Березкина // Учебное пособие по
спецкурсу - Гродно: ГрГУ, 1986. - 119 с.