Теоретические аспекты анализа данных при прогнозировании валютных курсов

Контрольная работа

Теоретические аспекты анализа данных при прогнозировании валютных курсов

Содержание

1. Машинное обучение и статистические методы анализа данных

. Описание используемых методов

. Оценка точности прогнозирования

. Предварительная обработка данных

Литература

. Машинное обучение и статистические методы анализа данных

На данный момент машинное обучение является одной из наиболее развивающихся областей прикладной математики, позволяющих решать большой спектр задач предсказания и распознавания. Многие экономисты используют методы анализа данных для предсказания валютных курсов. Так, например, Martin Evans и Richard Lyons в своей статье «Micro-Based Exchange-Rate Forecasting» используют метод k ближайших соседей и метод опорных векторов для прогнозирования основных мировых валютных пар (EUR/USD, GBP/USD, USD/JPY). В своей работе ученые строят прогнозы, основываясь на таких факторах, как биржевые котировки сырьевых товаров и процентных ставках. Они сравнивают данные методы с моделью, построенной с помощью анализа временных рядов. Они приходят к выводу, что для интрадейт-трейдинга модель, основанная на техническом анализе, дает более высокую точность и поэтому более применима. Стоит отметить, что ученые предсказывали конкретные уровни значений или то, вырастет курс или упадет, а не изменения курса на определенный процент.

Также делает и Barbara Rossi в статье «Exchange Rate Predictability». В своей работе тестирует, насколько точно можно предсказать изменение курсов, но не берет в расчет предсказания экстремумов.

Любая задача машинного обучения подразумевает наличие выборки - совокупности данных, представляемой в виде списков или таблиц, в которых содержится некоторая информация об анализируемом объекте. Задача заключается в построении модели того, как устроен анализируемый объект, на основе анализа имеющихся данных.

Задачи машинного обучения делятся на 2 типа: “обучение с учителем” и “обучение без учителя”. Первый тип задач, как правило, заключается в поиске зависимости между некоторыми характеристиками модели, называемыми факторами, и исследуемой величиной, называемой откликом. К обучению с учителем относятся такие задачи, как линейная регрессия, логистическая регрессия, метод опорных векторов, метод ближайших соседей и другие. Обучение без учителя подразумевает динамически обучаемую во времени модель.

Большинство задач машинного обучения, связанных с прогнозированием, можно разделить на 3 больших этапа: выбор модели, ее обучение и предсказание с использованием построенной модели. Обучение представляет собой простой подбор параметров модели, основанный на обучающей выборке. Параметры подбираются таким образом, чтобы заранее подобранный функционал ошибки предсказания, характеризующий то, насколько аккуратно построенная модель предсказывает исследуемую величину, достигал своего минимума.

Еще одной важной задачей при построении модели является ее оценка качества предсказания, которая будет характеризовать то, насколько адекватно будет полагаться на прогноз, полученный с помощью построенной модели.

. Описание используемых методов

Основными методами, которые мы будем использовать для анализа курса, являются методы классификации, регрессии и анализа временных рядов. Пусть множество T соответствует тем дням, данные по которым мы будем использовать для построения модели, а множество P будет обозначать те дни, для которых мы планируем делать предсказание.

Задача классификации подразумевает, что прогнозируемая величина Y(t) принимает дискретные значения, которые предсказываются на основе значений некоторых факторов X₁(t)… X_n(t).

Задача регрессии подразумевает, что предсказываемая величина Y(t) принимает непрерывное значение. Как и для задачи классификации, значение отклика прогнозируется по значениям факторов X₁(t) … X_n(t).

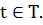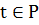Обе две задачи подразумевают то, что у нас имеются данные, соответствующие X₁(t) … X_n(t) и Y(t), для дней  На основе этих данных будет происходить “обучение” модели, после которого будет установлена связь между X₁(t) … X_n(t) и Y(t). Далее на основе данных по X₁(t) … X_n(t), где , и уже обученной модели строится прогноз для соответствующих Y(t).

Анализ временных рядов также имеет дело с непрерывными значениями Y(t), только в данном случае прогноз строится на основе значений предсказываемой величины в предыдущие моменты времени, а именно, ищется зависимость между Y(t) и Y(t-1), Y(t-2), …, Y(t-p), где p - некоторое фиксированное число, которое мы тоже стремимся оптимизировать.

Нетрудно заметить, что для этой задачи не требуется никаких дополнительных данных, кроме значений Y(t). Обучение модели происходит на основе знаний о Y(t) при 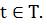В результате обучения устанавливается связь между Y(t) и Y(t-1), Y(t-2), …, Y(t-p). Дальнейшее предсказание производится только для тех моментов времени t, для которых известны значения Y(t-1), Y(t-2), …, Y(t-p).

Классификация

Частным случаем задачи прогнозирования является задача с бинарным откликом, а именно, когда отклик может принимать всего 2 значения, например 0 и 1. На практике такие задачи встречаются крайне часто, например, когда мы хотим предсказать имело ли место какое-то событие или нет. В терминах, определенных выше, если событие имело место, то мы приписываем функции отклика значение, равное единице, в противном случае - нулю. Для данной задачи мы рассматриваем 4 возможных события:

·        Курс вырос, а именно ;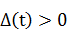

·        Курс вырос более чем на 1 процент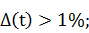

·        Курс упал более чем на 1 процент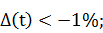

·        Абсолютное значение изменения курса превышает 1%.

Геометрически задача классификации с бинарным откликом может быть интерпретирована следующим образом: обучающая выборка, состоящая из векторов (X₁(t), …X_n(t)), где n - количество факторов, соответствует множеству точек в n-мерном конфигурационном пространстве (одно значение t соответствует одной точке). Каждая из данных точек покрашена в один из двух цветов, например, красный и синий. Задача заключается в том, чтобы по данному расположению красных и синих точек в конфигурационном пространстве, построить разделяющую поверхность, которая бы наилучшим образом отделила красные точки от синих. В дальнейшем мы будем считать, что построенная разделяющая поверхность разбила конфигурационное пространство на две части: отвечающую синему цвету и отвечающую красному цвету. Предсказание новых откликов по новым значениям факторов строится так: для новой точки в конфигурационном пространстве выясняем, какому классу эта точка принадлежит (синему или красному) и ставим ей в соответствие тот прогноз, который соответствует полученному цвету.

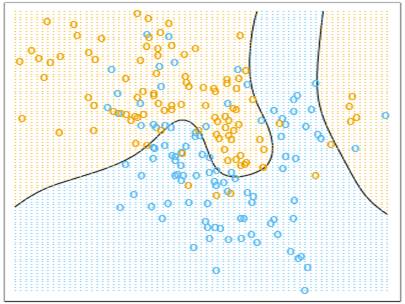
Рис. 1: Случай n=2, двумерное конфигурационное пространство, разделяющая поверхность обозначена черным цветом.

Аналитически это правило можно записать следующим образом: если в конфигурационном пространстве ввести систему координат x₁, …, x_n, то построенная разделяющая поверхность может быть задана уравнением

.

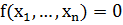Тогда для новых значений 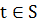 прогноз для отклика Y(t) строится следующим образом: подставляем новые значения факторов в функцию 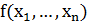, если 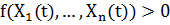, то Y(t) полагаем равным единице, в противном случае Y(t) равно нулю.

Метод ближайших соседей

Одним из наиболее простых методов бинарной классификации является метод ближайших k-соседей. Прежде чем перейти к описанию самого метода стоит отметить, что данный алгоритм классификации является метрическим, это означает, что на конфигурационном пространстве должна быть задана функция расстояния (или иначе, метрика). В качестве расстояния между точками может быть взята обычная евклидова метрика, а именно, расстояние между двумя точками X=(X₁, …, X_n) и Y=(Y₁, …, Y_n) вычисляется по формуле

.

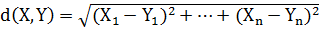Простейший случай метода ближайших k-соседей устроен, по сути, как процесс голосования. Первоначально мы фиксируем число k, которое отвечает количеству соседей, участвующих в голосовании. Для нового значения факторов, мы смотрим положение соответствующей точки в конфигурационном пространстве, далее вычисляем расстояния (относительно введенной метрики) до оставшихся точек выборки, и выбираем k ближайших соседей среди выборки. Прогноз отклика по новым значениям факторов равен метке того класса, которого содержится больше среди полученных соседей.

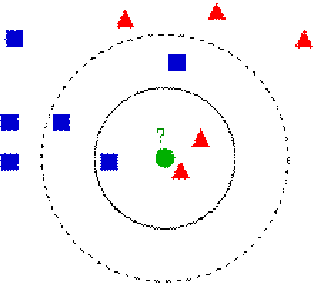
Рис.2: Случай n=2, классификация нового объекта (зеленый круг). При k=3 (черная окружность) среди соседей классифицированного объекта присутствуют два представителя первого класса и один - второго, поэтому новый объект получает метку 1 класса. При k=5 (черная пунктирная окружность) объект получает метку второго класса.

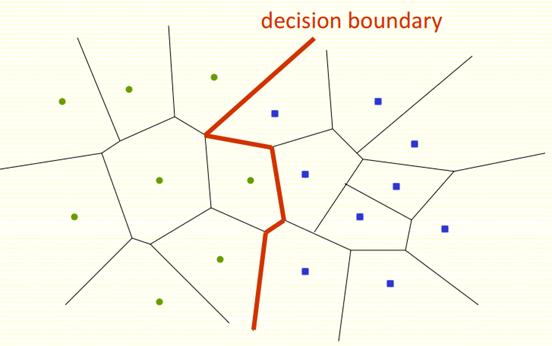
Рис. 3: Решающее правило для двухклассовой классификации с помощью метода ближайших соседей при k=1. Разделяющей поверхностью в данном случае является красная ломаная. Часть плоскости слева от нее принадлежит первому классу, справа - второму.

Обозначим X(t) = (X₁(t), …, X_n(t)), тогда прогноз для дня 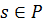 аналитически можно записать следующим образом:

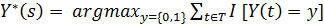 w(s, t),

где .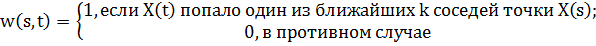

У данной модели присутствует три параметра: количество соседей, метрика и весовая функция w(s, t). В общем случае в качестве весовой функции можно взять некоторую функцию 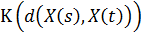, зависящую от расстояния между точками X(s) и X(t+1). Например, если мы хотим, чтобы голос соседа имел тем больший вес, чем ближе он располагается относительно точки X(t), то мы можем .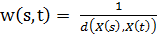

Метод опорных векторов (SVM)

Как уже было отмечено ранее, основной задачей любого метода классификации является построение разделяющей поверхности с уравнением 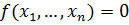. Решающим правилом (или иначе классификатором), определяющим, к какому из классов следует отнести новый объект, является 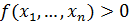 или 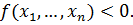 Точки, принадлежащие самой разделяющей поверхности, можно отнести как к первому классу, так и ко второму.

Метод опорных векторов строит разделяющую поверхность таким образом, чтобы суммарное расстояние от близлежащих к ней элементов обучающей выборки, называемых опорными векторами, было максимальна. Такая поверхность называется оптимальной.

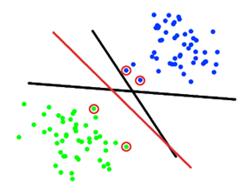
Рис. 4: Случай n=2, пример нескольких разделяющих поверхностей (две черные и одна красная прямые) из которых только одна является. Красным выделены опорные векторы.

В простейшем случае разделяющая поверхность будет являться гиперплоскостью и может быть задана в виде:

.

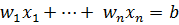В данном случае функция, задающая разделяющее пространство будет равна:

,

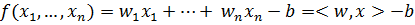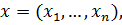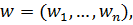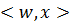где вектор  вектор  а  обозначает скалярное произведение векторов x и w. Если мы смогли построить оптимальную разделяющую гиперплоскость, то нормировав правильным образом коэффициенты гиперплоскости, можно добиться того, чтобы для любого 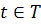 выполнялось следующие условия:

·        Если Y(t) равно 1, тогда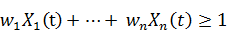

·        Если Y(t) равно 0, тогда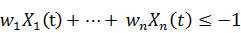

Это означает, что между гиперплоскостям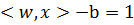и  и 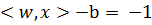 не содержится ни одной точки выборки. Иными словами, задача построения оптимальной гиперплоскости равносильна тому, чтобы максимизировать “зазор” между этими двумы плоскостями. Расстояние от каждого из классов до разделяющей гиперплоскости равно 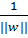, где 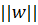 обозначает евклидову норму вектора:

.

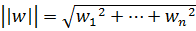Соответственно, величина “зазора” равна 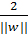. Поэтому оптимальной разделяющей гиперплоскостью будет являться такая гиперплоскость, у которой бы норма w была бы минимальная при условиях, описанных выше.

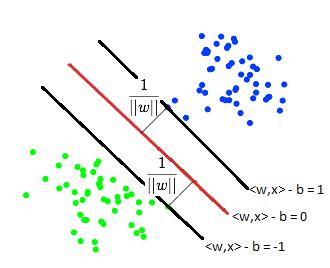
Рис. 5: Случай n=2, три гиперплоскости (в данном случае прямые) отделяющие два класса. “Зазор” образован двумя черными прямыми.

Задача, описанная выше, записывается аналитически следующим образом:

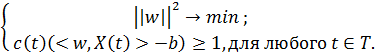
Здесь c(t) = 1 при Y(t)=1 и c(t) = -1 при Y(t)=0. Данная задача может быть решена с помощью оптимизационного метода Лагранжа, который заключается в подборе таких положительных параметров 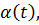 чтобы Лагранжиан

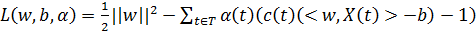
достигал своего минимума по w и b при условии максимизации по 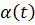. Стоит отметить, что  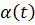могут быть найдены стандартными методами поиска экстремумов и будут зависеть от значений Y(t) и X(t). Предсказание отклика для нового дня 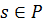 будет следующим:

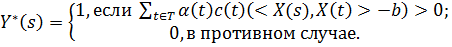
Стоит уделить некоторое внимание проблеме линейной неразделимости двух классов, соответствующих 0 и 1. Не для любой выборки будут существовать такие плоскост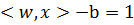и  и 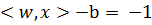, чтобы ни одной точки из выборки не попало в зазор между ними (см. Рис. 5). В этом случае существует несколько подходов, одним из которых является метод спрямляющего пространства.

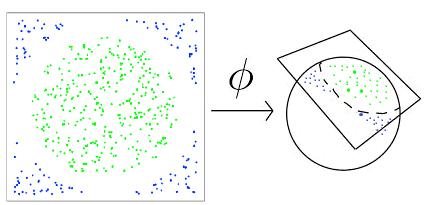
Рис. 6: Случай n=2, пример линейно неотделимых классов. Если вложить двумерное конфигурационное пространство в трехмерное, то полученная выборка будет уже линейно отделимой. В данном случае выборка перемещена на сферу с помощью отображения .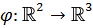

Основной задачей метода спрямляющего пространства является правильный подбор отображения 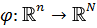, где 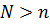. Новой разделяющей поверхностью будет уже не гиперплоскость, как это было в линейном случае, а

Новые значения 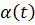, полученные в методе Лагранжа, будут выражаться уже не только через Y(t) и X(t), но и через скалярные произведения 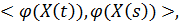 где 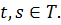 Таким образом, дополнительным параметром метода будет являться ядро отображения:

.

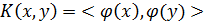Метод спрямляющего пространства предлагает не что иное, как использовать в алгоритме SVM вместо обычного евклидова скалярного произведения - ядро. Подобрав правильным образом ядро, задача может быть сведена к случаю линейно отделимой выборки. Наиболее популярным выбором для ядра является:

·        Полиномиальное ядро: 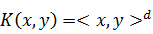 или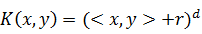

·        Радиальное ядро: ,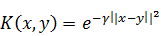

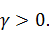
Дерево принятия решений

Дерево принятий решений представляет собой очень наглядную конструкцию, позволяющую не только классифицировать новые объекты выборки, но и проследить процесс принятия решения, а именно, оно отвечает на вопрос: в каких пределах должен лежать каждый из факторов, для того, чтобы объект мог быть отнесен к первому классу? Дерево принятия решения выглядит следующим образом: у дерева есть вершины и ребра, у некоторых вершин есть потомки, те вершины, у которых нет потомков, называются листьями, вершина, которая не является ничьим потомком, называется корнем.

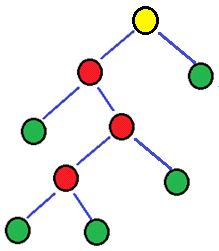
Рис. 7: Пример дерева, синим обозначены ребра, зеленым - листья, желтым - корень, красным, зеленым и желтым - вершины дерева.

статистический метод анализ данные

Как правило, рассматриваются бинарные деревья, а именно, деревья, у которых каждая вершина, не являющаяся листом, имеет ровно двух потомков. Каждой не листовой вершине приписывается атрибут, например “X₁>0.5”. Каждому ребру приписывается ответ на атрибут, соответствующий вершине, из которой исходит данное ребро. В бинарном дереве ответами являются “да” и “нет”. Листовым вершинам приписывается значение отклика (в нашем случае это 0 или 1). Элементы выборки (новые значения факторов) стоит классифицировать с помощью дерева принятия решений следующим образом: начинает с корня дерева, смотрим, какая из ветвей соответствует новому элементу, переходим по ней к потомку, аналогично, выбираем правильную ветвь, переходим по ней и так далее до тех пор, пока не дойдем до листа. В листе будет содержаться номер класса, которому стоит присвоить новый элемент выборки.

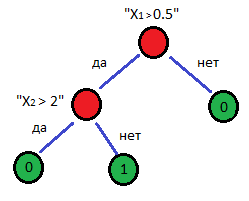
Рис. 8: Пример дерева принятия решения с двумя факторами. Классу 1 соответствуют те элементы выборки, для которых выполнено “X₁ 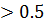” и “X₂ 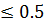”. Классу 0 соответствуют те элементы выборки, для которых либо “X₁ 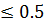”, либо “X₁ 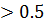” и “X₂ ”.

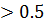В качестве атрибутов можно выбирать не только простейшие неравенства, задающие ограничения на один из факторов, но и более сложные неравенства. Для начала разберемся, как, с геометрической точки зрения, устроен процесс добавления нового атрибута на примере дерева, изображенного на Рис. 7. Будем двигаться от корня к листьям. Атрибут “X₁>0.5”, расположенный в корне, разбивает всю плоскость на 2 полуплоскости: левая ветвь, идущая от корня, соответствует полуплоскости X₁>0.5, правая соответствует X₁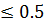. Так как правая ветвь ведет в лист, которому приписан нулевой класс, это значит, что полуплоскость X₁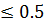 целиком присваивается нулевому классу. Левая ветвь ведет в новый атрибут “X₂>2”, это означает, что полуплоскость X₁>0.5, соответствующая этой ветви, снова делится на две части. Левая ветвь нового атрибута соответствует “четвертьплоскости”, ограниченной системой неравенств 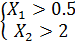, а правая ветвь соответствует “четвертьплоскости” .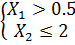

Так как обе эти ветви оканчиваются листьями, которым приписан нулевой и первый класс соответственно, это значит, что первой “четвертьплоскости” целиком присваиваются отклик, равный 0, а второй “четвертьплоскости” - отклик, равный 1. Результат изображен на рисунке 8.

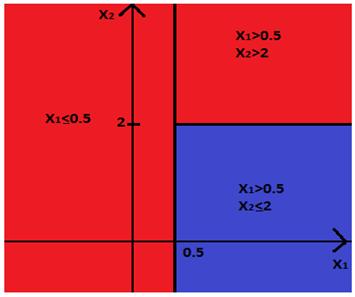
Рис. 9: Геометрическая интерпретация дерева принятия решений, изображенного на рисунке 7.

Для того чтобы описать процесс обучения дерева принятия решения, нужно ввести понятие энтропии. Пусть есть некоторое множество А, элементы которого принадлежат одному из двух классов (в нашем случае это классы, соответствующие отклику 0 и 1). Обозначим А₀ элементы из первого класса, а А₁ - из второго. Тогда энтропией называется функция:

.

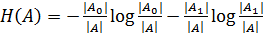Логарифм, как правило, берется по основанию два. Если элементы первого и второго класса в множестве А содержатся в одинаковой пропорции (то есть 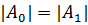), тогда энтропия равна 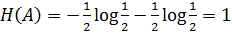. Если в множестве присутствуют элементы только одного класса, то 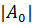 или 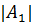 равно нулю, тогда 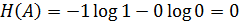. Здесь по определению полагается, что 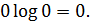 Таким образом, чем более однородное множество мы рассматриваем, тем меньше энтропия этого множества.

Далее нам потребуется понятие прироста информации. Пусть множество А разбито каким-то образом на 2 множества B и C, тогда приростом информации для данного разбиения называется

.

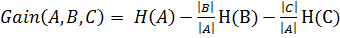Обучение алгоритма происходит следующим образом: вычисляется энтропия обучающей выборки, если энтропия не близка к нулю, то выбирается вид первого атрибута, например, “X₁>a”. Здесь а - параметр, который мы будем сейчас подбирать. Для каждого фиксированного параметра а атрибут “X₁>a” делит выборку на 2 части: в первую группу попадают те элементы, для которых выполняется неравенство X₁>a, во вторую - для которых верно обратное неравенство. Далее для каждого разбиения выборки таким способом на 2 части вычисляем прирост информации с помощью формулы, указанной выше, где в качестве множества А берем всю выборку, а в качестве В и С берем первую и вторую группу, полученную с помощью разбиения атрибутом “X₁>a”. То значение параметра, которое максимизирует прирост информации и будет являться искомым. Подобрав первый атрибут, мы получили корень дерева принятия решений. Атрибут поделил всю выборку на две части, которые соответствуют левой и правой ветви дерева. Далее процедура повторяется для каждой из полученных двух частей выборки, причем на каждом новом шаге мы можем менять атрибут. Алгоритм остановится, когда либо энтропия текущего множества будет достаточно мала, либо прирост информации при любом параметре а будет достаточно мал.

Помимо функции энтропии в теории обучения деревьев принятия решения также используется индекс Джинни:.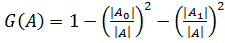

Регрессия

Регрессия является одним из самых популярных подходов для восстановления зависимости между факторами и непрерывным откликом. Задача может быть сформулирована следующим образом: по данным факторов X(t)=(X₁(t), …, X_n(t)) и откликам Y(t) надо построить функцию 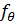 (x₁, …, x_n), такую что  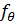(X₁(t), …, X_n(t)) приближает значения Y(t) наилучшим образом. В данном случае  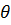- вектор параметров, которые и являются искомыми величинами в задаче. Задачу можно разделить на следующие этапы:

.        Выбираем класс функций, которые будем рассматривать в качестве функций предсказания, например, линейные функции, полиномы и т.д. Эта функция будет иметь некоторое число параметров (вектор 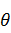), которые мы будем искать. Например, в общем виде линейная функция представима как 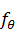 (x₁, …, x_n) =  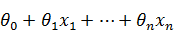и имеет в качестве параметров коэффициенты при соответствующих x_i.

.        Выбираем функцию, характеризующую точность прогноза. Положим 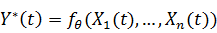, тогда в качестве функционала ошибки можно взять, например, сумму квадратов ошибок:

3.        .

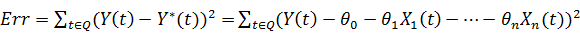.        Далее подбираем параметры 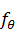 (x₁, …, x_n) таким образом, чтобы функционал ошибки достиг своего минимального значения. Данный подход называется методом наименьших квадратов. В случае с линейной регрессией результат метода наименьших квадратов известен. Обозначим через X матрицу, составленную из строк (X₁(t), …, X_n(t)), где 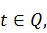 а Y будет обозначать вектор-столбец, составленный из соответствующих Y(t). Тогда вектор-столбец параметров выражается в матричном виде следующим образом: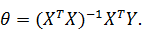

Регуляризация регрессии

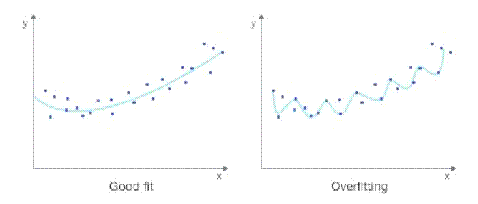
Одной из основных проблем машинного обучения является переобучение (overfitting). Оно заключается в том, что модель слишком хорошо подстраивается под данные, теряя при этом свою простоту. Например, если приближать выборку полиномом 100 степени, то нам, безусловно, удастся достаточно точно приблизить данные из обучающей выборки. Тем не менее, такая точность не только не гарантирует хорошую оценку предсказания на тестовой выборке, но и может, за счет излишней сложности модели, сделать ее хуже, чем она могла бы получиться для более простой модели.

 <#"874191.files/image082.gif">

·        .

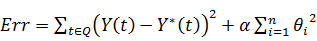Обе регуляризации, описанные выше, штрафуют модель за большое количество ненулевых коэффициентов или за слишком большие коэффициенты регрессии.

Анализ временных рядов

Как уже было отмечено выше, данные, необходимые для построения модели временных рядов не подразумевают наличие каких-либо факторов. Обучение производится лишь на основе данных об отклике. В общем виде задача заключается в подборе количества предшествующих факторов, с помощью которых будет предсказываться новое значение, типа зависимости и коэффициентов зависимости. Как правило, предполагается, что новое значение отклика равно линейной комбинации предыдущих p значений плюс некоторая ошибка. Существует множество различных моделей зависимости, наиболее простыми из них являются:

·        Авторегрессионная модель AR(p)

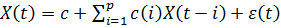
·        Модель скользящего среднего MA (q)

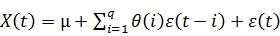
·        Модель авторегресии скользящего среднего ARMA(p,q)

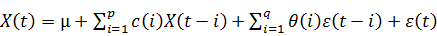
Каждая модель содержит некоторое множество неопределенных коэффициентов: 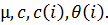 Дополнительными неопределенными величинами являются p и q. Все неизвестные величины можно восстановить, исходя из принципа минимизации функционала ошибки.

. Оценка точности прогнозирования

Обозначим Q - те моменты времени, по которым мы будем оценивать качество прогноза. Для построения оценки точности необходимо, чтобы для каждого t из Q были известны истинные значения отклика Y(t). Пусть Y*(t) обозначает значение прогноза, построенного с помощью обученной модели, для всех 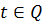. Оценка точности модели производится с помощью функционала ошибки, который отображает, насколько хорошо предсказанное значение Y*(t) приближает реальное значение Y(t).

Для задачи классификации оценкой точности может послужить, например, процент совпавших значений Y(t) и Y*(t), а именно:

,

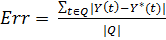где |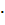| означает абсолютное значение, если аргумент является числом и обозначает количество элементов, если аргумент - множество. Очевидно, что величина ошибки лежит в пределах от 0 до 1, чем меньше ошибка, тем, соответственно, точнее предсказание модели. Если нам важно понять, какие значения (0 или 1) модель предсказывает хуже, то, для более точной характеристики качества прогнозирования можно посчитать следующие величины:

·        n₁₁ - количество совпавших единичных значений;

·        n₁₀ - количество ложно предсказанных единиц;

·        n₀₁ - количество ложно предсказанных нулей;

·        n₀₀ - количество совпавших нулевых значений.

Для задачи регрессии с непрерывным значением Y(t) традиционным выбором является:

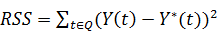·        - функционала ошибки является сумма квадратов ошибок. Чем меньше эта величина тем точнее можно считать модель;

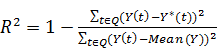·        - коэффициент детерминации. Чем ближе величина к 1, чем точнее предсказание;

Для модели временных рядов, можно использовать те же самые метрики. В случае временных рядов число параметров мы тоже выбираем сами: например, количество предшествующих значений p, от которых мы будем строить зависимость, влияет на количество коэффициентов, которые мы будем оптимизировать в модели. Поэтому мы можем попытаться соблюсти баланс между точностью модели и количеством параметров с помощью следующих функционалов ошибок:

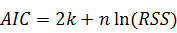·        - информационный критерий Акаике. Здесь k - число параметров модели. Чем меньше значение AIC, тем оптимальнее модель.

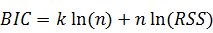·        - информационный критерий Байеса.

Стоит отметить, что выбранный функционал ошибки будет использован, прежде всего, для обучения модели, целью которого является подбор таких параметров модели, чтобы функционал ошибки принимал минимальное значение из возможных. Помимо выбора функционала ошибки, одним из важных вопросов задаче оценки точности построенной модели является то, каким образом мы выбираем множество Q.

Скользящий контроль (Cross-Validation)

При построении оценки качества модели стоит принимать во внимание тот факт, что использование одних и тех же данных для обучения и для оценки качества (например, когда в качестве множества Q берем все множество T) может привести к переоценке точности модели. Поэтому логичней всего было бы разбить данные на 2 группы: первую группу можно было бы использовать для обучения, а вторую для подсчета точности. С другой стороны, при таком разбиении данные могут распределиться неоднородно: например, в первую и вторую группу могут попасть те данные, которые относились соответственно к периоду до и после отмены Центральным Банком Российской федерации системы валютных коридоров. Такая ситуация приведет к тому, что наша модель “приспособится” лишь к определённому режиму курсов валют, и предсказание для другого режима не сможет считаться релевантным.

Чтобы избежать подобной ситуации при построении модели принято использовать метод скользящего контроля или, иначе, метод кросс-валидации. Общий принцип данного подхода заключается в том, что вся выборка делится на две части: обучающую и контрольную. Как уже было сказано выше, по первой выборке производится настройка параметров модели, по второй - оценка качества предсказания. Данная процедура производится несколько раз, окончательная оценка качества модели является усредненным значением по всем полученным оценкам. Основным параметром кросс-валидации является то, в каком соотношении выборка делится на обучающие и контрольные, к примеру, мы можем делить данные пополам, или в отношении 2:1, или 4:1. Как правило, данные делятся на K равных частей из которых K-1 часть берется в качестве обучающей выборки, а оставшаяся часть - в качестве тестовой. Кроме того, дополнительным параметром является то, сколько раз и каким образом производится разбиение выборки при фиксированном K. Например, мы можем проделать процедуру всего один раз, либо взять для оценки качества все возможные разбиения данных на обучающие и тестовые. Существует несколько типов кросс-валидации:

·        Hold-out (или контроль на отложенных данных) - разбиение производится один раз. Оценка точности модели совпадает с оценкой для данного разбиения.

·        K-fold (или контроль по K блокам) - данные делятся на K частей, каждая из этих частей берется в качестве тестовой выборки. В результате получаем K различных оценок точности модели, окончательная оценка получается путем усреднения полученных оценок. Наиболее популярным выбором для K является значение, равное пяти.

·        Leave-one-out (LOO или контроль по отдельным объектам) - является частным случаем K-fold при K равном размеру выборки. Таким образом, в качестве тестовой выборки берется последовательно по одному элементу, а количество построенных оценок качества модели равно размеру выборки.

·        RxK-fold (или контроль по RxK блокам) - процедура K-fold повторяется R раз, причем каждый раз выборка случайным образом делится на K частей.

У каждого из вышеперечисленных методов есть свои плюсы и минусы, например, Leave-one-out требует больших вычислений и, как следствие, не может быть использован при большом количестве данных. K-fold при K=5, наоборот, плохо подходит при сравнительно небольшом количестве данных. Hold-out в силу отсутствия усреднения может привести к неточным оценкам и ситуации, описанной выше.

. Предварительная обработка данных

Одним из факторов, влияющих на точность модели, является ненормированность данных. Рассмотрим простейший пример: пусть мы хотим классифицировать какой-то объект, с помощью метода ближайших соседей. Пусть у объекта первый фактор лежит в пределах от 0 до 1, а второй фактор - в пределах от -1000 до 1000. Тогда выборка будет более протяженной вдоль второго фактора, и, при подсчете расстояний, больший вес будет иметь вклад, даваемый вторым фактором, вклад первого фактора будет практически незаметен. Таким образом, близость между точками будет определяться только расположением вдоль второго фактора, что может привести к некоторым ошибкам классификации.

Чтобы избежать такой однобокости модели, можно произвести одну из следующих нормировок данных:

·        Из каждого фактора вычесть его математическое ожидание и поделить на стандартное отклонение 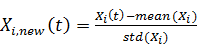. Здесь,  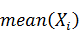обозначает оценку математического ожидания фактора 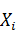,  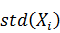- оцека стандартного отклонения.

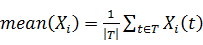
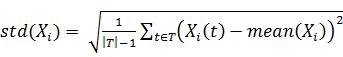
·        Из каждого фактора вычесть его максимальное значение и поделить на размах

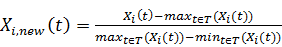
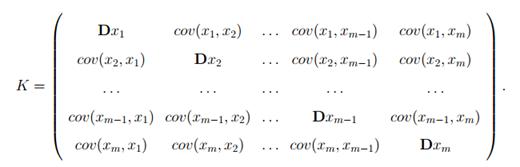
Присутствие элементов, не равных нулю, вне диагонали говорит о зависимости между факторами. Для решения данной проблемы используются следующие подходы:

.        Существует возможность выбора одного из факторов (например, фактора X₁) в качестве основного, для всех остальных же строятся линейные регрессии вида 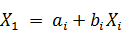_. Тогда в нашей модели, по сути, мы будем учитывать только влияние фактора  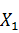на отклик, а влияние оставшихся факторов будет выражаться через коэффициенты линейных регрессий и значения первого фактора.

.        Более продвинутым подходом является использование метода главных компонент. По сути дела, он заключается в поиске новой системы координат, в которой бы матрица ковариаций K приняла бы диагональный вид. Поиск базиса осуществляется по следующему алгоритму:

·        Централизуем наши данные. То есть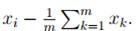

·        Как мы знаем, если зафиксировать единичный вектор (направление) a_i, то любой вектор 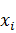 может быть представлен в виде проекции нашего вектора на направление a₁, вычисляемой по формуле 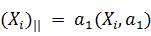, и ортогональной проекции 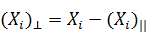. Круглые скобки  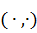в данном случае означают скалярное произведение. На втором шаге мы ищем первую главную компоненту - такой единичный вектор a₁, который минимизирует сумму квадратов длин всех ортогональных проекций 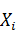. Иначе говоря (если обозначить | 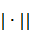длину вектора), то первая главная компонента равна:

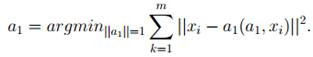
·        Вычитаем из каждого вектора его проекцию на первую главную компоненту

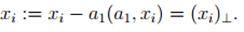
·        Точно так же, как на втором шаге, но уже для новых 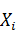, находим вторую главную компоненту a₂. Если такое вектор не единственен, то выбираем любой из них.

·        После нахождения 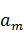 процедура прекращается. Построенные векторы будут образовывать искомый ортонормированный базис.

Литература

1.Haddad K. and M. Salehizadeh, 1988. An Application of Options to Foreign Exchange Rate Forecasting. Quarterly Journal of Business and Economics, 27(1). pp. 42-69.

.        Martin D. D. Evans, Richard K. Lyons, 2005. Meese-Rogoff Redux: Micro-Based Exchange-Rate Forecasting. The American Economic Review, 95 (2). pp. 405-414.

.        Ian H. Giddy, Gunter Dufey, 1975. The Random Behavior of Flexible Exchange Rates: Implications for Forecasting. Journal of International Business Studies, 6(1). pp. 1-32.

.        Andrew C. Pollock, 1990. Alternative exchange rate forecasting models: an application to quarterly movements of the lira/pound-sterling. Giornale degli Economisti e Annali di Economia, 11/12. pp. 527-555.

.        Kenneth Rogoff, 2009. Exchange Rates in the Modern Floating Era: What Do We Really Know? Review of World Economics, 145 (1). pp. 1-12.

.        Barbara Rossi. Exchange Rate Predictability. Journal of Economic Literature, Vol. 51, No. 4 (DECEMBER 2013), pp. 1063-1119.

.        Richard J. Rogalski, Joseph D. Vinso. Price Level Variations as Predictors of Flexible Exchange Rates. Journal of International Business Studies, Vol. 8, No. 1 (Spring - Summer, 1977), pp. 71-81.

.        Heinrich W. Ursprung. On the Value of Free Foreign-Exchange Forecasts Managerial and Decision Economics, Vol. 8, No. 2 (Jun., 1987), pp. 161-165.

.        Thomas H. Lubecke, Robert E. Markland, Chuck C. Y. Kwok, Joan M. Donohue. Forecasting Foreign Exchange Rates Using Objective Composite Models. MIR: Management International Review, Vol. 35, No. 2 (2nd Quarter, 1995), pp. 135-152.

.        Walter Wasserfallen. The Behavior of Flexible Exchange Rates: Evidence and Implications. Financial Analysts Journal, Vol. 44, No. 5 (Sep. - Oct., 1988), pp. 36-44.

.        Jorge R. Calderon-Rossell, Moshe Ben-Horim. The Behavior of Foreign Exchange Rates.Journal of International Business Studies, Vol. 13, No. 2 (Autumn, 1982), pp. 99-111.

.        Robert A. Driskill. Exchange-Rate Dynamics: An Empirical Investigation. Journal of Political Economy, Vol. 89, No. 2 (Apr., 1981), pp. 357-371.

.        J. V. Hansen, J. B. McDonald, R. D. Nelson. Some Evidence on Forecasting Time-Series with Support Vector Machines. The Journal of the Operational Research Society, Vol. 57, No. 9 (Sep., 2006), pp. 1053-1063.

.        Charles Engel, Kenneth D. West. Exchange Rates and Fundamentals. Journal of Political Economy, Vol. 113, No. 3 (June 2005), pp. 485-517.

.        B. Mizrach. Multivariate Nearest-Neighbor Forecasts of EMS Exchange Rates. Journal of Applied Econometrics, Vol. 7, Supplement: Special Issue on Nonlinear Dynamics and Econometrics (Dec., 1992), pp. S151-S163.

.        Agnieszka Markiewicz. MODEL UNCERTAINTY AND EXCHANGE RATE VOLATILITY. International Economic Review, Vol. 53, No. 3 (August 2012), pp. 815-843.

.        Luca Antonio Ricci. Exchange Rate Regimes, Location, and Specialization. IMF Staff Papers, Vol. 53, No. 1 (2006), pp. 50-62.

.        Simon Van Norden. Regime Switching as a Test for Exchange Rate Bubbles. Journal of Applied Econometrics, Vol. 11, No. 3 (May - Jun., 1996), pp. 219-251.

.        Barbara Rossi. Exchange Rate Predictability. Journal of Economic Literature, Vol. 51, No. 4 (DECEMBER 2013), pp. 1063-1119.

.        M. J. Manohar Rao. On Predicting Exchange Rates. Economic and Political Weekly, Vol. 35, No. 5, Money, Banking and Finance (Jan. 29 - Feb. 4, 2000), pp. 377-386.

.        Tony Caporale, Khosrow Doroodian. Exchange Rate Regimes and Uncertainty. Weltwirtschaftliches Archiv, Bd. 131, H. 3 (1995), pp. 569-576.