Внешняя медиана ориентированного графа
Министерство образования и науки
Российской Федерации
Федеральное государственное бюджетное
образовательное учреждение высшего образования
«Магнитогорский государственный
технический университет им. Г.И. Носова»
Институт энергетики и
автоматизированных систем
Кафедра вычислительной техники и
программирования
КУРСОВАЯ РАБОТА
по дисциплине: «Алгоритмы на сетях и
графах»
на тему: «Внешняя медиана
ориентированного графа»
Исполнитель:
Богатырёв А. В., студент 2 курса, группа АВп-14
Руководитель:
Файнштейн С. И., доцент кафедры ВТиП
Магнитогорск, 2016
ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МАГНИТОГОРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Г.И. НОСОВА»
Кафедра
вычислительной техники и программирования
ЗАДАНИЕ НА
КУРСОВУЮ РАБОТУ
Тема:
«Внешняя медиана ориентированного графа».
Студенту гр. АВп-14 Богатырёву А.В.
Исходные данные:
. СМК-О-СМГТУ-42-09 Курсовой проект (работа): структура, содержание,
общие правила выполнения и оформления
. ГОСТ 19.701-90 Схемы алгоритмов, программ, данных и систем. Обозначения
условные и правила выполнения
. Методические рекомендации для выполнения курсовой работы по дисциплине
«Структуры и модели данных» направления 230100 - Информатика и вычислительная
техника
Срок сдачи: «1» июня 2016 г.
Руководитель: ______________________/Файнштейн С.И./
Задание получил: ______________________/Богатырёв А.В./
Магнитогорск, 2016
Оглавление
Введение
. Теоретическое обоснование теории графов
.1 Основные понятия теории графов
.2 Понятие медианы
.3 Методы нахождения медиан графа
.4 Алгоритм нахождения медиан графа
.5 Задача оптимального размещения насосной станции для полива
полей
. Практическая часть
.1 Алгоритм решения задачи размещения точки насосной станции
.2 Программная реализация
.3 Пример работы программы
Заключение
Список используемой литературы
Приложение
. Алгоритм Флойда
. Поиск суммарного расстояния до вершин
. Функция нахождения индекса минимального значения в массиве
Введение
В ряде задач о размещении пунктов обслуживания требуется так расположить
пункт обслуживания на графе, чтобы сумма кратчайших расстояний от этого пункта
до вершин графа была минимально возможной. Оптимальное в указанном смысле место
размещения пункта называется медианой графа. Исходя из природы целевой функции,
такие задачи называются минисуммными задачами размещения. Эти задачи в
различных формах часто встречаются на практике: при выборе места расположения
коммутаторов в сети, подстанций в электросетях, баз снабжения(складов) в сети дорог(где
вершины представляют потребителей) или отделов сортировки в почтовой связи.
С этим типов задач контрастирует минимальная задача размещения,
возникающая при выборе места для таких пунктов обслуживания, как пожарное депо,
полицейский участок или амбулатория. Мы будет рассматривать задачу о нахождении
p-медианы данного графа G. Это задача об оптимальном
размещении заданного числа пунктов обслуживания, при котором сумма кратчайших
расстояний от вершин графа G от
ближайших к ним пунктов принимает минимально возможное значение. Задача
нахождения p-медианы может быть обобщена, если
каждой вершине Xi сопоставить
некоторый вес Vi(представляющий ее размеры или
важность), тогда целевой функцией станет сумма «взвешенных» расстояний.
1. Теоретическое обоснование теории графов
.1 Основные понятия теории графов
Граф
G задается множеством точек (вершин)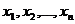 
(которое
обозначается через множество X) и множеством линий (ребер, дуг) 
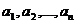(обозначаемых множеством A), соединяющих между собой
все или часть этих точек. Граф задается парой (X,А).
Граф
называют ориентированным (рис. 2), если его пары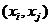 
и 
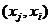(где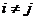 
) считают
различными. В графе ребро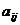 
соединяет точку 
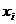с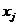 
и имеет направление из вершины 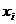в .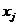
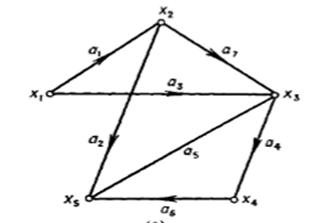
Рисунок
2. «Ориентированный граф»
Граф
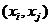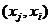называют неориентированным (рис.3), если порядок записи элементов в парах и (где 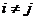) не имеет значения.
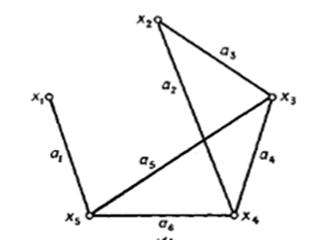
Рисунок
3.«Неориентированный граф»
Петлей
называется дуга, начальная и конечная вершины которой совпадают.
Граф
со взвешенными дугами - это граф, дугам которого 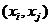приписаны
(сопоставлены) некоторые числа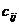 
,
называемые весом (длиной, стоимостью или ценой) пути.
Две
вершины называются смежными, если какая-нибудь из двух дуг 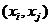и 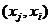или обе
одновременно присутствуют в графе.
Две
дуги называются смежными, если они различны и имеют общую вершину (независимо
от того, является ли эта точка началом или концом для каждой из дуг).
Помеченный
граф (или перенумерованный) - граф, вершины которого отличаются одна от другой
какими-либо пометками. В качестве пометок обычно используются буквы или целые
числа.
Степенью
вершины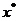 
в графе G называется число рёбер, инцидентных 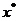(т. е. количество ребер, имеющих граничной вершину).
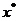Цепь
- это последовательность ребер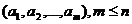 
, в
которой у каждого ребра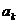 
одна из граничных вершин является также граничной
вершиной для ребра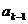 
, а другая - граничной вершиной для 
.
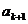Простая
цепь - цепь, у которой все ребра различны. В противном случае цепь называют
составной.
Цикл
- это конечная цепь, начинающаяся в некоторой вершине 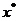и заканчивающаяся в той же вершине 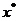. Если в цикле все ребра различны, то его называют
простым, в противном случае его называют составным.
Цикл
с отрицательной суммарной длиной - цикл, обходя который, путь будет иметь сколь
угодно малый вес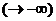 
.
Матрица
весов - матрица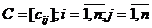 
, элементами которой являются длины дуг графа.
Путь
- это последовательность дуг, в которой конечная вершина всякой дуги, отличной
от последней, является начальной для следующей дуги.
Маршрут
- это последовательность ребер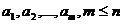 
в
которой каждое ребро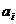 
, за исключением, возможно, первого и последнего
ребер, связано с ребрам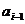и 
и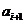 
своими
двумя концевыми вершинами.
Путь
между двумя вершинами называется кратчайшим, если его стоимость минимальна
среди стоимостей всех возможных путей между этими двумя вершинами .[4,6]
1.2 Понятие медианы
Для простоты изложения начнем с рассмотрения задачи о размещении точек
водоснабжения на графе.
Пусть необходимо выбрать место для размещения точек водоснабжения в
населенном пункте. В этой задачи требуется так расположить эти вершины, чтобы
сумма кратчайших расстояний от вершин графа до других населенных пунктов была
минимально возможной. Оптимальное в указанном смысле место расположения пункта
называется медианой графа. Под вершинами графа понимаются точки водоснабжения.
Исходя из природы целевой функции, такие задачи называются минисуммными
задачами размещения.
В данной работе мы будем рассматривать минисуммные задачи размещения. В
частности рассмотрим задачу о нахождении p-медианы данного графа G; это задача
о размещении заданного числа (скажем, p) точек водоснабжения, при которых сумма
кратчайших расстояний от вершин графа G до ближайших населенных пунктов
принимает минимально возможное значение.
Задача о p-медиане может быть несколько обобщена, если каждой вершине xj
сопоставить некоторый вес vj (представляющий, например, ее размер и важность);
тогда целевой функцией, подлежащей минимизации, станет сумма «взвешенных»
расстояний.
Пусть дан граф G = (X, Γ). Для каждой вершины xi ∈ X (здесь и далее суммирование
ведется по всем xi ∈ X)
σo(xi) = ∑ vj d(xi, xj) -
внешнее передаточное число,
σt(xi) = ∑ vj d(xj, xi) -
внутреннее передаточное число,
теория граф индекс массив
где d(xi, xj) - кратчайшее расстояние от вершины xi до вершины xj.
Вершина xo*, для которой σo(xo* ) = min [
σo(xi) ],
называется внешней медианой графа G, а вершина xt*, для которой σt(xt*) = min [
σt(xi) ],
называется внутренней медианой графа G.
Рассмотрим выбор точек водоснабжения.
Для этого вернемся к нашей задаче. Итак, повторюсь, что точки
водоснабжения можно представить в виде вершин графа, а дороги, проложенные до
населенных пунктов - дуги. На практике каждой вершине присваивается вес vj,
представляющий ее «важность» (например, vj может быть числом, равным длине
пути, измеряемый, например, в километрах).
В этом случае задача сводится к нахождению места для размещения точек
водоснабжения, чтобы сумма расстояний до населенных пунктов было минимальным.
Таким образом, возвращаясь к обозначениям, введенным выше, необходимо найти
такую вершину xo,t*, чтобы сумма внешних и внутренних передаточных чисел была наименьшей.
Тогда вершина xo,t* может быть названа внешне-внутренней медианой. Далее
покажем, что точка xo,t* является оптимальной, т. е. для любой другой точки
графа (вершины или произвольной точки дуги) общее расстояние при условии, что в
этой точке будет располагаться точка водоснабжения, будет не меньше, чем для
вершины xo,t*.
Обобщим понятие медианы, определив p-медиану.
Пусть Xp - подмножество множества вершин X графа G = (X, Γ), и положим, что Xp содержит p
вершин. Переопределим следующие обозначения
(Xp, xj) = min [ d(xi, xj) ]
и d(xj, Xp) = min [ d(xj, xi) ],
где минимум ищется по всем xi
∈ X.
Если xi′ - вершина из
Xp, на которой достигается минимум в предыдущих формулах, то говорят, что
вершина xj прикреплена xi′. Передаточные же числа множества вершин Xp
определяются аналогично передаточным числам одиночной вершины:
σo(xi) = ∑ vj d(Xp, xj) - внешнее передаточное
число,
σt(xi) = ∑ vj d(xj, Xp) - внутреннее передаточное
число.
Множество же Xo*, для
которого σo(Xo*) = min [ σo(xi) ] (минимум ищется по всем Xp ⊆
X), называется внешней p-медианой графа G, аналогично определяется внутренняя
p-медиана.
Понятно, что нахождение
p-медианы используя непосредственно вышеуказанные формулы нецелесообразно с
вычислительной точки зрения.
Далее рассмотрим абсолютные
p-медианы.
Для упрощения задачи будем
далее рассматривать неориентированный граф G. Т. о. индексы t и o будут
отсутствовать, т. к. внешние и внутренние передаточные числа будут совпадать.
Точку графа (вершина или точка дуги), для которой передаточное число будет
принимать наименьшее значение, будем называть абсолютной медианой графа G. [1]
1.3 Методы нахождения медиан графа
Существует несколько методов нахождения медиан графа.
К этим методам относятся:
). Метод Беллмана-Форда.
Данный метод был предложен независимо Ричардом Бел-лманом и Лестером
Фордом и позволяет найти кратчайшие пути из одной вершины ко всем остальным
вершинам, для случая, когда веса ребер могут быть отрицательными.
Алгоритм вернет значение true, если в графе нет отрицательных циклов, и
false, если таковой цикл имеется. Если в графе есть отрицательные циклы, то
задача о поиске кратчайших путей (по крайней мере, для некоторых вершин) не
существует [6].
) Метод Дейкстры.
Этот метод основан:
-
на приписывании вершинам графа временных пометок, причем пометка вершины дает
верхнюю границу длины пути от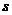 
к этой
вершине;
пометки
(их величины) постепенно уменьшаются с помощью некоторой итеративной процедуры;
на
каждом шаге итерации одна из временных меток становится постоянной, т. е. эта
пометка уже не является верхней границей, а дает длины кратчайшего пути от
вершины 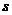к рассматриваемой вершине.
)
Эвристический метод.
Тейц
и Барт предложили эвристический метод для нахождения p-медианы. Метод состоит в
следующем: случайным образом выбираются p вершин, они образуют начальное
множество S, аппроксимирующее p-медианное множество Xp*. Затем выясняется,
может ли некоторая вершина xj ∈ X \ S
заменить вершину xi ∈ S (как медианная вершина), для чего строят новое
множество S* = (S ∪ {xj}) \ {xi} и сравнивают передаточные числа σ(S*) и σ(S).
Если σ(S*) < σ(S), то S заменяют на S*, которое лучше аппроксимирует p-медианное
множество Xp*. Затем аналогично исследуется множество S* и т. д., пока не будет
построено множество S^, которое нельзя будет изменить по вышеуказанному
принципу.
).
Метод Флойда.
Один
из наиболее эффективных методов решения задачи о нахождении медиан графа
предложил Флойд.
В
данной работе мы находим медианы неориентированного графа.
Этот
метод применяют, если необходимо найти кратчайшие пути между всеми парами
вершин. Метод базируется на использовании последовательности из n
преобразований начальной матрицы весов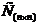 
. При
этом на каждой итерации матрица представляет собой длины кратчайших путей между
каждой парой вершин с тем ограничением, что путь между 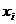и ;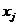 
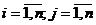(для любых 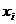и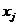) содержит в качестве промежуточных только вершины из
множества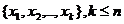 
.
1.4 Алгоритм нахождения медиан графа
Пользуясь рассмотренным выше методом Флойда распишем пошагово алгоритм
нахождения медиан графа.
Предположим,
что в начальной матрице весов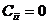 
для всех
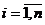и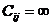 
, если в графе отсутствует дуга .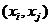
Присвоение
начальных значений
Шаг
1. Положить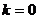
.
Итерация:
Шаг
2. 
.
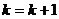Шаг
3. Для всех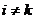 
, таких, что 
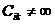, и для
всех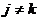 
, так,
что
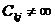, введем операцию: 
.
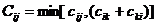Проверка
на окончание:
Шаг
4. (а) Если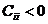 
, то в графе 
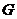существует
цикл
отрицательного
веса, содержащий вершину 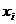и решения нет.
Остановка
алгоритма.
(б)
Если все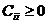 
и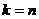 
, то
получено решение. Матрица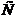 
дает
длины всех кратчайших путей. Остановка алгоритма.
(в)
Если все 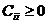и 
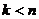, то
вернуться к шагу 2. [2]
1.5 Задача оптимального размещения насосной станции для полива полей
На сегодняшний день существует немало оптимизационных задач для размещения
точек в населенных пунктах и за их пределами. К этим задачам относятся
статистические, математические методы, а также методы для решения конкретных
задач. Статистические методы основаны на общенаучных и экономико-географических
методах обработки статистических данных, а с помощью математических методов
есть возможность быстро обрабатывать цифровой материал и получать
количественные оценки анализируемых явлений.
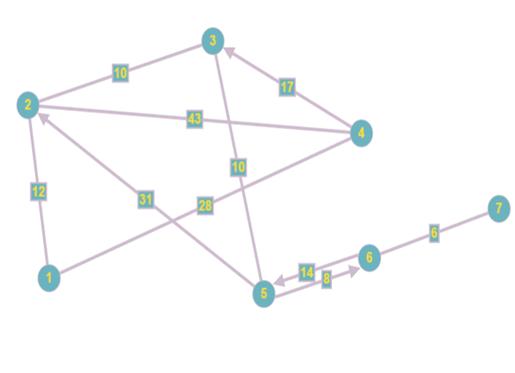
Рисунок 1. «Карта населенных пунктов»
В данной работе мы рассмотрим задачу оптимального размещения точки
насосной станции, в которой предусматривается, что сумма кратчайших расстояний
от точки до полей - минимальна. Будем располагать точку на графе, где
населенные пункты - вершины графа, оптимально-расположенная точка станции -
медиана графа. Оптимальное в указанном смысле место расположения точки
называется медианой графа. Для решения поставленной задачи будем использовать
алгоритм нахождения медиан заданного графа.
2. Практическая часть
2.1 Алгоритм решения задачи размещения точки насосной станции
На основании исходных данных(рисунок 1) формируем матрицу длин дуг D0,
каждый элемент которой равен длине кратчайшей дуги между вершинами i и j. Если
такой дуги нет, положим значение элемента равным ∞.
Таблица 1. Матрица D0.
|
D0=
|
0
|
12
|
∞
|
28
|
∞
|
∞
|
∞
|
|
12
|
0
|
10
|
43
|
∞
|
∞
|
|
∞
|
10
|
0
|
∞
|
10
|
∞
|
∞
|
|
28
|
43
|
17
|
0
|
∞
|
∞
|
∞
|
|
∞
|
31
|
10
|
∞
|
0
|
8
|
∞
|
|
∞
|
∞
|
∞
|
∞
|
14
|
0
|
6
|
|
∞
|
∞
|
∞
|
∞
|
∞
|
6
|
0
|
Для определения медианы графа, представленного на рисунке 1, необходимо
составить матрицу длин кратчайших дуг между каждой парой вершин используя
алгоритм Флойда-Уоршелла.
|
D7=
|
0
|
12
|
22
|
28
|
32
|
40
|
46
|
|
12
|
0
|
10
|
40
|
20
|
28
|
34
|
|
22
|
10
|
0
|
50
|
10
|
18
|
24
|
|
28
|
27
|
17
|
0
|
27
|
35
|
41
|
|
32
|
20
|
10
|
0
|
8
|
14
|
|
46
|
34
|
24
|
74
|
14
|
0
|
6
|
|
52
|
40
|
30
|
80
|
20
|
6
|
0
|
Основываясь на полученой нами матрице длин кратчайших путей, найдем
CВВ(i) для каждой вершины графа
ВВ(i)=Σd(i, j).ВВ(1)==Σjd(1, j)=180ВВ(2)==Σjd(2, j)=144ВВ(3)==Σjd(3, j)=134ВВ(4)==Σjd(4, j)=175ВВ(5)==Σjd(4, j)=144ВВ(6)==Σjd(4, j)=198ВВ(7)==Σjd(4, j)=228
Медианой графа является такая вершина x, для которой СВВ(x)=min{СВВ(i)}.
Минимальное значение имеет СВВ(3)=134, а это значит, что вершина 3 является
медианой графа.
2.2 Программная реализация
Нахождение медиан графа реализовано в среде разработки Microsoft Visual Studio 2015 на языке программирования C++.
Чтобы найти медианы графа необходимо задать граф.
Для задания матрицы весов и количества вершин существует возможность их
введения вручную
Количество вершин указывается в константе препроцессора #define MatrixLen 7, где 7 количество вершин. Матрица
расстояний задается в функции main
переменной matrix.
2.3 Пример работы программы
При запуске программы поочередно будет выведено:
· исходные данные
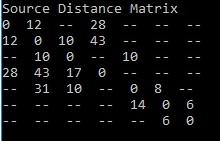
Рис. 2.3.1 - Исходные данные
· Матрица кратчайших путей
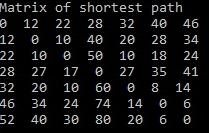
Рис. 2.3.2 - Матрица кратчайших путей
· Сумма расстояний от вершины до всех дуг
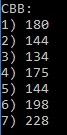
Рис. 2.3.3 - CBB
· Искомая медиана графа
Рис. 2.3.4 - Результат
Заключение
В результате курсового проектирования составлена и решена задача наиболее
выгодного расположения точки насосной станции в сельскохозяйственных угодьях.
Изучены основные алгоритмы, используемые в теории графов. В частности: метод
Беллмана-Форда, алгоритм Флойда и Дейкстры.
Список используемой литературы
1. Кристофидес
Н. Теория графов. Алгоритмический подход. М.: Мир, 1978, - 432 с.
. Миков
А.Ю, Файнштейн С.И. Алгоритмы на сетях и графах. МГТУ, 2016, - 75c
Приложение
Листинг программы:
1.
Алгоритм Флойда
(int k=0; k < MatrixLen; ++k)(int i = 0; i < MatrixLen;
++i)(int j=0; j < MatrixLen; ++j)(matrix[i][k] < INF &&
matrix[k][j] < INF)(matrix[i][k] + matrix[k][j] < matrix[i][j])[i][j] =
matrix[i][k] + matrix[k][j];
. Поиск
суммарного расстояния до вершин
for (int i = 0; i < MatrixLen; i++) {sum = 0;(int j = 0; j
< MatrixLen; j++) {<< matrix[i][j]<<" ";+=
matrix[i][j];
}[i] = sum;<<"\n";
}
. Функция
нахождения индекса минимального значения в массиве
int minIndex(int _arr[]) {
int min = 0;(int i = 1; i < MatrixLen; i++) {(_arr[min]
> _arr[i])= i;
}min;
}