Эксергетические потери. Индикаторная и теоретическая диаграмма поршневого компрессора. Истечение газов
Контрольная
работа по теплотехнике
Вопрос 1. Показать в диаграмме 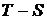 эксергетические
потери в двух последовательных процессах
эксергетические
потери в двух последовательных процессах
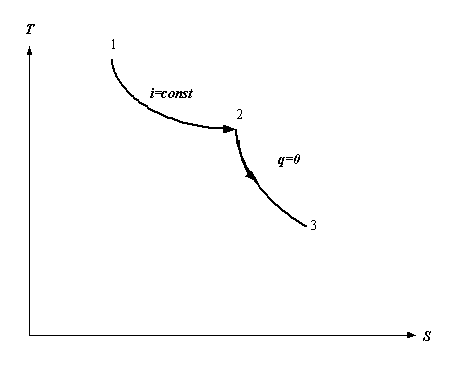
Рис. 1
Эксергия рабочего тела в состоянии 1
определяется по формуле
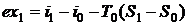 ,
,
где 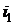 и
и 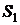 - энтальпия и энтропия рабочего
тела в рассматриваемом состоянии 1,
- энтальпия и энтропия рабочего
тела в рассматриваемом состоянии 1, 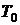 ,
, 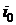 и
и 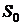 - температура, энтальпия и энтропия
рабочего тела при условиях окружающей среды.
- температура, энтальпия и энтропия
рабочего тела при условиях окружающей среды.
Эксергия рабочего тела в состоянии 2
определяется по формуле
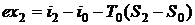 ,
,
где 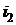 и
и 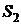 - энтальпия и энтропия рабочего
тела в рассматриваемом состоянии 2.
- энтальпия и энтропия рабочего
тела в рассматриваемом состоянии 2.
Потери эксергии в процессе 1-2 будут
равны
 .
.
Так как в процессе 1-2
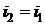 ,
,
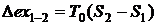 .
.

Рис. 2
На диаграмме 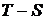 этим
потерям соответствует площадь
этим
потерям соответствует площадь 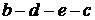 .
.
Необратимый адиабатный процесс 2-3
представим в виде двух последовательных процессов: обратимого адиабатного
процесса 2-a и изотермического процесса a-3, протекающего при температуре 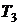 . В процессе
2-a потери эксергии отсутствуют, а в изотермическом процессе a-3
. В процессе
2-a потери эксергии отсутствуют, а в изотермическом процессе a-3 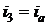 . Тогда
потери эксергии в процессе 2-3 будут равны
. Тогда
потери эксергии в процессе 2-3 будут равны
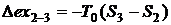
На диаграмме 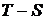 этим
потерям соответствует площадь
этим
потерям соответствует площадь
 .
.
Вопрос 15. Можно ли теплоту
некоторого источника полностью превратить в работу?
Первый закон (первое начало)
термодинамики в общем виде представляет собой закон сохранения и превращения
энергии. Этот закон налагает строгое условие на все природные процессы, которые
при всем их разнообразии ограничены условием сохранения энергии.
Запишем уравнение первого закона
термодинамики. Для этого допустим, что к рабочему телу подведено некоторое
количество теплоты Q. Эта теплота будет затрачена на изменение внутренней
энергии 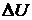 и на
совершение работы
и на
совершение работы 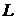 . Тогда для
m кг массы тела уравнение эквивалентности будет иметь вид
. Тогда для
m кг массы тела уравнение эквивалентности будет иметь вид
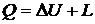 , (1)
, (1)
где 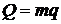 ,
, 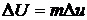 ,
,  .
.
Для одного кг массы уравнение (1)
примет вид
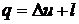 ,
,
где  ,
, 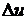 ,
, 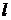 - удельные количества теплоты,
изменения внутренней энергии и работы.
- удельные количества теплоты,
изменения внутренней энергии и работы.
Для бесконечно малого процесса
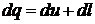 . (2)
. (2)
Уравнение (2) представляет собой
математическую запись первого закона термодинамики. Из этого уравнения следует,
что теплота, подведенная к рабочему телу, затрачивается на изменение внутренней
энергии и совершение работы.
В термодинамике в качестве рабочих
тел часто используются газы. При описании термодинамических процессов
предполагается, что газы идеальные. Для идеального газа работа 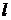 есть работа
по изменению объема, т. е.
есть работа
по изменению объема, т. е.
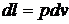 , (3)
, (3)
где 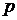 - давление,
- давление, 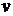 - удельный
объем.
- удельный
объем.
Из равенств (2) и (3) получим
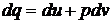 . (4)
. (4)
Состояние идеальных газов
описывается уравнением Клапейрона-Менделеева
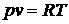 ,
,
где 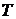 - температура,
- температура, 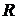 - газовая
постоянная.
- газовая
постоянная.
Для идеальных газов
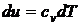 ,
,
где 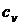 - теплоемкости газа при постоянном
объеме, и уравнение (4) принимает вид
- теплоемкости газа при постоянном
объеме, и уравнение (4) принимает вид
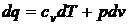 . (5)
. (5)
Рассмотрим изотермический процесс. В
таком процессе температура не изменяется, т. е. 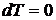 . Из равенства (5) для
изотермического процесса получим
. Из равенства (5) для
изотермического процесса получим
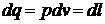 ,
,
т. е. полное превращение теплоты в
работу.
Рассмотрим круговой цикл тепловой
машины, изображенный на рисунке 1. Для того чтобы от тепловой машины можно было
получить полезную работу, необходимо выполнить следующие условия.
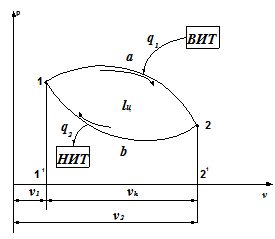
Рис. 3
Необходимо иметь рабочее тело - это тело,
посредством которого осуществляется взаимное превращение теплоты и работы.
Необходимо наличие по меньшей мере двух
источников теплоты с разными температурами - верхний (высший) источник теплоты
(ВИТ) или нагреватель и нижний (низший) источник теплоты (НИТ) или холодильник.
Работа тепловой машины должна быть цикличной, т.
е. рабочее тело, совершая ряд процессов, должно возвращаться в исходное
состояние.
В процессе расширения 1-а-2 от ВИТ с
температурой 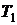 к рабочему
телу подводится теплота в количестве
к рабочему
телу подводится теплота в количестве 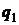 . При этом получается положительная
работа
. При этом получается положительная
работа 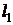 , численно
равная площади
, численно
равная площади 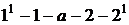 . В процессе
сжатия 2-b-1 от рабочего тела отводится теплота
. В процессе
сжатия 2-b-1 от рабочего тела отводится теплота 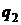 к НИТ с температурой
к НИТ с температурой 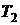 . В этом
процессе затрачивается работа
. В этом
процессе затрачивается работа 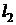 , равная площади
, равная площади 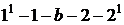 . Из первого
закона термодинамики получим работу цикла
. Из первого
закона термодинамики получим работу цикла
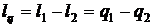 .
.
Чтобы получить полезную работу,
работа, затраченная на сжатие в процессе 2-b-1, должна быть меньше работы
расширения в процессе 1-а-2. Чтобы этого достичь, необходимо одновременно со
сжатием охлаждать рабочее тело, отнимая у него теплоту 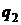 . Если при
сжатии не охлаждать рабочее тело, то процесс сжатия пойдет по пути 2-а-1 и на
сжатие будет потрачена та же самая работа
. Если при
сжатии не охлаждать рабочее тело, то процесс сжатия пойдет по пути 2-а-1 и на
сжатие будет потрачена та же самая работа 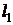 , которая была получена в процессе
расширения. В результате полезная работа цикла будет равна нулю.
, которая была получена в процессе
расширения. В результате полезная работа цикла будет равна нулю.
Таким образом, повторяя
последовательно цикл 1-а-2-b-1 с подводом и отводом теплоты, можно получить
непрерывно действующую тепловую машину.
Коэффициент полезного действия (кпд)
цикла тепловой машины определяется по формуле
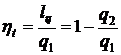 .
.
Кпд тепловой машины всегда меньше 1
(или 100%), так как не вся теплота 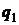 , подведенная к рабочему телу,
превращается в работу. Часть этой теплоты в количестве
, подведенная к рабочему телу,
превращается в работу. Часть этой теплоты в количестве 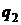 отводится в
окружающую среду.
отводится в
окружающую среду.
Отсюда вытекает следующая
формулировка второго закона термодинамики: “Стопроцентное превращение теплоты в
работу посредством тепловой машины невозможно”. Тепловой двигатель, который всю
подведенную теплоту превращает в работу, называется вечным двигателем второго
рода. Тепловая машина с кпд, равным единице, не противоречит первому закону
термодинамики, который констатирует лишь взаимопревращаемость энергий. Однако
такая машина противоречит второму закону термодинамики, который обусловливает
получение полезной работы некоторым компенсирующим процессом - передачей части
теплоты (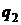 ) к НИТ.
) к НИТ.
Вопрос 2. Какая разница между
индикаторной и теоретической диаграммами поршневого компрессора
Компрессоры служат для получения
сжатого газа. Они нашли широкое применение в технике, являясь одним из основных
агрегатов в газотурбинных, а также в некоторых поршневых двигателях.
Компрессоры по способу сжатия газа подразделяются на поршневые и лопаточные
(турбинные). Кроме того, компрессоры могут быть одноступенчатыми или
многоступенчатыми.
Принципиальная схема
трехступенчатого поршневого компрессора представлена на рисунке 1. Здесь: 1-
цилиндр; 2 - поршень, 3 - шатун, 4 - коленчатый вал, 5 - подшипник, 6 -
всасывающий клапан, 7 - нагнетательный клапан, 8,9 - промежуточные охладители.
В направлении стрелок 10,11 осуществляется вход и выход охлаждающей воды.
Рис. 4
Принцип работы такого компрессора
состоит в следующем. Через клапан 6 первой ступени происходит всасывание газа.
После сжатия газ через охладитель 8 направляется во вторую ступень компрессора.
Причем всасывание газа во второй ступени происходит при давлении сжатия в
первой ступени. Всасывание газа в третьей ступени выполняется через
промежуточный охладитель 9 при давлении сжатия во второй ступени. Через
нагнетательный клапан третьей ступени осуществляется нагнетание газа в
резервуар.
Теоретическая диаграмма процессов
сжатия в трехступенчатом компрессоре в pv-координатах представлена на рисунке
2. Рассмотрим процессы цикла: 0-1 - линия всасывания газа в первой ступени
компрессора (не является термодинамическим процессом, т. к. происходит только
перемещение газа без изменения его термодинамических параметров); 1-2 -
политропный процесс сжатия в первой ступени; 2-а - линия нагнетания газа в
промежуточный охладитель 8; а-3 - линия всасывания во второй ступени
компрессора; 3-4 - политропный процесс сжатия во второй ступени; 4-b - линия
нагнетания в промежуточный охладитель 9; b-5 - линия всасывания в третьей
ступени компрессора; 5-6 - политропный процесс сжатия в третьей ступени; 6-с -
линия нагнетания газа в резервуар.
Рис. 5
Отрезки 2-3 и 4-5 изображают уменьшение
объема газа в процессе при постоянном давлении от охлаждения в охладителях 8 и
9.Охлаждение производится до одной температуры, равной температуре всасывания
газа в первой ступени 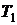 . Поэтому
температуры в точках 1, 3, 5 будут одинаковыми, и через них можно провести
изотерму 1-7.
. Поэтому
температуры в точках 1, 3, 5 будут одинаковыми, и через них можно провести
изотерму 1-7.
Отношение давлений для каждой
ступени обычно принимается одинаковым и равным некоторой величине 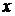 .
.
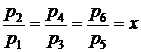 .
.
В случае равенства начальных
температур и показателей политропы конечные температуры также будут равны, т.
е. 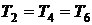 .
.
При равенстве температур газа на
входе в каждую ступень и равенстве отношений давлений затраты работы на сжатие
во всех ступенях будут одинаковыми
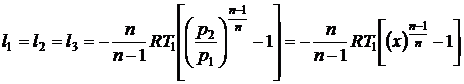 .
.
Работа на привод трехступенчатого
компрессора
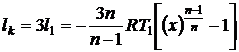 .
.
Эта работа может быть определена
площадью фигуры 0-1-2-3-4-5-6-с-0 на рисунке 2.
Компрессор называется идеальным,
если сжатый в цилиндре газ полностью, без остатка, выталкивается поршнем,
отсутствуют потери энергии в клапанах, отсутствуют утечки и перетечки газа
через неплотности, отсутствуют силы трения поршня о цилиндр.
Вредным пространством называется
некоторый свободный объем  между
поршнем и крышкой цилиндра в момент нахождения поршня в крайнем верхнем
положении. Его объем составляет 4-10% от рабочего объема
между
поршнем и крышкой цилиндра в момент нахождения поршня в крайнем верхнем
положении. Его объем составляет 4-10% от рабочего объема  цилиндра.
Газ, оставшийся во вредном пространстве первого цилиндра, имеет давление
цилиндра.
Газ, оставшийся во вредном пространстве первого цилиндра, имеет давление 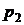 , газ,
оставшийся во вредном пространстве второго цилиндра, имеет давление
, газ,
оставшийся во вредном пространстве второго цилиндра, имеет давление 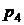 , а газ,
оставшийся во вредном пространстве третьего цилиндра - давление
, а газ,
оставшийся во вредном пространстве третьего цилиндра - давление 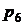 . При
обратном движении поршня происходит расширение газа, оставшегося во вредном
пространстве. Всасывание новой порции газа в цилиндр первой ступени начинается
лишь тогда, когда давление расширяющегося в нем газа станет меньше давления
. При
обратном движении поршня происходит расширение газа, оставшегося во вредном
пространстве. Всасывание новой порции газа в цилиндр первой ступени начинается
лишь тогда, когда давление расширяющегося в нем газа станет меньше давления 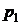 (окружающей
среды). Всасывание новой порции газа в цилиндр второй ступени начинается лишь
тогда, когда давление расширяющегося в нем газа станет меньше давления
(окружающей
среды). Всасывание новой порции газа в цилиндр второй ступени начинается лишь
тогда, когда давление расширяющегося в нем газа станет меньше давления 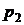 , а
всасывание новой порции газа в цилиндр третьей ступени начинается лишь тогда,
когда давление расширяющегося в нем газа станет меньше давления
, а
всасывание новой порции газа в цилиндр третьей ступени начинается лишь тогда,
когда давление расширяющегося в нем газа станет меньше давления 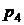 . При этом в
цилиндры поступает новая порция газа
. При этом в
цилиндры поступает новая порция газа 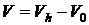 , объем которого меньше рабочего
объема
, объем которого меньше рабочего
объема 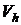 .
Действительная индикаторная диаграмма трехступенчатого компрессора с вредным
пространством показана на рисунке 3. (Объем вредного пространства во всех
цилиндрах предполагается одинаковым).
.
Действительная индикаторная диаграмма трехступенчатого компрессора с вредным
пространством показана на рисунке 3. (Объем вредного пространства во всех
цилиндрах предполагается одинаковым).
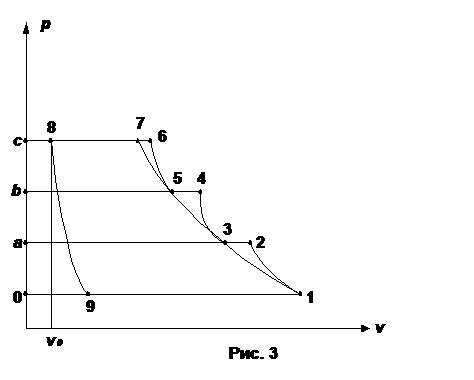
Рис. 6
Работа на привод такого компрессора
может быть определена площадью фигуры 0-1-2-3-4-5-6-8-9 на рисунке 3.
Вредное пространство уменьшает
количество всасываемого газа и, следовательно, уменьшает производительность
компрессора. Степень использования рабочего объема цилиндра оценивается
объемным кпд компрессора
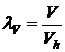 .
.
Объемный кпд уменьшается с
увеличением объема вредного пространства.
Для оценки степени совершенства
реального компрессора его сравнивают с идеальным. При этом для охлаждаемых
компрессоров вводится изотермический кпд
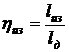 ,
,
где 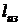 - работа на привод идеального
компрессора при изотермическом сжатии (определяется площадью 1-3-5-7-с-0 на рисунках
2 и3),
- работа на привод идеального
компрессора при изотермическом сжатии (определяется площадью 1-3-5-7-с-0 на рисунках
2 и3), 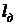 -
действительная работа на привод реального охлаждаемого компрессора
(определяется площадью фигуры 0-1-2-3-4-5-6-8-9 на рисунке 3).
-
действительная работа на привод реального охлаждаемого компрессора
(определяется площадью фигуры 0-1-2-3-4-5-6-8-9 на рисунке 3).
Вопрос 55. Можно ли скорость
истечения пара рассчитать по уравнению
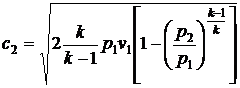 ?
?
Процессы движения газа, происходящие в различных
теплотехнических установках, связаны с преобразованием энергии в газовом
потоке. Расчет газового потока основывается на двух основных допущениях:
течение газа установившееся (не зависит от времени), от сечения к сечению
происходят бесконечно малые изменения параметров газа по сравнению со
значениями самих параметров.
При таких допущениях газ при движении будет
проходить ряд последовательных равновесных состояний.
Уравнение неразрывности (закон сохранения массы)
для одномерного установившегося потока газа имеет вид
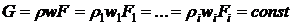 ,
,
где 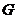 - массовый секундный расход газа,
- массовый секундный расход газа, 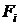 - площади
поперечных сечений канала,
- площади
поперечных сечений канала, 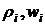 - плотность и скорость газа в
соответствующих сечениях(
- плотность и скорость газа в
соответствующих сечениях(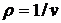 ).
).
Дифференциальное уравнение движения
газа в случае одномерного установившегося потока при отсутствии сил трения и
массовых внешних сил имеет вид
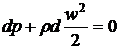 ,
,
где p - давление. Учитывая, что 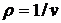 , получим
, получим
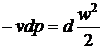 . (1)
. (1)
Величина 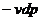 совпадает с
формулой для располагаемой работы в уравнении первого закона термодинамики вида
совпадает с
формулой для располагаемой работы в уравнении первого закона термодинамики вида
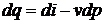 ,
,
где 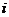 - удельная энтальпия. Отсюда
уравнение первого закона термодинамики для газового потока примет вид
- удельная энтальпия. Отсюда
уравнение первого закона термодинамики для газового потока примет вид
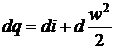 .
.
При адиабатном течении газа (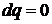 ) последнее
уравнение принимает вид
) последнее
уравнение принимает вид
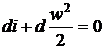 ,
,
после интегрирования получаем
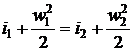 . (2)
. (2)
Таким образом, при адиабатном
течении газа сумма удельных энтальпии 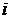 и кинетической энергии
и кинетической энергии 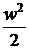 остается
неизменной. Увеличение удельной кинетической энергии газа связано с уменьшением
его энтальпии формулой
остается
неизменной. Увеличение удельной кинетической энергии газа связано с уменьшением
его энтальпии формулой
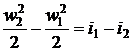 .
.
Уравнение (1) устанавливает основную
закономерность течения газа в каналах различного профиля при дозвуковых
скоростях. В конфузоре (сужающийся канал) давление по длине канала понижается
(dp<0) а скорость растет. В диффузоре (расширяющийся канал) течение газа
сопровождается его сжатием с увеличением давления (dp>0) и уменьшением скорости.
(При сверхзвуковых скоростях потока понижение давления в расширяющихся каналах
приводит к увеличению скорости). Каналы, в которых давление (т.е. потенциальная
энергия газа) понижается, а скорость (т.е. кинетическая энергия) растет,
называются соплами.
При адиабатном истечении газа через
суживающееся сопло из уравнения (2) получим
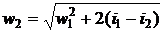 ,
,
где 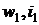 - скорость и энтальпия газа во
входном сечении сопла, а
- скорость и энтальпия газа во
входном сечении сопла, а 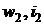 - скорость
и энтальпия газа в выходном сечении Т.е. увеличение скорости обусловлено
изменением энтальпии (переходом тепловой энергии в кинетическую).
- скорость
и энтальпия газа в выходном сечении Т.е. увеличение скорости обусловлено
изменением энтальпии (переходом тепловой энергии в кинетическую).
В случае, когда 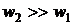 , величиной
, величиной 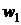 можно
пренебречь. Тогда скорость на выходе из сопла
можно
пренебречь. Тогда скорость на выходе из сопла
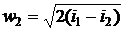 . (3)
. (3)
Для идеального газа 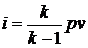 и из
последнего равенства получим
и из
последнего равенства получим
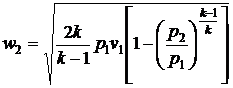 . (4)
. (4)
Водяной пар существенно отличается
от идеального газа, для которого получена формула (4). Поэтому для определения
скорости истечения водяного пара пользуются формулой (3), а значения энтальпии
в точках 1 и 2 находят с помощью 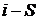 диаграммы водяного пара.
диаграммы водяного пара.
Задача 1. Параметры смеси газов.
Истечение газов
В помещении компрессорной станции
объемом 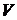 произошла
разгерметизация трубопровода, по которому транспортируется горючий газ под
давлением
произошла
разгерметизация трубопровода, по которому транспортируется горючий газ под
давлением 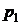 при
температуре
при
температуре 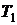 . Через
образовавшееся в трубопроводе сквозное отверстие площадью
. Через
образовавшееся в трубопроводе сквозное отверстие площадью 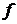 газ выходит
в помещение.
газ выходит
в помещение.
Рассчитать через какое время 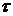 во всем
объеме компрессорной станции может образоваться взрывоопасная смесь, а также
среднюю молекулярную массу, плотность, удельный объем и изобарную удельную
массовую теплоемкость смеси, если ее температура
во всем
объеме компрессорной станции может образоваться взрывоопасная смесь, а также
среднюю молекулярную массу, плотность, удельный объем и изобарную удельную
массовую теплоемкость смеси, если ее температура 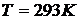 , а давление
, а давление 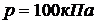 .
Коэффициент расхода отверстия
.
Коэффициент расхода отверстия 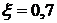 . Воздухообмен не учитывается.
. Воздухообмен не учитывается.
Исходные данные:
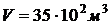 ,
, 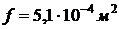 ,
,
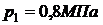 ,
, 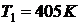 .
.
Газ - пропилен.
Показатель адиабаты газа (пропилен)
возьмем из приложения 1 к методическим указаниям: 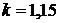 .
.
Определим значение критического
отношения давлений
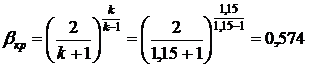 .
.
Отношение давлений в помещении и в
трубопроводе
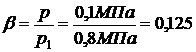 .
.
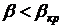 ,т.е. режим истечения критический,
массовый расход газа через отверстие определим по формуле
,т.е. режим истечения критический,
массовый расход газа через отверстие определим по формуле
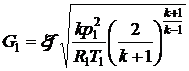 .
.
Здесь 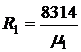 - газовая постоянная пропилена,
- газовая постоянная пропилена, 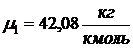 - его
молекулярная масса (из приложения 1 к методическим указаниям).
- его
молекулярная масса (из приложения 1 к методическим указаниям).
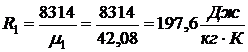 .
.
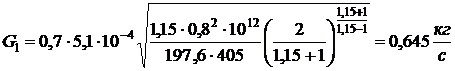 .
.
Из приложения 1 к методическим
показаниям находим НКПВ пропилена
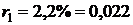 .
.
Масса газа в помещении при НКПВ
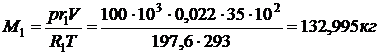 .
.
Время образования взрывоопасной
концентрации
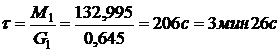 .
.
Объемная доля воздуха в смеси
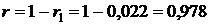 .
.
Молекулярная масса воздуха 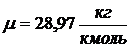 (из
приложения 1 к методическим указаниям). Тогда молекулярная масса смеси
(из
приложения 1 к методическим указаниям). Тогда молекулярная масса смеси
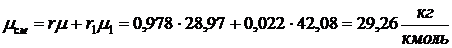 .
.
Газовая постоянная смеси
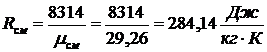 .
.
Плотность смеси
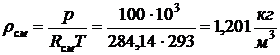 ,
,
удельный объем смеси
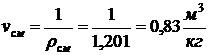 .
.
Массовая доля воздуха в смеси
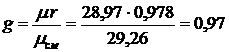 ,
,
массовая доля пропилена в смеси
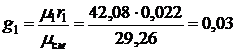 .
.
Мольная изобарная теплоемкость
воздуха и пропилена (из приложения 1 к методическим указаниям)
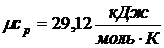 ,
,
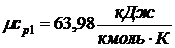 ,
,
тогда массовые удельные изобарные
теплоемкости воздуха и ацетилена
 ,
,
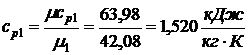 .
.
Изобарную удельную массовую
теплоемкость смеси найдем по формуле
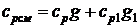 ,
,
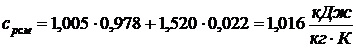 .
.
Задача 2. Конвективный теплообмен.
Теплопередача
Рукавная линия диаметром 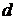 поперечно
обдувается воздухом со скоростью
поперечно
обдувается воздухом со скоростью 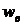 . Температура воздуха
. Температура воздуха 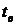 . По
рукавной линии со скоростью
. По
рукавной линии со скоростью 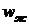 движется вода, температура которой
на входе в рукавную линию
движется вода, температура которой
на входе в рукавную линию 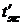 . Рассчитать
максимальную длину рукавной линии из условия, чтобы температура на выходе из
рукавной линии была
. Рассчитать
максимальную длину рукавной линии из условия, чтобы температура на выходе из
рукавной линии была 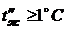 . Толщина
стенки рукавной линии
. Толщина
стенки рукавной линии 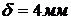 .
Эквивалентный коэффициент теплопроводности материала рукава принять
.
Эквивалентный коэффициент теплопроводности материала рукава принять
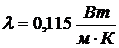 .
.
Исходные данные: 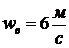 ;
; 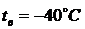 ;
;
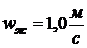 ;
; 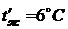 ;
; 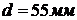 .
.
Средняя температура воды в рукаве
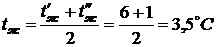 .
.
Из справочника (Теплотехнический
справочник. Под общ. ред. В. Н. Юренева и П. Д. Лебедева. В 2-х т. Т. 2. Изд.
2-е, перераб. М. Энергия, 1976) возьмем кинематическую вязкость воды 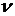 ,
коэффициент теплопроводности воды
,
коэффициент теплопроводности воды 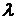 , плотность воды
, плотность воды 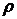 и
теплоемкость воды
и
теплоемкость воды 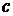 при
температуре
при
температуре 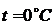
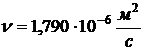 ,
, 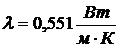 ,
, 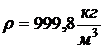 ,
, 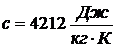 ,
,
и при температуре 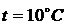
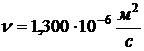 ,
, 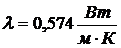 ,
, 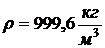 ,
, 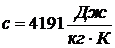 .
.
По этим значениям интерполяцией
определим вязкость 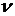 ,
коэффициент теплопроводности
,
коэффициент теплопроводности 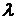 , плотность
, плотность 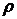 и
теплоемкость воды
и
теплоемкость воды 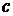 при
температуре
при
температуре 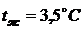
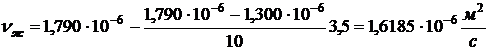 ,
,
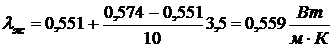 ,
,
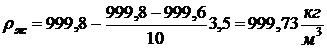 ,
,
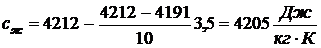 .
.
Для определения режима течения воды найдем число
Рейнольдса
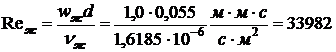 .
.
Число Рейнольдса 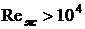 ,
коэффициент теплоотдачи от воды найдем по формуле
,
коэффициент теплоотдачи от воды найдем по формуле
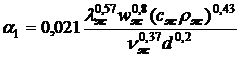 ,
,
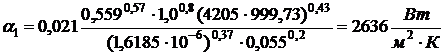 .
.
Из того же справочника возьмем
кинематическую вязкость воздуха 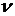 , коэффициент теплопроводности
воздуха
, коэффициент теплопроводности
воздуха 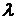 , плотность
воздуха
, плотность
воздуха 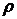 и изобарную
теплоемкость воздуха
и изобарную
теплоемкость воздуха 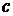 при
температуре
при
температуре 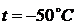
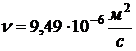 ,
, 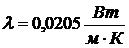 ,
, 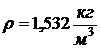 ,
, 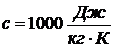 ,
,
и при температуре 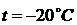
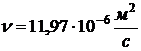 ,
, 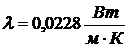 ,
, 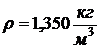 ,
, 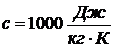 ,
,
тогда при температуре 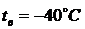
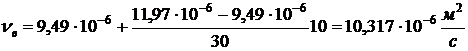 ,
,
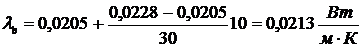 ,
,
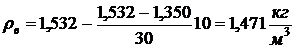 ,
,
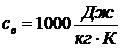 .
.
Наружный диаметр рукава 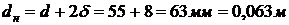 . Для
определения режима течения воздуха найдем число Рейнольдса
. Для
определения режима течения воздуха найдем число Рейнольдса
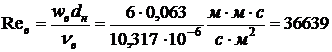 .
.
Число Рейнольдса 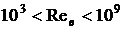 ,
коэффициент теплоотдачи от рукава к воздуху найдем по формуле
,
коэффициент теплоотдачи от рукава к воздуху найдем по формуле
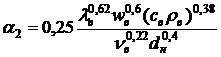 ,
,
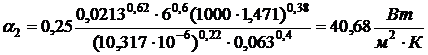 .
.
Коэффициент теплопередачи от воды к
воздуху найдем по формуле
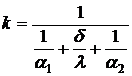 ,
,
где 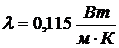 - эквивалентный коэффициент
теплопроводности материала рукава.
- эквивалентный коэффициент
теплопроводности материала рукава.
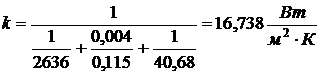 .
.
Массовый расход воды в рукаве
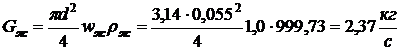 .
.
Количество теплоты, отдаваемое водой
воздуху, найдем через изменение энтальпии воды
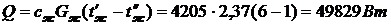 .
.
Средний диаметр рукава 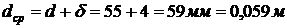 . Тогда
максимальная длина рукавной линии
. Тогда
максимальная длина рукавной линии
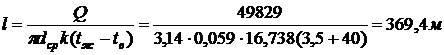 .
.
Задача 3. Лучистый теплообмен
Определить минимальное расстояние,
обеспечивающее безопасность соседнего с горящим объекта, при исходных данных:
проекция факела пламени горящего объекта имеет прямоугольную форму размером 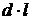 , его
температура
, его
температура 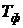 , а степень
черноты
, а степень
черноты 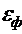 . На
поверхности негорящего объекта: допустимое значение температуры
. На
поверхности негорящего объекта: допустимое значение температуры 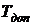 , допустимое
значение плотности теплового потока (критическая плотность)
, допустимое
значение плотности теплового потока (критическая плотность) 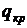 , степень
черноты поверхности
, степень
черноты поверхности 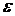 .
.
Кроме того, оценить безопасное
расстояние от факела для личного состава, работающего на пожаре без средств
защиты, при условии а) кратковременного пребывания; б) длительной работы. При
кратковременном тепловом воздействии для кожи человека 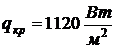 , при
длительном
, при
длительном 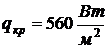 . При
решении задачи учитывать только теплообмен излучением. Коэффициент безопасности
принять равным
. При
решении задачи учитывать только теплообмен излучением. Коэффициент безопасности
принять равным 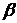 .
.
Исходные данные:
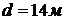 ;
; 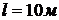 ;
; 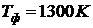 ;
; 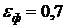 ;
;
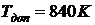 ;
; 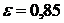 ;
; 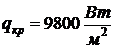 ;
; 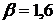 .
.
Минимальное расстояние,
обеспечивающее безопасность соседнего с горящим объекта, найдем из условия
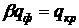 , (1)
, (1)
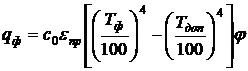
результирующая плотность теплового
потока между факелом и поверхностью тела,
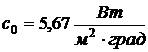
коэффициент излучения абсолютно
черного тела,
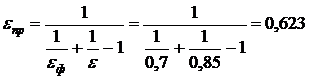
приведенная степень черноты системы,
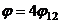
средний по поверхности полный
коэффициент облученности, 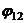
коэффициент облученности, зависящий
от расстояния между факелом и облучаемым телом.
Из равенства (1) получим
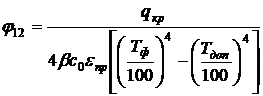 .
.
Для объекта 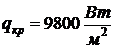 и
и 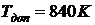
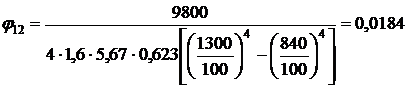 .
.
Для личного состава при
кратковременном пребывании
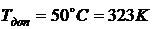 и
и 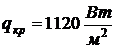
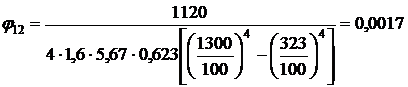 .
.
Для личного состава при длительном пребывании
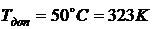 и
и 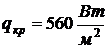
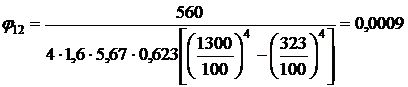 .
.
Коэффициент облученности 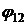 будем
определять по формуле для двух плоскопараллельных поверхностей, расстояние
между которыми равно
будем
определять по формуле для двух плоскопараллельных поверхностей, расстояние
между которыми равно 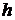 (Теплотехнический
справочник. Под общ. ред. В. Н. Юренева и П. Д. Лебедева. В 2-х т. Т. 2. Изд.
2-е, перераб. М. Энергия, 1976 стр. 191).
(Теплотехнический
справочник. Под общ. ред. В. Н. Юренева и П. Д. Лебедева. В 2-х т. Т. 2. Изд.
2-е, перераб. М. Энергия, 1976 стр. 191).
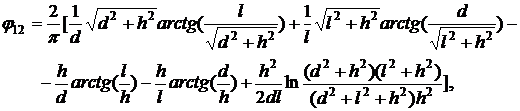
которая при 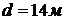 и
и 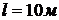 принимает
вид
принимает
вид
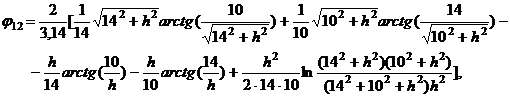
или
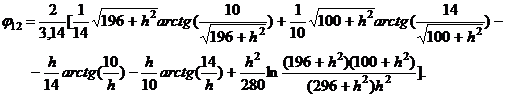
Зададим 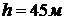 , при этом
значении
, при этом
значении
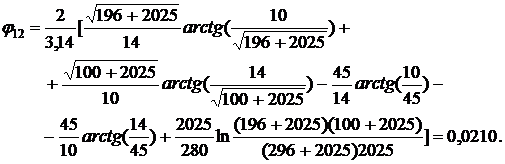
Зададим 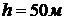 , при этом
значении
, при этом
значении
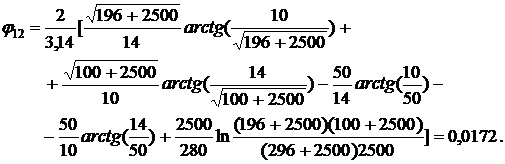
Зададим 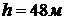 , при этом
значении
, при этом
значении
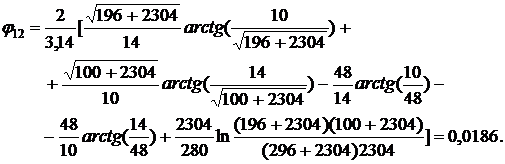
При этом значении
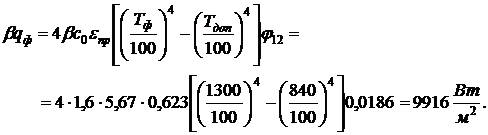
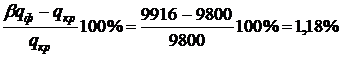
Минимальное расстояние,
обеспечивающее безопасность соседнего с горящим объекта, 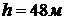 .
.
Зададим 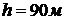 , при этом
значении
, при этом
значении
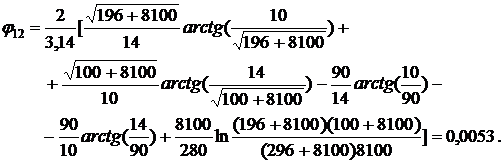
Зададим 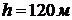 , при этом
значении
, при этом
значении
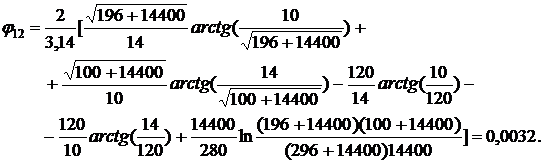
Зададим 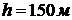 , при этом
значении
, при этом
значении

Зададим 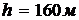 , при этом
значении
, при этом
значении
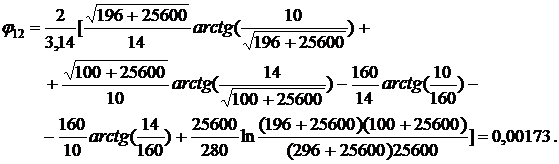
При этом значении
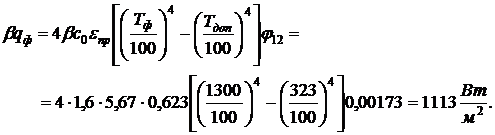
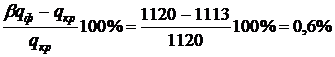 .
.
Минимальное расстояние,
обеспечивающее безопасность личного состава при кратковременном пребывании, 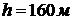 .
.
Зададим 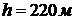 , при этом
значении
, при этом
значении
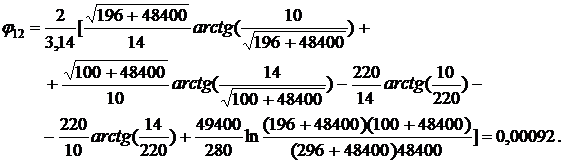
Зададим 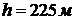 , при этом
значении
, при этом
значении
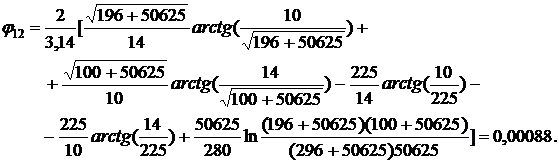
При этом значении
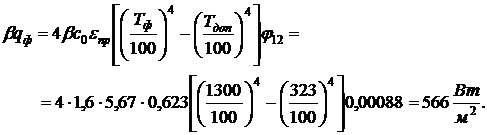
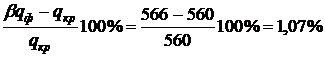 .
.
Минимальное расстояние,
обеспечивающее безопасность личного состава при длительном пребывании, 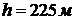 .
.
Задача 4. Температурный режим при
пожаре в помещении
Производство, связанное с обращением
ГЖ, размещено в помещении размерами в плане 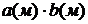 и высотой
и высотой 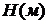 . При аварии
технологических аппаратов возможны и розлив жидкости на пол, и возникновение
пожара. Предусмотрены устройства, ограничивающие растекание жидкости на полу на
площади квадрата
. При аварии
технологических аппаратов возможны и розлив жидкости на пол, и возникновение
пожара. Предусмотрены устройства, ограничивающие растекание жидкости на полу на
площади квадрата 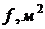 расстояние
от границы горения до стены с оконными и дверными проемами, через которые будет
происходить газообмен при пожаре в помещении с внешней средой,
расстояние
от границы горения до стены с оконными и дверными проемами, через которые будет
происходить газообмен при пожаре в помещении с внешней средой, 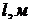 .
.
Механическая вентиляция при
возникновении пожара выключается. За счет естественного газообмена в помещение
поступает такое количество воздуха, что на 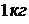 горящей жидкости в среднем
приходится
горящей жидкости в среднем
приходится 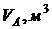 воздуха.
воздуха.
Рассчитайте возможную температуру
среды в помещении при возникновении пожара:
а) среднеобъемную через 5, 15 и 30
мин его развития;
б) локальную в точке над факелом под
перекрытием через 5, 15 и 30 мин его развития;
в) локальную в точках, находящихся
на высоте 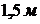 от пола и
расстояниях от границы горения
от пола и
расстояниях от границы горения 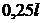 ,
, 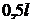 ,
, 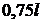 и
и 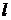 , через 2 мин его развития.
, через 2 мин его развития.
Постройте графики:
а) изменения среднеобъемной
температуры среды в помещении при пожаре во времени;
б) изменения температуры среды в
точке над факелом под перекрытием во времени;
в) изменения температуры среды на
высоте 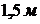 в
зависимости от расстояния от границы горения для 2 мин развития пожара.
в
зависимости от расстояния от границы горения для 2 мин развития пожара.
По графику установите, на каком
расстоянии от выхода значение температуры среды достигнет 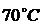 .
.
Исходные данные:
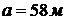 ,
, 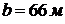 ,
, 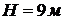 ,
, 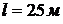 ,
,
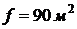 ,
, 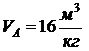 ,
,
жидкость - бутиловый спирт.
Низшая теплота сгорания рабочей массы бутилового
спирта
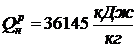 ,
,
теоретический объем воздуха,
необходимый для его горения
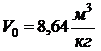 ,
,
теоретический объем продуктов
горения (при коэффициенте избытка воздуха 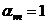 )
)
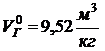
(из приложения 2 к методическим
указаниям).
Коэффициент избытка воздуха
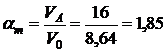 ,
,
тогда приведенный объем продуктов
горения
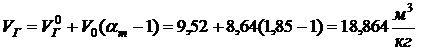 .
.
Площадь поверхности теплообмена
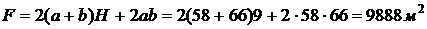 .
.
Массовая скорость выгорания жидкости
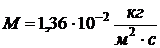
(из приложения 2 к методическим
указаниям), тогда масса жидкости, сгоревшей за 2 мин пожара
 ,
,
масса жидкости, сгоревшей за 5 мин
пожара
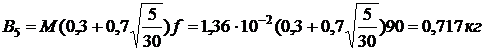 ,
,
масса жидкости, сгоревшей за 15 мин
пожара
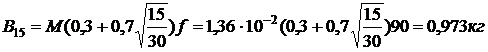 ,
,
масса жидкости, сгоревшей за 30 мин
пожара
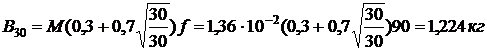 .
.
Пусть 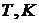 - среднеобъемная температура среды
в помещении при пожаре,
- среднеобъемная температура среды
в помещении при пожаре,  -
коэффициент полноты горения. Тогда приведенная степень черноты системы «среда -
поверхность ограждения»
-
коэффициент полноты горения. Тогда приведенная степень черноты системы «среда -
поверхность ограждения»
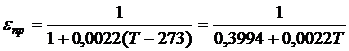 ,
,
удельная объемная изобарная
теплоемкость продуктов горения
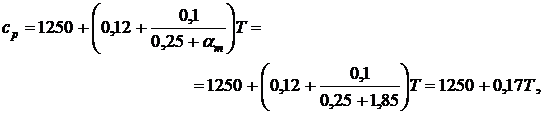
температура продуктов горения
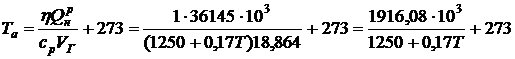 .
.
Среднеобъемная температура среды в
помещении при пожаре для любого момента времени 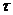 определяется по формуле
определяется по формуле
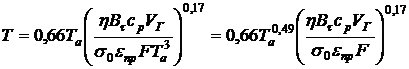 ,
,
где 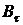 - масса жидкости, сгоревшей за
- масса жидкости, сгоревшей за 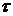 мин пожара,
мин пожара,
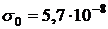 - константа
излучения абсолютно черного тела. Подставим в эту формулу известные значения
величин и выражений
- константа
излучения абсолютно черного тела. Подставим в эту формулу известные значения
величин и выражений
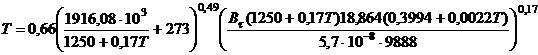
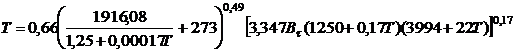 .
.
Для определения среднеобъемной
температуры среды в помещении при пожаре через 2 мин после возникновения пожара
получим уравнение
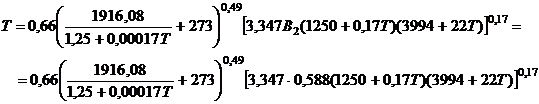
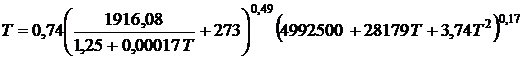 . (1)
. (1)
Для определения среднеобъемной
температуры среды в помещении при пожаре через 5 мин после возникновения пожара
получим уравнение
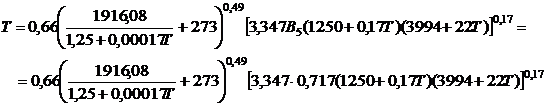
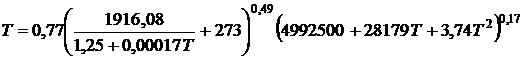 . (2)
. (2)
Для определения среднеобъемной
температуры среды в помещении при пожаре через 15 мин после возникновения
пожара получим уравнение
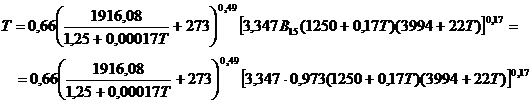
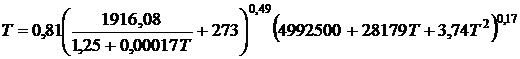 . (3)
. (3)
Для определения среднеобъемной
температуры среды в помещении при пожаре через 30 мин после возникновения
пожара получим уравнение
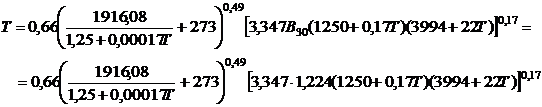
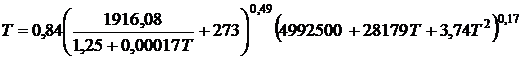 . (4)
. (4)
Уравнения (1), (2), (3) и (4) будем
решать методом итераций.
Решаем уравнение (1).Зададим
начальное значении 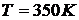 . Найдем
первое приближение
. Найдем
первое приближение
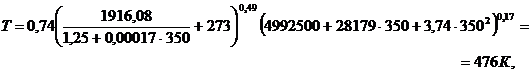
найдем второе приближение
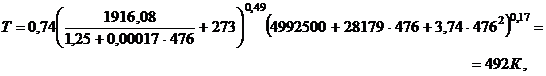
третье приближение
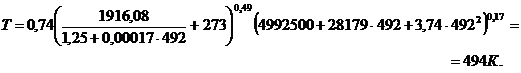
Последние два значения температуры
отличаются на
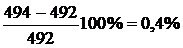 ,
,
поэтому считаем, что среднеобъемная
температура среды в помещении при пожаре через 2 мин после возникновения пожара
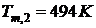 .
.
Решаем уравнение (2).Зададим
начальное значении 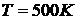 . Найдем
первое приближение
. Найдем
первое приближение
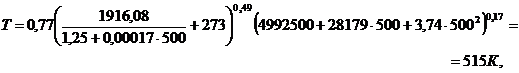
найдем второе приближение
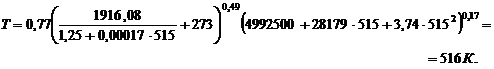
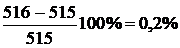 ,
,
поэтому считаем, что среднеобъемная
температура среды в помещении при пожаре через 5 мин после возникновения пожара
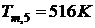 .
.
Решаем уравнение (3).Зададим
начальное значении 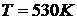 . Найдем
первое приближение
. Найдем
первое приближение
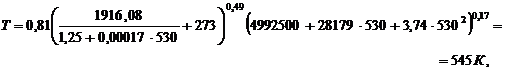
найдем второе приближение
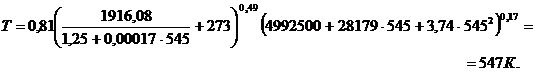
Последние два значения температуры
отличаются на
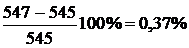 ,
,
поэтому считаем, что среднеобъемная
температура среды в помещении при пожаре через 15 мин после возникновения
пожара 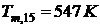 .
.
Решаем уравнение (4).Зададим
начальное значении 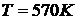 . Найдем
первое приближение
. Найдем
первое приближение
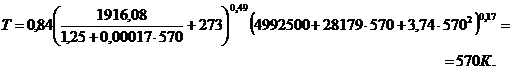
Полученное значение температуры не
отличается от предыдущего, поэтому считаем, что среднеобъемная температура
среды в помещении при пожаре через 30 мин после возникновения пожара 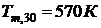 .
.
График изменения среднеобъемной
температуры среды в помещении при пожаре во времени представлен на рисунке 1.

Рис. 7
Локальное значение температуры среды
в помещении при пожаре для любого момента времени 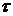 определяется
по формуле
определяется
по формуле
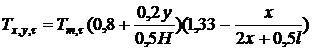 .
.
Тогда локальная температура в точке
над факелом под перекрытием 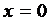 ,
, 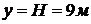 через 2, 5, 15 и 30 мин после
начала пожара будет равна
через 2, 5, 15 и 30 мин после
начала пожара будет равна

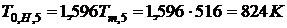 ,
,
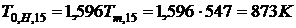 ,
,
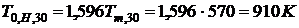 .
.
График изменения температуры среды в
точке над факелом под перекрытием во времени представлен на рисунке 8.

Рис. 8
Локальная температура в точках,
находящихся на высоте 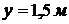 от пола и
расстояниях от границы горения
от пола и
расстояниях от границы горения 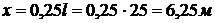 ,
, 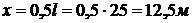 ,
, 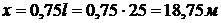 и
и 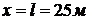 , через 2 мин после начала пожара
будет равна
, через 2 мин после начала пожара
будет равна
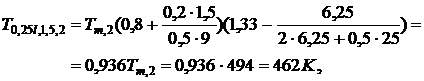
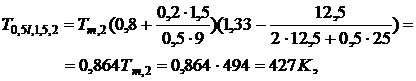
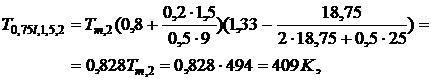
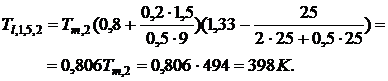
График изменения температуры среды
на высоте 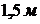 в
зависимости от расстояния от границы горения для 2 мин развития пожара
представлен на рисунке 9.
в
зависимости от расстояния от границы горения для 2 мин развития пожара
представлен на рисунке 9.

Рис. 9
Температура среды достигнет 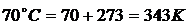 при
при 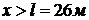 .
.
Задача 5. Нестационарная теплопроводность.
Изменяющиеся граничные условия 3 рода
тело энергия эксергия
газ
Рассчитайте температурное поле по
толщине перекрытия через 0,5 ч после начала пожара, используя полученные при
решении задачи 4 результаты расчета температуры среды над факелом под перекрытием
(график изменения температуры среды под перекрытием). Перекрытие представляет
собой сплошную железобетонную плиту толщиной 18 см. Коэффициент
теплопроводности слоя бетона 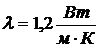 . Начальная температура перекрытия
. Начальная температура перекрытия 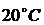 , такую же
температуру имеет воздух над перекрытием.
, такую же
температуру имеет воздух над перекрытием.
Максимальное значение температуры
среды за время пожара по результатам решения задачи 4
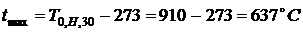 .
.
Тогда максимальное значение
коэффициента теплоотдачи на обогреваемой поверхности
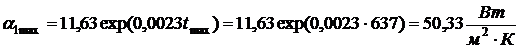 ,
,
максимальная толщина расчетного слоя
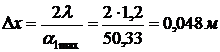 ,
,
минимальное количество расчетных
слоев
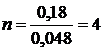 .
.
Задаем количество расчетных слоев по
толщине перекрытия 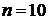 , толщина
каждого расчетного слоя
, толщина
каждого расчетного слоя
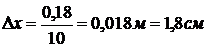 .
.
Теплоемкость железобетона 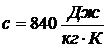 , его
плотность
, его
плотность 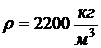 (Ерохин В.
Г., Маханько М. Г. Сборник задач по основам гидравлики и теплотехники. М.:
Энергия, 1979). Тогда коэффициент температуропроводности материала перекрытия
(Ерохин В.
Г., Маханько М. Г. Сборник задач по основам гидравлики и теплотехники. М.:
Энергия, 1979). Тогда коэффициент температуропроводности материала перекрытия
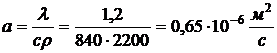 .
.
Максимальный интервал времени для
расчета
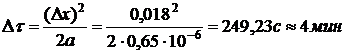 .
.
Дифференциальное уравнение
одномерной нестационарной теплопроводности имеет вид
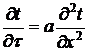 . (1)
. (1)
Разобьем перекрытие по толщине на 10
слоев. Координаты точек разбиения обозначим через 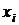 .
.
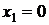 ,
, 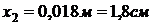 ,
, 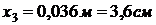 ,
, 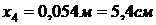 ,
,
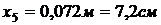 ,
, 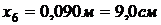 ,
, 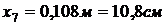 ,
,
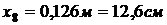 ,
, 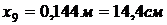 ,
, 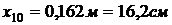 ,
,
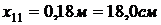 .
.
Зададим интервал времени 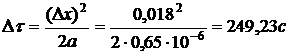 . Моменты
времени, в которые будет вычисляться температура обозначим через
. Моменты
времени, в которые будет вычисляться температура обозначим через 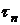
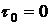 ,
, 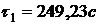 ,
, 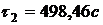 ,
, 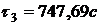 ,
, 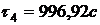 ,
,
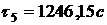 ,
, 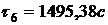 ,
, 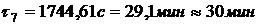 .
.
Обозначим значение температуры в
точке 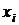 в момент
времени
в момент
времени 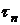 через
через 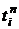 , т. е.
, т. е.
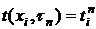 .
.
Тогда конечно-разностный аналог
уравнения (1) запишется в виде
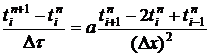 ,
,
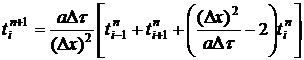 . (2)
. (2)
При 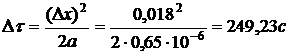 это уравнение принимает вид
это уравнение принимает вид
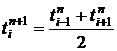 . (3)
. (3)
В начальный момент времени 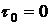 :
:
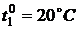 ,
, 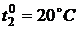 ,
, 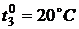 ,
, 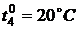 ,
, 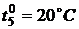 ,
, 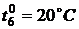 ,
,
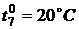 ,
, 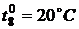 ,
, 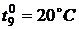 ,
, 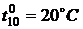 ,
, 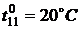 .
.
По формуле (3) найдем значения
температуры во внутренних точках в момент времени 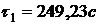
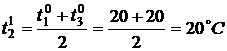 ,
, 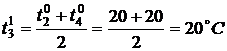 ,
,
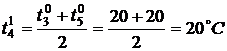 ,
, 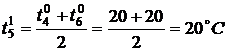 ,
,
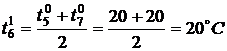 ,
, 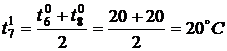 ,
,
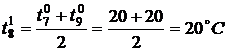 ,
, 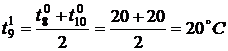 ,
,
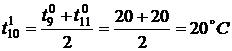 .
.
Температуры среды за время пожара в
момент времени 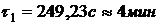 по
результатам решения задачи 4 (с графика на рис. 2)
по
результатам решения задачи 4 (с графика на рис. 2)
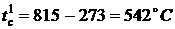 ,
,
коэффициента теплоотдачи на
обогреваемой поверхности
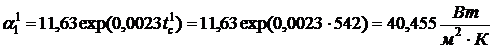 .
.
Температуру перекрытия в точке 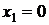 найдем из
равенства
найдем из
равенства
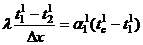
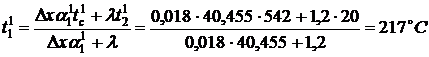 .
.
Температура воздуха над перекрытием 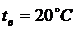 Коэффициента
теплоотдачи на холодной поверхности перекрытия
Коэффициента
теплоотдачи на холодной поверхности перекрытия
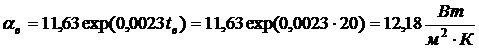 .
.
Температуру перекрытия в точке 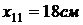 найдем из
равенства
найдем из
равенства
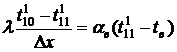
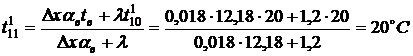 .
.
По формуле (3) найдем значения
температуры во внутренних точках в момент времени 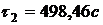
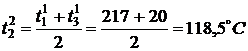 ,
, 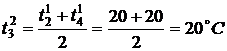 ,
,
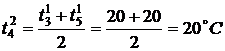 ,
, 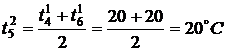 ,
,
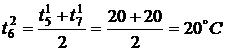 ,
, 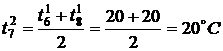 ,
,
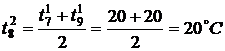 ,
,  ,
,
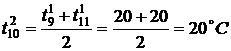 .
.
Температуры среды за время пожара в
момент времени 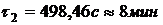 по
результатам решения задачи 4 (с графика)
по
результатам решения задачи 4 (с графика)
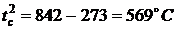 ,
,
коэффициента теплоотдачи на
обогреваемой поверхности
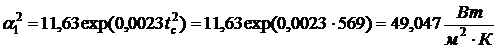 .
.
Температура перекрытия в точке 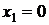
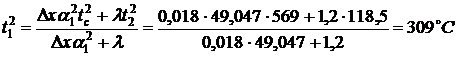 .
.
Температура перекрытия в точке 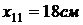
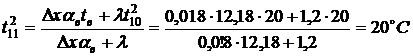 .
.
По формуле (3) найдем значения
температуры во внутренних точках в момент времени 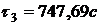
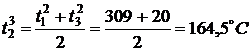 ,
, 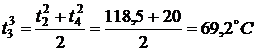 ,
,
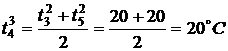 ,
, 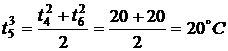 ,
,
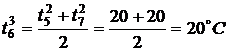 ,
, 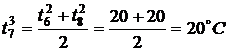 ,
,
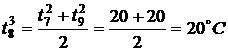 ,
, 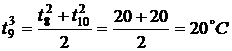 ,
,
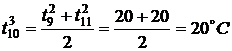 .
.
Температуры среды за время пожара в
момент времени 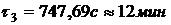 по
результатам решения задачи 4 (с графика)
по
результатам решения задачи 4 (с графика) 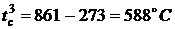 ,
,
коэффициента теплоотдачи на
обогреваемой поверхности
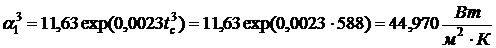 .
.
Температура перекрытия в точке 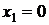
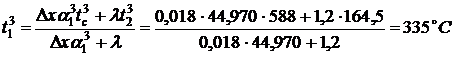 .
.
Температура перекрытия в точке 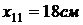
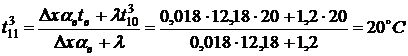 .
.
По формуле (3) найдем значения
температуры во внутренних точках в момент времени 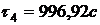
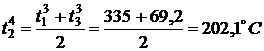 ,
, 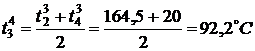 ,
,
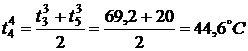 ,
, 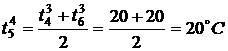 ,
,
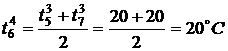 ,
, 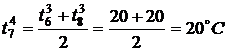 ,
,
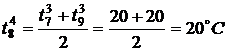 ,
, 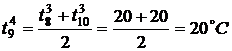 ,
,
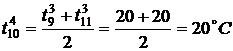 .
.
Температуры среды за время пожара в
момент времени 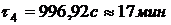 по
результатам решения задачи 4 (с графика)
по
результатам решения задачи 4 (с графика)
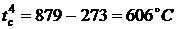 ,
,
коэффициента теплоотдачи на
обогреваемой поверхности
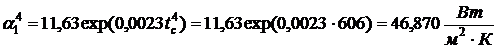 .
.
Температура перекрытия в точке 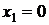
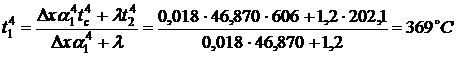 .
.
Температура перекрытия в точке 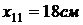
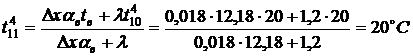 .
.
По формуле (3) найдем значения
температуры во внутренних точках в момент времени 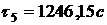
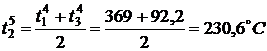 ,
, 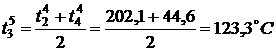 ,
,
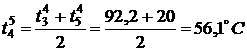 ,
, 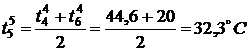 ,
,
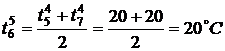 ,
, 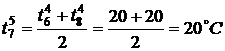 ,
,
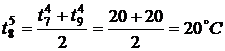 ,
, 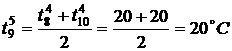 ,
,
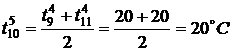 .
.
Температуры среды за время пожара в
момент времени 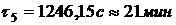 по
результатам решения задачи 4 (с графика)
по
результатам решения задачи 4 (с графика)
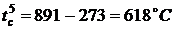 ,
,
коэффициента теплоотдачи на
обогреваемой поверхности
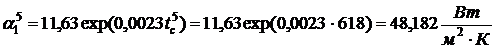 .
.
Температура перекрытия в точке 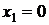
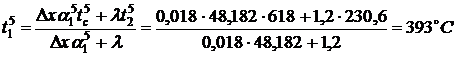 .
.
Температура перекрытия в точке 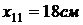
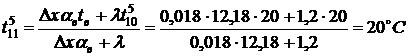 .
.
По формуле (3) найдем значения
температуры во внутренних точках в момент времени 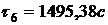
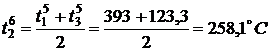 ,
, 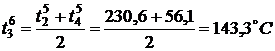 ,
,
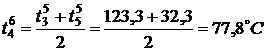 ,
, 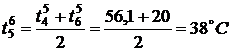 ,
,
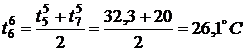 ,
, 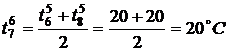 ,
,
 ,
, 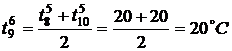 ,
,
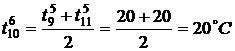 .
.
Температуры среды за время пожара в
момент времени 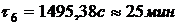 по
результатам решения задачи 4 (с графика)
по
результатам решения задачи 4 (с графика)
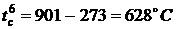 ,
,
коэффициента теплоотдачи на
обогреваемой поверхности
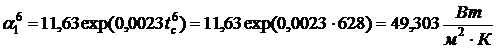 .
.
Температура перекрытия в точке 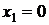
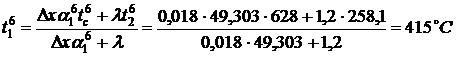 .
.
Температура перекрытия в точке 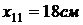
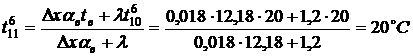 .
.
По формуле (3) найдем значения
температуры во внутренних точках в момент времени 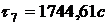
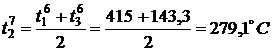 ,
, 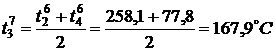 ,
,
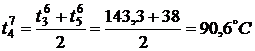 ,
, 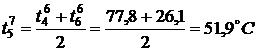 ,
,
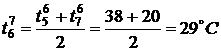 ,
, 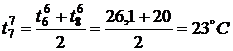 ,
,
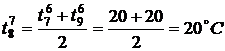 ,
, 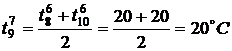 ,
,
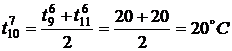 .
.
Температуры среды за время пожара в
момент времени 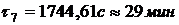 по
результатам решения задачи 4 (с графика)
по
результатам решения задачи 4 (с графика)
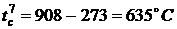 ,
,
коэффициента теплоотдачи на
обогреваемой поверхности
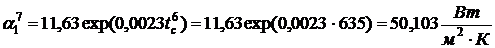 .
.
Температура перекрытия в точке 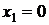
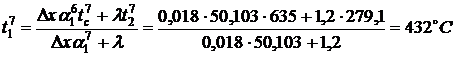 .
.
Температура перекрытия в точке 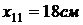
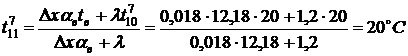 .
.
Результаты расчетов приведены в
таблице.
График распределения температуры по толщине
перекрытия через 29 минут после начала пожара приведен на рисунке.

Рис. 10
Задача 6. Нестационарная
теплопроводность. Не изменяющиеся граничные условия 3 рода
Железобетонная плита перекрытия
толщиной 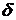 обогревается
с одной стороны средой с температурой
обогревается
с одной стороны средой с температурой 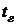 в течение
в течение 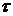 мин.
Коэффициент теплообмена на обогреваемой поверхности плиты
мин.
Коэффициент теплообмена на обогреваемой поверхности плиты 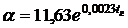 . Начальная
температура перекрытия
. Начальная
температура перекрытия 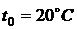 ,
Коэффициент теплопроводности железобетона
,
Коэффициент теплопроводности железобетона 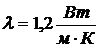 , коэффициент температуропроводности
, коэффициент температуропроводности
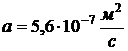 .
.
Рассчитать температуру на расстоянии
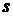 от
обогреваемой поверхности плиты: а) принимая перекрытие за неограниченную
пластину; б) принимая перекрытие, как полуограниченное тело.
от
обогреваемой поверхности плиты: а) принимая перекрытие за неограниченную
пластину; б) принимая перекрытие, как полуограниченное тело.
Исходные данные: 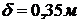 ,
, 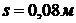 ,
, 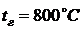 ,
, 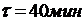 .
.
Коэффициента теплоотдачи на
обогреваемой поверхности
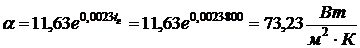 .
.
Принимаем перекрытие за
неограниченную пластину. Найдем числа Био и Фурье
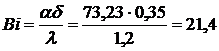 ,
,
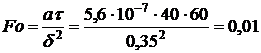 .
.
При одностороннем нагревании
неограниченной пластины толщиной 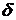 в течении времени
в течении времени 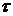 температура
на расстоянии
температура
на расстоянии 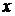 от необогреваемой
поверхности определяется по формуле
от необогреваемой
поверхности определяется по формуле
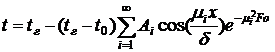 , (1)
, (1)
где 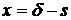 ,
, 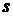 - расстояние от обогреваемой
поверхности,
- расстояние от обогреваемой
поверхности,
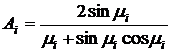 ,
,
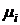 - корни характеристического
уравнения
- корни характеристического
уравнения 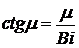 .
.
Так как число Фурье 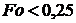 в формуле
(1) ограничимся тремя первыми членами ряда. Тогда
в формуле
(1) ограничимся тремя первыми членами ряда. Тогда
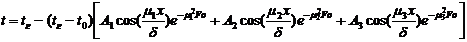 , (2)
, (2)
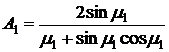 ,
, 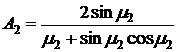 ,
, 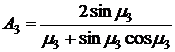 .
.
Из учебника (Исаченко В. П., Осипова
В. А., Сукомел А. С. Теплопередача. М.: Энергия, 1975, стр.79) возьмем значение
первых трех корней характеристического уравнения при 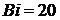
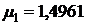 ,
, 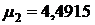 ,
, 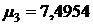
и при 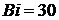
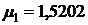 ,
, 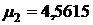 ,
, 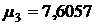 .
.
Значения 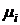 при
при 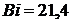 найдем
интерполяцией
найдем
интерполяцией
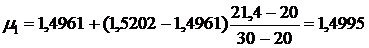 ,
,
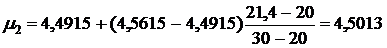 ,
,
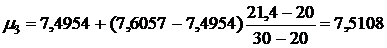 .
.
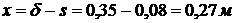 ,
,
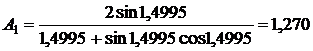 ,
,
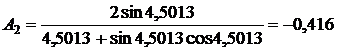 ,
,
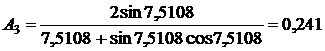 ,
,
 ,
,
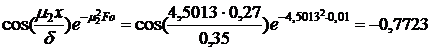 ,
,
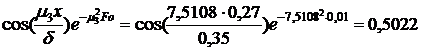 ,
,
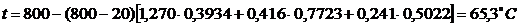 .
.
Принимаем перекрытие за полуограниченное
тело. Найдем аргументы функции Крампа
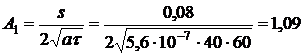 ,
,
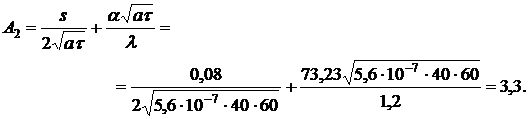
Из таблицы значений функции Крампа
(Юдаев Б. Н. Теплопередача. М.: Высшая школа, 1973, стр.97) находим, что при
при 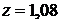
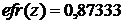 а при
а при 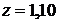
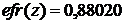 . Тогда при
. Тогда при 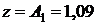
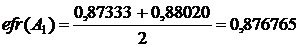 .
.
Из той же таблицы при 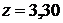
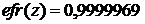 . Тогда
. Тогда
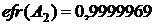 .
.
Температуру на расстоянии 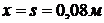 от
обогреваемой поверхности найдем по формуле
от
обогреваемой поверхности найдем по формуле
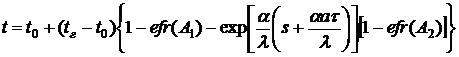 ,
,
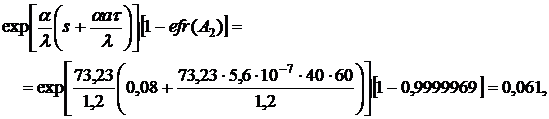
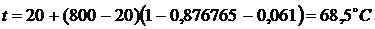 .
.