SVD-сжатие, модификации
Министерство
образования и науки российской федерации
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
Кубанский
государственный университет
Факультет
математики и компьютерных наук
Кафедра
математических и компьютерных методов
Направление 02.03.01 Математика и
компьютерные науки
Выпускная квалификационная работа
бакалавра
Тема:
SVD-сжатие, модификации
Выполнила К.Г. Твердова
курс, группа 43.1
Руководитель, д.ф.-м.н.,
профессор В.Г. Лежнев
Краснодар, 2015
СОДЕРЖАНИЕ
Введение
. Сингулярное
разложение
1.1
Определение SVD
.2 Методы
нахождения сингулярного разложения
.3 Алгоритм
SVD
.4
Сингулярное разложение и собственные значения матрицы
2.
Пространства матрицы и SVD
2.1
Сингулярное разложение и нормирование матриц
3. SVD-сжатие
. Метод
максимизации столбцов
.
Практическая часть
Заключение
Список
использованных источников
ВВЕДЕНИЕ
Жизнь современного общества невозможно представить без широкого
применения информационных технологий. Бурное развитие Интернета, компьютерной,
копировальной и фототехники привело к широкому использованию цифровых
изображений и обусловило большой интерес к разработке эффективных алгоритмов
сжатия таких изображений.
Применение алгоритмов, обеспечивающих высокую степень сжатия, позволяет
увеличить скорость передачи данных по каналам связи и эффективность их
хранения.
Эта проблема и была поставлена для решения в данной работе. Здесь
предполагается реализация возможности сжатия изображения с помощью SVD-сжатия.
Для решения поставленной цели необходимо рассмотреть ряд сопутствующих
задач:
1. Рассмотреть особенности сингулярного разложения
2. Разработать алгоритм, реализующий сжатие изображения
. Применить теорию о сингулярном разложении для сжатия изображения
при помощи MathCAD, разработав программу для сжатия
изображения
. Произвести анализ динамики сингулярных чисел
. Сделать выводы
1. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ
.1
Определение SVD
Теорема. Для любой вещественной (п х п)-матрицы A существуют две вещественные ортогональные (п х п)-матрицы U и V такие, что
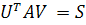
Более того, можно выбрать U и V
так, чтобы диагональные элементы 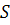 имели вид
имели вид
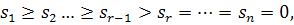
где r - ранг матрицы A. В частности, если A невырождена, то
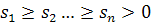
Индекс r элемента 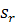 есть фактическая размерность
собственного пространства матрицы A.
есть фактическая размерность
собственного пространства матрицы A.
Столбцы матриц U и V называются соответственно левыми и
правыми сингулярными векторами, а значения диагонали матрицы 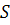 называются сингулярными значениями
[1].
называются сингулярными значениями
[1].
Пусть A - (m х n)-матрица
и ей в соответствие поставлен линейный оператор, также обозначаемый A. Формулу сингулярного разложения 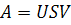 T можно переформулировать в
геометрических терминах. Линейный оператор, отображающий элементы пространства Rm в элементы пространства Rn представим в виде последовательно
выполняемых линейных операций вращения, растяжения и вращения. Число ненулевых
элементов на диагонали матрицы
T можно переформулировать в
геометрических терминах. Линейный оператор, отображающий элементы пространства Rm в элементы пространства Rn представим в виде последовательно
выполняемых линейных операций вращения, растяжения и вращения. Число ненулевых
элементов на диагонали матрицы 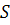 есть фактическая размерность матрицы A.
есть фактическая размерность матрицы A.
Поэтому компоненты сингулярного разложения наглядно показывают
геометрические изменения при отображении линейным оператором A множества векторов из одного
векторного пространства в другое.
.2 Методы
нахождения сингулярного разложения
Для нахождения сингулярного разложения существует 4 основных метода -
QR-итераций, Якоби, метод «разделяй-и-влавствуй», бисекции [2].
В настоящее время «разделяй-и-влавствуй» один из самых быстрых алгоритмов
отыскания сингулярных чисел и сингулярных векторов матриц порядка больше 25.
Однако алгоритм «разделяй-и-властвуй» не гарантирует высокой относительной
точности для малых сингулярных чисел.
Метод бисекции способен вычислять сингулярные числа на заданном
интервале. Таким образом, для реализации сингулярного разложения были выбраны
метод Якоби и QR-итераций, т.к. метод Якоби является наиболее точным, а
QR-итераций наиболее быстрым и надежным.
В отличие от QR-алгоритма, метод Якоби не предполагает первоначального
приведения к трехдиагональной форме, а работает с исходной плотной матрицей. Он
работает медленнее, однако способен вычислять сингулярные числа и сингулярные
векторы намного точнее, чем другие алгоритмы.
.3 Алгоритм SVD
Рассмотрим приближенное линейное описание матрицы 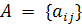 вида
вида
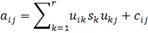 , (1)
, (1)
где 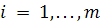 и
и 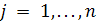 .
.
Значения 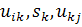 для данного значения k найдены из условия минимума выражения
для данного значения k найдены из условия минимума выражения
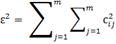 , (2)
, (2)
при ограничениях нормировки
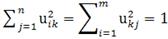 , (3)
, (3)
и упорядоченности 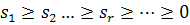
Выражения (1), (2), (3) запишем в матричных обозначениях:
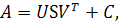
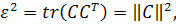
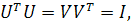
где матрицы 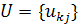 ,
, 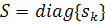 ,
, 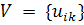 . Если значение r достаточно велико, то
. Если значение r достаточно велико, то 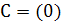 .
.
Так будет заведомо при 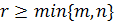 . Минимальное значение r, при котором выполнимо равенство
. Минимальное значение r, при котором выполнимо равенство 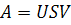 T, равно рангу матрицы A.
T, равно рангу матрицы A.
Один из возможных алгоритмов нахождения сингулярного разложения
заключается в следующем. Найдем последовательно векторы uk, vk и сингулярные числа 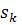 для
для 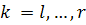 . В качестве этих векторов берутся
нормированные значения векторов ak и bk соответственно:
. В качестве этих векторов берутся
нормированные значения векторов ak и bk соответственно:
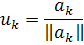
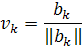

Процедура нахождения векторов uk, vk
начинается с выбора наибольшей по норме строки b11 матрицы A. Для
k = 1 формулы нахождения векторов a1i, b1i имеют вид:
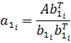
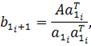
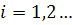
Для вычисления векторов uk, vk при 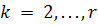 используется вышеприведенная
формула, c той разницей, что матрица A заменяется на скорректированную на k-м шаге матрицу
используется вышеприведенная
формула, c той разницей, что матрица A заменяется на скорректированную на k-м шаге матрицу 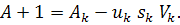
.4
Сингулярное разложение и собственные значения матрицы
Сингулярное разложение обладает свойством, которое связывает задачу
отыскания сингулярного разложения и задачу отыскания собственных векторов.
(Собственный вектор x матрицы A - такой вектор, при котором
выполняется условие 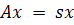 ), число
), число 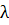 называется собственным числом. Так как матрицы U и V ортогональные, то есть
называется собственным числом. Так как матрицы U и V ортогональные, то есть
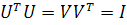 , (4)
, (4)
где I - единичная матрица размерности 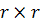 , то из (4) следует, что
, то из (4) следует, что
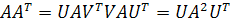 ,
,
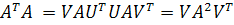 (5)
(5)
Умножая оба выражения справа соответственно на U и V получаем
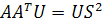 ,
,
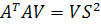 (6)
(6)
Из выражения (6) следует, что столбцы матрицы U являются собственными векторами матрицы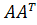 , а квадраты сингулярных чисел
, а квадраты сингулярных чисел 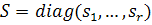 ее собственными значениями. Также
столбцы матрицы V являются
собственными векторами матрицы
ее собственными значениями. Также
столбцы матрицы V являются
собственными векторами матрицы 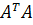 , а квадраты сингулярных чисел являются ее собственными
значениями.
, а квадраты сингулярных чисел являются ее собственными
значениями.
2.
ПРОСТРАНСТВА МАТРИЦЫ И SVD
Сингулярное разложение позволяет найти ортогональные базисы различных
векторных пространств разлагаемой матрицы. В теореме о сингулярном разложении
рассматривается матрица размером (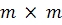 ),
),
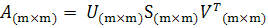
Существует так называемое экономное представление сингулярного разложения
матрицы.
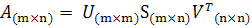
Согласно этому представлению при 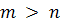 , диагональная матрица
, диагональная матрица 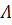 имеет пустые строки, а при
имеет пустые строки, а при 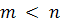 - пустые столбцы. Поэтому существует
еще одно экономное представление [1]:
- пустые столбцы. Поэтому существует
еще одно экономное представление [1]:
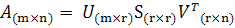 ,
,
в котором 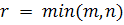
Нуль-пространство матрицы A -
набор векторов х, для которого справедливо высказывание 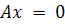 . Собственное пространство матрицы A - набор векторов b, при котором уравнение
. Собственное пространство матрицы A - набор векторов b, при котором уравнение 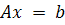 имеет ненулевое решение для х.
Обозначим
имеет ненулевое решение для х.
Обозначим 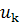 и
и 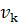 - столбцы матриц U и V.
- столбцы матриц U и V.
Тогда разложение 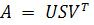 может быть записано в виде:
может быть записано в виде:
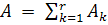 ,
,
где 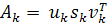 .
.
Если сингулярное значение 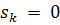 , то
, то 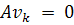 и
и 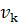 находится в нуль-пространстве матрицы A, а если сингулярное значение
находится в нуль-пространстве матрицы A, а если сингулярное значение 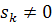 , то вектор
, то вектор 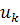 находятся в собственном пространстве
матрицы A.
находятся в собственном пространстве
матрицы A.
Следовательно, можно сконструировать базисы для различных векторных
подпространств, определенных матрицей A.
Набор векторов 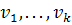 в векторном пространстве V формирует базис для V, если любой
вектор х из V можно представить в виде линейной комбинации векторов
в векторном пространстве V формирует базис для V, если любой
вектор х из V можно представить в виде линейной комбинации векторов 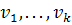 единственным способом.
единственным способом.
Пусть V0 будет набором тех столбцов 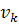 , для которых
, для которых 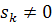 , а V1 - все остальные столбцы
, а V1 - все остальные столбцы 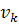 .
.
Также, пусть U0 будет набором столбцов 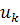 , для которых
, для которых 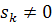 , а U1 - все остальные столбцы
, а U1 - все остальные столбцы 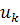 , включая и те, для которых
, включая и те, для которых 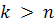 .
.
Тогда, если r - количество
ненулевых сингулярных значений, то имеется r столбцов в наборе V0 и 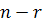 столбцов в наборе V1 и U1, а также
столбцов в наборе V1 и U1, а также 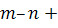
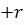 столбцов в наборе U0.
столбцов в наборе U0.
Каждый из этих наборов формирует базис векторного пространства матрицы A:
V0 - ортонормальный базис для
ортогонального комплементарного нуль-пространства A,
V1
- ортонормальный
базис для нуль-пространства A,
U0 - ортонормальный базис для
собственного пространства A,
U1 - ортонормальный базис для
ортогонального комплементарного нуль-пространства A.
2.1
Сингулярное разложение и нормирование матриц
Рассмотрим изменение длины вектора х до и после его умножения справа матрицу
A. Евклидова норма вектора определена
как:
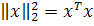
При умножении вектора x на
матрицу A справа, длина результирующего
вектора Ax изменяется.
Если матрица A ортогональна,
длина вектора Ax остается неизменной. В противном случае,
с помощью выражения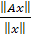 , можно вычислить, насколько матрица A растянула вектор x.
, можно вычислить, насколько матрица A растянула вектор x.
Таким образом, евклидова норма матрицы, есть максимальный коэффициент
растяжения вектора.
Евклидова норма матрицы определяется так. Пусть x является n-мерным
вектором, и A - матрица размерности 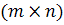 . Тогда Евклидова норма матрицы
. Тогда Евклидова норма матрицы
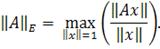
Альтернативной Евклидовой норме является норма Фробениуса:
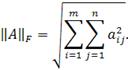
Если известно сингулярное разложение, то обе эти нормы легко узнать.
Пусть 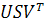 -сингулярное разложение (
-сингулярное разложение (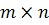 )-матрицы A.
)-матрицы A.
Тогда
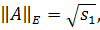 и
и
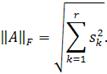
Сингулярные значения матрицы A - это длины осей эллипсоида, заданного множеством 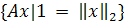 .
.
3. SVD-СЖАТИЕ
Матрица изображения А = (aij), размерности n x n, представима в виде A = USVT, где U, V - ортогональный матрицы, а S-диагональная, на главной диагонали
которой расположены (в порядке убывания) неотрицательные значения sk - сингулярные числа матрицы.
Величина
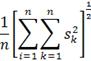
определяет среднеквадратичную норму функции-изображения, которая наиболее
подходит для сравнения изображений. При этом удобно использовать равенство
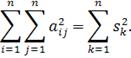
Для многих классов изображений сингулярные числа sk очень быстро убывают. Можно оставить
малое количество сингулярных чисел, норма очень мало изменится, изображения
на-глаз, будут почти не различимы. Этот феномен и дает возможность
сжатия-восстановления (с потерями).
Черно-белое изображение размерности nxn пикселей можно рассматривать как матрицу той же
размерности, значениями элементов который служат числа - соответствующие
интенсивности белого цвета для каждого пикселя. Поэтому, как и для любой
матрицы, к изображению можно применить сингулярное разложение.
Рассмотрим алгоритм SVD
сжатия изображений. Так как сингулярные значения быстро убывают, то, начиная с
некоторого номера p, их вклад в
общую сумму 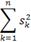 достаточно мал, и эти оставшиеся значения можно не учитывать
при восстановлении исходного изображения. В формуле A = USVT нет необходимости целиком сохранять матрицы U, S, V, что позволяет
производить сжатие изображения.
достаточно мал, и эти оставшиеся значения можно не учитывать
при восстановлении исходного изображения. В формуле A = USVT нет необходимости целиком сохранять матрицы U, S, V, что позволяет
производить сжатие изображения.
Справедливо приближенное неравенство
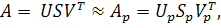
где Sp = diag (s1,…, sp, 0,…, 0), в матрицах 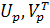 первые p столбцов и первые p строк соответственно совпадают со столбцами и строками матриц U, V, а остальные элементы равны нулю.
первые p столбцов и первые p строк соответственно совпадают со столбцами и строками матриц U, V, а остальные элементы равны нулю.
Следовательно, вместо матрицы A размерности n x n требуется сохранять матрицы размерности n x p, p x n и строку из p
чисел sk. Т.е. получим сжатие с коэффициентом
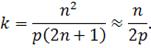
Анализ влияния сохраняемого количества сингулярных значений на качество
сжатого черно-белого изображения. Выбор числа p можно характеризовать значениями параметра 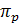 :
:
4. МЕТОД
МАКСИМИЗАЦИИ СТОЛБЦОВ
Рассматривается алгоритм, позволяющий решать частную задачу сингулярного
разложения матрицы - получение определенного числа главных сингулярных чисел.
Максимизация столбца. Пусть А = (aij) - вещественная квадратная матрица
порядка n. Будем обозначать ak = (a1k, …, ank)T ее
k-ый столбец, а через |ak|, (ak, ap) - евклидову норму и скалярное
произведение вектор-столбцов.
Обозначим через 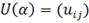 ортогональную матрицу с элементами
ортогональную матрицу с элементами 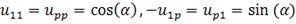 , а остальные диагональные элементы
равны единице, внедиагональные - нулю.
, а остальные диагональные элементы
равны единице, внедиагональные - нулю.
Рассмотрим матрицу 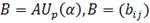 . Для столбцов матрицы В имеем
. Для столбцов матрицы В имеем
Угол 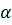 будем выбирать так, что норма первого столбца
будем выбирать так, что норма первого столбца 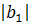 была бы максимальной.
Максимизирующий угол
была бы максимальной.
Максимизирующий угол 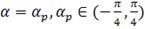 , определяется следующим правилом:
, определяется следующим правилом:
а) если 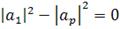 , то
, то
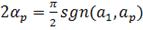 , (7)
, (7)
б) иначе 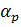 определяется равенство
определяется равенство
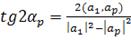 (8)
(8)
Свойство 1. Если 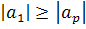 , то
, то 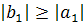 , т.е. норма первого столбца не убывает при рассматриваемом
преобразовании матрица А.
, т.е. норма первого столбца не убывает при рассматриваемом
преобразовании матрица А.
Свойство 2. Если 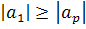 , то
, то 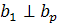 , т.е. новые столбцы
, т.е. новые столбцы 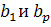 ортогональны.
ортогональны.
Итерационная последовательность матриц. Пусть 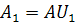 , где
, где 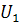 - ортогональная матрица перестановки
первого столбца с максимальным по норме столбцом матрицы А. Рассмотрим
последовательность
- ортогональная матрица перестановки
первого столбца с максимальным по норме столбцом матрицы А. Рассмотрим
последовательность 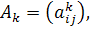
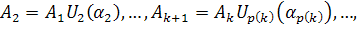 (9)
(9)
где 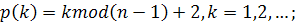 целочисленный индекс p = p(k) изменяется циклически от 2 до n при возрастании k. Номер матрицы
целочисленный индекс p = p(k) изменяется циклически от 2 до n при возрастании k. Номер матрицы 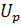 обозначает номер столбца, который
преобразуется вместе с первым. Матрицы
обозначает номер столбца, который
преобразуется вместе с первым. Матрицы 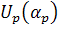 с углом
с углом 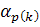 определяются, кроме
определяются, кроме 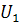 , правилами пункта 1. Так как первый
столбец
, правилами пункта 1. Так как первый
столбец 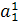 является наибольшим в матрице
является наибольшим в матрице 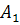 , то выполняются свойства 1 и 2 для
столбцов всех матриц
, то выполняются свойства 1 и 2 для
столбцов всех матриц 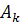 .
.
Лемма. Последовательность 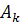 сходится поэлементно при
сходится поэлементно при 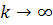 [3].
[3].
Обозначим предельную матрицу 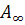 ,
, 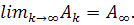 Пусть
Пусть 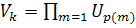 , тогда
, тогда 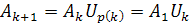 . Ортогональные матрицы
. Ортогональные матрицы 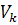 также сходятся, обозначим их
предельную матрицу
также сходятся, обозначим их
предельную матрицу 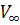 . Справедливо равенство
. Справедливо равенство 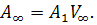
Следствие. Первый столбец 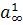 предельной матрицы
предельной матрицы 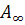 уже не может быть увеличен нашей
итерационной процедурой.
уже не может быть увеличен нашей
итерационной процедурой.
Отсюда следует, что этот столбец 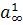 ортогонален всем остальным, иначе
можно было построить матрицу
ортогонален всем остальным, иначе
можно было построить матрицу 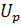 , которая увеличила бы норму
, которая увеличила бы норму 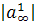 .
.
Сингулярное разложение. Процедурой (7) - (9) будем называть построение
последовательности (9), максимизирующей указанный столбец. Эта процедура для
первого столбца приводит к матрице 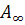 , первый столбец которой ортогонален
остальным, обозначим эту матрицу через
, первый столбец которой ортогонален
остальным, обозначим эту матрицу через 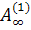 , то есть
, то есть 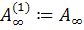 и
и 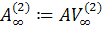 .
.
Для второго столбца матрицы 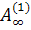 может быть осуществлена процедура
(7) - (9) (предварительно поставив на его место максимальный по норме среди
старших по номеру), индекс p = p(k) изменяется циклически от 3 до n при возрастании k. Полученную в пределе матрицу обозначим
может быть осуществлена процедура
(7) - (9) (предварительно поставив на его место максимальный по норме среди
старших по номеру), индекс p = p(k) изменяется циклически от 3 до n при возрастании k. Полученную в пределе матрицу обозначим 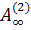 ; ее первые два столбца ортогональны
остальным. Предельную ортогональную матрицу в этой процедуре будем обозначать
; ее первые два столбца ортогональны
остальным. Предельную ортогональную матрицу в этой процедуре будем обозначать 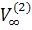 , т.е.
, т.е. 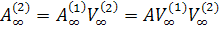 .
.
Для 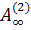 проведем максимизацию нормы третьего столбца, предельные
матрицы обозначим через
проведем максимизацию нормы третьего столбца, предельные
матрицы обозначим через 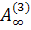 и через
и через 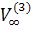 . Продолжая таким образом, получим после применения (n - 2) раза этой процедуры к матрице
. Продолжая таким образом, получим после применения (n - 2) раза этой процедуры к матрице 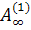 матрицу
матрицу 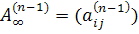 , столбцы которой взаимно
ортогональны, и выполняется равенство
, столбцы которой взаимно
ортогональны, и выполняется равенство 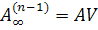 , где
, где 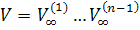 - ортогональная.
- ортогональная.
Пусть 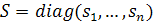 , где sk - норма k-го столбца
матрицы
, где sk - норма k-го столбца
матрицы 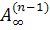 . Мы имеем
. Мы имеем  , W - ортогональная, и для матрицы А получаем SVD-разложение A.
, W - ортогональная, и для матрицы А получаем SVD-разложение A.
скорость
связь сжатие изображение
5. ПРАКТИЧЕСКАЯ ЧАСТЬ
Для BMP-матриц выбранных изображений
получить сингулярные числа и коэффициенты сжатия 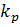 .
.
Оставляя первые p
сингулярных чисел получить BMP-матрицы
сжатых изображений, получить их представления на экране; выбрать значения p, для которых сжатые будут очень
хорошего качества, хорошего, удовлетворительного, плохого и идентифицируемого.
Исследовать разницу сжатий изображений различных размеров.
По этим p сингулярным числам определить F-нормы сжатых изображений, числа 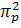 - отношения сжатой F-нормы к F-норме исходного изображения и коэффициенты сжатия
- отношения сжатой F-нормы к F-норме исходного изображения и коэффициенты сжатия 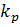 .
.
Результаты исследования динамики сингулярных чисел p (табл. 1) и коэффициентов сжатия 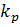 (табл. 2) различных размерностей:
(табл. 2) различных размерностей:
Таблица 1
|
Качество
|
p = 256
|
p = 512
|
p = 768
|
|
Очень хорошее
|
p = 110-80
|
p = 170-140
|
p = 210-150
|
|
Хорошее
|
p = 70-50
|
p = 100-90
|
p = 130-90
|
|
Удовлетворительное
|
p = 50-30
|
p = 70-40
|
p = 70-50
|
|
Плохое
|
p = 30-15
|
p = 40-30
|
p = 40-35
|
|
Идентифицируемое
|
p = 20-9
|
p = 20-15
|
p = 25-18
|
Таблица 2
|
Качество
|
p = 256
|
p = 512
|
p = 768
|
|
Очень хорошее
|
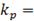 1.597-1.161 1.597-1.161
|
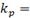 1.827-1.504 1.827-1.504
|
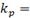 3.275-2.089 3.275-2.089
|
|
Хорошее
|
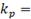 2.555-1.825 2.555-1.825
|
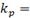 2.842-2.558 2.842-2.558
|
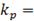 5.458-3.374 5.458-3.374
|
|
Удовлетворительное
|
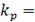 4.258-2.555 4.258-2.555
|
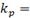 6.394-3.654 6.394-3.654
|
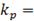 6.266-9.825 6.266-9.825
|
|
Плохое
|
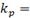 8.517-4.258 8.517-4.258
|
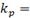 8.525-6.394 8.525-6.394
|
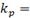 10.965-14.036 10.965-14.036
|
|
Идентифицируемое
|
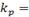 17.05-12.788 17.05-12.788
|
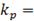 17.544-27.291 17.544-27.291
|
На результаты исследования влияли качество и композиции изображений, а
при p = 768 влиял размер, так как
использовались матрицы изображения размерности m x n.
Также было выполнено сжатие цветного изображения.
Таблица 3
Изображение размера 256х256
|

|

|
|
Исходное
|
Очень хорошее
|
|
p = 256
|
90
|
|
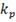 = 0.499 = 0.499
|
1.419
|
|
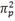 = 1 = 1
|
0.999
|
|

|

|
|
Хорошее
|
Удовлетворительное
|
|
60
|
40
|
|
2.129
|
3.194
|
|
0.996
|
0.992
|
|

|
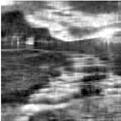
|
|
Плохое
|
Идентифицируемое
|
|
25
|
15
|
|
5.11
|
8.517
|
|
0.984
|
0.969
|
Таблица 4
Изображение
512х512
|

|

|
|
Исходное
|
Очень хорошее
|
|
p = 512
|
170
|
|
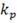 = 0.5 = 0.5
|
1.504
|
|
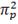 = 1 = 1
|
0.992
|
|

|

|
|
Хорошее
|
Удовлетворительное
|
|
100
|
60
|
|
2.558
|
4.263
|
|
0.98
|
0.965
|
|

|

|
|
Плохое
|
Идентифицируемое
|
|
30
|
20
|
|
8.525
|
12.788
|
|
0.942
|
0.928
|
Таблица 5
Изображение 1024х768
|

|

|
Очень хорошее
|
|
p = 768
|
210
|
|
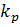 = 0.571 = 0.571
|
2.089
|
|
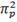 = 1 = 1
|
0.998
|
|

|

|
|
Хорошее
|
Удовлетворительное
|
|
130
|
70
|
|
3.374
|
6.266
|
|
0.993
|
0.984
|
|

|

|
|
Плохое
|
Идентифицированное
|
|
40
|
25
|
|
10.965
|
17.544
|
|
0.973
|
0.962
|
Таблица 6
Изображение цветное 1280х1024
|

|

|
|
Исходное 1280х1024
|
Очень хорошее
|
|
P = 1024
|
220
|
|
K = 0.555
|
2.585
|
|
П = 1
|
0.993
|
|

|

|
|
Хорошее
|
Удовлетворительное
|
|
150
|
80
|
|
3.791
|
7.108
|
|
0.986
|
0.97
|
|

|

|
|
Плохое
|
Идентифицированное
|
|
50
|
30
|
|
11.373
|
18.955
|
|
0.957
|
0.943
|
ЗАКЛЮЧЕНИЕ
Для поставленной в работе задачи было выполнено:
. изучено сингулярное разложение и SVD-сжатие изображений,
2. разработан алгоритм сжатия изображения в MathCAD,
. изучена особенность динамики сингулярных чисел,
. проведен анализ динамики сингулярных чисел и коэффициентов
сжатия при сжатии изображения,
. произведено сжатие цветного изображения.
В практической части были использованы BMP-изображения различных размеров: 256х256, 512х512,
1024х768. По p сингулярным числам найдены F- норма Фробениуса сжатых
изображений, числа 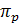 - отношения сжатой F-нормы к F-норме исходного
изображения и коэффициенты сжатия
- отношения сжатой F-нормы к F-норме исходного
изображения и коэффициенты сжатия 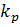 .
.
При SVD-сжатии изображение преобразуют в
вектор, сингулярные числа которого расположены в порядке убывания их
значимости, картинка может быть восстановлена с использованием некоторого
количества первых сингулярных чисел. Чем большее элементов будет использовано,
тем лучше будет качество восстановленного изображения.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Форсайт
Дж., Малькольм М., Моулер К. Машинные методы математических вычислений: Пер. с
англ. - М.: Мир, 1980. - 279 с.
2. Деммель
Дж. Вычислительная линейная алгебра - М.: Мир, 2001. - 429 с.
. Прэтт
У. Цифровая обработка изображений: Пер. с англ. - М.: Мир, 1982. - Кн. 1 - 312
с.
. Сингулярная
разложение [Электронный ресурс]
. Стрижов
В.В. Информационное моделирование [Электронный ресурс]
. Логинов
Н.В. Сингулярное разложение матриц. - М.: МГАПИ, 1996. - 80 с.
. Смирнов
С.И., Михайлов В.В., Остриков В.Н. Применение рандомизированного метода главных
компонент для сжатия данных гиперспектральной съемки // Современные проблемы
дистанционного зондирования Земли из космоса. - М.: Издательство КИРАН, 2014. -
С. 9-17.
9. Харебов
К.С. Компьютерные методы решения задачи наименьших квадратов и проблемы
собственных значений. - Владикавказ: Издательство СОГУ, 1995. - 76 с.
10. Фаддеев
Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. - М.: Физматгиз,
1963. - 536 с.
. Марчук
Г.И. Методы вычислительной математики. - М.: Наука, 1980. - 456 с.
. Кабанихин
С.И., Кривотько О.И. Сингулярное разложение в задаче об источнике // Сибирский
журнал вычислительной математики. - Новосибирск: Издательство СО РАН, 2012. -
Т. 15, №2. - С. 101-107.
. Загребнюк
В.И., Насиров Ф.В. Разложение цветных изображений на сингулярные компоненты //
Восточно-европейский журнал передовых технологий. - Харьков: Технологический
центр, 2013. - Т. 4, №2 (64). - С. 15 - 19.
. Савостьянов
Д.В. Быстрая полинейная аппроксимация матриц и интегральные уравнения. - М. ИВМ
РАН, 2006. - 144 с.
. Голуб
Дж., Ван Лоун Ч. Матричные вычисления: Пер. с англ. - М.: Мир, 1999. - 548 с.
. Ибрагимов
И.В. Новый подход к решению задачи обобщённого сингулярного разложения //
Матричные методы и вычисления. - М.: ИВМ РАН, 1999. - С. 193-201.
. Сильвестров
И.Ю. Анализ сингулярного разложения линеаризованного оператора динамической
теории упругости для случая вертикального сейсмического профилирования //
Вычислительные технологии. - Новосибирск: Издательство СО РАН, 2007. - Т. 12,
№6. - С. 90-100.