Струны Лиувилля в космосе

Струны Лиувилля в космосе

Контрольная работа

Cтруны Лиувилля в космосе

Введение

На рубеже столетий концепция квантового поля и связанных с ним элементарных частиц стала вытесняться концепцией струн. Так, согласно мнению С. Вейнберга [ В], «известные сейчас наиболее удачные теории поля, в том числе электродинамику, нужно рассматривать как «эффективную теорию поля». Последние слова означают низкоэнергетическое приближение более фундаментальной теории, которая... представляет собой нечто вроде теории струн…».

Наиболее вероятным кандидатом на роль объединенной теории всех известных сегодня взаимодействий считается 26 мерная «гетероическая струна», что в переводе с греческого языка означает «гибридную силу» [K]. Эта струна компактифицируется на 16- мерной решетке группы Каца-Муди 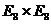 с 480 генераторами, что приводит к свободной от внутренних аномалий теории. Эта конструкция существует как единый объект при высоких энергиях 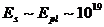 Гэв. Дальнейшая редукция этого прямого произведения групп к группам меньшей размерности при понижении энергии 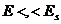 может выглядеть как [K]

,

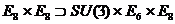а для группы Каца -Муди :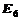

,

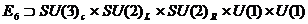то есть при понижении энергии от предельно больших значений 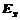, при которых реализуется описание мира в виде многомерных квантовых поверхностей-струн, к наблюдаемым сегодня энергиям могут последовательно выделяться новые физические взаимодействия вплоть до неоткрытых сегодня неизвестных полевых взаимодействий, описываемых группой 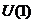. Однако, гетероические струны образовывают геометрические структуры с точной симметрией, которые не учитывают квантовые флуктуации. И тем более, при их построении не учитывается возможность возникновения квантового статистического ансамбля флуктуаций геометрии, которые могут привести к радикальной модификации теории.

Рассмотрим для примера простейшую модель квантовой механики - линейный гармонический осциллятор. Расчет среднеквадратичной флуктуации энергии осциллятора дает

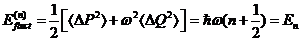 (1)

где 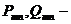 матричные элементы операторов импульса и координаты.

То есть, среднеквадратичная флуктуация есть величина, равная самой энергии осциллятора.

Квантовые поправки, связанные с флуктуациями, оказываются особенно существенными вблизи, например, точек фазовых переходов.

В квазиклассическом приближении они формируют основную стуктуру полного эффективного действия в квантовой теории поля и известный из эксперимента облик некоторых квантовых объектов. Например, адроны при высоких энергиях и больших переданных импульсах хорошо описываются структурными функциями валентных кварков. При небольших переданных импульсах вклад флуктуаций в наблюдаемые величины достигает десятков процентов и именно с вычислением этого вклада в КХД связывается надежда на объяснение конфайнмента кварков. Эта возможность связана с равенством нулю массы покоя глюона, в результате чего глюон является чисто релятивистским объектом. Масса покоя гравитона, как ожидается, тоже равна нулю. Поэтому, квантовые флуктуации гравитационного поля должны быть велики в сильных полях тяготения. Такие поля могут существовать только в малых пространственно-временных масштабах при характерных длинах 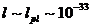 см. В эпоху «Большого Взрыва» каждый пузырек этой многомерной пены представляет собой новый совершенно особенный мир, существующий планковское время 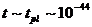 с (Рис1.).

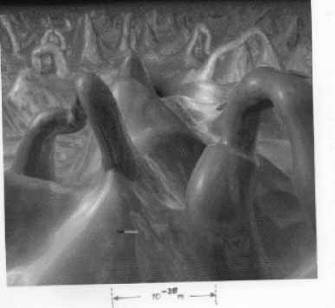
Рисунок 1. Пространственно-временная пена пена квантовых флуктуаций.

1. Струнный формализм

Точным решением теории гетероических струн является D -брана [ ]. Этот объект представляет собой многомерную, вообще говоря, искривленную поверхность, на которой задаются моды собственных колебаний струны. Примем далее рациональную систему единиц 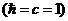. Тогда масса браны 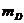 будет связана с константой струнного взаимодействия 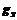 формулой

(а)

(б)              (в)

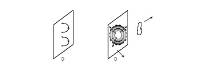
Рисунок 2. Рассеяние низкоэнергетического замкнутого струнного состояния (частицы) на D - бране : (a) - асимптотическое состояние  прошлого, (b) - время взаимодействия (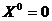), при котором  возникает коллективное возбуждение на D - бране в виде двух открытых струн, (в) - асимптотичекое будущее, которому соответствует рекомбинация струнного состояния на бране с образованием замкнутого струнного состояния (частицы), тогда как  D- брана получает отдачу, и при этом возникают флуктуации ее внутреннего состояния.

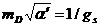 (2)

где  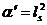- наклон Редже (струнная шкала длины).

Предположим, что D-брана достаточно тяжела, чтобы ее движения можно было описывать квазиклассическим путем. Это соответствует маленьким собственным размерам (в пределе D - частица является 0 -мерной) и большим массам D - частиц . Будем описывать рассеяние наблюдаемой физической частицы (например, фотона или гравитона) на такой D - бране. (Рис2.)

Тогда оператор отдачи, описывающий возбуждение мирового листа при рассеянии, примет вид [ ]

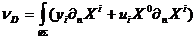 (3)

здесь 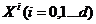 - коллективные моды колебаний D-браны.

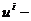скорость отдачи при рассеянии,

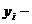начальная позиция D-браны на мировом листе.

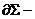граница , внутри которой сосредоточена струна на мировом листе.

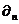-нормальная производная к границе D-браны.

Среди коллективных переменных, входящих в (3), выделяется нулевая колебательная мода 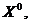 называемая «время цели» (см.Рис.2), описывающая сближение замкнутой струны с D-браной и удовлетворяющая граничным условиям Ньюмена

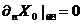
при 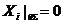 для других переменных с .

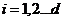После взаимодействия с замкнутой струной D- частица характеризуется парой логарифмических операторов

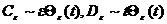 (4)

где 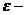 параметр внутренней симметрии, описывающий связь геометрии мирового листа со шкалой энергии. Параметр 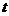 ниже

будет отождествлен со временем цели  .

комплексная тэта функция, позволяющая обрезать ультафиолетовые расходимости в средних значениях и корреляционных функциях, заданных на мировом листе, на котором сосредоточена струнная конструкция.

Эти расходимости регуляризовываются в пределе 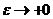, 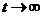(что соответствует окончанию процесса рассеяния). При этом 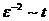, а двухточечные корреляционные функции логарифмических операторов (4) ведут себя как 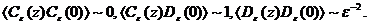 (5)

То есть, основной вклад в динамику рассеяния будет вносить последняя корреляционная функция, составленная из операторов .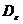

Знание правил (5) работы со средними логарифмических операторов позволяет, в принципе, вычислять средние значения любых переменных, заданных на рассматриваемой струнной конструкции.

Мы постараемся далее избегать этих сложных вычислений и получать

Значимые результаты теории из простых качественных феноменологических соображений.

Пространственно-временная пена квантовых флуктуаций делает структуру пространства-времени (и в частности, струнную структуру) похожей на кристаллическую решетку твердого тела, по которой распространяются коллективные возбуждения в виде квазичастиц-экситонов. Квазичастицы, которые распространяются на фоне основного состояния пространства-времени, носят название D (Дирихле) частиц. А струны, с помощью которых строится вся эта конструкция - струнами Лиувилля. Далее мы свяжем эти названия с конкретным содержанием развиваемой теории. D- частицы можно рассматривать на фоне плоского или искривленного пространства-времени. Тогда они считаются одним из примеров дефектов этого пространства, подобным дефектам в кристалле.

Введенная выше пара логарифмических операторов (4) позволяет расчитать деформацию D- браны после рассеяния, которая состоит из

) сдвига браны в целом

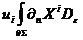 (6)

) квантовых флуктуаций в начальном положении D- частицы

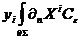 (7)

Если значения импульса налетающей реальной частицы до и после столкновения равны 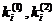, то импульс отдачи при рассеянии будет равен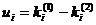

Нулевая мода колебаний струны может быть интерпретирована как время событий, происходящих на D- бране в процессе столкновения с замкнутой струной (время цели) 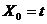[ ]. Тогда функция 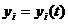 приобретает физический смысл траектории D- частицы на мировом листе в этом времени. Деформация пространственно - временных свойств самой D - браны в процессе столкновения может быть описана скалярной вершинной функцией

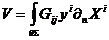 , (10)

где результирующая струнная метрика, заданная на D - бране имеет вид

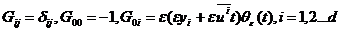, (11)

где

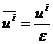 - ренормированный параметр скорости отдачи струны Лиувилля в процессе столкновения.

По метрике (20) можно построить эффективное действие для струны Лиувилля , описывающее квантовые эффекты на D- бране.

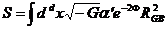 (12)

где 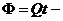 линейное по времени фоновое скалярное поле, называемое иначе дилатонным полем. 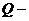 дефицит центрального топологического заряда D- траны, связанный с деформацией метрики (11) в окружающем искривленном пространстве-времени.

Квадратичный инвариант кривизны Гаусса-Боннэ

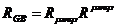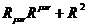 - 4  (13)

является комбинацией инвариантов тензора кривизны Римана .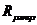

Напомним, что скаляр кривизны

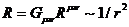, (14)

где 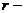радиус кривизны пространства-времени.

Как видим, струна Лиувилля, как объект, обладает набором релятивистских свойств, искривляя пространство-время, в котором находится дефект, в виде D- частицы. Это искривление носит точечный характер. Например, квадрат инварианта кривизны

то есть является 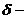функционалом «времени цели», что соответствует

описанию процесса столкновения частицы с точечным дефектом.

С другой стороны, струна Лиувилля обладает и чисто классическими свойствами, характерными для частиц в классической механике.

Пусть например, мировой лист подвергается конформной деформации во времени .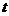

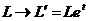 (16)

При этом пара логарифмических операторов 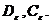 преобразуется как

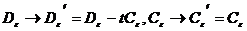 , (17)

что соответствует изменению функций, описывающих положение

D - частицы в пространтве следующим образом

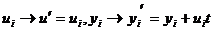 , (18)

То есть массивная D-частица, искривляющая окружающее пространство, по релятивистским законам квантовой теории гравитации движется по мировому листу как классический объект, подчиняющийся преобразованиям Галилея (18) с фиксированной скоростью 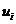. Это - следствие сложной струнной структуры дефекта в виде D-частицы. Параметр внутренней конформной симметрии струны оказывается связанным при этом со «временем цели», описывающим процесс рассеяния, асимптотическим соотношением

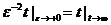 (19)

Формула (19) фиксирует окончание рассеяния в момент времени

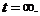
Таким образом, струна Лиувилля, как физический объект, обладает классическими и релятивистскими свойствами одновременно. Соотношение (19) позволяет записать метрику на струне (11) после окончания рассеяния на ней физической частицы в виде

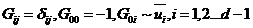 (20)

В пространстве- времени (20) отсутствуют все возмущения, вносимые в процессе рассеяния полем D- частицы, но остались недиагональные компоненты метрики пространства-времен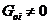и . Таким образом, отдача D - частиц при рассеянии модифицирует свойства наблюдаемого пространства-времени, индуцируя в нем нелоренцеву метрику с отличными от нуля недиагональными компонентами! Так как в определение скорости 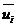входит параметр энергетической шкалы 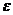, то эффективная (и безразмерная ! ) метрика 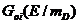 зависит от энергии, что является следствием сохранения импульса при рассеянии физической частицы на D - частице. Метрика плоского пространства (20) отличается от метрики Лоренца, что приводит к нарушению Лоренц - инвариантности в соответствующей эффективной теории поля уже при достаточно высоких энергиях

1. Распространение света в пространстве-времени c нарушенной Лоренц-инвариантностью

Рассмотрим эффективное четырехмерное пространств время, созданное квантовыми флуктуациями и дефектами на плоском лоренц-инвариантном фоне. При энергиях 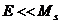 фундаментальная струнная структура будет проявляться в нем в виде флуктуаций метрики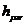  

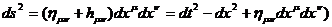 (22)

где ,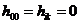

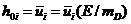
Здесь и ниже греческие индексы пробегают значения ,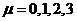

Латинские индексы пробегают значения .

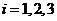Выберем в этом пространстве-времени 2 бесконечно близкие точки, лежащие на двух разных геодезических линиях. Тогда площадь параллелограмма, построенного на соединяющей их прямой линии, как на диагонали, будет равна

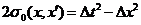 (23)

Здесь 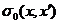- площадь в плоском пространстве-времени Лоренца с метрикой 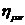, константа скорости света в этом пространстве .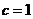

Разложим соответствующую площадь 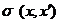 в пространстве- времени (22) в ряд по малым возмущениям .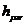

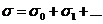 (24)

Пусть 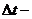время, соответствущее распространению светового сигнала между точками с расстоянием 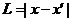(расстояние между источником излучения и детектором). Тогда его можно будет вычислить по формуле

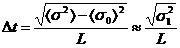 (25)

При прямом расчете (25) полезно учесть изменение величины скорости светового сигнала в пространственно - временной пене квантовых флуктуаций по сравнению с сигналом в плоском пространстве-времени. Пусть сигнал распространяется вдоль оси 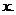 Приравняем друг другу световые интервалы плоского пространства-времени и пространства- времени, искаженного квантовыми флуктуациями.

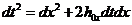, (26)

где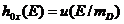

Найдем новую скорость света 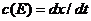 в искаженном флуктуациями пространстве, соответствующую положительному корню этого квадратного уравнения

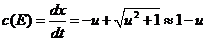 (27)

Пусть 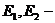два энергетических канала детектора. Тогда световой сигнал, получаемый в этих каналах, будет приниматься с разными скоростями 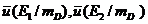 и, следовательно, в одном из каналов (с меньшей энергией) будет принят через время 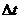. То есть, в этом канале свет будет запаздывать во времени.

Найдем теперь время запаздывания сигнала 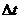 формуле (25). Для конечных промежутков времени распространения сигнала из (25) следует, что

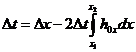, (28)

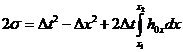 (29)

Из (23), (28),(29) с учетом 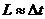 найдем первую поправку к площади 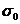 в ряде (24)

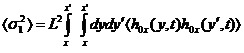 (30)

Среднеквадратичные деформации мирового листа по смыслу соответствуют двухточечному коррелятору 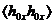 на деформированной D-бране. В последней стадии рассеяния при 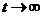этот коррелятор есть 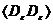 и его расчет может быть выполнен в микроскопической теории - теории струн Лиувилля. Однако, с точностью до численного коэффициента порядка единицы этот коррелятор можно найти с помощью простой оценки. Пусть 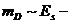 масса D-частицы. 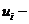скорость отдачи при рассеянии фотона на D-частице. Тогда 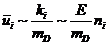 (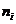- единичный вектор). Теперь можно оценить искомый коррелятор

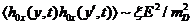 (31)

Теперь из (25) следует оценка для времени задержки сигнала, которую удобно привести сразу в системе единиц СГС:

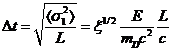 (32)

Из (32) видно, что время задержки излучения тем больше, чем выше энергия. Поэтому, экспериментальные методики поиска основаны на регистрации одинаковых по форме импульсов в разных энергетических каналах установок, принимающих гамма-излучение от внегалактических объектов - блазаров (активных ядер галактик) и гамма-всплесков. Если схожие по форме импульсы регистрируются установкой в разные моменты времени, близкие друг другу, то это может свидетельствовать о том, что импульсы с более низкой энергией задерживаются при их распространении в пространстве по сравнению с импульсами высокой энергии.

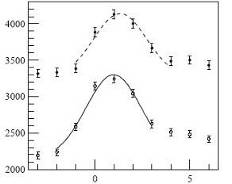
Время счета в секундах

Рисунок 3. Сравнение полезного сигнала в двух энергетических каналах аппарата BATSE космической обсерватории GRO.

Штрихпунктирная линия обозначает фит Гаусса для сигнала в канале 1(E = 25- 55 кэв). Сплошная линия обозначает фит Гаусса для сигнала в канале 3 (E= 110-320 кэв).

Грубая обработка полезного сигнала аппарата BATSE космической лаборатории GRO для гамма - всплеска GRB 970508 представлена на Рис 3.

4.       Дисперсионные соотношения и энергия покоя частиц в пространственно - временной пене

Выясним, как меняются дисперсионные соотношения для частиц , одетых пространственно- временной пеной квантовых флуктуаций. Фундаментальную структуру пространства времени, как указывалось выше, образуют струны Лиувилля. Будем считать, что амплитуда флуктуаций при энергиях 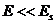 мала, и метрика на струне слабо отклоняется от метрики Лоренца

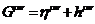 , (33)

где возмущение 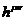 имеет вид (22).

Дисперсионное соотношение для частицы должно в этой метрике иметь вид:

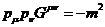 , (34)

что является ковариантным обобщением обычного дисперсионного соотношения для частицы в метрике Лоренца[].

Усредним (34) по ансамблю квантовых флуктуаций (по колебательным модам струны Лиувилля). Получим

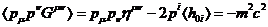. (35)

Среднее значение 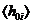 соответствует линейной корреляционной функции. Поэтому, для вычисления поправки к дисперсионному соотношению за счет отличия метрики 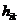 от нуля , надо квадрировать ковариантное дисперсионное соотношение (34).

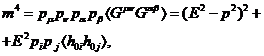 (36)

Выполним усреднение в (36) с учетом изотропии мира и соотношения (31). Учтем, что

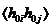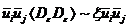~ , (37)

где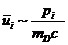  

после чего дисперсионное соотношение (36) примет вид.

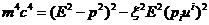 (38)

Для безмассовых частиц и частиц малой массы 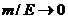 отсюда получается соотношение:

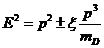 (39)

,

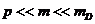то дисперсионное соотношение для частиц примет вид:

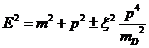 (40)

Дисперсионные соотношения (39), (40) получаются в случае рассеяния одной замкнутой струны (частицы) на дефекте (D - частице). Однако, более реальной при детектировании частиц ситуацией является регистрация пучка частиц, собранных в луч.

Этот луч при распространении в пространственно - временной пене может рассеиваться на D - частице. При таком рассеянии частицы, образующие луч попадают в меняющийся в пространстве гравитационный потенциал. Эти вариации гравитационного поля, в котором распространяется пучок частиц, в месте нахождения частиц пучка меняют метрику D - браны, входящей в состав струны Лиувилля, потому что сама струна является нелокальным протяженным объектом, тогда как частицы, практически, остаются точечными. Оценим вариации метрики струны Лиувилля при рассеянии на ней точечных частиц. Вариации метрики в n - мерном пространстве - времени можно рассчитать по формуле

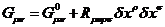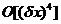 +  , (41)

где 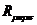- компоненты тензора Римана.

Эта формула позволяет рассчитать метрику в точке 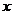, бесконечно близкой к точке 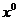. Если  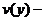скорость частиц в пучке как функция их положения в пространстве, то эта скорость будет существенным образом изменяться на расстоянии 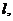 где 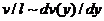 . Тогда кривизна в (41) может быть оценена как 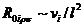 при изменении расстояния между частицами пучка 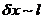 ,а компонента метрики  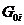примет вид 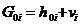. Здесь величина 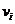- есть средняя скорость пучка частиц 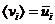. Поэтому , конечная поправка к дисперсионному соотношению (35), возникающая за счет вариации метрики в пучке частиц вместо 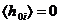 принимает вид 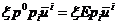, а само дисперсионное соотношение с учетом этого коллективного эффекта есть

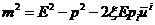 (42)

Это дисперсионное соотношение для массивных частиц содержит кубичную по импульсу и линейную по постоянной 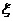 поправку к дисперсионному соотношению свободной «голой» частицы. Какое из соотношений (39), (40) или (42) реализуется в природе должен установить эксперимент. Исследуем (42) для того, чтобы проверить, как изменяются стандартные формулы Специальной Теории Относительности (СТО) с учетом спонтанного нарушения Лоренц -инвариантности (ЛИ) для частиц, «одетых» пространственно-временной пеной квантовых флуктуаций. Перепишем (42) в явном виде, не фиксируя заранее знак величины 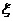 и обозначая массу покоя через  ().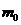

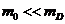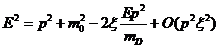 (43)

Квадрируя (43) получим:

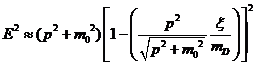 (44)

В нерелятивистском пределе 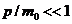 отсюда получается:

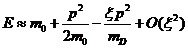 (45)

Эффективная масса покоя, входящая в кинетическую энергию 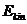, оказывается, поэтому, равной

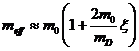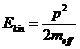, при  (46)

Эти результаты можно переписать иначе иначе, вводя вместо энергии покоя «голых» релятивистских частиц новую энергию покоя, связанную со спонтанным нарушением ЛИ в пространственно-временной пене квантовых флуктуаций

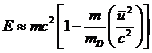 , (47)

где .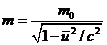

Формулы (45), (46) подсказывают первый наивный способ проверки представлений теории струн Лиувилля по ее низкоэнергетическим следствиям. Казалось бы, это можно сделать измеряя массы и энергию покоя элементарных частиц. Однако, максимальная масса известных сегодня частиц ограничена цифрой 174 Гэв (масса t - кварка). Поэтому, отношение масс в формуле (45) ограничено малой величиной 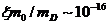. Трудно представить себе эксперимент, который смог бы уловить на этом уровне точности различие между массами 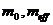. Более надежную, на сегодняшний день информацию информацию о значении массы 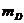 поставляют астрономические наблюдения. В результате этих наблюдений удается зарегистрировать гамма-лучи высоких энергий ( E~ 100 кэв - 1Тэв для гамма всплесков) [ ] и (E~ 10 Тэв ) для блазаров []. Это излучение проходит во Вселенной большие расстояния L ~ 100-1000 Мпск., прежде чем оно регистрируется детекторами на Земле и ИСЗ. При таких больших энергиях и расстояниях для детектируемого излучения становятся существнными волновые эффекты - фазовые и поляризационные. 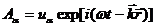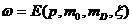Действительно, в световой волне  фаза  фаза 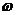 чувствительна выбору массы 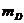 при больших временах наблюдения за световой волной t . Поэтому, наблюдая за тонкими поляризационными эффектами в гамма- излучении ( которое является следствием излучения электромагнитных волн электронами при ускорении частиц в магнитных полях) можно поставить ограничения как на массу 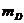, так и на константы 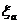, которые должны быть разными для частиц a различных типов. Так , для электронов 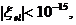 для фотонов .

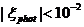5.       Зависимость наблюдаемых эффектов теории некритических струн Лиувилля от красного смещения внегалактических объектов.

При расстояниях до внегалактических объектов L~ 100 Mпск и более надо учитывать эффекты глобальной кривизны пространства - времени и, в частности, зависимость расстояния до разбегающихся галактик от красного смещения 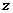. Тогда, зависимость времени запаздывания для излучения 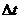 от красного смещения дается формулой.

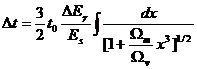 (48)

где 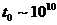 лет - возраст Вселенной.  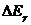- разность энергий в двух разных энергетических каналах приемника излучения.

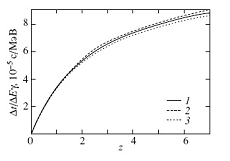
Рисунок 4. Теоретические кривые зависимости отношения 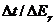 от красного смещения z для разных типов космологических моделей 1- для плоской модели Вселенной , 2-для закрытой космологической модели, 3-для открытой космологической модели.

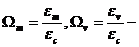 отношение плотностей энергии барионной материи и космического вакуума к критической плотности Вселенной [] В результате, запаздывание сигналов от внегалактических объектов можно представить графически (Рис.4)

Как видно из (Рис.4) , эффект запаздывания излучения от удаленных космологических источников (при z > 2) можно использовать для определения топологии расширяющегося искривленного мира, то есть, для выяснения того, что именно представляет собой 3 -мерное сечение нашего мира - плоскость, шар или гиперболоид []. Измерить современными методами столь малые различия во временах регистрируемых сигналов  ,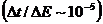

к сожалению, крайне сложно из-за больших ошибок в измерении параметров источников излучения. Однако, в близком будущем необходимая точность может быть достигнута.

Дисперсионные соотношения для частиц при учете изменения их длин волн из-за космологического эффекта Доплера [ЛЛ] принимают вид:

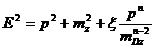 (49)

где n<2 - целое число,

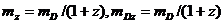
Это изменение дисперсионных соотношений может привести , например, к существенным различиям в спектрах космических лучей, приходящих на Землю из нашей галактики ( близкие объекты) и от далеких объектов Метагалактики с z ~1. Существуют, например, объяснения провала Грэйсена - Зацепина - Кузьмина в спектре космических лучей и различием данных AGASA и HI RES, связанные с эффектами красного смещения [St]. Однако, окончательные выводы здесь пока еще невозможны в связи с плохой точностью измерений и малой статистикой регистрируемых событий. В этой связи большие надежды связываются с открытием второго - нейтринного окна во Вселенную [ ].

Заключение

Модель некритических струн Лиувилля, появившаяся в конце 20 - начале 21 века, является естественным развитием основных представлений физики высоких энергий. В этой модели создан гибкий хорошо адаптированный к возможным экспериментальным открытиям математический аппарат. Из незатронутых в настоящем обзоре вопросов следует упомянуть нелинейную квантовую механику, на которой базируется рассматриваемая струнная модель и ее суперсимметричное обобщение. Однако, уже простой обзор этой модели показывает, что она приводит к ряду нетривиальных предсказаний, которые можно пытаться тестировать экспериментальными методами. В частности, она предсказывает появление в пространственно - временной пене квантовых флуктуаций дефектов типа D - частиц и (как следствие) спонтанное нарушение Лоренц - инвариантности плоского пространства- времени Минковского. Кроме того, теория предсказывает изменение дисперсионных соотношений для частиц, которые одеваясь пространственно - временной пеной, становятся квазичастицами. Возможными экспериментальными следствиями этих теоретических предсказаний являются запаздывание сигналов от внегалактических источников излучения и тонкие поляризационные эффекты в излучении, принимаемом от внегалактических объектов. Эти предсказания теории некритических струн, известные сегодня, не являются исчерпывающими. Впереди новые неожиданные выводы теории и попытки их экспериментального обнаружения.

Список литературы

пространство время внегалактический энергия

1. Кейн Г. // Современная физика элементарных частиц. М. Мир, 2010. Верешков Г.М. // Структура, физическое содержание и проблемы стандартной модели, Труды второй Баксанской Молодежной Школы Экспериментальной и Теоретической Физики, т.2., Приэльбрусье, Кабардино-Балкария 18-24 апреля 2001г. , Нальчик,2002.

2. Эйнштейн А. // Альберт Эйнштейн. Собрание научных трудов. Т.1, М. Наука, 1965.

3.  Боголюбов Н.Н., Ширков Д.В. // Квантовые поля, М. Наука, 1980.

4. Каку М. // Введение в теорию суперструн. М. Мир, 2009.

5. Берестецкий В.Б., Лифшиц Е.М., Питаевский Л.П.// Квантовая Электродинамика.М.Наука,1980.

7. Сахаров А.Д. , ДАН СССР, 1967,т.177, с. 70.; Зельдович Я.Б.,  Новиков И.Д.// Теория тяготения и эволюция звезд, М. Наука 1971.

. Верешков Г.М., Гришкан Ю.С. и др. // ЖЭТФ , 1981 т. 80, с. 1665.9.Sahni V., Starobinsky A.A. // Int. J. Mod. Phys.2010, v.9,p.373.

10. Weller J., Albrecht A. // astro-ph/ 0106079.

11. Ландау Л.Д. , Лифшиц Е.М. // Статистическая физика, ч.I, М., Наука, 1970.

. Вейнберг С. // Гравитация и космология. М. Мир. 1975.

13.Wang .X. Tegmark M. , Zaldiaga M, // astro-ph 10105091;  Efstatiou G. Et al. // astro-ph /0109152.

14.Зельдович Я.Б., Новиков И.Д. // Строение и эволюция Вселенной, М. Наука,1975.

15. Coleman S., Glashow S.L. , Phys. Rev. D., 2009, v. 59, 116008.

. Amelino-Kamelia G., Piran T., Phys.Rev. D. ,2001,v..64.,036005.

17. Вертрградрва Е.Г., Гришкан Ю.С. , Петков В.Б. Письма Астрон. Ж.В печати.