Решение задач линейной алгебры в Ms Excel

Содержание

Введение

1. Метод Гаусса и одно из его приложений в экономике (задача о рационе)

1.1 Простейшая задача о рационе

.2 Метод Гаусса

.3 Метод Гаусса в Excel

2.   Модель Леонтьева межотраслевого баланса

.     Метод наименьших квадратов (МНК)

3.1 Алгебраический метод наименьших квадратов

3.1.1 Анализ данных эксперимента

3.2 МНК в Excel

Заключение

Список литературы

Введение

Данная работа посвящена решению задач линейной алгебры в Excel,точнее решению систем линейных уравнений. Будут рассмотрены три метода: метод Гаусса, метод, основанный на нахождении обратной матрицы и метод наименьших квадратов.

В первом параграфе работы в качестве примера использования систем линейных уравнений в экономике приведена простейшая задача о рационе и её решение методом Гаусса в частном случае, когда количество неизвестных совпадает с количеством уравнений.

Во втором параграфе рассматривается модель Леонтьева межотраслевого баланса. Это модель, позволяющая анализировать состояние экономики и моделировать различные сценарии ее развития. Возникающая в этом методе система линейных уравнений традиционно решается нахождением обратной матрицы. Чтобы пояснить, запишем модель Леонтьева в матричной форме:

(E-A)*X=Y

Если у нас имеется матрица (Е-А)^-1 ,то умножая обе части равенства на эту матрицу, получим: Х=(Е-А)^-1*У.

Третий параграф описывает решение задач, сводящихся к решению систем линейных уравнений, при помощи МНК (метода наименьших квадратов).

В каждом параграфе будет приведена реализация в Excel.

.        Метод Гаусса и одно из его приложений в экономике  (задача о рационе)

1.1 Простейшая задача о рационе

Формулировка задачи. Допустим, на ферме занимаются выращиванием телят. Известно, что для хорошего роста теленка в день ему необходимо потреблять m веществ в количестве 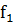 ,…, 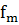соответственно.

На ферму ежедневно завозится n кормов в количестве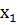,…,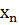. Известно, что доля итогового вещества в j-ом корме равна 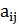. Тогда общее количество вещества определяется по формуле

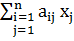
(слагаемое 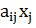- количество итогового вещества в j корме; i=1,…,n).

В результате получаем систему

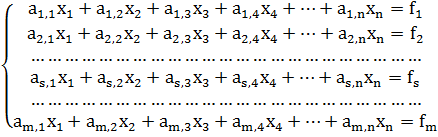 (1)

Если m ≠n ,то система называется прямоугольной и методы её решения рассматриваются в другом параграфе. В данном случае будем считать, что m=n. Такая система является квадратной и к ней применим метод Гаусса.

1.2 Метод Гаусса

Алгоритм Метода Гаусса состоит из двух основных частей: прямой ход и обратный ход.

Прямой ход заключается в том, что система приводится к треугольному виду (верхняя унитреугольная форма). Обратный ход - непосредственное нахождение неизвестных. Причем, корни находятся в обратном порядке: сначала 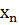, затем  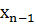и т.д.

)        Прямой ход состоит из следующих шагов.

На первом шаге элементарными преобразованиями исключается 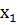из всех уравнений, начиная со второго.

Второй шаг заключается в исключение 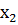 из всех уравнений, начиная с третьего.

На s шаге 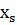 исключается из всех уравнений, начиная с s+1 (s=1,…,n-1).

При этом каждый шаг начинается с обработки s уравнения: строка под номером sделится на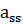,чтобы коэффициент при  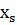стал равен 1.

Описанный алгоритм носит циклический характер.

После завершения этого процесса получаем систему:

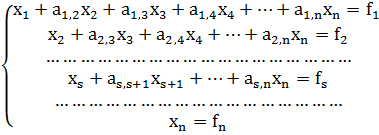 (2)

)        Обратный ход.

В результате выполнения алгоритма прямого хода система (1) приняла треугольный вид (2). Для нахождения решения остается из системы (2) найти 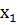, , 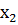…, 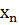. Метод нахождения достаточно очевиден: из последнего уравнения находим .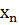

Затем, подставив найденное значение 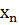 в (n-1)-ое уравнение, найдем 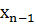, и т.д. Таким образом, s-ое неизвестное  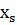находим из s-го уравнения:

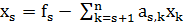.         1.0.

Причем, если условиться считать, что значение суммы, в которой нижний индекс суммирования больше верхнего (пустая сумма), равно нулю, в формуле 1.0. можно считать, что индекс s принимает натуральные значения от n до 1.

1.3 Метод Гаусса в Excel

В Excel Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. Существует более рациональный способ реализации данного метода в Excel.

Решим задачу о рационе в Excel.

Формулировка:    

Допустим, на ферме занимаются выращиванием телят. Известно, что для хорошего роста теленка в день ему необходимо потреблять 4 вещества в количестве 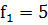,,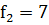 , 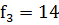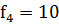соответственно.

На ферму ежедневно завозится 4 корма в количестве 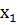,…,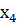. Известно, что доля итогового вещества в j-ом корме равна 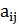. Тогда общее количество вещества определяется по формуле

=

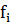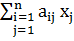
(слагаемое 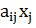- количество итогового вещества в j корме; i=1,…,n).

В результате получаем систему

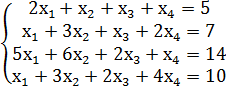(1)

Введем исходные данные в Excel:

Отображение в режиме формул:

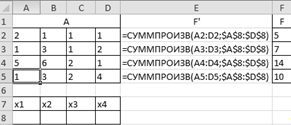
Где А - матрица коэффициентов,

F- вектор свободных членов,

F’ содержит формулу, вычисляющую левую часть уравнения.

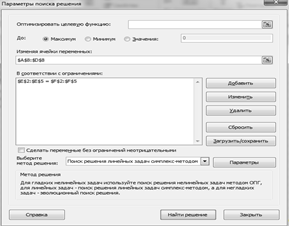
Далее для нахождения корней составленной системы линейных уравнений воспользуемся функцией Поиск решения:

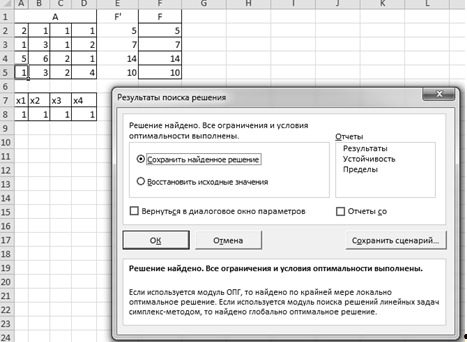
Результат вычислений:

2.      Модель Леонтьева межотраслевого баланса

Макроэкономика функционирования многоотраслевого хозяйства требует баланса между отдельными отраслями. Каждая отрасль, с одной стороны, является производителем, а с другой - потребителем продукции, выпускаемой другими отраслями. Возникает довольно непростая задача расчета связи между отраслями через выпуск и потребление продукции разного вида. Впервые эта проблема была сформулирована в виде математической модели в 1936 г. в трудах известного американского экономиста В.В.Леонтьева, который попытался проанализировать причины экономической депрессии США 1929-1932 гг. Эта модель основана на алгебре матриц.

Суть сводится к следующему.

Основу информационного обеспечения модели межотраслевого баланса составляет технологическая матрица, содержащая коэффициенты прямых материальных затрат на производство единицы продукции. Эта матрица является также основой экономико-математической модели межотраслевого баланса. Предполагается, что производствао единицы продукции в j-й отрасли требует определенное количество затрат промежуточной продукции i-й отрасли, равное а_ij. Оно не зависит от объема производства в отрасли и является довольно стабильной величиной во времени. Величины а_ij называются коэффициентами прямых материальных затрат и рассчитываются следующим образом:

Коэффициент прямых материальных затрат показывает, какое количество продукции i-й отрасли необходимо, если учитывать только прямые затраты, для производства единицы продукции j-й отрасли.

Систему уравнений баланса можно переписать в виде

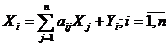
Если ввести в рассмотрение матрицу коэффициентов прямых материальных затрат А= (а_ij), вектор-столбец валовой продукции X и вектор-столбец конечной продукции Y:

,                      ,

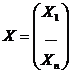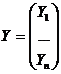то система уравнений в матричной форме примет вид:

Х=АХ + У.

Полученная система уравнений называется экономико-математической моделью межотраслевого баланса (моделью Леонтьева, моделью "затраты-выпуск"). С помощью этой модели можно выполнять три варианта расчетов:

o   Задав в модели величины валовой продукции каждой отрасли (X_i), можно определить объемы конечной продукции каждой отрасли (Y_i):

 = (Е - А)Х (2).

o   Задав величины конечной продукции всех отраслей (У_г), можно определить величины валовой продукции каждой отрасли (Х)

o   Для ряда отраслей задав величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.

В формулах Е обозначает единичную матрицу n-го порядка, а (Е - А)^-1 обозначает матрицу, обратную к матрице (Е - А). Если определитель матрицы (Е - А) не равен нулю, т.е. эта матрица невырожденная, то обратная к ней матрица существует. Обозначим эту обратную матрицу через В=(Е -А)^-1, тогда систему уравнений в матричной форме (2) можно записать в виде

= ВY.

Элементы матрицы В будем обозначать через b_ij, тогда из матричного уравнения для любой i-й отрасли можно получить следующее соотношение:

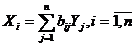
Из последних соотношений следует, что валовая продукция выступает как взвешенная сумма величин конечной продукции, причем весами являются коэффициенты b_ij, которые показывают, сколько всего нужно произвести продукции i-й отрасли для выпуска в сферу конечного использования единицы продукции j-й отрасли. В отличие от коэффициентов прямых затрат а_ij коэффициенты b_ij называются коэффициентами полных материальных затрат и включают в себя как прямые, так и косвенные затраты всех порядков. Если прямые затраты отражают количество средств производства, израсходованных непосредственно при изготовлении данного продукта, то косвенные относятся к предшествующим стадиям производства и входят в производство продукта не прямо, а через другие (промежуточные) средства производства.

Пример нахождения вектора валовой продукции

Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат и вектор конечной продукции:

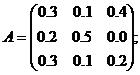
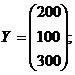
Найти вектор валовой продукции.

Решение.

1.      Определим матрицу коэффициентов полных материальных затрат.. Находим матрицу (Е-А)

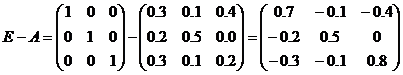
b.      Вычисляем определитель этой матрицы

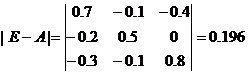
c.       Транспонируем матрицу (Е-А)

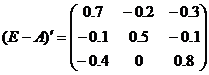
d.      Находим алгебраические дополнения для элементов матрицы (Е-А)’

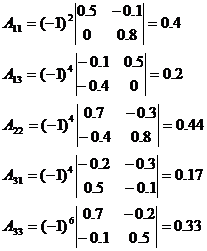
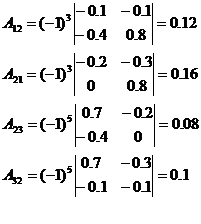
Таким образом, присоединенная матрица имеет вид:

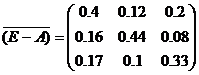
e.       Находим матрицу коэффициентов полных материальных затрат:

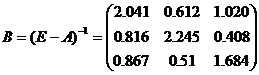
2.      Найдем величины валовой продукции трех отраслей (вектор X),:

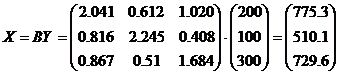
Нахождения вектора валовой продукции в Excel.

Модель Леонтьева межотраслевого баланса в режиме формул:

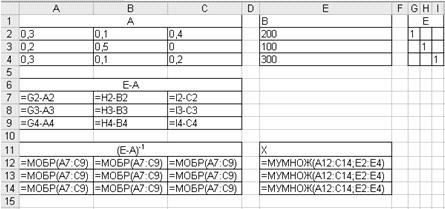
Результаты расчетов представленной модели:

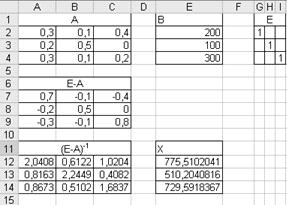
Искомый вектор валового выпуска отраслей занимает диапазон Е12:Е14.

В процессе решения задачи использовались следующие функции:

. МОБР - возвращает обратную матрицу для матрицы, хранящейся в массиве.

Синтаксис: МОБР (массив).

Массив - числовой массив с равным количеством строк и столбцов.

После введения функции в левую верхнюю ячейку диапазона массива следует выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а затем нажать клавиши CTRL+SHIFT+ENTER.

. МУМНОЖ - возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2.

Синтаксис: МУМНОЖ(массив1;массив2).

Массив1, массив2 - перемножаемые массивы.

После введения функции в левую верхнюю ячейку диапазона массива следует выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а затем нажать клавиши CTRL+SHIFT+ENTER.

3.      Метод наименьших квадратов (МНК)

Система m линейных уравнений с n неизвестными имеет вид:

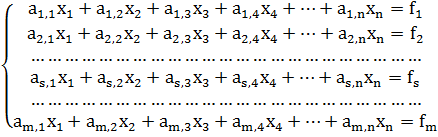
Возможны три случая: m<n, m=n, m>n. Случай, когда m=n, рассматривался в предыдущих параграфах. При m<n, если система mлинейных уравнений с nнеизвестными является совместной, то она не определена и имеет бесконечно много решений.

В случае, если m>nи система является совместной, то матрица А имеет по крайней мере m - nлинейно зависимых строк. Здесь решение может быть получено отбором n любых линейно независимых уравнений (если они существуют)и применением формулы Х=А^-1×В, то есть, сведением задачи к ранее решенной. При этом полученное решение всегда будет удовлетворять и остальным m - nуравнениям.

Однако при применении компьютера удобнее использовать более общий подход - метод наименьших квадратов.

.1 Алгебраический метод наименьших квадратов

Под алгебраическим методом наименьших квадратов понимается метод решения систем линейных уравнений

Ax∼= B (1.1)

путем минимизации евклидовой нормы

‖Ax − b‖ → inf . (1.2)

3.1.1 Анализ данных эксперимента

Рассмотрим некоторый эксперимент, в ходе которого в моменты времени

<<... <

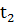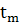
производится, например, измерение температуры Q(t). Пусть результаты измерений задаются массивом

, , ..., .

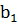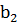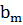Допустим, что условия проведения эксперимента таковы, что измерения проводятся с заведомой погрешностью. В этих случаях закон изменения температуры Q(t) ищут с помощью некоторого полинома

(t) = + + + ... +,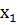

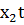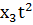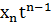определяя неизвестные коэффициенты 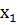, , 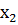..., 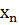из тех соображений, чтобы величина E(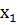, ...,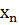), определяемая равенством

гаусс алгебраический exel аппроксимация

E(,...,) =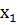

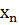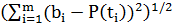
Если заменить P(t) его выражением, то получим

=

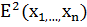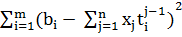
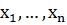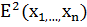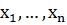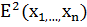Поставим задачу определения массива так, чтобы величина была минимальна, т.е. определим массив методом наименьших квадратов. Для этого приравняем частные производные по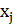к нулю:

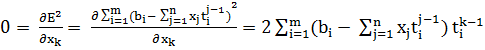
Если ввести m × n матрицу A = (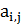), i = 1, 2..., m; j = 1, 2, ..., n, где

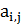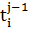=, i = 1, 2..., m; j = 1, 2, ..., n,

то выписанное равенство примет вид

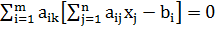 (k=1,2,…,n)

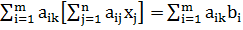 (k=1,2,…,n)

Перепишем написанное равенство в терминах операций с матрицами. Имеем по определению умножения матрицы на столбец

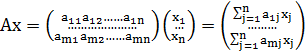
Для транспонированной матрицы аналогичное соотношение выглядит так

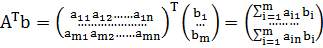
Введем обозначение: i -ую компоненту вектора Ax будем обозначать 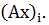В соответствии с выписанными матричными равенствами будем иметь

=

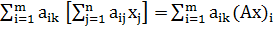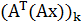
(k=1,2,…,n)

В матричной форме это равенство перепишется в виде

A^Tx=A^TB (1.3)

Здесь A - прямоугольная m× n матрица. Причем в задачах аппроксимации данных, как правило, m > n. Уравнение (1.3) называется нормальным уравнением.

Можно было с самого начала, используя евклидову норму векторов, записать задачу в эквивалентной матричной форме:

==

=

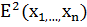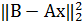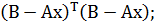
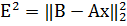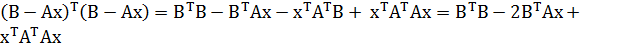
Наша цель минимизировать эту функцию по x. Для того чтобы в точке решения достигался минимум, первые производные по x в этой точке должны равняться нулю. Производные данной функции составляют

−2A^TB + 2A^TAx

и поэтому решение должно удовлетворять системе линейных уравнений

(A^TA)x = (A^TB).

Эти уравнения называются нормальными уравнениями. Если A - m× n матрица, то A>A - n × n - матрица, т.е. матрица нормального уравнения всегда квадратная симметричная матрица. Более того, она обладает свойством положительной определенности в том смысле, что (A>Ax, x) = (Ax, Ax) ≥ 0.

Замечание. Иногда решение уравнения вида (1.3) называют решением систе- мы Ax = В, где A прямоугольная m × n (m > n) матрица методом наименьших квадратов.

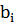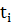Задачу наименьших квадратов можно графически интерпретировать как минимизацию вертикальных расстояний от точек данных до модельной кривой (см. рис.1.1). Эта идея основана на предположении, что все ошибки в аппроксимации соответствуют ошибкам в наблюдениях. Если имеются также ошибки в независимых переменных , то может оказаться более уместным минимизировать евклидово расстояние от данных до модели.

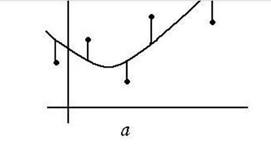
рис.1.1.

3.2 МНК в Excel

Приведенный ниже алгоритм реализации МНК в Excel подразумевает, что все исходные данные уже известны. Обе части матричного уравнения A×X=B системы умножаем слева на транспонированную матрицу системы А^Т:

А^ТАХ=А^ТВ

Затем обе части уравнения умножаем слева на матрицу (А^ТА)^-1. Если эта матрица существует, то система определена. С учетом того, что

(А^ТА)^-1*(А^ТА)=Е, получаем

Х=(А^ТА)^-1А^ТВ.

Полученное матричное уравнение является решением системы m линейных уравнений с nнеизвестными при m>n.

Рассмотрим применение вышеописанного алгоритма на конкретном примере.

Пример. Пусть необходимо решить систему

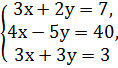
Решение.

В Excelлист с решением в режиме отображения формул для данной задачи выглядит следующим образом:

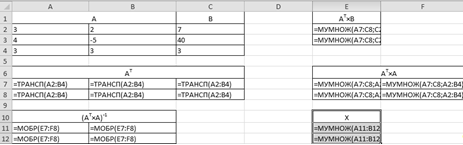
Результаты расчетов:

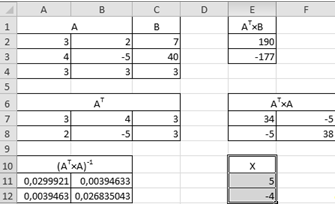
Искомый вектор Х расположен в диапазоне Е11:Е12.

При решении заданной системы линейных уравнений использовались следующие функции:

. МОБР - возвращает обратную матрицу для матрицы, хранящейся в массиве.

Синтаксис: МОБР(массив).

Массив - числовой массив с равным количеством строк и столбцов.

После введения функции в левую верхнюю ячейку диапазона массива следует выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а затем нажать клавиши CTRL+SHIFT+ENTER.

. МУМНОЖ - возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2.

Синтаксис: МУМНОЖ(массив1;массив2).

Массив1, массив2 - перемножаемые массивы.

После введения функции в левую верхнюю ячейку диапазона массива следует выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а затем нажать клавиши CTRL+SHIFT+ENTER.

. ТРАНСП - преобразует вертикальный набор ячеек в горизонтальный, или наоборот. В результате использования этой функции появляется массив с числом строк, равным числу столбцов исходного массива, и числом столбцов, равным числу строк начального массива.

Заключение

В курсовой работе описаны некоторые классические ([4],[7]) методы решения систем линейных уравнений. Описан также метод наименьших квадратов и решение системы с прямоугольной матрицей, в которой число уравнений больше, чем число неизвестных. Решение этой системы также свелось к решению методом Гаусса системы с квадратной матрицей, получаемой из исходной системы умножением обеих частей на транспонированную матрицу.

Следует отметить ( см. [2], [3], [4], [6], [7]), что в современных научных вычислениях в основном фигурируют методы решения больших, т.е. с размерностью более 1000, систем линейных алгебраических уравнений. В указанных книгах описаны существенно более изощренные методы решения алгебраических систем, для реализации которых на Excel’е требуется написание на языке Visual Basic новых макросов. Но, так как для решения больших систем Excel не пригоден в связи с низкой производительностью, то реализация этих методов в Excel не имеет смысла.

Список литературы

[1] Гельман В.Я. Решение математических задач средствами Excel.-Москва-

Санкт-Петербург : Питер,2003.

[2] Каханер Д. Моулер К., Нэш С. Численные методы и программное обеспечение.-М.: Мир, 1998.

[3] Кормен Т., Лейзерсон Ч., Ривест Р. АЛГОРИТМЫ (построение и анализ). - М.: МЦНМО, 2000.

[4] Райс Дж. Матричные вычисления и математическое обеспечение.- М.: Мир, 1984.

[5] Васильев А.Н. Научные вычисления в Microsoft Excel .- Москва-Киев: Диалектика, 2004.

[6] Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. - М.:Мир, 1980.

[7] Press W.H., Teukolsky S.A., Flannery B.P. Numerical Recipes in C.- Cambridge University Press, 1991.