Разработка программного проекта определения локальных экстремумов функции
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РФ
Федеральное государственное бюджетное
образовательное учреждение высшего профессионального образования
"Норильский Индустриальный
институт"
Кафедра Информационных систем и
технологий
курсовая
работа
По дисциплине:
Высокоуровневые методы информатики и
программирования
На тему: «Разработка программного
проекта определения локальных экстремумов функции»
Разработал
студент
Лапшин И.А.
группа ИС -
14(дневн)
Руководитель:
к.т.н.,профессор,
Фомичева С.Г.
Норильск, 2015
Оглавление
Назначение и цели создания проекта
Формализация задачи
Укрупненная блок-схема алгоритма
Листинг программы и модулей
Результат работы приложения
Файл-справка
Заключение
Список использованной литературы
алгоритм инсталляция приложение экстремум
функция
Введение
Объектно-ориентированные языки программирования давно пользуются большой
популярностью среди программистов, так как они позволяют использовать
преимущества объектно-ориентированного подхода не только на этапах
проектирования и конструирования программных систем, но и на этапах их
реализации, тестирования и сопровождения.
Первый объектно-ориентированный язык программирования Simula 67 был
разработан в конце 60-х годов в Норвегии. Авторы этого языка очень точно
угадали перспективы развития программирования: их язык намного опередил свое
время. Однако современники (программисты 60-х годов) оказались не готовы
воспринять ценности языка Simula 67, и он не выдержал конкуренции с другими
языками программирования (прежде всего, с языком Fortran). Прохладному
отношению к языку Simula 67 способствовало и то обстоятельство, что он был
реализован как интерпретируемый, а не компилируемый язык, что было совершенно
неприемлемым в 60-е годы, так как интерпретация связана со снижением скорости выполнения
программ.
Но достоинства языка Simula 67 были замечены некоторыми программистами, и
в 70-е годы было разработано большое число экспериментальных
объектно-ориентированных языков программирования: например, языки CLU, Alphard,
Concurrent Pascal и др. Эти языки так и остались экспериментальными, но в
результате их исследования были разработаны современные
объектно-ориентированные языки программирования: C++, C Sharp, Smalltalk,
Delphi и др.
Появление Delphi не могло пройти незамеченным среди многочисленных
пользователей компьютера. Оценки экспертов, изучающих возможности этого нового
продукта фирмы Borland, обычно имеют положительную основу. Основное достоинство
Delphi состоит в том, что здесь реализованы идеи визуального программирования.
Среда визуального программирования превращает процесс создания программы в
приятное и легко понимаемое конструирование приложения из большого набора
графических и структурных примитивов. - чрезвычайно быстро развивающаяся
система. Первая версия - Delphi 1. 0 была выпущена в феврале 1995 г. А затем
новые версии выпускались ежегодно.
Каждая последующая версия Delphi дополняла предыдущую.
Большинство версий Delphi выпускается в нескольких вариантах: Standart -
стандартном, Professional профессиональном, Client/Server - клиент/сервер,
Enterprise - разработка баз данных предметных областей. Различаются варианты в
основном разным уровнем доступа к системам управления базами данных. Последние
варианты - Client/Server и Enterprise, в этом отношении наиболее мощные.оказал огромное
влияние на создание концепции языка C# для платформы .NET. Многие его элементы
и концептуальные решения вошли в состав C Sharp.
Назначение и цели
создания проекта
Условие задачи: Задача нахождения локального экстремума функции одного
аргумента. Построить график функции F(x), позволяющий выполнять зуммирование и
скроллинг изображения.
Говоря о назначении моего проекта, можно вспомнить, что точки минимума и
максимума функции (точки экстремума) необходимы при исследовании функций в
математическом анализе, а так же при решении задач в механике и многом другом.
Моя проект ориентирован на учеников старших классов и студентов, которым может
понадобиться простая и удобная программа для вычисления экстремумов функций.
Назначение проекта:
. Нахождение экстремумов функции, выбранной пользователем.
2. Построение графика функции для графического решения задачи.
. Сохранение данных в файл и загрузка данных из этого файла.
К большому сожалению моя программа не может конкурировать с известными
аналогами: MathCad, SciLab, SAGE. Но в дальнейшем, благодаря изучению новых
языков программирования я мечтаю об усовершенствовании данной программы. Я
задаюсь целью вычисления экстремумов сложных функций, вводимых пользователем
вручную.
Цели, которые я ставил перед собой, приступая к работе:
. Узнать больше о нахождение экстремумов функций одной переменной.
2. Придумать функции для выбора пользователем.
. Ознакомиться с возможностями визуальной среды программирования
Delphi и сделать удобный интерфейс для расчета. Написать программу для расчета
экстремумов функций.
. Протестировать данную программу на разных операционных системах.
Для функций, выбранных пользователем, необходимо определить алгоритм
вычисления экстремумов. А так же использовать компоненты, позволяющие выполнять
зуммирование (приближение или отдаление изображения графика) и скроллинг (сдвиг
изображения в выбранном направлении). Необходимо сделать удобный для
пользователя выбор и описание функции. В описание функции входит: назначение
пользователем промежутков построения графика, коэффициентов функции, а также
шаг дискретизации.
Нахождение экстремумов функции может подразумевать под собой не только
аналитический путь: решение сложных уравнений с использованием первой
производной; оно также допускает и графический способ решения: построение и
анализ графика функции.
В своем проекте я пошел по второму пути, но это не значит что он более
легкий. Продумать все до мельчайших деталей очень сложно, т.к. в ходе
выполнения курсовой работы появляются все новые и новые вопросы, не терпящие
отлагательств. Тонких нюансов возникает огромнейшее количество. К примеру:
защита данных от некорректного ввода пользователем, так же называемая в
простонародье, как «защита от дураков». Только на выполнение этой задачи уходит
не малое количество времени.
Также нужно продумать вопросы, которые могут возникнуть у пользователя
при использовании данной программы, и создать справку с ответами на вопросы
такого рода.
Формализация задачи
Пусть функция f задана на некотором множестве X⊂ R и 
∈ X.
Определение 1: Точка называется точкой локального максимума (минимума) функции f,
если существует такая окрестность U() точки , что для всех x ∈ X ⋂ U() выполняется неравенство
f(x) ≤ f() (соответственно f(x) ≥f())
Если для всех x ∈ X ⋂ U() и x ≠ выполняется неравенство f(x) < f() (соответственно f(x) > f()), то точка называется точкой строгого
локального максимума (минимума).
В дальнейшем для простоты точки (строгого) локального максимума и
минимума функции будем кратко называть ее точками (строгого) максимума и
минимума. Точки максимума и минимума (строгого) функции называют ее точками
экстремума (строгого). Из теоремы Ферма для функций, определенных в некоторой
окрестности точки, сразу следует необходимое условие локального экстремума в
этом точке.
Теорема 2 (необходимое условие экстремума): Если функция имеет в точке локального
экстремума производную, то эта производная равна нулю.
Действительно, из того, что у функции в точке существует производная,
следует, что функция определена в некоторой окрестности этой точки, а так как
эта точка является точкой локального экстремума, то ее окрестность можно
выбрать так, что сужение на выбранную окрестность функции примет в
рассматриваемой точке наибольшее или наименьшее значение. Из теоремы Ферма,
примененной к указанному сужению функции, следует, что если в указанной точке
производная существует, то она равна нулю.
Замечание 2. Напомним, что под производной всегда понимается конечная
производная, если специально не оговорено, что допускаются и бесконечные
производные. Из комментариев к теореме Ферма следует, что в точке локального
экстремума может существовать знаконеопределенная бесконечная производная, но
не может существовать бесконечная производная определенного знака. Может
случиться, что в точке локального экстремума вообще не существует производной -
ни конечной, ни бесконечной (см. рис. №1).
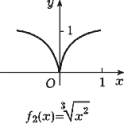
(Рис. №1)
Отметим, что условия равенства нулю производной или ее несуществования в
данной точке, будучи необходимыми условиями экстремума, не являются
достаточными условиями для наличия экстремума в этой точке. Например, у функции
f(x) =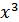 
производная f '(x) = 3
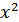в точке x =0 равна нулю, а
экстремума в этой точке нет (рис. №2).
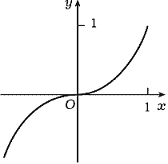
(Рис. №2)
Определение 2. Если функция определена в некоторой окрестности точки x0 и
в этой точке производная функции либо существует и равна нулю, либо не
существует, то точка называется критической точкой этой функции. Критические
точки функции, в которых производная функции равна нулю, называются также и
стационарными точками.
Теорема 2 означает, что все точки локального экстремума функции находятся среди
множества ее критических точек.
Определение 3. Точка называется точкой возрастания (убывания) функции f, если у существует такая окрестность U(), что при x ∈ X ⋂ U(), и x < , выполняется неравенство f(x) ≤
f() (соответственно f(x) ≥ f()), а при x ≥ - неравенство f(x) ≥ f() (соответственно f(x) ≤ f()). Если при x ≠ выполняется, кроме того, неравенство
f(x) ≠ f(), то точка называется точкой строгого возрастания (строгого убывания)
функции f. Точки строгого экстремума, точки строгого возрастания и убывания
удобно описывать в терминах знака приращения
∆y = f( + ∆x) - f()
функции f. В точке строгого максимума приращение функции в некоторой
окрестности этой точки имеет отрицательное значение при ∆x ≠ 0, в
точке строгого минимума - положительное, в точке строгого возрастания при ∆x
< 0 - отрицательное, при ∆x > 0 - положительное, а в точке строгого
убывания - положительное при ∆x < 0 и отрицательное при ∆x >
0 (рис. №3). Конечно, здесь всегда предполагается, что приращение аргумента ∆x
таково, что точка + ∆x принадлежит области определения X функции f.
Таким образом, при переходе через точку строгого экстремума (т. е. при изменении знака
приращения аргумента ∆x) приращение функции не меняет знака, а при
переходе через точки строгого возрастания и убывания меняет знак. Нетрудно
сформулировать в терминах знака производной в точке достаточные условия того,
что эта точка является точкой строгого возрастания или убывания (в этом случае
согласно определению производной функция заведомо определена в некоторой
окрестности рассматриваемой точки).
(Рис. №3)
Если функция f имеет в точке 
положительную производную
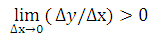
то для всех достаточно малых ∆x выполняется неравенство
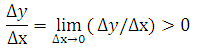
Отсюда следует, что при∆ x < 0 имеет место ∆y < 0, а
при∆ x > 0 также и ∆y > 0, т. е. точка является точкой строгого
возрастания.
Аналогично рассматривается случай f'().
Таким образом, если в точке существует не равная нулю
производная (конечная или определенного знака бесконечная), то эта точка
является либо точкой строгого возрастания, либо точкой строгого убывания, а
следовательно, не может быть точкой экстремума. Тем самым мы еще раз доказали,
что если в точке экстремума существует конечная или определенного знака
бесконечная производная, то она равна нулю. Отметим, что доказанная лемма дает
лишь достаточные, но не необходимые условия для точек строгого возрастания и
строгого убывания функций, имеющих в этих точках конечные или бесконечные
производные. Это видно уже на примере функции f(x) = x3, у которой точка x = 0
является точкой строгого возрастания, а производная в ней равна нулю: f'(0) = 0
(см. рис. 82).
Замечание 3. Аналогично лемме нетрудно доказать, что если в точке
производная, конечная или бесконечная, неотрицательна (неположительна), то эта
точка является точкой возрастания (соответственно убывания) функции, но, вообще
говоря, нестрогого.
Отметим, что у функции, равной тождественно постоянной на множестве ее
задания, все точки этого множества являются как точками экстремума, так и
точками возрастания и убывания функции.
Все это делает целесообразным введение понятий как точек экстремума,
точек возрастания и убывания функции, так и точек строгого экстремума, точек
строгого возрастания и строгого убывания функции.
Теорема 3. Пусть функция непрерывна в некоторой окрестности точки,
дифференцируема в ее проколотой окрестности, и производная с каждой стороны от
рассматриваемой точки сохраняет один и тот же знак.
Для того чтобы функция в этой точке имела строгий максимум (строгий
минимум), необходимо и достаточно, чтобы при переходе через нее производная
меняла знак с плюса на минус (соответственно с минуса на плюс).
Для того чтобы эта точка была точкой строгого возрастания (строгого
убывания) функции, необходимо и достаточно, чтобы производная с обеих сторон от
рассматриваемой точки была положительной (отрицательной).
Таким образом, образно говоря, в условиях теоремы точка является точкой
строгого максимума (строгого минимума) функции тогда и только тогда, когда в
этой точке строгое возрастание (строгое убывание) функции сменяется ее строгим
убыванием (соответственно строгим возрастанием). Подобным образом точка
является точкой строгого возрастания (строгого убывания) функции тогда и только
тогда, когда с обеих сторон от этой точки функция строго возрастает
(соответственно строго убывает) (см. теорему 1).
Пусть функция f непрерывна в окрестности U() точки , дифференцируема в проколотой
окрестности
Ủ() и производная сохраняет постоянный знак во всех точках
проколотой окрестности Ủ(), лежащих с каждой стороны от точки . Для любой точки x ∈ Ủ(), согласно формуле Лагранжа, имеем ∆y
= f'(ε)∆x, где точка ε
лежит между точками и x = + ∆x. Таким образом,
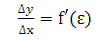(1)
Поэтому если производная f'(x) меняет знак с плюса на минус при переходе
через точку :'(x) > 0 при ∆x < 0 и f'(x) < 0 при ∆x
> 0, (1)>0 то при ∆x < 0 и (1)<0 при ∆x > 0. Отсюда ∆y
< 0 при всех ∆x, + ∆x Ủ(), т.е. приращение функции ∆y
не меняет знака при переходе через точку и является отрицательным. Это
означает, что точка является точкой строгого локального максимума.
Аналогично, из формулы (1) следует, что если производная f'(x) меняет
знак с минуса на плюс при переходе через точку , то (1)<0 при ∆x < 0 и
(1)>0 при ∆x > 0, а поэтому при переходе через точку приращение функции ∆y не
меняет знака и положительно. Это означает, что точка является точкой строгого локального
минимума.
Если производная f'(x) не меняет знака при переходе через точку , то из формулы (1) следует, что и
отношение ∆y/∆x также не меняет знака при переходе через эту точку
и его знак совпадает со знаком производной. Поэтому если f'(x) > 0, x ∈ Ủ(), то ∆y < 0 при ∆x
< 0 и ∆y > 0 при ∆x > 0, т.е. точка является точкой строгого
возрастания, а если f'(x) < 0, x ∈ Ủ(), то аналогично получаем, что точка является точкой строгого убывания.
Мы доказали, что каждое из рассмотренных условий о знаке производной с
разных сторон от точки является достаточным условием соответственно для строгого
локального максимума, строгого локального минимума, строгого возрастания или
убывания функции в точке. Поскольку были рассмотрены все возможные случаи
знаков производной с каждой стороны от точки , то все сформулированные условия
являются не только достаточными, но и необходимыми для соответствующих
утверждений (рис. №4).
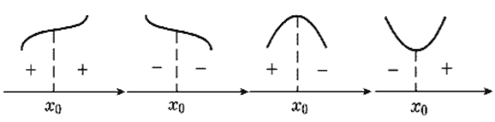
(Рис. №4)
Следует обратить внимание на то, что рассмотренным здесь случаем когда
производная с каждой стороны от данной точки не меняет своего знака (а поэтому
можно говорить об изменении знака производной при переходе через точку), не
исчерпываются возможные ситуации даже для дифференцируемых функций: может
случиться, что для сколь угодно малой окрестности по одну из сторон от точки или по обе стороны производная
меняет знак. В этих точках приходится применять другие методы для исследования
функций на экстремум. Таким образом, в более широком классе функций,
дифференцируемых в окрестности рассматриваемой точки, кроме, быть может, самой
этой точки, условие изменения знака производной в данной точке является лишь
достаточным условием экстремума.
Докажем еще одни достаточные условия для точек строгого экстремума и
точек строгого возрастания (строгого убывания) в терминах производных любого
порядка в данной точке. Эти условия для точек строгого возрастания и убывания
обобщают условия, указанные в приведенной выше лемме. Для задачи же об
экстремумах они представляют собой принципиально новый подход к отысканию точек
экстремума, имеющий широкие обобщения.
Теорема 4. Пусть функция y = f(x) n раз дифференцируема в точке , n > 1 и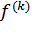 
() = 0, x = 1, 2, ..., n - 1,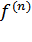 
() ≠0. (2)
Тогда если n = 2m, m ∈ N, т.е. n - четное число, то функция f имеет в точке строгий экстремум, а именно строгий
максимум при 
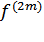() < 0 и строгий минимум при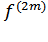
() > 0. Если же n = 2m - 1, m ∈ N, т. е. n - нечетное число, то
функция f не имеет в точке экстремума; в этом случае при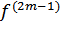 
() > 0 точка является точкой строгого возрастания
функции f, а при 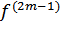() < 0 - ее точкой строгого убывания.
Предпошлем доказательству одно простое замечание: если β(x) = o(α(x)), x→, где функции α и β заданы в некоторой окрестности точки
∈ R, то существует такая окрестность
U() этой точки, что при x ∈ U() справедливо неравенство
|β(x)| = |α(x)|/2. (3)
В самом деле,
| β (x)| =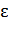 
(x)α(x), (4)
где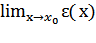 
= 0, и, следовательно, существует такая окрестность U(), что при x ∈ U() выполняется неравенство
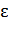| (x)| < 1/2. (5)
Из (4) и (5) следует неравенство (3).
Напишем формулу Тейлора порядка n для функции f в окрестности точки .В силу условий (2) будем иметь
∆y = f( + ∆x) - f() = 
∆
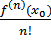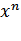+ o(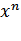), ∆x→0. (6)
Так как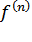 
() ≠0, то(
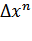)= o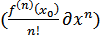
, ∆x→0,
т.е. второй член правой части равенства (6) является бесконечно малым по
сравнению с первым. Поэтому, согласно (3), существует такая окрестность U() точки , что при x ∈ U() для функции o(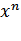) в формуле (6) выполняется
неравенство
|o(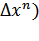
|<
= 
|∆|
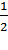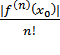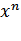и, следовательно, при достаточно малых ∆x знак правой части
равенства (6), а потому и знак приращения функции ∆y, совпадает со знаком
первого слагаемого правой части. Если n = 2k, то в формуле (6) приращение
аргумента ∆x возводится в четную степень, поэтому знак приращения функции
∆y не зависит от знака ∆x≠0 и, следовательно, является точкой строгого экстремума,
причем строгого максимума при 
() < 0 (в этом случае ∆y < 0, ∆x≠0) и
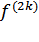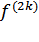строгого минимума при () > 0 (в этом случае y > 0, ∆x≠0). Если же
n = 2k - 1, то ∆x возводится в нечетную степень, и поэтому знак ∆y
меняется вместе с изменением знака ∆x, следовательно, точка не является точкой экстремума. Если ∆x
меняет знак с минуса на плюс, то при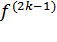 
() > 0 приращение ∆y также
меняет знак с минуса на плюс и, следовательно, является точкой возрастания функции
f, а при 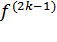() < 0 приращение ∆y меняет
знак с плюса на минус и, следовательно, точка является точкой убывания функции f.
Отметим специально частный случай теоремы 4 при n = 2. Если f'(x) = 0,
а f"(x) > 0, то точка является точкой строгого минимума, а если f'(x) = 0, а
f"(x) < 0, (рис. №5), то - точкой строгого максимума. Подчеркнем, что
все условия экстремума, полученные в этом параграфе, относятся к внутренним
точкам промежутка, на котором была определена функция. На концах промежутка
требуется проводить отдельные исследования и при применении методов
дифференциального исчисления использовать в концевых точках понятие
односторонних производных.
Минимум Максимум
(Рис. №5)
Укрупненная блок-схема алгоритма
procedure TfrmMain.edXminKeyPress(Sender: TObject; var Key: Char);
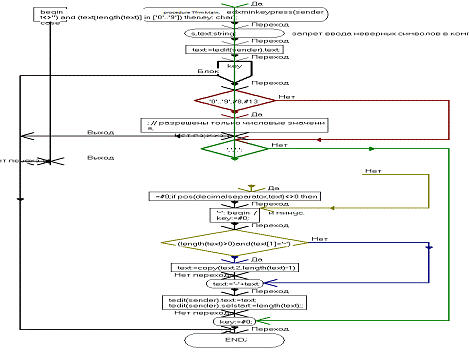
procedure TfrmMain.Button1Click(Sender: TObject);
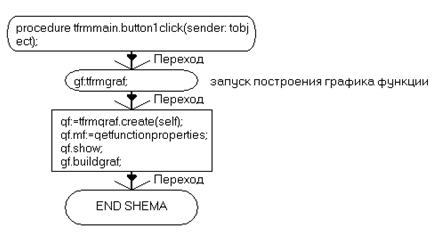
procedure TfrmMain.mniPropSaveClick(Sender: TObject);
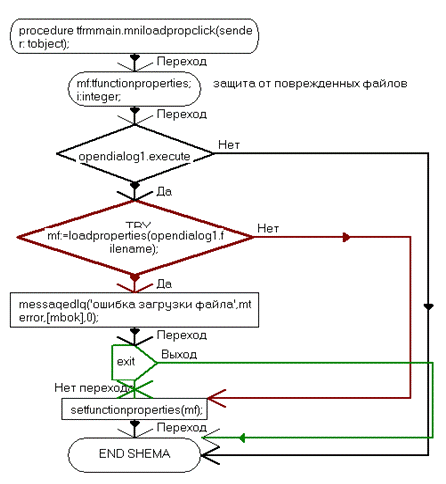
procedure TfrmMain.mniLoadPropClick(Sender: TObject);
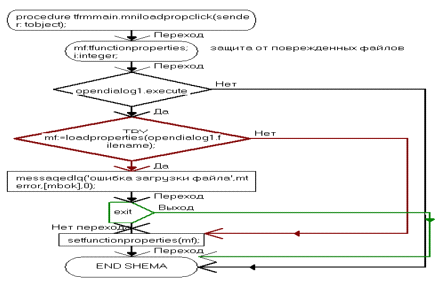
procedure TfrmMain.cbFunctionCloseUp(Sender: TObject);
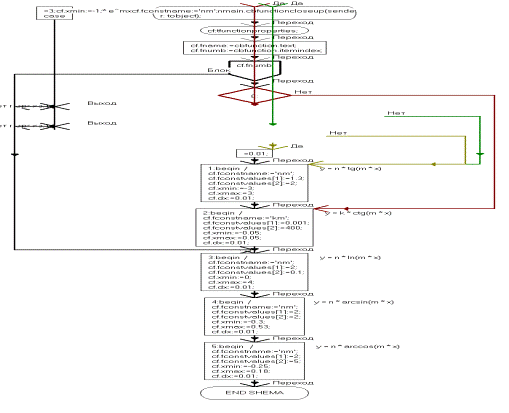
procedure TfrmMain.SetFunctionProperties(mf: TFunctionProperties);
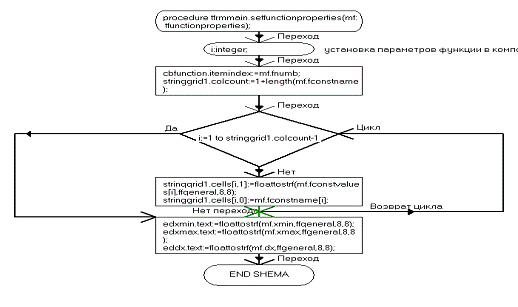
function TfrmMain.GetFunctionProperties: TFunctionProperties;
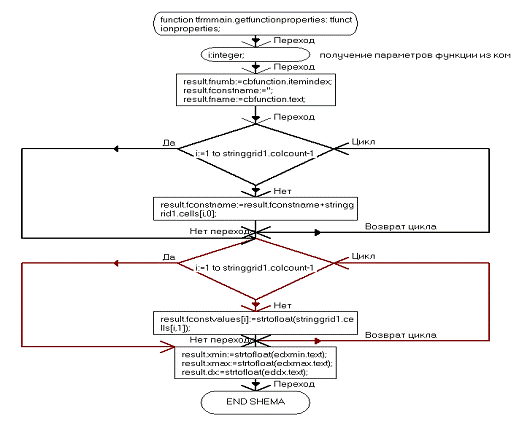
procedure TfrmMain.FormCreate(Sender: TObject);
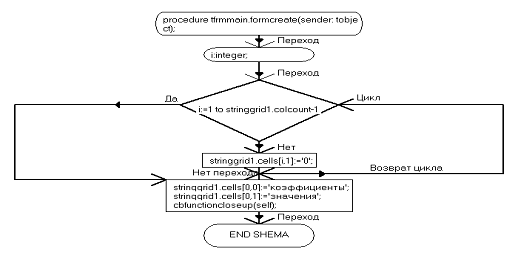
procedure TfrmMain.N1Click(Sender: TObject);
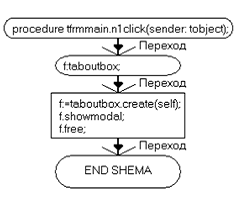
procedure TfrmMain.N2Click(Sender: TObject);
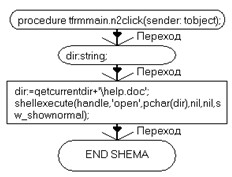
procedure TfrmGraf.CreateParams(var Params: TCreateParams);
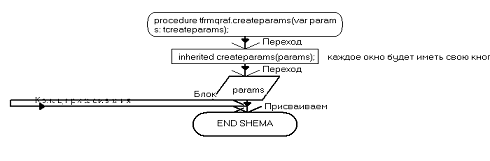
procedure TfrmGraf.mniZoomPClick(Sender: TObject);
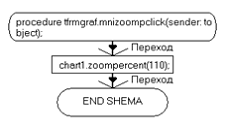
procedure TfrmGraf.mniZoomMClick(Sender: TObject);
procedure TfrmGraf.mni100Click(Sender: TObject);
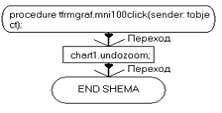
procedure TfrmGraf.mniFileClick(Sender: TObject);
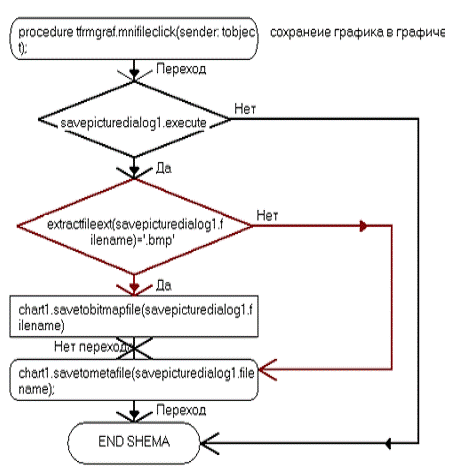
procedure TfrmGraf.FormClose(Sender: TObject; var Action: TCloseAction);
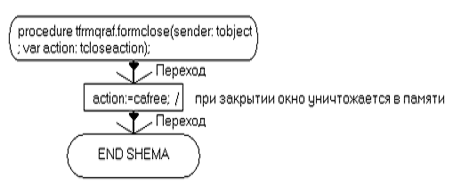
procedure TfrmGraf.SetFunctionProperties;
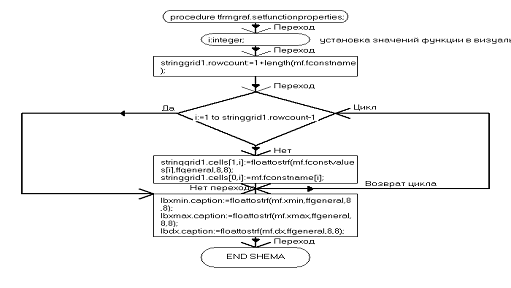
procedure TfrmGraf.BuildGraf;
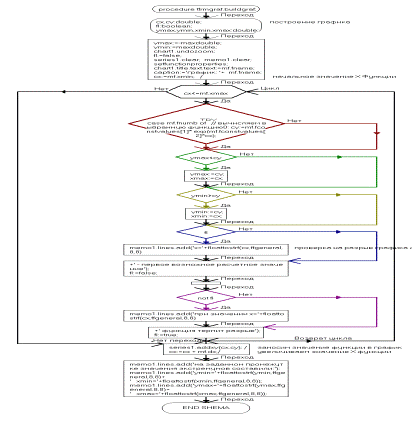
procedure TfrmGraf.mniPropSaveClick(Sender: TObject);
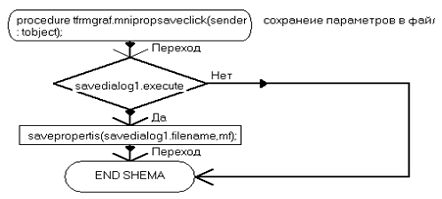
procedure TfrmGraf.mniLoadPropClick(Sender: TObject);
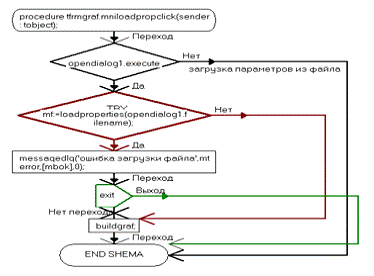
procedure TfrmGraf.FormCreate(Sender: TObject);
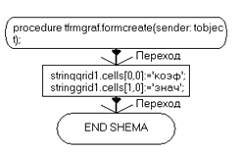
procedure TfrmGraf.Button1Click(Sender: TObject);
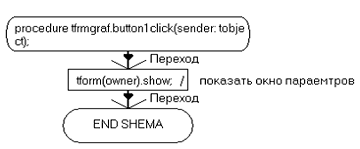
Листинг программы и модулей
unit Unit1;, Messages, SysUtils, Variants, Classes, Graphics, Controls,
Forms,, StdCtrls, Grids, ExtCtrls, UmGlobal, Menus, ShellAPI;= class(TForm):
TPanel;: TComboBox;: TGroupBox;: TGroupBox;: TStringGrid;: TGroupBox;: TLabel;:
TEdit;: TLabel;: TEdit;: TGroupBox;: TLabel;: TEdit;: TButton;: TSaveDialog;:
TOpenDialog;: TMainMenu;: TMenuItem;: TMenuItem;: TMenuItem;: TMenuItem;:
TMenuItem;: TMenuItem;edXminKeyPress(Sender: TObject; var Key:
Char);StringGrid1KeyPress(Sender: TObject; var Key: Char);Button1Click(Sender:
TObject);mniPropSaveClick(Sender: TObject);mniLoadPropClick(Sender:
TObject);cbFunctionCloseUp(Sender: TObject);GetFunctionProperties:
TFunctionProperties;SetFunctionProperties(mf:TFunctionProperties);FormCreate(Sender:
TObject);N1Click(Sender: TObject);N2Click(Sender: TObject);
{ Private declarations }
{ Public declarations };: TfrmMain;Unit2,unit3;
{$R *.dfm}TfrmMain.edXminKeyPress(Sender: TObject; var Key: Char);
//запрет ввода неверных символов в компонеты ввода
Edits,text:string;:=TEdit(Sender).text;key of
'0'..'9',#8,#13:; // разрешены только числовые значения,
',','.': begin //разделитель дробной части,(Text<>'') and
(Text[Length(Text)] in ['0'..'9']) then:=DecimalSeparator:=#0;pos(DecimalSeparator,text)<>0
then:=#0;;
'-': begin // и минус.:=#0;(Length(text)>0)and(Text[1]='-')
then:=Copy(text,2,Length(text)-1)Text:='-'+Text;(Sender).text:=Text;(Sender).SelStart:=Length(Text);;;key:=#0;;;TfrmMain.StringGrid1KeyPress(Sender:
TObject; var Key: Char);
//запрет ввода неверных символов в
StringGridtext:string;:=TStringGrid(Sender).Cells[TStringGrid(Sender).Col,(Sender).Row];key
of
'0'..'9',#8:; // разрешены только числовые значения,
',','.': begin //разделитель дробной части,(Text<>'') and
(Text[Length(Text)] in ['0'..'9'])
then:=DecimalSeparatorKey:=#0;pos(DecimalSeparator,text)<>0 then
key:=#0;;
'-': begin // и минус:=#0;(Length(text)>0)and(Text[1]='-')
then:=Copy(text,2,Length(text)-1)Text:='-'+Text;(Sender).Cells[TStringGrid(Sender).Col,(Sender).Row]:=Text;.ProcessMessages;(Windows.getFocus,EM_SETSEL,length(text),length(text));;
#13: // Enter(TStringGrid(Sender).Col+1)<TStringGrid(Sender).ColCount
then(Sender).Col:=TStringGrid(Sender).Col+1;key:=#0;;;TfrmMain.Button1Click(Sender:
TObject);
// запуск построения графика
функцииgf:TfrmGraf;:=TfrmGraf.create(Self);.mF:=GetFunctionProperties;.Show;.BuildGraf;;TfrmMain.mniPropSaveClick(Sender:
TObject);
// сохранеие выбранных параметров
функцииcf:TFunctionProperties;:=GetFunctionProperties;SaveDialog1.Execute
then(SaveDialog1.FileName,cF);;TfrmMain.mniLoadPropClick(Sender: TObject);
// защита от поврежденных
файловmf:TFunctionProperties;:integer;OpenDialog1.Execute
then:=LoadProperties(OpenDialog1.FileName);('Ошибка загрузки файла',mtError,[mbOk],0);;;(mf);;;TfrmMain.cbFunctionCloseUp(Sender:
TObject);cF:TFunctionProperties;.FName:=cbFunction.Text;.FNumb:=cbFunction.ItemIndex;
// при выборе функции задаем некоторые начальные значанения (для
примера)cF.FNumb of
:begin // y = n * e^mx.FConstName:='nm';.FConstValues[1]:=2;.FConstValues[2]:=3;.Xmin:=-1;.Xmax:=1;.dX:=0.01;;
:begin // y = n * tg(m *
x).FConstName:='nm';.FConstValues[1]:=1.3;.FConstValues[2]:=2;.Xmin:=-3;.Xmax:=3;.dX:=0.01;;
:begin // y = k * ctg(m * x).FConstName:='km';.FConstValues[1]:=0.001;.FConstValues[2]:=400;.Xmin:=-0.05;.Xmax:=0.05;.dX:=0.01;;
:begin // y = n * ln(m *
x).FConstName:='nm';.FConstValues[1]:=2;.FConstValues[2]:=0.1;.Xmin:=0;.Xmax:=4;.dX:=0.01;;
:begin // y = n * arcsin(m * x).FConstName:='nm';.FConstValues[1]:=2;.FConstValues[2]:=2;.Xmin:=-0.3;.Xmax:=0.53;.dX:=0.01;;
:begin // y = n * arccos(m *
x).FConstName:='nm';.FConstValues[1]:=2;.FConstValues[2]:=5;.Xmin:=-0.25;.Xmax:=0.18;.dX:=0.01;;;(cF);;TfrmMain.SetFunctionProperties(mf:
TFunctionProperties);
// установка параметров функции в компонеты ввода
StringGridI:integer;.ItemIndex:=mf.FNumb;.ColCount:=1+Length(mf.FConstName);I:=1
to StringGrid1.ColCount-1
do.Cells[i,1]:=FloatToStrF(mf.FConstValues[i],ffGeneral,8,8);.Cells[i,0]:=mf.FConstName[i];;.Text:=FloatToStrF(mf.Xmin,ffGeneral,8,8);.Text:=FloatToStrF(mf.Xmax,ffGeneral,8,8);.Text:=FloatToStrF(mf.dX,ffGeneral,8,8);;TfrmMain.GetFunctionProperties:
TFunctionProperties;
// получение параметров функции из компонентов ввода
StringGridi:integer;.FNumb:=cbFunction.ItemIndex;.FConstName:='';.FName:=cbFunction.Text;i:=1
to StringGrid1.ColCount-1
do.FConstName:=Result.FConstName+StringGrid1.Cells[i,0];I:=1 to
StringGrid1.ColCount-1
do.FConstValues[i]:=StrToFloat(StringGrid1.Cells[i,1]);.Xmin:=StrToFloat(edXmin.Text);.Xmax:=StrToFloat(edXmax.Text);.dX:=StrToFloat(eddX.Text);;TfrmMain.FormCreate(Sender:
TObject);i:integer;i:=1 to StringGrid1.ColCount-1
do.Cells[i,1]:='0';;.Cells[0,0]:='Коэффициенты';.Cells[0,1]:='Значения';(self);;TfrmMain.N1Click(Sender:
TObject);f:TAboutBox;:=TAboutBox.create(self);.ShowModal;.free;;TfrmMain.N2Click(Sender:
TObject);dir:string;:=GetCurrentDir+'\help.doc';(handle,'open',PChar(dir),nil,nil,SW_SHOWNORMAL);;.Unit2;,
Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, umGlobal, ImgList, Menus, TeeProcs, TeEngine, Chart, ExtCtrls,,
Buttons, Series,math, StdCtrls, Grids;= class(TForm): TPanel;: TPanel;:
TChart;: TMainMenu;: TMenuItem;: TMenuItem;: TMenuItem;: TMenuItem;:
TImageList;: TMenuItem;: TSpeedButton;: TSpeedButton;: TSpeedButton;:
TSavePictureDialog;: TLineSeries;: TMenuItem;: TMenuItem;: TMenuItem;:
TSaveDialog;: TOpenDialog;: TStringGrid;: TLabel;: TLabel;: TLabel;: TLabel;:
TLabel;: TLabel;: TLabel;: TLabel;: TMemo;: TButton;mniZoomPClick(Sender: TObject);mniZoomMClick(Sender:
TObject);mni100Click(Sender: TObject);mniFileClick(Sender:
TObject);FormClose(Sender: TObject; var Action:
TCloseAction);BuildGraf;mniPropSaveClick(Sender:
TObject);mniLoadPropClick(Sender: TObject);SetFunctionProperties;FormCreate(Sender:
TObject);Button1Click(Sender: TObject);CreateParams(var Params: TCreateParams);
override;
{ Private declarations }
{ Public declarations }:TFunctionProperties;;: TfrmGraf;
{$R *.dfm}TfrmGraf.CreateParams(var Params: TCreateParams);
// каждое окно будет иметь свою кнопку на панели
задачCreateParams(Params);Params do:= ExStyle or
WS_EX_APPWINDOW;;TfrmGraf.mniZoomPClick(Sender:
TObject);.ZoomPercent(110);;TfrmGraf.mniZoomMClick(Sender:
TObject);.ZoomPercent(90);;TfrmGraf.mni100Click(Sender: TObject);.UndoZoom;;TfrmGraf.mniFileClick(Sender:
TObject);
// сохранеие графика в графическом видеsavepicturedialog1.Execute
thenextractfileext(SavePictureDialog1.FileName)='.bmp'
then.SaveToBitmapFile(savepicturedialog1.FileName).SaveToMetafile(savepicturedialog1.FileName);;TfrmGraf.FormClose(Sender:
TObject; var Action: TCloseAction);:=caFree; // при закрытии окна оно
уничтожается в памяти;TfrmGraf.SetFunctionProperties;
// установка значений функции в визуальные элементы
формыI:integer;.RowCount:=1+Length(mf.FConstName);I:=1 to
StringGrid1.RowCount-1
do.Cells[1,i]:=FloatToStrF(mf.FConstValues[i],ffGeneral,8,8);.Cells[0,i]:=mf.FConstName[i];;.Caption:=FloatToStrF(mf.Xmin,ffGeneral,8,8);.Caption:=FloatToStrF(mf.Xmax,ffGeneral,8,8);.Caption:=FloatToStrF(mf.dX,ffGeneral,8,8);;TfrmGraf.BuildGraf;
// построение
графикаcX,cY:double;:boolean;,Ymin,Xmin,Xmax:double;:=-MaxDouble;:=MaxDouble;.UndoZoom;:=False;.Clear;
Memo1.Clear;;.Title.Text.Text:=mf.FName;:='График: '+ mf.FName;:=mF.Xmin; //
начальное значение X ФункцииcX<=mF.Xmax domf.FNumb of // вычисляем выбранную
функцию
: cY:=mF.FConstValues[1]* exp(mF.FConstValues[2]*cX);
: cY:=mF.FConstValues[1]* Tan(mF.FConstValues[2]*cX);
: cY:=mF.FConstValues[1]* CoTan(mF.FConstValues[2]*cX);
: cY:=mF.FConstValues[1]* Ln(mF.FConstValues[2]*cX);
: cY:=mF.FConstValues[1]* ArcSin(mF.FConstValues[2]*cX);
: cY:=mF.FConstValues[1]* ArcCos(mF.FConstValues[2]*cX);;Ymax<cY
then:=cY;:=cX;;Ymin>cY then:=cY;:=cX;;fl then //проверка на разрыв графика
функции.Lines.Add('Х='+Floattostrf(cX,ffGeneral,8,8)
+' - первое возможное расчетное значение');:=False;not Fl
then.Lines.Add('При значении Х='+Floattostrf(cX,ffGeneral,8,8)
+' функция терпит разрыв');:=True;;.Addxy(cX,cY); // заносим значение
функции в график:=cX + mF.dX;// увеличиваем значение Х функции;.Lines.Add('На
заданном промежутке значения экстремумов
составили:');.Lines.Add('Ymin='+floatToStrF(Ymin,ffGeneral,8,8)+
'
Xmin='+floatToStrF(Xmin,ffGeneral,8,8));.Lines.Add('YMax='+floatToStrF(Ymax,ffGeneral,8,8)+
' Xmax='+floatToStrF(Xmax,ffGeneral,8,8));;TfrmGraf.mniPropSaveClick(Sender:
TObject);
// сохранеие параметров в файлSaveDialog1.Execute
then(SaveDialog1.FileName,mF);;TfrmGraf.mniLoadPropClick(Sender: TObject);
// загрузка параметров из файлаOpenDialog1.Execute
then:=LoadProperties(OpenDialog1.FileName);('Ошибка загрузки
файла',mtError,[mbOk],0);;;;;;
TfrmGraf.FormCreate(Sender:
TObject);.Cells[0,0]:='Коэф';.Cells[1,0]:='Знач';;TfrmGraf.Button1Click(Sender:
TObject);(Owner).Show; // показать окно параемтров;.Windows, SysUtils, Classes,
Graphics, Forms, Controls, StdCtrls,, ExtCtrls;= class(TForm): TPanel;:
TImage;: TLabel;: TLabel;: TLabel;: TLabel;: TButton;: TLabel;
{ Private declarations }
{ Public declarations };: TAboutBox;
{$R *.dfm}.TFunctionProperties=record //описание функции общедоступой для
всех форм:string[40];:byte;:string[5];:array[1..5] of
double;:double;:double;:double;;SavePropertis(FileName:string;
fP:TFunctionProperties);LoadProperties
(FileName:string):TFunctionProperties;SavePropertis(FileName:string;
fP:TFunctionProperties);f:file of TFunctionProperties;(f,FileName);(f);(f,
fP);(f);;LoadProperties (FileName:string):TFunctionProperties;f:file of
TFunctionProperties;(f,FileName);(f);(f, Result);(f);;.Graf;,in 'Unit1.pas'
{frmMain},in 'UmGlobal.pas',in 'Unit2.pas' {frmGraf},in 'Unit3.pas' {AboutBox};
$R *.res}.Initialize;.CreateForm(TfrmMain, frmMain);.Run;.
Результат работы приложения
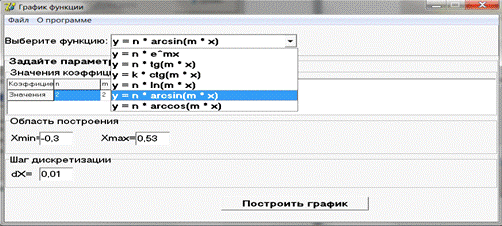
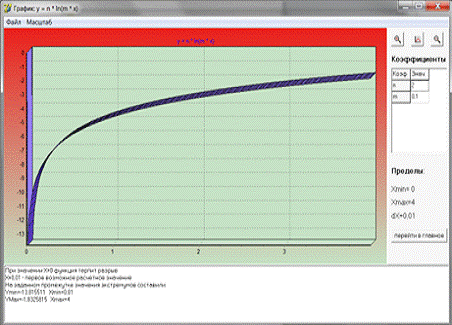
В этом окне показывается график функции с возможностью зуммирования,
скролинга и перемещения графика. Внизу выводятся значения экстремумов на
заданном промежутке.
Сохраненный график в формате wmf:
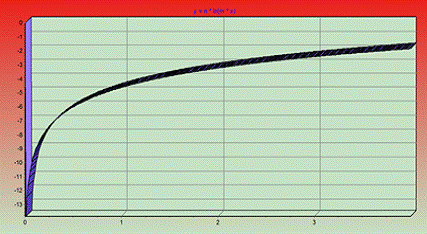
Файл-справка
О программе
НАХОЖДЕНИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА
ФУНКЦИИ ОДНОГО АРГУМЕНТА.
Данная программа разработана для расчета экстремумов и построения
графиков данных функций:
. y = n * e^mx
2. y = n * tg(m * x)
. y = k * ctg(m * x)
. y = n * ln(m * x)
. y = n * arcsin(m * x)
. y = n * arccos(m * x)
Значения получаются приближенными, при точных расчетах использовать
данную программу не рекомендуется.
Расчет экстремума.
1. При запуске программы необходимо выбрать функцию из списка.
2. После - расставить значения коэффициентов строках для заполнения:
Значения коэффициентов(n,m,k);
Область построения(Xmin,Xmax);
Шаг дискретизации(dX);
3. Нажать на кнопку «Построить график». Откроется новое окно, где
есть возможность увидеть график, приблизить его, зажав левую клавишу мыши и
потянув по диагонали вправо-вниз что бы увеличить (влево-вверх что бы
уменьшить). Скроллинг изображения производиться зажатием правой кнопки мыши.
Под графиком выведены значения экстремумов на данном промежутке.
4. Также можно охранить свои параметры и график, кликнув на пункт меню
“Файл”→ ”Сохранить параметры функции/график”
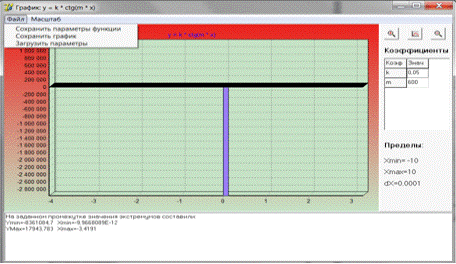
5. Загрузить свои параметры можно так же нажав на пункт меню “Файл”→
”Загрузить параметры”
Спасибо за использование данной программы!
Заключение
Данная программа проверена на операционных системах Microsoft XP/7/8.1.
Для ее корректной работы требуется 1,01 Мб.
Ошибок при запуске не обнаружено. Удобство программы было отмечено
некоторыми пользователями. Они были довольны интерфейсом и быстродействием
программ. В среднем для прорисовки графика и нахождения экстремумов требуется
1-3 секунды.
Многие из тех, кто уже попробовал данную программу, начинают предлагать
идеи по расширению функционала проекта. Так как идей поступает очень много -
данный проект будет развиваться и возможно, в ближайшем будущем сможет
потеснить аналоги от крупных компаний хотя бы благодаря удобству в
использовании. Скорее всего, он будет перенесен на более совершенные языки
программирования. Таким образом, в основном эта программа рассчитана на старшие
классы, но ей так же могут воспользоваться и студенты первых курсов.
Список использованной литературы
1.Круценюк, К. Ю. Численные методы решения уравнений (Excel,
Turbo Pascal, Delphi) [Текст] : учеб. пособие / К. Ю. Круценюк ; Норильский
индустр. ин-т. - Норильск : НИИ, 2010. - 76 с. - Библиогр.: с. 73-74 ( 24
назв.).
.Круценюк, К. Ю. Технология визуального программирования
(DELPHI для экономистов) [Текст]: лабораторный практикум / К. Ю. Круценюк ;
Норильский индустр. ин-т. - Норильск : НИИ, 2008. - 92 с. - Библиогр.: с. 90 (
19 назв.).
.Delphi 7 [Текст] / Хомоненко А.Д. [ и др.] ; под ред. А.Д.
Хомоненко. - СПб. : БХВ-Петербург, 2006. - 1216 с. : ил. - Предм. указ.: с.
1196-1200.
.С.Г. Фомичева. Визуальная среда программирования
Delphi/Учеб. пособие Норильск, НИИ,1999.
.Пискунов Н.С. Дифференциальное и интегральное исчисления:
Учеб. Для втузов. В 2-х т. Т. I: - М.: Интеграл - Пресс, 2001. - 416 с.
.Научная библиотека: 4.17. Локальный экстремум функции,
http://sernam.ru/lect_math2.php?id=57
.Школьная коллекция: Локальный экстремум,
http://school-collection.edu.ru/catalog/res/e0bd4447-c571-4282-a3e5-7915a08c949e/view/
.Нуклипс: 15.2. Локальные экстремумы функций,
http://nuclphys.sinp.msu.ru/mathan/p1/m1502.html
.Mazprofs: Возрастание, убывание и экстремумы функции,
http://mathprofi.ru/vozrastanie_ubyvanie_ekstremumy_funkcii.html
.Math24: Локальные экстремумы функции, http://www.math24.ru/локальные-экстремумы-функции.html
.Википедия: Экстремум,
https://ru.wikipedia.org/wiki/Экстремум
.Википедия: Delphi (язык программирования),
https://ru.wikipedia.org/wiki/Delphi_(язык_программирования)