Закон сохранения момента количества движения в физике магнитных явлений
Реферат
Закон сохранения момента количества
движения в физике магнитных явлений
Содержание
1. Момент количества движения. Пространственное квантование
2. Магнитный момент в магнитном поле
3. Спин и собственный магнитный момент электрона
4. g-фактор
5. Принцип запрета Паули
6. Обменная энергия
7. Обменное взаимодействие
8. Энергия обменного взаимодействия
Литература
1.
Момент количества движения. Пространственное квантование
В физике огромную роль играют законы сохранения. Атомная
физика и физика магнитных явлений не являются в этом смысле исключениями.
Электроны в атоме движутся в поле силы, обладающей сферической симметрией, или,
попросту говоря, сила, действующая на электрон со стороны ядра, зависит от
расстояния электрона от ядра, но не зависит от направления. Классическая
механика "предусмотрела" для такого случая специальный закон
сохранения - закон сохранения момента количества движения: L = [pr] не
зависит от времени.
А что по этому поводу говорит квантовая механика? Закон
сохранения момента количества движения, конечно, имеет место и в квантовой
механике (это общее правило: каждый "классический" закон сохранения
имеет квантовый аналог; обратное неверно - есть квантовые законы сохранения, не
имеющие аналога в классической физике).
Существование закона сохранения момента количества движения
означает, что электрон, находящийся в определенном стационарном состоянии (т.е.
в состоянии с определенной энергией), может иметь определенный момент
количества движения. Строгое квантовомеханическое рассмотрение движения частицы
в силовом поле с центральной симметрией показывает: сохраняющийся момент
количества движения частицы может характеризоваться длиной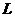 
и проекцией 
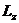на какую-либо ось (мы ее назвали осью z).
Сразу же возникает вопрос: "На какую ось?". Безразлично!
Именно этим безразличием подчеркивается изотропия силы, действующей на частицу.
Конечно, если есть какая-либо причина, выделяющая определенное направление, то
речь должна идти о проекции на это направление.
Квантовая механика не только ограничивает задание момента
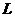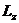количества движения двумя величинами ( и ) вместо трех (классический вектор
характеризуется тремя проекциями), но и формулирует жесткие ограничения на эти
величины. Проекция момента количества движения на ось z может принимать
значения
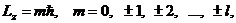(1)
а длина вектора момента количества движения
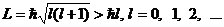(2)
Таким образом, момент количества движения принадлежит к таким
физическим величинам, которые квантуются, т.е. могут иметь только определенные
дискретные значения, пропорциональные постоянной Планка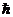 
.
Когда хотят назвать величину вектора момента количества движения,
называют просто значение числа l. В
дальнейшем мы всегда будем под моментом количества движения понимать безразмерную
величину l, а множитель 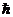опускать.
Обратите внимание: частица может обладать нулевым моментом
количества движения!
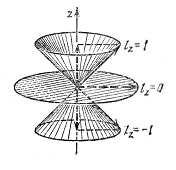
Рис. 1. Наглядная классическая картина, изображающая пространственное
квантование.
Как правило, когда мы говорим, что частица имеет определенный
момент количества движения, это означает, что она находится в состоянии с
заданным значением l. При этом проекция L на ось может иметь
одно из 2 l + 1 значений. Более наглядно: момент количества движения
может иметь только дискретные направления в пространстве (правда, не надо
забывать, что ось z - ось квантования - имеет произвольное направление). Это
квантовое свойство вектора момента количества движения называют пространственным
квантованием (рис.1).
Проекци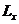и 
и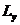 
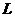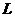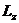вектора при заданных и не имеют определенных значений; можно говорить только о
вероятности того или иного значения этих проекций. Если воспользоваться
классическим образом, то сохраняющийся вектор момента количества движения
удобно представлять себе как вектор, прецессирующий вокруг оси z. Угол между 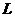и осью z определяется значением 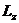, т.е. m (см. (1) и рис.1).
Наглядное представление о "прецессирующем" моменте
количества движения объясняет, почему максимальное значение проекции 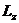меньше 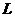(см. (1) и (2)). Если бы 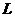равнялось 
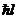, то остальные две проекци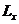и и 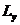в этом состоянии равнялись бы нулю, т.е.
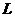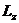имели бы наряду с и определенные значения, что невозможно.
Классический момент количества движения и квантовый не разделены
непреодолимой стеной. При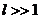 
пространственное квантование не слишком
существенно, а величина L, равная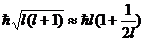 
почти неотличима от классического значения 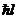. Более строго: свойства классического
момента количества движения могут быть получены в результате предельного
перехода к большим значениям l. Это
пример общего принципа, согласно которому квантовая механика содержит в себе
классическую в виде предельного случая.
физика магнитное явление энергия
Момент количества движения нас интересует здесь, поскольку он
связан с магнитным моментом. Квантовая механика подтвердила, что для электрона
гиромагнитное отношение
.
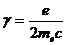Следовательно, если электрон массой me находится
в состоянии с проекцией момента количества движения, равной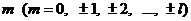 
, то проекция его магнитного момента равна
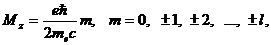(3)
Напрашивается такой вывод: движущийся электрон может претендовать
на роль элементарного магнитика, правда, если он находится в состоянии с
отличным от нуля моментом количества движения, т.е. если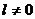 
. С другой стороны, важно подчеркнуть:
вращающийся вокруг ядра электрон может находиться в состоянии с равным нулю
моментом количества движения. Конечно, это следствие отсутствия траектории!
Квантовая механика, объяснив устойчивость атомов, одновременно показала, что
электроны в атоме движутся так, что проекции их моментов количества движения
суть целые числа в единицах 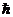; существование связи между магнитным моментом и моментом
количества движения показывает, что движущийся вокруг ядра электрон можно
рассматривать как устойчивый магнитный момент, правда, обладающий квантовыми
свойствами. Главное из них - пространственное квантование.
Устойчивость магнитного момента электрона, вращающегося вокруг
ядра, очень важна для понимания атомной природы магнетизма.
Электроны в атоме имеют определенное состояние. Это состояние устойчиво
- в том смысле, что изменить его можно, только сообщив электронам некоторую
конечную порцию энергии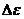 
(по атомным масштабам - большую).
Каждое состояние характеризуется определенным моментом количества
движения, а значит, и магнитным моментом. Следовательно, магнитный момент атома
устойчив (в той же мере, что и состояние электронов атома).
2. Магнитный
момент в магнитном поле
До сих пор магнитный момент выступал в роли источника магнитного
поля. И об этой его роли мы еще много будем говорить. Но сейчас, когда мы
узнали, что в природе существуют устойчивые магнитики, следует обсудить, как
они будут вести себя, если их поместить во внешнее, т.е. созданное другими
источниками, магнитное поле. При этом магнитики мы будем считать столь
устойчивыми, что их величина не зависит от величины магнитного поля. Когда речь
идет об атомных магнитиках, то это не есть какое-то специальное ограничение.
Наоборот, чаще всего очень трудно создать столь большое магнитное поле, чтобы
оно изменило величину атомного магнитного момента, правда, если он отличен от
нуля. Поэтому, когда речь идет о поведении магнитного момента в магнитном поле,
то имеют в виду возможность его перемещения - движения как целого и поворотов.
Начнем с постоянного и однородного магнитного поля. Свойство магнитной стрелки
ориентироваться определенным образом в магнитном поле хорошо известно. И так же
хорошо известно, что именно это ее свойство - основа применения магнитной
стрелки в целях ориентации. Стрелка компаса ориентируется потому, что это
энергетически выгодно. Энергия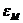 
магнитного момента М в магнитном поле Н есть
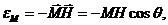(4)
где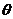 
- угол между магнитным моментом и
магнитным полем. Ясно, что при 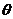=0 энергия минимальна.
Если магнитный момент отклонен на угол 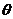от магнитного поля, со стороны магнитного
поля действует момент силы, направленный перпендикулярно к плоскости,
проходящей через магнитное поле Н, в которой в данный момент времени
находится магнитный момент. В результате магнитный момент будет вращаться,
описывая конус вокруг магнитного поля. Так как магнитный момент отличается от
момента количества движения множителем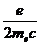 
то частота его обращения есть
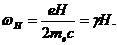(5)
Мы видим, что гиромагнитное отношение (мы по-прежнему обозначили
его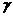 
) выступает в новой роли, связывая
магнитное поле Н с частотой прецессии магнитного момента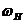 
. В этой роли мы его будем встречать значительно чаще, чем в той, в
которой оно появилось у нас первый раз. Формулы (4) и (5) справедливы для
классического магнитного момента. В случае квантового магнитного момента надо учесть
пространственное квантование. Как говорилось выше, момент может находиться в 
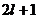состояниях. Каждому состоянию
соответствует свой магнитный уровень энергии, равный
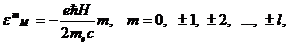(6)
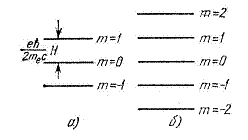
Рис. 2. Эквидистантные уровни энергии магнитного момента в
постоянном магнитном поле:
а) l=1, б) l=2.
Такая система уровней называется эквидистантной (рис. 2):
расстояние между соседними уровнями не зависит от 
и равно
(7)
Если электрону "вздумается" перейти с уровня на уровень,
ему придется поглотить или испустить квант электромагнитной энергии, равный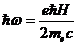 
. Таким образом, частота электромагнитного
поля, поглощаемого или испускаемого при переходе с одного магнитного уровня на
другой, равна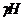 
. Она совпадает с частотой классического
вращения магнитного момента вокруг направления поля.
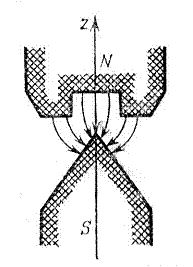
Рис. 3. Вблизи оси магнита магнитное поле направлено вдоль оси z и увеличивается по мере приближения к острию, т.е. зависит
от z.
А теперь пусть магнитное поле Н, по-прежнему направленное
вдоль оси z, само зависит от координаты z (рис. 3). Следовательно, зависит от z и энергия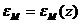 
. Зависимость энергии от координаты
означает, что на магнитный момент действует сила, равная
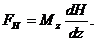(8)
В случае классического магнитного момента вместо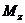 
надо подставить 
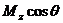, а в случае квантового - одно из 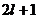значений проекции магнитного момента на
ось z (см. (3)).
3. Спин и
собственный магнитный момент электрона
К сожалению, историческая последовательность открытий в
физике, как, впрочем, и в любой науке, не следует логике рассказа о науке.
Удобно было бы этот раздел начать так.
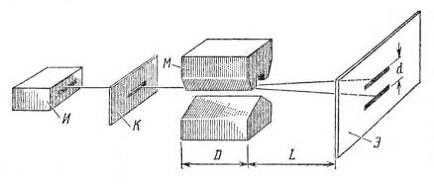
Рис. 4. Схема опыта Штерна-Герлаха: И - источник атомов водорода,
К - коллиматор, М - магнит (D - расстояние,
которое проходит пучок в магнитном поле с отличным от нуля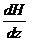 
), Э - экран (d - расстояние между следами пучков), L - расстояние от магнита до экрана.
Существование силы (8), действующей на магнитный момент, позволяет
по отклонению пучка атомных частиц, проходящих через неоднородное магнитное
поле, измерить их магнитный момент, а главное, убедиться в справедливости
выводов квантовой механики о пространственном квантовании. Действительно, после
того как пучок атомов, обладающих магнитным моментом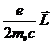 
, пройдет неоднородное магнитное поле,
должны образоваться 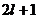пространственно разделенных пучков
(рис.4). Такой эксперимент был поставлен немецкими физиками О. Штерном и В.
Герлахом в 1922 г. Через неоднородное магнитное поле они пропустили пучок
атомов водорода. Результат оказался совершенно неожиданным, хотя подтвердил
факт пространственного квантования: пучок разделился на два. Казалось бы, пучок
вовсе не должен был разделиться, ведь электроны в атоме водорода имеют нулевой
момент количества движения. Предположим, при прохождении атомов через прибор
они почему-то возбуждаются - переходят в состояние с большей энергией и
ненулевым моментом количества движения. Но тогда число пучков на выходе из
прибора должно быть нечетным: 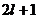. А эксперимент совершенно определенно показал: пучок делится на
два! Делится так, будто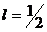 
- в резком противоречии с выводами
квантовой механики.
Так удобно было бы начать этот раздел, а потом разъяснить, что
неожиданный результат опыта Штерна и Герлаха объясняется тем, что электрон
обладает спином.
Или можно было бы поступить иначе. Рассказать об опыте,
проделанном Эйнштейном и де Гаазом (1915 г.), непосредственно измерившими
гиромагнитное отношение, которое оказалось в два раза больше предсказываемого
теорией. А потом объяснить, что расхождение теории с экспериментом объясняется
существованием у электрона спина.
К сожалению (повторим еще раз), события происходили не в логически
удобной последовательности. Эйнштейн и де Гааз, по-видимому, из-за ошибки в
расчете, получили значение гиромагнитного отношения, равное 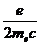, т.е. не обнаружили расхождения с теорией
тех лет. Более того, их статья так и называется "Экспериментальное
доказательство молекулярных токов Ампера". Подчеркнем: Эйнштейн прекрасно
понимал, что гипотеза Ампера противоречит классической физике. Именно поэтому и
был задуман эксперимент по наблюдению гиромагнитного эффекта. Он должен был
подтвердить (и, по мнению авторов, подтвердил) существование молекулярных
токов. Гиромагнитное отношение впоследствии неоднократно измерялось. Оно
оказалось вдвое больше, чем следует из формулы приведенной выше.
Штерн и Герлах поставили свой опыт в 1922 г., когда о
существовании у электрона спина уже подозревали. Подозрение возникло при
анализе атомных спектров - главного источника сведений о структуре атомов в те
годы.
Но что же такое спин? И какое отношение он имеет к физике
магнитных явлений?
У квантовой частицы, кроме момента количества движения, обязанного
ее движению в пространстве (его называют орбитальным моментом количества
движения, хотя ни о какой орбите, как мы помним, говорить нельзя), может
существовать момент количества движения, присущий самой частице. Этот момент
называют собственным (внутренним) моментом, или спином. Слово спин
(spin) по-английски означает веретено, но представление о частице с отличным от
нуля спином, как о шарике или волчке конечного радиуса, вращающегося вокруг
своей оси, ни в какой мере, даже самой грубой, не соответствует действительности.
Прежде всего, потому, что вообще элементарной частице (например, электрону) не
удается приписать конечный радиус. Многочисленные попытки оказывались
неудачными, так как входили в противоречие с требованиями теории
относительности. То, что спин не есть результат пространственного вращения
частицы, наиболее отчетливо видно из следующего: значения проекции собственного
момента количества движения частиц могут быть не только целыми (см. (1) и (2)),
но и полуцелыми.
Для электрона: s = 1 /2;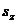 
= ± 1 /2; 2s + 1 = 2.
Протоны, нейтроны и нейтрино тоже имеют спин, равный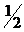 
. У фотона спин равен единице, а у всех 
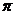-мезонов (их три: нейтральный 
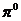и два заряженных, 
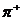и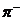 
с зарядами ± е) спин равен нулю.
Как мы видим, существование собственного момента расширило
возможные значения момента количества движения: спин может принимать целые (s =
0, 1, 2 и т.д.) и полуцелые (s = 1/2, 3/2, 5/2 и т.д.) значения. Нулевой спин
причисляют к целым спинам.
Частицы с нулевым и целым спином называют бозонами (по
имени индийского физика Бозе), а частицы с полуцелым спином - фермионами
(по имени Ферми). Почему все частицы делят на два класса, мы поймем позже.
Спин элементарной частицы - присущее ей внутреннее свойство, как
заряд и масса. Электрон или протон не могут расстаться со своим спином, как не
могут потерять часть своего заряда или массы. Именно в этом и проявляется
элементарность электрона, протона, нейтрона и других частиц, которые принято
считать элементарными. Их элементарность не препятствует взаимным превращениям.
Но это совсем другая тема.
Дирак построил теорию электрона, т.е. сформулировал уравнение,
которому должна удовлетворять волновая функция электрона. Это уравнение (его
так и называют - уравнением Дирака) учитывает не только волновые свойства
электрона, но и требования теории относительности. Квантовую механику,
согласующуюся с требованиями теории относительности, называют релятивистской
квантовой механикой. При ее создании не знали частиц со спином, отличным от
1/2. Дираку казалось, что равенство спина половине - логическое следствие
релятивистской квантовой теории. После открытия частиц со спином, отличным от
1/2, было понято, что уравнение Дирака - не единственное возможное уравнение.
Волновые функции частиц с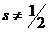 
подчиняются уравнениям, отличающимся от
уравнения Дирака, которое безукоризненно описывает свойства электрона - частицы
со спином 1/2.
Логическим следствием релятивистской квантовой механики заряженной
частицы с зарядом е, массой me и спином 1/2 оказалось существование у такой частицы магнитного
момента, имеющего две проекции, равные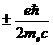 
. Сравните это выражение с формулой (3)! Видно, что для
собственного спинового момента количества движения гиромагнитное отношение
равно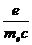 
, т.е. вдвое больше, чем для орбитального
момента. Классическое (орбитальное) гиромагнитное отношение в единицах 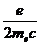мы будем обозначать 
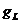, а спиновое 
.
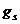Подчеркнем: 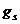= 2 в единицах 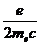при любом значении s (даже целом!). Букву
g без индекса мы оставим для полного гиромагнитного отношения, учитывающего и
орбитальный и спиновый моменты. Его называют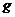 
-фактором, или фактором Ланде.
Как мы уже говорили, существование у электрона спина действительно
объясняет и опыт Штерна-Герлаха, и опыт Эйнштейна - де Гааза. В обоих случаях
проявился не орбитальный, а собственный момент количества движения электронов.
Таблица I
В небольшой таблице (табл. I) мы собрали сведения о спинах и
магнитных моментах трех наиболее важных частиц - частиц, из которых построены
все окружающие нас тела и мы сами.
То обстоятельство, что нейтрон, хотя он и нейтральный,
обладает магнитным моментом, а магнитный момент протона в 2,8 раза больше, чем
предсказывает формула Дирака, нашло свое объяснение в современной теории
элементарных частиц.
В телах число электронов равно числу протонов, а собственный
магнитный момент электрона во много раз больше магнитного момента протона.
Ясно, что именно электроны играют главную роль в магнитных свойствах тел
различной природы. Правда, удается не только обнаружить и измерить магнитные
моменты атомных ядер (хорошо известны магнитные моменты практически всех
атомных ядер), но и исследовать магнитные свойства веществ, обусловленные
существованием ядерных магнитных моментов. Часть физики магнитных явлений,
занятая исследованиями магнитных свойств ядерных частиц, называется ядерным
магнетизмом. О ядерном магнетизме мы, к сожалению, почти ничего не
расскажем.
4. g-фактор
В подавляющем большинстве случаев элементарным магнитиком можно
считать собственный магнитный момент электрона. Его проекция на ось равна (с
точностью до знака) магнетону Бора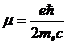 
. Если электрон движется так, что его орбитальный момент отличен
от нуля, магнитные моменты, орбитальный и спиновый, складываются. Но как
складывать "квантовые векторы", т.е. векторы, обладающие дискретными
значениями проекции на избранную ось?"Классические" векторы
складывают по правилу параллелограмма. Для этого надо знать длину каждого
вектора и угол между ними. Когда складывают "квантовые" векторы,
поступают следующим образом. Пусть есть два вектора, 
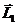и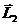 
таких, что 
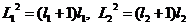, а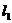 
, 
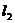- целые или полуцелые числа.
Спрашивается, каким может быть вектор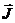
, равный сумме 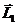и 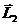? Для получения ответа спроектируем эти
векторы на общую ось. Ясно, что максимальная и минимальная проекции суммы двух
векторов есть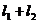 
и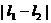 
. Это означает, что максимальная проекция вектора 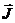, т.е. J может принимать значения
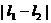от до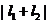 
. Вычислим, чтобы попрактиковаться, возможные дискретные значения
скалярного произведения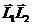 
через 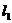, 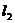и J. Для этого равенство
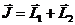
возведем в квадрат (по обычным правилам), а для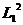 
,
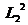и 
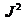воспользуемся "квантовыми"
выражениями:
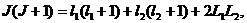т. e.
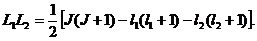(9)
Подставляя вместо J его возможные значения от 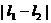до 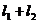, получим набор возможных дискретных значений скалярного
произведения .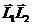
Векторы 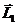и 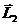могут относиться к одной частице (скажем, один из векторов -
орбитальный момент, а другой - спиновый) или к разным (например, можно задать
вопрос, чему равен момент двух частиц, если момент одной частицы 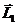, а другой ?).
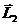Правило сложения векторов поможет нам выяснить, каким может быть
спин системы, состоящей из нескольких электронов.
Начнем с двух электронов. Так как каждый из спинов может
ориентироваться только по оси, либо против оси, то возможны только такие
ситуации:
) спины "антипараллельны" друг другу - суммарный спин
равен нулю (S = 0);
) спины "параллельны" друг другу - суммарный спин равен
единице (S = 1).
Слова "параллельны" и "антипараллельны" взяты
в кавычки, так как у спина электрона, как у всякого момента, две его проекции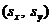 
не имеют определенного значения.
Между состояниями с S = 0 и S = 1 есть существенное различие. Состояние с нулевым спином -
единственное (его так и называют - синглет). Состояний же со спином, равным
единице, может быть три: с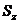 
= - 1, 0 и 1. Это состояние называют триплетом.
Чтобы еще более отчетливо почувствовать различие между
классическими и квантовыми моментами, вычислим значение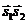 
при S = 0 и при S = 1 (
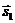и 
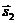- векторы спинов первого и второго электронов, 
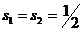). Заметим что спин, равный половине,
наименьший из встречающихся в природе моментов, кроме нулевого, конечно. Для
него отличие квантовых свойств от классических максимально. Согласно формуле
(9)
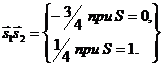
(10)
Таблица II
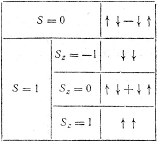
Если бы моменты были классическими, то произведения 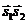для "параллельных" и
"антипараллельных" спинов отличались бы только знаком и равнялись бы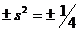 
.
Какие значения имеют проекции спинов каждого электрона в
синглетном и триплетном состоянии, видно из табл. II (стрелка вниз изображает
состояние отдельного электрона с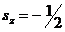 
, стрелка вверх - с 
).
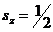Обратите, пожалуйста, внимание на то, что спиновая конфигурация
может быть антисимметричной (S = 0) и
симметричной (S = 1). Глядя на таблицу, нетрудно понять, что речь идет о
перестановке электронов. Понимание симметрии спиновых конфигураций поможет
разобраться в таком важном для теории магнетизма понятии, как обменная
энергия.
Три электрона, как легко сообразить, могут иметь спин, равный 1/2
или 3/2. Вообще четное число электронов создает конфигурации с целым спином (в
частности, с нулевым), а нечетное число электронов - с полуцелым.
Рассмотрим теперь систему из нескольких электронов. Орбитальный
момент электронов пусть равен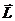 
, а спиновый - 
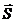. Напомним, что задание моментов означает задание их длин L
и S и проекций на выбранную ось 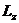, (одно из чисел: 
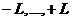) и (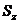
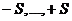). Каким магнитным моментом будет обладать эта система электронов?
Если несколько уточнить вопрос, то ответ придет почти автоматически.
Вращательные свойства системы характеризуются полным моментом количества
движения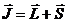 
, максимальная проекция которого J,
согласно предыдущему, может принимать значения от 
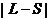до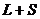 
. Магнитный момент 
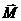пропорционален 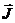, причем коэффициент пропорциональности мы назвали гиромагнитным
отношением. Итак,
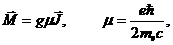(11)
и задача сводится к отысканию величины g-фактора как функции L,
S и J. Напомним, что задача возникла из-за того, что
гиромагнитные отношения для орбитального и собственного моментов разные (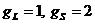
). Учитывая различие g-факторов, для
магнитного момента можно написать следующее выражение:
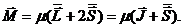(12)
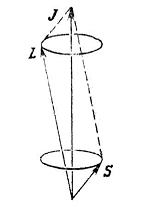
Рис. 5. Классическая картина "прецессии" орбитального 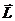и спинового 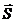моментов вокруг полного момента .
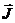Черта над векторам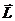и и 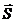означает, что берутся их средние
значения. Дело в том, что сохраняется (имеет определенное стационарное
значение) только полный момент количества движения 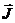(поэтому над ним нет черты), а векторы 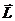и 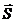прецессируют вокруг 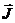(рис. 5).
Нас, согласно формуле (12), будет интересовать вектор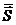 
, который, естественно, направлен вдоль
вектора 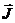(это отчетливо видно из рис. 5), т.е. 
.
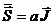Константу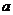 
легко определить из следующей цепочки
равенств:
.
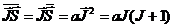Заметьте: для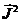 
мы опять воспользовались квантовой формулой. Значение 
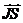вычисляется совершенно аналогично тому,
как была получена формула (9):
.
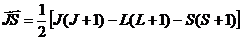Следовательно,
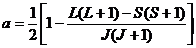
Сравнивая формулы (11) и (12), получаем искомое выражение для g-фактора:
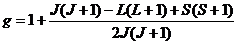. (13)
Если спин отсутствует (S = 0), то, естественно, J = L и g = 1; если же L = 0, а J = S, то g = 2. При J = 0, что возможно при L = S, выражение (11) не определено, но,
конечно, никакого магнитного момента нет, так как все проекции вектора 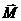равны нулю.
Фактор Ланде g может быть равным нулю и при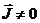 
, например, при L = 2, S = 3/2 и J = 1/2. Этот пример показывает, что g-фактор отнюдь не "располагается" между единицей и
двойкой.
Подведем итог: если система электронов имеет определенный полный
момент количества движения 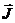, являющийся суммой орбитального 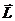и спинового 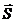моментов, то магнитный момент такой
системы электронов равен "квантовому" вектору 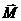(см. (11)), проекции которого на
избранную ось есть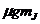 
, где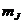 
принимает одно из следующих значений: 
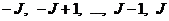а g-фактор определен формулой (13).
5. Принцип
запрета Паули
Одинаковые частицы в классической и квантовой физике ведут
себя совершенно по-разному. Классические частицы, даже абсолютно одинаковые,
движутся каждая по своей траектории. Если в начальный момент времени положение
каждой из частиц было зафиксировано, то в любой последующий момент,
зафиксировав снова частицы в пространстве, - на их траекториях, можно указать,
где какая частица находится, т.е. отличить одну от другой. В квантовой механике
ситуация совсем иная, так как частицы движутся не по траекториям. Зафиксировав
частицу в начальный момент времени, мы принципиально не имеем возможности найти
ее среди ей подобных в последующие моменты времени.
В квантовой механике одинаковые частицы
совершенно неразличимы.
Такое утверждение составляет содержание принципа
тождественности одинаковых частиц. Из принципа тождественности следует, что
перестановка одинаковых частиц не приводит к изменению квантового состояния
системы.
Рассмотрим волновую функцию двух частиц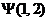 
. Цифры 1 и 2 символически обозначают
координаты (с учетом переменной, указывающей направление спина) первой и второй
частиц. Перестановка двух частиц (первая частица становится на место второй,
вторая - на место первой) описывается перестановкой аргументов у функции :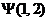
.
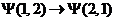При такой операции состояние системы не должно измениться. Но это
означает, что при перестановке волновая функция может только приобрести
постоянный множитель. Обозначим его буквой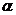 
. Тогда 
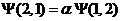. Проделав перестановку частиц два раза,
т.е. вернувшись к их исходному расположению, убеждаемся, что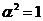 
и, следовательно, либо 
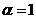, либо 
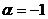. Значение множителя 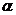определяется не состоянием системы, а типом частиц, составляющих
систему.
Так как множитель а равен или +1, или - 1, то существуют два типа
частиц:
для одних перестановка не приводит к изменению волновой функции:
(Б)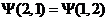 
(14);
для других при перестановке частиц волновая функция меняет знак:
(Ф)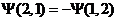 
(15).
Мы описали сейчас свойство частиц, не имеющее никакого
классического аналога. Квантовая механика привела к открытию свойств, не
связанных с силовым взаимодействием между частицами; частицы могут даже не
взаимодействовать друг с другом, но выписанные выше перестановочные законы
должны обязательно выполняться. Природа (квантовая механика) диктует
частицам правила поведения в коллективе - ведь ясно, что, обобщая соотношения
(14) и (15), мы можем рассматривать совокупности любого числа частиц. Часть
физики, занимающаяся исследованием поведения больших (макроскопических)
совокупностей частиц, носит название статистической физики. О частицах,
для которых выполняется соотношение (14), говорят, что они подчиняются статистике
Бозе-Эйнштейна, а о частицах, для которых, выполняется соотношение (15), - статистике
Ферми-Дирака. Поэтому слева от равенств (14) и (15) поставлены буквы (Б) и
(Ф).
Есть ли у частицы какое-либо "личное" свойство, которое
определяет ее подчиненность одной из двух статистик? Оказывается есть. Как
показал Паули,
частицы с нулевым и целым спином подчиняются статистике
Бозе-Эйнштейна, частицы с полуцелым спином - статистике Ферми-Дирака.
Становится понятным, почему частицы с целым или нулевым спином
были названы бозонами, а частицы с полуцелым спином - фермионами.
Теперь вернемся к вопросу о том, сколько электронов может
находиться в одном состоянии. Во-первых, напомним, что у электрона спин равен
половине и, следовательно, электроны - фермионы. И, во-вторых,
сформулируем один из фундаментальных принципов атомной физики - принцип
запрета Паули:
Сейчас мы докажем принцип запрета Паули, используя антисимметрию
волновой функции двух электронов. К тому, что мы знаем о волновой функции, надо
добавить: волновая функция двух невзаимодействующих частиц строится в виде
билинейной комбинации волновых функций отдельных частиц. Итак, пусть один
электрон находится в состоянии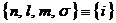 
, а другой в состоянии 
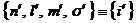. Тогда, при перестановке частиц, в согласии с правилом (15),
.
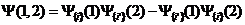Отсюда: если состояния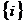 
и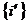 
совпадают 
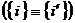, волновая функция тождественно равна нулю - такого состояния нет.
Мы видим, что фермионы - индивидуалисты, они не терпят себе
подобных. Каждая физическая система стремится находиться в состоянии с
наименьшей энергией. Это обстоятельство плюс принцип Паули позволяют понять
структуру атомов и вместе с этим - природу периодического закона Менделеева. По
сути, задача сводится к расположению Z электронов атома с атомным номером Z по
состояниям, учитывая, что:
Таблица IV
) состоянием с различными и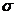 
, но одинаковым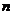и 
и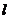 
отвечает одинаковая энергия, и
) полный набор квантовых чисел 
может иметь только один электрон.
Число состояний с определенным значением 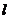равно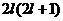 
. Так как 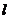не может быть больше 
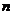, то каждому значению соответствует всего несколько 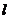: при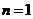 
только 
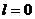(s-состояние), при 
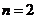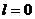имеем и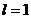 
- s - и р-состояния и т.д. Легко
подсчитать, сколько электронов могут иметь совпадающие 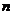и 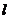при произвольных их значениях и составить таблицу.
Таблица III показывает распределение числа состояний по группам с
определенным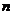и и 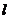. Сравнение этой таблицы с периодической системой Менделеева
показывает, что периоды периодической системы - следствие последовательного
заполнения электронами состояний с разным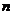и и 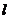, расположенных по группам. Первая группа
заполняется в атомах Н и Не. В Не заполнена одна оболочка. Заполнение второй и
третьей соответствует двум первым (малым) периодам периодической системы,
содержащим по восемь элементов (они заканчиваются на Ne и Аr). Далее - два больших периода по 18 элементов (до Кr и Хе соответственно) и большой период, содержащий 32
элемента (до Rn); последняя группа состояний только начинает заполняться в
существующих элементах.
Повторение химических свойств атомов при переходе от периода к
периоду связано с тем, что в химических свойствах наиболее существенную роль
играют внешние электроны - электроны, находящиеся вне полностью заполненной
оболочки (мы, к сожалению, не можем на этом подробно останавливаться).
Порядок расположения состояний в табл. III, соответствующий
последовательности их заполнения электронами, конечно, связан с зависимостью
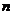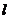энергии электронов от и . Глядя на первые строки таблицы, можно сформулировать простое
правило: сначала заполняются состояния с наименьшими 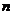и всеми допустимыми 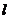, а потом происходит переход к следующему 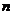. Однако в четвертой строке и во всех
последующих дело обстоит не так просто. Например, раньше (по таблице) должны
заполняться состояния 4s, а потом 3d. В действительности, если взглянуть на
электронные конфигурации группы железа (от Sc до Ni), то видно, что идет соревнование между заполнением 4s и 3d
оболочек: например, после V, у которого три электрона в состоянии 3d и два в
4s, идет Сr, у которого пять электронов в состоянии
3d и один в 4s, а у Мn при пяти
электронах в состоянии 3d два в состоянии 4s.
Чтобы приблизиться к теме нашего рассказа о магнитных свойствах,
заметим, что совокупности электронов, полностью заполняющих группу состояний с
заданным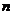и и 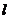, обладают суммарным нулевым моментом, как орбитальным, так и
спиновым. Это связано с тем, что для заполнения необходимо использовать
электроны с противоположными проекциями моментов.
Для примера в табл. IV приведены электронные конфигурации
нескольких элементов.
В последнем столбце таблицы расположен символ (терм), в котором
собраны нужные сведения о свойствах электронной конфигурации данного атома в
основном состоянии. Структура символа такова: латинская большая буква
обозначает полный орбитальный момент электронной конфигурации со следующим
соответствием: S Р D F. далее по алфавиту: L = 0 1 2 3.
Индекс внизу обозначает величину полного момента 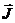, индекс наверху - мультиплетность, т.е.
значени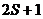е 
, где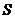 
- полный спин электронов атома. У Be терм 
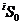, т.е. L = 0, J = 0, S = 0; у Аl терм 
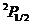, т.е. L=l, J =1/2, S=1/2. Глядя на терм
атома, по сформулированному выше правилу легко вычислить g-фактор и определить
магнитный момент атома. Разработаны достаточно точные расчетные методы,
существуют сравнительно простые правила (правила Хунда), позволяющие определить
термы всех атомов. Тем самым квантовая механика решила вопрос о магнитных
моментах мельчайших структурных единиц вещества - атомов. Хотя среди атомов
встречаются такие, у термов которых справа стоит нуль, т.е. J = 0 (например, у
всех атомов инертных газов), у большинства атомов есть отличный от нуля полный
момент и, следовательно, они - микроскопические магнитики.
В заключение этого параграфа приведем электронную структуру
"самого магнитного" атома - атома железа (феррума) Fe, по имени
которого получило свое название "самое магнитное" свойство - ферромагнетизм
Fe: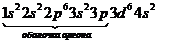 
терм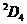 
.
6. Обменная
энергия
Рассмотрим термы атомов. Например, электронная конфигурация Mn (Z
= 25) такова: оболочка Ar +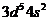 
, а его терм 
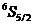. Почему спин электронов марганца равен
5/2? Ведь ясно, что принцип Паули не запрещает электронам иметь и другие
проекции спинов. Что заставило все пять электронов выстроиться
"параллельно"?
Другой пример не из теории атома, а из теории молекул. Простейшая
молекула - молекула водорода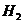 
. Два электрона движутся вокруг двух протонов, создавая устойчивую
конфигурацию. Два электрона могут иметь спин S, равный 1 или 0. Электроны в 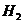имеют спин, равный нулю. Почему? Эти
вопросы требуют ответа и ответ этот нетривиален. Дело в том, что причина
осуществления той или другой спиновой конфигурации не связана с магнитным
взаимодействием электронов, хотя ясно, что выбор спиновой конфигурации
определяется энергетической выгодностью: осуществляется та, которая обладает
меньшей энергией.
В начале предыдущего параграфа мы показали, что магнитное
взаимодействие мало и им можно без существенных потерь пренебречь. Но в таком
случае остается только электростатическое взаимодействие, которое не
чувствительно к спиновому состоянию электронов. Действительно, электроны, спины
которых "параллельны", и электроны, спины которых
"антипараллельны", отталкиваются друг от друга с одинаковой силой,
обратно пропорциональной квадрату расстояния между ними. Почему же спин у
электронов марганца равен 5/2, а у электронов в молекуле водорода - нулю?
Казалось бы, не должно быть никакой связи между энергией электронной системы и
ее спином, во всяком случае до тех пор, пока мы не учтем магнитное
взаимодействие. В действительности, связь есть. Она возникает из-за
антисимметрии волновой функции электронов.
Рассмотрим для простоты систему, состоящую из двух электронов,
связанных только электростатическими силами. Пренебрежение магнитным
взаимодействием означает, что, решая задачу об энергии системы, мы можем вообще
забыть о спинах электронов. Пусть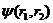 
- волновая функция, описывающая орбитальное движение электронов.
Мы подчеркнули это, явно выписав аргументы волновой функции - координаты электронов
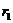и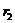 
; спиновые переменные опущены. Совсем забывать о спиновых
переменных нельзя, так как полная волновая функция 
должна быть антисимметричной (см. (15)).
Нам придется ограничиться констатацией того, что полная волновая функция есть произведение спиновой функции 
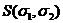, описывающей спиновое состояние
электронов (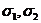
- спиновые переменные), и орбитальной 
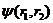, описывающей их орбитальное движение:
.
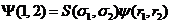Мы видели, что спиновая конфигурация может быть симметричной (при
S = 1) или антисимметричной (при S = 0). Но вся
функция - антисимметрична. Следовательно,
симметричной спиновой функции соответствует антисимметричная орбитальная, и
наоборот. Отсюда вытекает следующее утверждение:
при S = 0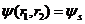 
- симметричная функция,
при S = 1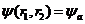 
- антисимметричная функция.
Симметричные и антисимметричные функци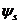и 
и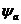 
описывают разные орбитальные движения электронов и поэтому
им отвечают разные энергии. Какая энергия окажется меньше, зависит от
конкретной задачи. В молекуле водорода минимальная энергия соответствует
симметричной волновой функции, описывающей орбитальное движение. Именно поэтому
электронный спин у 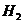равен нулю.
Полученному здесь результату - зависимости энергии системы
электронов от симметрии волновой функции, а, как следствие, - от спина, - можно
придать форму, которая позволит говорить о своеобразном обменном
взаимодействии между электронами.
Обозначим через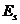 
энергию электронов, соответствующую волновой функции 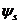, а через 
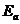- энергию, соответствующую 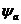. Из сказанного выше существует соответствие между энергией
системы и ее спином:
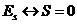
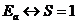
Мы составим из спинов электронов выражение (оно носит название спинового
гамильтониана и обозначается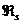 
), которое при S = 0 принимает значение 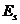, а при S = 1 - значение .
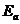Для этого воспользуемся формулой (10):
.
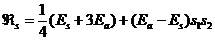Значения, которые принимает спиновый гамильтониан 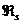, суть возможные значения энергии системы
из двух электронов (те самые 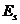и 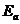, о которых сказано выше).
Первое слагаемое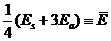 
не зависит от спина системы и, как легко убедиться, есть
усредненное по возможным спиновым состояниям значение энергии (три состояния с S = 1 и одно с S = 0), а второе слагаемое зависит от спина
системы электронов. Разность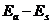 
принято записывать в виде некоторого параметра А со знаком минус.
Тогда спиновому гамильтониану двух электронов можно придать вид
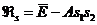. (16)
Такая запись позволяет связать энергетическую выгодность состояний
с S = 0 и S = 1со знаком параметра А. При А < 0 выгодно
"антипараллельное" расположение спинов, а при А > 0 -
"параллельное". Параметр А называют обменным интегралом, а
второе слагаемое в (16) - обменной энергией или обменным взаимодействием.
Поясним происхождение терминов. Эпитет "обменный" возник
из-за того, что симметричная и антисимметричная волновые функции описывают
состояние электронов, меняющихся своими местами. Более того, параметр А есть
мера частоты перемены мест. Его называют обменным интегралом, так как
для вычисления параметра А необходимо проинтегрировать определенные выражения,
содержащие волновые функции. Термин обменное взаимодействие
подчеркивает, что структура спинового гамильтониана такова, будто между двумя
электронами существует какое-то специфическое силовое взаимодействие, величина
которого зависит от взаимного расположения спинов электронов. В этом смысле оно
напоминает магнитное взаимодействие. Мерой интенсивности служит обменный
интеграл А.
Подчеркнем несколько очень важных для дальнейшего обстоятельств.
) Обменное взаимодействие изотропно. Поворот всех спинов на один и
тот же угол не изменяет значения обменной энергии. Это, в частности, видно из
того, что в формулу (16) входит скалярное произведение спинов, не меняющееся
при повороте обоих спинов на один и тот же угол.
) Интенсивность обменного взаимодействия А определяется величиной
электростатической энергии электронов и поэтому не мала, хотя, как правило,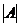 
все же несколько меньше, чем средняя
энергия электростатического взаимодействия (в наших обозначениях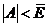 
).
) Знак обменного интеграла, согласно сказанному выше, может быть и
положительным, и отрицательным. Когда речь идет о внутриатомном обменном
взаимодействии, чаще всего А > 0 (что зафиксировано одним из правил Хунда);
при межатомном взаимодействии чаще встречаются ситуации с А < 0, хотя случаи
А > 0 не просто существуют, но и служат объяснением наиболее яркого
магнитного свойства - ферромагнетизма.
В случае межатомного обменного взаимодействия (когда
взаимодействующие электроны принадлежат разным атомам) обменный интеграл А
существенно зависит от расстояния между атомами, резко (экспоненциально)
уменьшаясь при удалении атомов друг от друга на расстояния, превосходящие
размер атома. Доказать, это, конечно, можно, только подставив конкретные
волновые функции в конкретный обменный интеграл, а представить себе, наверное,
не так трудно, если вспомнить, что обменное взаимодействие - результат обмена
местами электронов.
В заключение приведем небольшую схему, фиксирующую логику этого
пособия:
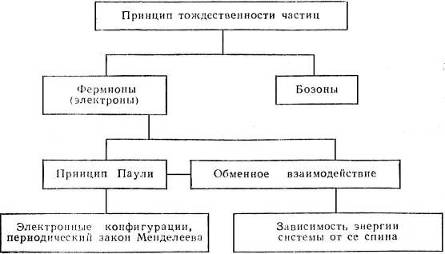
7. Обменное
взаимодействие
Обменное взаимодействие, специфическое квантово-механическое взаимодействие тождественных
частиц, в частности электронов <#"866375.files/image168.gif"> (17)
(18)
где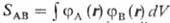 
-интеграл перекрывания электронных
волновых функций атомов <#"866375.files/image171.gif"> и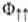 
на соответствующие спиновые функции (спин-функции). Из требования
антисимметричности вытекает, что функция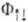 
отвечает противоположному направлению спинов
<#"866375.files/image174.gif"> - параллельно направленным спинам
<#"866375.files/image175.gif"> и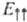 
соответственно)
вычисляется как среднее значение оператора <#"866375.files/image177.gif"> (19) где
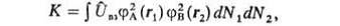(20)
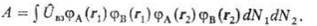(21)
Интеграл К представляет классическую энергию кулоновского
взаимодействия пространственно распределенных зарядов; интеграл А называется
обменным интегралом, характеризует энергию обменного взаимодействия и не имеет классического
аналога. Он появляется вследствие того, что каждый электрон
<#"866375.files/image180.gif"> вероятность для
электронов <#"866375.files/image181.gif"> уменьшается по сравнению с
невзаимодействующей системой независимых атомов
<#"866375.files/image182.gif"> N2/2 при N >> 1, в то
время как энергия обменного взаимодействия пропорциональна числу ближайших
пар-соседей, т.е. она пропорциональна N.
В случае многоэлектронных систем знак энергии обменного
взаимодействия зависит от строения электронной оболочки взаимодействующих
объектов (атомов <#"866375.files/image183.gif">, зависящий от взаимной
ориентации спинов. Эта добавочная энергия - энергия обменного взаимодействия
атомов сортов i и j, имеющих спиновые моменты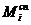 
и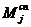 
:
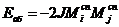, (22)
где J − обменный интеграл, имеющий размерность
энергии. Наличие обменного интеграла в выражении для обменной энергии связано с
перекрытием областей распределения электронного заряда атомов i и j. Обменная энергия не
имеет классического аналога, хотя и имеет электростатическое происхождение. Она
характеризует различие энергии кулоновского взаимодействия системы в случаях,
когда спины параллельны и когда они антипараллельны.
Получить некоторое представление о физической природе энергии
обменного взаимодействия можно, сравнив эту величину с тепловой энергией,
необходимой для разрушения магнитного упорядочения. Так, у железа при
температуре Кюри q тепловая энергия, приходящаяся на один атом (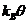
), необходимая для
разрушения магнитного упорядочения, равна примерно 0,1 эВ. Следовательно,
величина энергии упорядочивающего обменного взаимодействия, приходящаяся на
один атом, должна быть того же порядка.
Если предположить не квантовый механизм упорядочения,
например упорядочение под действием энергии Е, вызывающей ориентацию
диполя с магнитным моментом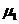 
в поле другого диполя моментом 
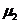, то такая энергия
выражается соотношением 
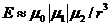, где r − расстояние между
диполями. Оценка этой энергии для магнитных моментов величиной порядка одного
магнетона Бора дает значение приблизительно 0,001 эВ при равновесных
расстояниях между ближайшими соседними атомами в твердых телах. Следовательно,
эффект дипольного взаимодействия по величине, по крайней мере, на два порядка
слабее того, который обуславливает наблюдаемую на опыте величину обменной
энергии.
Таким образом, обменное взаимодействие, ответственное за
возникновение ферромагнетизма, нельзя описать с помощью классических моделей,
оно представляет собой квантовомеханический эффект.
Установлено, что значение обменного интеграла J зависит от отношения
межатомного расстояния d к диаметру a недостроенной внутренней электронной
оболочки атома вещества (рис.6). Ферромагнетизм наблюдается только для
элементов, у которых обменный интеграл положителен (J > 0), что выполняется
для d/a > 1,5. Например, из элементов группы железа
ферромагнетиком является только альфа-железо (a-Fe), кобальт (Co) и
никель (Ni). Гамма-железо (g-Fe) и другие элементы этой группы
ферромагнетиками не являются. Однако, в ряде случаев при изменении постоянной
решетки за счет легирования другим элементом можно добиться того, что данный
элемент (слабо легированный) становится ферромагнетиком. Такой эффект
наблюдается у марганца (Mn) при легировании его азотом в малых
концентрациях, когда отношение d/a оказывается порядка 1,5.
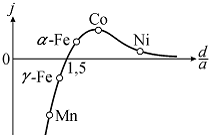
Рис. 6. Зависимость обменного интеграла J от отношения межатомного
расстояния к радиусу недостроенной внутренней оболочки
Кроме того, имеется множество химических соединений и
сплавов, в составе которых могут присутствовать не ферромагнитные элементы, но
сами эти соединения и сплавы являются ферромагнетиками. Например, сплавы
Mn-Cu-Al и соединения MnSb, MnBi, CrO2, MnOFe2O3 и т.д. Эти факты свидетельствуют о том, что
кристаллическое строение вещества является одним из факторов, определяющим
принадлежность данного вещества к ферромагнетикам.
Литература
1. Матвеев
А.Н. Атомная физика. М.: Высшая школа, 2009.
2. Гольдин
Л.Л., Новикова Г.И. Квантовая физика. Вводный курс. М.: Институт компьютерных
исследований, 2002.
. Блохинцев
Д.И. Основы квантовой механики. М.: Наука, 2003.
. Иродов
И.Е. Квантовая физика. Основные законы. М.: Лаборатория Базовых Знаний, 2011.