Генерация бесселевых пучков в полихроматическом свете
РЕФЕРАТ
Генерация бесселевых пучков в полихроматическом
свете.// Дипломная работа на соискание квалификационного уровня “специалист“ по
специальности “Квантовая электроника”/ Таврический национальный университет -
Симферополь, 2010. -43 с., 3 главы, 10 рис., 8 источников.
Предмет
исследования - бесселевый пучок нулевого и первого порядка
Объект исследования
- коническая линза (аксикон), для генерации полихроматических бесселевых пучков
нулевого и первого порядка
Цель работы -
генерация полихроматических пучков Бесселя-Гаусса нулевого и первого порядков и
исследование их фазовой структуры.
Для реализации поставленной цели были
сформулированы следующие задачи:
. Выяснить условия необходимые для формирования
полихроматических пучков Бесселя-Гаусса.
. Собрать и отъюстировать установку для
генерации полихроматических пучков Бесселя-Гаусса и исследовать их фазовую
структуру.
. Сформировать полихроматический пучок
Бесселя-Гаусса первого порядка с единичным зарядом на оси.
Научная новизна
- создание новых методов измерения характеристик материалов, а также
экспериментальные исследования, проводимые на их основе, позволяют не только
расширить знания фундаментальных оптических свойствах, но и открывают
перспективы конструирования принципиально новых приборов.
СОДЕРЖАНИЕ
РЕФЕРАТ
ВВЕДЕНИЕ
ГЛАВА
1.БЕССЕЛЕВЫЕ ПУЧК
1.1
Бесселевы функции с любым индексом
.2
Бесселевы функции первого рода
.3
Асимптотическое представление бесселевых функций с целым индексом для больших
значений аргумента
ГЛАВА
2.ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ
ПОЛИХРОМАТИЧЕСКИХ
БЕССЕЛЕВЫХ ПУЧКОВ
2.1
Описание полихроматических бесселевых пучков
.2
Теоретическое описание полихроматических бесселевых пучков
ГЛАВА
3. ГЕНЕРАЦИЯ ПОЛИХРОМАТИЧЕСКИХ БЕССЕЛЕВЫХ
ПУЧКОВ
НУЛЕВОГО И ПЕРВОГО ПОРЯДКОВ
3.1
Генерация полихроматических бесселевых пучков нулевого порядка
.1.1
Экспериментальная установка для генерации полихроматических бесселевых пучков
нулевого порядка
.1.2
Интерференция полихроматических бесселевых пучков нулевого порядка
.2
Генерация полихроматических бесселевых пучков первого порядка
.2.1
Экспериментальная установка для генерации полихроматических бесселевых пучков
первого порядка
.2.2
Интерференция полихроматических бесселевых пучков первого порядка
.3
Техника безопасности
ЗАКЛЮЧЕНИЕ
СПИСОК
ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
В настоящее время после создания аксикона или
конической линзы, сильно возрос интерес к исследованию Бессель-Гауссовым пучкам
получаемым на аксиконе. В настоящее время хорошо исследованы свойства данного
класса пучков для монохроматического излучения. Однако при генерации пучков
Бесселя-Гаусса возникает ряд сложностей.
Стимулом для проведения данной работы, послужила
статья французских учёных, о возможности генерации Бесселевых пучков в
полихроматическом свете. В этой статье показано что поскольку оптический путь
всех волн, которые образуют Бесселев пучок одинаков после прохождения аксикона,
то для формирования достаточно использовать источники с пространственной
когерентностью.
Исходя из выше сказанного, была сформулирована
цель моей работы:
Цель работы -
генерация полихроматических пучков Бесселя-Гаусса нулевого и первого порядков и
исследование их фазовой структуры.
Для реализации поставленной цели были
сформулированы следующие задачи: бесселевый пучок генерация интерференция
. Выяснить условия необходимые для формирования
полихроматических пучков Бесселя-Гаусса.
. Собрать и отъюстировать установку для
генерации полихроматических пучков Бесселя-Гаусса и исследовать их фазовую
структуру.
. Сформировать полихроматический пучок
Бесселя-Гаусса первого порядка с единичным зарядом на оси.
ГЛАВА 1 БЕССЕЛЕВЫЕ ПУЧКИ
1.1Бесселевы
функции с любым индексом
Чтобы объяснить происхождение бесселевых
функций, рассмотрим уравнение Лапласа в пространстве[1,2]:
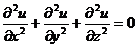 . (1.1)
. (1.1)
Если перейти к цилиндрическим координатам по
формулам:
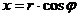 ,
,  ,
, 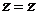 ,
,
то уравнение (1) примет следующий
вид:
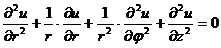 . (1.2)
. (1.2)
Поставим задачу: найти все такие решения
уравнения, которые могут быть представлены в виде произведения трех функций,
каждая из которых зависит только от одного аргумента, то есть найти все решения
вида:
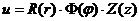 ,
,
где 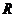 ,
, 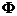 ,
, 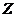 предполагаются дважды непрерывно
дифференцируемыми.
предполагаются дважды непрерывно
дифференцируемыми.
Пусть 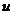 есть решение упомянутого вида.
Подставляя его в (1.2), получим:
есть решение упомянутого вида.
Подставляя его в (1.2), получим:
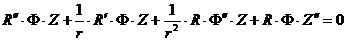 ,
,
откуда (после деления на 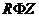 )
)
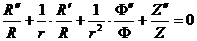 .
.
Записав это в виде:
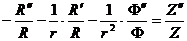 ,
,
найдем, что левая часть не зависит
от 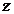 , правая не
зависит от
, правая не
зависит от 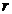 ,
, 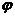 ;
следовательно, общая величина этих выражений есть некоторая постоянная
;
следовательно, общая величина этих выражений есть некоторая постоянная 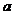 . Отсюда:
. Отсюда:
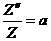 ;
; 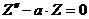 ;
;
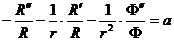 ;
; 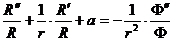 ;
;
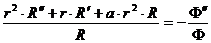 .
.
В последнем равенстве левая часть не
зависит от 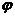 , правая не
зависит от
, правая не
зависит от 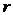 ;
следовательно, общая величина этих выражений есть некоторая постоянная
;
следовательно, общая величина этих выражений есть некоторая постоянная 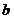 . Отсюда:
. Отсюда:
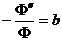 ,
, 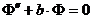 ;
;
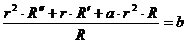 ,
,  .
.
Таким образом, 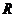 ,
, 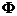 ,
, 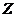 должны
удовлетворять линейным дифференциальным уравнениям второго порядка:
должны
удовлетворять линейным дифференциальным уравнениям второго порядка:
 , (1.3)
, (1.3)
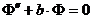 ,
, 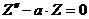 ,
,
из которых второе и третье есть
простейшие линейные уравнения с постоянными коэффициентами, а первое является
линейным уравнением с переменными коэффициентами нового вида.
Обратно, если 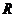 ,
, 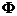 ,
, 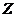 удовлетворяют
уравнениям (1.3), то
удовлетворяют
уравнениям (1.3), то 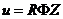 есть
решение уравнения (1.2). В самом деле, подставляя
есть
решение уравнения (1.2). В самом деле, подставляя 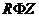 в левую
часть (1.2) и деля затем на
в левую
часть (1.2) и деля затем на 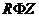 , получим:
, получим:
Таким образом, общий вид всех трех
решений уравнения (1.2), которые являются произведением трех функций, каждая из
которых зависит от одного аргумента, есть 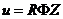 , где
, где 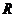 ,
, 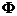 ,
, 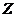 - любые решения уравнений (1.3) при
любом выборе чисел
- любые решения уравнений (1.3) при
любом выборе чисел 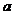 ,
, 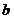 .
.
Первое из уравнений 1.3 в случае 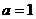 ,
, 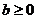 называется
уравнением Бесселя. Полагая в этом случае
называется
уравнением Бесселя. Полагая в этом случае 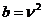 , обозначая независимую переменную
буквой
, обозначая независимую переменную
буквой 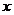 (вместо
(вместо 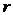 ), а
неизвестную функцию - буквой
), а
неизвестную функцию - буквой 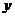 (вместо
(вместо 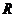 ), найдем,
что уравнение Бесселя имеет вид:
), найдем,
что уравнение Бесселя имеет вид:
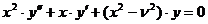 . (1.4)
. (1.4)
Это линейное дифференциальное
уравнение второго порядка с переменными коэффициентами играет большую роль в
приложениях математики. Функции, ему удовлетворяющие, называются бесселевыми,
или цилиндрическими, функциями.
1.2 Бесселевы
функции первого рода
Будем искать решение уравнения Бесселя (1.4) в
виде ряда:
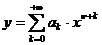 .
.
Тогда
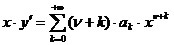 ,
,
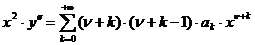 ,
,
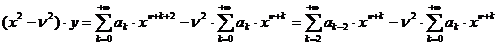 ,
,
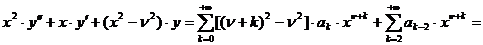
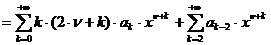 .
.
Следовательно, приходим к требованию
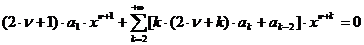 ,
,
или к бесконечной системе уравнений
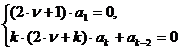
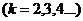 ,
,
которая распадается на две системы:
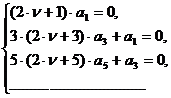
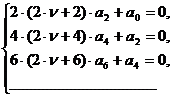
Первая из них удовлетворится, если
взять  … Во второй
системе
… Во второй
системе 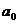 можно взять
произвольно; тогда
можно взять
произвольно; тогда 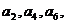 … однозначно
определяются (если
… однозначно
определяются (если 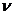 не является
целым отрицательным числом). Взяв
не является
целым отрицательным числом). Взяв
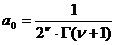 ,
,
найдем последовательно:
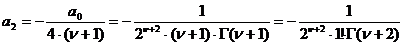 ,
,
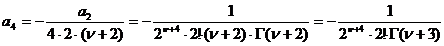 ,
,
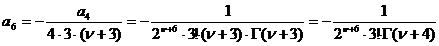 ,
,
и в качестве решения уравнения (1.4)
получим ряд:
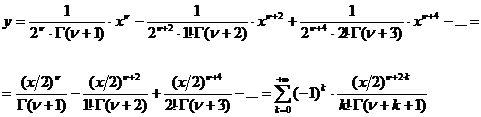
Этот ряд, формально удовлетворяющий
уравнению (1.4), сходится для всех положительных значений 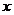 и,
следовательно, является решением уравнения (1.4) в области
и,
следовательно, является решением уравнения (1.4) в области 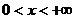 (в случае
целого
(в случае
целого 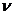 в области
в области 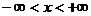 ).
).
Функция
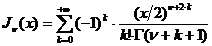 (1.5)
(1.5)
называется бесселевой функцией
первого рода с индексом 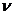 . Она
является одним из решений уравнения Бесселя (1.4). В случае целого
неотрицательного индекса
. Она
является одним из решений уравнения Бесселя (1.4). В случае целого
неотрицательного индекса 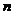 получим:
получим:
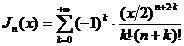 , (1.6)
, (1.6)
и, в частности,
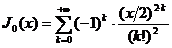 .(1.7)
.(1.7)
1.3 Асимптотическое представление
бесселевых функций с целым индексом для больших значений аргумента
Пусть 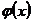 - положительная функция и
- положительная функция и 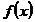 -
какая-нибудь (вообще комплекснозначная) функция, определенные для достаточно
больших значений
-
какая-нибудь (вообще комплекснозначная) функция, определенные для достаточно
больших значений 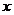 . Запись
. Запись
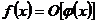 при
при 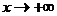
означает, что найдутся такие числа 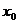 и M, что при
и M, что при 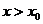 имеем
имеем 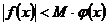
Подобная запись употребляется и в
других аналогичных случаях. Например, если 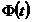 - положительная функция и
- положительная функция и 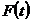 -
какая-нибудь функция, определенные для достаточно малых положительных значений
-
какая-нибудь функция, определенные для достаточно малых положительных значений 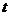 , то запись
, то запись
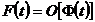 при
при 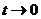
означает, что найдутся такие числа 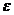 и
и 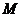 , что
, что 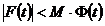 на
на 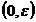 .
.
Вспомогательная лемма
Если 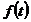 дважды
непрерывно дифференцируема на
дважды
непрерывно дифференцируема на 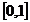 , то для функции
, то для функции
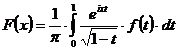
имеет место асимптотическое
представление
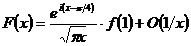 при
при 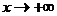 .
.
Докажем эту лемму. Заменяя на 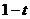 , получим:
, получим:
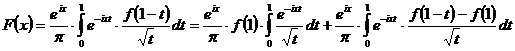 . (1.8)
. (1.8)
Рассмотрим на каком-либо интервале 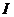 (конечном
или бесконечном) два дифференциальных уравнения
(конечном
или бесконечном) два дифференциальных уравнения
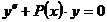 ,
, 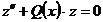 , (1.9)
, (1.9)
где 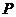 и
и 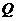 - непрерывные функции на
- непрерывные функции на 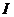
Рассмотрим интеграл, фигурирующий в
первом слагаемом правой части формулы (1.9). Заменяя 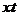 на
на 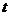 , найдем:
, найдем:
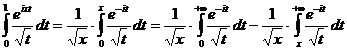 ,
,
но, заменив на 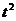 , получим:
, получим:
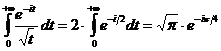 .
.
Если 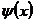 положительна, убывает и стремиться
к нулю при
положительна, убывает и стремиться
к нулю при 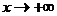 , то
, то 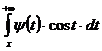 и
и 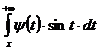 , а
следовательно, и
, а
следовательно, и 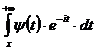 есть
есть 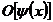 при
при 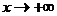 , поэтому
, поэтому
 при
при 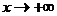 ,
,
откуда
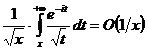 при
при 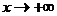 .
.
Итак, получаем асимптотическое
представление:
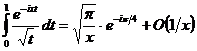 при
при 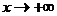 .(1.10)
.(1.10)
Рассмотрим теперь интеграл,
фигурирующий во втором слагаемом правой части формулы (1.9). Имеем:
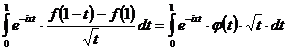 ,
,
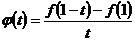 .
.
Очевидно, 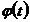 дважды
непрерывно дифференцируема на
дважды
непрерывно дифференцируема на 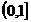 , но существуют
, но существуют 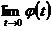 и
и 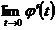 , поэтому
, поэтому 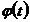 становится
непрерывно дифференцируема на
становится
непрерывно дифференцируема на 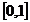 . Интегрирование по частям дает:
. Интегрирование по частям дает:
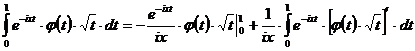 ,
,
где первое слагаемое правой части 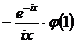 есть
есть 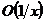 при
при 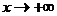 , а интеграл
во втором слагаемом несобственный при нижнем пределе мажорируется интегралом
, а интеграл
во втором слагаемом несобственный при нижнем пределе мажорируется интегралом
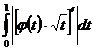 ,
,
который сходится, так как
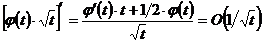 при
при 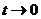 ;
;
Итак, имеем:
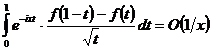 при
при 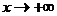 . (1.11)
. (1.11)
Из (1.8), (1.9), (1.10) получаем
искомое асимптотическое представление:
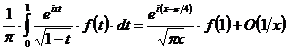 при
при 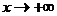 .(1.12)
.(1.12)
Из этой формулы, переходя к
сопряженным величинам, найдем еще:
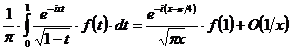 при
при 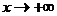 .(1.13)
.(1.13)
Формулы (1.12) и (1.13) верны и для
комплекснозначных функций 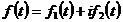 .
.
Вывод асимптотической формулы для Jn(x)
Заменяя 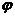 на
на 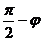 , получим:
, получим:
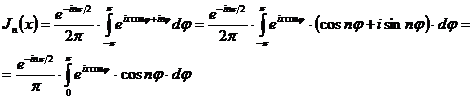
(учитывая, что 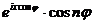 есть четная
функция от
есть четная
функция от 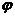 , а
, а 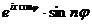 есть
нечетная функция от
есть
нечетная функция от 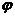 ).
Подстановка
).
Подстановка 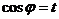 дает:
дает:
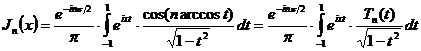 ,
,
где 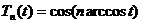 есть, очевидно, полином n-й степени
(полином Чебышева), так как из формулы Муавра видно, что
есть, очевидно, полином n-й степени
(полином Чебышева), так как из формулы Муавра видно, что 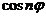 есть
полином n-й степени
относительно
есть
полином n-й степени
относительно 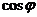 . Но
. Но
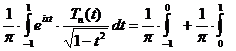
и, заменяя в первом из этих
интегралов 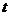 на
на 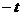 , получим:
, получим:
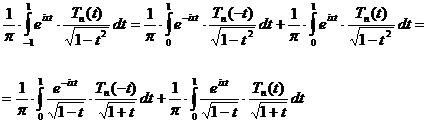
Так как 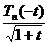 и
и 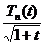 на
на 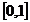 имеют
производные всех порядков, то к двум последним интегралам применимы формулы
(1.12) и (1.13), и мы получаем:
имеют
производные всех порядков, то к двум последним интегралам применимы формулы
(1.12) и (1.13), и мы получаем:
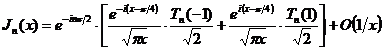 ;
;
но 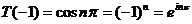 ;
; 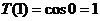 , следовательно,
, следовательно,
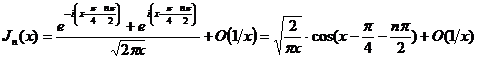 .
.
Итак, имеем искомое асимптотическое
представление бесселевой функции первого рода с целым индексом для больших
значений аргумента:
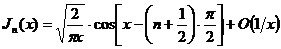 при
при 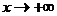 .(1.14)
.(1.14)
Эта формула показывает, что 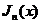 с точностью
до слагаемого порядка
с точностью
до слагаемого порядка  является
затухающей гармоникой с волной постоянной длины и амплитудой, убывающей обратно
пропорционально квадратному корню из абсциссы.
является
затухающей гармоникой с волной постоянной длины и амплитудой, убывающей обратно
пропорционально квадратному корню из абсциссы.
В частности,
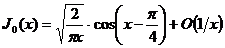 при
при 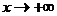 ; (1.15)
; (1.15)
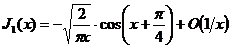 при
при 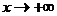 . (1.16)
. (1.16)
Графики этих функций изображены ни
рис1.
Рассмотрим несколько примеров
решения уравнения Бесселя.
. Найти решение уравнения Бесселя
при 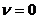
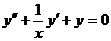 ,
,
удовлетворяющее начальным условиям
при 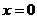 ,
, 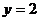 и
и 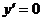 .
.
Решение.
На основании формулы 5 находим одно
частное решение:
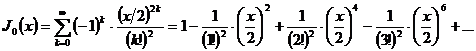 .
.
. Найти одно из решений уравнения:
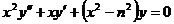 ,
, 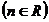 .
.
Решение.
Сделаем замену
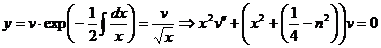 .
.
При 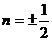 получим:
получим:
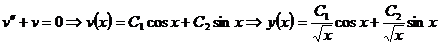 .
.
При 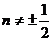 будем искать решение в виде
обобщенного степенного ряда:
будем искать решение в виде
обобщенного степенного ряда:
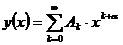 .
.
Уравнение на 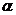 имеет вид
имеет вид 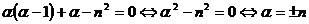 ;
;
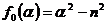 ,
, 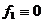 ,
, 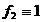 ,
, 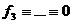 , поэтому
, поэтому
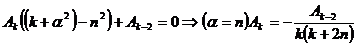 ,
,
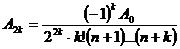 ,
, 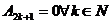 .
.
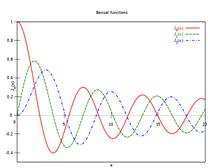
Рис.1.1 График распределения
интенсивности функции бесселя 0,1и2 порядков.
ГЛАВА 2. ИССЛЕДОВАНИЕ
ПОЛИХРОМАТИЧЕСКИХ БЕССЕЛЕВЫХ ПУЧКОВ
.1 Описание полихроматических
бесселевых пучков
Распространение инвариантных световых полей,
таких как бесселевые световые пучки, представляют интерес в широкой области
текущих предложений таких, как микроманипуляция атомами и мезоразмерными
частицами, генерация плазмы при помощи лазерного излучения, и изучение
оптического углового момента. Рассматривая оптические поля, как суперпозиции
конических волны, мы обсудим как когерентное свойство света играют ключевую
роль в их формировании. В качестве примера мы покажем, что пучки Бесселя могут
быть созданы из временно некогерентных широкодиапазонных источников света,
включая галогенную лампу. Используя суперконтинуальный источник света мы
поясним, как световые пучки зависят от функции ширины спектра падающего
светового поля [3].
Хорошо известно, что дифракция является
характерной волновой природы света, который возникает, когда любой волновой
фронт точечно модулированным по амплитуде и/или по фазе. Части волнового
фронта, которые распространяются после модуляции, интерферируют и возникают
дифракционные порядки. С точки зрения квантовой механики, дифракция является
центром понимания Гейзенбергского принципа неопределённости и напрямую связана
с понятием де Бройлевским представлением о частице, которой можно приписать
длину волны, которая обратно пропорциональна моменту частицы. В этой связи решения
уравнения Гельмгольца, которые являются инвариантными распространения или
"псевдо-недифрагирующими" получили значительный интерес и применение
в последние годы. Дурнин был первым, кто указал, что набор решений скалярного
волнового уравнения может быть недефрагируемым. Бесселевый пучок нулевого
порядка является одним из таких решений, представляя из себя пучок с узкой
центральной областью, окружённой ряда концентрических колец.
Фаза плоской волны распространяющейся на
расстоянии ∆z вдоль оси z
претерпевает сдвиг kz∆z,
kz будучи компонентом волнового вектора который направлен вдоль
направления распространения. Результатом этого является изменение
интерференционной картины при наложении плоской волны. Существуют, однако,
оптические элементы, которые устанавливают тот же самый фазовый сдвиг на все
наложенные плоские волны, если свет распространяется, например, по конусу. В
этом случае интерференционная картина не изменяется с расстоянием, поэтому эти
лучи являются инвариантами распространения. Такой конус может быть легко
сформирован при помощи освещения аксикона, что создаёт приближение к
Бесселевому пучку в лаборатории. Этот пункт также подразумевает, что свет,
формирующий центральный максимум этого луча, прошёл равноудаленные
(эквидистантные) пути, которые в свою очередь означают, что мы может
рассмотреть использование временно- некогерентных световых пучков для их
образования. В действительности, до определения бесселевого пучка, Мак Леод
создал фокальную линию в белом свете, используя аксикон в качестве фокусирующего
элемента.
Бесселевые пучки изучались в режимах от
ультрафиолетовых импульсов, до режима непрерывного излучения. Они нашли важные
применения в атоме оптике, оптических микроманипуляциях, лазерной плазмы,
нелинейной оптике и интерференции. Изучение фемтосекундных лазеров показало
важную роль которую оказывает длительность импульса на создание бесселевых
пучков, и, фактически, это связано с , так называемыми Х-волнами, которые
поддерживают их с точечно-временной локализацией при распространении. В этой
работе мы подробно обсудим, как когерентные свойства падающего светового поля
влияют на формирование беселевых пучков в отсутствие дисперсии для непрерывного
и фемтосекундного режимов. Наши исследования показывают, что источники чисто
белого света действительно могут генерировать бесселевые пучки и что мы можем
использовать формирование таких пучков, чтобы интерпретировать информацию о
свойствах временной и пространственной когерентности падающего светового поля.
Ключевым критерием длины распространения бесселевых или недифрагирующих
световых полей является требованием пространственной когерентности источника
света, и мы реализовали псевдо недифрагирующее световое поле, используя
источник света, обладающий пространственной когерентности, но с отсутствием временной
когерентности. Мы сравним свойства недифрагирующих световых полей созданных с
использованием различных источников света. В представленной работе мы
предлагаем новые применения этих пучков в частности при построении изображений
и микроманипуляциях.
.2 Теоретическое описание
полихроматических бесселевых пучков
Во-первых, мы разработаем простую теорию
широкодиапазонных бесселевых пучков описывающую наши наблюдений. В частности,
мы рассмотрим, распространений импульсного бесселевого пучка несшего порядка
через воздух, для которого хроматическая дисперсия пренебрежимо мала.
Электрическое поле описывается в скалярном медленно изменяющимся приближением
при помощи огибающей E(r,z,t), где исключается несущая exp(iω0
(z-ct)/c) с центральной частотой ω0,
и мы предполагаем наличие радиальной симметрии вдоль оси z.
Тогда профиль интегральной плотности потока, с интенсивностью, интегрируемой по
времени импульса может быть записан:
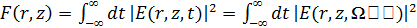 (2.1)
(2.1)
где было использовано приближение Парсеваля, а
также получено спектральное разрешение огибающей E
(r,z,Ω)
из E (r,z,t)
при помощи Фурье - преобразований, где Ω описывает отстройку по частоте
от несущей
Ω=ω-ω0.
Для описанного случая импульс на входе z=0
имеет коллимированный Гауссовый профиль, и мы можем описать спектральную часть
огибающей как
E(r, z=0, Ω) =E0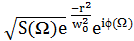 ,
(2.2)
,
(2.2)
где w0 - это размер Гауссова
пятна на входе, S(Ω) -
нормированный спектр импульса, Φ(Ω)- частотно
зависимая фаза, и E0-
амплитуда поля. Входящее поле сначала проходит через аксикон, с коэффициентом
преломления n
и
углом γ,
а
затем распространяется вдоль оси z.
Хорошо известно, что входящий Гауссовый пучок трансформируется в пучок Бесселя
на длине распространения в окрестности z=zmax/2,
где zmax=w0/θ,
а
θ=(n-1)γ
. Тогда,
спектрально представленное поле в плоскости наблюдения может быть описано как
E(r,
z=zmax/2,
Ω)= E0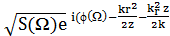 f (z,Ω)J0
(kr(Ω)r),
(2.3)
f (z,Ω)J0
(kr(Ω)r),
(2.3)
где f(z,
Ω)≈f(z,0)-
медленно меняющаяся функция частоты и z
окрестность
zmax
/2
и kr
(Ω)=(ω0+
Ω)(n - 1) γ/c
- это радиальная компонента волнового вектора. Подставляя приближённое решение
для бесселевого пучка (2.3) в (2.1), мы получаем нормированный профиль
интегральной плотности потока
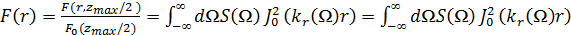 , (2.4)
, (2.4)
где 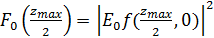 .
.
Профиль интегральной плотности потока F(r)
в уравнении (2.4), должен быть сравнён с экспериментальным интегральным
профилем потока для импульсных бесселевых пучков с различными спектрами S
(Ω). В качестве
простой модели мы рассмотрим Гауссов спектр:
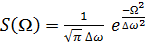 (2.5)
(2.5)
где Δω - ширина
импульса. Отметим, что в формуле (2.4) для профиля интегральной плотности
потока и спектр S (Ω), и аргумента
функции Бесселя 0(kr
(Ω) r) зависит от Ω,
вот
каким образом спектр импульса влияет на профиль интегральной плотности потока
пучка. В основном, профиль флюенса - сумма по полосе пропускания импульса
Бесселевых пучков J0(kr
(Ω) r) ,
которые изменяются как cos2 (kr
(Ω) r - π/4) = [1+cos (2kr
(Ω) r - π/2)]/2 для kr (Ω)r>>
1. При
среднем прохождении импульса Δω выполняется
колебания cos2 (kr (Ω) r - π/4)
от
Бесселевых пучков в значительной степени будет отменен по радиусам, что π
разность
фаз или больше существует между спектром край Ω =
Δω и в центре Ω=0,2(kr
(∆ω)-(kr
(0))r≥π,
которая определяет критический радиус π
разности фаз
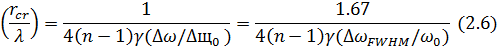
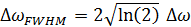 .
.
Другими словами , число колец бесселевого пучка
в белом свете может быть рассмотрено как изменение ширины импульса Δω.
Число
колец может быть приближённо равно как
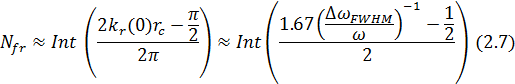
Пример этого показан на Рис.2.1, где λ=
790nm = 2πc/ω0,
∆ωFWHM/
ω0=0.11,
n= 1.5, а γ=1o,
rcr= 331μm,
Nfr
≈7.
Пунктирная линия показывает результат непрерывного бесселевого пучка (∆ωFWHM/
ω0→) с множеством
колец, в то время как сплошная линия показывает результаты для импульсного
бесселевого пучка с ∆ωFWHM/
ω0= 0,114 и
насчитывается около шести колец, которые действительно затухают за пределами rcr=
330μm. Мы заметим, что
для исходного гауссового пучка с размерами пятна w0 , исчезновение
колец будет наблюдаться в том случае, если w0> rcr, в
то время как w0 задаёт пространственный масштаб конечной реализации
бесселевого пучка генерированным аксиконом.
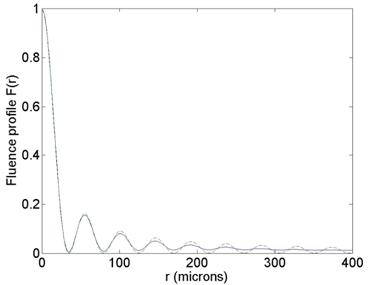
Рис. 2.1. Расчетный Бесселевый луч с
λ
=0.79 μm, Δω / ω = 0.19, n=1.5
и
γ =1º, =330 μm
ГЛАВА 3. ГЕНЕРАЦИЯ ПОЛИХРОМАТИЧЕСКИХ
БЕССЕЛЕВЫХ ПУЧКОВ НУЛЕВОГО И ПЕРВОГО ПОРЯДКОВ
.1 Генерация полихроматических
бесселевых пучков нулевого порядка
В настоящее время после создания аксикона или
конической линзы, сильно возрос интерес к исследованию Бессель-Гауссовым пучкам
получаемым на аксиконе. В настоящее время хорошо исследованы свойства данного
класса пучков для монохроматического излучения. Однако при генерации пучков
Бесселя-Гаусса возникает ряд сложностей.
Стимулом для проведения данной работы, послужила
статья французских учёных, о возможности генерации Бесселевых пучков в
полихроматическом свете. В этой статье показано что поскольку оптический путь
всех волн, которые образуют Бесселев пучок одинаков после прохождения аксикона,
то для формирования достаточно использовать источники с пространственной
когерентностью.
.1.1 Экспериментальная установка для
генерации полихроматических бесселевых пучков нулевого порядка
Для генерации полихроматических бесселевых
пучков нулевого порядка была создана следующая экспериментальная установка
(Рис. 3.1).

Рис. 3.1. Экспериментальная установка для
генерации полихроматических бесселевых пучков нулевого порядка 1- зеркало; 2-
лампа; 3- линзы; 4,6,8- микрообъектив;5- оптоволокно; 7- аксикон;9- CCD
камера.
Свет от ксеноновой лампы высокого давления
ДКсШ180 при помощи зеркальнолинзового конденсора и 20-ти кратного
микрообъектива фокусировался на входной торец оптического волокна [4,6]
(Рис.3.2) с диаметром сердцевины 7,5мкм и диаметром оболочки 27,5мкм.

Необходимость в использовании оптического
волокна возникла в связи с тем, что свет от ксеноновой лампы не когерентен, а для
генерации пучка Бесселя необходим когерентный источник света [5]. Были изучены
различные типы оптических волокон для создания такого типа источника с
диаметрами сердцевины от 4 до 120 мкм. Если мы берем волокно с большим
диаметром сердцевины, то интенсивность светового потока достаточная для
генерации, но сама картина пучка Бесселя выглядит размытой или исчезает вообше
из-за малой длины когерентности. Если же мы возьмем волокно с малым диаметром
сердцевины, то в результате мы получим достаточно контрастный пучок Бесселя, но
интенсивность данной картины не позволяет зафиксировать нужное нам изображение.
После прохождения света в волокне мы проводили
коллимирование излучение на выходе при помощи 10-ти кратного микрообъектива
(6). Пучок после коллимации имел диаметр 5мм. В дальнейшем наш пучок направляли
на коническую линзу [5] - аксикон (7). Поведение пучка при прохождении аксикона
схематически изображено на Рис.3.3.
Растянутую фокальную зону после аксикона мы
проецировали 8-ти кратным микрообъективом (8) на CCD матрицу - камеры (9).
Результаты,
полученные
на данной экспериментальной установке, приведены на Рис.3.4.
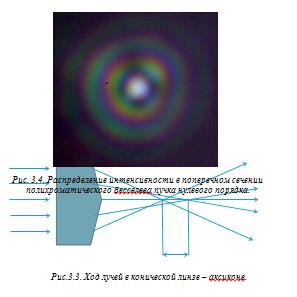
Как известно получение интерференционной картины
возможно только в том случае, если интерференционные волны когерентны между
собой. В нашей же экспериментальной установке для генерации полихроматических
бесселевых пучков нулевого порядка мы использовали ксеноновую лампу, которая не
имеет когерентность, и хотя для увеличения длины когерентности мы использовали
оптическое волокно в качестве точечного источника, получение классической
интерференции явилось очень затруднительным. Поэтому для получения
интерференционной картины мы пользовались методом деления волногофронта с
помощью бипризмы Френеля [7]. Две призмы (Рис. 3.5) с малыми преломляющими
углами склеены друг с другом. Источник S
расположен на расстоянии r
от
этих призм. Волновой фронт
света,
исходящего от источника S,
с
помощью призм разбивается на две части, и обе волны встречаются за призмами.
Так как оба фронта вызваны одним и тем же источником, то в области перекрывания
возникнет интерференционная картина. Наблюдателю, находящемуся в месте
расположения экрана, кажется, что световые лучи идут из двух источников:
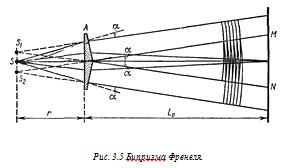
Следовательно, роль виртуальных когерентных
источников в данном случае выполняют источники S1
и S2,
являющиеся
мнимыми изображениями источника S.
В
опыте с бипризмой Френеля вследствие малости преломляющих углов апертура
интерференции практически не отличается от апертуры перекрывающихся пучков, что
приводит к уменьшению общей освещенности интерференционной картины.
На Рис 3.6 представлена интерференционная
картина полихроматических бесселевых пучков нулевого порядка.

Полученная интерференционная картина
представляет собой регулярные интерференционные полосы вблизи оси. Это
указывает на то, что в центре пучка гладкий волновой фронт. Однако темные
полосы имеют нерегулярный характер. Это видно по искажению картины, появляются
вилки. Вообще вилки в интерференционной картине соответствуют оптическим
вихрям, переносимые пучком. Наличие вилок соответствуют топологическому
квадруполю, а его возникновение связано с аберрациями, вызванными неточностями
изготовления линз. Ориентация вилок соответствует знаку заряда. Верхние и
нижние заряды одинаковы, но противоположны по знаку.
.2 Генерация полихроматических
бесселевых пучков первого порядка
Далее передо мной стояла задача о получении
Бессель-Гауссового пучка первого порядка.
В данном пучке на оси расположен единичный
оптический вихрь с топологическим зарядом l=1.
Поэтому для получения Бессель-Гауссова пучка первого порядка необходимо
сгенерировать оптический вихрь в полихроматическом свете. Для этой цели мы
использовали коноскопическую картину, которая получается на одноосном кристалле
[7,8] помешенном между двумя параллельными поляризаторами. Вид теоретически
рассчитанной картины распределения интенсивности представлены на следующем
слайде.
Как видно из рисунка, в центральной части
формируется квадруполь состоящий из единичных оптических вихрей. Поэтому если
оптическую ось пучка направить вдоль направления одного из вихрей то после
выходного поляризатора мы получим пучок с оптическим вихрем на оси.
3.2.1 Экспериментальная установка
для генерации полихроматических бесселевых пучков первого порядка
На слайде представлена установка для генерации
Бессель-Гауссового пучка первого порядка. Первая часть установки совпадает с
установкой для генерации Бессель-Гауссового пучка нулевого порядка, а вторая
часть установки представляет из себя кристалл NbLiO3
помещенный между 2х параллельных поляризаторов и двумя линзами с фокусным
расстоянием 10 см, 1я из которых создают расходящийся пучок в кристалле, а
вторая колемирует. Распределение интенсивности в поперечном сечении
регистрировалась CCD
камерой. Результатом прохождения Бессель-Гауссового пучка через систему:
поляризатор-линза-кристалл-линза-поляризатор явилось формирование пучка с
выраженным минимумом интенсивности на оси. Наличие такого минимума на оси может
свидетельствовать о локализации в данной точки топологического заряда. Для
подтверждения данного предположения мы также использовали выше упомянутый
интерференционный метод
Для генерации полихроматических бесселевых
пучков нулевого порядка была усовершенствована экспериментальная установка для
генерации полихроматических бесселевых пучков нулевого порядка приведенная на
Рис. 3.1. Изменения в данной экспериментальной установке приведены на Рис.3.6
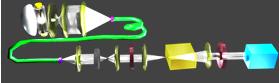
Рис. 3.6. Экспериментальная установка для
генерации полихроматических бесселевых пучков первого порядка 1- зеркало; 2-
лампа; 3- линзы; 4,6,8- микрообъектив; 5- оптоволокно; 7- аксикон; 9,13-
палеризатор; 10,12- линзы; 11- кристалл NbLiO3; 14- CCD
камера.
Свет от ксеноновой лампы высокого давления
ДКсШ180при помощи линзового конденсора и 20-ти кратного микрообъектива
направлялся на оптическое волокно (Рис.3.2) с диаметром сердцевины 7,5мкм и
диаметром оболочки 27,5мкм .
После прохождения света в волокне мы проводили
коллимирование излучение на выходе при помощи 20-ти кратного микрообъектива .
В дальнейшем наш пучок мы направляли на
коническую линзу - аксикон. Поведение пучка при прохождении аксикона
представлено на Рис.3.3. Растянутую фокальную зону после аксикона мы
проецировали 10-ти кратным микрообъективом на входную грань одноосного
кристалла для генерации полихроматического вихря с топологическим зарядом l=1.
Но для генерации «белого» полихроматического вихря необходимо, чтобы на
анизотропный кристалл попадал линейно поляризованный пучок. Для этого между
проецируюшим микрообъективом и анизотропным кристаллом размещался
поляризационный фильтр, который преобразовывал пучок в пучок с линейной
поляризацией. В дальнейшем после анизотропного кристалла пучок проходил второй
поляризационный фильтр и попадал на матрицу CCD - камеры. Результаты,
полученные на данной экспериментальной установке, приведены на Рис.3.7.
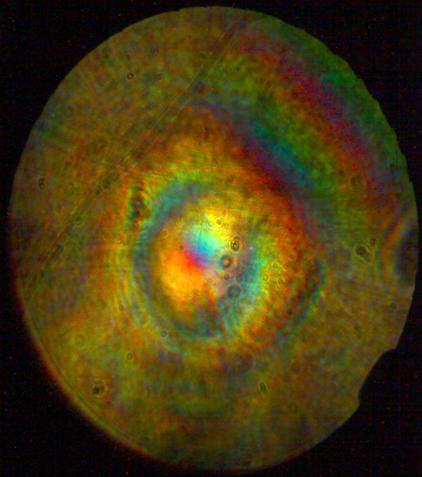

.2.2 Интерференция полихроматических
бесселевых пучков первого порядка
Как мы говорили в пункте 3.1.2 получение
интерференционной картины возможно только в том случае, если интерференционные
волны когерентны между собой. В нашей же экспериментальной установке для
генерации полихроматических бесселевых пучков нулевого порядка мы использовали
ксеноновую лампу, которая имеет очень малую длину когерентности, и хотя для
увеличения длины когерентности мы использовали оптическое волокно в качестве
точечного источника, получение классической интерференции явилось очень
затруднительным. Поэтому для получения интерференционной картины мы
использовали бипризму Френеля [7] (Рис. 3.5).
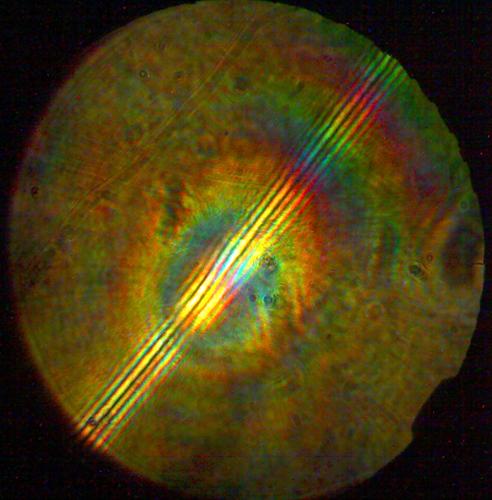
На Рис (3.8) представлена интерференционная
картина полихроматических бесселевых пучков первого порядка.
При рассмотрении интерференционной картины явно
видно наличие цветной вилки положение которой совпадает с положением минимума
на оси пучка. Это свидетельствует о том, что наши предположения о наличии
оптического вихря на оси пучка подтвердилось. Также в интерференционной картине
присутствуют парные противонаправленные вилки, местонахождение которых
соответствует положению исходного квадруполя пучка Бесселя-Гаусса.

3.3 Техника безопасности
Техника безопасности при работе с оптоволокном
- Если в здании, где вы работаете, установлено
активное сетевое оборудование, удостоверьтесь, подлежащее тестированию
оптоволокно отсоединено от него.
Для защиты глаз используйте специальные защитные
очки с покрытием, блокирующим проходящее по оптоволокну излучение светодиодов и
лазеров, которые используются в оптических трансиверах. Лазеры класса 1 не
могут повредить глаза, поскольку обладают невысокой мощностью, однако лазеры
более высоких гласов уже достаточно опасны для глаз.
Обеспечьте надежную связь между работниками,
тестирующими оптоволокно - это необходимо для координации действий и
обеспечения должной безопасности.
Большинство химикатов, которые используются для
очистки оптоволокна - вредны для здоровья. Поэтому следует стараться не вдыхать
их - избегать работы в замкнутых пространствах и хорошо проветривать помещения.
Что делать в случаях, если это невозможно, описано в стандартах ANSI Z.I 17.1
Safety Requirements for Confined Spaces.
Рабочее место должно быть организовано таким
образом, чтобы было просторно - хорошо оборудованное место позволит должным
образом и без травматизма подготовить оптоволоконный кабель к монтажу разъемов,
и смонтировать разъемы. Если терминирование кабелей происходит в тесном
пространстве, можно использовать небольшой раскладной стол.
Изучите правильные методики подготовки кабеля к
монтажу разъемов - большинство травм при работе с кабелем связано с
использованием ручных инструментов. Поэтому надо четко знать, как безопасно
удалять внешнюю оболочку кабеля и его броню.
Помните, что в процессе терминирования кабеля
оптоволокно вставляют в наконечник разъема, и небольшая часть кабеля без
буферного покрытия выступает оттуда. Обнаженное оптоволокно может поранить
человека.- Производя зачистку оптоволокна, направляйте инструмент от себя,
чтобы, если он соскользнет, избежать ранения.
Снимая буфер, обрезайте его небольшими
кусочками, чтобы избежать поломки кабеля.
Тем не менее, травму можно получить, даже
несмотря на все возможные меры предосторожности, однако требования техники
безопасности значительно сокращают количество несчастных случаев.
Данные требования относятся не только к процессам
тестирования и терминирования оптоволокна. Также очень важно оставлять место
монтажа в порядке после проведения работ - если на месте работы остались
осколки волокна, то может пораниться другой человек, не знающий специфики
работы с оптоволокном.
При работе с лампами высокого давления
Строго следуйте схеме подключения, проверяйте
изоляцию, проверяйте соответствие фаз.
Не используйте лампы без защитного стекла, если
в инструкции прямо не написано, что возможно применение без него.
При смене лампы проверяйте отсутствие на ней
жирных пятен или капель. Иначе лампа может взорваться.
Используйте светильники с возможностью горячего
перезапуска или применяйте реле отложенного времени.
Используйте только качественные комплектующие.
Не смотрите на горелку лампы без защитных
приспособлений. Черевато ожогом сетчатки. Вот информация от пострадавших. Сам
не врач, подтвердить или опровергнуть не могу.
Наружная колба нагревается выше 300 градусов. Ни
в коем случае не трогайте рабочую лампу.
Горелка и внешняя колба иногда взрываются. Особенно
в конце срока службы.
ЗАКЛЮЧЕНИЕ
В результате проделанной работы можно
сформулировать следующие выводы :
. Получен полихроматический пучок
Бесселя-Гаусса нулевого порядка
. Получена интерференционная картина
полихроматического пучка Бесселя-Гаусса нулевого порядка в которых наблюдаются
интерференционные вилки расположенные на первом кольце, что свидетельствует о
наличии оптического квадруполя
. Получен полихроматический
Бессель-Гаусов пучок первого порядка.
. Получена интерференционная картина пучка
Бессель-Гаусса 1го порядка, которая показывает присутствие оптического вихря на
оси пучка
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Пискунов
Н. С. «Дифференциальное и интегральное исчисления», учебное пособие для втузов,
М: Наука, 1985г., 560 стр.
2. Романовский
П. И. «Ряды Фурье. Теория поля. Аналитические и специальные функции.
Преобразование Лапласа», учебное пособие для втузов, М: Наука, 1983г., 336 стр
3. P.
Fischer, C.T.A. Brown, J.E. Morris, C. López-Mariscal, E.M. Wright, W.
Sibbett and K. Dholakia White light propagation
invariant beams // OPTICS EXPRESS, 2005, Vol. 13, No. 17, р.6657
4. Снайдер
А., Лав Дж. Теория оптических волноводов. - М: Радио и связь, 1987. - 656 с.
. Борн
М., Вольф Э. Основы оптики. - М: Наука, 1973. - 719с.
6. Nye
J.F. Natural Focusing and Fine Structure of Light. Caustics and Wave
Dislocations. Institute of Physics Publishing: Bristol and Philadelphia, 1999. 327
p
7. А.Снайдер,
Дж.Лав Теория оптических волноводов // Москва «Радио и связь», 1987, 656 стр.
. Азаам
Р. Башара Н. Эллипсометрия и поляризованный свет - М: Мир, 1981. - 584 с.
9.