Математическое моделирование температурных полей при теплотехнических процессах
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ
ОБРАЗОВАНИЯ
ГОМЕЛЬСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ИМЕНИ П.О. СУХОГО.
Энергетический
факультет
Кафедра
« Информационные технологии »
Курсовая
работа
по
дисциплине « Информатика »
на
тему: « Математическое моделирование температурных полей при теплотехнических
процессах »
Исполнитель:
студентка гр. ТЭ-22
Архипович Т.А.
Руководитель:
преподаватель
Ильющенко Г.Л.
Гомель
Содержание
Введение
.
Основные подходы к математическому моделированию решений дифференциальных
краевых задач
.1
Моделирование теплопередачи в твердых телах
.2
Метод конечных разностей
.3
Метод конечных элементов
.
Алгоритмический анализ задачи
.1
Постановка задачи
.2
Исходные данные
.3
Графическая схема алгоритма метода прогонки
.4
Обобщенная графическая схема алгоритма решения задачи
.
Аппаратное и программное обеспечение
.Математическое
моделирование температурных полей
Заключение
Список
литературы
Введение
Вычислительная техника используется сейчас не только
в инженерных и экономических науках, но и в таких традиционно нематематических
специальностях, как медицина, лингвистика, психология и др. В связи с этим
можно констатировать, что применение ЭВМ приобрело массовый характер. Для
решения производственных задач требовалось много времени и сил, но после
Научно-Технической Революции, которая привела к развитию информационных
технологий, время для этих задач стало уменьшаться.
Использование ПЭВМ в решении производственных
задач позволяет повысить эффективность труда, производства и многих других
показателей. Но и как раньше, для широкого применения ЭВМ в разработке
производственного продукта требуются высоко квалифицированные кадры, от которых
требуются знания в автоматизации труда. Возникла многочисленная категория
специалистов - пользователей ЭВМ, для которых необходима литература по
дисциплинам, непосредственно связанным с применением вычислительной техники.
Основной такой дисциплиной является
вычислительная математика. Она изучает методы построения и исследования
численных методов решения математических задач, которые моделируют различные
процессы.
Проектирование - сложный иерархический процесс,
включающий множество взаимосвязанных стадий и этапов. Математическое
моделирование технических объектов занимает центральное место в построении
эффективной технологии автоматизированного проектирования.
Инженер-проектировщик должен иметь четкое представление о видах математических
моделей и способах их построения, режимах функционирования технических объектов
и методах их моделирования, разработке алгоритмических моделей и их эффективной
реализации с использованием современных средств вычислительной техники.
При создании машин, технических комплексов и
других объектов широко используется моделирование. Как средство познания и
преобразования материального мира моделирование применяется в экспериментальных
и теоретических научных исследованиях.
Моделирование представляет собой процесс
замещения объекта исследования некоторой его моделью и проведение исследований
на модели с целью получения необходимой информации об объекте. Модель - это
физический или абстрактный образ моделируемого объекта, удобный для проведения
исследований и позволяющий адекватно отображать интересующие исследователя
физические свойства и характеристики объекта. Удобство проведения исследований
может определяться различными факторами: легкостью и доступностью получения
информации, сокращением сроков и уменьшением материальных затрат на
исследование и др.
Различают моделирование предметное и абстрактное.
При предметном моделировании строят физическую модель, которая соответствующим
образом отображает основные физические свойства и характеристики моделируемого
объекта. При этом модель может иметь иную физическую природу в сравнении с
моделируемым объектом. Если модель и объект одной и той же физической природы,
то моделирование называется физическим.
Физическое моделирование сложных технических
систем сопряжено с большим временными и материальными затратами.
Абстрактное моделирование связано с построением
абстрактной модели. Такая модель представляет собой математические соотношения,
графы, схемы, диаграммы и т. п. Наиболее мощным и универсальным методом
абстрактного моделирования является математическое моделирование. Оно широко
используется как в научных исследованиях, так и в проектировании.
Математическое моделирование позволяет
посредством математических символов и зависимостей составить описание
функционирования технического объекта в окружающей внешней среде, определить
выходные параметры и характеристики, получить оценку показателей эффективности
и качества, осуществить поиск оптимальной структуры и параметров объекта.
Применение математического моделирования при проектировании в большинстве
случаев позволяет отказаться от физического моделирования, значительно
сократить объемы испытаний и доводочных работ, обеспечить создание технических
объектов с высокими показателями эффективности и качества. одним из основных
компонентов системы проектирования в этом случае становится математическая
модель.
Математическая модель - это совокупность
математических объектов и отношений между ними, адекватно отображающих
физические свойства создаваемого технического объекта. В качестве
математических объектов выступают числа, переменные, множества, векторы,
матрицы и т. п. Процесс формирования называется математическим моделированием.
В конструкторской практике под математическим моделированием обычно понимается
процесс построения математической модели, а проведение исследований на модели в
процессе проектирования называют вычислительным экспериментом. Такое деление
удобно для проектировщиков и функционально вполне обосновано, поэтому в
дальнейшем будем придерживаться этой терминологии.
Для осуществления вычислительного эксперимента
на ЭВМ необходимо разобрать алгоритм реализации математической модели.
Алгоритм - это предписание, определяющее
последовательность выполнения операций вычислительного процесса. Алгоритм
автоматизированного проектирования представляет собой совокупность предписаний,
обеспечивающих выполнение операций и процедур проектирования, необходимых для
получения проектного решения. Для наглядности алгоритмы чаще всего представляют
в виде схем или графов. Алгоритм, записанный в форме, воспринимаемой
вычислительной машиной, представляет собой программную модель. Процесс
программирования называют программным моделированием.
1. Основные подходы к математическому
моделированию решений дифференциальных краевых задач
.1 Моделирование теплопередачи в твердых телах
При построении математических моделей тепловых
систем на микроуровне дискретизацию объектов осуществляют посредством методов
сеток.

Рис.1 Объект, представляющий собой изотропное
тело.
На рис.1 показан пример дискретизации двумерного
теплового объекта - твердого тела, температура которого зависит от времени t и
геометрических координат x и y. Сетка, наложенная на твердое тело, выделяет
дискретные элементы в виде прямоугольных пластин. Характерная особенность этих
элементов заключается в том, что каждый из них обладает одновременно
инерционными и диссипативными свойствами. Следовательно, выделенные дискретные
элементы тепловой системы являются сложными.
Задача анализа теплопередачи в твердом теле на
микроуровне моделирования заключается в определении температуры в узлах сетки.
На ранних стадиях проектирования часто рассматривают одномерный процесс
теплопередачи. Так, при анализе теплонапряженности дисковых фрикционных муфт и
тормозов автомобилей, тракторов, станков и др. машин пренебрегают
теплопередачей в радиальном и окружном направлениях, анализируя лишь изменение
температуры по толщине дисков.
Одномерными можно также считать задачи анализа
теплопередачи через стенки теплообменников, корпусных деталей машин, стены
зданий и сооружений и др. деталей технических объектов. Математические модели
таких объектов можно привести к моделям макроуровня.
Исходная математическая модель микроуровня
представляет собой дифференциальные уравнения в частных производных,
описывающие процессы, происходящие в моделируемом объекте, и граничные условия.
Рассмотрим процесс преобразования этой дифференциальной краевой задачи к задаче
макроуровня, математической моделью которой является система обыкновенных
дифференциальных уравнений.
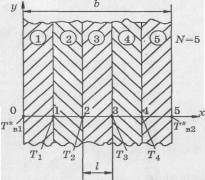
На рис.2 представлена динамическая модель
одномерной тепловой системы, используемая для анализа изменения температуры
вдоль координаты х. Дискретные элементы представляют собой пластины (слои).
Узлы сетки, в которых определяется температура, расположены на поверхностях
этих пластин. Узлы отображены на оси х и обозначены цифрами. Пронумеруем узлы
от 0 до n+1. Узлы с номерами 0 и n+1 называются граничными, а узлы вектора
(1,п) - внутренними. Количество слоев N = n+1.
Рис.2. Дискретизация одномерного теплового
объекта
Дифференциальное уравнение теплопроводности
Фурье для одномерной сплошной среды
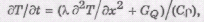 (1)
(1)
где Т - температура; ρ
- плотность;
λ
- коэффициент теплопроводности; С - удельная теплоемкость материала; GQ --
количество тепловой энергии, генерируемой или поглощаемой в единицу времени в
единице объема. При анализе теплопередачи в твердых телах без фазовых
превращений можно принимать GQ = 0.
Это уравнение описывает физические свойства
системы с распределенными параметрами. Для перехода к системе с
сосредоточенными параметрами, получаемой путем дискретизации сплошной среды,
используем конечно-разностную аппроксимацию второй частной производной
 (2)
(2)
где l - шаг дискретизации по оси х.
Введем обозначения:
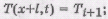 (3)
(3)
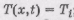 (4)
(4)
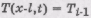 (5)
(5)
где i - номер узла сетки. Тогда выражение (2)
можно записать в виде
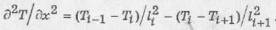 (6)
(6)
Подставив выражение (6) в уравнение (1), получим
систему обыкновенных дифференциальных уравнений
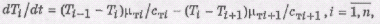 (7)
(7)
где cTi, μTi
- соответственно теплоемкость и коэффициент теплового сопротивления i-го
дискретного элемента
, li - соответственно объем и длина i-го
дискретного элемента. Система уравнений описывает физические свойства твердого
тела при одномерной теплопередаче. Решение этих уравнений позволяет определить
изменение температуры Тi(t) во всех внутренних узлах твердого тела 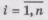 в
переходном процессе неустановившейся телепередачи, обусловленном изменением
воздействий на твердое тело окружающей его внешней среды.
в
переходном процессе неустановившейся телепередачи, обусловленном изменением
воздействий на твердое тело окружающей его внешней среды.
Проанализируем структуру дифференциального
уравнения, записанного относительно производной температуры i-гo внутреннего
узла системы, кроме узлов с номерами i=1 и i=п. Уравнение для i-го узла можно
записать в виде (9)
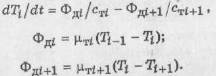 (9а)
(9а)
Эти 3 выражения представляют собой компонентные
уравнения диссипативных элементов i-гo и (i+1)-го слоев твердого тела
(дискретных элементов).
Граничные узлы с номерами i=0 b i=n+1
принадлежат одновременно твердому телу и внешней среде. Эти узлы находятся на
граничной поверхности твердого тела, посредством которой осуществляется его
взаимодействие с внешней средой. По аналогии с другими системами,
рассмотренными в предыдущих параграфах данной главы, отнесем эти узлы к внешней
среде, генерирующей на граничных поверхностях внешние воздействия на объект.
Рис. 3. Орграфы тепловой системы:
а - при источниках внешних воздействии типа
потока; б - при теплоизолированной правой границе и источнике типа потока на
левой границе; в - при источниках внешних воздействий типа потенциала
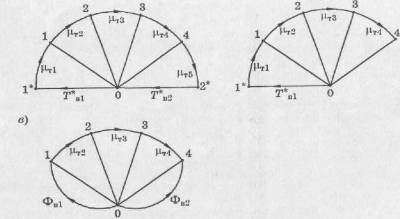
С учетом изображенного на рис. 3, а построен
орграф тепловой системы. При этом сделано предположение, что направление
теплового потока в твердом теле совпадает с положительным направлением оси х.
Узлы орграфа 1...4 отображают соответствующие внутренние узлы твердого тела
1...4 (см. рис.2), а узлы, отмеченные звездочкой, т. е. узлы 1* и 2*,
отображают граничные узлы i=0 и i=5, соответственно. Все узлы орграфа соединены
между собой ветвями диссипативных элементов с обозначениями параметров этих
элементов μТi. Ветви,
соединяющие узлы орграфа 1...4 с базовым узлом 0, не принадлежат инерционным
элементам, как это было в механических, гидравлических и других системах. Это
обусловлено тем, что дискретные элементы тепловой системы сложные, обладающие
одновременно инерционными и диссипативными свойствами, отобразить которые
отдельными элементами невозможно. Формальное изображение этих ветвей на
орграфе, с одной стороны, подчеркивает наличие инерционных свойств у тепловых
объектов, а с другой, - отображает связь фазовых координат типа потока Тi,
характеризующих состояние узлов орграфа, с системой отсчета этих координат,
начало которой отображает базовый узел.
Рассмотрим условия равновесного состояния
граничных узлов 1* и 2*. Для узла 1* условие равновесия потенциалов имеет вид
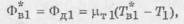 (10)
(10)
а для узла 2*
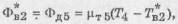 (11)
(11)
где ФВ1, ФВ2 - тепловые потоки, генерируемые
соответственно
на левой и правой граничных поверхностях; Тв1 ,
Тв2 - температуры граничных узлов 1* и 2* (т. е. узлов 0 и 5 на рис. 1).
Поскольку выражение (10) и (11) аналогичны
выражениям (9а) , то система уравнений (7) с учетом уравнений (9) может быть
записана в виде
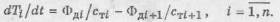 (12)
(12)
Составим матрицу инциденций, соответствующую
орграфу на рис. 3,а. Матрица А приведена в таблице 1
Таблица 1.

Принимая во внимание, что кроме внешних
воздействии типа потока (температуры граничных узлов или окружающей среды) к
твердому телу могут быть приложены воздействия типа потенциала (генерируемые на
граничной поверхности тепловые потоки, например, в результате трения
соприкасающихся тел), и используя матрицу инциденций:
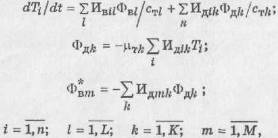 (13), (14), (15)
(13), (14), (15)
где Ивil,Идik, Идтk - инциденторы (элементы
матрицы А),
отображающие инцидентность ветвей источников
потенциалов и ветвей диссипативных элементов соответствующим узлам орграфа; L
-количество источников потенциалов ФB ; К - количество диссипативных элементов
тепловой системы; М - количество источников внешних воздействии типа потока Твт
.
Вышеописанные уравнения описывают алгоритм
структурно-матричного метода формирования математической модели тепловой системы.
При этом необходимо учитывать граничные условия.
Граничные условия I рода.
Задаются значения температур граничных узлов
Т*в1 и Тв2 В этом случае на основе вышеописанных уравнений непосредственно
получаем математическую модель теплового объекта в виде системы уравнений. При
этом потенциалы диссипативных элементов Фдк определяются по компонентным
уравнениям, а последнее уравнение позволяет определить значения тепловых
потоков Ф*в1 Ф*в2 на левой в правой граничных поверхностях, необходимые для
поддержания заданных значений температур граничных узлов Т*в1 и Г*в2 -Тепловые
потоки Ф*в1 и Ф*в2 генерируются источниками тепловой анергии внешней среды (или
представляют собой стоки - в случае отвода тепла от твердого тела). Но при
граничных условиях I рода потенциалы источников внешних воздействий неизвестны,
поэтому в уравнении принимается Ф*вl= 0.
Для решения полученной системы дифференциальных
уравнений необходимо задать начальные условия Ti0, 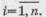
Таким образом, при формировании математической
модели тепловой системы с граничными условиями I рода используется динамическая
модель с источниками внешних воздействий типа потока, характеризуемыми
температурами граничных поверхностей Т*в1 и Т*в2.
Граничные условия II рода. Задается градиент
температуры на граничных поверхностях. В одномерном случае необходимо задать
значения дТ/дх при х = 0 и при х =b , где b - размер твердого тела вдоль оси х
. Их можно легко свести к граничным условиям III рода. Однако при равенстве
нулю градиента температуры на граничных поверхностях целесообразно
непосредственно использовать граничные условия II рода. Этот случай
соответствует теплоизолированной граничной поверхности.
Предположим, что пятый слой теплового объекта на
рис.2 выполнен из теплоизоляционного материала, характеризуемого малым
значением коэффициента теплопроводности λ5.
При этом μТ5→0, а Тв2≈Тв4.
Следовательно, теплообмен с окружающей средой через правую граничную
поверхность будет незначительным и им можно пренебречь. В орграфе при этом
граничный узел 2* может быть исключен (рис. 3, б). Составим матрицу инциденций
для твердого тела с теплоизолированной правой границей и с заданными граничными
условиями I рода на левой границе. Матрица Л приведена в табл.2
Таблица 2
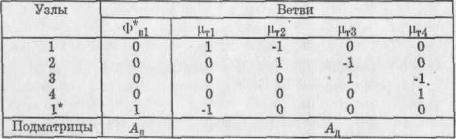
Математическая модель объекта в этом случае
будет такой же, как и в предыдущем, но только в ней ФД5=0.
Граничные условия III рода.
На граничной поверхности задаются условия
теплообмена с внешней средой. Возможны три вида теплообмена: генерирование на
граничных поверхностях тепловых потоков в процессе трения контактирующих
поверхностей (например, во фрикционных механизмах), конвективный теплообмен
твердого тела с окружающей газовой или жидкостной средой и теплообмен
излучением.
Граничные условия в первом случае имеют вид
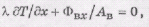 (16) где Фвх -
проекция теплового потока на ось х, АВ - площадь поверхности граничного
теплообмена.
(16) где Фвх -
проекция теплового потока на ось х, АВ - площадь поверхности граничного
теплообмена.
Составим граничные условия для х=0 и х=b (рис.
2), заменив при этом частные производные дT/дx отношениями конечных разностей
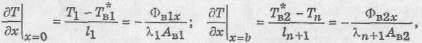 (17), (18)
(17), (18)
где Т*В1, Т*В2 - температуры граничных узлов,
обусловленные тепловыми потоками ФB1 и ФВ1 на граничных поверхностях.
Если тепловые потоки ФB1 и ФВ2 на левой и правой
граничных поверхностях твердого тела направлены от внешней среды к телу, т. е.
тепловая энергия подводится к нему с двух сторон, то проекции тепловых потоков
на ось х будут равны:
Фв1х=Фв1; ФВ2Х = - ФВ2. В этом случае получаем
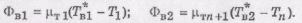 (19), (20)
(19), (20)
Легко заметить, что в этом случае в системе
уравнений потенциалы диссипативных элементов первого и последнего слоев
твердого тела Фд1 и ФД5 должны быть заменены на потенциалы источников внешних
воздействий ФВ1 и ФВ2 Эта замена на орграфе отражается исключением граничных
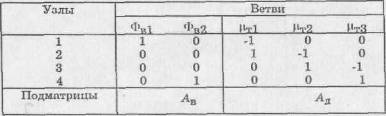
узлов (рис.3, в). Матрица инциденций, соответствующая данному орграфу,
приведена в табл.3.
Выражения используются для определения
температуры граничных узлов
 (21)
(21)
Таблица 3
.2 Метод конечных разностей
Достоинство этого метода состоит в том , что он
сводит решение краевой задачи для дифференциального уравнения к решению системы
алгебраических уравнений относительно значений искомой функции на заданном
множестве точек. Это достигается путем замены производных, входящих в
дифференциальное уравнение, их конечно-разностными аппроксимациями.
Сущность задачи заключается в покрытии области R
сеткой и замене непрерывного множества независимых переменных X в области R конечным
множеством точек Хк, являющихся узлами сетки. Сетка может быть прямоугольной,
косоугольной, с постоянными или переменными расстояниями между узлами (шагами
сетки). Наиболее часто используют сетку с постоянными расстояниями между
узлами, которая называется регулярной. Алгебраизация дифференциальных уравнений
в методе конечных разностей осуществляется за счет аппроксимации производных.
Как было отмечено, сеточные методы сводят
исходную краевую задачу к системе алгебраических уравнений. Для решения системы
алгебраических уравнений с трехдиагональной матрицей коэффициентов разработан и
широко применяется метод, который называется методом прогонки.
Метод прогонки является модификацией метода
Гаусса для частного случая разреженных систем - системы уравнений с
трехдиагональной матрицей. Он состоит из двух этапов - прямой и обратной
прогонки. Прямая прогонка состоит в том, что каждое неизвестное xi выражается
через xi+1 с помощью прогоночных коэффициентов Ai, Bi:
xi=Aixi+1+Bi i=1,2,3…,n-1.
Обратная прогонка состоит в последовательном
вычислении неизвестных xi. Сначала находим xn , затем последовательно вычисляем
все неизвестные xn-1, xn-2 , xi.
Традиционно метод конечных разностей применяют
при моделировании движения жидкостей или газов в трубопроводах и теплообменных
процессов.
.3 Метод конечных элементов
При решении задач, связанных с
определением напряжений и деформаций в элементах конструкций технических
объектов, чаще всего используется метод конечных элементов. Дискретизация
такого объекта осуществляется с использованием конечных элементов, a
алгебраизация задачи заключается в выборе аппроксимирующих функций для каждого
конечного элемента. Малые размеры конечных элементов позволяют использовать
простые аппроксимирующие функции 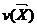 , причем одного и того же типа для
всех конечных элементов определенной формы. Обычно в качестве
, причем одного и того же типа для
всех конечных элементов определенной формы. Обычно в качестве 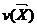 для
отдельного конечного элемента применяют полиномы не выше третьей степени,
например, в одномерном случае
для
отдельного конечного элемента применяют полиномы не выше третьей степени,
например, в одномерном случае
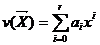 (22)
(22)
Функции v(Х) в методе конечных
элементов представляют в форме
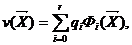 (23)
(23)
где коэффициенты qi имеют вполне
определенный физический смысл - это значения аппроксимирующей функции в узловых
точках: 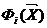 - функции,
которые называются координатными (или функциями формы); r - число узловых точек
в конечном элементе.
- функции,
которые называются координатными (или функциями формы); r - число узловых точек
в конечном элементе.
В общем случае аппроксимации вектора
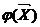 в m-мерном
пространстве выражение (23) принимает вид
в m-мерном
пространстве выражение (23) принимает вид
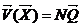
где 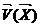 - вектор размерности
- вектор размерности 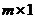 ;
; 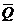 - вектор
размерности
- вектор
размерности 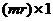 ; N -
интерполяционная матрица порядка
; N -
интерполяционная матрица порядка 
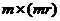 , элементами которой являются
координатные функции.
, элементами которой являются
координатные функции.
Важной процедурой МКЭ является выбор
функционала, который характеризует качество используемой аппроксимации. Для
механических систем в качестве такого функционала используют выражение
потенциальной энергии:
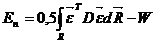 (24)
(24)
Минимизируя потенциальную энергию
Еп, находят вектор перемещений 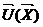 .
.
Связь деформации 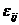 с
перемещениями ui можно выразить в матричной форме
с
перемещениями ui можно выразить в матричной форме
или более лаконично
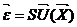 ,(25)
,(25)
где S - матрица-оператор
дифференцирования.
Таким образом
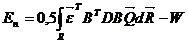 ,где
,где 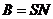 .
.
Обозначим 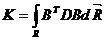 (26)
(26)
Матрица К является матрицей
жесткости. Тогда . В
соответствии с принципом Лагранжа дифференцируем Еп по вектору
. В
соответствии с принципом Лагранжа дифференцируем Еп по вектору 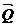 , и
приравниваем к нулю. В результате получаем систему алгебраических уравнений
, и
приравниваем к нулю. В результате получаем систему алгебраических уравнений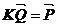 ,где
,где 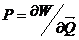 вектор
правых частей, который называется вектором нагрузок.
вектор
правых частей, который называется вектором нагрузок.
Матрица жесткости К всей исследуемой
детали составляется из матриц жесткости Кij отдельных КЭ. Матрицы Кij содержат
информацию о конфигурации и упругих свойствах материала конечных элементов и
подсчитываются по формуле (26), в которой при этом под R понимается подобласти,
относящиеся к рассматриваемому КЭ.
. Алгоритмический анализ задачи
.1 Постановка задачи
В качестве исходной математической
модели используем уравнение энергии, в котором исключим оператор конвективного
переноса и учтем одномерность задачи, t = t(x, τ). В
результате получим
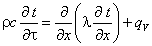 .(27)
.(27)
температурный поле
моделирование теплотехнический
На левом и правом торцах объекта
происходит тепловое взаимодействие со средой, и здесь необходимо задать
граничные условия. Универсальным способом описать самые различные ситуации
будет применение граничных условий третьего рода на левом (x = 0) и правом (x =
L) торцах объекта:
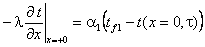 ;
;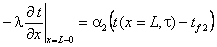 ,(28), (29)
,(28), (29)
где α и tf -
коэффициенты теплоотдачи и температуры окружающей среды на торцах стержня.
В этих соотношениях приравнены
значения плотности теплового потока,
поступающего из окружающей
среды и вычисленного по уравнению Ньютона-Рихмана (правые части)
и отводимого внутрь тела
посредством теплопроводности и вычисленного по закону Фурье (левые части).
Следует выделить, что такое
равенство справедливо при отсутствии фазовых превращений на поверхности
раздела.
На правом торце задана температура,
которая пульсирует около определенного значения Tf2 c амплитудой Ampl, а на
левом торце - постоянная температура Tf1:
tf1=const=Tf2(1+Ampl´sin(vt))
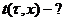
Задача решается методом конечных
разностей, о котором было сказано ранее.
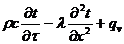 (29)
(29)
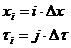
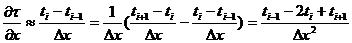 (30)
(30)
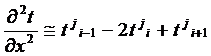 (31)
(31)
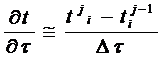 (32)
(32)
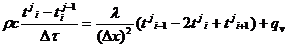 (33)
(33)
В (5) использована неявная
разностная схема, которая характеризуется абсолютной устойчивостью. Выполним
аппроксимацию граничных условий:
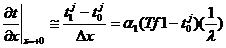 (34)
(34)
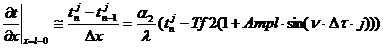 (35)
(35)
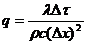
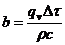
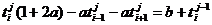
При i =(1..n-1):
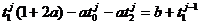
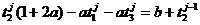
(36)
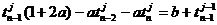
Структура получившейся линейной
системы уравнений с коэффициента-ми A, B, C, D является трехдиагональной.
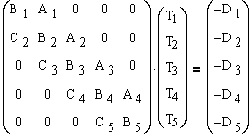
Из (34) следует
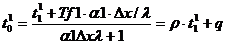
Из (35) следует
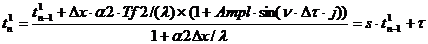
При i =(1..n-1)
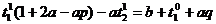
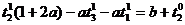
(37)
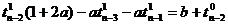
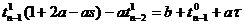
Система (9) позволяет найти величины
t1, t2… в момент времени t=1, то есть позволяет найти распределение температуры
t во внутренних узлах стержня в начальный момент времени. Далее следует
многократно решать систему (8) для нахождения распределения температуры в
последующие моменты времени. Для этого удобнее всего использовать метод
прогонки, о котором упоминалось ранее. Для расчета в MathCAD нужно использовать
программный фрагмент, при этом следует выполнить следующие этапы расчета:
Нужно задать функцию пользователя,
служащую для решения системы методом прогонки
Реализовать алгоритм циклического
вызова для каждого момента времени
Организовать вывод результата в
матрицу, столбцы которой являются векторами решений в последний момент времени.
.2 Исходные данные
В разрабатываемом курсовом проекте
используются следующие данные
Материал и размеры стержня
l
= 31 (Вт/м К) Теплопроводность
с = 810 (Дж/кг К) Удельная
теплоемкость
r
= 7850 (кг/м ) Плотность= 0.3 (м) Длина стержня
Параметры теплового воздействия=
0.310 Амплитуда= 3 Частота изменения температуры
Шаги пространственно-временной сетки
Dx
= 0.005 (м) Шаг по координате перемещения
Dt
= 0.15 (с) Шаг по координате времени
Температуры внешней среды на концах
стержня= 285 (К) Температура в начале стержня= 720 (К) Температура в конце
стержня
Начальная температура стержня
= 310 (К)
Объемная плотность теплового потока
2.3 Графическая схема алгоритма
метода прогонки



3. Аппаратное и программное обеспечение
С того момента как появились системы класса
MathCad, они имели удобный пользовательский интерфейс - совокупность средств
общения с пользователем в виде перемещаемых и масштабируемых окон, клавиш и
иных элементов. У этой системы есть эффективные средства типовой научной
графики, они просты в применении и понятны. Еще одно достоинство системы
MathCad это то, что они ориентированы на массового пользователя.- математически
ориентированные системы. Помимо вычислений они позволяют решать задачи, которые
не всегда решаемы с помощью текстовых редакторов или электронных таблиц.
Системы MathCad облегчают набор сложных математических формул и дают возможность
представить результаты вычислений в графическом виде; а также с их помощью
можно подготовить тексты статей, книг, диссертаций, научных отчётов, дипломных
и курсовых проектов.
В последнее время особый интерес проявляется к
системам символьной математики, способным выполнять не только числовые, но и
аналитические вычисления. Прежде чем появились системы символьной математики,
прошло много лет. К ним относится новое поколение систем MathCad под Windows и
ряд других математических систем, таких, как Maple и Mathematica. Применение их
облегчает сложные математические, финансово-экономичекие и статические расчёты,
для проведения которых приходилось привлекать научную элиту. Ранее не было
удобных и красивых интерфейсов математических программ, особенно в области
символьной математики. Основное внимание было уделено математической
корректности программ и богатству их функциональных возможностей. Вид документа
в MathCad практически ничем не отличается от вида научной статьи. В MathCad
удачно решена проблема передачи изменений числовых данных в формулах по всей
цепочке вычислений.
Для работы программы MathCad 3.0 необходим ПК
класса 386 или 486 с установленной на нем операционной системой Windows
3.1/3.11.
К средствам новых версий MathCad относятся
настройка под любой известный тип печатающего устройства, богатый набор
шрифтов, возможность использования всех инструментов Windows, прекрасная
графика и современный многооконный интерфейс. В версию MathCad 2001 PRO также
включены эффективные средства цветового оформления документов, создания
анимационных графиков и звукового сопровождения. Предусмотрен импорт любых
графических изображений - от простых и специальных графиков функций до
многокрасочных репродукций художественных произведений; также текстовый,
формульный и графический редакторы, объединенные с мощным вычислительным
потенциалом. Существует также возможность объединения с другими мощными
математическими и графическими системами для решения самых сложных задач.
Системы MathCad 2001 PRO поставляются на CD-ROM.
При этом полная инсталляционная версия MathCad 2001 PRO с документацией
занимает 260 Мб. Система ориентирована на операционные системы Windows
98/2000/XP и имеет возможности подготовки документов в формате, принятом для
глобальной сети Internet.
Для установки системы MathCad 2001 PRO нужен ПК
с емкостью ОЗУ не менее 64 Мб. Инсталляция в минимальном объеме требует 101 Мб
на жестком диске. Для полного использования системы должны быть
проинсталлированы приложения, с которыми она может работать совместно: Microsoft
Internet Explorer, Excel, MatLAB и др.
4. Математическое моделирование температурных
полей
Чтобы решить данную задачу необходимо
Ввести все исходные данные и вспомогательные
параметры (Таблица 1)
Затем необходимо поделить стержень на nx+1
участков по перемещению и по времени
Для τ =1 ввести
начальное значение температурного поля
Для текущего шага по времени определить
коэффициенты A, B, C, D методом прогонки
Сделать прямой цикл прогонки и определить
температуру в конце стержня
Сделать обратный цикл прогонки и определить
температуру в остальных точках стержня
В расчете используется функция с параметрами nx,
nτ.
Результатом
которой является двумерная матрица. В функции используется пользовательская
функция tf2, а также глобальные переменные ТО, а, а2, а3, b,
∆τ
Также в программе используется цикл -for от
начала до конца стержня и для определения температурного поля в следующий
момент времени.
Затем мы определяем коэффициенты прогонки для
начала стержня. После чего, уже определяем прогоночные коэффициенты для
остальных узлов стержня и температуру в конце стержня. В обратном цикле for
определяем температуру в остальных точках.
Затем строим графики T(x) и T(τ),
по
которым можно определить изменение температуры стержня в начале, в середине и
конце.
Также можем сделать вывод о том, что со стороны
начала стержня окружающая среда практически не влияет на изменение температуры.
Заключение
В данном курсовом проекте разработана
математическая модель нестационарного температурного поля, стержня или плоской
стенки с боковым теплообменом с учетом влияния на границах окружающей среды.
Математическая модель выполнена в системе
программирования MathCAD. Одним из его наиболее важных качеств, является то,
что при малых затратах времени и сил можно быстро автоматизировать технические
расчеты. В документе MathCAD возможно получить двумерные и трехмерные графики
на основе найденного температурного поля.
Список используемой литературы
Турчак
Л.И. Основы численных методов. - М.: Наука, 1987.
Тарасик
В.П. Математическое моделирование технических систем. - Мн.: ДизайнПРО, 1997. -
640 с.
Токочаков
В.И. Методические указания к лабораторным занятиям по теме "Применение
численных методов в задачах теплообмена" курса "Основы
конструирования и САПР" для студентов специальности Т.01.02.03. - Гомель:
ГПИ, 1995. (м/у 2004).
Трохова
Т.А. Практическое пособие по теме "Основные приемы работы в системе
MathCAD, версии 6.0." для студентов всех специальностей дневного и
заочного отделений. - Гомель: ГГТУ, 1998. (м/у 2286).
Токочаков
В.И. Практическое руководство к лабораторным занятиям по теме "Применение
численных методов в задачах теплообмена" курса "Основы
конструирования и САПР" для студентов специальности Т.01.02. Часть 2. -
Гомель: ГПИ, 1997. (м/у 2206).