Клеточные автоматы
Министерство
образования Российской Федерации
Московский
государственный технический университет
им. Н.Э.
Баумана
Факультет
«Информатики и систем управления»
Кафедра
«Защита информации»
клеточные автоматы
Научно-исследовательская
работа
Руководитель
_______________ Панин С.Д.
Исполнитель,
студ.
гр. ИУ10-102 ____________ Сопов А.Н.
студ.
гр. ИУ10-102 ____________ Киенко В.В.
Содержание
ВВЕДЕНИЕ
КЛЕТОЧНЫЕ АВТОМАТЫ
ПРАВИЛА И ВИДЫ ФИГУР
ПРАКТИЧЕСКАЯ ЧАСТЬ
ВЫВОД
СПИСОК ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
Идея клеточных автоматов появилась в конце
сороковых годов 20 века. Она была задумана и сформулирована Джоном фон Нейманом
и Конрадом Цусе независимо друг от друга как универсальная вычислительная среда
для построения, анализа и сравнения характеристик алгоритмов.
В данной работе приводится следующее определение
клеточных автоматов. «Клеточные автоматы являются дискретными динамическими
системами, поведение которых полностью определяется в терминах локальных
зависимостей. В значительной степени также обстоит дело для большого класса
непрерывных динамических систем, определенных уравнениями в частных
производных. В этом смысле клеточные автоматы в информатике являются аналогом
физического понятия «поля»… клеточный автомат может мыслиться как стилизованный
мир. Пространство представлено равномерной сеткой, каждая ячейка или клетка
которой содержит несколько битов данных; время идет вперед дискретными шагами,
а законы мира выражаются единственным набором правил, скажем, небольшой
справочной таблицей, по которой любая клетка на каждом шаге вычисляет своё
новое состояние по состояниям её близких соседей. Таким образом, законы системы
являются локальными и повсюду одинаковыми. «Локальный» означает, что для того,
чтобы узнать, что произойдет здесь мгновение спустя, достаточно посмотреть на
состояние ближайшего окружения: никакое дальнодействие не допускается.
«Одинаковость» означает, что законы везде одни и те же: я могу отличить одно
место от другого только по форме ландшафта, а не по какой-то разнице в
законах.»
Следует отметить, что клеточные автоматы - это
не просто машины, работающие с разбитым на клетки полем. Область применение
клеточных автоматов почти безгранична: от простейших «крестиков-ноликов» до
искусственного интеллекта. Тема клеточных автоматов очень актуальна, так как
может привести к разгадкам многих вопросов в окружающем мире. Создатель игры
«Жизнь» Конуэй, считал, что нашу вселенную можно представить клеточным
автоматом, который управляет движением элементарных частиц в соответствии с
некоторыми правилами (кстати, сейчас Конуэй придумал еще одно применение
клеточных автоматов в этой области: представим себе достаточно большое
количество «первичного бульона» из хаотически распределенных клеток, если можно
ожидать появления из такого хаоса структур, способных самовоспроизводить себя,
то это еще одно подтверждение теории зарождения жизни на Земле).
КЛЕТОЧНЫЕ АВТОМАТЫ
Клеточные автоматы используются для
моделирования гидродинамических и газодинамических течений. Уравнения
гидродинамики соответствуют математической модели, описывающей поведение
решетчатого газа, одного из клеточных автоматов, на макроуровне. Структуры,
возникающие в этих клеточных автоматах, похожи на возмущение поведения
поверхности потока жидкости механическим препятствием. Примитивные одномерные
клеточные автоматы могут моделировать процесс горения различного характера. В
настоящее время теория клеточных автоматов наиболее перспективно прилагаема к
вопросу о разработке самовосстанавливаемых электронных цепей.
Клеточные автоматы применимы не только в
математике и физике, а также в биологии, экономике, социологии, информатике и
т.д. С помощью клеточных автоматов успешно решались задачи моделирования
течений со свободной границей, распространения тепловых потоков, роста и
динамики доменов, роста дендритов, описания движения толпы. Их можно
использовать при составлении генетических алгоритмов. Представим себе клеточный
автомат, для клеток которого дополнительным условием выживания является
выработка некоторой последовательности выходных данных (назовем ее условно
реакцией) в ответ на последовательность входных данных (раздражение, являющееся
свойством среды), предсказывающее последующее состояние среды. Чтобы такой
автомат функционировал, добавляется также механизм случайного изменения правил
выработки реакции (мутации) и передачи вновь возникающим клеткам информации о
правилах реагирования соседей (наследования). Помимо исследования условий
развития моделей живых систем, такой подход позволяет решать и некоторые
практические задачи, в частности поиск кратчайшего пути на графе. Структура
графа кодируется некоторым образом в хромосомах клеток. Предполагается, что
алгоритмы, приобретенные вследствие мутаций и наследования, будут
соответствовать решениям задачи.
По своему поведению клеточные автоматы делятся
на четыре класса. К первому классу относятся автоматы, приходящие через
определенное время к устойчивому однородному состоянию. Автоматы второго класса
через некоторое время после пуска генерируют стационарные или периодические во
времени структуры. В автоматах третьего класса по прошествии некоторого времени
перестает наблюдаться корреляция процесса с начальными условиями. Наконец,
поведение автоматов четвертого класса сильно определяется начальными условиями
и с их помощью можно генерировать весьма различные шаблоны поведения. Такие
автоматы являются кандидатами на прототип клеточной вычислительной машины. В
частности, с помощью специфических клеточных конфигураций игры «Жизнь», которая
как раз и является автоматом четвертого типа, можно построить все дискретные
элементы цифрового компьютера.
Отметим еще одно применение клеточных автоматов
в информатике - шифрование и сжатие данных.
Клеточные автоматы применимы при реализации
эффективной системы распознавания образов. Один из возможных путей ее создания
- построение динамической системы, аттракторами которой в ее конфигурационном
пространстве были бы типичные картины-образы. Начальные условия всегда окажутся
в области притяжения одной из картин, с течением времени система трансформирует
начальные параметры, приведя их к наиболее близкой структуре - аттрактору. То
есть произойдет автоматическое распознавание образа. Причем можно создавать
обучающиеся системы распознавания, в них законы эволюции имеют состояние
программирования. Использовать клеточные автоматы можно и при решении
оптимизационных задач. Часто в различных сферах деятельности возникают задачи
нахождения оптимального варианта из неограниченного числа возможных. Точного
решения, как правило, не требуется, но дискретный компьютер не способен даже
приблизительно дать оптимальный результат.
Таким образом, клеточные автоматы нашли и
находят широкое применение во многих сферах человеческой деятельности, многие
задачи которых стало возможным решить только с помощью компьютера.
Наверное, наиболее известным из клеточных
автоматов можно считать клеточный автомат под названием игра «Жизнь». Создана
игра «Жизнь» была в 1970 году Джоном Хортоном Конуэем, математиком
Кембриджского университета. Возникающие в процессе игры ситуации очень похожи
на реальные процессы, происходящие при зарождении, развитии и гибели колонии
живых организмов. По этой причине «Жизнь» можно отнести к быстро развивающиеся
в наши дни категории игр, имитирующих процессы, происходящие в живой природе.
правила и виды фигур
клеточный автомат игра информатика
Рассматривается бесконечная плоская решётка
квадратных ячеек-клеток. Время в этой игре дискретно (t=0, 1, 2, ...). Клетка
может быть живой или мёртвой. Изменение её состояния в следующий момент времени
t+1 определяется состоянием её соседей в момент времени t (соседей у клетки
восемь, четверо имеют с ней общие рёбра, а четверо только вершины). Основная
идея состоит в том, чтобы, начав с некоего расположения клеток, проследить за
эволюцией исходной позиции под действием «генетических законов» Конуэя, которые
управляют рождением, гибелью и выживанием клеток. Конуэй тщательно подбирал
свои правила и долго проверял их на «практике», добиваясь, чтобы они по
возможности удовлетворяли трём условиям:
• Не должно быть ни одной исходной конфигурации,
для которой существовало бы простое доказательство возможности неограниченного
роста популяции.
• В то же время должны существовать такие
начальные конфигурации, которые заведомо обладают способностью беспредельно
развиваться.
• Должны существовать простые начальные
конфигурации, которые в течении значительного промежутка времени растут,
претерпевают различные изменения и заканчивают свою эволюцию одним из следующих
трёх способов: полностью исчезают (либо из-за перенаселенности, то есть слишком
большой плотности живых клеток, либо наоборот, из-за разреженности клеток,
образующих конфигурацию); переходят в устойчивую конфигурацию и перестают
изменяться вообще или же, наконец, выходят на колебательный режим, то есть
бесконечный цикл превращений с определенным периодом.
Следствием этих требований явились следующие
правила игры «Жизнь»:
. Выживание. Каждая клетка, имеющая две или три
соседние живые клетки, выживает и переходит в следующее поколение.
. Гибель. Каждая клетка, у которой больше трёх
соседей, погибает из-за перенаселённости. Каждая клетка, вокруг которой
свободны все соседние клетки или же занята всего одна клетка, погибает от
одиночества.
. Рождение. Если число занятых клеток, с
которыми граничит какая-нибудь пустая клетка, в точности равно трём, то на этой
клетке происходит рождение нового организма.
Зададимся вопросами: Какие основные типы
структур (то есть конфигураций, определяющих поведение сообществ на больших
временах) могут существовать в такой системе? Каковы здесь законы организации
структур? Могут ли они взаимодействовать, и к чему это приводит? Выясним, какие
закономерности являются следствиями представленных выше правил.
Первая закономерность - свойство локализации -
структуры, разделённые двумя «мёртвыми» (пустыми) клетками не влияют друг на
друга.
Вторая закономерность - система клеток, которую
описывает игра «Жизнь», развивается необратимо. В самом деле, конфигурация в
момент времени t полностью определяет будущее (состояние в моменты t+1, t+2 и
так далее). Но восстановить прошлое системы по её настоящему не удаётся.
Картина здесь такая же, как в одномерных отображениях, только прообразов у
данной конфигурации может быть бесконечно много. (Докажем это утверждение:
воспользуемся свойством локализации и расположим вокруг данной конфигурации
множество локализованных одиночных клеток или их пар так, чтобы они не влияли
на неё и друг на друга. Понятно, что все они исчезнут на следующем шаге, никоим
образом не повлияв на будущее системы). Здесь мы можем заметить признаки
нелинейных диссипативных структур: эти структуры определяли поведение системы
при t стремящемся к бесконечности в случае различных начальных данных.
Третья закономерность - как показывают
длительные наблюдения за процессом развития колоний, конфигурации, не обладавшие
в начале игры симметрией, обнаруживают тенденцию к переходу в симметричные
формы. Обретённые свойства симметрии в процессе дальнейшей эволюции не
утрачиваются, симметрия конфигурации может лишь обогащаться.
Условимся классифицировать конфигурации клеток по
следующим параметрам:
• По количеству клеток в комбинации:
единичная клетка, дуплет (2 клетки в комбинации), триплет (3 клетки) и т.д.
• По перспективе развития: развивающиеся
(неограниченный рост), стабильные (количество клеток в популяции колеблется около
какого-то среднего значения), вымирающие (популяция стабильно уменьшается),
периодические (количество клеток принимает несколько фиксированных значений
через определенный период).
Теперь рассмотрим типичные структуры,
появляющиеся в игре «Жизнь». Простейшими являются стационарные, то есть не
зависящие от времени структуры (сам Конуэй называет их «любителями спокойной
жизни»). Их примеры показаны на рисунке 1. С помощью этих стационарных структур
можно получить множество других. В самом деле, если мы имеем такую структуру,
то конфигурация, полученная поворотом на 90О, также будет стационарной.
Конфигурации в нижних рядах показывают, как можно достраивать определённые
структуры до любых размеров. Используя свойство локализации можно строить
«большие» стационарные структуры из «малых»-элементарных.

Рис.1. Примеры стационарных структур,
реализующихся в игре «Жизнь»
Можно считать, что стационарные структуры
повторяют себя на каждом шаге по времени. Но есть и другие конфигурации,
повторяющие себя через N шагов, так называемые N-циклы (периодические
структуры).
Примеры 2-циклов показаны на рисунке 2. При
эволюции различных сообществ часто встречается 2-цикл, показанный во второй
строке и называемый «семафором».

Рис. 2. Примеры периодических структур
(2-циклы), реализующихся в игре «Жизнь» (жаба, семафор, часы)
Известно много различных периодических
конфигураций. Однако эффективные алгоритмы, позволяющие строить различные
конфигурации с данным периодом N, по-видимому, в настоящее время не созданы.
Эволюция взятых наугад начальных данных часто
приводит к возникновению простейших локализованных структур (показанных на
рисунке 1) и семафоров. Однако возможны и более сложные типы эволюции,
например, когда сообщество клеток симметрично «достраивается», и возникают
циклы большого периода, имеющие сложную форму.
В игре «Жизнь» существуют конфигурации, которые
могут передвигаться по плоскости. Одной из них является «планер» (или
«глайдер») - конфигурация из 5 клеток (рис. 3)

Рис 3. Планер (глайдер) - перемещающаяся
конфигурация из 5 клеток
После второго хода планер немного сдвигается и
отражается относительно диагонали. В результате двух последующих ходов планер
«выходит из пике», ложится на прежний курс и сдвигается на одну клетку вправо и
одну клетку вниз относительно начальной позиции.
Скорость, с которой шахматный король
перемещается по доске в любом направлении, Конуэй называет «скоростью света».
Выбор Конуэя пал именно на этот термин из-за того, что в изобретённой им игре
большие скорости просто не достигаются. Ни одна конфигурация не воспроизводит
себя достаточно быстро, чтобы двигаться с такой скоростью. Конуэй доказал, что
максимальная скорость на диагонали составляет одну четверть скорости света.
Поскольку планер переходит сам в себя после четырёх ходов и при этом опускается
на одну клетку по диагонали, то говорят, что он скользит по полю со скоростью,
равной одной четвертой скорости света. Конуэй также показал, что скорость любой
конечной фигуры, перемещающейся по вертикали или по горизонтали на свободные
клетки, не может превышать половину скорости света. (Скорость движения равна
дроби, в числителе которой стоит число ходов, необходимых для воспроизведения
фигуры, а в8
знаменателе - число клеток, на которое она при
этом смещается). Понятно, что в силу симметрии есть планеры, распространяющиеся
вдоль любой диагонали квадрата в обоих направлениях.
Впрочем, некоторые конфигурации могут
передвигаться не вдоль диагоналей, а по вертикальным и горизонтальным прямым.
Таковы, например, три «корабля» показанные на рисунке 4. (Обратим внимание на
то, что далеко не любая конфигурация такого типа будет кораблём). Кстати,
планер является кораблём легчайшего веса. Во время движения из кораблей
возникают «искры», которые тут же гаснут при дальнейшем движении кораблей.

Рис. 4. Корабли - конфигурации, реализующиеся в
игре «Жизнь», способные перемещаться
Одиночные корабли без эскорта не могут занимать
в длину больше шести клеток, в противном случае на поле начинают появляться
различные мелкие фигуры, препятствующие движению корабля. Конуэй обнаружил, что
более длинным кораблям (которые он называл «сверхтяжёлыми») необходим эскорт из
двух или большего числа кораблей меньших размеров. Корабли эскорта не дают
возникать препятствиям на пути сверхтяжёлого корабля. Конуэй вычислил, что
корабль длиной в сто клеток требует эскорта, состоящего из тридцати трёх (!)
кораблей.
Итак, мы располагаем планерами и различными
кораблями. Возникает вопрос, что происходит, когда они сталкиваются между собой
или с различными стационарными конфигурациями (стационарами). Столкновения
могут быть очень разнообразны в зависимости от курса планера и его фазы при
столкновении. Столкновение двух планеров или планера со стационаром может
приводить к их «аннигиляции». В столкновении может рождаться целый набор
семафоров и стационаров.
Обратим внимание на следующую закономерность.
Если конфигурация все время локализована в квадрате размером NxN, то она
является набором стационаров и циклов, период которых не превышает 2N. В самом
деле, каждая клетка может находиться в одном из двух состояний, а всего клеток
в области N2 , поэтому при t>2N конфигурации начнут повторяться.
Рассматривая непрерывные среды, можно говорить о
резонансном возбуждении - начальных данных, приводящих к более сложной эволюции
решений, чем в остальных случаях. В игре «Жизнь» есть аналог такого поведения.
Обратим внимание на конфигурацию, показанную на рисунке 5, называемую
«r-пентемино». Возникающие клетки занимают всё большую часть плоскости,
рождается несколько планеров, причем это сообщество будет развиваться далее. Ни
одна из других конфигураций, состоящих из пяти клеток, не приводит к такому
сложному поведению.

Как правило, эволюция взятых наугад конфигураций
приводит к появлению наборов стационаров, семафоров, планеров. При этом общее
число клеток при t, стремящемся к бесконечности, оказывается ограниченным (это
было заложено в требованиях Конуэя), однако, при некоторых начальных данных
эволюция системы может качественно меняться. Такое поведение характерно для
ряда биологических систем, в частности, эволюционных процессов. Маловероятное
событие может качественно изменить поведение системы, привести к появлению
новых видов. Именно поэтому игра «Жизнь» находит применение в экологических
моделях, при моделировании морфогенеза, в других биологических задачах.
Чем большую площадь занимает сообщество, тем
сложнее оно может себя вести. Поэтому большой интерес вызывают неограниченно
растущие в пространстве конфигурации. Одну из них, называемую «катапультой» или
«планерным ружьём», предложил в 1970 году Р. Госпер-младший. Видно, что
катапульта через каждые 30 шагов повторяет себя и выпускает планер (см. рисунок
6). Планерное ружьё заполняет пространство потоком планеров. Конуэй высказал
гипотезу, согласно которой не существует ни одной начальной конфигурации,
способной беспредельно расти. Иначе говоря, любая конфигурация, состоящая из
конечного числа живых клеток, не может перейти в конфигурацию, в которой число
живых клеток превосходило бы некий конечный предел. Но гипотеза оказалась
ошибочной! Опровержение - планерное ружьё.
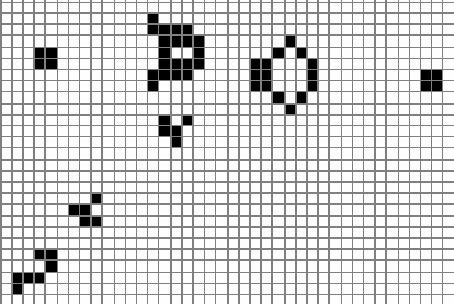
Рис. 6. Планерное ружьё (катапульта) -
конфигурация, генеририрующая за каждые 30 ходов планер.
Есть ещё более сложные сообщества клеток,
которые могут двигаться, оставляя за собой большой набор семафоров и стационаров.
Одно из них - «паровоз» (он имеет довольно сложную структуру). Поиск таких
конфигураций - довольно трудоёмкий процесс, требующий применения специальных
алгоритмов и под силу квалифицированным специалистам.
Также были найдены особые конфигурации, которые
Джон Тьюки назвал «садами Эдема». «Сады Эдема» не могут возникнуть в ходе
работы клеточного автомата, поскольку их не способна породить никакая
конфигурация. В силу этого они должны быть заданы с самого начала - в нулевом
поколении. Не имея предшественников, они не могут быть самовоспроизводящимися.
Алви Р. Смит нашел способ применить теорему Мура к игре Конуэя и показал, что
конфигурация по типу «садов Эдема» возможна и в «Жизни». Формулы, выведенные
Муром, позволили Смиту утверждать, что подобная конфигурация всегда может быть
заключена в квадрат со стороною в 10 000 000 000 клеток.
Приведённые примеры показывают, что в
обсуждаемой дискретной системе существует большое количество различных типов
упорядоченности, которые определяют асимптотическое поведение некоторого
множества конфигураций (в этом смысле они оказываются эквивалентны аттракторам
динамических систем). Однако можно доказать большее - в игре «Жизнь» существуют
сколь угодно сложные типы упорядоченности, эта дискретная система оказывается эквивалентна
универсальной вычислительной машине.
ЭВМ можно рассматривать как конечный набор
простейших логических элементов, осуществляющих операции И, ИЛИ, НЕ,
определённым образом соединённых проводами, по которым распространяется набор
импульсов, кодирующих последовательность нулей и единиц. В качестве генератора
таких импульсов в игре «Жизнь» выступает планерное ружьё. Наличие планера в
потоке естественно интерпретировать как единицу, отсутствие как ноль.
Столкновение планеров, приводящих к их аннигиляции, позволяет построить элемент
НЕ, направив два потока под прямым углом (если планер в определённом месте есть
в первом потоке, то после столкновения планер в другом потоке на этом месте
исчезнет). Более сложным образом конструируются другие элементы.
Для анализа ситуаций, возникающих в игре
«Жизнь», применяется компьютер. В программе, моделирующей этот клеточный
автомат, используется квадратная матрица, которая и является полем для игры.
При смене хода анализируется каждый элемент старой матрицы и строится на её
основе новая, которая соответствует конфигурации на следующем шаге эволюции.
Для более детального исследования игра Конуэя расширена на несколько популяций,
каждая из которых развивается по своим правилам. Правила для каждой популяции
выбираются из следующих:
• Условия рождения и смерти. Задаются
четыре параметра (параметры можно менять в процессе игры): минимальное и
максимальное количество соседей своей популяции, при котором рождается клетка;
минимальное и максимальное количество соседей, при котором клетка выживает и
переходит в следующее поколение.
• Соседями клетки могут быть любые клетки,
находящиеся в квадрате 3х3 с центром в данной клетке.
Игра «Жизнь» нашла свое применение в биологии
как игра «Аква-Тор», которая моделирует поведение системы, состоящей из двух
популяций, условно называемых «травоядные» и «хищники».
ПРАКТИЧЕСКАЯ
ЧАСТЬ
#include <iostream>
#include <ctime>namespace
std;main()
{int iFieldWidth(20) ,
iFieldHeight(10);char chLiveCell('#') , chDeathCell('.');iGenerations(5);bCellArry[iFieldWidth
* iFieldHeight] = {false};bTempCellArry[iFieldWidth * iFieldHeight] =
{false};((unsigned)time(NULL));(int y=0; y < iFieldHeight; y++)
{(int x=0; x < iFieldWidth; x++)
{(bCellArry[x + y * iFieldWidth])
{<< chLiveCell;
}
{<< chDeathCell;
}
}<< '\n' ;}<< '\n'
;<< '\n' ;(int y=0; y < iFieldHeight; y++)
{(int x=0; x < iFieldWidth; x++)
{[x + y * iFieldWidth] = rand() %
2;(bCellArry[x + y * iFieldWidth])
{<< chLiveCell;
}
{<< chDeathCell; } }<<
'\n' ;}<< '\n' ;<< '\n' ;(int g=0 ; g<iGenerations ; g++)
{(int y=0; y < iFieldHeight; y++)
{(int x=0, iCellCounter = 0; x <
iFieldWidth; x++)
{( ((x-1) >=0 ) && ((y-1)
>=0) )
{(bCellArry
[(x-1)+(y-1)*iFieldWidth]) iCellCounter++ ;
}((y-1) >=0 )
{(bCellArry [x+(y-1)*iFieldWidth])
iCellCounter++ ;
}( ((x+1) <= iFieldWidth)
&& ((y-1) >=0 ))
{(bCellArry[ (x+1) + (y-1) *
iFieldWidth]) iCellCounter++ ;
}((x-1) >=0 )
{(bCellArry[(x-1) + y*iFieldWidth])
iCellCounter++;
}((x+1) <= iFieldWidth-1 )
{(bCellArry[(x+1) + y*iFieldWidth] )
iCellCounter++;
}( ((x-1) >= 0 ) &&
((y+1) <= iFieldHeight-1))
{(bCellArry[(x-1) + (y+1) *
iFieldWidth]) iCellCounter++;
}((y+1) <= iFieldHeight-1)
{(bCellArry [x+(y+1) * iFieldWidth])
iCellCounter++;
}(((x+1) <= iFieldWidth -1)
&& ((y+1) <= iFieldHeight-1))
{(bCellArry [(x+1) + (y+1) *
iFieldWidth]) iCellCounter++;
}((iCellCounter < 2 ) ||
(iCellCounter > 3 ))
{[x + y * iFieldWidth] =
false;<< chDeathCell;
}
{((!bCellArry [x + y * iFieldWidth])
&& (iCellCounter !=3))
{[x + y * iFieldWidth] =
false;<< chDeathCell;
}
{[x + y * iFieldWidth] =
true;<< chLiveCell;
}
}= 0;
}<< '/n' ;
}<< '/n' ;<< '/n' ;(int
i=0 ; i < (iFieldWidth * iFieldHeight) ; i ++ )
{[i] = bTempCellArry[i];
}
}0; }
1) Задаем
начальное
состояние

) Вывод пяти поколений
ВЫВОД
Хотя игра состоит всего из трех
простых правил, тем не менее, она более сорока лет привлекает пристальное
внимание учёных. Игра «Жизнь» и ее модификации повлияла (в ряде случаев
взаимно) на многие разделы таких точных наук как математика, информатика,
физика. Кроме того, многие закономерности, обнаруженные в игре, имеют свои
аналогии в других, подчас совершенно «нематематических» дисциплинах. Возможно,
эта игра связана и с другими научными явлениями, в том числе и с теми, о
которых современной науке пока неизвестно. Также возможно, что не открытые на
сегодня законы Природы и Общества станут более понятными благодаря «Жизни» и ее
модификациям.
СПИСОК ЛИТЕРАТУРЫ
1. <http://habrahabr.ru/>
. <http://life.written.ru/>
. <http://crm.ics.org.ru/>
. <http://www.ict.edu.ru/>