Теоремы Перрона-Фробеніуса та Маркова

Теоремы Перрона-Фробеніуса та Маркова

Теоремы Перрона-Фробеніуса та Маркова

В роботі дано елементарне доведення відомих теорем Перрона-Фробеніуса та Маркова для матриць другого порядку. Робота має певну методичну цінність і може бути використана на заняттях шкільних гурків та факультативів

   Відомо [[1]-[10]], яку важливу роль відіграють невід’ємні матриці в математичних моделях економіки, біології, теорії ймовірностей тощо.

   Одними з основоположних фактів теорії цих матриць є теореми Перрона. Перрона-Фробеніуса та Маркова. Доведення цих теорем в загальному випадку потребує застосування теорем з таких неелментарних розділів математики, як теорія екстремумів функції багатьох змінних, жорданова нормальна форма тощо.

   Мета роботи дати елементарне доведення вищезгаданих теорем Перрона, Перрона-Фробеніуса та Маркова для матриць другого проядку, яке цілком доступне і для школярів 9-го класу. Це дозволить, наприклад, на заняттях шкільних математичних гуртків чи факультативів розглянути та проаналізувати змістовні математично-економічні та теоретико-ймовірносні моделі (наприклад, модель Леонтьєва, випадкове блукання на відрізку) з повним доведенням всіх тверджень.

1. Необхідні відомості з теорії матриць.

Матриця розмірів m x n – це прямокутна таблиця чисел з m рядків та n стовпців. Позначається матриця так:

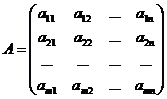
   Квадратною матрицею n-го порядку зветься матриця розміром n x n. Важливою числовою характеристикою матриці є її визначник, який позначається detA. Для 2x2 матриці 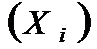 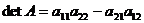. Матриці А та В однакових розмірів називаються рівними, якщо іх відповідні елементи однакові, що записують так: А=В.

   З матрицями можна здійснювати такі операції:

1. Множити на число

Приклад: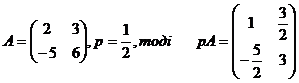

2. Додавати матриці однакових розмірів:

Приклад: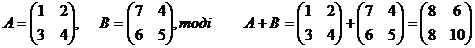

3. Множити матриці:

Приклад: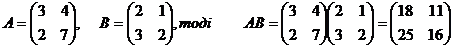

   Взагалі, добутком матриці А розмірів m x r та матриці В розмірів r x n називається матриця С розмірів m x n, яка позначається АВ. Елемент c_ij цієї матриці – це сума попарних добутків елементів i-го рядка матриці А та елементів j-го рядка матриці В, а саме: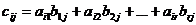

   Якщо А та В квадратні матриці однакового порядку, то їх завжди можна перемножити.

   Квадратна матриця порядку n, у якої єлементи 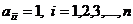, а інші елементи є нулями, називається одиничною матрицією порядку n. Однична матриця має таку властивість: АЕ=ЕА=А, де А – квадратна матриця порядку n, Е – одинична матриця такого ж порядку.

   Нехай А – квадратна матриця, тоді матриця А^-1 зветься оберненою до матриці А, якщо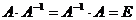

   Не в кожної матриці є обернена до неї, а саме А^-1 існує тоді і тільки тоді, коли .

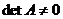   Беспосередньо можна первірити, що для

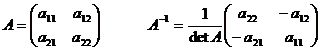
Визначення: Число l називається власним значенням n x n матриці А, якщо знайдется стовпчик 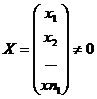такий, що АХ=lХ. При цьому Х називається власним вектором матриці А, що відповідає власному значенню l.

   Якщо власний вектор Х відповідає власному значенню l, то сХ, де с - const, також власний вектор, що відповідає l. Власне значення є коренем характеристичного рівняння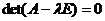 . Звідки видно, що не у кожної матриці є власні значення.

Визначення: Матриця А зветься додатною, якщо всі її елементи додатні, це позначається А>0.

   Теорема Перрона: Нехай А - додатна матриця, тоді А має додатне власне значення r>0 таке, що:

   1. r- відповідає єдиний (з точністю до множення на число) власний вектор.

   2. інші власні значення по модулю < r.

3. власний вектор, що відповідає r, можна вибрати додатним (тобто з додатними елементами).

Доведення теореми для 2х2 матриць.

Нехай .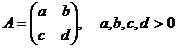

Тоді .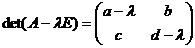

Напишемо характеристичне рівняння для матриці А:

.

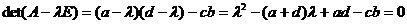Це квадратне рівніння з дискримінантом:

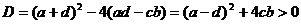
І тому

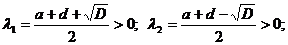
Тобто твердження теореми 1 і 2 доведені, якщо r=l₁.

Знайдемо власний вектор , що відповідає власному значенню l₁ з рівності

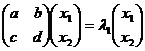
Тоді

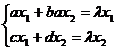, або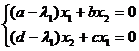             

Враховуючи, що

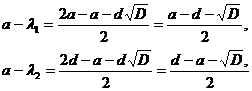
перепишемо систему у вигляді:

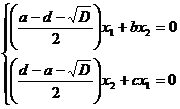
Але 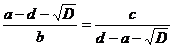 і тому рівняння системи пропорціональні, а це означає, що одне з них можна відкинути.

Знайдемо x₁ з першого рівняння системи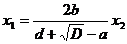

Щоб довести, що власний вектор можна вибрати додатним, достатньо перевірити, що 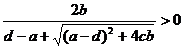,тому що поклавши отримаємо x₁>0.

   Враховуючи, що b>0 треба довести, що ,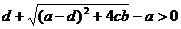

але це випливає з того, що 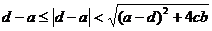, бо cb>0.

   Таким чином третє твердження доведено, а з ним доведена теорема.

Визначення: Матриця А n-го порядку зветься нерозкладною, якщо однаковим переставленням рядків та стовпців її не можна привести до виду 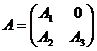, де А₁, А₂ - квадратні матриці розмірів k x k та (n-k) x (n-k) відповідно. Для 2х2 матриць 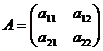 це означає, що  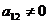та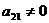

Визначення: Матриця А зветься невід’ємною, якщо всі її елементи невід’ємні.

Зауваження: Фробеніус довів, що твердження теореми Перрона залишаються в силі для нерозкладних невід’ємних матриць. Це можна довести, просто повторивши наше доведення теореми Перрона для 2х2 матриць у випадку, коли один або обидва діагональних елемента дорівнюють нулю.

Визначення: Квадратна матриця називається стохастичною, якщо

1)

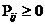
2)

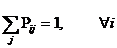
Теорема Маркова: Нехай для стохастичної матриці P існує натуральне число k₀ таке, що 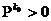 (тобто всі елементи додатні). Тоді

   1. 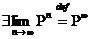 (існування границі матриці означає, що існує границя кожного її елементу)

   2. Матриця 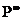 - має однакові рядки.

   3. Всі елементи цих рядків додатні.

Доведення теореми для 2х2 матриць.

Запишемо стохастичну матрицю у вигляді 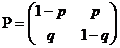, де

Запишемо її характеристичне рівняння: ,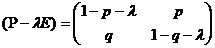

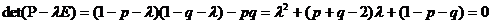
Це квадратне рівняння з дискрімінантом:

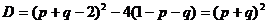
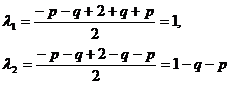
З урахуванням 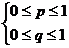 маємо 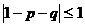, але якщо 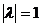, то це значить, що p=q=1 або p=q=0, відкіля матриця P буде мати вигляд 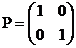, або 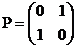 і тоді Pⁿ містить нулі 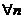, що суперечить умові. Таким чином .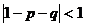

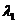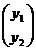Беспосередньою перевіркою з урахуванням стохастичності встановлюємо, що власному значенню  відповідає власний вектор , де x₁=x₂, тобто, наприклад  власний вектор. Знайдемо власний вектор , що відповідає власному значенню .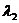

За визначенням

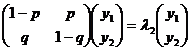
Звідки

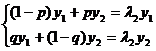
Згадуючи, що 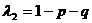 отримуємо

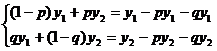
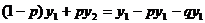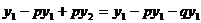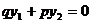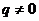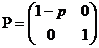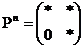   Очевидно, що рівняння системи пропорційні, тому одне з них можна відкинути. Знайдемо y₁ з першого рівняння:  або  звідки , але  , бо в протилежному випадку дана матриця мала б вигяд: , а тоді матриця  мала б нульовий елемент 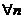, що суперечить умові. Тому можна записати, що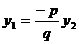

Доведемо тепер твердження 1 теореми.

   Розглянемо матрицю S, стовпцями якої є власні вектори матриці P. Нам необхідно отримати зручну формулу для Pⁿ.

Позначимо .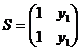

Оскілки 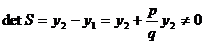, то існує S^-1. Перепишемо рівняння 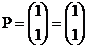 та 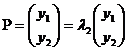 у матричній формі

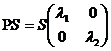 або .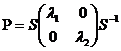

Відкіля 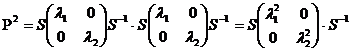 і взагалі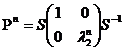

Знайдемо границю Pⁿ:

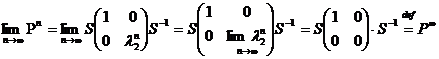
   Твердження 1 теореми доведено.

   Доведемо тепер, що рядки матриці 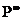 однакові. Для цього обчиcлимо .

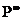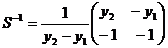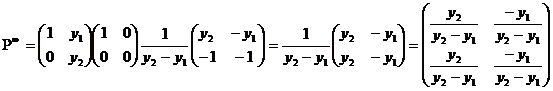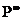Оскільки , то Ми бачимо, що рядки матриці  - однакові. Доведемо тепер, що їх елементи додатні. Для цього врахуємо отриману раніше залежність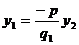

Для того, щоб довести треба довести, що 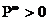, треба довести, що  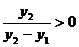та .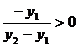

Маємо

,

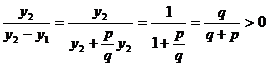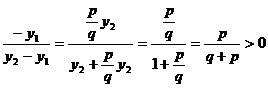, тому що p>0 і q >0

Теорема доказана.

Зауваження1 В процесі доведення ми вивели, що для 2х2 матриць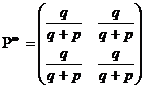

Зауваження2 Позначимо 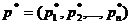 рядки граничної матриці 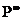. Тоді 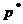можна знайти з умови:

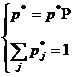
Доведення.

Оскільки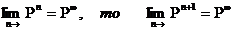

Зівдки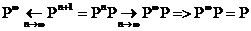

Або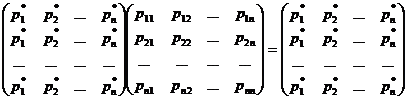

Звідки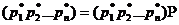

Зокрема, для 2х2 матриці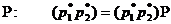

Умовою 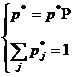 рядок 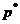 визначається однозначно, що для 2х2 матриці можна перевірити.

    В роботі дані для матриць другого порядку елементарні доведення таких фундаментальних теорем теорії невід’ємних матриць. як теореми Перрона, Перрона-Фробеніуса, Маркова.

   У відомій нам літературі повне доведення цих теорем дається для загального випадку матриць n-го порядку з використанням неелемнтарних теорем і методів. А математичний апарат, який використовується в даній роботі, це: аналіз поведінки розв’язків квадратного рівняння та розв’язків системи двох лінійних рівнянь в залежності від коефіцієнтів.

   Робота може бути використана при проведенні додаткових занять, присвячених розгляду вибраних неелементарних питань математики, за допомогою методів, які доступні школярам.

Список літератури:

1.   С.А. Ашманов. Математические модели и метод в экономике.
МГУ. 1980

2.   С.А. Ашманов. Введение в математическую экономику. “Наука”.
М., 1984

3.   Р. Беллман. Введение в теорию матриц. “Наука”. М. 1969

4.   Ф.Р. Гантмахер. Теория матриц. “Наука”. М.,1967

5.   Б.В. Гнеденко. Курс теории вероятностей. “Наука”. М., 1988

6.   С. Карлин. Математические метод в теории игр, программирования и экономике. “Мир”. М., 1964

7.   Дж. Кемени, Дж. Скелл, Дж. Томпсон. Введение в конечную математику. Иностранная литература. М. 1963

8.   П. Ланкастер. Теория матриц. “Наука”. М. 1978

9.   Ю.М. Свирежев, Д.О.Логофет. Устойчивость биологических сообществ. “Наука”. М. 1978

10.В. Феллер. Введение в теорию вероятностей и ее приложение.
Т1. “Мир”.М. 1984