|
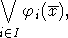
|
(1)
|
где
 - рекурсивно
перечислимое по Тьюрингу множество бескванторных попарно несовместных формул
сигнатуры
- рекурсивно
перечислимое по Тьюрингу множество бескванторных попарно несовместных формул
сигнатуры  . Обратно, любая
р.п. дизъюнкция бескванторных формул сигнатуры
. Обратно, любая
р.п. дизъюнкция бескванторных формул сигнатуры  определяет рекурсивно перечислимое множество
определяет рекурсивно перечислимое множество 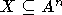 .
.
Это
вариант леммы Энгелера для вычислимости в списочной надстройке, ее
доказательство можно найти в [1]. Из леммы 1 и теоремы Поста следует, что если 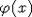 - бескванторная формула, то
множество
- бескванторная формула, то
множество 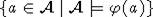 рекурсивно.
рекурсивно.
Определение
2. Множество X m сводится к Y ( ), если существует всюду определенная вычислимая
функция
), если существует всюду определенная вычислимая
функция  , что
, что 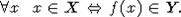
Множества
X и Y m-эквивалентны (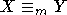 ),
если
),
если 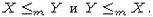
m-степень
множества X есть множество 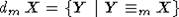 .
.
m-степень
рекурсивна (р.п.), если она содержит хотя бы одно рекурсивное (р.п.) множество.
Так
же, как и в классической теории алгоритмов, доказывается следующая лемма (см.,
например, [4]).
Лемма
3. Справедливы следующие утверждения:
1)
отношение 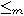 рефлексивно и
транзитивно;
рефлексивно и
транзитивно;
3)
 .
.
Известно
[4], что в арифметике существует только три рекурсивные m-степени: 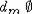 ,
, 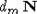 и степень всех остальных рекурсивных множеств. В
данной работе описывается структура рекурсивных m-степеней в полях с
трансцендентными элементами.
и степень всех остальных рекурсивных множеств. В
данной работе описывается структура рекурсивных m-степеней в полях с
трансцендентными элементами.
Итак,
пусть 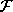 - поле,
рассматриваемое в сигнатуре
- поле,
рассматриваемое в сигнатуре 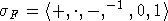 - его простое подполе. Предполагаем, что
- его простое подполе. Предполагаем, что 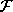 содержит трансцендентные над
содержит трансцендентные над 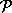 элементы.
элементы.
Лемма
4. Множество 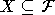 рекурсивно
рекурсивно  одно из множеств X или [
одно из множеств X или [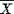 ] состоит из конечного набора
алгебраических над
] состоит из конечного набора
алгебраических над 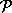 элементов
и вместе с каждым элементом содержит все алгебраически сопряженные с ним (т.е.
корни того же самого минимального многочлена).
элементов
и вместе с каждым элементом содержит все алгебраически сопряженные с ним (т.е.
корни того же самого минимального многочлена).
Доказательство.
Пусть 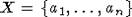 ,
,  - минимальные многочлены для элементов
X, причем вместе с каждым ai множество X содержит и все остальные корни fi(x).
Тогда
- минимальные многочлены для элементов
X, причем вместе с каждым ai множество X содержит и все остальные корни fi(x).
Тогда 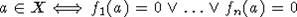 - рекурсивное
отношение.
- рекурсивное
отношение.
Пусть
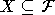 рекурсивно над
рекурсивно над 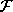 '. Тогда X и [
'. Тогда X и [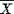 ] определяются рекурсивными
дизъюнкциями бескванторных формул
] определяются рекурсивными
дизъюнкциями бескванторных формул 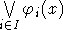 и
и 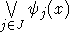 вида (1).
вида (1).
Случай
1. Одна из 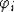 есть конечная
конъюнкция неравенств вида
есть конечная
конъюнкция неравенств вида 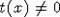 . Такой
. Такой 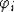 будут удовлетворять все элементы поля
будут удовлетворять все элементы поля 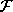 , за исключением конечного
числа алгебраических элементов, т.е. X есть множество требуемого вида.
, за исключением конечного
числа алгебраических элементов, т.е. X есть множество требуемого вида.
Случай
2. Все 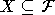 содержат хотя бы
одно равенство вида t(x) = 0. Тогда множество X не содержит ни одного
трансцендентного элемента, следовательно, существует
содержат хотя бы
одно равенство вида t(x) = 0. Тогда множество X не содержит ни одного
трансцендентного элемента, следовательно, существует 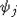 , которой удовлетворяют трансцендентные
элементы, но тогда
, которой удовлетворяют трансцендентные
элементы, но тогда 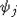 содержит
только одни неравенства
содержит
только одни неравенства 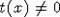 .
Таким образом, мы приходим к случаю 1 с заменой X на его дополнение.
.
Таким образом, мы приходим к случаю 1 с заменой X на его дополнение.
Лемма
5. Если функция 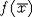 вычислима
в системе
вычислима
в системе 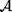 , то для любых
, то для любых
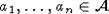
 принадлежит подсистеме системы
принадлежит подсистеме системы 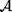 , порожденной элементами
, порожденной элементами 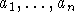 .
.
Доказательство.
См. в [1].
Теорема
6. Пусть 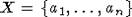 ,
, 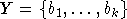 рекурсивные множества. Тогда
рекурсивные множества. Тогда
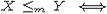 каждое поле
каждое поле 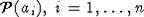 содержит одно из полей
содержит одно из полей 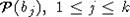 .
.
Доказательство.
Пусть 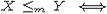 . Тогда найдется
вычислимая функция f(x), что
. Тогда найдется
вычислимая функция f(x), что 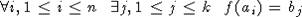 . По лемме 5, f(ai), есть значение некоторого
терма сигнатуры
. По лемме 5, f(ai), есть значение некоторого
терма сигнатуры 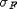 т.е.
рациональной функции с коэффициентами из поля
т.е.
рациональной функции с коэффициентами из поля 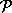 . Значит,
. Значит, 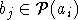 , т.е.
, т.е. 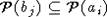 .
.
Обратно,
пусть 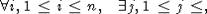 ,
, 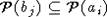 , т.е. ti(ai) = bi для некоторого
набора рациональных функций
, т.е. ti(ai) = bi для некоторого
набора рациональных функций 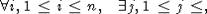 . Тогда
. Тогда 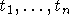 посредством вычислимой функции
посредством вычислимой функции
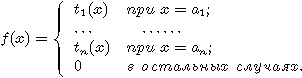
Непосредственно
из определения следует, что 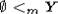 для любого конечного Y.
для любого конечного Y.
Следствие
7. Справедливы следующие утверждения:
1)
если X конечное рекурсивное множество и 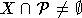 , то любое конечное рекурсивное Y сводится к X;
, то любое конечное рекурсивное Y сводится к X;
2)
для рекурсивного X имеем: 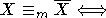 и
и 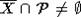 ;
;
3)
среди рекурсивных m-степеней существует наибольшая, это степень множества X из
п.2.
Доказательство.
1. Следует из теоремы.
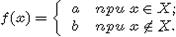
3.
Пусть X конечное рекурсивное множество и 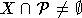 . Пусть Y произвольное рекурсивное. Если Y
конечно, то
. Пусть Y произвольное рекурсивное. Если Y
конечно, то 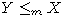 по п.1. Если
Y коконечно, то
по п.1. Если
Y коконечно, то 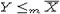 по лемме
3, но
по лемме
3, но 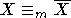 . Таким образом,
упорядочение рекурсивных m-степеней в поле
. Таким образом,
упорядочение рекурсивных m-степеней в поле 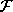 имеет вид:
имеет вид:
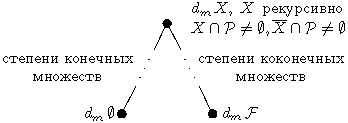
Если
в поле 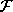 достаточно много
алгебраических элементов, например, если
достаточно много
алгебраических элементов, например, если 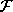 алгебраически замкнуто, то существует
бесконечное число рекурсивных m-степеней.
алгебраически замкнуто, то существует
бесконечное число рекурсивных m-степеней.
Следствие
8. Пусть поле 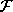 алгебраически
замкнутое характеристики 0, a рекурсивная m-степень,
алгебраически
замкнутое характеристики 0, a рекурсивная m-степень, 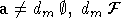 и не является наибольшей среди рекурсивных.
Тогда:
и не является наибольшей среди рекурсивных.
Тогда:
1)
существует счетное число рекурсивных степеней, несравнимых с a;
2)
существует счетное число попарно несравнимых степеней 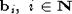 , таких, что
, таких, что 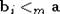 ;
;
3)
существует счетное число попарно несравнимых степеней 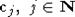 , таких, что
, таких, что 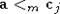 ;
;
4)
порядок на рекурсивных m-степенях плотный.
Доказательство.
Пункты 1) - 3) следуют из теоремы 6 и свойств алгебраических расширений полей.
Для доказательства 4) рассмотрим рекурсивные множества 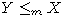 . Можно считать, что
. Можно считать, что 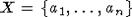 и
и 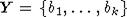 , причем X и Y не содержат элементов из
, причем X и Y не содержат элементов из 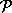 . Тогда
. Тогда 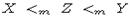 , где
, где 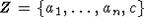 ,
, 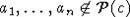 , но
, но  .
.
Список литературы
Ашаев
И.В., Беляев В.Я., Мясников А.Г. Подходы к теории обобщенной вычислимости //
Алгебра и логика. 32. N 4 (1993). С. 349-386.
Кфури
А. Дж., Столбоушкин А.П., Ужичин П. Некоторые открытые вопросы в теории схем
программ и динамических логик // УМН. 1989. Т.44. Вып.1 (265). С. 35-55.
Гончаров
С.С., Свириденко Д.И. 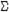 -программирование//
Логико-математические проблемы МОЗ (Вычислительные системы. Вып. 107).
Новосибирск, 1985. С. 3-29.
-программирование//
Логико-математические проблемы МОЗ (Вычислительные системы. Вып. 107).
Новосибирск, 1985. С. 3-29.
Роджерс
Х. Теория рекурсивных функций и эффективная вычислимость. М: Мир, 1972.
Blum L., Shub M., Smale S. On a theory of computation and complexity
over the real numbers: NP-completeness, recursive functions and universal
machines //Bull. Amer. Math. Soc. 1989. V.21. N1. P.1-46.
Friedman H. Algorithmic procedures, generalized Turing algorithms,
and elementary recursion theory //Logic Colloquium'69 (R.O. Gandy and C.E.M.
Yates, eds). North Holland,
1971. Р. 361-390.
Для
подготовки данной работы были использованы материалы с сайта http://www.omsu.omskreg.ru/