Проекция инвариантной меры с орбиты коприсоединенного представления на подалгебру Картана

Проекция инвариантной меры с орбиты коприсоединенного представления на подалгебру Картана

Проекция инвариантной меры с орбиты коприсоединенного представления на подалгебру Картана

С.В. Никитин, Омский государственный университет, кафедра математического анализа

1. Введение

В 1973 г. Костант в своей работе [1] показал, что если G компактная группа и 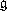ее алгебра Ли, то для элемента X из подалгебры Картана алгебры 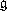выполнено равенство

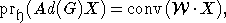
где - ортогональная проекция (относительно формы Киллинга); 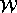- группа Вейля алгебры 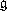, 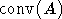означает выпуклую оболочку множества A.

Теорема Костанта о выпуклости является обобщением более ранних результатов Шура и Хорна. В 1923 г. Шур доказал, что диагональ 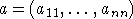эрмитовой матрицы A=(aij) порядка n с собственными числами 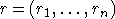содержится в выпуклой оболочке множества 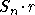, где Sn - симметрическая группа, действующая на 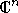перестановками координат. Затем Хорн показал, что каждая точка этой выпуклой оболочки может быть получена таким способом.

Таким образом, проекция орбиты 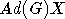- это выпуклый многогранник с вершинами в точках 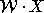. В 1982 г. Guillemin и Stenberg [2], а также Atiyah [3] дали интерпретацию теоремы Костанта как теоремы о выпуклости отображения моментов. Следующий естественный шаг - нахождение проекции инвариантной меры с орбиты на подалгебру Картана. Существует формула Duistermaat-Heckman'а [4, 5] для преобразования Лапласа проекции инвариантной меры, по которой она может быть восстановлена, но представляет интерес и прямая геометрическая конструкция для нахождения проекции инвариантной меры, которая предложена в этой статье.

2. Предварительные сведения

Пусть 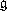- конечномерная вещественная простая компактная алгебра Ли, - ее подалгебра Картана. Группа Ли G алгебры 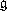действует на 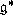с помощью коприсоединенного представления 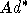: 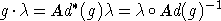, где 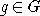, 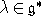. Определим орбиту элемента :

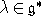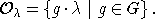
На каждой орбите 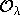существует единственная с точностью до пропорциональности инвариантная мера 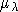, т.е. такая, что для любой непрерывной функции 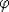и для любого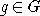

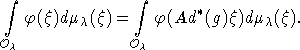
Пусть 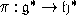ортогональная проекция. Определим проекцию меры 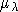на 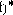- это мера 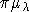, задаваемая соотношением:

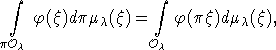
где 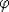- финитная непрерывная функция на 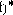. Мера 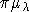абсолютно непрерывна и 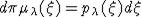, где 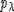- плотность проекции меры 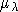. Нахождению плотности 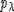и посвящена эта статья.

Введем некоторые обозначения: 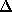- система корней алгебры , 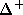- множество положительных корней, 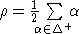- их полусумма. Пусть 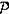- решетка весов алгебры , кроме того, пусть 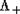обозначает множество 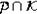, где 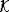- камера Вейля. 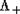представляет собой множество всех старших весов . Каждому неприводимому представлению группы G соответствует единственный старший вес 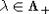. Если 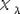- характер этого представления, то формула Кириллова утверждает, что

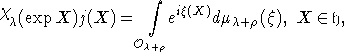
где

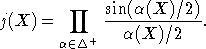
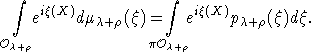
Таким образом, формулу Кириллова можно переписать в следующем виде:

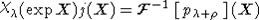
или

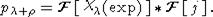
Пусть 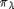неприводимое представление . Обозначим множество весов 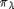как 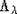. Если 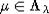, то 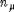обозначает кратность веса 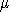в представлении 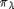. Известно, что

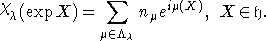
Поэтому, применяя преобразование Фурье к обеим частям равенства, получаем:

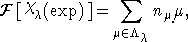
где 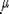- дельта-функция в точке 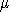. Найдя функцию 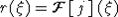, мы получим выражение для функции :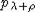

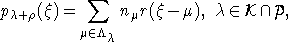
или

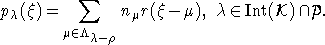
Точное выражение для функции 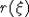в дальнейшем не требуется, нам достаточно знать, что это положительная, финитная, кусочно-непрерывная функция.

3. Функция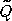

В этом разделе мы определим функцию 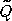, через которую выражается функция 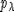, а также укажем некоторые ее свойства.

В дальнейшем мы будем использовать следующие обозначения: d - ранг алгебры, т.е. размерность подалгебры Картана , s - число положительных корней, r - разность s-d, которая строго больше нуля для всех алгебр Ли (кроме алгебры A1). Для того чтобы определить 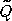, мы рассмотрим систему положительных корней 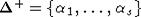как проекцию набора из s попарно ортогональных векторов. Остановимся на этом более подробно.

Пусть 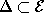, где 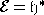- векторное пространство, порожденное 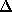, т.е. линейная оболочка множества 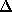, 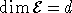. Рассмотрим некоторое векторное пространство L, в которое 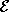вложено как подпространство векторов, имеющих ненулевыми первые d координат. Имеется естественная ортогональная проекция 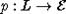. Нетрудно проверить, что если выбрать подходящую (достаточно большую) размерность пространства L, то в L можно найти набор из s векторов 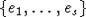таких, что (ei,ej)=0, если 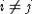и, кроме того, 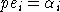. Пространство V - линейная оболочка векторов , которые образуют в нем ортогональный базис. Введем следующее обозначение:

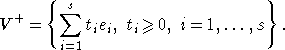
V+ - это конус в пространстве V, порожденный векторами 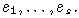. Определим на 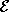функцию 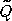следующим образом:

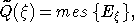
где mes - мера Лебега на .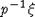

Замечание.    В случае алгебры Ли A1 множество 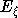0-мерно. В этом случае можно считать, что функция 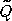имеет следующий вид:

Функция 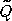определена всюду в 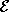, непрерывна, кусочно-полиномиальна и определяется алгеброй с точностью до пропорциональности, т.е. при выборе другого базиса 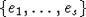функция 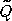лишь умножается на константу.

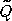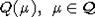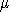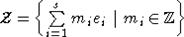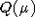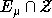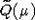Можно рассматривать функцию как непрерывное продолжение дискретной функции Костанта. Функция Костанта , где - решетка корней алгебры; - это число способов представить в виде суммы положительных корней, Q(0)=1. Пусть - решетка в V. Тогда равно числу элементов в множестве , а - это мера или объем 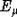. Для примера функция Костанта 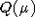и функция 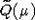для алгебры Ли A2 связаны следующим образ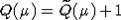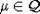ом: , . Формула Костанта для кратностей весов в неприводимом представлении со старшим весом такова:

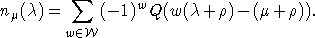
4. Основной результат

Теорема.    Пусть 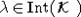. Тогда проекция инвариантной меры с орбиты коприсоединенного представления, проходящей через точку , имеет плотность :

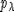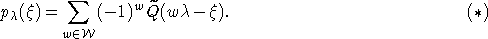
Кроме того, функция 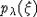является непрерывной, кусочно-полиномиальной, инвариантной относительно действия группы Вейля 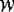функцией, носитель которой содержится в множестве .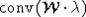

НАБРОСОК ДОКАЗАТЕЛЬСТВА. Докажем равенство (*) для 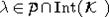. Сечение 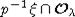орбиты 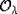, проходящее через точку 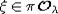, имеет размерность r, поэтому 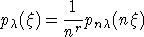. Таким образом, мы получаем:

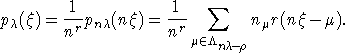
Для вычисления 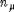используется формула Костанта для кратностей весов. Если 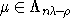, то

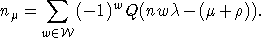
Затем обе части равенства умножаются на непрерывную финитную функцию 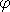, интегрируются по 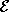и, наконец, n устремляется к бесконечности (при этом сумма в правой части рассматривается как интегральная сумма). После некоторых преобразований получается следующее равенство:

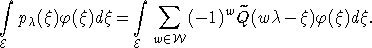
Так как это верно для любой непрерывной функции 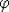, то получаем (*) для всех 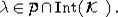После этого, используя однородность функции 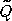, (*), доказывается для всех 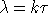, , 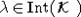где 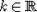, , 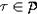а затем, используя предельный переход, и для всех 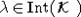. Непрерывность и кусочно-полиномиальность следуют из соответствующих свойств функции .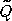

Докажем инвариантность относительно действия группы Вейля, т.е. равенство 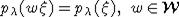. Так как для функции j(X) выполнено равенство j(wX)=j(X), то верно и 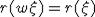. Далее, если 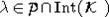, то

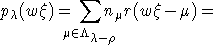
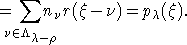
Затем равенство 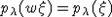доказывается для всех 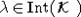. Из равенства (*) легко получить, что . Так как функция 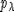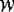-инвариантна, то .

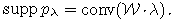Список литературы

Kostant B. On convexity, the Weyl group and the Iwasawa decomposition // Ann. Sci. Ecole Norm. Sup. 1973. N.6. С.413-455.

Guillemin V., Stenberg S. Convexity properties of the moment mapping // Invent. Math. 1982. N.67. С.491-513.

Atiyah M. Convexity and commuting hamiltonians // Bull. London Math. Soc. 1982. N.14. С.1-15.

Duistermaat J. J., and Heckman G. J. On the variation in the cohomology in the symplectic form of the reduced phase space // Invent. Math. 1982. N.69. С.259-268.

Neeb K.-H. A Duistermaat-Heckman formula for admissible coadjoint orbits, preprint.

Для подготовки данной работы были использованы материалы с сайта http://www.omsu.omskreg.ru/