Спектр спиновых волн в антиферромагнетиках с неколлинеарными магнитными подрешетками
Спектр спиновых волн в антиферромагнетиках с
неколлинеарными магнитными подрешетками
Кызыргулов И.Р.
Как
известно, кристалл 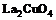 приближенно
имеет коллинеарную антиферромагнитную структуру [1, 2]. Ряд экспериментальных
работ указывает на наличие слабого ферромагнитного момента в плоскостях
приближенно
имеет коллинеарную антиферромагнитную структуру [1, 2]. Ряд экспериментальных
работ указывает на наличие слабого ферромагнитного момента в плоскостях 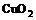 , направленного
перпендикулярно плоскости и имеющего противоположные направления в соседних
плоскостях [3, 4]. Ферромагнитный момент возникает при выходе магнитных
моментов ионов
, направленного
перпендикулярно плоскости и имеющего противоположные направления в соседних
плоскостях [3, 4]. Ферромагнитный момент возникает при выходе магнитных
моментов ионов 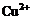 из
базисной (001) плоскости при повороте их на небольшой угол вследствие поворота
октаэдров
из
базисной (001) плоскости при повороте их на небольшой угол вследствие поворота
октаэдров  в ортофазе.
Другими словами, магнитные моменты подворачиваются в плоскости (010) на малый
угол [5]. Но поскольку в соседних плоскостях октаэдры развернуты в противофазе,
это приводит к противоположной направленности ферромагнитных моментов в
соседних плоскостях, что означает, антиферромагнитную модуляцию вдоль оси [001].
Из исследований инфракрасных спектров, неупругого рассеяния нейтронов и
двухмагнонного рассеяния света определена величина угла скоса, которая
оказалось равной
в ортофазе.
Другими словами, магнитные моменты подворачиваются в плоскости (010) на малый
угол [5]. Но поскольку в соседних плоскостях октаэдры развернуты в противофазе,
это приводит к противоположной направленности ферромагнитных моментов в
соседних плоскостях, что означает, антиферромагнитную модуляцию вдоль оси [001].
Из исследований инфракрасных спектров, неупругого рассеяния нейтронов и
двухмагнонного рассеяния света определена величина угла скоса, которая
оказалось равной 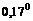 [4,
6].
[4,
6].
Исследуем
влияние неколлинеарности магнитных подрешеток на спектры спиновых волн в
кристалле 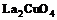 как поправку
к спектру, найденному в работе [7].
как поправку
к спектру, найденному в работе [7].
Будем
исходить из гамильтониана, в котором учитывается энергия магнитной системы:
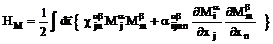 , (1)
, (1)
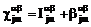 ,
,
где
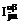 - тензор однородного
обменного взаимодействия,
- тензор однородного
обменного взаимодействия, 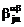 -
тензор анизотропии,
-
тензор анизотропии, 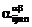 -
тензор неоднородного обменного взаимодействия,
-
тензор неоднородного обменного взаимодействия, 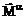 - намагниченности подрешеток,
- намагниченности подрешеток, 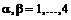 ,
, 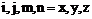 . Тензор
. Тензор 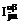 выберем в виде
выберем в виде
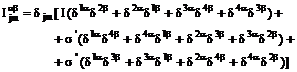 ,
,
где
I - постоянная внутриплоскостного взаимодействия (в CuO2 - плоскости), 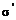 ,
, 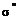 - постоянные межплоскостного взаимодействия.
- постоянные межплоскостного взаимодействия.
Далее
ввиду эквивалентности подкластеров можно ввести следующую систему обозначений:
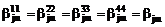 ,
,
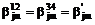 ,
, 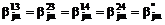 ,
,
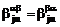 .
.
Аналогичных
обозначений будем придерживаться и для компонент тензоров 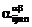 c учетом соотношения из
орторомбичности кристаллической структуры
c учетом соотношения из
орторомбичности кристаллической структуры
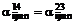 ,
, 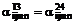 ,
, 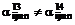 .
.
Эксперименты
по неупругому нейтронному рассеянию дают значение для постоянной
внутриплоскостного обменного взаимодействия 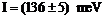 [8] и верхнюю оценку для постоянных
межплоскостного обменного взаимодействия
[8] и верхнюю оценку для постоянных
межплоскостного обменного взаимодействия 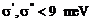 . Приведенные экспериментальные данные позволяют
считать в нашем приближении
. Приведенные экспериментальные данные позволяют
считать в нашем приближении 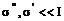 .
.
Запишем
гамильтониан (1) в представлении приближенного вторичного квантования.
Намагниченности подрешеток 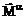 можно выразить через операторы
Гольштейна-Примакова:
можно выразить через операторы
Гольштейна-Примакова:
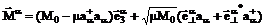 , (2)
, (2)
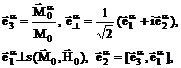 (2.1)
(2.1)
где
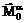 - равновесная намагниченность
- равновесная намагниченность
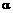 - той подрешетки,
- той подрешетки, 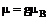 , g - фактор Ланде,
, g - фактор Ланде, 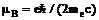 - магнетон Бора.
- магнетон Бора.
Подставляя
(2) в (1) и переходя к фурье-представлению операторов
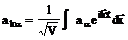 ,
,
получим:
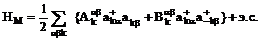 , (3)
, (3)
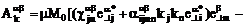
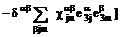 ,
(3.1)
,
(3.1)
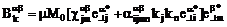 . (3.2)
. (3.2)
Перейдем
к исследованию конкретного случая. Введем сферические координаты базисных
векторов (2.1). Учитывая малую величину угла откоса, напишем:
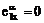 ,
, 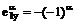 ,
, 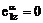 ,
,
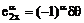 ,
, 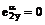 ,
,
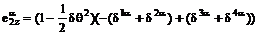 ,
,
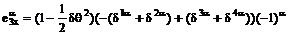 ,
,
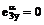 ,
, 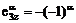 . (4)
. (4)
Тогда
в соответствии с системой инвариантов группы 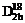 коэффициенты
коэффициенты 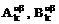 (3.1-3.2) будут иметь вид:
(3.1-3.2) будут иметь вид:
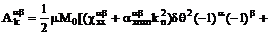
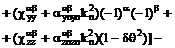
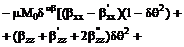
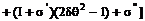 , (5.1)
, (5.1)
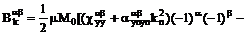
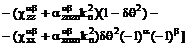 (5.2)
(5.2)
Отсюда,
используя выбор ортов (4) и учитывая направления равновесных намагниченностей,
получим:
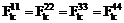 ,
, 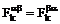 ,
,
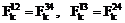 ,
, 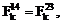 (6)
(6)
где
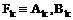 .
.
Выпишем
компоненты 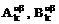 в явном виде
ввиду их важности для дальнейшего.
в явном виде
ввиду их важности для дальнейшего.
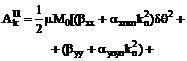
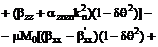
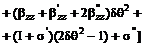 ,
,
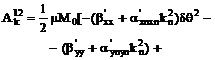
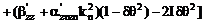 ,
,
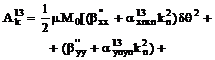
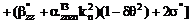 ,
,
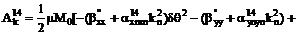
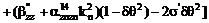 , (7)
, (7)
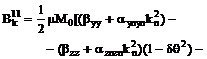
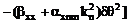 ,
,
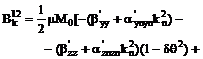
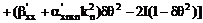 ,
,
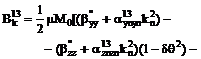
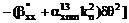 ,
,
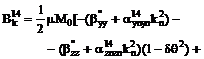
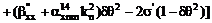 . (8)
. (8)
Для
упрощения диагонализации гамильтониана (3) введем вместо операторов 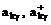 операторы
операторы 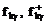 согласно следующим формулам:
согласно следующим формулам:
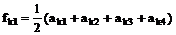 ,
,
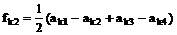 ,
,
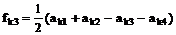 ,
,
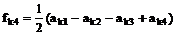 . (9)
. (9)
Тогда
с учетом (6) гамильтониан (3) в новых операторах 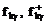 имеет вид:
имеет вид:
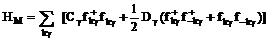 , (10)
, (10)
где
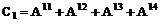 ,
,
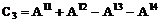 ,
,
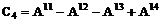 (11)
(11)
и
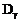 аналогично выражаются
через компоненты матрицы В.
аналогично выражаются
через компоненты матрицы В.
Разделим
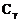 и
и 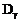 на слагаемые, не содержащие величину
на слагаемые, не содержащие величину 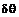 , и слагаемые, содержащие
, и слагаемые, содержащие 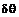 :
:
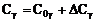 ,
, 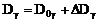 .
.
В
гамильтониане (10) с помощью канонического u-v-преобразования Боголюбова
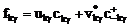 , (12)
, (12)
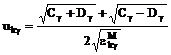 ,
,
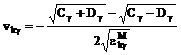 ,
,
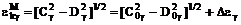
перейдем
к магнонным операторам 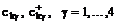 .
Диагонализованный гамильтониан имеет стандартный вид:
.
Диагонализованный гамильтониан имеет стандартный вид:
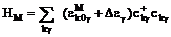 , (13)
, (13)
где
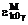 - энергия спиновых волн
коллинеарного антиферромагнетика,
- энергия спиновых волн
коллинеарного антиферромагнетика, 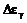 - поправка к энергии, связанная с
неколлинеарностью подрешеток.
- поправка к энергии, связанная с
неколлинеарностью подрешеток.
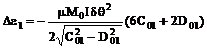 ,
,
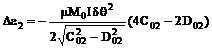 ,
,
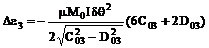 ,
,
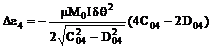 .
.
Если
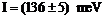 ,
, 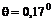 , то поправки к спектрам спиновых
волн, определяемые неколлинеарностью магнитных подрешеток, будут иметь порядок:
, то поправки к спектрам спиновых
волн, определяемые неколлинеарностью магнитных подрешеток, будут иметь порядок:
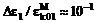 ,
, 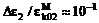 ,
,
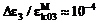 ,
, 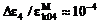 .
.
Линейная
зависимость поправки 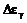 от
обменного параметра I и квадратичная зависимость от угла откоса
от
обменного параметра I и квадратичная зависимость от угла откоса 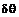 может привести в некоторых случаях к
немалым изменениям спектра спиновой волны.
может привести в некоторых случаях к
немалым изменениям спектра спиновой волны.
Выражаю
благодарность научному руководителю М.Х.Харрасову за предоставленную задачу и
постоянную помощь.
Список литературы
Vaknin
D., Sinha S.K., Moncton D.E. et al. // Phys. Rev. Lett. 1987.
V. 58. P. 2802-2805.
Shirare C., Endoh Y., Birgineau R.J. et al. // Phys. Rev. Lett.
1987. V. 59. P. 1613-1616.
Kastner M.A., Birgeneau R.J., Thurston T.R. et al. // Phys. Rev. B.
1988. V. 38. P. 6636-6640.
Thio T., Thurston T.R., Preyer N.W. et al. // Phys. Rev. B. 1988. V.
38. P. 905-908.
Endoh Y., Yamada K., Birgeneau R.J. et al. // Phys. Rev. B.
1983. V. 37. P. 7443-7453.
Боровик-Романов
А.С., Буздин А.И., Крейнес Н.М., Кротов С.С. // Письма в ЖЭТФ. 1988. Т. 47. С.
600-603.
Абдуллин
А.У., Савченко М.А., Харрасов М.Х. // ДАН. 1995. Т. 342.
¹ 6. С. 753-756.
Hayden S.M., Aeppli G., Osborn R. et al. // Phys. Rev. Lett.
1991. V. 67. P. 3622-3625.
Для
подготовки данной работы были использованы материалы с сайта http://www.bashedu.ru