Хроногеометрия несвязных гранично однородных порядков в аффинном пространстве
Хроногеометрия несвязных гранично однородных порядков
в аффинном пространстве
Н.Л. Шаламова, Омский государственный университет,
кафедра математическогомоделирования,
644077
Омск, пр. Мира,55-A
Изучение
упорядоченных аффинных пространств An, n>2, связано, как известно, прежде
всего с основаниями теории относительности [1]. Следуя же квантовой теории, мы
не можем распространять причинно-следственные связи на явления микромира и
поэтому вынуждены рассматривать так называемые "несвязные порядки".
Предполагая при этом, что скорость передачи взаимодействия и в микромире
ограничена, автор получает результаты, изложенные в данной статье.
Рассмотрим
в n-мерном аффинном пространстве An, n>2, несвязный порядок 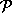 , заданный семейством
, заданный семейством 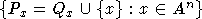 подмножеств An, для которого выполнены
условия: (1)
подмножеств An, для которого выполнены
условия: (1) 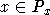 ; (2) если
; (2) если 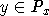 , то
, то 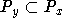 ; (3) если
; (3) если 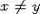 , то
, то 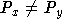 . Несвязность порядка
. Несвязность порядка 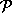 означает, что
означает, что 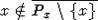 . Предполагаем далее, что верно следующее: (i)
. Предполагаем далее, что верно следующее: (i) 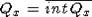 ; (ii)
; (ii) 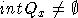 для любой
для любой 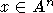 .
.
Замечание
1. Для любого множества A, будем через 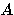 , int A, и
, int A, и 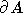 обозначать соответственно замыкание,
внутренность и границу множества A.
обозначать соответственно замыкание,
внутренность и границу множества A.
Назовем
внешним конусом множества Px следующее множество:
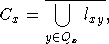
где
lxy - луч, идущий из точки x и проходящий через точку 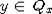 . Считаем далее, что Cx - конус "с острой
вершиной", то есть не содержит прямой. Известным является факт [1], что
семейство
. Считаем далее, что Cx - конус "с острой
вершиной", то есть не содержит прямой. Известным является факт [1], что
семейство 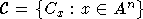 внешних
конусов задает порядок в An.
внешних
конусов задает порядок в An.
Гомеоморфизм
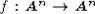 , для которого
f(Px)=Pf(x) для любой точки
, для которого
f(Px)=Pf(x) для любой точки 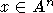 , назовем порядковым
, назовем порядковым 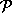 -автоморфизмом. Множество всех порядковых
-автоморфизмом. Множество всех порядковых 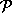 -автоморфизмов будет группой,
которую обычно обозначают
-автоморфизмов будет группой,
которую обычно обозначают 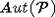 .
Подгруппа группы
.
Подгруппа группы 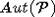 ,
сохраняющая фиксированную точку
,
сохраняющая фиксированную точку 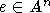 , обозначается
, обозначается 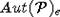 .
.
Порядок
 называется
называется  - однородным или гранично
однородным, если для любых
- однородным или гранично
однородным, если для любых 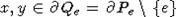 найдется
найдется 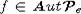 такой, что f(x)=y.
такой, что f(x)=y.
Имеет
место следующая
Теорема.
Пусть 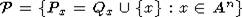 , n>2,
инвариантной относительно группы параллельных переносов несвязный порядок в
n-мерном аффинном пространстве An, для которого выполнены условия:
, n>2,
инвариантной относительно группы параллельных переносов несвязный порядок в
n-мерном аффинном пространстве An, для которого выполнены условия:
(1)
существует семейство 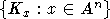 равных
и параллельных телесных одинарных замкнутых выпуклых конусов с острой вершиной
такое, что
равных
и параллельных телесных одинарных замкнутых выпуклых конусов с острой вершиной
такое, что 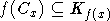 для любых
для любых 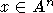 и
и 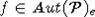 ;
;
(2)
порядок 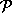 - гранично
однородный.
- гранично
однородный.
Тогда
любой порядковый 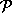 -автоморфизм
будет аффинным преобразованием.
-автоморфизм
будет аффинным преобразованием.
Доказательство
.
Для
любой точки 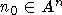 рассмотрим
следующее множество
рассмотрим
следующее множество
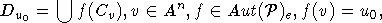
где
объединение берется по всем 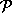 -автоморфизмам f из стабилизатора
-автоморфизмам f из стабилизатора 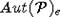 таких, что f(v) = uo .
таких, что f(v) = uo .
По
условию (1) 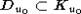 и, кроме
того, если
и, кроме
того, если 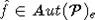 , то
, то
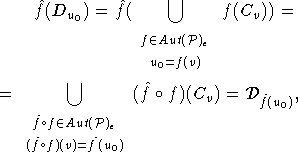
то
есть семейство 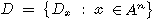 сохраняется
сохраняется
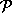 -автоморфизмами из
-автоморфизмами из 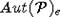 .
.
Замечание
2. Не следует думать, что в определении множества 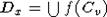 ,
, 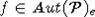 , f(v) = x точка v- фиксированная. Точка
, f(v) = x точка v- фиксированная. Точка 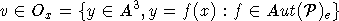 , то есть v- точка из орбиты
точки x, для которой определяется множество Dx.
, то есть v- точка из орбиты
точки x, для которой определяется множество Dx.
Рассмотрим
далее множества
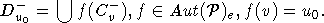
Легко
видеть, что 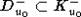 (здесь C-v,
K-v- это конусы, центрально симметричные конусам Cv и Kv относительно точки v).
В самом деле, для любой точки
(здесь C-v,
K-v- это конусы, центрально симметричные конусам Cv и Kv относительно точки v).
В самом деле, для любой точки 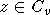 ,
,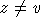 имеем
имеем 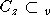 (семейство
(семейство 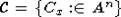 задает порядок в An). Поэтому для
задает порядок в An). Поэтому для 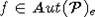 , f(v) = u0 имеем
, f(v) = u0 имеем 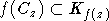 и
и 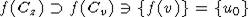 . Если же
. Если же 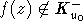 то
то 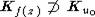 и
и 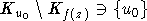 . Это противоречит тому, что
. Это противоречит тому, что 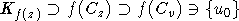 . Значит
. Значит 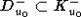 для любой точки
для любой точки 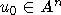 .
.
Отметим
теперь следующее: каждое множество Dx содержит Cx, а каждое множество D-x-
содержит конус C-x. Далее, поскольку Kx, K-x- выпуклые конусы с острой
вершиной, то существует гиперплоскость Tx такая, что 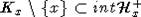 ,
, 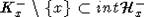 , где
, где 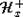 ,
, 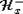 - полупространства, на которые Tx разбивает An.
Утверждается, что в качестве Tx можно выбрать такую гиперплоскость, которая
пересекает конус Cy,
- полупространства, на которые Tx разбивает An.
Утверждается, что в качестве Tx можно выбрать такую гиперплоскость, которая
пересекает конус Cy, 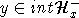 по
компактному множеству. Известно, что по отношению к замкнутому однородному
выпуклому телесному конусу Ce с острой вершиной все гиперплоскости, имеющие с
по
компактному множеству. Известно, что по отношению к замкнутому однородному
выпуклому телесному конусу Ce с острой вершиной все гиперплоскости, имеющие с 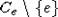 непустое пересечение, можно
разделить на три непересекающихся класса. К первому классу A1 отнесем все
гиперплоскости, пересекающие
непустое пересечение, можно
разделить на три непересекающихся класса. К первому классу A1 отнесем все
гиперплоскости, пересекающие 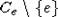 по компактному множеству. Во второй класс A2
попадут гиперплоскости, имеющие с
по компактному множеству. Во второй класс A2
попадут гиперплоскости, имеющие с 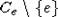 некомпактное пересечение и параллельные при этом
какой-либо прямолинейной образующей конуса Ce, принадлежащей его границе
некомпактное пересечение и параллельные при этом
какой-либо прямолинейной образующей конуса Ce, принадлежащей его границе 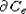 . Все остальные
гиперплоскости будут принадлежать к третьему классу A3. Нетрудно видеть, что
вышеупомянутая гиперплоскость Tx не может быть параллельна какой-либо
гиперплоскости из класса A3. Это следует из того, что
. Все остальные
гиперплоскости будут принадлежать к третьему классу A3. Нетрудно видеть, что
вышеупомянутая гиперплоскость Tx не может быть параллельна какой-либо
гиперплоскости из класса A3. Это следует из того, что 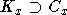 , а
, а 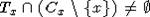 и также
и также 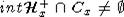 ,
, 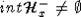 , что противоречит выбору Tx.
, что противоречит выбору Tx.
Если
же Tx параллельна гиперплоскости из класса A2, то 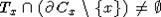 и
и 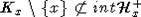 , что также противоречит выбору Tx. Значит Tx
параллельна некоторой гиперплоскости из класса A1. Итак, пусть
, что также противоречит выбору Tx. Значит Tx
параллельна некоторой гиперплоскости из класса A1. Итак, пусть 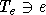 - эта та самая гиперплоскость, о
которой идет речь выше, то есть Te параллельна гиперплоскости Tv из класса A1 и
разбивает An на два полупространства
- эта та самая гиперплоскость, о
которой идет речь выше, то есть Te параллельна гиперплоскости Tv из класса A1 и
разбивает An на два полупространства 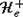 и
и 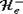 такие, что
такие, что 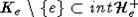 ,
, 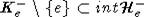 . Очевидно, что в этом случае найдется
гиперплоскость Ty0, параллельная Te, такая, что
. Очевидно, что в этом случае найдется
гиперплоскость Ty0, параллельная Te, такая, что 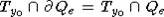 и множество
и множество 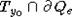 - компактно. Если теперь точка
- компактно. Если теперь точка 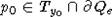 , то
, то 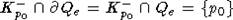 . Поскольку
. Поскольку 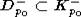 и порядок
и порядок 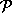 - гранично однородный, то для любой точки
- гранично однородный, то для любой точки 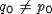 будет верно следующее:
будет верно следующее:
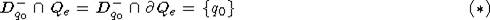
Действительно,
вследствие граничной однородности порядка 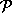 для любых точек
для любых точек 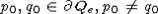 найдется
найдется 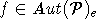 такой, что f(p0) = q0 и, значит, f(D)-p0 =
D-f(p0) = D-q0. Но
такой, что f(p0) = q0 и, значит, f(D)-p0 =
D-f(p0) = D-q0. Но 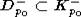 ,
поэтому
,
поэтому 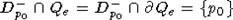 и,
следовательно,
и,
следовательно, 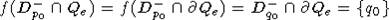 .
.
Покажем
теперь, что наш порядок 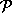 будет
максимально линейчатым, то есть для любой точки
будет
максимально линейчатым, то есть для любой точки 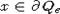 имеем
имеем 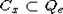 . Предположим, что это не так и найдется точка
. Предположим, что это не так и найдется точка 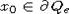 такая, что луч
такая, что луч 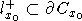 не лежит полностью в Qe, то есть
не лежит полностью в Qe, то есть 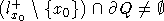 .
.
Если
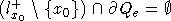 , то есть луч l+x0, за
исключением точки x0 лежит вне Qe, поступим следующим образом: Пусть
, то есть луч l+x0, за
исключением точки x0 лежит вне Qe, поступим следующим образом: Пусть 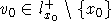 ,
, 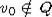 точка, которая вместе с некоторым шаром
точка, которая вместе с некоторым шаром 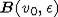 с центром в точке v0
положительного радиуса
с центром в точке v0
положительного радиуса 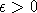 лежит
в
лежит
в 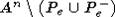 . Точка
. Точка 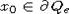 , значит найдется
, значит найдется 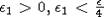 такое, что шар
такое, что шар 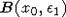 имеет непустое пересечение с
int Q. Выберем точку
имеет непустое пересечение с
int Q. Выберем точку 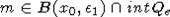 .
Нетрудно видеть, что для прямой lm, проходящей через точку m и параллельной лучу
l+x0 число точек пересечения с
.
Нетрудно видеть, что для прямой lm, проходящей через точку m и параллельной лучу
l+x0 число точек пересечения с 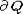 уже наверняка больше двух: первая точка лежит на
отрезке [m1, m), где
уже наверняка больше двух: первая точка лежит на
отрезке [m1, m), где 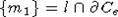 ,
вторая точка лежит на отрезке (m, m2), где
,
вторая точка лежит на отрезке (m, m2), где 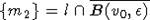 , так как
, так как 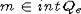 ,
, 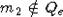 ,
, 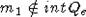 . В этом случае в качестве точки x0 возьмем
любую точку из множества
. В этом случае в качестве точки x0 возьмем
любую точку из множества 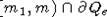 .
.
Пусть
точка 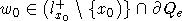 . Тогда по
доказанному выше
. Тогда по
доказанному выше 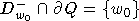 (см. (
(см. ( )), но, поскольку
)), но, поскольку 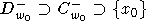 , множество
, множество 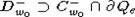 содержат, кроме точки w0 еще и точку
x0, что, очевидно, противоречит (
содержат, кроме точки w0 еще и точку
x0, что, очевидно, противоречит ( ). Значит порядок
). Значит порядок 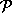 - максимально линейчатый и в соответствии с
результатами Э.Б.Винберга [2] и А.К.Гуца [3] любой порядковый
- максимально линейчатый и в соответствии с
результатами Э.Б.Винберга [2] и А.К.Гуца [3] любой порядковый 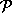 -автоморфизм
-автоморфизм 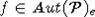 будет аффинным преобразованием.
будет аффинным преобразованием.
Теорема
доказана.
Следствие.
Пусть  , n>2, -
несвязный порядок в An, о котором идет речь в теореме и, кроме того, семейство
, n>2, -
несвязный порядок в An, о котором идет речь в теореме и, кроме того, семейство 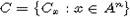 внешних конусов порядка
внешних конусов порядка 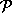 является семейством равных и
параллельных эллиптических конусов.
является семейством равных и
параллельных эллиптических конусов.
Тогда
любой порядковый 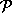 -автоморфизм
-автоморфизм
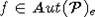 будет преобразованием
Лоренца.
будет преобразованием
Лоренца.
Список литературы
Гуц
А.К. Аксиоматическая теория относительности // Успехи мат. наук. 1982. Т. 37. N
2. C. 39-79.
Винберг
Э.Б. Строение группы автоморфизмов однородного выпуклого конуса // Труды ММО.
1965. Т.13. С.56-83.
Для
подготовки данной работы были использованы материалы с сайта http://www.omsu.omskreg.ru/