|
|
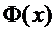
|
|
1,96
|
0,4750
|
Следовательно,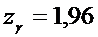 .
.
После определения 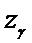 определяем
точность оценки по формуле:
определяем
точность оценки по формуле:
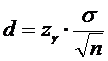 (5)
(5)
и
границы доверительного интервала:
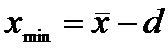 и
и 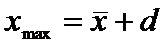 (6)
(6)
Таким образом, с надежностью 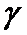 доверительный
интервал
доверительный
интервал 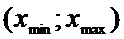 содержит в себе генеральное среднее
(математическое ожидание) а или в
содержит в себе генеральное среднее
(математическое ожидание) а или в 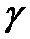 %
случаев построенный интервал накроет истинное значение параметра а.
%
случаев построенный интервал накроет истинное значение параметра а.
Задача. 1. Пусть имеется
генеральная совокупность с некоторой характеристикой, распределенной по
нормальному закону с дисперсией, равной  .
Произведена выборка объема n = 27 и получено выборочное среднее характеристики
.
Произведена выборка объема n = 27 и получено выборочное среднее характеристики
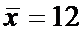 . Найти доверительный интервал,
покрывающий неизвестное математическое ожидание исследуемой характеристики
генеральной совокупности с надежностью
. Найти доверительный интервал,
покрывающий неизвестное математическое ожидание исследуемой характеристики
генеральной совокупности с надежностью 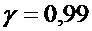 .
.
Дано: n = 27, 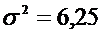 ,
,
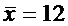 ,
,  .
.
Решение.
1)
По таблице 2 для функции
Лапласа из уравнения
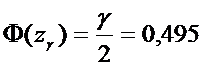
найдем значение 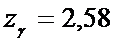 .
.
2) Определим точность оценки d:
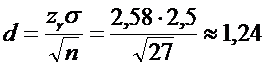 .
.
3)Находим границы доверительного интервала:

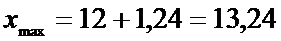
Отсюда
получаем искомый доверительный интервал:
(10,76; 13,24).
Случай
больших выборок. Приведенные выше
расчеты доверительного интервала применяются и в случаях с неизвестной
дисперсии, но только если объем выборок 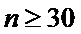 ,
т.е. в случаях больших выборок.
,
т.е. в случаях больших выборок.
В
этом случае в формулах (3) и (4) вместо 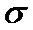 используется
его вычисленная по выборке несмещенная оценка
используется
его вычисленная по выборке несмещенная оценка 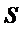 .
.
Для примера (из лекций) о концентрации нитратов в
огурцах найдем доверительный интервал генерального среднего с надежностью 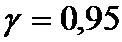 . При этом мы предполагаем нормальное
распределение концентрации нитратов.
. При этом мы предполагаем нормальное
распределение концентрации нитратов.
Имеем 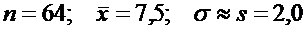 ,
, 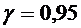 .
.
1)Для 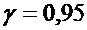
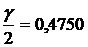 находим по таблице 2
находим по таблице 2 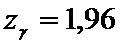 ,
,
2)Тогда 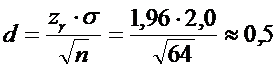 .
.
3) 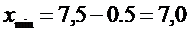 и
и 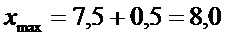 .
.
Отсюда
получаем искомый доверительный интервал: (7,0; 8,0).
Минимальный
объем выборки. Если требуется оценить
математическое ожидание с наперед заданной точностью оценки d
и надежностью 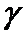 , то из формулы (3) получим
формулу для минимального объема выборки, который обеспечит эту точность:
, то из формулы (3) получим
формулу для минимального объема выборки, который обеспечит эту точность:
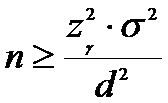 .
.
Задача
2. Морская глубина измеряется
прибором, систематическая ошибка измерения которого равна нулю, а случайная ошибка измерения распределена нормально со
среднеквадратическим отклонением 18м. Сколько надо сделать независимых
измерений, чтобы определить глубину моря с точностью 4 м при надежности 0,996?
Решение. Согласно условию задачи 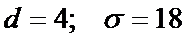 . По
таблице 2 для функции Лапласа из уравнения
. По
таблице 2 для функции Лапласа из уравнения
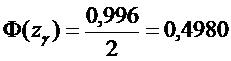
найдем
значение 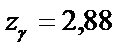 .
.
откуда
. 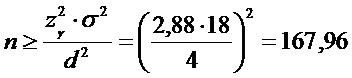
Поскольку
n – число целое, то  .
.
Обычно дисперсия распределения неизвестна и мы можем
только по выборке получить оценки
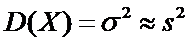 и
и
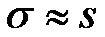 .
.
По данным выборки построим случайную величину
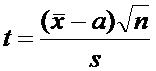 .
.
Условие определения доверительного интервала (2)
перепишем в виде
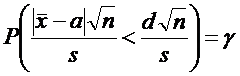
Введем
обозначение: 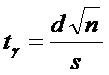 .
.
Тогда
последнее уравнение примет вид
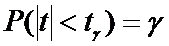 . (7)
. (7)
Значения
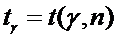 , удовлетворяющие уравнению (7) при
различных значениях
, удовлетворяющие уравнению (7) при
различных значениях 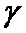 и n,
определяются по таблице 3.
и n,
определяются по таблице 3.
После определения 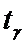 алгоритм
построения доверительного интервала аналогичен случаю известной дисперсии.
алгоритм
построения доверительного интервала аналогичен случаю известной дисперсии.
Случайная величина t имеет t-распределение
Стьюдента, вид которого, сильно зависит от объема выборки 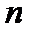 .
.
При 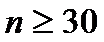 распределение
Стьюдента близко к нормальному распределению и можно пользоваться таблицей 2
для нормального распределения.
распределение
Стьюдента близко к нормальному распределению и можно пользоваться таблицей 2
для нормального распределения.
При 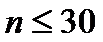 - случай малых
выборок - распределение Стьюдента далеко от нормального. Поэтому в этом
случае использование таблиц распределения Стьюдента необходимо.
- случай малых
выборок - распределение Стьюдента далеко от нормального. Поэтому в этом
случае использование таблиц распределения Стьюдента необходимо.
Алгоритм построения
доверительного интервала:
1)
Значения 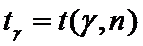 ,
удовлетворяющие уравнению (7) при различных значениях
,
удовлетворяющие уравнению (7) при различных значениях 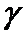 и
n, определяются по таблице 3
и
n, определяются по таблице 3
2)
Точность оценки находим по
формуле:
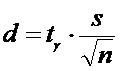 . (8)
. (8)
3)
Находим границы доверительного интервала 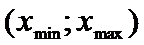 :
:
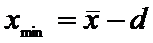
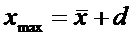 .
.
Пример
1лекции 1 (продолжение).
Дано:
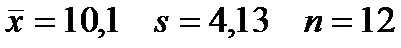 ,
, 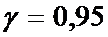
1)По
таблице 3
 .
.
2)Точность
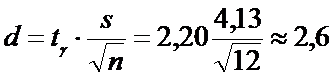
3)
Границы интервала:
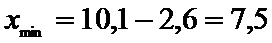
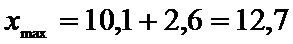 .
.
Получим доверительный интервал (7,5; 12,7).
В практической деятельности по контролю состояния
окружающей среды нередко возникает необходимость сравнить результаты измерений
с какой-либо заданной фиксированной величиной.
Наиболее типичный случай – сравнение с величиной
предельно допустимой концентрации (ПДК) загрязняющего вещества в объектах
окружающей среды.
Пусть фиксированная величина – ПДК, тогда
если 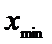 >
ПДК
>
ПДК 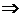 ПДК превышена (с надежностью
ПДК превышена (с надежностью 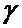 ):
):

если 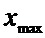 <
ПДК
<
ПДК 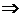 ПДК не превышена (с надежностью
ПДК не превышена (с надежностью 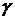 ):
):

если 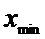 <ПДК <
<ПДК <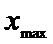
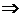 различия
недостоверны (с надежностью
различия
недостоверны (с надежностью 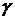 ):
):
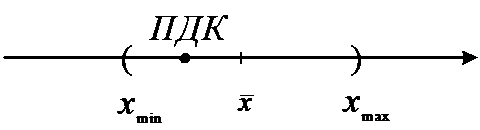 .
.
В 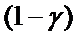 % случаев наши выводы
могут оказаться неверными.
% случаев наши выводы
могут оказаться неверными.
Задача
3. Произведено девять проб почвы с целью определения,
превышает ли концентрация загрязняющего вещества уровень ПДК, равный 4,2 мг/кг.
Получены следующие результаты в мг/кг:
4.7; 5.8; 3.9; 6.1; 5.1; 4.4; 4.6; 4.1; 4.5
Можно ли с надежностью 0.95 утверждать, что ПДК в
среднем превышена?
Решение.
1) Вычисляем выборочное среднее:
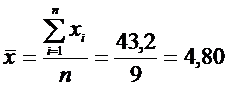
2)
Вычисляем дисперсию:
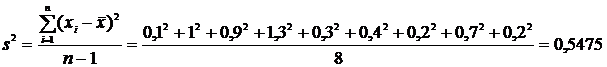
и
выборочное среднее отклонение 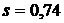 .
.
3)
Так как 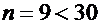 то по таблице 3
то по таблице 3
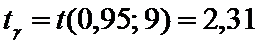 .
.
4) Точность оценки
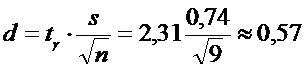 ,
,
5) Границы интервала:
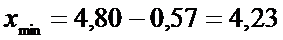
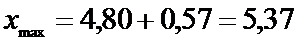 .
.
Получим доверительный интервал
(4,23;5,37) мг/кг.
6)Так как 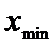 >
ПДК=4,2, то можно утверждать, что ПДК превышена.
>
ПДК=4,2, то можно утверждать, что ПДК превышена.
Ответ: Можно с заданной доверительной
вероятностью.
4. Задача.
4.
Пусть имеется генеральная совокупность с некоторой характеристикой,
распределенной по нормальному закону с дисперсией, равной  . Произведена выборка объема n = 27 и
получено выборочное среднее характеристики
. Произведена выборка объема n = 27 и
получено выборочное среднее характеристики 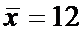 .
Найти доверительный интервал, покрывающий неизвестное математическое ожидание
исследуемой характеристики генеральной совокупности с надежностью
.
Найти доверительный интервал, покрывающий неизвестное математическое ожидание
исследуемой характеристики генеральной совокупности с надежностью 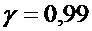 .
.
Дано: n = 27, 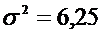 ,
, 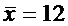 ,
,  .
.
Решение.
2) По таблице 2 для функции Лапласа из
уравнения
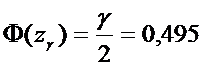
найдем значение 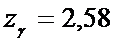 .
.
2) Определим точность
оценки d:
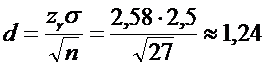 .
.
3)Находим границы
доверительного интервала:

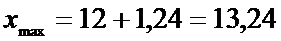
Отсюда получаем искомый доверительный
интервал:
(10,76; 13,24).
Случай больших выборок. Приведенные выше расчеты
доверительного интервала применяются и в случаях с неизвестной дисперсии, но
только если объем выборок 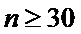 , т.е. в случаях
больших выборок.
, т.е. в случаях
больших выборок.
В этом случае в формулах (3) и (4)
вместо 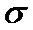 используется его вычисленная по выборке
несмещенная оценка
используется его вычисленная по выборке
несмещенная оценка 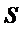 .
.
Для примера (из
лекций) о концентрации нитратов в огурцах найдем доверительный интервал
генерального среднего с надежностью 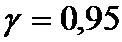 . При этом мы
предполагаем нормальное распределение концентрации нитратов.
. При этом мы
предполагаем нормальное распределение концентрации нитратов.
Имеем 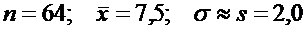 ,
, 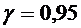 .
.
1)Для 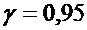
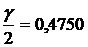 находим
по таблице 2
находим
по таблице 2 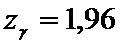 ,
,
2)Тогда 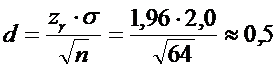 .
.
3) 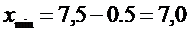 и
и 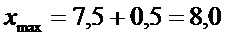 .
.
Отсюда получаем искомый доверительный
интервал: (7,0; 8,0).
Минимальный объем выборки. Если требуется оценить
математическое ожидание с наперед заданной точностью оценки d и надежностью 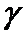 , то из формулы (3) получим формулу для
минимального объема выборки, который обеспечит эту точность:
, то из формулы (3) получим формулу для
минимального объема выборки, который обеспечит эту точность:
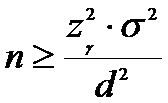 .
.
Задача 5. Морская глубина измеряется
прибором, систематическая ошибка измерения которого равна нулю, а случайная ошибка измерения распределена нормально со
среднеквадратическим отклонением 18м. Сколько надо сделать независимых
измерений, чтобы определить глубину моря с точностью 4 м при надежности 0,996?
Решение. Согласно условию задачи 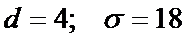 . По таблице 2 для функции Лапласа из
уравнения
. По таблице 2 для функции Лапласа из
уравнения
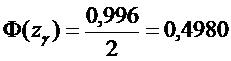
найдем значение 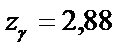 .
.
откуда
. 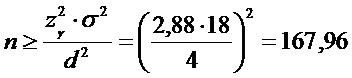
Поскольку n – число целое, то  .
.
Статистической гипотезой называется предположение о виде распределения или о
параметрах известных распределений.
Гипотезы
о значениях параметров распределения или о сравнительной величине параметров
двух распределений называются параметрическими гипотезами.
Гипотезы
о виде распределения называются непараметрическими гипотезами.
Проверить статистическую гипотезу – это значит проверить, согласуются ли данные,
полученные из выборки с этой гипотезой.
Гипотезу, выдвинутую для проверки ее согласия с
выборочными данными, называют нулевой гипотезой и обозначают H0.
Вместе с гипотезой H0 выдвигается альтернативная
или конкурирующая гипотеза, которая противоречит основной и которая
обозначается H1.
ПРИМЕРЫ
Гипотеза 1. При исследовании местности было
произведено несколько проб древесины и вычислено, что среднее число пораженных
деревьев на 1 га равно 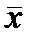 . Через некоторое время
произведено повторное исследование, и среднее число пораженных деревьев стало
. Через некоторое время
произведено повторное исследование, и среднее число пораженных деревьев стало 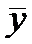 , причем
, причем 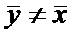 .
.
Встает вопрос, расхождение случайно и связано с
недостаточным числом измерений или закономерно и связано с изменением течения
болезни?
Пусть случайная величина Х
−первоначальное состояние всех деревьев;
случайная
величина Y − состояние через некоторое время.
Тогда
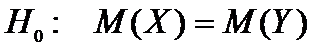
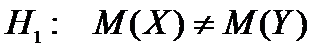 .
.
Гипотеза
2. На акватории в контрольной точке ниже выпуска сточных вод предприятия взяты
пробы воды для определения содержания в воде некоторого загрязняющего вещества.
Полученная средняя концентрация равна 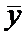 ,
причем
,
причем 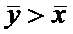 , где
, где 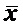 -
фоновая концентрация загрязняющего вещества, полученная до начала работы
предприятия.
-
фоновая концентрация загрязняющего вещества, полученная до начала работы
предприятия.
Если
полученное превышение значимо, то предприятие может быть подвергнуто
экономическим санкциям. Поэтому утверждение о превышении фоновой концентрации
должно быть подвергнуто статистической проверки.
Пусть
Х – фоновая концентрация вещества,
Y – концентрация вещества после начала работы
предприятия.
Задача
проверки гипотез имеет вид:
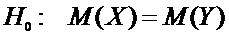
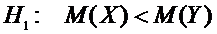 .
.
Принятие гипотезы в результате проверки
не означает утверждения, что гипотеза верна. Это лишь означает, что результаты
наблюдений не дают оснований её отвергнуть.
Если основная гипотеза отвергается, то
принимается альтернативная гипотеза.
Ошибка 1 рода
состоит в том, что будет отвергнута правильная гипотеза.
Ошибка 2 рода
состоит в том, что будет принята неправильная гипотеза.
|
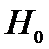
|
принимается
|
отвергается
|
|
верна
|
Решение правильное
|
Ошибка 1 рода
|
|
неверна
|
Ошибка 2 рода
|
Решение правльн
|
Вероятность 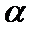 допустить ошибку 1
рода называют уровнем значимости.
допустить ошибку 1
рода называют уровнем значимости.
На практике задача сравнения дисперсий возникает, если
требуется сравнить точность приборов, инструментов, методов измерений,
технологий.
Очевидно, предпочтительнее взять тот прибор,
инструмент и т.п., который обеспечивает наименьшее рассеяние результатов
измерений, т.е. наименьшую дисперсию.
Проведем
измерения на двух приборах.
Пусть все возможные измерения первым прибором − Х
и этим прибором проведено 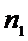 измерений, и по ним
вычислена
измерений, и по ним
вычислена 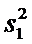 − оценка
− оценка 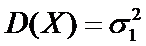 .
.
Пусть все возможные измерения первым прибором − Y
и этим прибором проведено 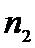 измерений, и по ним
вычислена
измерений, и по ним
вычислена 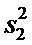 − оценка
− оценка 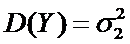 ,
причем
,
причем 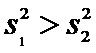 .
.
Требуется по выборочным средним и заданном 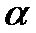 проверить значимость этого различия.
проверить значимость этого различия.
Краткое
условие:
Х: 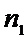
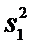 ,
,
Y: 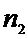
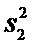 , причем
, причем 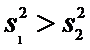 .
.
Сформулируем
гипотезу:
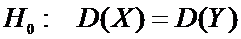

Зададим
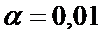 или
или 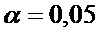 в
зависимости от конкретной задачи.
в
зависимости от конкретной задачи.
Вычислим
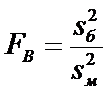 ,
,
где 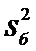 - большая дисперсия,
а
- большая дисперсия,
а 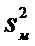 - меньшая дисперсия.
- меньшая дисперсия.
Соответствующая
случайная величина F − статистический критерий данной задачи
− имеет распределение Фишера – Снедекора.
Если
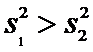 , то выборочное значение критерия
, то выборочное значение критерия
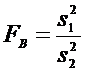 .
.
Критическая
область - правосторонняя.
Для
определения 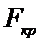 найдем степени свободы:
найдем степени свободы:
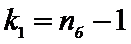 ,
, 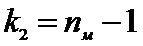
где
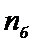 - объем выборки с большей дисперсией
- объем выборки с большей дисперсией 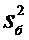
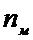 - объем выборки с меньшей дисперсией
- объем выборки с меньшей дисперсией 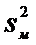 .
.
По
таблице 7 определим
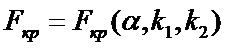 .
.
Сравниваем
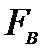 с
с 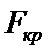 :
:
-
если 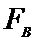
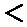
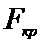 ,
, 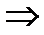 принимаем
принимаем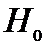 , (различие в оценках дисперсии
незначимо и точности обоих приборов одинаковы);
, (различие в оценках дисперсии
незначимо и точности обоих приборов одинаковы);
-
если 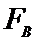
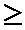
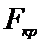 ,
, 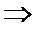 принимаем
принимаем
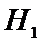 . (отклоняем гипотезу
. (отклоняем гипотезу 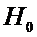 . Второй прибор точнее.)
. Второй прибор точнее.)
Задача
6.
Для проверки точности дозировки двух автоматов по упаковке химического вещества
отобраны от первого автомата 12 проб, от второго – 15 проб. По отобранным
пробам рассчитаны оценки дисперсии: 11,41 и 6,52 соответственно. Можно ли на
основе сделанных измерений и по уровню значимости 0,05 сделать вывод, что
второй прибор точнее.
Краткое
условие:
Х: 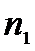 =12
=12 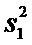 =11,41
=11,41
Y: 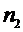 =15
=15 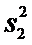 =6,52,
=6,52,
Согласно
условию 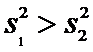 .
.
Решение.
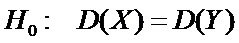
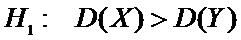 .
.
Так
как 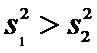 вычисляем
вычисляем
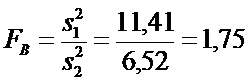 .
.
Для
определения 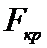 определим
определим
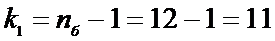
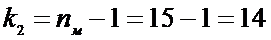 .
.
По
таблице 7
 .
.
Так
как

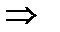 принимаем
принимаем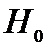 .
.
Это
означает, что точности автоматов по упаковке химического вещества одинаковы.
Схема
решения:
|
Ho
|
H1
|
Статистика критерия
|
Критические точки
|
Условие принятия Ho
|
|
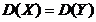
|
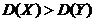
|

|
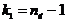
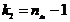
таблица
7
|
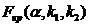
|
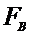 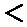 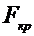
|
|
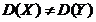
|
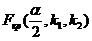
|
7. Проверка
гипотезы о числовом значении среднего нормального распределения
Рассмотрим производство, при котором автоматически
должен соблюдаться некоторый параметр производимых изделий.
Значение параметра для каждого отдельного изделия
может, естественно, как отклоняться от заданного номинала.
Очевидно, что для того, чтобы проверить правильность
настройки станка, надо убедиться в том, что среднее значение параметра у
производимых на нем изделий будет соответствовать номиналу, т.е. проверить
гипотезу
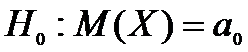 .
.
Здесь Х – нормально распределенная генеральная
совокупность значений этого параметра.
(случай известной дисперсии)
Предположение о том, что дисперсия известна, оправдано
для случай большой выборки. Так же это оправдано, если данным методом ранее уже
было произведено множество измерений и дисперсия определена.
Пусть из совокупности Х с известной
дисперсией 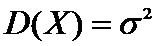 сделана выборка объемом
сделана выборка объемом 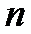 , и по наблюдениям вычислено
, и по наблюдениям вычислено 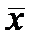 . Пусть
. Пусть 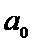 -
предполагаемое значение для М(Х) и
-
предполагаемое значение для М(Х) и 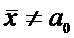 .
Требуется по выборочным средним и заданном уровне значимости проверить
значимость этого различия.
.
Требуется по выборочным средним и заданном уровне значимости проверить
значимость этого различия.
Кратко:
Х: 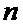
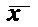
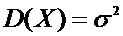 известна.
известна.
Для
поставленной задачи выдвинем гипотезу
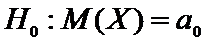 .
.
Альтернативная
гипотеза может иметь вид:
а) 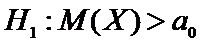 или
или 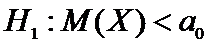 ,
,
б) 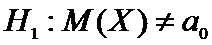 .
.
Случайная величина N имеет
нормальное распределение N(O,1),
По
выборке вычисляем
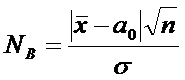 .
.
Случайная величина N имеет
нормальное распределение N(O,1),
Схема
решения:
|
Ho
|
H1
|
Статистика критерия
|
Критические точки
|
Условие принятия Ho
|
|
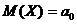
|
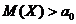
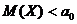
|
таблица 2
|
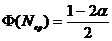
|
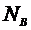 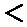 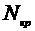
|
|
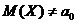
|
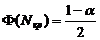
|
Задача
7. Установлено, что средний вес таблетки лекарства
сильного действия должен быть равен  мг. Выборочная
проверка 121 таблетки полученной партии лекарства показала, что средний вес
таблетки этой партии
мг. Выборочная
проверка 121 таблетки полученной партии лекарства показала, что средний вес
таблетки этой партии 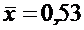 мг. Требуется проверить
значимость этого превышения нормы при уровне значимости 0,01. Многократными
предварительными опытами по взвешиванию таблеток, поставляемых фармацевтическим
заводом, было установлено, что вес таблеток распределен нормально со средним
квадратичным отклонением
мг. Требуется проверить
значимость этого превышения нормы при уровне значимости 0,01. Многократными
предварительными опытами по взвешиванию таблеток, поставляемых фармацевтическим
заводом, было установлено, что вес таблеток распределен нормально со средним
квадратичным отклонением 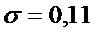 мг.
мг.
Решение.
Кратко:
Х: 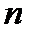 =121
=121 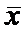 =0,53
=0,53 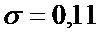 .
.
Для
поставленной задачи выдвинем гипотезы
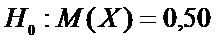
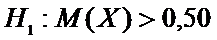 .
.
По
выборке вычисляем
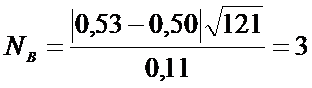 .
.
Критическая
точка 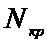 является решением уравнения
является решением уравнения
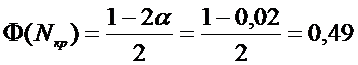 ,
,
и
по таблице 2 находим 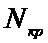 =2,34.
=2,34.
Так
как
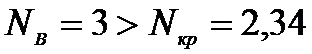
отвергаем
гипотезу 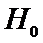 и принимаем гипотезу
и принимаем гипотезу 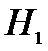 , что означает, различие в весе таблетки
значимо.
, что означает, различие в весе таблетки
значимо.
А
это значит, что партия таблеток не может быть пущена в продажу.
Фармацевтическая фирма терпит убытки.
Если
бы эти таблетки были пущены в продажу, то была бы совершена ошибка 2 рода, и
она могла бы иметь очень серьезные последствия для здоровья людей.
(случай неизвестной дисперсии)
Схема
решения:
|
Ho
|
H1
|
Статистика критерия
|
Критические точки
|
Условие принятия Ho
|
|
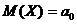
|
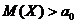
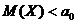
|
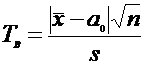
|
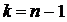
таблица 6
|
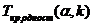
|
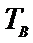 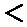 
|
|
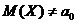
|
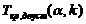
|
9. Проверка гипотезы
о равенстве средних двух нормальных совокупностей
(зависимые выборки)
Ранее при сравнении средних двух серий измерений
предполагалось, что эти измерения проводятся независимо друг от друга.
Такое условие не выполняется, если следим за развитием
болезни у одних и тех же больных.
Пусть, например, группа объектов подвергается какому-то
воздействию. Измеряется некоторый признак до и после воздействия.
Требуется проверить влияние воздействия на данный
признак.
В этом случае задачу сравнения средних двух
совокупностей можно переформулировать.
Будем рассматривать разность значений признака до и
после лечения у одних и тех же объектов.
Тогда это значение предположительно равно нулю
(нулевая гипотеза) и можно применить весь аппарат проверки гипотезы о равенстве
среднего предполагаемому значению.
Пусть значение признака в первой серии взяты из
генеральной совокупности Х, а во второй – Y.
Из этих совокупностей произведены выборки одинакового
объема  , варианты которых равны
, варианты которых равны 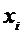 и
и 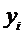 .
Рассмотрим случайную величину
.
Рассмотрим случайную величину
D= Y
-X,
варианты
которой имеют значения
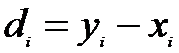 .
.
Тогда условие задачи сводится к проверке гипотезы
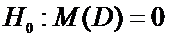
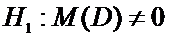 .
.
Задача
8. Пусть 10 пациентов получали изучаемый метод лечения,
и у каждого пациента измерялось значение признака до после лечения:
|
до
|
0,8
|
0,9
|
2,5
|
1,2
|
1,3
|
1,5
|
1,6
|
2,1
|
2,0
|
1,0
|
|
после
|
4,8
|
5,9
|
6,5
|
4,7
|
6,3
|
6,5
|
5,1
|
6,1
|
4,0
|
6,0
|
Требуется,
при 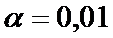 проверить оказало ли лечение влияние на
изучаемый признак.
проверить оказало ли лечение влияние на
изучаемый признак.
Решение.
Вычислим значения разностей 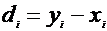 :
:
|
di
|
4,0
|
5,0
|
4,0
|
3,5
|
5,0
|
5,0
|
3,5
|
4,0
|
2,0
|
5,0
|
и
рассчитаем требуемые числовые характеристики:
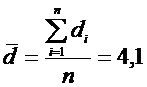
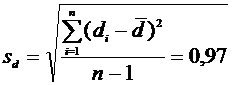 .
.
По
полученным данным рассчитаем
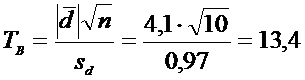 .
.
Определим границы
двусторонней критической области:
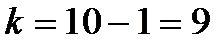 ,
,
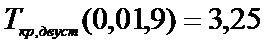 .
.
Так как 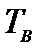
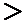
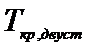 , то принимаем гипотезу
, то принимаем гипотезу 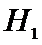 . Следовательно, лечение оказало влияние
на изучаемый признак.
. Следовательно, лечение оказало влияние
на изучаемый признак.
Аналогичные задачи возникают,
если одни и те же пробы почвы анализируются разными методами.
10. Точечные статистические оценки
параметров двумерных совокупностей
Пусть требуется обработать результаты наблюдений двух
величин X и Y.
Таблицы наблюдений
Если число наблюдений n небольшое,
то результаты наблюдений 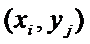 представляются в
виде таблицы наблюдений
представляются в
виде таблицы наблюдений
Для вычисления числовых характеристик в этом случае
таблицу наблюдений удобно дополнить до следующей таблицы:
|
№
|
1
|
2
|
|
n
|
суммы
|
|
xi
|
x1
|
x2
|
…
|
xn
|
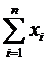
|
|
yi
|
y1
|
y2
|
…
|
yn
|
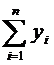
|
|
xi2
|
x12
|
x22
|
…
|
xk2
|
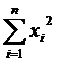
|
|
yi2
|
y12
|
y22
|
…
|
yn2
|
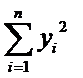
|
|
xi yi
|
x1y1
|
x2y2
|
…
|
xnyn
|
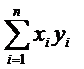
|
Используя последний столбец таблицы, находим оценки
числовых характеристик.
Оценками математических ожиданий являются выборочные
средние значения

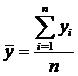 , (4)
, (4)
Несмещенные
оценки дисперсий 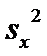 и
и 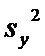 :
:
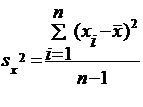
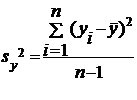 (5)
(5)
Расчетные
формулы:
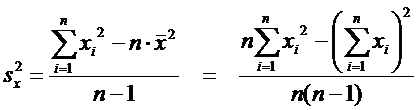 , (6)
, (6)
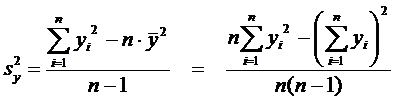 . (7)
. (7)
Несмещенная оценка корреляционного момента называется эмпирический
корреляционный момент:
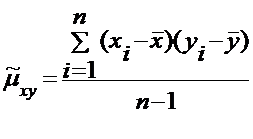 (8)
(8)
Оценка
коэффициента корреляции:
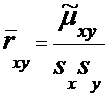 , (9)
, (9)
и
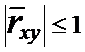 (10)
(10)
Расчетные
формулы:
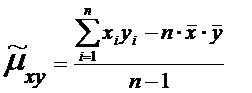
или
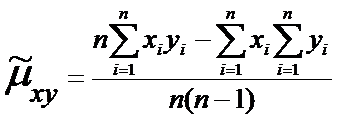 (11)
(11)
и
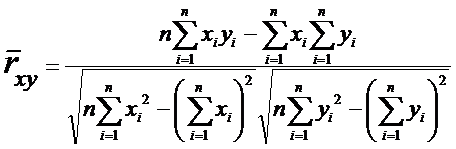 (12)
(12)
Замечание. Применяются также выборочные оценки дисперсий:
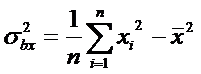
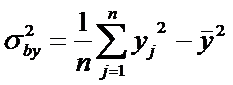 .
.
и выборочный
корреляционный момент
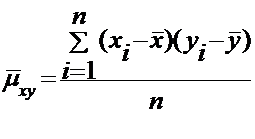
или
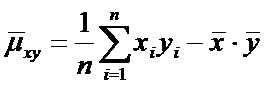
При
этом
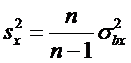
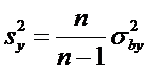

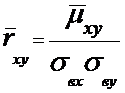
Выборочный корреляционный момент и выборочные
дисперсии являются смещенными оценками корреляционного момента и дисперсий.
Пример. Дана таблица наблюдений
|
номер наблюдения
|
x
|
y
|
|
1
|
1
|
3,3
|
|
2
|
1,4
|
2,0
|
|
3
|
1,8
|
5,8
|
|
4
|
2,2
|
4,1
|
|
5
|
2,6
|
5,2
|
|
6
|
3
|
7,3
|
Решение:
Для вычисления оценок
числовых характеристик заполним следующую таблицу
|
номер наблюдения
|
1
|
2
|
3
|
4
|
5
|
6
|
суммы
|
|
xi
|
1,0
|
1,4
|
1,8
|
2,2
|
2,6
|
3,0
|
12,0
|
|
yi
|
3,3
|
2,0
|
5,8
|
4,1
|
5,2
|
7,3
|
27,7
|
|
xi2
|
1,00
|
1,96
|
3,24
|
4,84
|
6,76
|
9,00
|
26,8
|
|
yi2
|
10,89
|
4,00
|
33,64
|
16,81
|
27,04
|
53,29
|
145,67
|
|
xi
yi
|
3,30
|
2,80
|
10,44
|
9,02
|
13,52
|
21,90
|
60,98
|
По суммам в последнем столбце
рассчитаем числовые характеристики
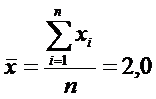
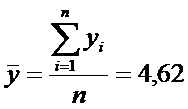 ,
,
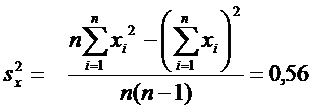 ,
,
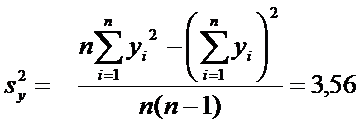
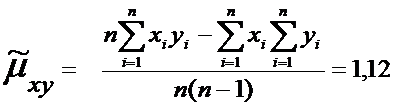
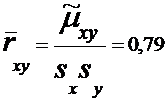
Проверка значимости коэффициента корреляции
Пусть известно, что проведены наблюдения для нормально
распределенной двумерной характеристики (X; Y).
При 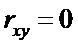 между переменами
отсутствует линейная корреляция. Если оценка
между переменами
отсутствует линейная корреляция. Если оценка  , то,
так как число наблюдений ограничено, нельзя заключить, что коэффициент
корреляции
, то,
так как число наблюдений ограничено, нельзя заключить, что коэффициент
корреляции 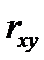 также отличен от нуля.
также отличен от нуля.
Тем самым требуется проверить, действительно ли
величины X и Y линейно коррелированны или это вызвано случайными
факторами.
Для этого при заданном уровне значимости 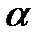 проводится проверка гипотезы
проводится проверка гипотезы
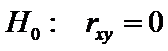 ,
,
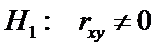 .
.
При
справедливости гипотезы 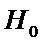 статистический
критерий
статистический
критерий
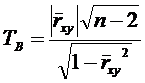 (13)
(13)
имеет
распределение Стьюдента с 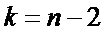 степенями свободы.
степенями свободы.
Поэтому
гипотеза 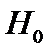 отвергается, если
отвергается, если
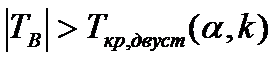 , (14)
, (14)
а
значения  определяется по таблице 6.
определяется по таблице 6.
11. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Пусть исходная информация
задана таблицей наблюдений
Тогда
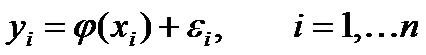 (2)
(2)
В основе метода
наименьших квадратов (метод МНК) лежит критерий минимизации суммы
квадратов ошибок 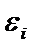 ., т.е.
., т.е.
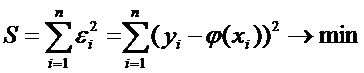 (3)
(3)
1)
Линейная регрессия.
Пусть
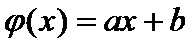 (4)
(4)
где 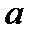 и
и
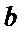 - некоторые параметры. Тогда задача
(2) имеет вид
- некоторые параметры. Тогда задача
(2) имеет вид
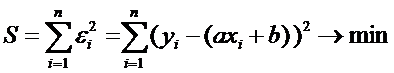 (5)
(5)
Нахождение минимума функции
двух переменных 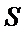 сводится к решению системы
уравнений
сводится к решению системы
уравнений
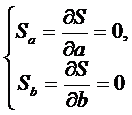 (6)
(6)
или
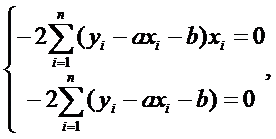
Раскрыв скобки, и проведя
преобразования, получим
систему
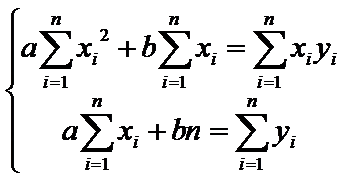 . (7)
. (7)
Решая эту систему, найдем,
что
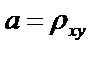 , а
, а 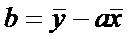 (8)
(8)
т.е. получим коэффициенты выборочного
уравнения линейной регрессии. тем самым прямая, построенная по методу МНК
совпадает с выборочным уравнением линейной регрессии.
2) Квадратичная регрессия
Пусть
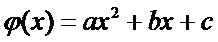 (9)
(9)
где 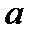 ,
,
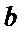 и
и 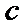 -
некоторые параметры. Тогда задача (2) имеет вид
-
некоторые параметры. Тогда задача (2) имеет вид
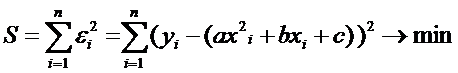 (10)
(10)
Нахождение минимума функции
двух переменных 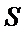 сводится к решению системы
уравнений
сводится к решению системы
уравнений
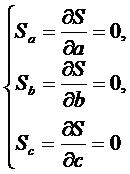 (11)
(11)
или
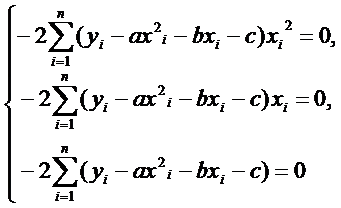 (12)
(12)
3)
Другие виды функции регрессии.
Если диаграмма рассеяния
имеет вид
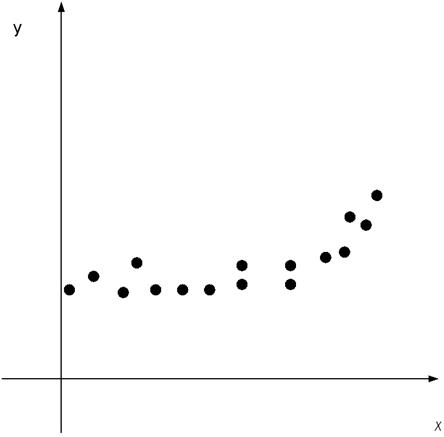
то
функцию регрессии ищут в виде
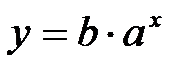
Поиск
неизвестных коэффициентов 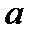 и
и 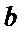 производится путем логарифмирования
уравнения:
производится путем логарифмирования
уравнения:
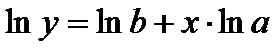
Обозначим
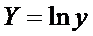 ,
, 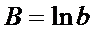 и
и 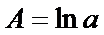 . Тогда в новых переменных уравнение
регрессии примет линейный вид:
. Тогда в новых переменных уравнение
регрессии примет линейный вид:
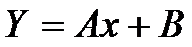 ,
,
и
коэффициенты А и В ищем методом МНК для линейной регрессии.
Пример.
В результате многолетних исследований толщины слоя ила после разлива на
пойменных лугах в зависимости от толщины снежного покрова получены следующие
данные
|
толщина снежного покрова ,
см
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
толщина слоя ила, см
|
0,5
|
1,0
|
1,4
|
1,7
|
1,8
|
1,9
|
2,0
|
Требуется
найти зависимость между толщиной снежного покрова и толщиной слоя ила.
Решение. Пусть x – толщина слоя снега, а y – толщина
слоя ила. Предполагаем, что зависимость между ними имеет вид
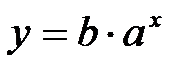
Введя обозначения 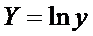 ,
, 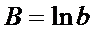 и
и 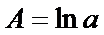 , для линейной регрессии:
, для линейной регрессии:
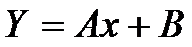 ,
,
Система (7) имеет вид
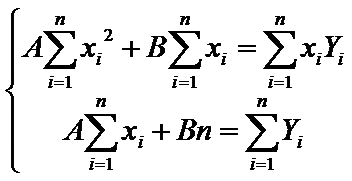 (13)
(13)
составим таблицу
|
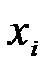
|
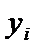
|
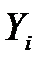
|
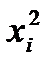
|
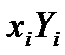
|
0,5
|
-0,3010
|
1
|
-0,3010
|
|
2
|
1,0
|
0
|
4
|
0
|
|
3
|
1,4
|
0,1461
|
9
|
0,4383
|
|
4
|
1,7
|
0,2304
|
16
|
0,9216
|
|
5
|
1,8
|
0,2553
|
25
|
1,2765
|
|
6
|
1,9
|
0,2788
|
36
|
1,6728
|
|
7
|
2,0
|
0,3010
|
49
|
2,1070
|
|
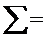 28 28
|
10,3
|
0,9106
|
140
|
6,1152
|
Система (13) тогда имеет вид
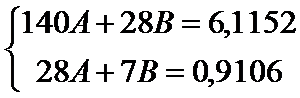 ,
,
Решив систему, и сделав
преобразование 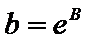 ,
, 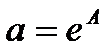 получим:
получим:
 .
.
Следовательно,
уравнение регрессии для зависимости толщины слоя ила от толщины снежного
покрова имеет вид:
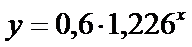 .
.
Если диаграмма рассеяния
имеет вид
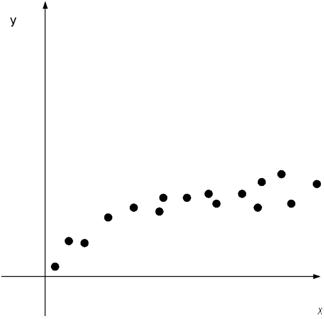
то функцию регрессии ищем в
виде
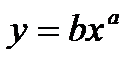
Это уравнение также может
быть линеаризовано путем перехода к переменным
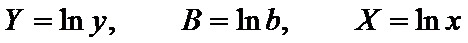 ,
,
в которых уравнение имеет вид
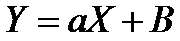 .
.
Если диаграмма рассеяния
имеет вид
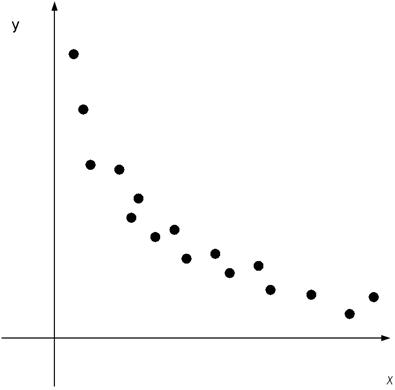
то зависимость между
переменными можно искать в виде
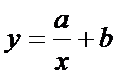
которое может быть
линеаризовано, положив 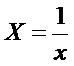 . Тогда уравнение
имеет вид
. Тогда уравнение
имеет вид
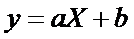 .
.
12. Выборочная линейная
регрессия
Определение. Выборочным уравнением линейной регрессии Y на X называется уравнение

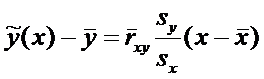 (1)
(1)
где
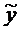 - значения линии регрессии, причем
величина
- значения линии регрессии, причем
величина
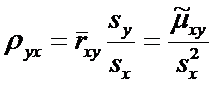 (2)
(2)
называется
коэффициентом линейной регрессии Y на X.
Выборочное уравнение линейной регрессии (1) может быть
приведено к виду
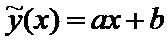 , (3)
, (3)
в
котором
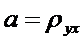 и
и 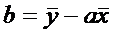 . (4)
. (4)
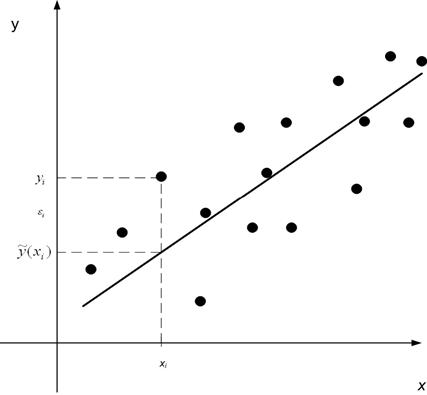
Рассмотрим положение точек наблюдения 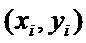 относительно выборочной линейной
регрессии.
относительно выборочной линейной
регрессии.
Если
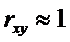 , то
, то
Если
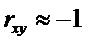 , то
, то
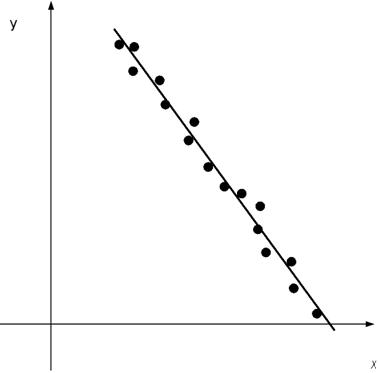
Если
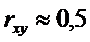 , то
, то
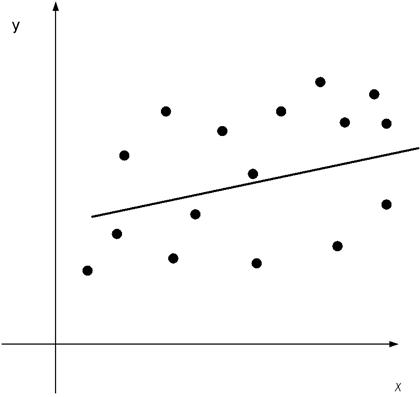
Если
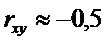 , то
, то
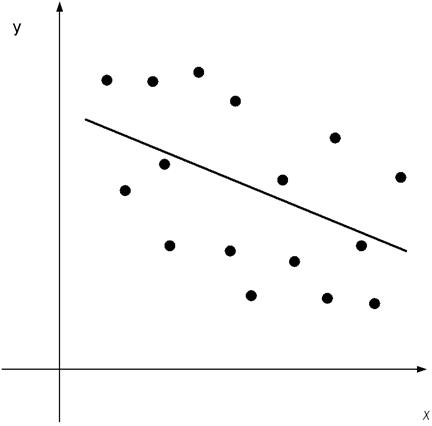
Если
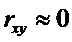 , то
, то
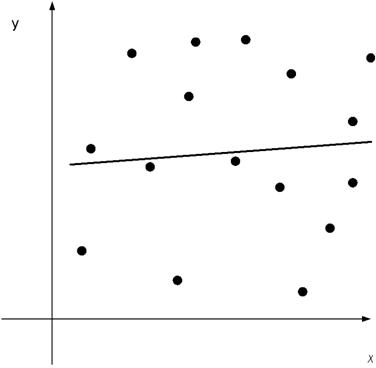
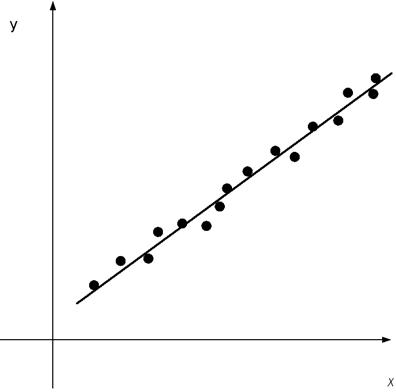
Чем ближе  к единице, тем
«теснее» расположены точки наблюдений относительно выборочного уравнения
линейной регрессии.
к единице, тем
«теснее» расположены точки наблюдений относительно выборочного уравнения
линейной регрессии.
Тогда выборочное уравнение линейной регрессии может
приближенно описывать функцию регрессии 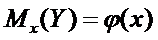 ,
т.е. считаться её оценкой.
,
т.е. считаться её оценкой.
Чем меньше  , тем расплывчатее
«облако» наблюдений, тем в меньшей степени уравнение линейной регрессии
отражает связь между наблюдениями.
, тем расплывчатее
«облако» наблюдений, тем в меньшей степени уравнение линейной регрессии
отражает связь между наблюдениями.
Коэффициент корреляции 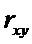 является
показателем тесноты линейной зависимости между переменными.
является
показателем тесноты линейной зависимости между переменными.
13. Доверительный
интервал для линейной регрессии
Пусть 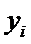 - измерения величины
y при различных значениях
- измерения величины
y при различных значениях 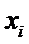 независимой
величины x.
независимой
величины x.
Считаем, что Y –
случайная величина, а X – неслучайная.
По этим измерениям ищем функцию регрессии 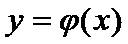 , предполагая, что она линейная.
, предполагая, что она линейная.
Оценим функцию регрессии с помощью выборочной линейной
функцией регрессии:
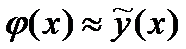
Для любых пар наблюдений 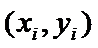 можно
записать соотношение
можно
записать соотношение
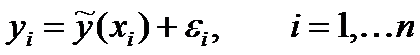 , (5)
, (5)
где
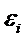 - случайные ошибки измерений, а
- случайные ошибки измерений, а
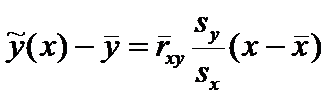 .
.
Пусть случайные ошибки измерений удовлетворяют
условиям:
1)
они независимы;
2)
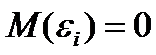 ,
что означает отсутствие систематической ошибки измерений;
,
что означает отсутствие систематической ошибки измерений;
3)
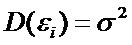 ,
что означает, что разброс ошибок измерений не зависит от значения x.
,
что означает, что разброс ошибок измерений не зависит от значения x.
4)
Случайные ошибки измерений
распределены по нормальному закону.
Воздействие
случайных ошибок определяется с помощью остаточной дисперсии
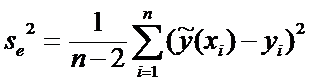 . (6)
. (6)
Выборочное линейное уравнение регрессии приближенно
описывает зависимость у от x:
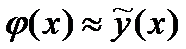 .
.
ЗАДАЧА: определить область на плоскости, в которой с
заданной вероятностью 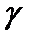 находится функция регрессии
находится функция регрессии 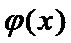 .
.
Данная область называется доверительный интервал
для условного математического ожидания 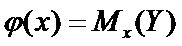 и
определяется неравенством
и
определяется неравенством
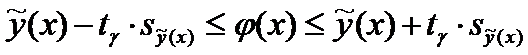 ,(7)
,(7)
где
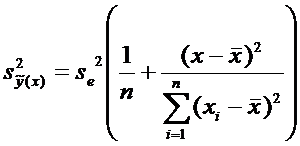 (8)
(8)
и 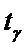 определяется по таблице 3 по формуле
определяется по таблице 3 по формуле
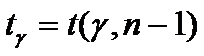 (9)
(9)
или
по формуле
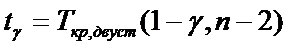 , (10)
, (10)
используя
таблицу 6.
Используя
уже полученные оценки, формулу (8) можно преобразовать к виду
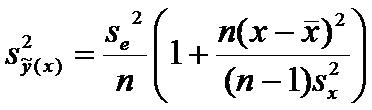 (11)
(11)
откуда
находим
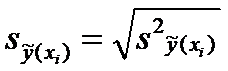 . (12)
. (12)
Величина доверительного интервала зависит от значения 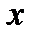 .
.
Построение доверительного интервала
Введем
обозначения для значений нижней и верхней границ доверительного интервала при
значениях 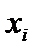 :
:
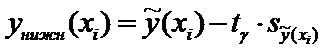 (13)
(13)
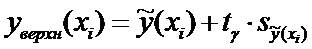 (14)
(14)
Для построения доверительного интервала добавим строки
в таблицу для вычисления точечных оценок:
Таблица
|
№
|
1
|
2
|
|
n
|
суммы
|
|
xi
|
x1
|
x2
|
…
|
xn
|
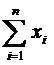
|
|
yi
|
y1
|
y2
|
…
|
yn
|
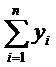
|
|
xi2
|
x12
|
x22
|
…
|
xk2
|
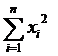
|
|
yi2
|
y12
|
y22
|
…
|
yn2
|
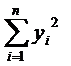
|
|
xi
yi
|
x1y1
|
x2y2
|
…
|
xnyn
|
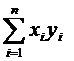
|
|
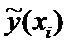
|
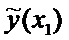
|
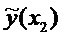
|
…
|
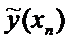
|
|
|
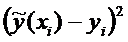
|
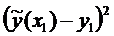
|
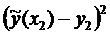
|
…
|
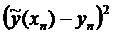
|
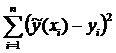
|
|
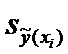
|
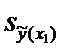
|
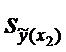
|
…
|
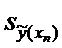
|
|
|
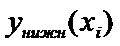
|
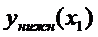
|
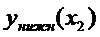
|
…
|
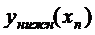
|
|
|
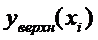
|
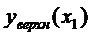
|
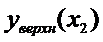
|
…
|
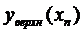
|
|
График линейной регрессии строится по двум точкам,
причем точка 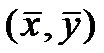 лежит на этой прямой. Границы
доверительного интервала имеют форму гиперболы, причем наименьшее расстояние
между ветвями имеет место в точке
лежит на этой прямой. Границы
доверительного интервала имеют форму гиперболы, причем наименьшее расстояние
между ветвями имеет место в точке 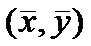 .
.
Ошибка! Ошибка связи.
Заметим, что отдельные наблюдения могут выходить за
пределы построенной области.
По
мере удаления x от 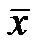 величина
доверительного интервала увеличивается.
величина
доверительного интервала увеличивается.
Таким
образом, прогноз значений зависимой переменной y по
уравнению регрессии оправдан, если значение независимой переменной x
не выходит за диапазон ее значений по выборке.
14.
Проверка гипотез об однородности выборок с помощью
критерия «хи-квадрат» (задача с последнего семинара).
16. Критерий Вилкоксона проверки однородности двух
выборок (лекция 12).
23. Ориентированные графы. Матрица смежности вершин.
Если
в графе G все элементы множества U — дуги, то граф называется ориентированным
(орграфом).
Матрицей
смежности обыкновенного графа
(орграфа), содержащего n вершин, называется квадратная матрица An´n , каждый
элемент которой aij , i,j=1,...,n,
определяется следующим образом:
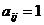 , если существует ребро (дуга),
соединяющее вершины xi и xj ;
, если существует ребро (дуга),
соединяющее вершины xi и xj ;
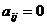 , в противном случае.
, в противном случае.
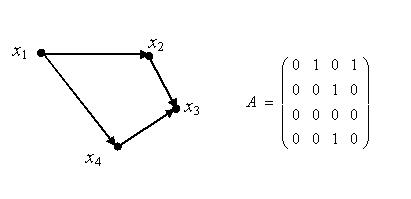
Матрица
смежности ориентированного графа.
24. Знаковый и взвешенный
орграф.
Взвешенный граф можно задать с
помощью специальной матрицы смежности, в которой при наличии ребра (дуги),
соединяющего вершины xi и xj в качестве соответствующего
элемента указывается вес этого ребра (дуги).
При изображении графа его вершины можно располагать
произвольно и по своему усмотрению выбирать форму соединяющих их линий. В тех
случаях, если имена вершин несущественны. естественно не различать графы,
отличающиеся лишь именами (порядком) вершин. О таких графах говорят, что они изоморфны.
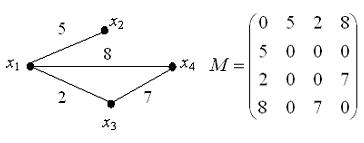
Матрица
смежности взвешенного неориентированного графа
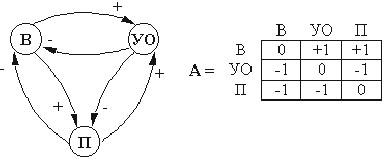
Знаковый
орграф и его матрица.