|
Тип заготовки
|
Кількість
заготовок, шт.
|
|
Перший спосіб
розкрою
|
Другий спосіб
розкрою
|
|
А
|
2
|
6
|
|
В
|
5
|
4
|
|
С
|
2
|
3
|
|
Величина відходів,
см2
|
12
|
16
|
1. Математична модель задачі
12Х1+ 16X2 -> min
2Х1+6Х2 >= 24
5Х1+ 4Х2 >= 31
2Х1+ 3Х2 >=18
Хі >= 0 (i=1,2)
Хі - ціле.
2.
Обґрунтування вибору методу розв’язання задачі
Оскільки в поставленій задачі цільова функція прямує до
мінімуму (мінімізація величини відходів) і вона лінійно залежить від елементів
рішення та є обмеження, які представляють собою лінійні нерівності, тоді
поставлена задача є задачею лінійного програмування. Та оскільки є вимога, що
змінні є цілими числами (кількість заготовок - ціле число), тоді відповідно
задача являється задачею цілочисельного лінійного програмування. Математична
модель поставленої задачі відповідає математичній моделі задачі цілочисельного
лінійного програмування:
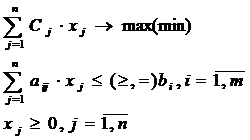
Існує два методи рішення задач цілочисельного лінійного
програмування:
1. Метод відсікання (алгоритм Гоморі): суть методу
полягає в тому, що при отриманні нецілочисельного рішення необхідно побудувати
рівняння, яке відсіче отриманий оптимальний результат і залишить всі інші
значення ОДР. Після цього задача знову вирішується. Таким чином задача
вирішується до тих пір, поки не буде отримано цілочисельне рішення задачі.
2. Метод гілок і границь: метод являє собою
комбінаторний метод, який передбачає побудову розгалуження простору рішень і
відкидання областей, які не вміщують допустимі цілочисельні рішення. В методі
вирішується послідовність релаксованих задач і на кожній ітерації виконується
оцінка верхньої границі оптимального рішення. Процес рішення задачі є процесом
породження гілок і побудови границь цільової функції.
Для вирішення цієї задачі в рамках курсового проекту
використаємо алгоритм Гоморі.
3.
Алгоритм розв’язання задачі (Алгоритм Гоморі)
1. Симплекс методом вирішуємо задачу:
визначаємо індексний рядок:
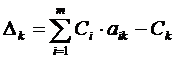
вибір розв’язального стовпчика:
При ц.ф. max: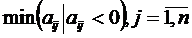
, якщо всі 
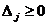, то рішення пункту знайдено;
При ц.ф. min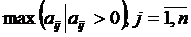 
, якщо всі 
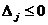, то рішення пункту знайдено;
вибір розв’язального рядка і визначення розв’язального
елемента:
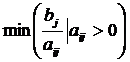, Якщо всі 
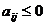, то задача не має рішення і є необмеженою;
У розв’язальному рядку записується:
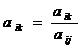
У розв’язальному стовпчику записується: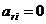 
, для всіх r, крім r=i,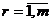 
Для всіх інших елементів, крім r=i та k=j, використовується
правило прямокутника:
,
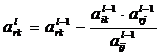- номер ітерації;
перераховуємо таблиці.
Якщо отриманий оптимальний результат є цілочисельним, тоді
рішення задачі знайдено.
. Нехай серед координат отриманого оптимального рішення є не
цілі числа. Оберемо серед цих змінних ту, яка має найбільшу дробову частину: xs=bs.
Цій змінній відповідає якийсь рядок. Для цього рядка справедлива рівність:
.
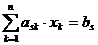Рівняння:
,
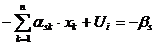буде додаватись в останню симплекс таблицю для продовження
рішення. Змінна Ui буде (n+1) змінною і буде братися в якості
базисної, для неї буде вводитись додатковий стовпчик.
. Двоїстим симплекс методом вирішується отримана задача:
від’ємне дробове число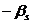 
визначає вектор, який
виводиться з базису. Вектор, який вводиться в базис обчислюється за формулою:
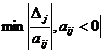
- відносно розв’язального елементу
перераховується симплекс таблиця.
Якщо в результаті рішення отримаємо цілі значення, то рішення
задачі знайдено. В противному випадку робимо 2 та 3 пункти.
Для розв’язання задачі використовуємо комп’ютерний
математичний пакет: MathCAD та табличний процесор MS Exel.
4.
Розв’язання задачі вручну
За умовою задачі ми склали математичну модель задачі.
Приводимо задачу до канонічного виду:
12x1+ 16x2+ x3+ x4+ x5 -> min
2x1 + 6x2-1x3 + 0x4
+ 0x5 = 24
5x1 + 4x2 + 0x3-1x4
+ 0x5 = 31
2x1 + 3x2 + 0x3 + 0x4-1x5
= 18
Хі >= 0 (i=1,3) Хі - ціле.
Зведемо завдання до знаходження максимуму. Для цього
помножимо всі рядки на (-1) і шукатимемо опорний план.
-2x1-6x2 + 1x3 + 0x4
+ 0x5 = -24
x1-4x2 + 0x3 + 1x4
+ 0x5 = -31
x1-3x2 + 0x3 + 0x4
+ 1x5 = -18
|
Базис
|
БР
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
x3
|
-24
|
-2
|
-6
|
1
|
0
|
0
|
|
x4
|
-31
|
-5
|
-4
|
0
|
1
|
0
|
|
x5
|
-18
|
-2
|
-3
|
0
|
0
|
1
|
|
F(X0)
|
0
|
12
|
16
|
0
|
0
|
0
|
Визначаємо роз’вязальні рядок і стовпець.
На перетині роз’вязальних рядка і стовпця знаходиться
роз’вязальний елемент, рівний (-4)
|
Базис
|
БР
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
x3
|
-24
|
-2
|
-6
|
1
|
0
|
0
|
|
x4
|
-31
|
-5
|
-4
|
0
|
1
|
0
|
|
x5
|
-18
|
-2
|
-3
|
0
|
0
|
1
|
|
F(X)
|
0
|
12
|
16
|
0
|
0
|
|
θ
|
0
|
12 : (-5) = -22/5
|
16 : (-4) = -4
|
-
|
-
|
-
|
|
Базис
|
БР
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
x3
|
221/2
|
51/2
|
0
|
1
|
-11/2
|
0
|
|
x2
|
73/4
|
11/4
|
1
|
0
|
-1/4
|
0
|
|
x5
|
51/4
|
13/4
|
0
|
0
|
-3/4
|
1
|
|
F(X0)
|
-124
|
-8
|
0
|
0
|
4
|
0
|
У базисному стовпці всі елементи додатні.
Переходимо до основного алгоритму симплекс-методу.
Поточний опорний план неоптимальний, оскільки в індексному
рядку знаходяться від’ємні коефіцієнти.
Як роз’вязальний виберемо стовпець, відповідний змінній x1,
оскільки це найбільший коефіцієнт по модулю.
Обчислимо значення Di по рядках як частку від ділення: bi
/ ai1
і з них выберемо найменше:(221/2 : 51/2
, 73/4 : 11/4 , 51/4
: 13/4 ) = 3
Отже, 3-тій рядок є роз’вязальний .
Роз’вязальний елемент рівний (13/4)
знаходиться на пересіченні роз’вязального стовпця і роз’вязального рядка.
|
Базис
|
B
|
x1
|
x2
|
x3
|
x4
|
x5
|
min
|
|
x3
|
221/2
|
51/2
|
0
|
1
|
-11/2
|
0
|
41/11
|
|
x2
|
73/4
|
11/4
|
0
|
-1/4
|
0
|
61/5
|
|
x5
|
51/4
|
13/4
|
0
|
0
|
-3/4
|
1
|
3
|
|
F(X1)
|
124
|
-8
|
0
|
0
|
4
|
0
|
0
|
Отримуємо нову симплекс-таблицю:
|
Базис
|
B
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
x3
|
6
|
0
|
0
|
1
|
6/7
|
-31/7
|
|
x2
|
4
|
0
|
1
|
0
|
2/7
|
-5/7
|
|
x1
|
3
|
1
|
0
|
0
|
-3/7
|
4/7
|
|
F(X1)
|
100
|
0
|
0
|
0
|
4/7
|
44/7
|
Кінець ітерацій: індексний рядок не містить від’ємних
елементів - знайдений оптимальний план
Остаточний варіант симплекс-таблиці:
|
БазисBx1x2x3x4x5
|
|
|
|
|
|
|
|
x3
|
6
|
0
|
0
|
1
|
6/7
|
-31/7
|
|
x2
|
4
|
0
|
1
|
2/7
|
-5/7
|
|
x1
|
3
|
1
|
0
|
0
|
-3/7
|
4/7
|
|
F(X2)
|
100
|
0
|
0
|
0
|
4/7
|
44/7
|
Оптимальний план можна записати так:3 = 62
= 41 = 3(X) = 0•6 + 16•4 + 12•3 = 100
5.
Аналіз результатів роботи в програмі MathCAD
Для свого вирішення задачі використаємо
функцію:
Minimize(f, var1, var2, ...) повертає
значення var1, var2, які задовольняють обмеження вирішують блок і, які змушують
function f набути його найменшого значення.
Аргументи: var1, var2 ... прості змінні- функція, визначена
вище, вирішують блок. Наприклад, г аргументу міг послатися на function г(x,y)
:=x/y.
Використання функціЇ:
1. Визначте функцію, щоб мінімізувати.
2. Визначте значення припущення для змінних, що
вирішуються.
. Надрукуйте слово Given, що означає умова
завдання.
. Внизу Given, type рівності і нерівності, які
служать обмеженнями, використовуючи логічні оператори.
. Введіть функцію Мінімізувати з відповідними
аргументами.
Примітки:
· Ці функції повертають скаляр, коли лише одна змінна
включена. Інакше вони повертають вектор.
· Якщо немає жодних обмежень слово Given
не необхідне.
Вводимо вхідні дані та отримаємо наступний результат:
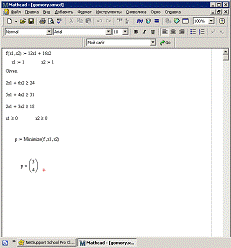
Вектор Р відображає значення шуканих мінних. Отже, х1=3,
х2=4.
Знайдений результат відповідає результату, обчисленому
вручну. Задача вирішена
Висновок
- система комп'ютерної алгебри з класу систем
автоматизованого проектування, орієнтована на підготовку інтерактивних
документів з обчисленнями і візуальним супроводженням, відрізняється легкістю
використання.має простий і інтуїтивний для використання інтерфейс користувача.
Для введення формул і даних можна використовувати як клавіатуру, так і
спеціальні панелі інструментів.
Робота здійснюється в межах робочого аркуша, на якому
рівняння і вирази відображаються графічно, на противагу текстовому запису в
мовах програмування.
Незважаючи на те, що ця програма здебільшого орієнтована на
користувачів-непрограмістів, Mathcad також використовується в складніших
проектах, щоб візуалізувати результати математичного моделювання, шляхом
використання поширених обчислень і традиційних мов програмування.
Список використаної літератури
mathcad математичний комп'ютерний
1. Методи оптимізації. Методичні вказівки до
виконання лабораторних робіт / Уклад. Г.А. Гайна, Н.Л. Попович. - К.: КНУБА,
2011.
2. Методичні вказівки до виконання курсової
роботи з дисципліни “Методи оптимізації” / Уклад. Г.А. Гайна. - К.: КНУБА,
2009.
. Гайна Г.А. Методи оптимізації: алгоритми,
приклади, задачі: Навчальний посібник. - К.: КНУБА, 2008. - 144с.