Сравнительный анализ методов квадратичной интерполяции и золотого сечения
Курсовая работа
Сравнительный анализ
методов квадратичной интерполяции и золотого сечения
Введение
экстемум интерполяция
итерация
Задачей оптимизации в математике, информатике и исследовании
операций называется задача нахождения экстремума (минимума или максимума)
целевой функции в некоторой области конечномерного векторного пространства,
ограниченной набором линейных и / или нелинейных равенств и / или неравенств.
Методы квадратичной интерполяции и золотого сечения
принадлежат к методам одномерной минимизации.
Целью этих методов является нахождение безусловного минимума
функции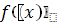
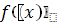 одной переменной, т.е. такую точку
одной переменной, т.е. такую точку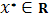
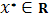 , что при
, что при 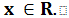
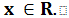
Метод квадратичной интерполяции основан на последовательном
применении процедуры оценивания с использованием квадратичной аппроксимации.
Метод золотого сечения - метод поиска значений
действительно-значной функции на заданном отрезке. В основе метода лежит
принцип деления в пропорциях золотого сечения. Наиболее широко известен как
метод поиска экстремума в решении задач оптимизации. Интервал неопределенности
делится на две равные части так, что отношение длины большого отрезка к длине
всего интервала равно отношению длины меньшего отрезка к длине большего
отрезка.
Целью курсовой работы является сравнительный анализ методов
квадратичной интерполяции и дихотомии.
1. Метод квадратичной интерполяции
Постановка задачи
Требуется найти безусловный минимум функции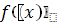
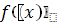 одной переменной, т.е. такую точку
одной переменной, т.е. такую точку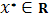
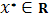 , что при
, что при 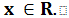
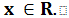
Стратегия поиска
Метод квадратичной интерполяции (метод Пауэлла) относиться к
последовательным стратегиям. Задается начальная точка и с помощью пробного шага
находятся три точки так, чтобы они были как можно ближе к искомой точке
минимума. В полученных точках вычисляются значения функции. Затем строится
интерполяционный полином второй степени, проходящий через имеющиеся три точки.
В качестве приближения точки минимума берется точка минимума полинома. Процесс
поиска заканчивается, когда полученная точка отличается от наилучшей из трех опорных
точек не более чем на заданную величину.
Алгоритм
Задать начальную точку 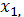
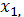 величину шага ∆x>0,
величину шага ∆x>0, 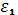
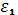 и
и 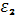
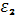 - малые положительные числа, характеризующие точность.
- малые положительные числа, характеризующие точность.
Вычислить 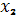
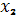 =
= 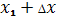
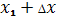 .
.
Вычислить 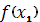
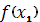 =
= 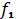
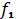 и
и 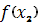
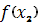 =
= 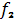
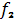 .
.
Сравнить 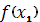
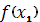 с
с 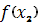
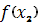 :
:
а) если 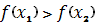
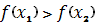 , положить
, положить 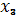
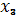 =
= 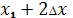
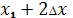 . (рис 1, а).
. (рис 1, а).
б) если 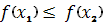
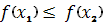 , положить
, положить 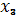
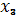 =
= 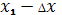
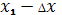 . (рис 1, б).
. (рис 1, б).
Вычислить 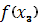
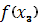 =
= 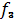
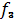 .
.
Найти 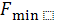
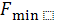 = min{
= min{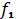
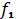 ,
, 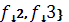
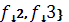 ,
, 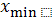
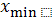 =
= 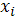
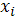 :
: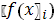
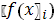 =
= 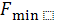
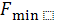 .
.
1.
Вычислить
точку минимума интерполяционного полинома, построенного по трем точкам:
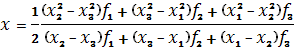
и величину функции 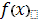
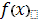 (рис 1).
(рис 1).
Если знаменатель в формуле для 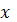
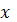 на некоторой итерации обращается в нуль, то результатом
интерполяции является прямая. В этом случае рекомендуется обозначить
на некоторой итерации обращается в нуль, то результатом
интерполяции является прямая. В этом случае рекомендуется обозначить 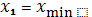
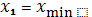 и перейти к шагу 2.
и перейти к шагу 2.
1.
Проверить
выполнение условия окончания:
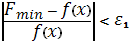
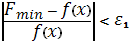 ,
,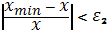
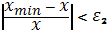
Тогда:
а) если оба условия выполнены, процедура закончена и 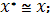
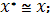
б) если хотя бы одно из условий не выполнено и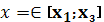
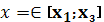 ,
,
выбрать наилучшую точку 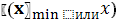
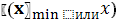 и две точки по обе стороны
и две точки по обе стороны
от нее. Обозначить эти точки в естественном порядке и перейти к
шагу 6;
в) если хотя бы одно из условий не выполнено и 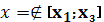
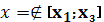 , то
, то
положить 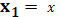
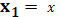 и перейти к шагу 2.
и перейти к шагу 2.
2. Метод золотого сечения
Постановка задачи
Требуется найти безусловный минимум функции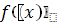
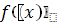 одной переменной, т.е. такую точку
одной переменной, т.е. такую точку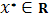
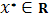 , что при
, что при 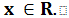
Стратегия поиска
Метод относится к последовательным стратегиям. Задается начальный
интервал неопределенности и требуемая точность. Алгоритм уменьшения интервала
опирается на анализ значений функций в двух точках (см. рис. 2). В качестве точек
вычисления функции выбираются точки золотого сечения. Тогда с учетом свойств
золотого сечения на каждой итерации, кроме первой, требуется только одно новое
вычисление функции. Условие окончания процесса поиска стандартные: поиск
заканчивается, когда длина текущего интервала неопределенности оказывается
меньше установленной величины.
Алгоритм
0. Задать начальный интервал неопределенности 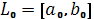
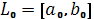 , точность
, точность 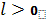
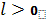 .
.
. Положить 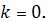
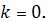
. Вычислить 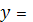
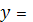 ,
, 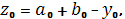
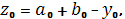
. Вычислить
 .
.
. Сравнить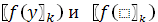
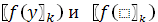 .
.
а) если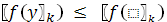
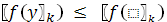 , то положить
, то положить 
 и
и 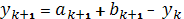
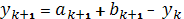 ,
, 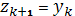
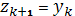 (рис. 3а). Перейти к шагу 6.
(рис. 3а). Перейти к шагу 6.
б) если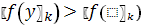
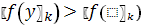 , положить
, положить 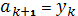
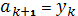 ,
, 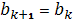
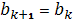 и
и 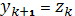
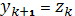 ,
, 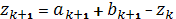
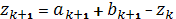 (рис. 3б).
(рис. 3б).
. Вычислить 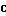
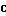 и проверить условие окончания:
и проверить условие окончания:
а) если 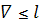
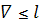 , процесс поиска завершается и
, процесс поиска завершается и 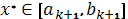
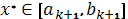 . В качестве приближенного решения можно взять середину последнего
интервала:
. В качестве приближенного решения можно взять середину последнего
интервала: 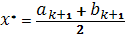
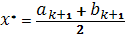 ;
;
б) если 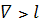
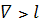 , положить
, положить 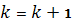
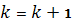 и перейти к шагу 4.
и перейти к шагу 4.
3.
Решение задач
.1
Перечень функций для исследования
Найти минимум функции:
1)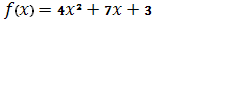
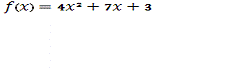 [-4; 0]
[-4; 0]
) [1; 4]
) [-5; 0]
)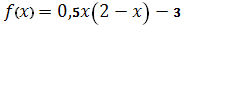
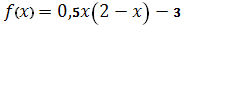 [0; 5]
[0; 5]
)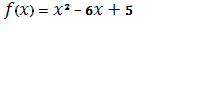
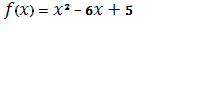 [0; 7]
[0; 7]
3.2
Решение методом квадратичной интерполяции
Пример 1. Найти минимум функции 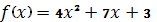
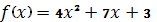
0.1. 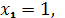
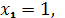 ∆x=1,
∆x=1, 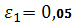
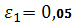 ,
, 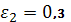
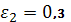 .
.
.2. 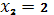
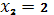
.3. 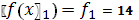
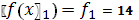 ;
;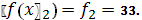
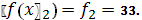
.4. 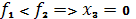
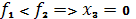
.5. 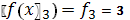
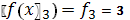
.6. 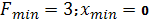
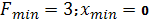
.7. 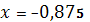
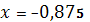 ;
;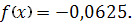
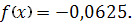
.8. 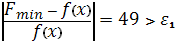
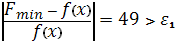 ;
; 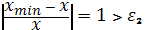
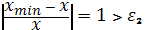
.2. 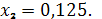
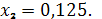
.3. 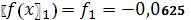
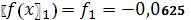 ;
; 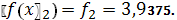
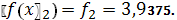
.4. 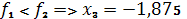
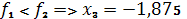 .
.
.5. 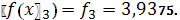
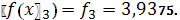
1.6. 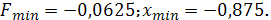
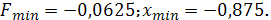
.7. 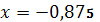
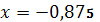 ;
;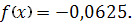
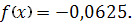
.8. 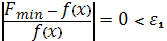
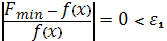 ;
; 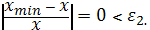
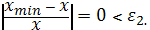
.9 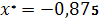
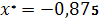 .
.
Пример 2. Найти минимум функции 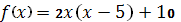
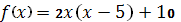
0.1. 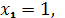
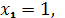 ∆x=1,
∆x=1, 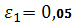
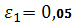 ,
, 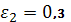
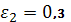 .
.
.2. 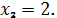
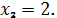
.3. 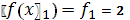
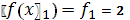 ;
; 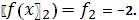
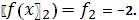
.4. 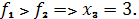
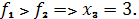
.5. 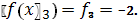
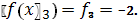
.6. 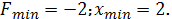
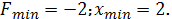
.7. 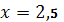
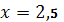 ;
;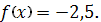
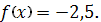
.8. 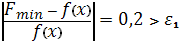
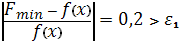 ;
; 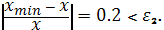
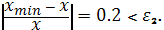
.9. 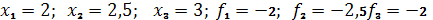
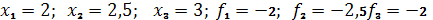
1.6. 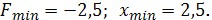
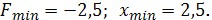
1.7. 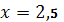
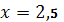 ;
; 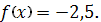
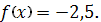
.8. 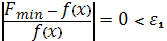
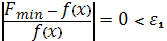 ;
; 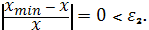
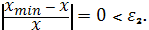
.9. 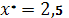
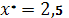 .
.
Пример 3. Найти минимум функции 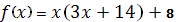
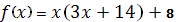
0.1. 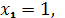
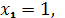 ∆x=1,
∆x=1, 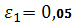
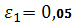 ,
, 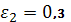
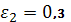 .
.
.2. 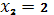
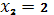
.3. 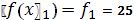
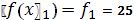 ;
; 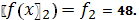
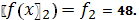
0.4. 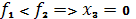
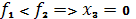 .
.
.5. 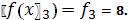
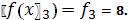
.6. 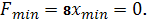
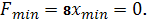
.7. 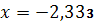
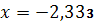 ;
;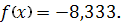
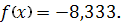
.8. 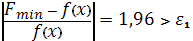
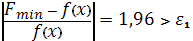 ;
; 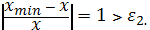
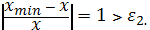
.9. 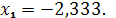
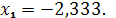
1.2. 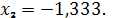
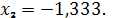
.3. 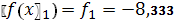
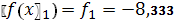 ;
; 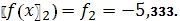
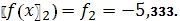
.4. 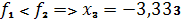
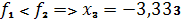 .
.
.5. 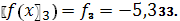
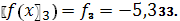
1.6. 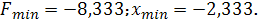
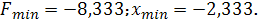
.7. 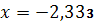
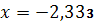 ;
;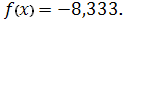
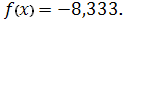
.8. 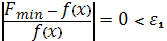
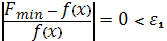 ;
; 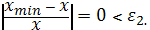
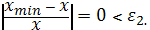
1.9 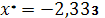
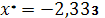 .
.
3.3
Решение методом золотого сечения
Пример 1. Найти минимум функции 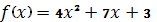
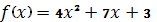
0.1 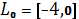
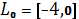 ,
,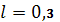
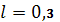 .
.
.2 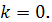
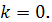
.3 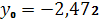
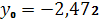 ,
, 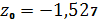
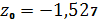 .
.
0.4 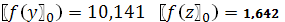
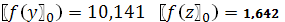 .
.
.5 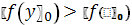
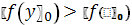 .
.
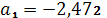
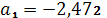 ,
,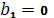
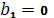 ,
, 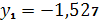
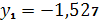 ,
, 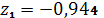
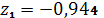 .
.
.6 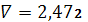
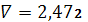 ,
, 
 .
.
.4 
 .
.
.5 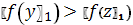
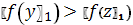 .
.
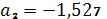
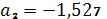 ,
, 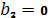
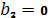 ,
, 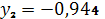
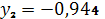 ,
, 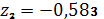
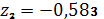 .
.
.6 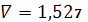
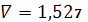 ,
, 
 .
.
.4 
 .
.
.5 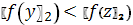
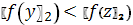 .
.
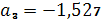
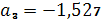 ,
, 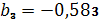
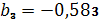 ,
, 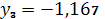
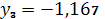 ,
, 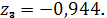
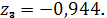
.6 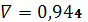
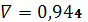 ,
, 
 .
.
.4 
 .
.
.5 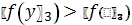
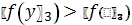 .
.
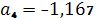
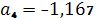 ,
, 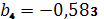
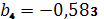 ,
, 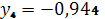
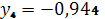 ,
, 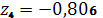
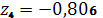 .
.
.6 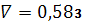
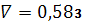 ,
, 
 .
.
.4 
 .
.
.5 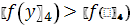
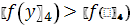 .
.
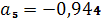
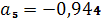 ,
, 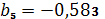
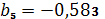 ,
, 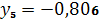
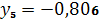 ,
, 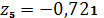
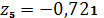 .
.
.6 
 ,
, 
 .
.
.4 
 .
.
.5 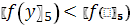
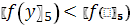 .
.
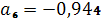
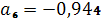 ,
, 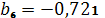
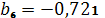 ,
, 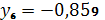
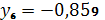 ,
, 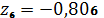
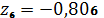 .
.
.6 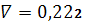
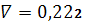 ,
, 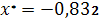
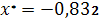 .
.
Пример 2. Найти минимум функции 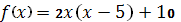
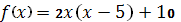
0.1 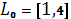
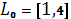 ,
,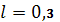
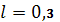 .
.
.3 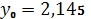
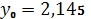 ,
, 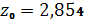
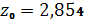 .
.
0.4 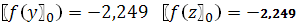
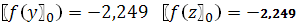 .
.
.5 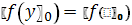
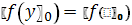 .
.
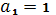
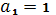 ,
, 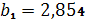
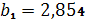 ,
, 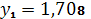
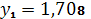 ,
, 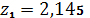
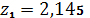 .
.
.6 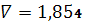
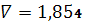 ,
, 
 .
.
.4 
 .
.
.5 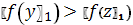
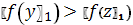 .
.
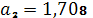
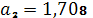 ,
, 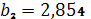
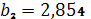 ,
, 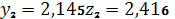
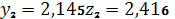 .
.
.6 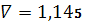
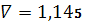 ,
, 
 .
.
.4 
 .
.
.5 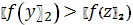
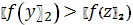 .
.
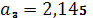
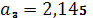 ,
, 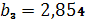
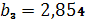 ,
, 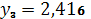
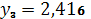 ,
, 

.6 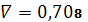
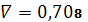 ,
, 
 .
.
.4 
 .
.
.5 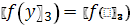
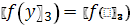 .
.
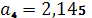
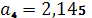 ,
, 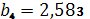
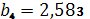 ,
, 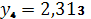
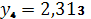 ,
, 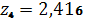
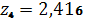 .
.
.6 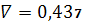
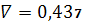 ,
, 
 .
.
.4 
 .
.
.5 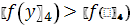
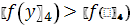 .
.
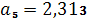
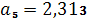 ,
, 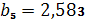
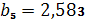 ,
, 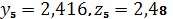
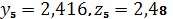 .
.
.6 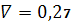
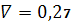 ,
, 
 .
.
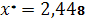
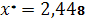 .
.
Пример 3. Найти минимум функции 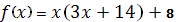
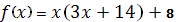
0.1 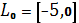
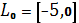 ,
,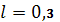
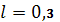 .
.
.2 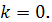
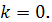
.3 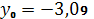
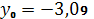 ,
, 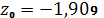
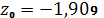 .
.
0.4 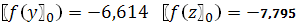
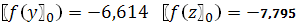 .
.
.5 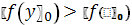
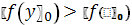 .
.
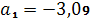
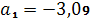 ,
, 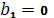
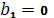 ,
, 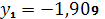
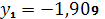 ,
, 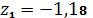
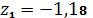
.6 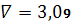
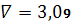 ,
, 
 .
.
.4 

1.5 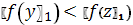
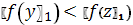 .
.
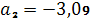
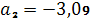 ,
, 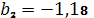
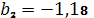 ,
, 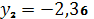
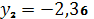 ,
, 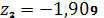
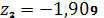 .
.
.6 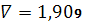
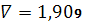 ,
, 
 .
.
.4 
 .
.
.5 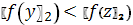
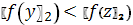 .
.
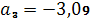
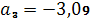 ,
, 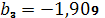
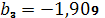 ,
, 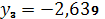
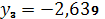 ,
, 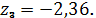
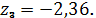
.6 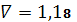
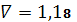 ,
, 
 .
.
.4 
 .
.
.5 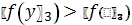
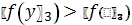 .
.
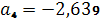
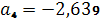 ,
, 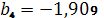
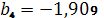 ,
, 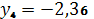
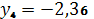 ,
, 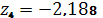
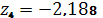 .
.
.6 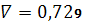
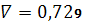 ,
, 
 .
.
.4 
 .
.
.5 
 .
.
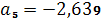
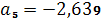 ,
, 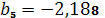
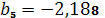 ,
, 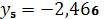
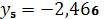 ,
, 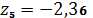
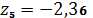 .
.
.6 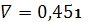
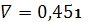 ,
, 
 .
.
.4 
 .
.
.5 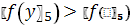
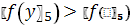 .
.

 ,
, 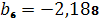
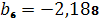 ,
, 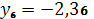
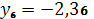 ,
, 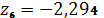
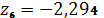 .
.
.6 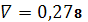
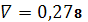 ,
, 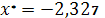
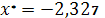 .
.
4.
Сравнительный анализ методов
Наилучшими критериями сравнения методов поиска являются их
эффективность и универсальность. Под эффективностью алгоритма обычно понимают
число вычислений функции, необходимое для достижения требуемого сужения
интервала неопределенности
.1
Преимущества и недостатки
Преимущества метода квадратичной интерполяции:
Методом квадратичной интерполяции решение происходит быстрее
для гладких функций.
Недостатки метода квадратичной интерполяции:
Для быстpоизменяющихся функций методом квадратичной
интерполяции решение происходит медленнее методов исключения интеpвалов.
Преимущества метода золотого сечения:
Метод золотого сечения, обладающий высокой эффективностью,
наиболее подходят для решения одномерных унимодальных задач оптимизации. С
точки зрения эффективности метод золотого сечения занимает промежуточное
положение между методами дихотомии и чисел Фибоначчи.
Недостатки метода золотого сечения:
При решение методом золотого сечения происходит большое
количество итераций. Велика возможность ошибиться при расчетах, поскольку
происходит частая замена либо используется большое количество переменных.
4.2 Количество итераций
Количество итераций при решении методом квадратичной
интерполяции.
|
№
|
Функция
|
Количество
итераций
|
|
1
|
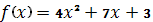
|
2
|
|
2
|
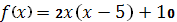
|
|
3
|
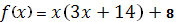
|
2
|
|
4
|
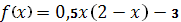
|
2
|
|
5
|
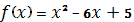
|
1
|
Количество итераций при решении методом золотого сечения
|
№
|
Функция
|
Количество
итераций
|
|
1
|
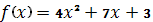
|
6
|
|
2
|
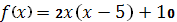
|
5
|
|
3
|
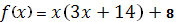
|
6
|
|
4
|
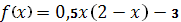
|
6
|
|
5
|
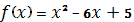
|
7
|
.3
Точность к min
Точность вычисления методом квадратичной интерполяции
|
№
|
Функция
|
Минимум
|
Точность
|
|
1
|
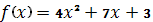
|
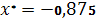 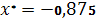 . .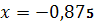
|
|
|
2
|
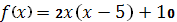
|
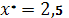 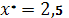 . .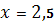
|
|
|
3
|
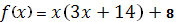
|
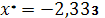 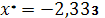 . .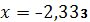
|
|
|
4
|
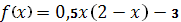
|
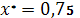 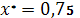 . .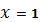
|
|
|
5
|
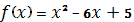
|
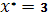
|
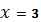
|
Точность вычисления методом золотого сечения
|
№
|
Функция
|
Минимум
|
Точность
|
|
1
|
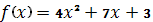
|
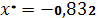 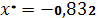 . .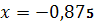
|
|
|
2
|
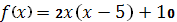
|
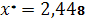 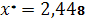 . .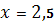
|
|
|
3
|
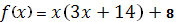
|
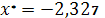 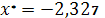 . .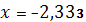
|
|
|
4
|
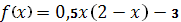
|
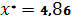
|
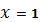
|
|
5
|
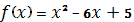
|
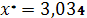
|
Заключение
Рассмотрев все результаты исследования методов квадратичной
интерполяции и золотого сечения, можно прийти к выводу, что каждый из них имеет
свои достоинства и недостатки. Однако, пользователь всегда сможет найти
подходящий алгоритм для решения своей конкретной проблемы. В руках опытного
программиста метод золотого сечения и метод квадратичной интерполяции
представляет собой мощный инструмент для поиска точных ответов в случае
дискретных, и приближённых, но весьма точных, - в случае непрерывных задач.
Список литературы
1. А.В.
Пантелеев, Т.А. Летова «Методы оптимизации в примерах и задачах»
. А.В.
Аттетков, СВ. Галкин, B.C. Зарубин «МЕТОДЫ ОПТИМИЗАЦИИ». - Москва: Издательство
МГТУ им. Н.Э. Баумана, 2003.