Методы теории вероятностей в анализе безопасности и надежности летательных аппаратов
Введение
Теория вероятностей возникла в
середине 17 в. То, что случайные явления представляют собой не исключение, а
правило в реальном мире, было замечено еще в древности. Об этом словами
Лукреция Кара прекрасно говорит Альфред Реньи. Попытки математически подойти к
изучению случайных явлений делались задолго до Паскаля и Ферма. Во всяком
случае, факты устойчивости частот случайных событий, связанных с
демографическими данными и потреблением больших городов, были известны еще в
Древнем Китае и Древнем Риме. Изучать случайные события с помощью точных
методов пытались Кардано и Галилей. Однако начало теории вероятностей на самом
деле положила только переписка Паскаля и Ферма по поводу вопросов кавалера де
Мере. К тому времени процесс научного познания уже победил; научное мышление
уверенно одолевало воззрения теологов, и свободный полет творческой мысли
неизбежно приводил к одному из основных вопросов познания: каковы типы
закономерностей, господствующих в Природе? Нет ли наряду с механистическим
детерминизмом детерминизма более общего, позволяющего охватить явления природы
шире и глубже?
На этот вопрос теперь дан
определенный ответ: закономерности случайных явлений дают нам детерминизм более
широкого типа, который в качестве предельного случая включает детерминизм
полный, практически в реальных явлениях не наблюдаемый.
Начиная с Паскаля, Ферма и Гюйгенса,
в научный обиход вошли первые понятия теории вероятностей - математической
науки о случайных событиях. Эти понятия формировались на примерах изучения
азартных игр, но создатели начал теории вероятностей отчетливо понимали общее
натурфилософское значение своих рассмотрений. В связи со сказанным полезно
привести подлинные слова Гюйгенса, которые содержатся в его трактате «Об
азартных играх»: «…я полагаю, что при внимательном изучении предмета читатель
заметит, что имеет дело не только с игрой, но что здесь закладываются основы
очень интересной и глубокой теории». Последующее развитие науки в полной мере
подтвердило эту точку зрения.
С течением времени изменялся и
расширялся объект изучения теории вероятностей. Если в самом начале ее
появления, фактически вплоть до конца XVIII века, основной интерес представляло
исследование вероятностей случайных событий, то уже в XIX веке центр тяжести
переносится на исследование случайных величин. Впрочем, само это понятие
формировалось очень долго, и его элементы встречаются уже в работе Гюйгенса.
Позднее случайными величинами занимались Муавр, Котс, Даниил Бернулли, Лаплас,
Лежандр, Гаусс. Работы упомянутых ученых (кроме Муавра) относились к теории
ошибок наблюдений, и здесь по необходимости должно изучать не столько случайные
события, сколько случайные величины. Логически четкий смысл понятие случайной
величины приобрело только в работах акад. А.Н. Колмогорова, а понятие функции
распределения одной из работ А. Ляпунова.
На этом, однако, не прекратилось
расширение объекта изучения. Во второй четверти нашего столетия в теорию
вероятностей было введено важнейшее понятие - понятие случайного процесса. Его
формирование протекало под влиянием физики, биологии, инженерного дела. Суть в
том, что как физика и биолога, так и инженера в первую очередь интересует
процесс развития явления во времени, а потому рассмотрение только случайных
величин, которые не связаны с течением времени, имеет лишь ограниченное
значение. И хотя определение случайного процесса связано с именами таких
выдающихся исследователей, как А.Я. Хинчин, А.Н. Колмогоров, Е.Е. Слуцкий,
следует все же отметить, что у них были и предшественники - Лаплас, Башелье,
Пуанкаре, А.А. Марков. По предложению французского математика Адамара в честь
Маркова назван важнейший класс случайных процессов (марковские процессы), для
которых все влияние прошлого на развитие процесса в будущем заключается в
достигнутом им в настоящий момент состоянии. Вскоре задачи геофизики и других
областей естествознания привели к необходимости рассмотрения не только
случайных величин, зависящих от одного параметра - времени, но и от многих
параметров - времени и положения. Так появились новые объекты изучения -
случайные поля.
Само собой разумеется, что
центральное понятие теории вероятностей - вероятность - не могло оставаться
неизменным на протяжении почти трехсот лет. Хорошо известно, что классическое
определение, возникшее в переписке Паскаля и Ферма, оказалось недостаточным
тогда, когда наука столкнулась с необходимостью изучения задач страхования,
ошибок наблюдения. Разрыв логических основ теории вероятностей с потребностями
практики сказывался уже в начале прошлого века и стал совершенно нетерпим в
наши дни. Вот почему в последние пятьдесят лет ученые уделяли такое внимание
логическим вопросам, вопросам разумного расширения действия понятий теории
вероятностей. Это было вызвано потребностями как бурно прогрессирующей
практики, предъявившей к теории вероятностей многообразные требования, так и
самой математики.
Теоретические основы науки о
авиационной техники в СССР были заложены в 50-60-х гг. Их базу составили
количественные методы расчёта и анализа и инженерные методы обеспечения при
создании и испытаниях изделий авиационной техники. Разработка методов
количеств, оценки уровня, дифференцированный подход к оценке влияния различных
видов отказов систем на выполняемые летательным аппаратом функции позволили
перейти к активному управлению процессом обеспечения на этапах проектирования,
экспериментальной отработки и лётно-доводочных испытаний летательных аппаратов.
Была создана основа для объективной сравнительной оценки уровней летательных
аппаратов различных типов и динамики их изменения во время эксплуатации. Реализация
этих методов стала возможной благодаря созданию и широкому внедрению единой
отраслевой системы учёта и сбора информации об отказах, выявляемых в
эксплуатации, а также благодаря разработке вероятностно-статистических и
расчётно-аналитических методов. В 70-х гг. наука о надёжности в авиации
получила дальнейшее развитие. Основу её составили комплексные программы
обеспечения, опирающиеся на научные методы проектирования, испытаний и
эксплуатационной оценки изделий авиационной техники. Цель работы по обеспечению
и анализу - изучение причин зарождения и развития неисправностей и создание
изделий с заданным и контролируемым уровнем. Сложность решения проблемы
возрастает одновременно с увеличением сложности создаваемых изделий и их
насыщением автоматическими устройствами и системами, поддерживающими рабочие
режимы вблизи пределов устойчивости работы и прочности конструкции. Благодаря
применению научных методов обеспечения, учёту предшествующего опыта уровень
вновь создаваемых изделий возрастает по сравнению с уровнем прототипов.
1. Сравнительный анализ
вероятностей катастрофы летательного аппарата.
транспорт вероятность летательный
1.1 Постановка задачи
задания №1
Летательный аппарат (ЛА) состоит из
- m двигателей с вероятностей отказа P1, P2,… Pm;
- n дублирующих систем энергосбережения с вероятностей отказа
P1Э, P2Э,… PnЭ;
N c вероятностей отказа Рс каждая.
Катастрофа наступает, если выходит
из строя любая (r+1) и более двигателей, либо если все системы энергоснабжения,
либо если хотя бы одна из N вспомогательных подсистем.
В случаи отказа любого r из m двигателей катастрофа
наступает с вероятностью РD.
Определить вероятность катастрофы ЛА
и сравнить ее с вероятностью катастрофы ЛА без дублирующих систем (один
двигатель с вероятностью катастрофы P1, одна система энергосбережения с вероятностей отказа P1Э и N вспомогательных
подсистем с вероятностей отказа Рс каждая), предполагая, что
все упомянутые выше системы и подсистемы ЛА функционируют независимо друг от
друга.
В обоих случаях сравнить вероятности
катастроф, связанных с отказом
двигателей;
систем энергосбережения;
вспомогательных подсистем.
Дано
m = 5; Р1 =6∙10-4, Р2
=5∙10-4, Р3=7∙10-4, Р4=2∙10
-4, Р5=4∙10 -4
r=4 РD=0.1;
n=4 Р1Э=3∙10-4, Р2Э=4∙10-4,
Р3Э=10 -4, Р4Э=6∙10 -4;
N=3∙103 Pc=6∙10-9.
Решение.
Математическая часть
Введем обозначение событий:
- D1, D2, D3, D4 - отказ 1-го, 2-го, 3-го и 4-го двигателей соответственно;
- В1, В2, В3, - отказ 1-й, 2-й,
и 3-й системы энергоснабжения соответственно;
· Сi - отказ i-ой вспомогательной
подсистемы, i = 1,2,…, N;
· Ек - катастрофа;
- Ekd, Eкэ, Eкc - катастрофы, связанные с
отказом двигателей, систем энергоснабжения и вспомогательных подсистем
соответственно.
А) Рассмотрим случай ЛА
с дублирующими системами:
В этом случае:
ЕK=ЕKD+ЕKЭ+EКС. (1.1)
Перейдем к противоположным событиям,
будем иметь:
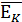
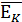 =
=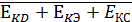
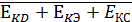 (1.2)
(1.2)
Из равенства (1.2) в силу соотношения
двойственности получим:
ЕK=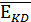
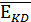 ∙
∙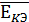
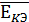 ∙
∙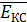
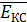 (1.3)
(1.3)
Тогда вероятность катастрофы будет
определяться по формуле:
P(EK)=1 - P(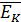
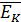 )=1-P(
)=1-P(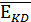
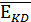 ∙
∙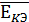
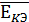 ∙
∙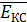
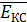 ) (1.4)
) (1.4)
Из равенства (1.4) в силу
независимости событий ЕKD, ЕKЭ, EКС получим:
P(EK)=1- P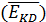
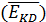 ∙ P(
∙ P(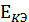
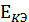 )∙ P(EKC)=1 - (1-P(EKD))∙(1-P(EKЭ))∙P(EKC)). (1.5)
)∙ P(EKC)=1 - (1-P(EKD))∙(1-P(EKЭ))∙P(EKC)). (1.5)
Рассмотрим структуру
событий ЕKD, ЕKЭ,
EКС
и найдем их вероятности, то есть вероятности катастроф, связанных с отказом
·двигателей ЕКD
·систем энергоснабжения ЕKЭ
·вспомогательных подсистем ЕKC
1) Рассмотрим структуру событий ЕKD и найдем P(EKD)= PKD
Так как событие ЕKD - это событие,
состоящее в том, что катастрофа произошла из-за отказа двигателей, а по условию
задачи катастрофа, связанная с отказом двигателей наступает, если выходят из
строя любых (r+1) и более двигателей из m двигателей, а в случае отказа любого г из m двигателей катастрофа наступает с вероятностью РD. Значит:
ЕKD= ЕKDr+ ЕKD≥
(r+1), где
Так как в нашем случае число
двигателей m = 5, r = 4; то r + 1 = 4 + 1 = 5.
Значит:
ЕKD= ЕKD4+ ЕKD≥5 где:
ЕКD4 - событие, состоящее в
том, что катастрофа произошла из-за отказа любого r =4 из m=5 двигателей;
ЕKD>5 - событие, состоящее в
том, что катастрофа произошла из-за выходы из строя любых (r + 1) = 5 и более двигателей, а в
нашем ЕKD>5= ЕKD5 - это событие, состоящее
в том, что катастрофа произошла из-за отказа пяти двигателей. Из этого следует,
что:
ЕKD≥5
= ЕKD5 = D1∙ D2∙ D3∙ D4∙ D5 (1.6)
В свою очередь катастрофа, связанная
с отказом ровно r = 4 двигателей (при работающих остальных), не обязательно влечет
за собой катастрофу (ас вероятностью PD), значит
EKD4=EK∙
ED4
Тогда:
EKD= EKD4+ EKD≥5= EK∙ ED4+ EKD≥5
P(EKD)=P(EKD4+ EKD≥5)= P(EKD4)+ P(EKD≥5)=P(EK∙
ED4)+P(EKD≥5)
а для нашего случая и учитывая
(1.6), получим:
P(EKD)=P(EKD4+ EKD≥5)= P(EKD4)+ P(EKD≥5)=P(EK∙ ED4)+P(EKD≥5)= P(EK∙ ED4)+P(EKD5) = P(EK∙ ED4)+ P(D1∙ D2∙ D3∙ D4∙ D5)
С другой стороны, катастрофа,
связанная с отказом ровно r=4 двигателей при
работающих остальных из пяти имеющихся у ЛА по условию задачи, есть следующее
событие:
ED4
= D1∙
D2
∙ D3∙D4
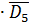
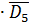 +
D1∙
D2
∙ D3∙
+
D1∙
D2
∙ D3∙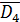
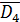 ∙ D5 +
D1∙
D2
∙
∙ D5 +
D1∙
D2
∙ 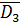
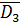 ∙D4∙D5
+
∙D4∙D5
+
+
D1∙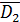
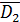 ∙ D3∙D4∙D5 +
∙ D3∙D4∙D5 +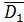
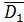 ∙ D2
∙ D3∙D4
∙ D5 (1.8)
∙ D2
∙ D3∙D4
∙ D5 (1.8)
то есть не работают 5-й, 4-й, 3-й,
2-й, 1-й двигатели из пяти, имеющихся у ЛА.
Замечание.
Тот факт, что события EKD4 и EKD≥5
несовместны, можно доказать следующим
образом:
EKD4∙
EKD≥5
=< согласно (1.7) >= EK∙
ED4∙
EKD≥5=<
согласно (1.6) >= EK∙
ED4∙
ЕKD5 =
=< согласно (1.6) и (1.8) = EK(D1∙
D2
∙ D3∙D4
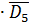
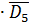 +
D1∙
D2
∙ D3∙
+
D1∙
D2
∙ D3∙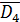
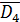 ∙ D5 +
D1∙
D2
∙
∙ D5 +
D1∙
D2
∙ 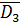
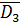 ∙D4∙D5
+ D1∙
∙D4∙D5
+ D1∙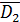
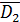 ∙ D3∙D4∙D5 +
∙ D3∙D4∙D5 +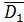
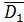 ∙ D2
∙ D3∙D4
∙ D5)
∙ D1∙
D2∙
D3∙
D4∙
D5
= EK
((D1∙
D2∙
D3∙
∙ D2
∙ D3∙D4
∙ D5)
∙ D1∙
D2∙
D3∙
D4∙
D5
= EK
((D1∙
D2∙
D3∙
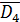
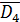 ∙D5
∙D5
 D1∙
D2∙
D3∙
D4∙D5)+(D1∙
D2∙
D1∙
D2∙
D3∙
D4∙D5)+(D1∙
D2∙
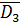
 ∙ D4∙D5
∙ D1∙
D2∙
D3∙
D4∙D5)+(D1∙
∙ D4∙D5
∙ D1∙
D2∙
D3∙
D4∙D5)+(D1∙
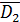
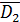 ∙ D3∙
D4∙D5
∙ D1∙
D2∙
D3∙
D4∙D5)+(
∙ D3∙
D4∙D5
∙ D1∙
D2∙
D3∙
D4∙D5)+(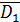
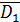 ∙ D2∙
D3∙
D4∙D5
∙ D1∙
D2∙
D3∙
D4∙D5)+(D1∙
D2∙
D3∙
D4∙
∙ D2∙
D3∙
D4∙D5
∙ D1∙
D2∙
D3∙
D4∙D5)+(D1∙
D2∙
D3∙
D4∙
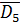
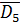 ∙D1∙
D2∙
D3∙
D4∙
∙D1∙
D2∙
D3∙
D4∙
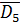
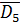 )=
)=
= EK((D1∙
D1)∙(D2
∙D2)∙(D3∙
D3)∙(D4∙
D4)
∙(D5
∙ 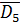
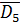 ) + (D1∙
D1)∙(D2∙
D2)∙(D3∙
D3)∙(D4∙
) + (D1∙
D1)∙(D2∙
D2)∙(D3∙
D3)∙(D4∙
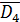
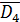 )∙(D5
∙ D5)+(D1∙
D1)∙(D2∙
D2)∙(D3∙
)∙(D5
∙ D5)+(D1∙
D1)∙(D2∙
D2)∙(D3∙
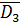
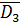 )∙(D4∙
D4)
∙(D5
∙ D5)
+(D1∙
D1)∙(D2∙
)∙(D4∙
D4)
∙(D5
∙ D5)
+(D1∙
D1)∙(D2∙
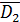
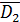 )∙(D3∙
D3)∙(D4∙
D4)
∙(D5
∙ D5)+(D1∙
)∙(D3∙
D3)∙(D4∙
D4)
∙(D5
∙ D5)+(D1∙
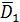
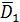 )∙(D2∙
D2)∙(D3∙
D3)∙(D4∙
D4)
∙(D5
∙ D5)
)∙(D2∙
D2)∙(D3∙
D3)∙(D4∙
D4)
∙(D5
∙ D5)
Используя тот факт, что A∙A = A и A∙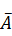
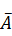 =Ø,
получим
=Ø,
получим
EKD4∙ EKD≥5
=EK((D1 ∙D2 ∙ D3 ∙D4∙ Ø) + (D1 ∙D2 ∙D3∙ Ø∙ D5)+ (D1 ∙D2 ∙ Ø ∙ D4∙D5) + (D1 ∙ Ø ∙ D3 ∙D4∙D5) + (Ø ∙D2 ∙D3 ∙D4∙ D5)) = Ø
А как известно, что, если
произведение двух событий равно невозможному событию (пустому множеству), то
такие события являются несовместными.
По определению условной вероятности
имеем:
P(EKD)=P(EK
/ ED4)∙P(ED4)+P(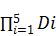
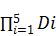 )
)
а в силу независимости
событий Di, i=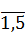
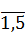 , далее имеем:
, далее имеем:
P(EK / ED4)
∙ P(ED4)+
P(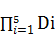
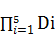 )
)
Используя (1.7) и
несовместимость его (ED4)
слагаемых
P(EK / ED4)∙(P(D1∙
D2
∙ D3∙D4
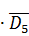
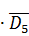 ) +
P(D1∙
D2
∙ D3∙
) +
P(D1∙
D2
∙ D3∙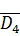
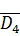 ∙ D5 )
+ P(D1∙
D2
∙
∙ D5 )
+ P(D1∙
D2
∙ 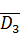
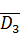 ∙D4∙D5)+
P(D1∙
∙D4∙D5)+
P(D1∙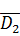
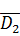 ∙ D3∙D4∙D5)
+ P(
∙ D3∙D4∙D5)
+ P(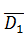
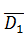 ∙ D2
∙ D3∙D4
∙ D5))+
∙ D2
∙ D3∙D4
∙ D5))+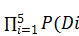
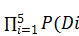 )
)
В силу всех независимых
событий Di 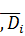
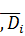 , i=
, i=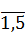
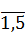 и потому, что
и потому, что
P(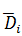
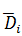 )=1-P(Di),
получим далее:
)=1-P(Di),
получим далее:
P(EK / ED4)∙
 [(P(D1)∙P(D2)∙P(D3)∙(P(D4)
∙(1-P(D5))+ (P(D1)∙P(D2)∙P(D3)∙(1-P(D4)) ∙P(D5)+P(D1)∙P(D2)∙(1-P(D3))∙P(D4) ∙P(D5) +P(D1)∙(1-P(D2))∙P(D3)∙P(D4) ∙P(D5) +(1-P(D1)∙ P(D2)∙ P(D3)∙P(D4) ∙P(D5)]+
[(P(D1)∙P(D2)∙P(D3)∙(P(D4)
∙(1-P(D5))+ (P(D1)∙P(D2)∙P(D3)∙(1-P(D4)) ∙P(D5)+P(D1)∙P(D2)∙(1-P(D3))∙P(D4) ∙P(D5) +P(D1)∙(1-P(D2))∙P(D3)∙P(D4) ∙P(D5) +(1-P(D1)∙ P(D2)∙ P(D3)∙P(D4) ∙P(D5)]+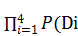
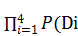 )
)
Так как P(Di)=Pi,
i=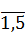
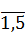 и P(EK
/ ED4)=PD,
имеем
и P(EK
/ ED4)=PD,
имеем
P(EKD)=PD∙[P1∙
P2∙
P3
∙P4∙(1-P5)+P1∙
P2∙
P3
∙(1 - P4)∙P5
+ P1∙
P2∙(1
- P3)∙
P4∙P5
+ P1∙(1
- P2)∙
P3∙
P4∙P5
+(1 - P1)∙
P2∙
P3∙
P4∙P5]+
P1∙
P2∙
P3
∙ P4
∙P5=PD∙[P1∙
P2∙
P3∙
P4+
P1∙
P2∙
P3∙P5+
P1∙
P2∙
P4∙P5+
P1∙
P3∙
P4∙P5+
P2∙
P3∙
P4∙P5]∙(1-5PD)∙ P1∙
P2∙
P3
∙ P4∙P5≡PKD;
Если выполняется условие
P
«PD для всех i=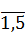
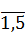 (1.9)
(1.9)
и учитывая, то что значение
вероятности случайного события есть величина, меньшая единицы, то
P1∙ P2∙ P3 ∙ P4∙ P5→0
А значит тоже
(1-5PD)∙ P1∙ P2∙ P3 ∙ P4∙ P5→0
И тогда имеем
P(EKD)≡PKD≈PD∙(P1∙ P2∙ P3∙ P4+ P1∙ P2∙ P3∙P5+ P1∙ P2∙ P4∙P5+ P1∙ P3∙ P4∙P5+ P2∙ P3∙ P4∙P5) (1.10)
Подставив значения, данные из
условия задания, получим
P(EKD)≡PKD≈PD∙(P1∙ P2∙ P3∙ P4+ P1∙ P2∙ P3∙P5+ P1∙ P2∙ P4∙P5+ P1∙ P3∙ P4∙P5+ P2∙ P3∙ P4∙P5)=0.1∙(6∙10-4∙5∙10-4∙7∙10-4∙2∙10-4+6∙10-4∙5∙10-4∙7∙10-4∙4∙10-4+6∙10-4∙5∙10-4∙2∙10-4∙4∙10-4+6∙10-4∙7∙10-4∙2∙10-4∙4∙10-4+5∙10-4∙7∙10-4∙2∙10-4∙4∙10-4)=
=0.1∙10-16∙(420+840+240+336+280)=21.16∙10-16
(1.10)
) Рассмотрим структуру событий Екэ
и найдем P(EКЭ)=PКЭ
EКЭ≡ B1∙ B2∙ B3∙ B4 - катастрофа, связанная
с отказом всех трех систем энергоснабжения (п= 4 по условию
задачи).
В силу независимости
всех событий Bi, i=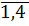
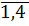 имеем
имеем
P(EКЭ)
≡P(B1∙B2∙B3∙
B4)=P(B1)
∙P(B2)
∙P(B3)
∙P(B4)
=P1э∙P2э∙P3э∙P4э
(1.12)
Подставив значения,
данные из условия задания, получим
P(EКЭ)≡P(B1∙B2∙B3∙ B4)=P(B1) ∙P(B2) ∙P(B3) ∙P(B4)=P1э∙P2э∙P3э∙P4э =3∙10-4∙4∙10-4∙10-4∙6∙10-4=120∙10-16
(1.13)
) Рассмотрим структуру события екс
и найдем P(екс) = Pкс.
Событие Екс наступает,
если отказывает хотя бы одна из вспомогательной подсистемы, значит
екс≡C1+C2+
… +CN=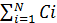
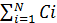
В силу закона двойственности
екс≡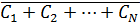
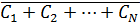 =
= 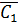
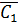 ∙
∙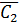
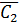 ∙…∙
∙…∙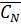
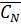 =
=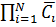
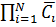
в силу независимости
событий 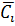
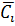 , i=
, i=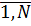
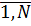 получим
получим
P
(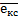
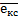 ) ≡P(
) ≡P(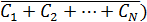
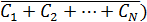 =P(
=P(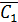
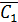 ) ∙ P(
) ∙ P(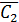
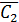 )∙…∙ P(
)∙…∙ P(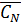
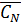 )=
)=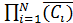
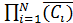 =
=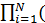
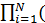 1-P(Ci))
1-P(Ci))
Так как P(Ci)=Pc,
i=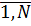
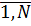 получим
получим
P
(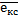
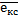 )=
)=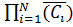
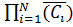 =
=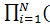
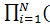 1-Pс)=(1-Pc)N
1-Pс)=(1-Pc)N
тогда
P(екс)=(1-
P (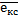
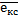 )=1 - (1-Pc)N≡PKC
)=1 - (1-Pc)N≡PKC
Если выполняется NPC<<1=>
P
(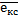
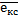 )=(1-Pc)N=1-NPC+
)=(1-Pc)N=1-NPC+
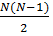
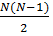 PC2-…
(-1)N PcN ≈ 1-NPC
(1.14)
PC2-…
(-1)N PcN ≈ 1-NPC
(1.14)
Подставив значения,
данные из условия задания, получим
P(екс)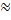
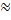 1-1+NPC=NPC=3∙103∙6∙10-9=18∙10-6
(1.15)
1-1+NPC=NPC=3∙103∙6∙10-9=18∙10-6
(1.15)
.2 Расчетная часть
Переходим к числовым расчетам.
Вычислим вероятность катастрофы по выведенной нами формуле (1.5). Так как в
нашем случае выполняется условие (1.9), то
P(EК)=1
- (1 - P(EKD))∙(1-P(екс))∙P(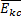
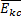 ))=1-
))=1-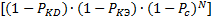
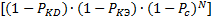 ==1
- (1 - PD∙(P1∙
P2∙
P3∙
P4+
P1∙
P2∙
P3∙P5+
P1∙
P2∙
P4∙P5+
P1∙
P3∙
P4∙P5+
P2∙
P3∙
P4∙P5)+
(1-5
==1
- (1 - PD∙(P1∙
P2∙
P3∙
P4+
P1∙
P2∙
P3∙P5+
P1∙
P2∙
P4∙P5+
P1∙
P3∙
P4∙P5+
P2∙
P3∙
P4∙P5)+
(1-5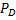
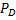 ) P1P2P3P4
P5)∙(1-P1Э∙
P2Э∙
P3Э
P4Э)∙(1-Pc)N
) P1P2P3P4
P5)∙(1-P1Э∙
P2Э∙
P3Э
P4Э)∙(1-Pc)N
Если выполняется условие NPC<<1 и PKD<<1 и PКЭ<<1, то будем далее иметь
PKD+ PКЭ+ NPC=21.16∙10-16+120∙10-16+18∙10-6
≈18∙10-6
Так как 21.16∙10-16≤120∙10-16≤18∙10-6,
видно, что PКЭ ≤ PKD ≤ Pкс из этого следует, что вероятность катастрофы, связанной с отказом
вспомогательных подсистем, является определяющей.
В) Теперь рассмотрим
случай ЛА без дублирующих систем:
P’КЭ= P’1Э; ≤ P’KD = P1=>
P’ (EK)=P1+P1Э+NPC=6∙10-4+3∙10-4+18∙10-6=918∙10-6
P’KЭ < P’КD < PКС, а из этого следует, что вероятность катастрофы, связанной с
отказом двигателя и систем энергоснабжения, является определяющей.
И, наконец, сравним вероятности P’ (EK) и P’ (EK):
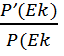
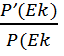 =
=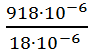
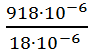 =51
=51
Вывод
На основании вышеизложенного можно
заключить, что наиболее вероятной является катастрофа, связанной с отказом
одной из вспомогательных подсистем, а отсутствие дублирующих систем увеличивает
вероятность катастрофы в 51 раз, при этом определяющим фактором становится
отказ двигателя или системы энергоснабжения.
2. Определение
надежности элементов системы энергоснабжения самолета задача №2
.1 Постановка задачи
задания №2
Испытываются m элементов системы энергоснабжения самолета, которые работают
независимо один от другого. Длительность времени безотказной работы элементов
распределена по показательному закону с функциями надежности Ri(t), 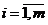 для
каждого из
для
каждого из 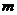 элементов,
где
элементов,
где 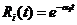 ;
;
Определить вероятность
того, что в интервале (0;в)
часов откажут
а) только один элемент;
b)
только два элемента;
c)
все m элемента.
Дано:
m
= 3;
б1
= 0,37; б2
= 0,47; б3
= 0,17;
в
= 5;
Решение.
Математическая часть
Введем обозначения:
A1,
A2,
A3,
A4
- событие, состоящее в том, что отказал только один элемент, только два, все
три элемента, ни один элемент не отказал.
p1,
p2,
p3
- вероятность отказа 1-го, 2-го, 3-го элемента в заданном
интервале (0; 5) соответственно; тогда
q1,
q2,
q3
- вероятность безотказной работы 1-го, 2-го, 3-го элемента в
заданном интервале (0; 5) соответственно;
Вероятность p1
отказа 1-го элемента в заданном интервале (0; 5) будет равна:
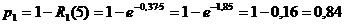 , следовательно:
, следовательно:
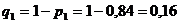 .
.
Вероятность p2
отказа 2-го элемента в заданном интервале (0; 5) будет равна:
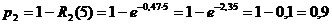 , следовательно:
, следовательно:
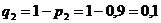 .
.
Вероятность p3
отказа 3-го элемента в заданном интервале (0; 5) будет равна:
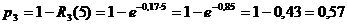 , следовательно:
, следовательно:
 .
.
2.2 Расчетная часть
Переходим к расчету
искомых вероятностей, которые находится следующим образом:
Вероятность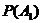 отказа
только одного элемента в заданном интервале (0; 5) будет равна:
отказа
только одного элемента в заданном интервале (0; 5) будет равна:
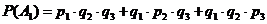 ;
;
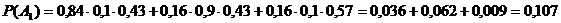
Вероятность 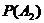 отказа
только двух элементов в заданном интервале (0; 5) будет равна:
отказа
только двух элементов в заданном интервале (0; 5) будет равна:
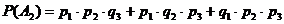
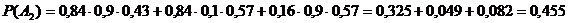
Вероятность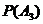 отказа только трех элементов в заданном интервале (0; 5) будет равна:
отказа только трех элементов в заданном интервале (0; 5) будет равна:
 .
.
Вероятность  безотказной
работы всех трёх элементов за время испытания в заданном интервале (0; 5) будет
равна:
безотказной
работы всех трёх элементов за время испытания в заданном интервале (0; 5) будет
равна:
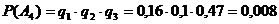 .
.
Вывод
На основании изложенного
можно заключить, что при заданных данных во время испытаний в заданном
интервале (0; 5) наиболее вероятным являются отказ только двух элементов, а наименее
вероятным является отказ только одного элемента, так как:
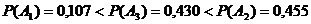
Вероятность того, что
все три элемента безотказно отработают во время испытаний в заданном интервале
(0; 5) является небольшой, а именно:
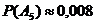
Список использованной
литературы
1. Сотсков Ю.Н.,
Нарольская А.Н. Теория расписаний. Методичеcкое пособие. - Мн.: РИО МГВАК,
2008.
. Сапцин В.М. Высшая
математика. Часть 1. - Мн.: РИО МГВАК, 2002.
. Барковская Л.С.,
Станишевская Л.В., Черторицкий Ю.Н. Теория вероятностей. Практикум. - Мн.: РИО
УО «БГЭУ», 2004.