|
Производная алгебраической суммы функций
|
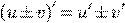
|
|
Производная произведения функций
|
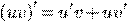
|
|
Производная частной функций
|
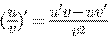
|
|
Производная сложной функций
|
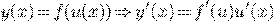
|
Пример 1.
Найти
производную (вынос постоянного числа за знак производной) 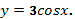
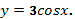
Решение.
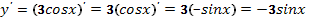
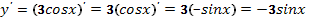 .
.
Пример
2. Найти производную частного функции 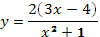
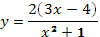 .
.
Решение.
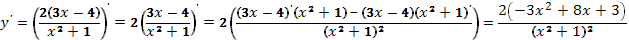

Упражнения.
Вычислить
производную функции:
)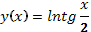
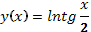
)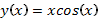
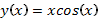
)
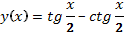
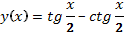 .
.
Ответы
упражнениям.
)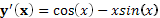
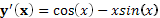 2)
2)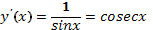
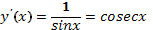 3)
3) 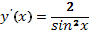
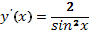 .
.
дифференциальный уравнение экономический
Дифференциальное уравнение n-го
порядка записывается в виде:
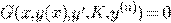 .
.
Обыкновенным ДУ первого порядка является уравнение вида:
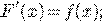
уравнением в частных производных первого порядка является уравнение вида:
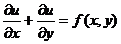 ;
;
уравнением 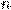 -го порядка, разрешенным относительно старшей производной
является уравнение вида:
-го порядка, разрешенным относительно старшей производной
является уравнение вида:
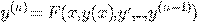 .
.
Решением дифференциального уравнения называется такая функция 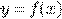 , которая при подстановке ее в данное
уравнение обращает его в тождество. Задача о нахождении решения некоторого
дифференциального уравнения --- задача интегрирования данного дифференциального
уравнения.
, которая при подстановке ее в данное
уравнение обращает его в тождество. Задача о нахождении решения некоторого
дифференциального уравнения --- задача интегрирования данного дифференциального
уравнения.
Общее решение ДУ --- это такое его решение,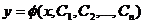 , которое является функцией
независимой переменной и произвольных постоянных, число которых равно порядку
уравнения.
, которое является функцией
независимой переменной и произвольных постоянных, число которых равно порядку
уравнения.
Частное решение ДУ --- это решение, получаемое из общего решения, при
некоторых конкретных числовых значениях произвольных постоянных.
2.2 Теорема 1
(условия существования и единственности задачи Коши)
Задача Коши:
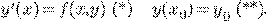
Пусть в ДУ (*) правая часть и ее частная производная по 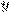 непрерывны на открытом множестве
непрерывны на открытом множестве 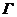 координатной плоскости ОХУ. Тогда
справедливы утверждения:
координатной плоскости ОХУ. Тогда
справедливы утверждения:
. Для всякой точки 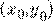 из открытого множества
из открытого множества 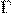 найдется решение
найдется решение 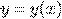 уравнения (*), удовлетворяющее
начальному условию (**)
уравнения (*), удовлетворяющее
начальному условию (**) 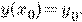
. Если два решения 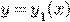 и
и 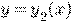 уравнения (*) совпадают хотя бы для одного значения
уравнения (*) совпадают хотя бы для одного значения 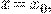 т.е. если
т.е. если 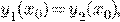 то эти решения совпадают при всех
значениях переменной
то эти решения совпадают при всех
значениях переменной 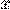 , для которых они определены.
, для которых они определены.
Примеры.
.  Это ДУ первого порядка. Общее
решение
Это ДУ первого порядка. Общее
решение 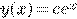 . Условие Теоремы 1 выполнено для
всей OXY. Решением задачи Коши с начальными условиями
. Условие Теоремы 1 выполнено для
всей OXY. Решением задачи Коши с начальными условиями 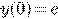 является функция
является функция 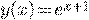 .
.
. 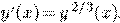 Это ДУ первого порядка. Общее
решение ДУ
Это ДУ первого порядка. Общее
решение ДУ 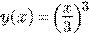 . Условие Теоремы 1 для всей OXY не выполнено (т.к. частная
производная
. Условие Теоремы 1 для всей OXY не выполнено (т.к. частная
производная 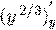 не существует при
не существует при 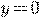 ). Поэтому единственность решения
нарушается в точке
). Поэтому единственность решения
нарушается в точке 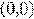 .
.
Упражнения.
1)
Найти частное решение дифференциального уравнения 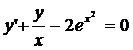 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 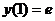 .
.
)
Найти решение задачи Коши для данного дифференциального уравнения 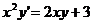 ,
, 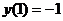 .
.
Ответы
к упражнениям.
)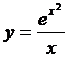 . 2)
. 2)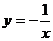 .
.
2.3 Неполные
ДУ первого порядка
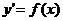 или
или  . Решение выглядит так
. Решение выглядит так 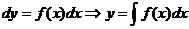 .
.
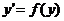 или
или 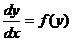 . Решение выглядит так
. Решение выглядит так 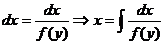 .
.
Примеры.
)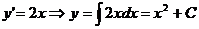
)
 .
.
Упражнения.
1)
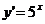
)
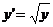 .
.
Ответы
к упражнениям.
)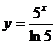 2)
2)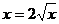 .
.
.4 ДУ с
разделяющимися переменными
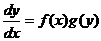 или
или 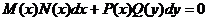 .
.
Тогда 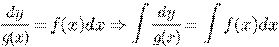 .
.
Пример.
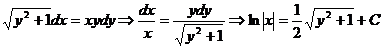 .
.
Упражнения.
)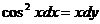
)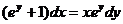 .
.
Ответы
к упражнениям.
)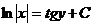 2)
2)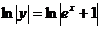 .
.
2.5
Однородные ДУ
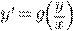
Сделаем замену
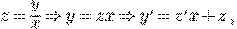
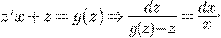
Функция 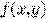 --- однородная
--- однородная 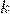 -го порядка (степени
-го порядка (степени 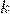 ), если
), если 
Функция 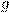 в уравнении --- однородная нулевой степени.
в уравнении --- однородная нулевой степени.
Уравнение 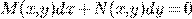 может быть сведено к однородному:
может быть сведено к однородному:
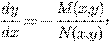
если 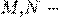 однородные функции степени
однородные функции степени 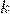 .
.
Примеры.
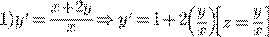
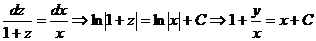 .
.
Упражнения.
)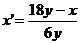
)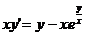 .
.
Ответы
к упражнениям.
)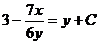 2)
2)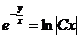 .
.
2.6 Линейные
ДУ первого порядка
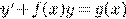 .
.
Сделаем замену
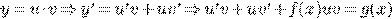
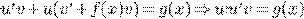 , т. к.
, т. к. 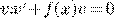 .
.
Пример.
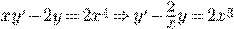
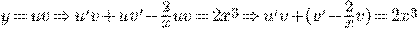
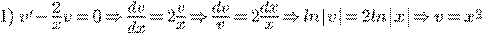
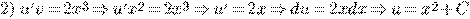
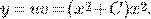
Упражнения.
)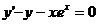 .
.
Ответы
к упражнениям.
1)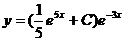 2)
2)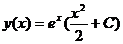 .
.
2.7 ДУ
Второго порядка, допускающие понижение порядка
В некоторых случаях решение ДУ второго порядка может быть сведено к
последовательному решению двух ДУ первого порядка. Тогда говорят, что ДУ
допускает понижение порядка.
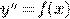 .
.
Уравнение можно переписать в виде
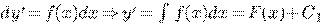
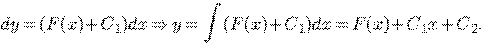
Пример.
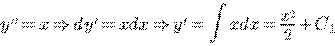 .
.
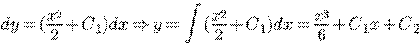 .
.
при 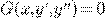 .
.
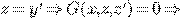 отсюда находим
отсюда находим 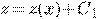
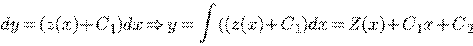 .
.
Пример.
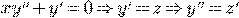
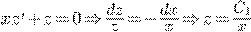
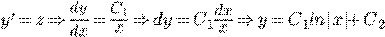 .
.
при 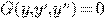 .
.
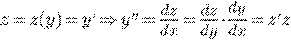
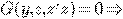 находим
находим 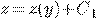
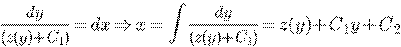 .
.
ПРИМЕР.
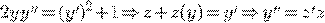
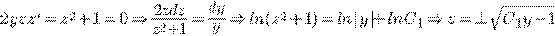
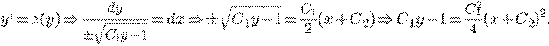
Упражнения.
1)
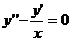
)
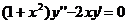
)
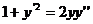 .
.
Ответы
к упражнениям.
)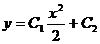 2)
2)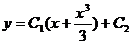 3)
3)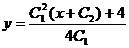 .
.
.8 Линейные
ДУ второго порядка с постоянными коэффициентами
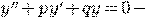 однородное ДУ.
однородное ДУ.
 неоднородное ДУ.
неоднородное ДУ.
2.9
Однородные линейные ДУ 2-го порядка с постоянными коэффициентами
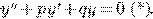
Ищем решение Эйлера:
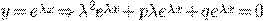
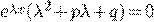 где
где 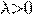
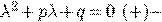 характеристическое уравнение ДУ (*).
характеристическое уравнение ДУ (*).
Корни характеристического уравнения и линейно независимые решения ДУ (*)
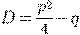
при 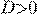 имеем
имеем
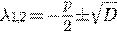
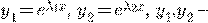 линейно независимые решения.
линейно независимые решения.
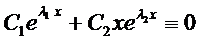
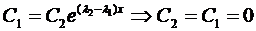
при 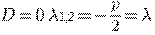
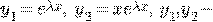 линейно независимые решения.
линейно независимые решения.
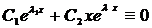
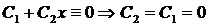
при 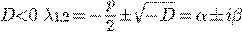
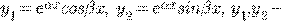 линейно независимые решения.
линейно независимые решения.
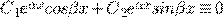
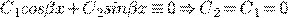 .
.
Теорема. Если 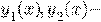 два линейно независимых решения ДУ (*),то общее решение (*)
имеет вид:
два линейно независимых решения ДУ (*),то общее решение (*)
имеет вид: 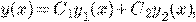 где
где 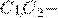 произвольные постоянные.
произвольные постоянные.
.10
Неоднородные линейные ДУ 2-го порядка с постоянными коэффициентами
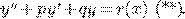
Метод вариации произвольных постоянных.
Решение ищем в виде линейной комбинации решений (*), где произвольные
постоянные являются функциями от 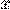 :
:

функции 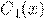 и
и 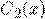 находим, решая систему из двух уравнений:
находим, решая систему из двух уравнений:
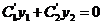 ,
, 
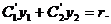
Пример 1.
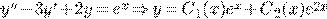
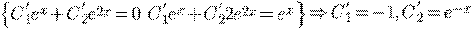
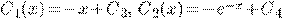
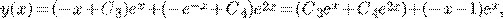
где 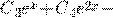 общее решение (*),
общее решение (*), 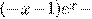 частное решение (**).
частное решение (**).
Теорема. Общее решение ДУ (**) равно сумме общего решения однородного ДУ
(*) и частного решения неоднородного ДУ (**).
Частные решения неоднородного ДУ (**) для некоторых видов правой части.
) Правая часть 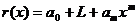 .
.
Частное решение 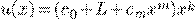
Пример 2.
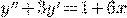
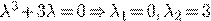
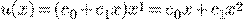
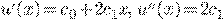
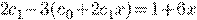
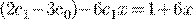
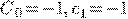
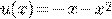 .
.
) Правая часть 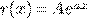 .
.
Частное решение 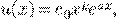
где 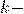 кратность
кратность 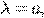 как корня характеристического уравнения (+).
как корня характеристического уравнения (+).
Пример 3.
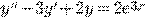
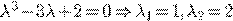
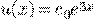
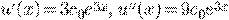
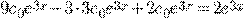
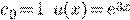 .
.
) Правая часть 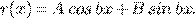
Частное решение 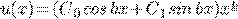 ,
,
где 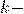 кратность
кратность 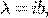 как корня характеристического уравнения (+).
как корня характеристического уравнения (+).
Пример 4.
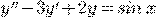
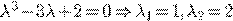
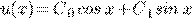
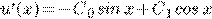
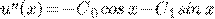
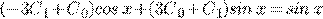
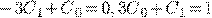
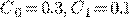
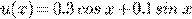 .
.
) Правая часть 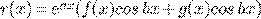 .
.
Частное решение 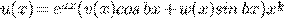 ,
,
где 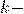 кратность
кратность 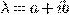 , как корня характеристического уравнения (+), степень
, как корня характеристического уравнения (+), степень 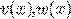 равна наибольшей из степеней
многочленов
равна наибольшей из степеней
многочленов 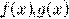 .
.
Упражнения.
1)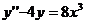
)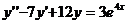
)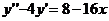 .
.
Ответы
к упражнениям.
)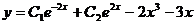
)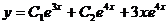
)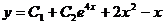 .
.
2.11 Система
дифференциальных уравнений
Нормальная система ДУ 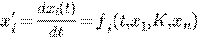 при
при 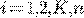
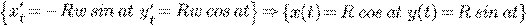
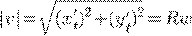 .
.
Иногда система ДУ сводится к ДУ более высокого порядка, зависящего только
от одной функции:
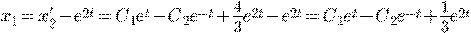 .
.
Автономная система ДУ
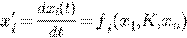 при
при 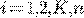 .
.
2.12
Использование дифференциальных уравнений для решения экономических задач
Дифференциальные уравнения находят достаточно широкое применение в
моделях экономической динамики, в которых отражается не только зависимость
переменных от времени, но и их взаимосвязь во времени.
Пример 1.
Рассмотрим процесс возрастания денежной суммы, положенной в банк при
условии начисления 100 r сложных процентов в год. Пусть 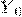 обозначает начальную денежную сумму,
а
обозначает начальную денежную сумму,
а 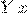 --- денежную сумму по истечении
--- денежную сумму по истечении 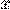 лет.
лет.
Если бы проценты начислялись один раз в год, мы бы имели
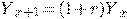
где 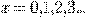
Если бы проценты начислялись два раза в год (по истечении каждого
полугодия), то мы бы имели
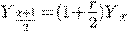
где 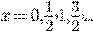
Вообще, если проценты начисляются 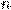 раз в год и
раз в год и  принимает последовательно значения
принимает последовательно значения 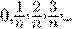
Тогда 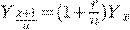 то есть
то есть 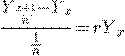 .
.
Если обозначить 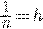 , то предыдущее равенство перепишется так
, то предыдущее равенство перепишется так
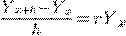 .
.
Неограниченно увеличивая 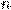 (при
(при 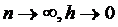 ) мы в пределе приходим к процессу возрастания денежной суммы
при непрерывном начислении процентов
) мы в пределе приходим к процессу возрастания денежной суммы
при непрерывном начислении процентов
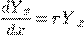 ,
,
то есть при непрерывном изменении 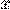 закон возрастания выражен
дифференциальным уравнением 1-го порядка. Отметим для четкости, что
закон возрастания выражен
дифференциальным уравнением 1-го порядка. Отметим для четкости, что 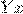 --- неизвестная функция,
--- неизвестная функция, 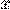 --- независимая переменная,
--- независимая переменная, 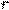 --- постоянная. Для решения данного
уравнения перепишем его следующим образом:
--- постоянная. Для решения данного
уравнения перепишем его следующим образом:
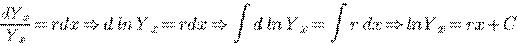
откуда 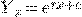 , или
, или 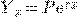 , где через
, где через 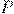 обозначено
обозначено 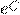 .
.
Учитывая начальное условие 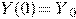 , найдем
, найдем 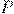 :
: 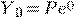 , следовательно,
, следовательно, 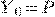 .
.
Решение имеет вид: 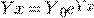 .
.
Найти функцию спроса, если 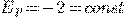 и
и 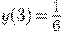 . Эластичность спроса (относительно
цены) определяется формулой
. Эластичность спроса (относительно
цены) определяется формулой
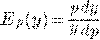 .
.
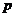 ---
первоначальное значение цены,
---
первоначальное значение цены,
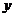 ---
первоначальное значение объема спроса.
---
первоначальное значение объема спроса.
Из
определения эластичности следует, что 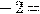
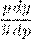 , т.е.
искомая функция задается уравнением с разделяющимися переменными. Решая это
уравнение, получаем
, т.е.
искомая функция задается уравнением с разделяющимися переменными. Решая это
уравнение, получаем 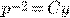 .
.
Учитывая
начальное условие 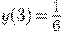 , имеем
, имеем 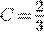 .
Окончательно
.
Окончательно 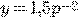 .
.
Упражнения.
)
В поселке с населением 3000 человек распространение эпидемии гриппа (без
применения экстренных санитарно-профилактических мер) описываемых уравнением 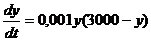 , где
, где 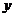 - число
заболевших в момент времени
- число
заболевших в момент времени 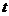 ;
; 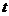 - число недель. Сколько больных будет в поселке через
две недели, если в начальный момент было трое больных?
- число недель. Сколько больных будет в поселке через
две недели, если в начальный момент было трое больных?
)
Функция спроса и предложения имеют вид:
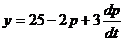 ,
, 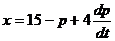 .
.
Найти
зависимость равновесной цены от времени, если в начальный момент 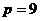 .
.
В
простейших ситуациях спрос на товар (предложение товара) предполагается
зависящим от его цены. В более сложных случаях в расчет принимается также
зависимость спроса (предложения) от скорости изменения цены.
)Найти
функцию дохода 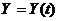 , если известно, что величина потребления задается
функцией
, если известно, что величина потребления задается
функцией 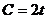 ; коэффициент капиталоемкости пророста дохода
; коэффициент капиталоемкости пророста дохода 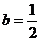 ,
, 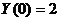 .
.
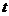 ---
единица времени.
---
единица времени.
Коэффициент
капиталоемкости --- отношение применяемого в производственном процессе, фирме
или отрасли капитала к объему выпуска в течение определенного периода времени,
как правило, одного года.
Ответы
к упражнениям.
)
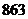 2)
2)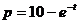 3)
3)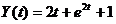 .
.
3. Тест
Найти дифференциал функций:
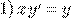
a)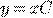 b)
b)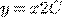 c)
c)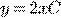 d)
d)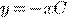
)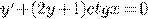 )
)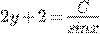 b)
b)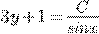 c)
c)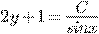 d)
d)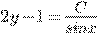
)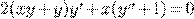 )
)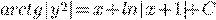 b)
b)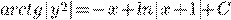 )
)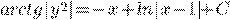 d)
d)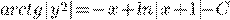
)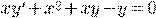 )
)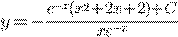 b)
b)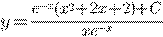 c)
c)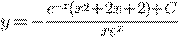 )
)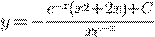
) )
)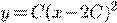 b)
b)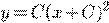 c)
c)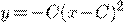 d)
d)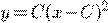
) )
)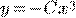 b)
b)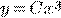 c)
c)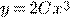 d)
d)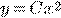
)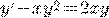 )
)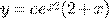 b)
b)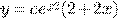 c)
c)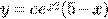 d)
d)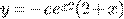
)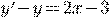 )
)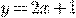 b)
b)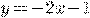 c)
c) d)
d)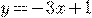
9)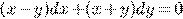 )
)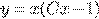 b)
b)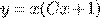 c)
c)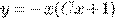 d)
d)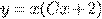
)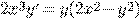 )
)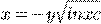 b)
b)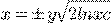 c)
c)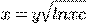 d)
d)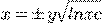
Ответы к тесту: 1)a 2)c 3)b 4)a 5)d 6)b 7)a 8)c 9)b 10)d
Используемая
литература
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика
в упражнениях и задачах. // М., Высшая школа. 1986 ( в 2 - х томах ).
. Под ред. проф. В.И. Ермакова. Сборник задач по высшей
математике. // М., Инфра - М., 2001.
. Васильев А.А. Практикум по высшей математике. Аналитическая
геометрия. ч. 2. Пределы последовательностей. // Сыктывкар, 2007.
. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А.
Сборник задач по высшей математике. // М., Айрис Пресс, 2001.
. Смирнов В.И. Курс высшей математики, том 3, часть 1 (10-е
издание). // М.: Наука, 1974