Группы симметрий правильных многогранников
План
Введение
Глава
1. Понятие группы
§1.
Определение группы
§2.
Разновидности групп
§3.
Действие группы на множестве
§4.
Группы симметрий
Глава
2. Лемма Бернсайда о количестве орбит
§1.
Формулировка и доказательство
§2.
Задачи о раскрасках
Заключение
Литература
Введение
Правильные многогранники известны человечеству с
давних времен. Так, например, недавно в Шотландии при раскопках были обнаружены
камни, ограненные в виде всех пяти правильных многогранников. Эти находки
относят ко второму тысячелетию до нашей эры.
Первое письменное упоминание о правильных
многогранниках принадлежит грекам. Пифагорейцам были известны тетраэдр, куб и
октаэдр. Описание додекаэдра и икосаэдра приписывается Теэтету Афинскому
(начало IV в. до н.э.); он же доказал, что других правильных многогранников не
существует.
Самый термин «группа» принадлежит французскому
математику Галуа - подлинному создателю теории групп. Идеи теории групп
«носились» в воздухе задолго до Галуа, и некоторые из ее теорем в наивной форме
были доказаны еще Лагранжем. Гениальные работы Галуа оказались непонятыми, и
возрождение интереса к ним началось только после книги Жордана «Курс теории
перестановок и алгебраических уравнений» (1870г.).
Группы симметрии многогранников изучались
многими математиками и кристаллографами. После того, как Лежандр (1833) впервые
ввёл математическое понятие симметрии в геометрию, Р.-Ж. Гаюи применил это
понятие в кристаллографии. В дальнейшем изучение возможных видов симметрии
многогранников было продолжено И.Ф.Х. Гесселем и О.Браве.
Глава 1. Понятие группы
§1.
Определение группы
Рассмотрим множество G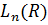 всех n
× n-матриц
с вещественными коэффициентами и с отличным от нуля определителем.
всех n
× n-матриц
с вещественными коэффициентами и с отличным от нуля определителем. 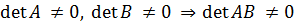 .
Видно, что А, B
.
Видно, что А, B 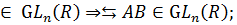 далее, (АВ) C = А
(ВC) и существует выделенная матрица Е такая, что АЕ = = ЕА = А для всех А
далее, (АВ) C = А
(ВC) и существует выделенная матрица Е такая, что АЕ = = ЕА = А для всех А . Кроме того, у каждой матрицы А
. Кроме того, у каждой матрицы А имеется «антипод»
- обратная матрица
имеется «антипод»
- обратная матрица 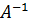 , для которой А
, для которой А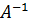 =
= 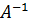 А
= Е.
А
= Е.
Множество G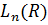 рассматриваемое вместе с законом композиции (бинарной операцией) (А, В)
рассматриваемое вместе с законом композиции (бинарной операцией) (А, В) 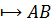 и
называемое полной линейной группой степени n над R, можно было бы коротко
определить, как подмоноид всех обратимых элементов моноида
и
называемое полной линейной группой степени n над R, можно было бы коротко
определить, как подмоноид всех обратимых элементов моноида 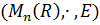 .
.
Пусть Х - произвольное множество. Бинарной алгебраической
операцией на Х называется произвольное (но фиксированное) отображение 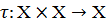 декартова
квадрата
декартова
квадрата 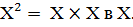 Чаще
всего бинарную операцию на Х обозначают каким-нибудь специальным символом:
Чаще
всего бинарную операцию на Х обозначают каким-нибудь специальным символом: 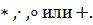
Бинарная операция 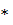 на
множестве Х называется ассоциативной, если
на
множестве Х называется ассоциативной, если 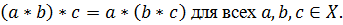
Множество Х с заданной на нём бинарной
ассоциативной операцией называется полугруппой. Полугруппу с единичным
(нейтральным) элементом принято называть ещё моноидом.
Как и для всякого множества, мощность моноида
М=(М, 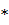 )
обозначается символом Card M или
)
обозначается символом Card M или 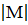 .
.
Подмножество 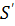 полугруппы
S с операцией
полугруппы
S с операцией 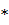 называется
подполугруппой, если х
называется
подполугруппой, если х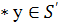 для всех x, у
для всех x, у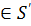 .
В этом случае говорят ещё, что подмножество
.
В этом случае говорят ещё, что подмножество 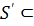 S
замкнуто относительно операции
S
замкнуто относительно операции 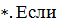 (М,
(М, 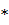 )
- моноид, а подмножество
)
- моноид, а подмножество 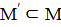 не только замкнуто
относительно операции
не только замкнуто
относительно операции  , но и содержит
единичный элемент, то
, но и содержит
единичный элемент, то 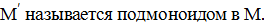
Определение. Моноид G, все элементы которого
обратимы, называется группой. Другими словами, предполагаются выполненными
следующие аксиомы:
(G0) на множестве G определена бинарная
операция: (х,у) ху
ху
(G1) операция ассоциативна: (ху)z = х(уz) для
всех х, у, z  G;
G;
(G2) G обладает нейтральным (единичным)
элементом е: хе = ех = х для всех x 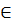 G
G
(G3) для каждого элемента x 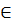 G
существует обратный
G
существует обратный 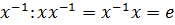
§2. Разновидности групп
Группа с коммутативной операцией называется
коммутативной, а еще чаще - абелевой. Почти всё сказанное выше о моноидах
переносится на группы.
Подмножество Н  G
называется подгруппой в G, если e
G
называется подгруппой в G, если e 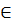 H;
H;
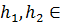 H
H
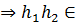 H
и
H
и 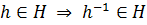 .
Подгруппа
.
Подгруппа 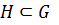 собственная, если
собственная, если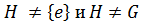
Приведём несколько примеров групп.
В полной линейной группе G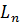 (R)
рассмотрим подмножество S
(R)
рассмотрим подмножество S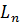 (R) матриц с
определителем 1:
(R) матриц с
определителем 1:
S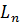 (R)
= {
(R)
= {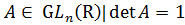 }.
}.
E  .
.
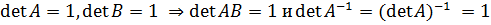 .
.
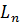 (R)
(R) подгруппа
в
подгруппа
в  ;
она носит название специальной линейной группы степени п над R. Ее называют еще
и унимодулярной группой.
;
она носит название специальной линейной группы степени п над R. Ее называют еще
и унимодулярной группой.
Используя рациональные числа вместо
вещественных, мы придем к полной линейной группе 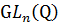 степени
n над Q и к ее подгруппе S
степени
n над Q и к ее подгруппе S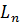 (Q). В свою очередь
S
(Q). В свою очередь
S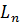 (Q)
cодержит подгруппу S
(Q)
cодержит подгруппу S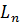 (Z) целочисленных
матриц с определителем 1. S
(Z) целочисленных
матриц с определителем 1. S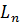 (Z) - также
является группой. Частично упорядоченное множество рассмотренных подгрупп
группы G
(Z) - также
является группой. Частично упорядоченное множество рассмотренных подгрупп
группы G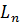 (R)
изображается диаграммой.
(R)
изображается диаграммой.

Положив в примерах 1) и 2) n=1, мы придем,
во-первых, к мультипликативным группам
 вещественных и
рациональных чисел. Эти группы бесконечны. Так как в (Z, ∙ , 1)
обратимыми элементами являются только 1 и -1, то
вещественных и
рациональных чисел. Эти группы бесконечны. Так как в (Z, ∙ , 1)
обратимыми элементами являются только 1 и -1, то 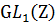 =
{± 1). Далее, S
=
{± 1). Далее, S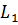 (R) = S
(R) = S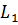 (Q)
= S
(Q)
= S (Z)
= 1. Но уже при п = 2 группа S
(Z)
= 1. Но уже при п = 2 группа S (Z) бесконечна: ей
принадлежат, например, все матрицы
(Z) бесконечна: ей
принадлежат, например, все матрицы
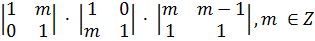
Бесконечные аддитивные группы:
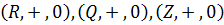
Циклические группы.
Пусть G - мультипликативная группа (т. е. с
операцией умножения), а - ее фиксированный элемент. Если любой элемент g 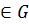 записывается
в виде
записывается
в виде 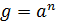 для
некоторого n
для
некоторого n 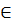 Z, то говорят, что
Z, то говорят, что
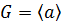 -
циклическая группа с образующим а (или циклическая группа, порожденная
элементом а). Аналогично циклическая группа определяется в аддитивном случае:
-
циклическая группа с образующим а (или циклическая группа, порожденная
элементом а). Аналогично циклическая группа определяется в аддитивном случае: 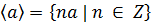 .
Это, конечно, не означает, что все элементы ап или па попарно различны.
Условимся в обозначении
.
Это, конечно, не означает, что все элементы ап или па попарно различны.
Условимся в обозначении 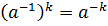 и убедимся в
справедливости следующего утверждения.
и убедимся в
справедливости следующего утверждения.
Теорема 1: Каковы бы ни были m, n 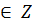 ,
,
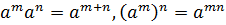
( соответственно 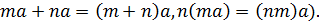
Доказательство: При неотрицательных m, n. Если 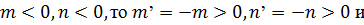
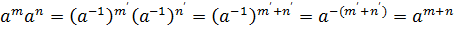 .
.
При 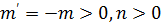 имеем
имеем
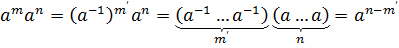
(или 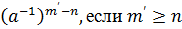 )
)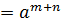 .
.
Аналогично рассматривается случай 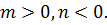
Равенство (ат)п=атп вытекает из предыдущего и
достаточно очевидно из определения степеней.
Простейшим примером циклической группы служит
аддитивная группа целых чисел (Z,+, 0), порожденная обычной единицей 1 или  1.
Множество {1,-1} является по умножению циклической группой порядка 2.
1.
Множество {1,-1} является по умножению циклической группой порядка 2.
Пусть снова G - произвольная группа, а -
некоторый ее элемент. Имеются две возможности: 1) Все степени элемента а
различны, .т. е.  . В этом случае
говорят, что элемент а
. В этом случае
говорят, что элемент а 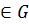 имеет бесконечный
порядок. 2) Имеются совпадения ат = ап при
имеет бесконечный
порядок. 2) Имеются совпадения ат = ап при 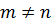 .
Если, например, т > п, то
.
Если, например, т > п, то  т. е. существуют
положительные степени элемента а
т. е. существуют
положительные степени элемента а 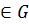 ,
равные единичному элементу. Пусть q- наименьший положительный показатель, для
которого
,
равные единичному элементу. Пусть q- наименьший положительный показатель, для
которого 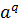 =
е. Тогда говорят, что а - элемент конечного порядка q. В конечной группе G
(Card G < ∞) все элементы, разумеется, будут конечного порядка.
=
е. Тогда говорят, что а - элемент конечного порядка q. В конечной группе G
(Card G < ∞) все элементы, разумеется, будут конечного порядка.
§3.
Действие группы на множестве
Группа G действует (слева) на множестве X, если
для любых элементов g 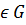 и х
и х 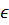 X
определен элемент gх
X
определен элемент gх 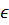 X, причем g2(g1х)
= (g2 g1)х и ех = х для всех х
X, причем g2(g1х)
= (g2 g1)х и ех = х для всех х 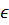 X, g1, g2
X, g1, g2 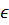 G.
Множествох = {gx | g
G.
Множествох = {gx | g 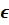 G}
G}
называется орбитой элемента х. Орбиты любых двух
элементов из X либо совпадают, либо не пересекаются, так что множество X
разбивается на непересекающиеся орбиты. Если орбита одна - все множество X, то
говорят, что С действует транзитивно на X. Иначе говоря, группа G действует
транзитивно на множестве X, если для любых двух элементов х, х' из X найдется
элемент g из G такой, что gх = х'.
Стабилизатором элемента х из X называется
подгруппа
StG(x)=
{g
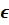 G
| gх
= х}.
G
| gх
= х}.
Множеством неподвижных точек элемента g из G
называется множество
Fiх(g) = {х 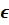 X | gх = х}.
X | gх = х}.
Мощности орбиты 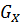 равна
индексу стабилизатора
равна
индексу стабилизатора  в группе G.
в группе G.
Пример:
Пусть К - фиксированный куб в трехмерном
евклидовом пространстве, G - группа всех движений этого пространства,
сохраняющих ориентацию и переводящих К в К. В группе G имеется тождественное
движение, вращения на 120° и 240° вокруг четырех осей, проходящих через
противоположные вершины куба, вращения на 180° вокруг осей, проходящих через
середины противоположных ребер, и вращения на 90°, 180° и 270° вокруг осей,
проходящих через центры противоположных граней. Итак, мы нашли 24 элемента в
группе G. Покажем, что других элементов в G нет. Группа G действует транзитивно
на множестве К0 вершин куба К, так как любые две вершины из К можно «соединить
цепочкой соседних», а соседние можно перевести друг в друга подходящим вращением.
Стабилизатор вершины x должен оставлять на месте также наиболее удаленную от
нее вершину х'. Поэтому он состоит из тождественного движения и вращений вокруг
оси хх' на 120° и 240°. Следовательно, |G| = |К°| • | |
= 8 • 3 = 24 и, значит, все указанные выше вращения составляют группу G.
|
= 8 • 3 = 24 и, значит, все указанные выше вращения составляют группу G.
Группа G называется группой вращений куба.
Докажем, что 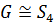 Вращения из G
переставляют четыре самых длинных диагонали куба. Возникает гомоморфизм: φ:
G
→
Вращения из G
переставляют четыре самых длинных диагонали куба. Возникает гомоморфизм: φ:
G
→ 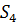 .
Ядро этого гомоморфизма равно {е}, так как только тождественное движение
оставляет каждую диагональ куба на месте. Поэтому G изоморфна подгруппе группы
.
Ядро этого гомоморфизма равно {е}, так как только тождественное движение
оставляет каждую диагональ куба на месте. Поэтому G изоморфна подгруппе группы 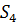 .
Сравнивая порядки этих групп, получаем, что G
.
Сравнивая порядки этих групп, получаем, что G 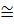
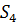 .
.
Одним из наиболее употребляемых примеров групп
и, в частности, групп перестановок, являются группы, которыми «измеряется»
симметричность геометрических фигур как плоских, так и пространственных.
Группа симметрий тетраэдра.
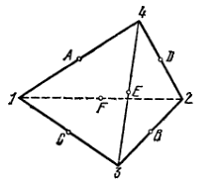
Тетраэдр (рис. 1) имеет 4 оси симметрии l1, l2,
l3, l4 3-го порядка, проходящие через его вершины 1, 2, 3, 4 и центры
противолежащих граней. Вокруг каждой оси, кроме тождественного, возможны еще
два вращения. Им соответствуют такие перестановки:
вокруг оси l1 
вокруг оси l2 
вокруг оси l3 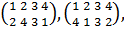
вокруг оси l4 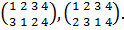
Кроме того, имеется 3 оси симметрии 2-го
порядка, проводящие через середины А, В, С, D, Е, F скрещивающихся ребер.
Поэтому имеется еще 3 (по числу пар скрещивающихся ребер) нетождественных
преобразования, которым соответствуют перестановки:
вокруг оси AB  ,
,
вокруг оси CD 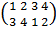 ,
,
вокруг оси EF 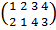 .
.
Итак, вместе с тождественным преобразованием
получаем 12 перестановок. При указанных преобразованиях тетраэдр
самосовмещяется, поворачиваясь в пространстве; его точки при этом не изменяют
своего положения относительно друг друга. Совокупность выписанных 12
перестановок замкнута относительно умножения, поскольку последовательное
выполнение вращений тетраэдра снова будет вращением. Таким образом, получаем,
группу, которая называется группой вращений тетраэдра.
При других преобразованиях пространства,
являющихся самосовмещениями тетраэдра, внутренние точки тетраэдра передвигаются
относительно друг друга. А именно: тетраэдр имеет 6 плоскостей симметрии,
каждая из которых проходит через одно из его ребер и середину противолежащего
ребра. Симметриям относительно этих плоскостей отвечают следующие транспозиции
на множестве вершин тетраэдра:
|
Плоскость
|
Транспозиция
|
|
ребро
(2, 3), точка A
|
(1,
4)
|
|
ребро
(2, 4), точка C
|
(1,
3)
|
|
ребро
(1, 2), точка E
|
(3,
4)
|
|
ребро
(1, 4), точка B
|
(2,
3)
|
|
ребро
(1, 3), точка D
|
(2,
4)
|
|
ребро
(3, 4), точка F
|
(1,
2)
|
Уже па основании этих данных можно утверждать,
что группа всевозможных симметрий тетраэдра состоит из 24 преобразований. В
самом деле, каждая симметрия, самосовмещая тетраэдр в целом, должна как-то
переставлять его вершины, ребра и грани. В частности в данном случае симметрии
можно характеризовать перестановками вершин тетраэдра. Поскольку тетраэдр имеет
4 вершины, его группа симметрий не может состоять больше чем из 24
преобразований. Иными словами, она либо совпадает с симметрической группой S4,
либо является ее подгруппой. Выписанные выше симметрии тетраэдра относительно
плоскостей определяют всевозможные транспозиции на множестве его вершин.
Поскольку эти транспозиции порождают симметрическую группу S4, получаем
требуемое. Таким образом, любая перестановка вершин тетраэдра определяется
некоторой его симметрией. Однако этого нельзя сказать о произвольной перестановке
ребер тетраэдра. Если условиться обозначать каждое ребро тетраэдра той же
буквой, что и его середину, то, скажем, перестановки на множестве ребер
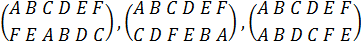
отвечают соответственно двум вращениям вокруг
оси l1, и вращению вокруг оси АB. Выписав перестановки на множестве {А, В. С,
D, Е, F} для всех преобразований симметрии, получим некоторую подгруппу
симметрической группы S6, состоящую из 24 перестановок. Группа перестановок
вершин тетраэдра и группа перестановок его ребер - разные группы перестановок,
поскольку они действуют на разных множествах. Но за ними «видна» одна и та же
группа - группа преобразований пространства, оставляющих тетраэдр на месте.
Группа симметрий куба. Симметрии куба, как и
симметрии тетраэдра, делятся на два типа - самосовмещения, при которых точки
куба не изменяют своего положения относительно друг друга, и преобразования,
оставляющие куб в целом на месте, но передвигающие его точки относительно друг
друга. Преобразования первого типа будем называть вращениями. Все вращения
образуют группу, которая называется группой вращений куба.
Имеется ровно 24 вращения куба вокруг различных
осей симметрии.
В самом деле, при поворотах куба место нижней
грани может занять любая из 6 граней куба (рис. 2). Для каждой из 6
возможностей - когда указано, какая именно грань расположена внизу, - имеется 4
различных расположения куба, соответствующих его поворотам вокруг оси,
проходящей через центры верхней и нижней граней, на углы 0, π/2,
π, Зπ/2.
Таким образом, получаем 6×4 = 24
вращений куба. Укажем их в явном виде.
Куб имеет центр симметрии (точка пересечения его
диагоналей), 3 оси симметрии четвертого порядка, 4 оси симметрии третьего
порядка и 6 осей симметрии второго порядка. Достаточно рассмотреть вращения
вокруг осей симметрии.
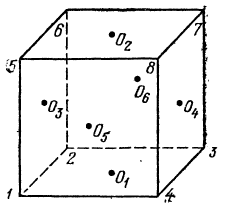
а) Оси симметрии четвертого порядка -это оси 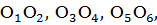 проходящие
через центры противоположных граней. Вокруг каждой из этих осей имеется по три
нетождественных вращения, а именно вращения на углы π/2,
π,
3π/2
проходящие
через центры противоположных граней. Вокруг каждой из этих осей имеется по три
нетождественных вращения, а именно вращения на углы π/2,
π,
3π/2 .
Этим вращениям соответствуют 9 перестановок вершин куба, при которых вершины
противоположных граней переставляются циклически и согласовано. Например,
перестановки
.
Этим вращениям соответствуют 9 перестановок вершин куба, при которых вершины
противоположных граней переставляются циклически и согласовано. Например,
перестановки
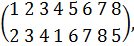

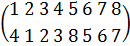
отвечают поворотам вокруг оси 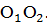
б) Осями симметрии третьего порядка являются
диагонали куба. Вокруг каждой из четырех диагоналей [1,7], [2, 8], [3, 5], [4,
6] имеется по два нетождественных вращения на углы 2π/3,
4π/3.
Например, вращения вокруг диагонали [1, 7] определяют такие перестановки вершин
куба:
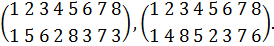
Всего получаем 8 таких вращений.
в) Осями симметрии второго порядка будут прямые,
соединяющие середины противолежащих ребер куба. Имеется шесть пар
противоположных ребер (например, [1,2], [7, 8]), каждая пара определяет одну
ось симметрии, т. е. получаем 6 осей симметрии второго порядка. Вокруг каждой
из этих осей имеется одно нетождественное вращение. Всего  6
вращений. Вместе с тождественным преобразованием получаем 9+8+6+1=24 различных
вращения. Все вращения куба указаны. Вращения куба определяют перестановки на
множествах его вершин, ребер, граней и диагоналей. Рассмотрим, как действует
группа вращений куба на множестве его диагоналей. Различные вращения куба
переставляют диагонали куба по-разному, т. е. им соответствуют различные
перестановки на множестве диагоналей. Поэтому группа вращений куба определяет
группу перестановок на множестве диагоналей, состоящую из 24 перестановок.
Поскольку куб имеет лишь 4 диагонали, группа всех таких перестановок совпадает
с симметрической группой на множестве диагоналей. Итак, любая перестановка
диагоналей куба соответствует некоторому его вращению, причём разным
перестановкам соответствуют разные вращения.
6
вращений. Вместе с тождественным преобразованием получаем 9+8+6+1=24 различных
вращения. Все вращения куба указаны. Вращения куба определяют перестановки на
множествах его вершин, ребер, граней и диагоналей. Рассмотрим, как действует
группа вращений куба на множестве его диагоналей. Различные вращения куба
переставляют диагонали куба по-разному, т. е. им соответствуют различные
перестановки на множестве диагоналей. Поэтому группа вращений куба определяет
группу перестановок на множестве диагоналей, состоящую из 24 перестановок.
Поскольку куб имеет лишь 4 диагонали, группа всех таких перестановок совпадает
с симметрической группой на множестве диагоналей. Итак, любая перестановка
диагоналей куба соответствует некоторому его вращению, причём разным
перестановкам соответствуют разные вращения.
Опишем теперь всю группу симметрий куба. Куб
имеет три плоскости симметрии, проходящие через его центр. Симметрии
относительно этих плоскостей в сочетании со всеми вращениями куба дают нам еще
24 преобразования, являющихся самосовмещениями куба. Поэтому полная группа
симметрий куба состоит из 48 преобразований.
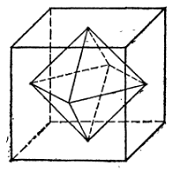
Группа симметрий октаэдра. Октаэдр один
из пяти правильных многогранников. Его можно получить, соединяя центры граней
куба и рассматривая тело, ограниченное плоскостями, которые определяются
соединительными прямыми для соседних граней (рис. 3). Поэтому любая симметрия
куба одновременно является симметрией октаэдра и наоборот. Таким образом,
группа симметрий октаэдра такая же, как и группа симметрий куба, и состоит из
48 преобразований.
один
из пяти правильных многогранников. Его можно получить, соединяя центры граней
куба и рассматривая тело, ограниченное плоскостями, которые определяются
соединительными прямыми для соседних граней (рис. 3). Поэтому любая симметрия
куба одновременно является симметрией октаэдра и наоборот. Таким образом,
группа симметрий октаэдра такая же, как и группа симметрий куба, и состоит из
48 преобразований.
Группа симметрий правильного многогранника
состоит из 2l преобразований, где l - число его плоских углов. Это утверждение
имеет место для всех правильных многогранников, его можно доказать в общем
виде, не находя всех симметрий многогранников.
Глава 2. Лемма Бернсайда о количестве орбит
§1.
Формулировка и доказательство
Лемма Бернсайда вычисляет количество орбит
действия группы на множестве с помощью суммы по всем элементам группы. Она
применяется в том случае, когда порядок множества X намного больше, чем порядок
группы G.
Пусть G - перестановок на множестве  Подмножество
Подмножество
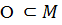 называется
орбитой группы G, если
называется
орбитой группы G, если
а) 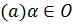 для
любого
для
любого 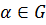 и
любого
и
любого 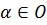 ;
т.е. действие перестановок из G на элементы O не выводит за пределы О;
;
т.е. действие перестановок из G на элементы O не выводит за пределы О;
б) два элемента из О можно перевести друг в
друга некоторой перестановкой из G.
Всякая группа перестановок G = { имеет орбиты.
имеет орбиты.
Для доказательства выберем произвольный элемент 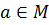 и
рассмотрим множество
и
рассмотрим множество  Оно будет орбитой
группы G, так как
Оно будет орбитой
группы G, так как
а) если 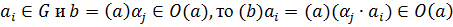 так
как
так
как 
б) если 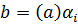 и
и
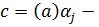 произвольные
элементы из
произвольные
элементы из 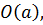 то
то  и
при этом
и
при этом 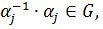 так
как G
так
как G группа.
группа.
Оказывается, что орбитами подобного вида
исчерпываются все типы орбит. Более точно, если О орбита
группы G и
орбита
группы G и 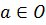 , то
, то 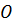 =
=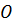 (а).
Справедливость этого утверждения вытекает непосредственно из определения орбиты
группы.
(а).
Справедливость этого утверждения вытекает непосредственно из определения орбиты
группы.
Ясно, что любые две орбиты О(а) и О (b) либо
совпадают (если b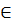 О(а)), либо не
пересекаются (если b
О(а)), либо не
пересекаются (если b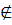 O(а)). Отсюда
следует, что множество М распадается в объединение непересекающихся подмножеств
- орбит группы G. В частности, может случиться, что единственной орбитой группы
G будет само множество М. Группы с таким свойством называются транзитивными.
Таким образом, группа перестановок G на множестве М транзитивна, если любой
элемент а
O(а)). Отсюда
следует, что множество М распадается в объединение непересекающихся подмножеств
- орбит группы G. В частности, может случиться, что единственной орбитой группы
G будет само множество М. Группы с таким свойством называются транзитивными.
Таким образом, группа перестановок G на множестве М транзитивна, если любой
элемент а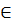 М
может быть получен из любого другого элемента b
М
может быть получен из любого другого элемента b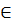 М
под действием подходящим способом выбранной перестановки
М
под действием подходящим способом выбранной перестановки 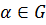 :
:
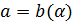 .
Все другие группы перестановок называются интранзитивными.
.
Все другие группы перестановок называются интранзитивными.
Пусть 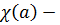 число
неподвижных точек перестановки
число
неподвижных точек перестановки 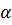 ,
, 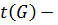 число
орбит группы перестановок
число
орбит группы перестановок 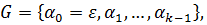 действующей на
множестве
действующей на
множестве 
Лемма Бернсайда: Для любой группы перестановок
имеет место равенство
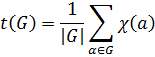
Доказательство: Рассмотрим отношение
«перестановка 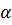 сохраняет
неподвижным элемент m» между перестановками группы G и элементами множества М.
Сопоставим парам (
сохраняет
неподвижным элемент m» между перестановками группы G и элементами множества М.
Сопоставим парам (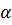 , т),
, т), 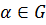 ,
m
,
m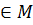 ,
вершины прямоугольной сети и отметим те из них, для которых соответствующая
пара (
,
вершины прямоугольной сети и отметим те из них, для которых соответствующая
пара (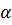 ,
т) находится в указанном отношении, т. е. m(a) = т (рис. 4). Иными словами,
построим график указанного отношения. Число отмеченных точек (точек,
принадлежащих графику) можно подсчитать двумя способами:
,
т) находится в указанном отношении, т. е. m(a) = т (рис. 4). Иными словами,
построим график указанного отношения. Число отмеченных точек (точек,
принадлежащих графику) можно подсчитать двумя способами:
определить число отмеченных точек на каждой
вертикали и просуммировать полученные величины или же определить число таких
точек по каждой горизонтали и затем вычистить их сумму.
Согласно определению отношения на каждой
вертикали отмечаются все точки, сохраняемые перестановкой 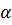 ,
соответствующей этой вертикали. Их число равно
,
соответствующей этой вертикали. Их число равно 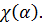 Поэтому
число всех точек графика равно
Поэтому
число всех точек графика равно
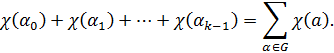
С другой стороны, на каждой горизонтали
отмечаются все перестановки, сохраняющие элемент m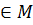 ,
отвечающий этой горизонтали. Мы знаем, что они образуют группу Gm -
стабилизатор элемента т - и их чисто равно
,
отвечающий этой горизонтали. Мы знаем, что они образуют группу Gm -
стабилизатор элемента т - и их чисто равно
Поэтому при втором способе подсчета числа
отмеченных точек графика рассматриваемого отношения получаем выражение

Однако если элементы i, j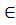 М содержатся в одной орбите, то
М содержатся в одной орбите, то 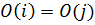 и поэтому
и поэтому 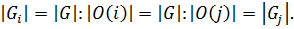 Пусть
Пусть
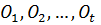 -
все орбиты группы G, такие, что
-
все орбиты группы G, такие, что 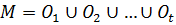 , и слагаемые в
этом объединении не пересекаются. Разобьем сумму (1) на части так, чтобы внутри
каждой из частей суммирование шло по элементам некоторой орбиты:
, и слагаемые в
этом объединении не пересекаются. Разобьем сумму (1) на части так, чтобы внутри
каждой из частей суммирование шло по элементам некоторой орбиты:
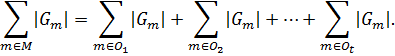
Каждое из t слагаемых в правой части этого
равенства можно преобразовать следующим образом:
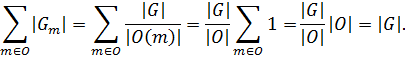
Поэтому
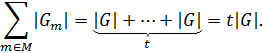
Таким образом, при втором способе подсчета мы
получили 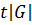 отмеченных
точек графика. Приравнивая величины, полученные при первом и втором способах,
получим
отмеченных
точек графика. Приравнивая величины, полученные при первом и втором способах,
получим
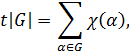
т.е.
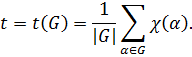
Лемма доказана.
§2. Задачи о раскрасках
Рассмотрим две комбинаторные задачи на
применение леммы Бернсайда. симметрия многогранник
лемма бернсайд
Задача 1: Сколькими способами можно раскрасить
вершины куба в три цвета (например, красный, синий и зеленый)?
Каждую из восьми вершин куба можно раскрасить
тремя способами, причем независимо от того, как раскрашены другие вершины, то
множество всех вершин куба можно раскрасить 38 = 6561 различными способами.
Однако при таком подходе к решению задачи молчаливо предполагается, что мы
умеем различать вершины куба перед окраской, т. е., скажем, куб жестко
закреплен или его вершины занумерованы. При этом полученный ответ можно
интерпретировать следующим образом: можно так раскрасить 38 абсолютно
одинаковых, жестко закрепленных кубов, что все они будут различаться. Дли 38+1
кубов этого сделать уже нельзя.
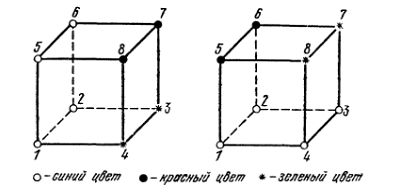
Ситуация существенно меняется, если мы откажемся
от предположения о том, что кубы жестко закреплены, так как по-разному
окрашенные кубы можно повернуть так, что в новом положении их окраски совпадут
(рис. 5).
Естественно считать, что два куба раскрашены
одинаково, если их раскраски совпадают после некоторого вращения одного из
кубов в пространстве. Будем говорить, что такие раскраски кубов геометрически
неотличимы. Поэтому естественным уточнением задачи о раскраске является
следующая задача: Сколькими геометрически различными способами можно раскрасить
вершины куба в три цвета.
Переформулируем теперь эту задачу так, чтобы
стала понятной ее связь с леммой Бернсайда. Пусть М - множество всевозможных
по-разному раскрашенных кубов одного размера, положение которых в пространстве
фиксировано,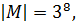 G -группа всех
вращений куба, состоящая из 24 перестановок. Группа G естественным образом
определяет группу перестановок на множестве М. Именно: если
G -группа всех
вращений куба, состоящая из 24 перестановок. Группа G естественным образом
определяет группу перестановок на множестве М. Именно: если 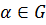 -
некоторое вращение, то каждому кубу из М можно сопоставить некоторый, вообще
говоря, другой куб. который получается из первого при вращении
-
некоторое вращение, то каждому кубу из М можно сопоставить некоторый, вообще
говоря, другой куб. который получается из первого при вращении 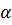 .
Это соответствие является, очевидно, перестановкой на множестве М, которую
будем обозначать
.
Это соответствие является, очевидно, перестановкой на множестве М, которую
будем обозначать 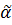 . Группу всех таких
перестановок множества М. определяемых перестановками из G, мы будем обозначать
. Группу всех таких
перестановок множества М. определяемых перестановками из G, мы будем обозначать
 .
Ясно, что
.
Ясно, что 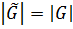 .
.
То, что два куба  и
и
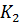 из
М раскрашены геометрически одинаково, означает, что один из них можно перевести
вращением в такое положение, в котором они неразличимы. Иными словами,
существует такая перестановка
из
М раскрашены геометрически одинаково, означает, что один из них можно перевести
вращением в такое положение, в котором они неразличимы. Иными словами,
существует такая перестановка 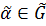 , что
, что 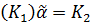 ,
т. е.
,
т. е.  и
и
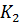 содержатся
в одной орбите группы
содержатся
в одной орбите группы  , действующей на
множестве М. Таким образом, для того чтобы определить число геометрически
различимых способов раскраски вершин куба, нужно найти количество орбит группы
, действующей на
множестве М. Таким образом, для того чтобы определить число геометрически
различимых способов раскраски вершин куба, нужно найти количество орбит группы  на
множестве М.
на
множестве М.
Считая вершины кубов занумерованными числами
1,2, 3, 4, 5, 6, 7, 8. раскраску каждого из 38 кубов можно однозначно
охарактеризовать «словом» из 8 букв, каждая из которых есть либо k, либо c,
либо з. То, что i-ая буква слова равна к (или с, или з), означает, что i-ая
вершина при выбранной нумерации окрашена в красный цвет (или в синий, или в
зеленый соответственно). Например, для кубов, изображенных на рис. 5, имеем
соответственно последовательности ссззсскк, ссссккзз. Перестановки из группы  переставляют
такие последовательности. Например, если
переставляют
такие последовательности. Например, если 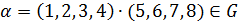 ,
то перестановка
,
то перестановка 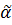 слово сссссссз
переводит в ссссзссс, слово ссззсскк переводит в сззссккс, слова сссссссс,
кккккккк, зззззззз оставляет неизменными и т. д. Выписать всю таблицу значений
для перестановки
слово сссссссз
переводит в ссссзссс, слово ссззсскк переводит в сззссккс, слова сссссссс,
кккккккк, зззззззз оставляет неизменными и т. д. Выписать всю таблицу значений
для перестановки 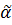 затруднительно,
поскольку она состоит из 38 строк.
затруднительно,
поскольку она состоит из 38 строк.
Для того чтобы применить лемму Бернсайда,
необходимо определить число неподвижных точек каждой перестановки из  .
Последовательность букв к, с, з будет неподвижной для перестановки
.
Последовательность букв к, с, з будет неподвижной для перестановки 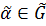 тогда
и только тогда, когда при разложении соответствующей перестановки
тогда
и только тогда, когда при разложении соответствующей перестановки 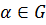 в
произведение циклов вершины куба, номера которых входит в один и тот же цикл,
окрашены одним цветом. Например, если
в
произведение циклов вершины куба, номера которых входит в один и тот же цикл,
окрашены одним цветом. Например, если 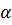 =
(1, 2, 3, 4)
=
(1, 2, 3, 4) 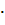 (5, 6, 7, 8), то
неподвижными относительно
(5, 6, 7, 8), то
неподвижными относительно 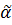 будут слова, составленные
целиком из одной буквы, и слова, составленные из двух разных букв, причем одна
из них стоит на первых четырех местах в слове, а вторая - из четырех
последующих. Поэтому имеется 9 неподвижных точек перестановки
будут слова, составленные
целиком из одной буквы, и слова, составленные из двух разных букв, причем одна
из них стоит на первых четырех местах в слове, а вторая - из четырех
последующих. Поэтому имеется 9 неподвижных точек перестановки 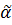 на
множестве М. Уже на этом примере видно, что подсчет числа неподвижных точек
перестановок из
на
множестве М. Уже на этом примере видно, что подсчет числа неподвижных точек
перестановок из  сильно упрощается,
если известны разложении в произведение циклов соответствующих перестановок из
G. Если перестановка
сильно упрощается,
если известны разложении в произведение циклов соответствующих перестановок из
G. Если перестановка 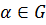 разложена в
произведение k-циклов, то число ее неподвижных точек равно
разложена в
произведение k-циклов, то число ее неподвижных точек равно 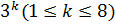 .
Поэтому сначала мы опишем разложения в произведение циклов для всех
перестановок из группы G вращений куба.
.
Поэтому сначала мы опишем разложения в произведение циклов для всех
перестановок из группы G вращений куба.
а) Вокруг каждой из трех осей, соединяющих
центры противоположных граней, имеется три нетождественных вращения. Им
соответствуют перестановки

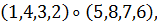
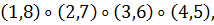
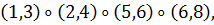
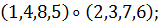
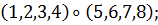
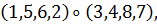
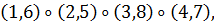
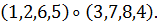
б) Вокруг каждой из четырех диагоналей, т. е.
осей, соединяющих противоположные вершины куба, имеется по два нетривиальных
вращения. Им соответствуют перестановки

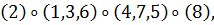
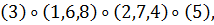
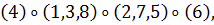
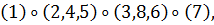

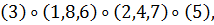
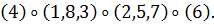
в) Вокруг каждой из шести осей, соединяющих
середины противоположных ребер, имеется одно нетривиальное вращение. Им
соответствуют перестановки

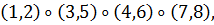

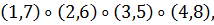
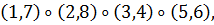
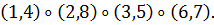
Вместе с тождественной получаем 24 перестановки.
Итак, в группе G вращений куба имеется
перестановка типа 
перестановок типа 
перестановок типа 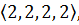
перестановок типа 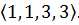
Перестановка первого типа имеет 38 неподвижных
точек, любая из перестановок второго типа - 32, третьего и четвертого типов -
34 неподвижных точек. Поэтому согласно Лемме Бернсайда имеем

Таким образом, число геометрически различимых
способов раскраски першим куба в три цвета равно 333.
Задача 2: Сколько различных ожерелий из семи
бусин можно составить из бусин двух цветов - красного и синего?
Для того чтобы стала понятной аналогия этой
задачи с предыдущей, переформулируем ее следующим равносильным образом:
Сколькими геометрически различными способами
можно раскрасить вершины правильного семиугольника в два цвета?
Здесь два способа раскраски неотличимы, если
один из них можно получить из другого, применяя к семиугольнику либо
преобразования вращения, либо симметрии относительно осей, т. е. перестановки
из группы диэдра D7. Если вершины семиугольника пронумерованы, имеется 27=128
различных вариантов их раскраски, так как каждую вершину независимо от других
можно раскрасить двумя способами.
Снова будем описывать раскраски словами длины 7,
составленными из букв к (вершина окрашена в красный цвет) и с (вершина окрашена
в синий цвет). На множестве N всех таких слов действует группа  перестановок,
задаваемых перестановками из D7. Например, если
перестановок,
задаваемых перестановками из D7. Например, если 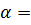 (1,
2, 3, 4, 5, 6, 7), то перестановка
(1,
2, 3, 4, 5, 6, 7), то перестановка 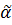 последнюю
букву каждого слова переставляет в его начало, а остальные буквы не изменяет.
Для того чтобы определить число орбит группы
последнюю
букву каждого слова переставляет в его начало, а остальные буквы не изменяет.
Для того чтобы определить число орбит группы  ,
на множестве N, необходимо найти типы перестановок из D7. Эта задача гораздо
проще аналогичного вопроса для группы G из задачи 1. Группа D7, состоит из 14
перестановок множества {1, 2, 3, 4, 5, б, 7}, которые распределены по возможным
типам так:
,
на множестве N, необходимо найти типы перестановок из D7. Эта задача гораздо
проще аналогичного вопроса для группы G из задачи 1. Группа D7, состоит из 14
перестановок множества {1, 2, 3, 4, 5, б, 7}, которые распределены по возможным
типам так:
перестановка имеет тип 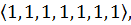
перестановок имеют тип 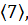
перестановок имеют тип 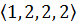 .
.
Слово неподвижно относительно перестановки 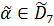 ,
тогда и только тогда, когда буквы, стоящие на местах с номерами из одного цикла
в перестановке
,
тогда и только тогда, когда буквы, стоящие на местах с номерами из одного цикла
в перестановке 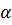 , совпадают.
Поэтому тождествен на я перестановка имеет 27 неподвижных точек на N,
перестановки второго типа - по 2, а перестановки третьего типа -по 24. Применяя
лемму Бернсайда, получаем
, совпадают.
Поэтому тождествен на я перестановка имеет 27 неподвижных точек на N,
перестановки второго типа - по 2, а перестановки третьего типа -по 24. Применяя
лемму Бернсайда, получаем
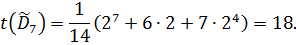
Итак, из бусин двух цветов можно составить 18
семи-бусенных ожерелий.
Заключение
Группы повсеместно используются в
математике
<http://ru.math.wikia.com/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0>
и естественных науках, часто для обнаружения внутренней симметрии
<http://ru.math.wikia.com/wiki/%D0%A1%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F>
объектов. Внутренняя симметрия обычно связана с инвариантными свойствами;
множество
<http://ru.math.wikia.com/wiki/%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE>
преобразований, которые сохраняют это свойство, вместе с операцией
<http://ru.math.wikia.com/wiki/%D0%91%D0%B8%D0%BD%D0%B0%D1%80%D0%BD%D0%B0%D1%8F_%D0%BE%D0%BF%D0%B5%D1%80%D0%B0%D1%86%D0%B8%D1%8F>
композиции, образуют группу, называемую группой симметрии.
В теории Галуа, которая и дала
начало понятию группы, группы используются для описания симметрии уравнений,
корнями которых являются корни некоторого полиномиального уравнения
<http://ru.math.wikia.com/wiki/%D0%9F%D0%BE%D0%BB%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F?action=edit&redlink=1>.
Из-за важной роли, которую они играют в этой теории, получили своё название
разрешимые группы
<http://ru.math.wikia.com/wiki/%D0%A0%D0%B0%D0%B7%D1%80%D0%B5%D1%88%D0%B8%D0%BC%D0%B0%D1%8F_%D0%B3%D1%80%D1%83%D0%BF%D0%BF%D0%B0>.
Абелевы группы
<http://ru.math.wikia.com/wiki/%D0%90%D0%B1%D0%B5%D0%BB%D0%B5%D0%B2%D0%B0_%D0%B3%D1%80%D1%83%D0%BF%D0%BF%D0%B0>
(т.е. группы, в которых операция коммутативна
<http://ru.math.wikia.com/wiki/%D0%9A%D0%BE%D0%BC%D0%BC%D1%83%D1%82%D0%B0%D1%82%D0%B8%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D1%8C>)
являются основой для построения более сложных объектов абстрактной алгебры,
таких как кольца
<http://ru.math.wikia.com/wiki/%D0%9A%D0%BE%D0%BB%D1%8C%D1%86%D0%BE_(%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0)>,
поля
<http://ru.math.wikia.com/wiki/%D0%9F%D0%BE%D0%BB%D0%B5_(%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0)>
и модули
<http://ru.math.wikia.com/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%BD%D0%B0%D0%B4_%D0%BA%D0%BE%D0%BB%D1%8C%D1%86%D0%BE%D0%BC?action=edit&redlink=1>.
Понимание теории групп также очень
важно для физики
<http://ru.math.wikia.com/wiki/%D0%A4%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0?veaction=edit&redlink=1>
и других естественных наук. В химии <http://ru.math.wikia.com/wiki/%D0%A5%D0%B8%D0%BC%D0%B8%D1%8F?action=edit&redlink=1>
группы используются для классификации кристаллических решёток
<http://ru.math.wikia.com/wiki/%D0%9A%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB%D0%BB%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%80%D0%B5%D1%88%D1%91%D1%82%D0%BA%D0%B0?veaction=edit&redlink=1>
и симметрий молекул
<http://ru.math.wikia.com/wiki/%D0%9C%D0%BE%D0%BB%D0%B5%D0%BA%D1%83%D0%BB%D0%B0?veaction=edit&redlink=1>.
В физике группы используются для описания симметрий, которым подчиняются
физические законы. Особенно важны в физике представления групп
<http://ru.math.wikia.com/wiki/%D0%9F%D1%80%D0%B5%D0%B4%D1%81%D1%82%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B3%D1%80%D1%83%D0%BF%D0%BF%D1%8B>,
в частности, групп Ли, так как они часто указывают путь к «возможным»
физическим теориям.
Литература
Богопольский
О. В. «Введение в теорию групп» 2002г.
Калужнин
Л.А., Сущанский В.И. «Преобразования и перестановки» 1985г.
Кострикин
А.И. «Введение в алгебру» 1977г.