Сравнительный анализ установившихся потоков газа при различных законах фильтрации
Министерство образования и науки
Российской Федерации
Федеральное государственное бюджетное
образовательное учреждение
высшего профессионального образования
Национальный минерально-сырьевой
университет «Горный»
КУРСОВАЯ РАБОТА
По дисциплине Подземная гидромеханика
(наименование учебной дисциплины
согласно учебному плану)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Тема работы: «сравнительный анализ
установившихся потоков газа при различных законах фильтрации»
Выполнил:
студент гр. НД-12-2 ____________________ /Исанбаева К.С./
ПРОВЕРИЛ:
Руководитель
работы доцент ________________ /Максютин А.В./
Санкт-Петербург
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение
высшего
профессионального образования
Национальный
минерально-сырьевой университет «Горный»
УТВЕРЖДАЮ
Заведующий кафедрой
___________ /________/
"___"__________2015 г.
Кафедра
разработки и эксплуатации нефтяных и газовых месторождений
КУРСОВАЯ
РАБОТА
По дисциплине
____Подземная гидромеханика
(наименование
учебной дисциплины согласно учебному плану)
ЗАДАНИЕ
Студенту группы __НД-12-2_ ____/Исанбаевой К.С,/___
(шифр группы) (Ф.И.О.)
Тема работы: «Сравнительный анализ установившихся потоков газа при
различных законах фильтрации»
. Исходные данные к работе: Задание на курсовую работу включает 2 части:
теоретическую и расчетную (4 задачи)
. Содержание пояснительной записки: В соответствии с методическими
указаниями к курсовой работе: задание на выполнение работы, расчетные формулы,
расчет, результаты, графики, заключение
__________________________________________________
. Перечень графического материала: эпюры, схемы
. Срок сдачи законченного проекта: 16 марта 2015 г.___
Руководитель проекта _доцент___ ________________ /Максютин А.В./
(должность) (подпись) (Ф.И.О.)
Дата выдачи задания: 17 февраля 2015 г.
АННОТАЦИЯ
Курсовая работа включает в себя 2 основные части: теоретическую и
расчетную. Темой теоретической части является сравнительный анализ
установившихся потоков газа при различных законах фильтрации. Расчетная часть
состоит из 4 задач. В расчетной части приводятся гидродинамические расчеты,
сопровождаемые графиками.
Работа содержит пояснительную записку объемом стр.36, вкл. рис. 25,
табл.9, библ. список из 6 наим.
ABSTRACT
work includes two main parts: theoretical and computational.
The theme of the theoretical part is a comparative analysis of the mouth -
steady-state flow of gas at various laws filtering. Calculated part consists of
four tasks. In the calculation of the hydrodynamic calculations are accompanied
by graphs.work contains an explanatory note volume p.36, Incl. Fig. 25, Tab.9 ,
the Bible. List of 6 Author.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
. ЦЕЛИ И ЗАДАЧИ КУРСОВОЙ РАБОТЫ
. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ ПО ТЕМЕ КУРСОВОЙ РАБОТЫ: «СРАВНИТЕЛЬНЫЙ
АНАЛИЗ УСТАНОВИВШИХСЯ ПОТОКОВ ГАЗА ПРИ РАЗЛИЧНЫХ ЗАКОНАХ ФИЛЬТРАЦИИ»
.1 Установившееся движение газов по линейному закону
фильтрации
.2 Плоскорадиальный фильтрационный поток газа по двухчленному
закону фильтрации
.3 Плоскорадиальный фильтрационный поток газа по степенному
закону фильтрации
.4 Обобщенная интерпретация законов фильтрации газа
. РАСЧЕТНАЯ ЧАСТЬ
.1 Задача №1
.2 Задача №2
.3 Задача №3
.3 Задача №4
. ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ПРИЛОЖЕНИЕ 1
ВВЕДЕНИЕ
Подземная гидромеханика - наука, изучающая законы течения природных
жидкостей - нефти, воды и газа в пористой среде - теоретическая основа
разработки нефтяных и газовых месторождений, одна из профилирующих дисциплин в
учебном плане нефтяных вузов. Подземная гидромеханика является основой
современной технологии нефтедобычи и добычи газа и имеет обширные области
приложения в гидрогеологии, гидротехнике, инженерной геологии. Объектом
изучения подземной гидромеханики является фильтрационный поток - поток жидкости
(газа, газожидкостной смеси) в поровой или трещинной среде.
Знание законов подземной гидромеханики необходимо при решении задач
выбора систем и режимов разработки залежей, рациональных для данных пластовых
условий.
Гидродинамическое моделирование разработки залежей основано на
использовании математических уравнений, полученных в рамках решения прямой
задачи подземной гидромеханики и описывающих процесс фильтрации в конкретных
условиях. С целью определения фильтрационных характеристик пласта для контроля
и регулирования разработки проводят гидродинамические исследования пластов и
скважин, обработка данных которых основана на решении обратной задачи подземной
гидромеханики.
1. ЦЕЛИ И
ЗАДАЧИ КУРСОВОЙ РАБОТЫ
Целями выполнения курсовой работы являются:
) углубление и закрепление теоретических знаний, полученных во время
лекционных, лабораторных и практических занятий;
) выработка навыков самостоятельного применения теории, привлечения
дополнительных данных, анализа практических данных, оценки и проверки
правильности решения;
) закрепление навыков расчета с применением вычислительной техники,
привлечения справочно-реферативной литературы, оформления и ведения
инженерно-технической документации.
Выполнение курсовой работы направлено на решение следующих задач:
) привитие навыков самостоятельной работы с учебной и научной
литературой;
) выработка аналитического мышления при изучении и решении поставленных
вопросов и задач;
) выработка умения грамотно и сжато излагать суть вопросов, поставленных
в теме курсовой работы;
) привитие навыков выполнения расчетов по формулам, применения системы
единиц измерения СИ и других систем единиц измерения;
) привитие навыков оформления курсовой работы согласно требованиям,
предъявляемых к инженерно-технической документации, в соответствии с ЕСКД.
2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ ПО ТЕМЕ КУРСОВОЙ РАБОТЫ: «СРАВНИТЕЛЬНЫЙ АНАЛИЗ
УСТАНОВИВШИХСЯ ПОТОКОВ ГАЗА ПРИ РАЗЛИЧНЫХ ЗАКОНАХ ФИЛЬТРАЦИИ»
При разработке газовых месторождений фильтрация газа и газоконденсатной
смеси в пласте проходит отлично от фильтрации жидкости. Особенность фильтрации
жидкостей и газов обусловлена различием их физических свойств, а также
характером их изменения при различных давлениях и температурах. При работе
газовых скважин скорость фильтрации газа из пласта к забою имеет значительные
величины, особенно в призабойной зоне.
В 1928 г. были впервые широко поставлены экспериментальные исследования
установившейся и неустановившейся фильтрации газов. Эти опыты были проведены в
СССР в бывшем Государственном исследовательском нефтяном институте (ГИНИ) Д. С.
Вилькером под руководством акад. Л. С. Лейбензона.
2.1 Установившееся движение газов по линейному закону фильтрации
Одномерное движение газов:
«Линейный закон фильтрации Дарси применим только в определенном диапазоне
режимов фильтрации, т.е. необходимо выделить верхнюю и нижнюю границы
применимости закона Дарси и соответствующие им две группы причин.
Верхняя граница применимости Дарси характеризуется некоторой
верхнекритической скоростью фильтрации. При высоких скоростях фильтрации выше
верхнекритической закон Дарси нарушается из-за проявления сил инерции.
Нижняя граница характеризуется проявлением неньютоновских реологических
свойств пластовых флюидов, их взаимодействием с твердым скелетом пористой среды
при достаточно малых скоростях фильтрации, меньших некоторой нижекритической
скорости фильтрации».
Основные характеристики фильтрационного потока газа можно получить,
используя аналогию между течением несжимаемой жидкости и течением газа. Для
этого вводится функция Лейбензона для идеального газа:
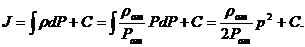 (2.1)
(2.1)
В отличие от одномерного движения несжимаемой жидкости, в котором
величина давления является линейной функцией, при фильтрации идеального газа
давление по длине пласта изменяется по параболическому закону.
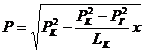 (2.2)
(2.2)
В отличие от фильтрации несжимаемой жидкости, расход газа прямо
пропорционален не разности давлений, а разности квадратов давлений.
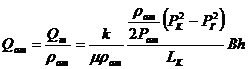 (2.3)
(2.3)
«По мере приближения к галерее скорость фильтрации газа увеличивается, в
отличие от одномерного движения несжимаемой жидкости, при котором скорость
фильтрации постоянна. При движении газа этот рост скорости фильтрации
происходит за счет расширения газа вследствие падения давления».
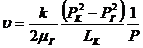 (2.4)
(2.4)
Радиальное движение газов:
Плоскорадиальный
фильтрационный поток идеального газа имеет место в круговом пласте постоянной
толщиной h c непроницаемой кровлей и
подошвой пласта, радиусом 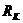 , в центре которого имеется гидродинамически
совешенная скважина радиусом
, в центре которого имеется гидродинамически
совешенная скважина радиусом 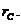 Для
изучения такого потока достаточно изучить движение вдоль одной любой
траектории, т.е. поток является одномерным по радиусу.
Для
изучения такого потока достаточно изучить движение вдоль одной любой
траектории, т.е. поток является одномерным по радиусу.
Для
идеального газа распределение давления представляет собой квадратную
логарифмическую зависимость и графически представляется
квадратно-логарифмической кривой. В газовом потоке имеет место резкое падение
давления вблизи скважины и весьма малое вдали от нее.
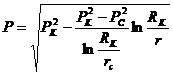 (2.5)
(2.5)
Дебит
газовой скважины пропорционален не разности давлений, называемой депрессией, а
разности квадратов давлений. Индикаторная линия при фильтрации газа строится в
координатах 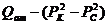 и в установившемся плоскорадиальном потоке имеет прямолинейный
характер.
и в установившемся плоскорадиальном потоке имеет прямолинейный
характер.
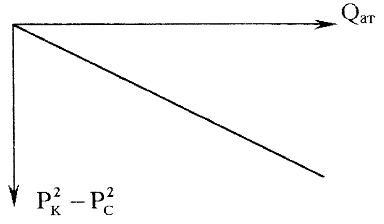
Рис.2.1.
Индикаторная диаграмма при фильтрации газа по закону Дарси
фильтрация движение газ закон
Средневзвешенное пластовое давление газа в круговом пласте близко к
контурному. Физически это объясняется значительной крутизной воронки депрессии
при притоке газа к скважине. Средневзвешенное давление используется при
определении запасов газа в пласте, а также для приближенного расчета
гидродинамических характеристик.
2.2 Плоскорадиальный фильтрационный поток газа по двухчленному
закону фильтрации
Рассмотрим способы определения основных характеристик фильтрационных
потоков при плоскорадиальном движении газа с большими скоростями, когда
причиной отклонения от закона Дарси являются значительные инерционные
составляющие общего фильтрационного сопротивления.
Для совершенного газа распределение давления в пласте дается формулой:
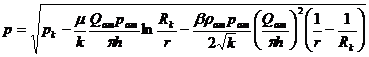 (2.6)
(2.6)
Индикаторные
линии, построенные в координатах 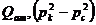 ,
являются параболами (рис.2.2).
,
являются параболами (рис.2.2).
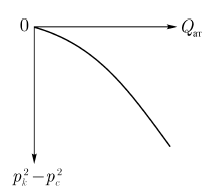
Рис.2.2. Индикаторная линия при фильтрации газа по двучленному закону
Уравнение притока к скважине для газа:
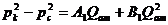 (2.7)
(2.7)
Коэффициенты фильтрационных сопротивлений, постоянные для данной
скважины. Они определяются опытным путем по данным исследования скважин при
установившихся режимах. Уравнение притока (2.7) с экспериментально
определяемыми коэффициентами широко используется в расчетах при проектировании
разработки месторождений. Кроме того, по значению A1, найденному в результате
исследования скважины, можно определить коллекторские свойства пласта,
например, коэффициент гидропроводности.
«В реальных условиях нельзя считать, что во всем пласте - от стенки
скважины до контура питания справедлив единый нелинейный закон фильтрации. При
значительных дебитах закон Дарси нарушается в некоторой области вблизи забоя
скважины, в то время как в остальной области пласта по-прежнему соблюдается
линейный закон. При увеличении дебита область, в которой нарушается закон
Дарси, увеличивается».
2.3 Плоскорадиальный фильтрационный поток газа по степенному закону
фильтрации
Функция давления для совершенного газа имеет вид:
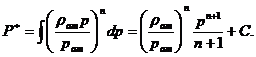 (2.8)
(2.8)
Расчетные формулы для плоскорадиальной фильтрации по степенному закону
для совершенного газа:
Для массового дебита
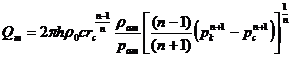 (2.9)
(2.9)
Для
объемного дебита, приведенного к атмосферным условиям
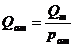 (2.10)
(2.10)
Для
распределения давления в пласте
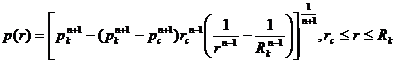 (2.11)
(2.11)
Для скорости фильтрации
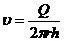 (2.12)
(2.12)
Если
в формулах (2.9)-(2.12) положить n = 2, то получим расчетные формулы для закона
фильтрации Краснопольского.
Кривая
распределения давления для несжимаемой жидкости имеет формулу гиперболы степени
n − 1, т.е. воронка депрессии, будет гиперболоидом вращения. Крутизна
воронки депрессии у стенки скважины будет больше, чем у логарифмической кривой.
Кривая p(r) для газа (формула (2.11) располагается еще выше, чем для жидкости
(при тех же значениях 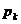 и
и 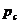 ).
).
На
рис.2.3 приведены индикаторные линии для течения газа при линейном законе
фильтрации (n = 1) и при нелинейных законах фильтрации 1 < n < 2 и n = 2.
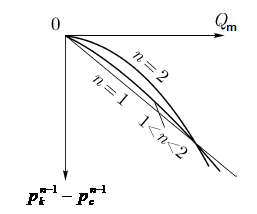
Рис.2.3. Индикаторные линии, соответствующие различным законам фильтрации
газа
Для
газа величина расхода пропорциональна радиусу скважины в степени 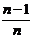 (для закона фильтрации Краснопольского
(для закона фильтрации Краснопольского 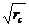 ), т.е. эта зависимость гораздо более сильная, чем в
случае соблюдения закона Дарси.
), т.е. эта зависимость гораздо более сильная, чем в
случае соблюдения закона Дарси.
Скорость
фильтрации вдоль линии тока изменяется при нелинейном законе фильтрации так же,
как и при линейном-обратно пропорциональна rp(r).
2.4 Обобщенная интерпретация законов фильтрации газа
Итак, движение газов в пористых средах, происходит как по линейному, так
и по нелинейному законам фильтрации. При решении различных задач подземной
гидродинамики для случаев нелинейной фильтрации за основу обычно берут формулу
Дарси, в которой градиент давления возводится в некоторый показатель степени,
или линейный закон фильтрации представляют двучленной формулой вида, одно из
слагаемых которой также выражает закон Дарси. Существуют также и одночленные
нестепенные формулы, выражающие нелинейный закон фильтрации, где вводится
некоторый коэффициент фильтрационного сопротивления λ как функция числа Рейнольдса Re.
«Существуют различные способы подхода к выводу формул, описывающих
нелинейные законы фильтрации. Наиболее распространенными оказались способы,
основанные на теории подобия и теории размерностей. Наиболее удачной
характеристикой режима фильтрации считается параметр Дарси (Да), введенный В.Н.
Щелкачевым (1946)».
3. РАСЧЕТНАЯ
ЧАСТЬ
3.1 Задача №1
Тема №1: Прямолинейно-параллельная установившаяся фильтрация однородной
несжимаемой жидкости по закону Дарси в однородном пласте (приток к галерее).
Дано:
Таблица 1
Номер
варианта Давление на контуре питания 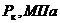 Давление
на стенке галереи
Давление
на стенке галереи 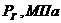 Длина пласта
Длина пласта 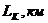 Проницаемость
k,
Проницаемость
k,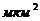 Динамическая вязкость
Динамическая вязкость 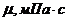 Ширина
пласта B, мТолщина пласта
Ширина
пласта B, мТолщина пласта
|
h , мПоритсость m, %
|
|
|
|
|
|
|
|
|
|
6
|
9,0
|
6,5
|
7,5
|
0,5
|
3,5
|
200
|
5
|
15
|
Определить закон распределения давления, градиента давления и скорости
фильтрации по длине пласта (в математическом и графическом виде), дебит
галереи, закон движения частиц жидкости и средневзвешенное по объему порового
пространства пластовое давление при исходных данных, приведенных в табл.1.
Прямолинейно-параллельным установившимся фильтрационным потоком считается
такой поток, в котором траектории движения частиц жидкости совпадают с линиями
токов, траектории параллельны, а скорости фильтрации во всех токах любого
поперечного сечения (перпендикулярного линиям токов) равны друг другу.
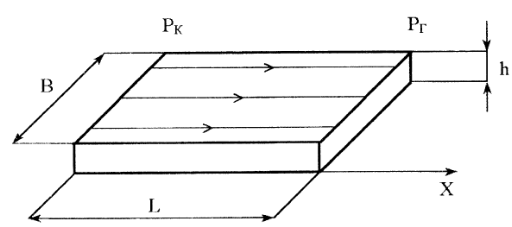
Рис.3.1. Схема прямолинейно-параллельного фильтрационного потока в пласте
. Закон распределения давления при установившейся фильтрации жидкости в
полосообразном пласте:
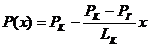 (3.1)
(3.1)
Где
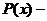 давление в произвольной точке
давление в произвольной точке 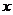 пласта, Па;
пласта, Па; 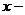 координата
точки пласта, отсчитываемая от контура питания, м.
координата
точки пласта, отсчитываемая от контура питания, м.
Подставив
исходные данные из табл.1 в (3.1), получим следующую зависимость:
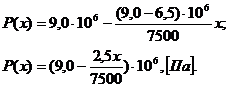 (3.2)
(3.2)
Изобразим
графически распределение давления, принимая 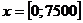 с шагом
с шагом 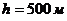 (рис.3.2).
(рис.3.2).
Пример
вычисления давления в точке 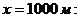
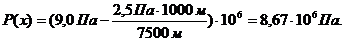
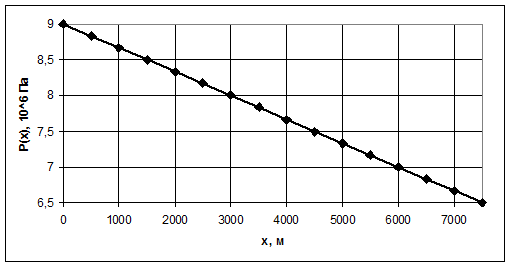
Рис.3.2. График распределения давления по длине линейного пласта
. Градиент давления определяется выражением:
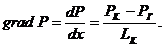 (3.3)
(3.3)
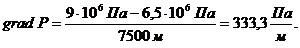
На
рис.3.3 представлен график распределения градиента давления по длине пласта.
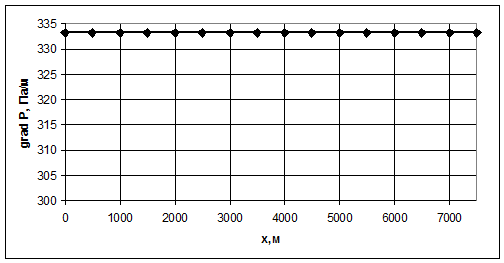
Рис.3.3. График распределения градиента давления по длине линейного
пласта
3. Скорость фильтрации согласно закону Дарси равна:
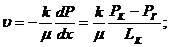 (3.4)
(3.4)
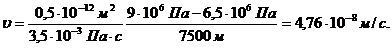
На
рис.4 представлен график распределения скорости фильтрации по длине пласта.
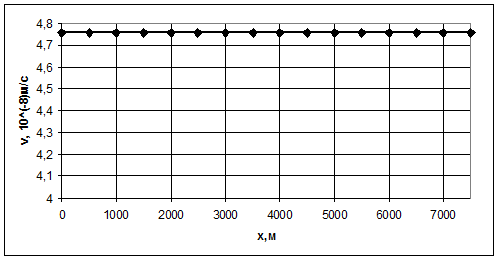
Рис.3.4. График распределения скорости фильтрации по длине линейного
пласта
4. Дебит галереи (объемный расход жидкости) равен:
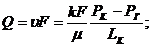 (3.5)
(3.5)
где
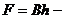 площадь поперечного сечения пласта,
площадь поперечного сечения пласта, 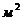 .
.
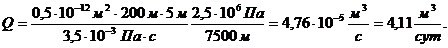
.
Закон движения жидких частиц определяется как:
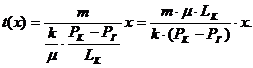 (3.6)
(3.6)
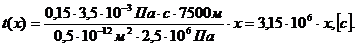
6.
Средневзвешенное по объему порового пространства пластовое давление
определяется как среднеарифметическое между давлением на контуре питания и на
галерее:
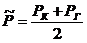 (3.7)
(3.7)
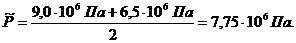
Таким
образом, теоретическое распределение давления в пласте при установившейся
фильтрации несжимаемой жидкости графически представляется в виде прямолинейного
графика - пьезометрической линии (рис.3.2), а распределение градиента давления
и скорости фильтрации по длине линейного пласта - постоянная величина (рис.3.3;
рис.3.4).
3.2 Задача №2
Тема №2: Плоскорадиальная установившаяся фильтрация однородной
несжимаемой жидкости по закону Дарси в однородном пласте (приток к совершенной
скважине).
Дано:
Таблица 2
Номер
варианта Давление на контуре питания 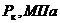 Давление
на стенке галереи
Давление
на стенке галереи 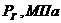 Радиус контура питания
Радиус контура питания
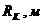 Радиус в
скважине
Радиус в
скважине
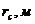 Динамическая
вязкость
Динамическая
вязкость 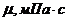 Толщина пласта
Толщина пласта
|
h , мПроницаемость k,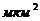 Поритсость m, % Поритсость m, %
|
|
|
|
|
|
|
|
|
|
6
|
9,0
|
6,5
|
2000
|
0,20
|
3,5
|
5
|
0,5
|
15
|
Определить закон распределения давления, градиента давления и скорости
фильтрации по длине пласта (в математическом и графическом виде), дебит
скважины, закон движения частиц жидкости и средневзвешенное по объему порового
пространства пластовое давление при исходных данных, приведенных в табл.2.
Решение
Особенности плоскорадиального потока:
1. Частицы жидкости движутся параллельно в одной и той же
плоскости, проходящей через ось скважины;
2. прямолинейные траектории движения частиц жидкости в любой
плоскости, перпендикулярной оси скважины, радиально сходятся в одной точке на
оси скважины;
. картины движения вдоль всех и любой траектории движения
одинаковы.
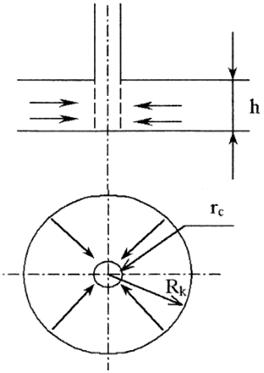
Рис.3.5. Схема плоскорадиального потока
. Распределение давления в круговом пласте:
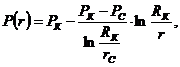 (3.8)
(3.8)
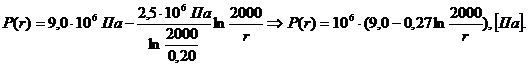
Изобразим
графически распределение давления, принимая текущий радиус 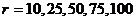 и далее через 200 м (рис.6).
и далее через 200 м (рис.6).
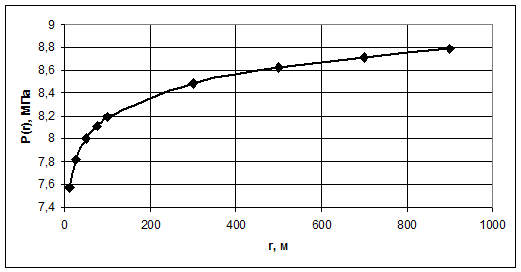
Рис.3.6. График распределения давления по пласту в зависимости от
текущего радиуса
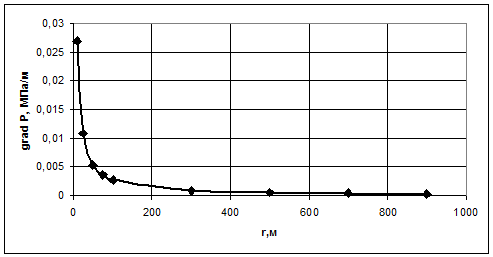
. Градиент давления:
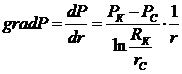
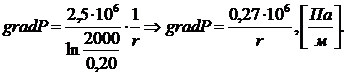 (3.9)
(3.9)
. Скорость фильтрации:
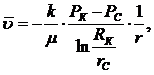 (3.10)
(3.10)
Знак «минус» в правой части равенства появляется из-за того, что скорость
фильтрации направлена в сторону уменьшения приведенного давления. Поэтому
векторы скорости фильтрации и градиента фильтрационного давления направлены в
разные стороны.
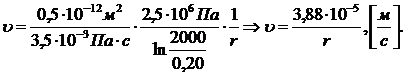
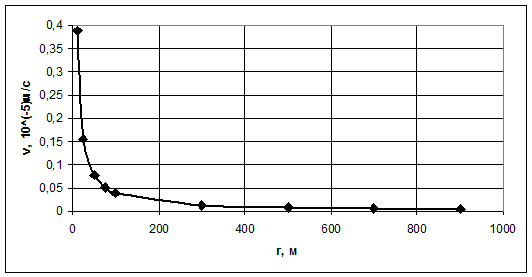
Рис.3.8. График распределения скорости фильтрации в зависимости от
текущего радиуса
4. Дебит (объемный расход) скважины (по формуле Дюпюи):
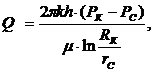 (3.11)
(3.11)
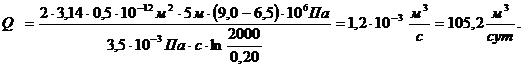
.
Закон движения жидких частиц:
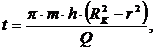 (3.12)
(3.12)
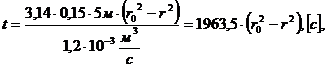
где
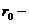 начальное положение частиц жидкости;
начальное положение частиц жидкости; 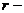 текущее положение частиц жидкости.
текущее положение частиц жидкости.
.
Средневзвешенное по объему порового пространства пластовое давление:
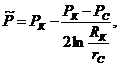 (3.13)
(3.13)
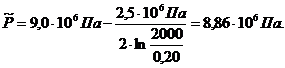
Таким
образом, распределение давления представляет собой логарифмическую зависимость
давления от радиуса и графически представляется логарифмической кривой, а
градиент давления и скорость фильтрации - обратную зависимость и графически
изображаются гиперболой.
3.3 Задача №3
Тема №3: Прямолинейно-параллельная установившаяся фильтрация однородной
несжимаемой жидкости в неоднородных пластах.
Дано:
Таблица 3
|
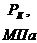 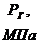 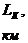 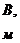 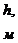 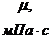 Слоисто
- неоднородныйЗонально - неоднородный Слоисто
- неоднородныйЗонально - неоднородный
|
|
|
|
|
|
|
|
|
|
|
|
|
|
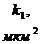 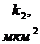 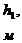 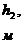 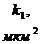 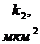 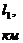 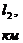
|
|
|
|
|
|
|
|
|
9,0
|
6,5
|
7,5
|
200
|
10
|
1,1
|
1
|
0,6
|
5
|
5
|
1
|
0,6
|
5,3
|
5
|
где
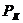 - давление на контуре питания;
- давление на контуре питания;
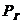 -
давление на стенке галереи;
-
давление на стенке галереи;
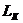 - длина
пласта;
- длина
пласта;
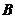 - ширина
пласта;
- ширина
пласта;
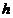 -
толщина пласта;
-
толщина пласта;
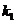 ,
, 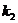 - проницаемость пропластков или зон пласта;
- проницаемость пропластков или зон пласта;
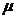 -
динамическая вязкость жидкости;
-
динамическая вязкость жидкости;
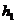 ,
, 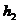 - толщина пропластков;
- толщина пропластков;
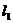 ,
, 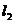 - длина зон пласта.
- длина зон пласта.
Определить закон распределения давления, градиента давления и скорости
фильтрации по длине пласта (в математическом и графическом виде), дебит галереи
и средний коэффициент проницаемости для двух случаев неоднородности пласта при
исходных данных, приведенных в табл.3.
Решение
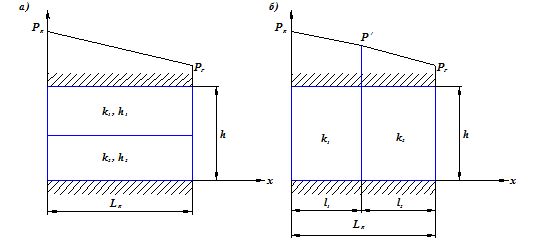
Рис.3.9.Схема прямолинейно-параллельного фильтрационного потока в
слоисто-неоднородном (а) и зонально-неоднородном (б) пластах
Случай слоисто-неоднородного пласта:
. Закон распределения давления в каждом из пропластков:
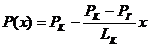 (3.14)
(3.14)
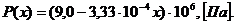

Рис.3.10. График распределения давления по пропласткам
. Градиент давления:
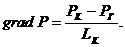 (3.15)
(3.15)
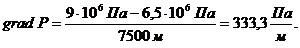
т.е.
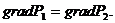

Рис.3.11. График распределения градиента давления по пропласткам
. Скорость фильтрации по пропласткам:
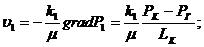 (3.16)
(3.16)
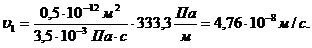
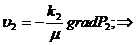
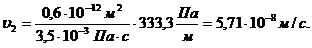
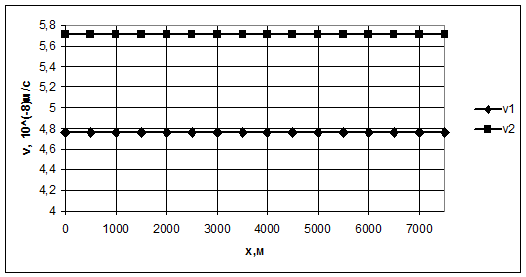
Рис.3.12.
График распределения скорости фильтрации в пласте 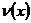 по пропласткам
по пропласткам
.
Дебит галереи:
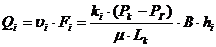 , (3.17)
, (3.17)
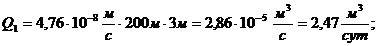
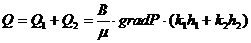 (3.18)
(3.18)
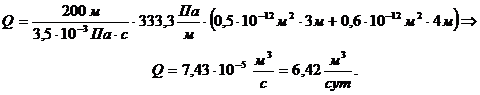
. Средняя проницаемость полосообразной залежи:
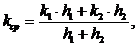 (3.19)
(3.19)
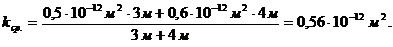
Случай зонально-неоднородного пласта:
. Закон распределения давления в каждом из пропластков:
Определим
давление 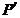 на границе двух зон, основываясь на уравнении
неразрывности
на границе двух зон, основываясь на уравнении
неразрывности 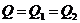 .
.
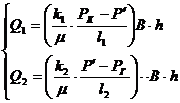
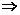
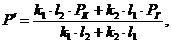 (3.20)
(3.20)
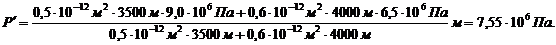
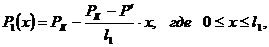 (3.21)
(3.21)
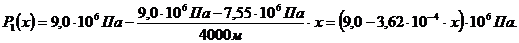
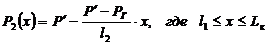 , (3.22)
, (3.22)
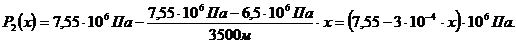
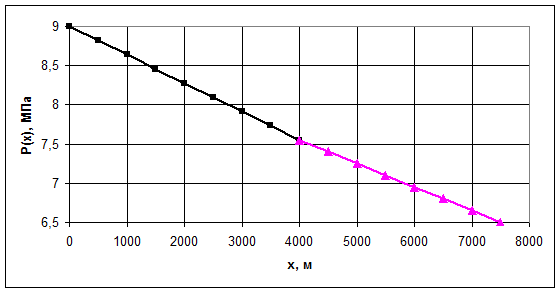
Рис.3.13. График распределения давления по пропласткам
. Градиент давления:
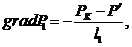
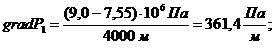 (3.23)
(3.23)
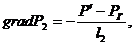 (3.24)
(3.24)
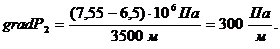
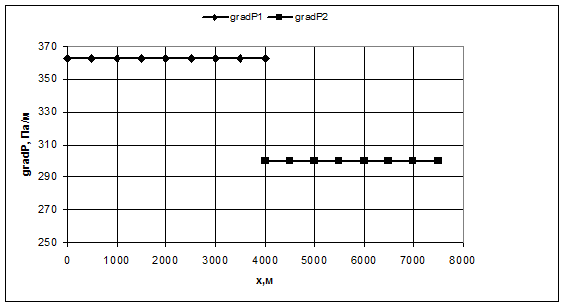
Рис.3.14. График распределения градиента давления по пропласткам
3. Скорость фильтрации по пропласткам:
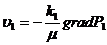 (3.25)
(3.25)
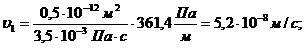
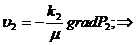
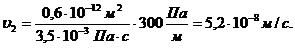
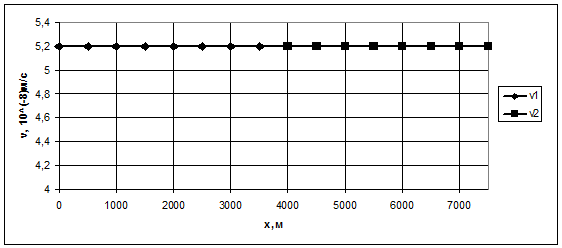
Рис.3.15. График распределения скорости фильтрации по пропласткам
4. Дебит галереи:
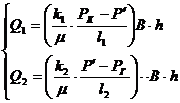 (3.26)
(3.26)
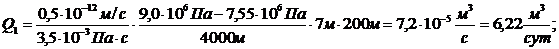
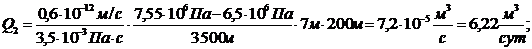
. Средний коэффициент проницаемости:
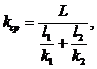 (3.27)
(3.27)
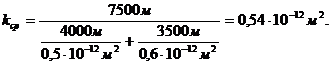
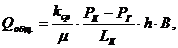 (3.28)
(3.28)
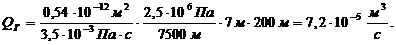
Таким
образом, объемные расходы жидкости по зонам 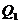 и
и 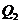 и общий объемный расход полосообразной залежи
и общий объемный расход полосообразной залежи 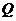 равны.
равны.
3.3 Задача №4
Тема №4: Плоскорадиальная установившаяся фильтрация однородной
несжимаемой жидкости в неоднородных пластах.
Дано:
Таблица 4
|
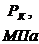 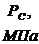 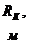 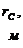 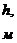 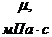 Слоисто
- неоднородныйЗонально - неоднородный Слоисто
- неоднородныйЗонально - неоднородный
|
|
|
|
|
|
|
|
|
|
|
|
|
|
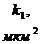 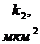 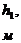 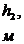 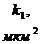 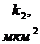 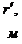
|
|
|
|
|
|
|
|
9,0
|
6,5
|
2000
|
0,20
|
7
|
3,5
|
0,5
|
0,6
|
3
|
4
|
0,5
|
0,6
|
1000
|
где
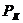 - давление на контуре питания;
- давление на контуре питания;
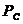 -
давление на забое скважины;
-
давление на забое скважины;
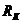 - радиус
контура питания;
- радиус
контура питания;
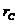 - радиус
скважины;
- радиус
скважины;
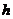 -
толщина пласта;
-
толщина пласта;
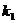 ,
, 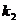 - проницаемость пропластков или зон пласта;
- проницаемость пропластков или зон пласта;
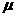 -
динамическая вязкость жидкости;
-
динамическая вязкость жидкости;
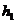 ,
, 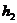 - толщина пропластков;
- толщина пропластков;
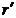 - радиус
границы между первой и второй зонами пласта.
- радиус
границы между первой и второй зонами пласта.
Определить закон распределения давления, градиента давления и скорости
фильтрации по длине пласта (в математическом и графическом виде), дебит
скважины и средний коэффициент проницаемости для двух случаев неоднородности
пласта при исходных данных, приведенных в табл.4.
Решение
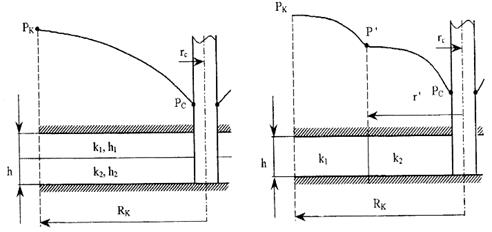
Рис.3.16. Плоскорадиальный поток в слоисто-неоднородном (а) и
зонально-неоднородном (б) пластах
. Закон распределения давления в каждом из пропластков:
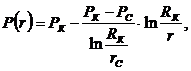 (3.29)
(3.29)
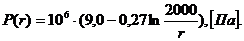

Рис.3.17.
График распределения давления в зависимости от текущего радиуса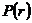
2. Градиент давления:
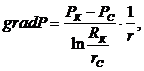 (3.30)
(3.30)
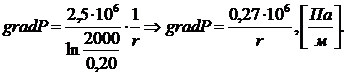
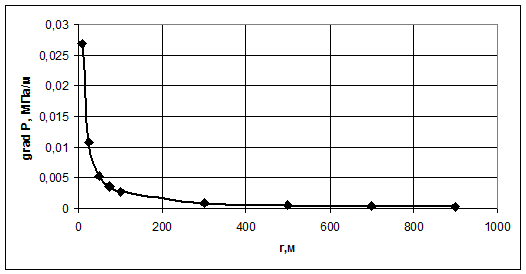
Рис.3.18.
График распределения градиента давления в зависимости от текущего радиуса 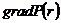
. Скорость фильтрации:
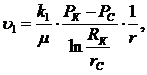 (3.31)
(3.31)
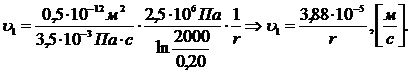
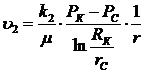 (3.32)
(3.32)
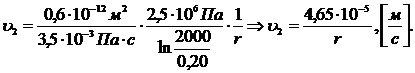
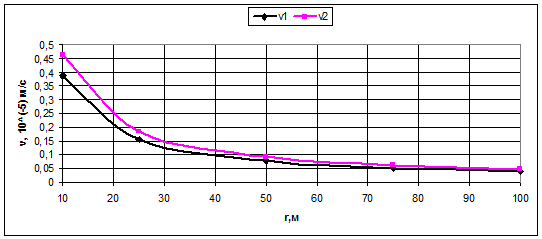
Рис.3.19.
График распределения скорости фильтрации 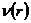
. Дебит скважины:
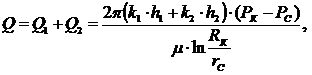 (3.33)
(3.33)
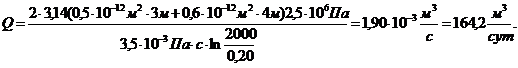
.
Средний коэффициент проницаемости:
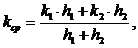 (3.34)
(3.34)
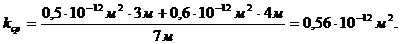
Случай
зонально-неоднородного пласта:
Давление
на границе двух зон 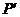 на основе уравнения неразрывности:
на основе уравнения неразрывности:
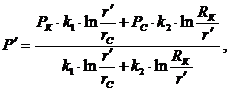 (3.35)
(3.35)
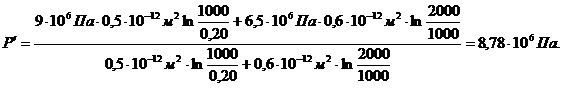
. Закон распределения давления в каждой зоне:
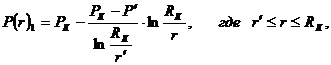 (3.36)
(3.36)
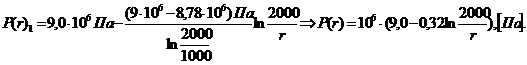
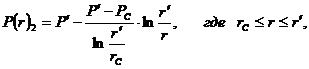 (3.37)
(3.37)
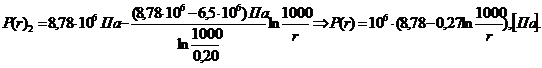
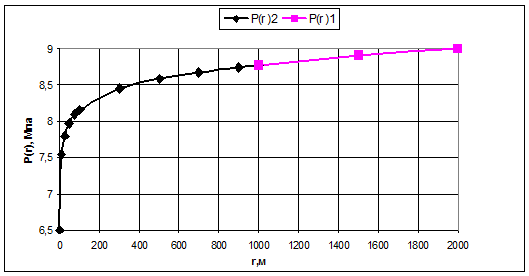
Рис.3.20.
График распределения давления в зависимости от текущего радиуса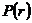
. Градиент давления:
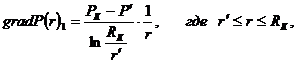 (3.38)
(3.38)
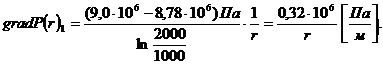
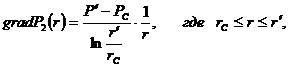 (3.39)
(3.39)
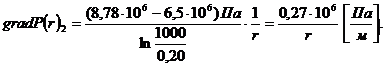
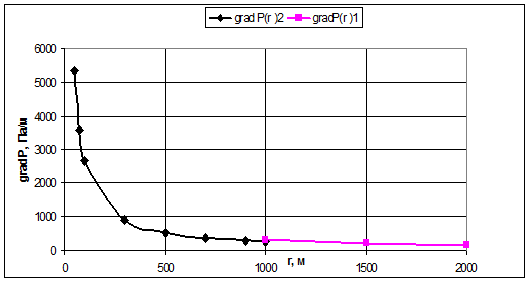
Рис.3.21.
График распределения градиента давления в зависимости от текущего радиуса 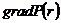
. Скорость фильтрации:
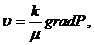 (3.40)
(3.40)
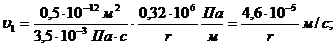
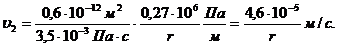
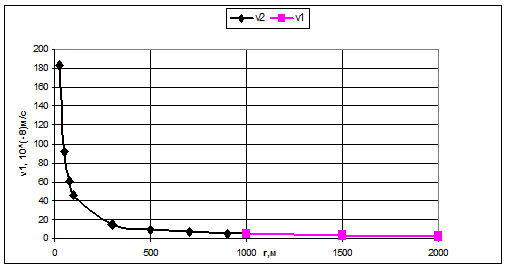
Рис.3.22.
График распределения скорости фильтрации в зависимости от текущего радиуса 
. Средний коэффициент проницаемости:
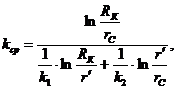 (3.41)
(3.41)
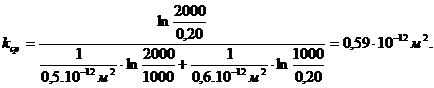
. Дебит скважины:
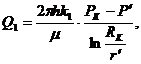 (3.42)
(3.42)
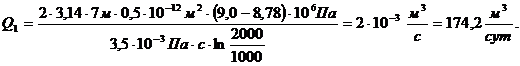
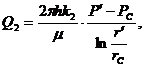 (3.43)
(3.43)
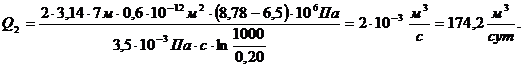
Дебит скважины в двухзональном пласте:
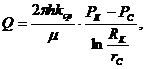 (3.44)
(3.44)
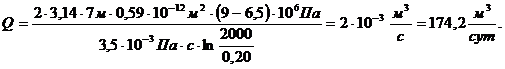
Таким
образом, дебит потока в силу установившегося движения несжимаемой жидкости
будет постоянен через любую цилиндрическую поверхность, соосную скважине 
4.
ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Тема курсовой работы посвящена изучению установившихся (стационарных)
одномерных фильтрационных потоков жидкости и газа.
В подземной гидромеханике под установившимся фильтрационным потоком
понимается такой поток, фильтрационные характеристики которого постоянны во
времени, т.е. распределение давления, градиента давления, скорости фильтрации,
массовый расход и др. параметры не изменяются во времени. Под одномерными
фильтрационными потоками понимают такие потоки, в которых давление является
функцией только одной координаты. В расчетной части курсовой работы изучаются
первые два одномерных потока - прямолинейно-параллельный и плоскорадиальный.
Сложные пространственные траектории реальных фильтрационных потоков могут
быть приближенно представлены как состоящие из одномерных фильтрационных
потоков.
Прямолинейно-параллельный поток может наблюдаться на отдельных участках
пластов залежей нефти и газа при движении жидкости от нагнетательных скважин к
эксплуатационным. Такие пласты часто называют полосообразными. Толщина пластов
h постоянна, граничный контур непроницаем и непроницаемы кровля и подошва
пласта. Батарея эксплуатационных скважин расположена параллельно начальному
контуру нефтеносности. Приближение тем больше, чем меньше расстояние между
скважинами и если заменить батарею сплошной прямолинейной выработкой -
галереей, то движение жидкости к галерее будет строго
прямолинейно-параллельным.
Плоскорадиальный поток имеет большое практическое значение, т.к. приток
нефти и газа к забоям эксплуатационных гидродинамически совершенных скважин подчиняется
законам плоскорадиальной фильтрации. Для эксплуатационной скважины поток
-радиально-сходящий, а для нагнетательной - радиально-расходящий.
Плоскорадиальным потоком будет занята вся зона от стенки скважины до контура
питания. Вблизи гидродинамически- несовершенной скважины линии тока
искривляются и поток можно считать плоско-радиальным только при некотором
удалении от скважины.
Радиально-сферический поток может реализовываться, когда скважина
вскрывает только плоскую горизонтальную, непроницаемую кровлю пласта. Пласт при
этом должен быть неограниченной толщины, а забой иметь полусферическую форму.
Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше
толщины пласта.
Реальные продуктивные пласты нефтяных и газовых месторождений имеют
неоднородное строение по фильтрационным параметрам пластов, в частности
неоднородность по проницаемости. Различают слоистую неоднородность (по толщине
пласта - сложен пропластками различной проницаемости) и зональную
неоднородность (по площади, по простиранию пласта, неоднородный пласт с
закономерным изменением в каком-либо направлении и др.).
В практике разработки нефтяных и газовых месторождений значительный
интерес представляет задача о притоке жидкости к скважине при наличии вокруг
забоя скважины кольцевой зоны с проницаемостью, отличной от проницаемости
остальной части пласта, т.е. пласт состоит из двух зон различной проницаемости.
Такая задача возникает в случаях таких, как торпедирование, кислотная обработка
призабойной зоны, вынос мелких фракций породы из этой зоны, установка
гравийного фильтра, глинизации или парафинизации призабойной зоны. Очень важной
при этом бывает необходимость установления влияния на продуктивность скважины
различия проницаемостей кольцевой призабойной зоны и остальной части пласта.
Описанные три вида одномерного потока играют большую роль при решении
многих задач нефте-газопромысловой практики. Они лежат в основе ряда
исследований закономерностей течения жидкости в пласте в зависимости от
принятой системы разработки или от конструктивных особенностей скважин.
Моделируя каждый из трёх видов одномерного потока, мы прибегаем к некоторой
схематизации реальных пластов и течений жидкости. Тем не менее, рассмотренные
схемы не только воспроизводят хотя и приближенно простейшие случаи течения
жидкости в реальном пласте, но и помогают изучать более сложные виды потоков
пластовой жидкости в тех случаях, в которых сложный фильтрационный поток удобно
представить себе состоящим из простейших видов потока.
ЗАКЛЮЧЕНИЕ
В данной курсовой работе были рассмотрены установившиеся одномерные
фильтрационные потоки жидкости и газа при различных законах фильтрации.
В теоретической части был произведен сравнительный анализ установившихся
потоков газа при линейных и нелинейных законах фильтрации.
Определение закона фильтрации жидкостей и газов представляет не только
теоретический интерес, но и имеет большое практическое значение, ибо без знания
закона фильтрации в пласте, особенно вблизи забоя скважин, нельзя рассчитать
возможные дебиты жидкости и газа, их изменения во времени при различных
условиях эксплуатации скважин, а также невозможно определение параметров пласта
(проницаемость, пористость и другие) по данным исследования (испытания)
нефтяных и газовых скважин.
СПИСОК
ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Басниев
К. С. Нефтегазовая гидромеханика / К.С. Басниев, Н.М. Дмитриев, Г.Д. Розенберг
- М.-Ижевск: Институт компьютерных исследований, 2005. - 544 с.
. Ольховская
В.А. Подземная гидромеханика. - Самара: Самарский Государственный Технический
Университет, 2004. - 148 с.
. Телков
А.П., Грачев С.И. Гидромеханика пласта применительно к прикладным задачам
разработки нефтяных и газовых месторождений: учебное пособие. В 2 ч. Ч.1. -
Тюмень: ТюмГНГУ, 2009. - 240 с.
. Щелкачев
В.Н., Лапук Б.Б. Подземная гидравлика. Ижевск: НИЦ «Регулярная и хаотическая
динамика», 2001. - 736с.
. Подземная
гидромеханика: Лабораторный практикум / М.К.Рогачев, А.Ю.Харин. -СПб: СПГГИ,
2006. - 83с.
. Подземная
гидромеханика: Методические указания к курсовой работе / М.К.Рогачев,
А.В.Максютин. - СПб: СПГГИ, 2011. - 90с.
ПРИЛОЖЕНИЕ 1
Таблица 5
Значения давления в отдельных точках пласта (Задача №1, задача
№3(слоисто-неоднородный пласт))
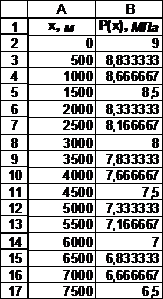
Таблица 6
Результаты расчета значений давления, градиента давления и скорости
фильтрации для конкретных значений текущего радиуса (Задача №2)

Таблица 7
Значения давлений в отдельных точках зонально-неоднородного пласта
(Задача №3)

Таблица 8
Результаты расчета значений давления, градиента давления и скорости
фильтрации для конкретных значений текущего радиуса слоисто-неоднородного
пласта (Задача №4)

Таблица 9
Результаты расчета значений давления, градиента давления и скорости
фильтрации для конкретных значений текущего радиуса зонально-неоднородного
пласта (Задача №4)
