Основы динамики космического полета
Введение
орбита планета спутник
Космос (греч. kosmos - строй, порядок, мир, Вселенная) первоначально у
древних греков (начиная с Пифагора 6 в до н.э.) - Вселенная как стройная
организованная система в противоположность хаосу беспорядочному нагромождению
материи.
Космос изучают с помощью разных
приборов и инструментов. Среди них телескопы, сложнейшее оптическое
оборудование, астрографы, астролябии. Ученые используют их для определения
состава планет, их температуры, величины и других данных.
октября 1957 г. с территории нашей
страны был запущен первый в мире искусственный спутник Земли. Проводились
координированные исследования верхних слоев атмосферы. Советский научный
эксперимент, осуществленный на такой большой высоте, имел тогда громадное
значение для познания свойств космического пространства и изучения Земли как
планеты Солнечной системы.
Первый спутник имел форму шара
диаметром 58 см с четырьмя прикрепленными стержневыми антеннами. Весил 83,6 кг.
Два его радиопередатчика, непрерывно излучали радиосигналы, которые мог
уверенно принимать широкий круг радиолюбителей. С его помощью была измерена
плотность верхних слоев атмосферы, исследованы особенности распространения
радиосигналов в ионосфере, проведены теоретические расчеты и проверены основные
технические решения, связанные с выведением искусственных летательных аппаратов
на орбиту. За 92 дня «Спутник-1» совершил 1440 оборотов вокруг Земли и
прекратил свое существование 4 января 1958 г., войдя в плотные слои атмосферы.
Простейший спутник был только первым
элементом в серии космических аппаратов, предполагавшей создание орбитальных
пилотируемых станций и межпланетных кораблей.
Особо следует отметить спутники
связи. Они расширяют возможности теле- и радиообщения между людьми на Земле.
Современные организации характеризуются большим объемом различной информации, в
основном электронной и телекоммуникационной, которая проходит через них каждый
день. Поэтому важно иметь высококачественный выход на коммутационные узлы,
которые обеспечивают выход на все важные коммуникационные линии. В России, где
расстояния между населенными пунктами огромное, а качество наземных линий
оставляет желать лучшего, оптимальным решением этого вопроса является
применение систем спутниковой связи.
Передача информации в цифровой форме
обладает рядом преимуществ по сравнению с другими методами передачи. К ним
относятся:
. простота и эффективность
объединения многих независимых сигналов и преобразования цифровых сообщений в
«пакеты» для удобства коммутации;
. меньшие энергозатраты по сравнению
с передачей аналогового сигнала;
. относительная нечувствительность
цифровых каналов к эффекту накопления искажений при ретрансляциях, обычно
представляющему серьезную проблему в аналоговых системах связи;
. потенциальная возможность
получения очень малых вероятностей ошибок передачи и достижения высокой
верности воспроизведения переданных данных путем обнаружения и исправления
ошибок;
. конфиденциальность связи;
. гибкость реализации цифровой
аппаратуры, допускающая использование микропроцессоров, цифровую коммутацию и
применение микросхем с большей степенью интеграции компонентов.
На сегодняшний день существует
большое количество ССС, основанных на различных спутниковых системах, различных
принципах и предназначенных для различных применений.
Поэтому данная тема курсовой работы
актуальна на сегодняшний день.
Целью данной курсовой работы
является изучение основ динамики космического полета.
Основными задачами при выполнении
работы являются:
) изучение литературы по теме
курсовой работы
) изучение основных принципов
и методов расчета траекторий полета
) раскрытие значения данной
темы
) возможность применения
изученного материала
1. Движение материальной
точки в центральном силовом поле Земли
1.1 Уравнения движения
точки в центральном силовом поле
. Рассмотрим движение материальной
точки В под действием центральной силы
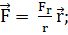
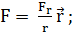 (1.1.1)
(1.1.1)
где 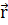 -
радиус-вектор, проведенный из центра сил О в движущуюся точку, Fr -
проекция вектора силы на направление радиуса-вектора, зависящая только от
расстояния r между точками О и В. В случае притяжения точки В к центру сил Fr= - |
-
радиус-вектор, проведенный из центра сил О в движущуюся точку, Fr -
проекция вектора силы на направление радиуса-вектора, зависящая только от
расстояния r между точками О и В. В случае притяжения точки В к центру сил Fr= - |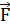 |,
в случае отталкивания Fr=
|
|,
в случае отталкивания Fr=
|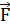 |.
|.
. Момент 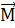 силы
силы
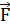 относительно
точки О равен нулю:
относительно
точки О равен нулю:
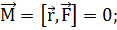
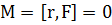 (1.1.2)
(1.1.2)
Поэтому в соответствии с
законом сохранения момент импульса материальной точки В относительно точки О
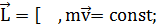
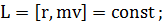 (1.1.3)
(1.1.3)
где т - масса точки В, a 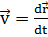 -
ее скорость.
-
ее скорость.
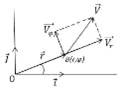
Рис 1
Вектор 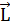 перпендикулярен к плоскости, проходящей через векторы
перпендикулярен к плоскости, проходящей через векторы 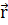 и
и 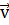 . Из
(рис 1.1) следует, что в центральном силовом поле эта плоскость не меняет своей
ориентации в пространстве, т.е. траектория точки В является плоской кривой.
Таким образом, положение точки В можно задать с помощью двух полярных координат
r и φ (рис. 1.1), а ее
скорость
. Из
(рис 1.1) следует, что в центральном силовом поле эта плоскость не меняет своей
ориентации в пространстве, т.е. траектория точки В является плоской кривой.
Таким образом, положение точки В можно задать с помощью двух полярных координат
r и φ (рис. 1.1), а ее
скорость 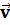 можно разложить на две взаимно перпендикулярные составляющие -
радиальную скорость
можно разложить на две взаимно перпендикулярные составляющие -
радиальную скорость 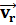 , и
трансверсальную
, и
трансверсальную 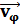 .
.
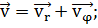
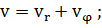
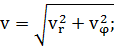
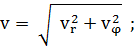 (1.1.4)
(1.1.4)
Действительно, 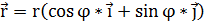 ,
где
,
где 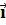 -
единичный вектор полярной оси, а
-
единичный вектор полярной оси, а  - единичный вектор,
образующий с
- единичный вектор,
образующий с 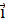 угол
угол
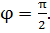 Скорость
точки В
Скорость
точки В 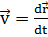 ,
или
,
или
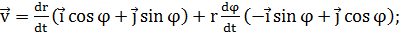 (1.1.6)
(1.1.6)
Единичный вектор - 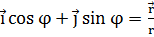 совпадает
по направлению с вектором
совпадает
по направлению с вектором 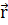 ,
а единичный вектор -
,
а единичный вектор - 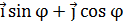 перпендикулярен
к
перпендикулярен
к 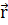 .
Поэтому первый член правой части написанного выше выражения для
.
Поэтому первый член правой части написанного выше выражения для 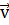 является
радиальной скоростью, а второй - трансверсальной.
является
радиальной скоростью, а второй - трансверсальной.
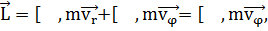 (1.1.7)
(1.1.7)
или, в силу взаимной
перпендикулярности векторов 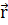 и
и 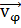
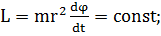 (1.1.8)
(1.1.8)
При повороте радиуса-вектора 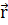 за время dt на малый угол dφ радиус - вектор прочерчивает круговой сектор, площадь которого
за время dt на малый угол dφ радиус - вектор прочерчивает круговой сектор, площадь которого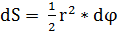
Поэтому величину
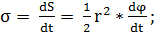 (1.1.9)
(1.1.9)
называют секториальной, или
секторной, скоростью. Из (1.1.8) видно, что при движении материальной точки в
центральном силовом поле секториальная скорость точки постоянна:
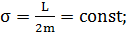 (1.1.10)
(1.1.10)
Этот закон впервые был установлен
Кеплером применительно к движению планет в поле тяготения Солнца. Его называют
вторым законом Кеплера.
3. Для определения траектории
материальной точки В воспользуемся законами сохранения момента импульса
(уравнение 1.1.8) и энергии:
W = Wк+ Wп = const; (1.1.11)
Кинетическая энергия может быть
представлена в виде:
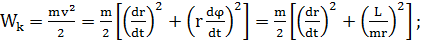 (1.1.12)
(1.1.12)
Подставив это значение Wк
в уравнение (1.1.11) и разрешив его относительно 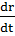 получим:
получим:
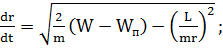 (1.1.13)
(1.1.13)
Из (1.1.8)
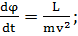 (1.1.14)
(1.1.14)
Таким образом
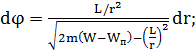 (1.1.15)
(1.1.15)
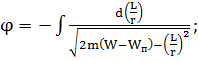 (1.1.16)
(1.1.16)
Для нахождения этого интеграла
необходимо знать зависимость потенциальной энергии Wп от r. Большой практический интерес
представляет движение материальной точки В в таком сферически симметричном
центральном силовом поле, для которого
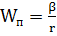 ;
(1.1.17)
;
(1.1.17)
где
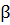 = const. В случае поля тяготения,
создаваемого материальной точкой с массой М,
= const. В случае поля тяготения,
создаваемого материальной точкой с массой М, 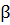 = -
= -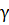 mМ < 0. Соотношение (1.1.16) справедливо также для потенциальной
энергии точечного электрического заряда q1 находящегося в электростатическом поле другого точечного заряда q2.
mМ < 0. Соотношение (1.1.16) справедливо также для потенциальной
энергии точечного электрического заряда q1 находящегося в электростатическом поле другого точечного заряда q2.
Подставим значение (1.1.17) для Wn в уравнение (1.1.16)
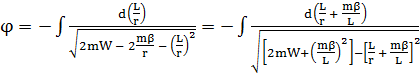 ;
(1.1.18)
;
(1.1.18)
Последний интеграл сводится к
табличному, если ввести обозначения:
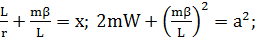 (1.1.19)
(1.1.19)
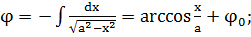 (1.1.20)
(1.1.20)
где φ0 - постоянная
интегрирования, которую можно обратить в нуль, выбрав начало отсчета угла φ таким образом, чтобы φ = 0 при х = а. Подставив
значения х и а, получим уравнение траектории точки В:
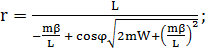
. Если точка В притягивается к
силовому центру, то 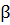 < 0
и уравнение ее траектории (1.1.22) можно переписать в такой форме:
< 0
и уравнение ее траектории (1.1.22) можно переписать в такой форме:
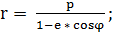 (1.1.23)
(1.1.23)
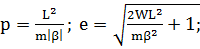 (1.1.24)
(1.1.24)
Траектория, или орбита, точки В
представляет собой кривую второго порядка, причем р - ее фокальный параметр, а
е - эксцентриситет.
Возможны следующие типы траекторий
точки В:
а) эллиптическая орбита (е <
1) приW < 0;
б) параболическая орбита (е =
1) при W = 0;
в) гиперболическая орбита (е
> 1) при W > 0;
г) прямолинейная траектория,
проходящая через центр сил (р = 0, е = 1) при L= 0.
В первых трех случаях центр сил
совпадает с одним из фокусов орбиты. Для планет, движущихся в поле тяготения
Солнца, W < 0. Поэтому для них справедлив первый закон Кеплера:
все планеты Солнечной системы
движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
В соответствии со вторым законом
Кеплера секториальная скорость 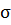 каждой
из планет постоянна. Следовательно, период Т обращения планеты по орбите равен
отношению площади S, ограниченной орбитой, к
каждой
из планет постоянна. Следовательно, период Т обращения планеты по орбите равен
отношению площади S, ограниченной орбитой, к 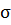 :
:
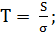 (1.1.25)
(1.1.25)
Площадь эллипса S =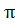 ab, где а и b - его большая и малая полуоси.
Учитывая, что
ab, где а и b - его большая и малая полуоси.
Учитывая, что
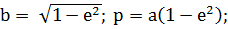 (1.1.26)
(1.1.26)
а также используя соотношение
(1.1.10), получаем
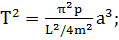 (1.1.27)
(1.1.27)
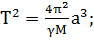 (1.1.28)
(1.1.28)
Уравнение (1.1.28) является
математической записью третьего закона Кеплера: квадраты периодов
обращения планет вокруг Солнца прямо пропорциональны кубам больших полуосей их
орбит.
. В случае движения материальной
точки В в сферически симметричном центральном поле сил отталкивания (β > 0) уравнение ее
траектории (1.1.22) также представляет собой уравнение кривой второго порядка:
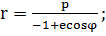 (1.1.29)
(1.1.29)
где р и e определяются по формулам (1.1.24).
Полная энергия материальной точки В:
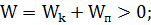 (1.1.30)
(1.1.30)
так как Wп> 0, а кинетическая энергия всегда положительна. Поэтому точка
В может двигаться только либо по гиперболической орбите, либо вдоль прямой,
проходящей через центр сил (при L = 0).
1.2 Уравнение орбиты
Для описания движения центра масс
тела или материальной точки необходимо ввести некоторое начало отсчета -
систему координат. При рациональном выборе системы координат часто удается
значительно упростить уравнения движения.
Различают инерциальную и
неинерциалъную системы координат. Инерциальной называют такую систему
координат, которая находится в состоянии покоя или равномерного прямолинейного
поступательного движения относительно «абсолютной» системы отсчета, например,
удаленных звезд, условно называемых неподвижными. Всякая другая система
координат является неинерциальной. Заметим, что часто при решении задач
механики некоторые неинерциальные системы координат оказывается возможным
рассматривать в качестве инерциальных. При этом допускается несущественная для
данной задачи погрешность, но зато удается значительно упростить задачу в
целом.
Уравнения движения в инерциальной
системе координат имеют наиболее простой вид и записываются на основе второго
закона Ньютона: произведение массы тела на его ускорение равно действующей
силе.
Абсолютное движение и
относительное движение. Рассмотрим движение
материальных точек М и т в некоторой инерциальной системе координат.
Единственной силой, под действием которой совершается движение, является сила
притяжения. Для материальной точки т эта сила определяется формулой
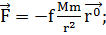 (1.2.1)
(1.2.1)
Здесь 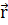 ° - единичный вектор, направленный от М к т, r - относительное расстояние. Сила,
действующая на материальную точку М, равна по величине |
° - единичный вектор, направленный от М к т, r - относительное расстояние. Сила,
действующая на материальную точку М, равна по величине |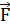 |, но направлена в
противоположную сторону.
|, но направлена в
противоположную сторону.
Запишем на основе второго закона
Ньютона уравнения абсолютного движения точек массами m и M:
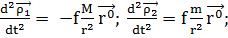 (1.2.2)
(1.2.2)
где 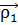 - радиус-вектор, проведенный из начала инерциальной системы
координат в точку т, а
- радиус-вектор, проведенный из начала инерциальной системы
координат в точку т, а 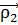 -
радиус-вектор, проведенный из начала инерциальной системы координат в точку М.
Понятно, что
-
радиус-вектор, проведенный из начала инерциальной системы координат в точку М.
Понятно, что
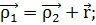 (1.2.3)
(1.2.3)
где 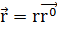
Вычитая из первого уравнения (2.1.2)
второе, получим с учетом (1.2.3) уравнение движения материальной точки т
относительно притягивающего центра М:
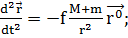 (1.2.4)
(1.2.4)
 ;
(1.2.5)
;
(1.2.5)
если обозначить
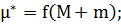 (1.2.6)
(1.2.6)
произведение постоянной притяжения
на сумму масс взаимно притягивающихся материальных точек.
Уравнение (1.2.5) является основным
в задаче двух тел. В координатной форме оно эквивалентно трем уравнениям
второго
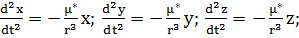 (1.2.7)
(1.2.7)
где 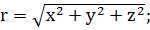
Движение
непритягивающего спутника. Во многих задачах
небесной механики т < М и оказывается возможным пренебречь ускорением,
которое спутник т сообщает притягивающему центру М. В результате придем к
ограниченной задаче двух тел (или задаче о непритягивающем спутнике). Тогда
можно совместить начало инерциальной системы координат с притягивающим центром
М (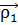 =
= 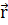 ,
, 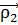 = 0) и записать уравнение относительного движения спутника в
следующем виде:
= 0) и записать уравнение относительного движения спутника в
следующем виде:
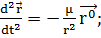 (1.2.8)
(1.2.8)
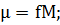 (1.2.9)
(1.2.9)
произведение постоянной притяжения
на массу притягивающего центра.
Из сравнения уравнений (1.2.5) и
(1.2.7) следует, что притягивающий спутник с массой т движется относительно
притягивающего центра с массой М так, как двигался бы непритягивающий спутник
вокруг притягивающего центра с массой М + т.
Интегралы уравнений
движения
Движение спутника относительно
притягивающего центра описывается системой дифференциальных уравнений шестого
порядка
Интеграл площадей. Умножим теперь уравнение движения (1.2.7) векторно на 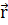 =
= 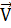 ,
полагая сначала, что
,
полагая сначала, что 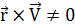 т.е.
векторы
т.е.
векторы 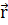 и
и 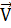 неколлинеарны.
Тогда
неколлинеарны.
Тогда
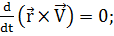 (1.2.10)
(1.2.10)
Отсюда найдем векторный интеграл
площадей
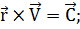 (1.2.11)
(1.2.11)
который эквивалентен трем скалярным
интегралам
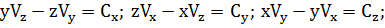 (1.2.12)
(1.2.12)
Здесь r = (x, у, z), V = (Vx, Vy, Vz), C = (Cx, Cy, Cz); проекции
векторов рассматриваются в системе координат, начало которой совпадает с
притягивающим центром, а оси имеют постоянную ориентацию в пространстве.
Если умножить уравнение (1.2.11)
скалярно на 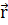 , то
получим
, то
получим
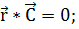 (1.2.13)
(1.2.13)
Отсюда следует, что вектор 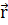 всегда находится в плоскости, проходящей через центр притяжения и
определяемой нормальным к ней вектором
всегда находится в плоскости, проходящей через центр притяжения и
определяемой нормальным к ней вектором 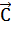 . Эта плоскость, т.е. плоскость движения спутника, называется
неизменяемой плоскостью Лапласа. Чтобы получить уравнение плоскости движения
спутника в координатной форме, умножим уравнения (1.2.12) соответственно на х,
у, z и
сложим. Тогда получим
. Эта плоскость, т.е. плоскость движения спутника, называется
неизменяемой плоскостью Лапласа. Чтобы получить уравнение плоскости движения
спутника в координатной форме, умножим уравнения (1.2.12) соответственно на х,
у, z и
сложим. Тогда получим
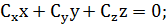 (1.2.14)
(1.2.14)
Уравнение орбиты. Согласно условию (1.2.14) движение спутника происходит в
неизменяемой плоскости, т.е. траектория представляет собой плоскую кривую,
которую называют орбитой спутника. Для получения уравнения орбиты используем
вектор Лапласа. Предварительно найдем скалярное произведение 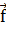 на
на 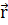 :
:
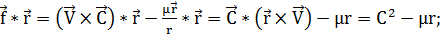 (1.2.15)
(1.2.15)
Но по определению скалярного
произведения
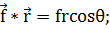 (1.2.16)
(1.2.16)
где 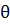 - уголя между векторами
- уголя между векторами 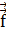 и
и 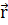 , тогда
, тогда
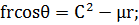 (1.2.17)
(1.2.17)
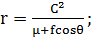 (1.2.19)
(1.2.19)
Вводя обозначения
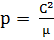 ; (1.2.20)
; (1.2.20)
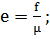 (1.2.21)
(1.2.21)
получим окончательно уравнение
орбиты спутника в полярных координатах
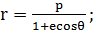 (1.2.22)
(1.2.22)
Здесь р - параметр орбиты,
определяющий ее линейные размеры, а е - эксцентриситет орбиты, характеризующий
ее форму.
С другой стороны, соотношение
(1.2.22) представляет собой уравнение конического сечения в полярных
координатах с полюсом в фокусе. Это коническое сечение симметрично относительно
вектора Лапласа, а полярный угол 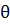 , который называют истинной аномалией, определяет поворот текущего
радиуса-вектора относительно оси симметрии. Полученный результат отражает
первый закон Кеплера:
, который называют истинной аномалией, определяет поворот текущего
радиуса-вектора относительно оси симметрии. Полученный результат отражает
первый закон Кеплера:
Движение спутника относительно
притягивающего центра всегда совершается по коническому сечению (по эллипсу,
окружности, гиперболе, параболе или прямой), в одном из фокусов которого
находится притягивающий центр.
Главная, или фокальная, ось орбиты,
совпадающая с направлением вектора Лапласа, называется в астрономии линией
апсид. Точки пересечения этой линии с орбитой называют апсидалъными, или просто
апсидами. Апсиды совпадают с вершинами конического сечения и имеют специальные
названия. В общем случае ближайшую к притягивающему центру апсиду называют
перицентром, а наиболее удаленную - апоцентром. Заметим, что перицентр
существует для любых орбит, а апоцентр - только для замкнутой. В зависимости от
притягивающего центра апсиды имеют свои собственные названия. Например, для
Земли это перигей и апогей, для Луны - периселений и апоселений, для Солнца -
перигелий и афелий и т.д.
Преобразуем теперь формулу (1.2.21)
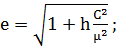 (1.2.23)
(1.2.23)
Из соотношений (1.2.20) и (1.2.23)
следует, что по заданным величинам произведения постоянной тяготения на массу
центрального тела (µ), постоянной интеграла энергии (h) и постоянной интеграла
площадей (С) можно вычислить параметр орбиты и ее эксцентриситет, т.е. задать
форму и размеры орбиты в ее плоскости.
1.3 Основные элементы
орбиты
Движение спутника относительно
притягивающего центра описывается тремя уравнениями второго порядка (1.2.7).
Следовательно, чтобы полностью определить движение спутника, надо задать шесть
производных постоянных. Например, можно задать три координаты и три
составляющие скорости в некоторой точке траектории. Обычно в астрономии
используются специальным образом подобранные постоянные, с помощью которых
удается наиболее просто и наглядно определить движение спутника
Выбор элементов орбиты. Шесть произвольных постоянных, которые позволяют полностью
определить положение спутника в любой момент времени, называют элементами
орбиты спутника.Ω - долгота восходящего узла (или просто долгота узла). Этот угол
фиксирует положение восходящего узла относительно некоторого начала отсчета
(рис. 1.2) и может изменяться в диапазоне
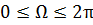 (1.3.1)
(1.3.1)
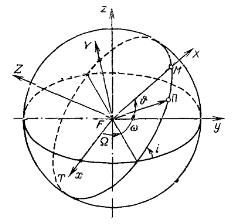
Рис. 2
угол i между плоскостью орбиты
спутника и основной координатной плоскостью
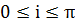 (1.3.2)
(1.3.2)
Этот угол часто называют наклонением
орбиты. Если 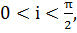 то
движение спутника называют прямым, а орбиту восточной, если же
то
движение спутника называют прямым, а орбиту восточной, если же 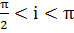 , то - обратным, а орбиту - западной. В случае i = 0 и i =
, то - обратным, а орбиту - западной. В случае i = 0 и i = 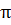 плоскость орбиты спутника совпадает с основной координатной
плоскостью; тогда понятие долготы восходящего узла теряет смысл. Такую орбиту
называют экваториальной. При i =
плоскость орбиты спутника совпадает с основной координатной
плоскостью; тогда понятие долготы восходящего узла теряет смысл. Такую орбиту
называют экваториальной. При i = 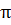 /2 плоскость орбиты совпадает с меридиональной плоскостью. Это -
полярная орбита.
/2 плоскость орбиты совпадает с меридиональной плоскостью. Это -
полярная орбита.
Для гиперболической и параболической
орбит возможны случаи, когда существует только один узел, восходящий или
нисходящий, т.е. траектория пересекает линию узлов только в одной точке. В подобных
случаях полагают, что второй узел расположен на линии узлов в бесконечно
удаленной точке.
С помощью углов Ω и i однозначно фиксируется положение
плоскости орбиты в выбранной системе координат (экваториальной или
эклиптической). Чтобы определить положение линии апсид орбиты в ее плоскости,
следует задать угол 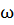 между
восходящим узлом и радиусом-вектором перицентра орбиты. Этот угол часто
называют аргументом перицентра, он может изменяться в пределах
между
восходящим узлом и радиусом-вектором перицентра орбиты. Этот угол часто
называют аргументом перицентра, он может изменяться в пределах
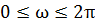 (1.3.3)
(1.3.3)
Орбита в своей плоскости
характеризуется эксцентриситетом е и параметром р. Для привязки движения
спутника по времени задают момент времени tп, когда спутник находится в перицентре.
Таким образом, для задания
пространственного движения спутника в астрономии обычно используют следующие
элементы орбиты:
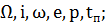 (1.3.4)
(1.3.4)
2. Околоземельные
спутники
2.1 Круговая орбита
спутника
Эллиптическая орбита. Наиболее часто
встречаются орбиты эллиптического типа (h < 0, 0 < е < 1). Как
известно, эллипс представляет собой геометрическое место точек, для которых
сумма расстояний от двух заданных точек (фокусов) есть величина постоянная. В
одном из фокусов эллипса находится притягивающий центр, а второй фокус
оказывается «пустым»
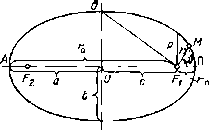
Рис 3
Основными параметрами эллиптической
орбиты (рис. 1.3) являются большая полуось a
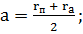 (2.1.1)
(2.1.1)
определяющая среднее расстояние до
притягивающего центра, и малая полуось b. Фокусное расстояние сназывают еще
линейным эксцентриситетом.
Из (1.2.22) расстояние от
притягивающего центра до спутника в перицентре
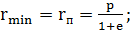 (2.1.2)
(2.1.2)
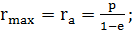 (2.1.3)
(2.1.3)
подставив радиусы в (2.1.1)
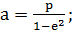 (2.1.4)
(2.1.4)
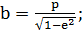 (2.1.5)
(2.1.5)
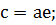 (2.1.6)
(2.1.6)
спутника в перицентре и апоцентре:
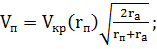 (2.1.7)
(2.1.7)
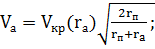 (2.1.8)
(2.1.8)
Установим связь между большой
полуосью а и постоянной интеграла энергии h. С этой целью запишем интеграл
энергии для спутника, находящегося в перицентре орбиты
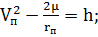 (2.1.9)
(2.1.9)
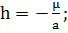 (2.1.10)
(2.1.10)
а интеграл энергии принимает вид
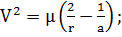 (2.1.11)
(2.1.11)
Воспользуемся уравнением (2.1.11)
для определения скорости спутника в точке, соответствующей концу малой полуоси
(точка В на рис. 1.3). В этой точке r = а и V2 = 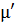 а =
а = 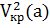 , т.е.
скорость спутника равна местной круговой скорости.
, т.е.
скорость спутника равна местной круговой скорости.
Круговая орбита. Эта орбита является частным случаем эллиптической (е = 0). Чтобы
спутник двигался по круговой орбите, его скорость должна равняться по величине
местной круговой скорости 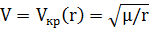 и быть направленной перпендикулярно радиусу - вектору. Нарушение
любого из двух указанных условий приводит к эллиптической орбите.
и быть направленной перпендикулярно радиусу - вектору. Нарушение
любого из двух указанных условий приводит к эллиптической орбите.
Уравнение круговой орбиты rкр = const, а понятия перицентра и истинной аномалии теряют смысл,
поскольку все точки круговой орбиты одинаково удалены от притягивающего центра.
Поэтому вместо истинной аномалии обычно рассматривают полярный угол, отсчет
которого ведут от некоторого фиксированного направления.
В отличие от параболической орбиты,
круговая орбита часто используется в модельных задачах механики космического
полета. Это объясняется тем, что для задания круговой орбиты достаточно одного
параметра (радиуса орбиты или ее высоты над поверхностью центрального тела).
.2 Суточный спутник
Суточный спутник. Если сидерический
(звездный) период обращения спутника равен звездным суткам (Т = 23 час 56,07
мин), то спутник называют суточным, или синхронным. Трасса невозмущенного
движения суточного спутника является замкнутой кривой, т.е. трассы всех
последующих витков совпадают с трассой первого витка. В этом случае можно
получить простое соотношение, связывающее текущие координаты трассы.
Пусть в начальный момент времени tQ
спутник находится в восходящем узле круговой суточной орбиты (рис 2.1). В
момент времени t трасса пройдет через точку О, для которой
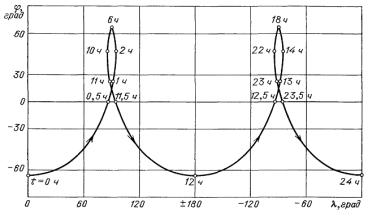
Рис 4
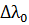 - долгота, отсчитываемая от восходящего узла В, и
- долгота, отсчитываемая от восходящего узла В, и 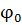 - широта.
- широта.
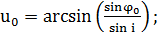 (2.2.1)
(2.2.1)
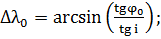 (2.2.2)
(2.2.2)
Орбитальная угловая скорость
суточного спутника равна угловой скорости вращения Земли 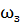 . Отсюда можно найти время перемещения по трассе из точки В в
точку О:
. Отсюда можно найти время перемещения по трассе из точки В в
точку О:
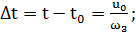 (2.2.3)
(2.2.3)
За это время Земля в свою очередь
повернется на угол
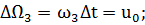 (2.2.4)
(2.2.4)
Теперь можно с учетом вращения Земли
определить долготу точки О как функцию ее широты
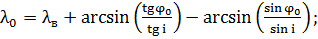 (2.2.5)
(2.2.5)
При каждом пересечении трассой
спутника экватора 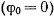 долгота
точки одна и та же:
долгота
точки одна и та же: 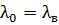 .
Поэтому трасса спутника имеет вид «восьмерки», т.е. представляет собой
замкнутую двойную петлю, причем одна петля расположена в северном полушарии, а
вторая в южном. На рис. 1.5 построены трассы суточных спутников в северном
полушарии при различных наклонениях орбиты. В южном полушарии картина
аналогична.
.
Поэтому трасса спутника имеет вид «восьмерки», т.е. представляет собой
замкнутую двойную петлю, причем одна петля расположена в северном полушарии, а
вторая в южном. На рис. 1.5 построены трассы суточных спутников в северном
полушарии при различных наклонениях орбиты. В южном полушарии картина
аналогична.
Рис 5
Особо следует выделить два
предельных случая: i = 0 и i = 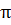 . При i
= 0 плоскость орбиты спутника совпадает с плоскостью экватора, и спутник
вращается с запада на восток с такой же угловой скоростью, что и Земля. Поэтому
для наблюдателя, который находится на поверхности Земли, спутник кажется
неподвижным. Следовательно, трасса его вырождается в точку. Такой суточный
спутник называют стационарным (неподвижным относительно поверхности Земли).
. При i
= 0 плоскость орбиты спутника совпадает с плоскостью экватора, и спутник
вращается с запада на восток с такой же угловой скоростью, что и Земля. Поэтому
для наблюдателя, который находится на поверхности Земли, спутник кажется
неподвижным. Следовательно, трасса его вырождается в точку. Такой суточный
спутник называют стационарным (неподвижным относительно поверхности Земли).
При i = 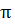 плоскость орбиты спутника также совпадает с плоскостью экватора,
но спутник движется на запад, против вращения Земли. Такой спутник в течение
суток дважды проходит над каждой точкой экватора.
плоскость орбиты спутника также совпадает с плоскостью экватора,
но спутник движется на запад, против вращения Земли. Такой спутник в течение
суток дважды проходит над каждой точкой экватора.
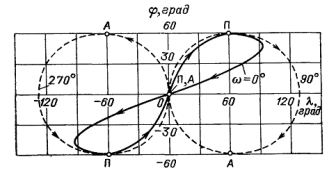
Рис 6
Стационарный спутник представляет
наибольший интерес для целей космической связи и наблюдения за поверхностью
Земли. Выведение стационарного спутника из точек старта, расположенных вне
плоскости экватора, требует больших энергетических затрат
Поэтому для решения многих задач
могут использоваться суточные (синхронные) спутники на круговых и эллиптических
орбитах, плоскость движения которых наклонена под большим углом к плоскости
экватора. За счет выбора элементов орбиты суточного спутника можно добиться
наибольшего эффекта в его использовании для целей связи или наблюдения. На рис.
1.6 построены трассы суточных спутников Земли с наклонением i = 60°,
эксцентриситетом е = 0,6 и различными положениями перигея, обозначенного буквой
П.
В Советском Союзе на геостационарную
орбиту выводятся связные спутники типа «Горизонт», «Радуга», «Экран». Всего в
различных точках геостационарной орбиты в 1987 году находились около ста
спутников, принадлежащих различным государствам.
3. Полет к Луне и
планетам
.1 Параметры орбиты Луны
Параметры орбиты Луны Плоскость
орбиты Луны наклонена к плоскости эклиптики (т.е. плоскости гелиоцентрической
орбиты барицентра системы Земля - Луна) на угол iл, величина которого меняется в диапазоне 4°59'-5° 19' с периодом
173 сут. Линия узлов лунной орбиты вращается в плоскости эклиптики навстречу
движению Луны (по часовой стрелке, если смотреть с северного полюса) с периодом
18,61 года. Поскольку средний угол между плоскостями земного экватора и
эклиптики составляет 23°27', то угол между плоскостями земного экватора и
лунной орбиты меняется в диапазоне 18°18'-28°36'. Следовательно, компланарный
перелет в плоскости орбиты Луны возможен всегда, если широта точки старта,
расположенной на поверхности Земли, удовлетворяет условию 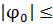 18°18'. Если широта точки старта находится в диапазоне 18°18'
18°18'. Если широта точки старта находится в диапазоне 18°18'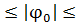 28°36', то компланарный перелет возможен в ограниченные интервалы
времени каждые 18,61 года. В случае
28°36', то компланарный перелет возможен в ограниченные интервалы
времени каждые 18,61 года. В случае 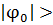 28°36' компланарный перелет в плоскости лунной орбиты невозможен.
28°36' компланарный перелет в плоскости лунной орбиты невозможен.
Угол наклона плоскости экватора Луны
к плоскости ее орбиты меняется от 6°31' до 6°51'. Геоцентрическая орбита Луны
близка к круговой, ее средний эксцентриситет е = 0,05490. Среднее расстояние от
Земли до Луны 38 4401 ± 1 км, минимальное расстояние 356 400 км, максимальное
расстояние 406 700 км. Средняя скорость геоцентрического движения Луны 1,023
км/с.
Звездным, или сидерическим, лунным
месяцем называют промежуток времени между двумя последовательными прохождениями
Луны через плоскость одного и того же круга широты (большого круга небесной
сферы, проходящего через светило и полюсы эклиптики). Сидерический месяц
составляет 27 сут 7 ч 43 мин 11,47 с, или 27,321661 средних солнечных суток
(длительностью 24 ч). Период обращения Луны вокруг собственной оси равен
сидерическому месяцу, поэтому Луна обращена к Земле всегда одной стороной.
Вместе с тем имеют место небольшие «покачивания» (либрация) Луны относительно
среднего положения. Различают оптическую (геометрическую) и физическую
либрации. Оптическая либрация является зрительным эффектом вследствие
относительного перемещения земного наблюдателя и Луны. Эта либрация обусловлена
неравномерностью обращения Луны вокруг Земли, несовпадением плоскостей лунной
орбиты и ее экватора, а также суточным перемещением земного наблюдателя.
Физическая либрация Луны является отклонением ее реального вращения вокруг
центра масс от вращения соответствующего сферического тела. Эта либрация
связана с близостью формы Луны к трехосному эллипсоиду, наибольшая ось которого
ориентирована вдоль среднего направления на Землю. Вследствие притяжения Земли
создается пара сил, приложенная к Луне и качающая ее вокруг центра масс на угол
порядка 2'. По своей сути физическая либрация Луны аналогична нутации Земли.
Благодаря оптической и физической либрациям можно наблюдать до 60% всей
поверхности Луны.
В зависимости от взаимного
расположения Земли, Луны и Солнца с земной поверхности можно видеть определенную
часть освещенного диска Луны, или различные фазы Луны. Фаза новолуния имеет
место, когда Луна находится между Солнцем и Землей, т.е. к Земле обращена
темная часть Луны. Когда Земля находится между Солнцем и Луной, имеет место
фаза полнолуния, т.е. с Земли виден полный освещенный диск Луны. Синодическим
месяцем называют промежуток времени между двумя последовательными новолуниями.
Средний синодический месяц составляет 29 сут 12 ч 44 мин 2,78 с, или 29,530588
средних суток. Он может меняться от 29,25 сут до 29,83 сут, т.е. на 13 ч
вследствие эллиптичности лунной орбиты.
3.2 Метод расчета
траектории полета к Луне
Приближенный расчет
траектории полета к Луне. В ряде случаев
оказывается допустимым существенное упрощение задачи вычисления траектории
полета к Луне. Это упрощение связано с заменой истинной траектории коническим
сечением, геоцентрическим вне сферы действия (или сферы влияния) Луны и
селеноцентрическим внутри сферы действия (влияния) Луны. Тем самым пренебрегают
возмущениями от нецентральности поля притяжения Земли, а также пренебрегают
возмущениями от Луны и Солнца на участке полета вне сферы действия Луны. Внутри
сферы действия Луны пренебрегают возмущениями от Земли и Солнца. Такой подход
допустим при расчете траекторий сближения, которые начинаются у Земли и на
первом же витке геоцентрического движения входят в сферу действия Луны с
существенно гиперболической селеноцентрической скоростью. Метод решения,
связанный с представлением траектории перелета в виде соединенных на границе
сферы действия Луны гео- и селеноцентрических конических сечений, когда
учитывают только основные гравитационные ускорения на каждом участке и
пренебрегают всякими возмущениями, принято называть методом игнорирования
возмущений
На геоцентрическом участке по
заданным начальным радиусу-вектору 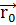 и вектору скорости
и вектору скорости 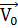 можно полностью определить все элементы орбиты, а затем параметры
движения КА в любой точке траектории. На входе в сферу действия Луны пересчитывают
радиус-вектор и вектор скорости КА из геоцентрической в селеноцентрическую
систему координат по формулам.
можно полностью определить все элементы орбиты, а затем параметры
движения КА в любой точке траектории. На входе в сферу действия Луны пересчитывают
радиус-вектор и вектор скорости КА из геоцентрической в селеноцентрическую
систему координат по формулам.
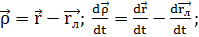 (3.2.1)
(3.2.1)
В соответствии со знаком радиальной
составляющей геоцентрической скорости  на входе в сферу действия Луны различают навесную эллиптическую
траекторию со входом на нисходящей ветви (
на входе в сферу действия Луны различают навесную эллиптическую
траекторию со входом на нисходящей ветви ( < 0) и настильную эллиптическую траекторию со входом на
восходящей ветви (
< 0) и настильную эллиптическую траекторию со входом на
восходящей ветви (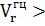 0).
Обе траектории показаны па рис. 1.7 Для гиперболической и параболической
геоцентрических траекторий вход в сферу действия Луны возможен только на
восходящей ветви.
0).
Обе траектории показаны па рис. 1.7 Для гиперболической и параболической
геоцентрических траекторий вход в сферу действия Луны возможен только на
восходящей ветви.
Внутри сферы действия Луны орбита
также определяется заданными начальными условиями в точке входа. Если КА
покидает сферу действия Луны, то в точке выхода следует выполнить обратный
переход отселеноцентрического к геоцентрическому движению. Геоцентрические
параметры в точке выхода будут полностью определять траекторию вне сферы действия
Луны. Эта геоцентрическая траектория в общем случае может быть эллиптической,
гиперболической или параболической.
Дальнейшее упрощение связано с
пренебрежением не только возмущениями, но и размерами сферы действия Луны по
сравнению с расстоянием Земля - Луна. Такой подход называют методом точечной
сферы действия. Суть его состоит в том, что рассматривают только два
геоцентрических конических сечения, которые моделируют траекторию пролета мимо
Луны, имеющую излом в точке соединения (точке «встречи» с Луной). Излом
обусловлен тем, что по предположению в указанной точке происходит мгновенное
изменение входного в сферу действия Луны вектора геоцентрической скорости на
выходной из сферы действия Луны вектор геоцентрической скорости.
Метод точечной сферы действия
существенно облегчает исследование множества траекторий, так как
рассматриваются только векторы скорости в точках входа в сферу действия Луны и
выхода из нее. При этом пренебрегают различием радиусов-векторов этих точек,
т.е. совмещают их. Сведение задачи к анализу многообразия скоростей позволяет
довольно просто построить векторы скорости в некоторых интересных случаях, а
затем использовать их, например, для выбора минимальных потребных скоростей и
др.
Метод точечной сферы действия удобен
для приближенного расчета траекторий сближения КА с Луной, которые начинаются и
кончаются вблизи Земли (облетные траектории). Он удобен также для расчета
межпланетных траекторий, проходящих вблизи Луны с целью использования ее
гравитационного поля для изменения вектора скорости КА (так называемый
пертурбационный маневр)
.3. Классификация
межпланетных траекторий
Классификация межпланетных
траекторий. В зависимости от решаемой задачи могут использоваться межпланетные
траектории различных классов. Принято выделять следующие основные классы:
. Траектория перелета к
планете назначения без возвращения к Земле.
. Траектории перелета к
планете назначения с возвращением к Земле.
. Траектории
последовательного облета нескольких планет.
В свою очередь каждый класс траекторий
может иметь несколько подклассов. Так, траектория полета к планете назначения
без возращения к Земле может проходить на заданном расстоянии от планеты,
заканчиваться выведением КА на орбиту вокруг планеты или посадкой на ее
поверхность. Пролетпая траектория не требует дополнительных энергетических
затрат, поэтому ее довольно просто реализовать. Вместе с тем пролет на
ограниченном расстоянии от планеты позволяет провести ряд интересных научных
исследований. При выведении КА на орбиту вокруг планеты назначения должен
осуществляться активный маневр с включением двигательной установки. Обычно
маневр выполняется вблизи перицентра пролетной гиперболической траектории. Если
планета имеет атмосферу, можно реализовать комбинированный маневр
аэродинамического торможения с последующим включением двигателя для выхода на
заданную орбиту. В некоторых случаях траектория перелета завершается посадкой
всего КА или отделяемого спускаемого аппарата. Возможна прямая посадка с
пролетной гиперболической траектории и посадка с околопланетной орбиты, на
которую предварительно выводится КА. Скорость КА может быть погашена с помощью
двигателя или за счет аэродинамического торможения, если у планеты есть
атмосфера. В некоторых случаях для уменьшения массы тормозной системы оказывается
целесообразным сочетание активного торможения (двигателем) с пассивным
(аэродинамический экран или парашют).
Большой практический интерес
представляет комбинированная схема полета, когда на участке сближения с
планетой отделяется спускаемый аппарат, совершающий посадку на поверхность
планеты и передающий полученную информацию через пролетный аппарат на Землю.
Такая схема позволяет максимально уменьшить массу передающей радиотехнической
аппаратуры на спускаемом аппарате и упростить его конструкцию. Пролетный
аппарат, который используется для контроля посадки спускаемого аппарата и в
качестве активного ретранслятора информации, имеет радиотехническую аппаратуру
требуемой мощности для надежной связи с Землей.
Траектории полета к планете
назначения с возвращением к Земле включают подклассы траекторий с задержкой у
планеты (на ее поверхности или на орбите вокруг планеты) и без задержки у
планеты. Если траектории без возвращения к Земле приемлемы только для доставки
автоматических аппаратов, то траектории с возвращением к Земле, являясь
обязательными для будущих пилотируемых полетов к планетам, могут использоваться
и при запуске автоматических аппаратов. Например, в тех случаях, когда
необходимо доставить на Землю образцы грунта или пробы атмосферы планеты. Возвращение
КА к Земле желательно проводить в два этапа. Сначала КА выводится на
промежуточную орбиту вокруг планеты, а затем стартует на гиперболическую
траекторию возвращения.
Траектории последовательного облета
нескольких планет можно разделить на подклассы траекторий с гравитационным
маневром, активным маневром за счет включения двигательной установки и
комбинированным активно-гравитационным маневром. Последний подкласс
представляет наибольший практический интерес.
3.4. Основные принципы
расчета траектории полета к планете
При расчете точной межпланетной
траектории КА должны учитываться следующие факторы, которые оказывают
воздействие на его движение:
. Притяжение Земли, Солнца,
Луны и планет Солнечной системы.
. Излучение Солнца.
. Эффекты общей теории относительности.
На начальном участке межпланетной
траектории, когда КА находится еще достаточно близко к Земле, необходимо
дополнительно учитывать влияние первой зональной гармоники в разложении
потенциала притяжения Земли по сферическим функциям. С увеличением расстояния
КА от Земли ее поле притяжения можно принимать в виде центрального.
Запишем в векторной форме уравнения
движения КА:
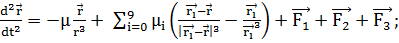 (3.4.1)
(3.4.1)
Здесь 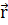 - геоцентрический радиус-вектор КА;
- геоцентрический радиус-вектор КА; 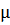 - произведение постоянной притяжения на массу Земли;
- произведение постоянной притяжения на массу Земли; 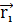 - геоцентрический радиус-вектор i-го небесного тела;
- геоцентрический радиус-вектор i-го небесного тела; 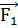 - возмущающее ускорение движения КА из-за нецентральности поля
притяжения Земли;
- возмущающее ускорение движения КА из-за нецентральности поля
притяжения Земли; 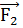 -
возмущающее ускорение движения КА вследствие солнечного излучения;
-
возмущающее ускорение движения КА вследствие солнечного излучения; 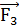 - возмущающее ускорение, характеризующее влияние эффектов общей
теории относительности на движение КА в пространстве, искривленном
гравитационным влиянием Солнца.
- возмущающее ускорение, характеризующее влияние эффектов общей
теории относительности на движение КА в пространстве, искривленном
гравитационным влиянием Солнца.
Поправка от нецентральности поля
притяжения Земли вычисляется по формуле
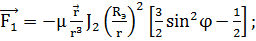 (3.4.2)
(3.4.2)
где 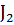 - коэффициент при первой зональной гармонике в разложении
потенциала поля притяжения Земли,
- коэффициент при первой зональной гармонике в разложении
потенциала поля притяжения Земли, 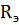 - экваториальный радиус Земли,
- экваториальный радиус Земли, 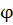 - геоцентрическая широта,
- геоцентрическая широта, 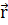 -
радиус-вектор рассматриваемой точки.
-
радиус-вектор рассматриваемой точки.
Для учета возмущения от солнечного
излучения можно использовать формулу вида
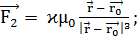 (3.4.3)
(3.4.3)
где 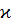 - коэффициент влияния солнечного излучения, зависящий от формы и
массы КА
- коэффициент влияния солнечного излучения, зависящий от формы и
массы КА
Влияние эффектов общей теории
относительности учитывается формулой
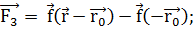 (3.4.4)
(3.4.4)
где
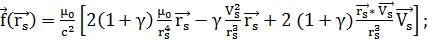 (3.4.5)
(3.4.5)
гдеs, Vs, - гелиоцентрические
радиус-вектор и скорость рассматриваемого тела; с - скорость света; 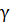 - параметр, характеризующий выбор системы координат поля
Шварцшильда. Обычно используется стандартная система координат (
- параметр, характеризующий выбор системы координат поля
Шварцшильда. Обычно используется стандартная система координат (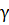 = 1). По существу релятивистская поправка
= 1). По существу релятивистская поправка 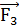 к геоцентрическому ускорению КА представляет собой разность
релятивистских поправок к гелиоцентрическому ускорению КА, т.е.
к геоцентрическому ускорению КА представляет собой разность
релятивистских поправок к гелиоцентрическому ускорению КА, т.е. 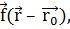 и гелиоцентрическому ускорению Земли, т.е.
и гелиоцентрическому ускорению Земли, т.е. 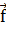 (-
(-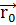 ).
).
Необходимые для численного интегрирования
уравнений движения КА координаты Луны и планет обычно вычисляются путем
интерполяции с использованием заданных табличных значений. Такие таблицы
строятся заблаговременно на основе одной из теорий Луны и планет.
Численное интегрирование уравнений
движения КА может осуществляться практически любым методом (Рунге-Кутта,
Адамса, Эйлера и др.). В целях экономии времени счета целесообразно
интегрировать с переменным шагом при контроле заданной точности. В пределах
сферы действия планеты шаг интегрирования обычно меняется в диапазоне 10 с - 30
мин, а на гелиоцентрическом участке его можно увеличивать до 1 час - 4 час.
Заключение
В наши дни полеты в космос,
постоянная работа людей на орбитальной станции, деятельность автоматических
космических аппаратов стали обычным явлением, своего рода рутиной. Связь,
телевидение, навигация, прогнозы погоды, исследования природных ресурсов
планеты уже не мыслимы без спутников. Трудно переоценить значение освоения
космоса для развития науки, техники, экономики. К исследованию и использованию
космического пространства подключаются все новые и новые страны. Люди уже
побывали на Луне, готовятся к осуществлению экспедиции на Марс. Однако
непреходящее значение и сегодня имеет тот факт, что у истоков всех этих
грядущих планов и свершений эры освоения космоса был запуск 4 октября 1957 г.
простейшего советского спутника.
Поэтому можно сказать, что при
выполнении данной курсовой работы нами были выполнены ранее поставленные
задачи. При ознакомлении с основной литературой по теме курсовой работы, мы
изучили основные понятия, принципы и методы расчета траектории, раскрыли
значение данной темы.
Материал данной курсовой работы
может быть использован при чтении соответствующих тем курса «Механика» а также
для организации самостоятельной работы студентов факультета математики, физики
и информатики.
Литература
1. Бутенин Н.Б., Лунц Я.Л., Меркин Д.Р. Курс теоретической
механики, в 2-х томах, т. 2. Динамика. URL: http://padaread.com/? book=31339
2. Охоцимский Д.Е., Сихарулидзе Ю.Г. Основы механики космического
полета.URL: http://padaread.com/? book=23015
3. Астродинамика // БСЭ. Гл.ред.: A.M. Прохоров. В 30-ти томах, Советская
Энциклопедия.URL: http://enc-dic.com/enc_sovet/Astrodinamika-70965.html
4. Небесная механика // БСЭ. Гл.ред.: A.M. Прохоров. 3-е изд. В 30-ти томах,
Советская Энциклопедия.URL: http://enc-dic.com/enc_sovet/Nebesnaja-mehanika-40445/
5. Орбиты небесных тел // БСЭ. Гл.ред.: A.M. Прохоров. 3-е изд. В 30-ти томах,
Советская Энциклопедия. URL: http://enc-dic.com/enc_sovet/Orbit-nebesnh-tel-44147/
6. Детлаф А.А., Яворский Б.М., Милковская Л.Б. Курс физики.
Том 1. Механика, основы молекулярной физики и термодинамики.URL:
http://padaread.com/? book=33351
. Словарь электронный. URL: http://enc-dic.com/word/k/Kosmos-13892.html
8. Дипломатия России. От польского приказа до наших дней.
Историко-документальный департамент МИД России. URL:
http://www.idd.mid.ru/inf/inf_12.html