Распространение радиоволн и антенно-фидерные устройства систем подвижной радиосвязи
Федеральное
агентство связи
Поволжский
Государственный Университет Телекоммуникаций
и
Информатики
Кафедра
Электродинамики и Антенн
Курсовая
работа по дисциплине
«Распространение
радиоволн и антенно - фидерные устройства
систем
подвижной радиосвязи»
Вариант
№4
Пояснительная
записка на 14 листах
Выполнил:
студент группы РС -
01
Ваничкин Д.Д.
Проверил: проф.
Кубанов В.П.
Самара
2013 год
Содержание
Рецензия
Параметры
антенн и фидеров. Элементарные излучатели электромагнитных волн - Задача 1
Линейные
симметричные электрические вибраторы - Задача 2
Антенные
решетки - Задача 3
Излучающие
поверхности - Задача 4
Распространение
радиоволн - Задача 5
Использованные
ресурсы
Параметры антенн и фидеров. Элементарные
излучатели электромагнитных волн - Задача 1
Антенна расположена в центре системы координат,
приведённой на рисунке 1. Характеристика направленности антенны описывается
функцией
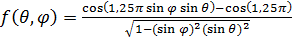 (1).
(1).
Для плоскости 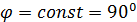 построить
нормированную диаграмму направленности этой антенны в полярной системе
координат и определить уровни первого бокового лепестка
построить
нормированную диаграмму направленности этой антенны в полярной системе
координат и определить уровни первого бокового лепестка 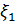 .
.
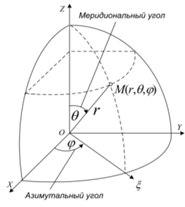
Рисунок 1
Решение. Согласно [1] заданная характеристика
направленности при 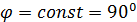 зависит только от
угла
зависит только от
угла 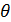 .
Запишем выражение для нормированной характеристики направленности в виде
.
Запишем выражение для нормированной характеристики направленности в виде
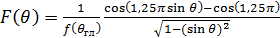 (2),
(2),
где 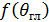 -
значение ненормированной функции
-
значение ненормированной функции 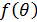 в
направлении
в
направлении 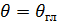 , соответствующем
её главному максимуму.
, соответствующем
её главному максимуму.
На рисунке 2 показана последовательность решения
с применением пакета программ Mathcad 14.
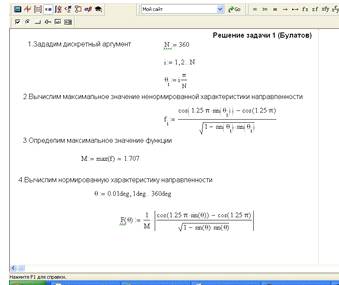
Рисунок 2
На рисунке 3 представлен результат расчёта
требуемой диаграммы направленности. С помощью нормированной диаграммы
направленности, построенной в прямоугольной системе координат с линейным
масштабом по оси ординат, определяем уровень первого бокового лепестка 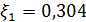 .
.
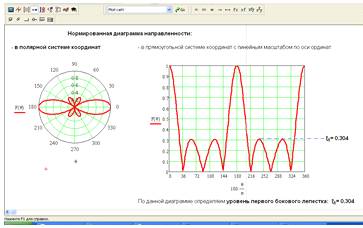
Рисунок 3
Линейные симметричные электрические вибраторы -
Задача 2
Определить ширину главного лепестка
нормированной амплитудной диаграммы направленности в 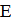 -
плоскости по уровню нулевого излучения
-
плоскости по уровню нулевого излучения 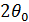 и
по уровню половинной мощности
и
по уровню половинной мощности 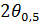 для линейного
симметричного электрического вибратора с длиной плеча
для линейного
симметричного электрического вибратора с длиной плеча 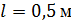 ,
если вибратор излучает на частоте
,
если вибратор излучает на частоте 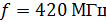 .
.
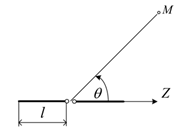
Рисунок 4
Решение. Расположим линейный симметричный
электрический вибратор вдоль оси 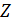 ,
как показано на рисунке 4.
,
как показано на рисунке 4. 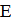 - плоскость
вибратора содержит его ось. Угол
- плоскость
вибратора содержит его ось. Угол 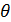 будет
аргументом амплитудной характеристики направленности в
будет
аргументом амплитудной характеристики направленности в 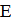 -
плоскости. Нормированная амплитудная диаграмма направленности вибратора
описывается формулой (1.15) из [2], которая имеет вид
-
плоскости. Нормированная амплитудная диаграмма направленности вибратора
описывается формулой (1.15) из [2], которая имеет вид
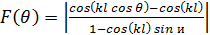 (3).
(3).
Подставив в эту формулу 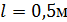 ,
,
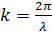 ,
с учётом того, что частоте
,
с учётом того, что частоте 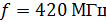 соответствует
длина волны
соответствует
длина волны 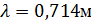 , получим расчётное
выражение в форме
, получим расчётное
выражение в форме
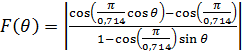 (4).
(4).
Последовательность решения, выполненного с
применением пакета программ Mathcad 14, показана на рисунке 5.
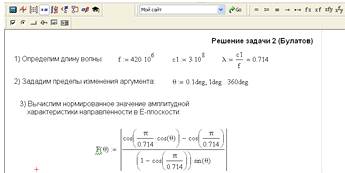
Рисунок 5
Результаты расчёта приведены на рисунке 6.
Диаграмма построена в прямоугольной (декартовой) системе координат с линейным
масштабом по оси ординат. С помощью этой диаграммы определяем ширину диаграммы
направленности по уровню нулевого излучения 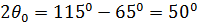 и
по уровню половинной мощности
и
по уровню половинной мощности 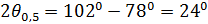 .
.
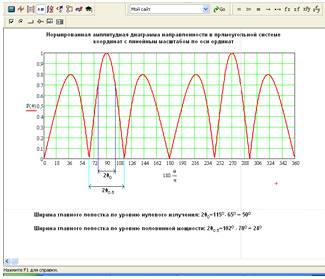
Рисунок 6
Антенные решетки - Задача 3
Антенная решётка, изображённая на рисунке 7,
состоит из 10 полуволновых линейных симметричных электрических вибраторов.
Расстояние 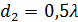 . Все вибраторы
возбуждаются синфазными токами равных амплитуд. Рассчитать нормированную амплитудную
характеристику направленности в
. Все вибраторы
возбуждаются синфазными токами равных амплитуд. Рассчитать нормированную амплитудную
характеристику направленности в 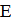 - плоскости и
построить её нормированную амплитудную диаграмму направленности в прямоугольной
системе координат с логарифмическим масштабом.
- плоскости и
построить её нормированную амплитудную диаграмму направленности в прямоугольной
системе координат с логарифмическим масштабом.
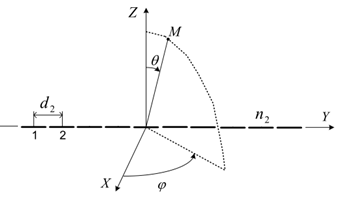
Рисунок 7
Решение. Линейные симметричные электрические
вибраторы для простоты показаны без зазоров в точках питания, т.е. в виде
непрерывных линий. Пусть 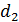 - расстояние между
серединами вибраторов, расположенных в одном ряду;
- расстояние между
серединами вибраторов, расположенных в одном ряду; 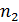 -
число вибраторов в одном ряду. В соответствии с теоремой перемножения,
ненормированная АХН рассматриваемой плоской решетки может быть представлена в
виде (формула (2.1) из [3]):
-
число вибраторов в одном ряду. В соответствии с теоремой перемножения,
ненормированная АХН рассматриваемой плоской решетки может быть представлена в
виде (формула (2.1) из [3]):
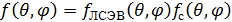 (5),
(5),
где 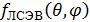 -
функция, характеризующая направленные свойства одного вибратора, а
-
функция, характеризующая направленные свойства одного вибратора, а 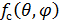 -
множитель системы.
-
множитель системы.
Как следует из формулы (2.2) в [3], при
ориентации вибратора вдоль оси Y АХН описывается выражением:
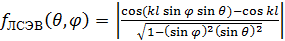 (6),
(6),
где 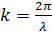 -
коэффициент фазы электромагнитной волны в свободном пространстве,
-
коэффициент фазы электромагнитной волны в свободном пространстве, 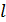 -
длина плеча вибратора.
-
длина плеча вибратора.
Согласно формуле (2.5) из [3], в случае
синфазного и равноамплитудного возбуждения вибраторов, и при 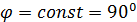 ,
множитель системы имеет вид:
,
множитель системы имеет вид:
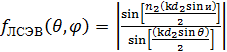 (7).
(7).
Заданная характеристика направленности при 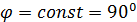 зависит
только от угла
зависит
только от угла 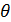 . Запишем выражение
для нормированной амплитудной характеристики направленности (АХН) в виде:
. Запишем выражение
для нормированной амплитудной характеристики направленности (АХН) в виде:
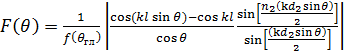 (8),
(8),
где 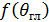 -
значение ненормированной функции
-
значение ненормированной функции 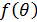 в
направлении
в
направлении 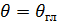 , соответствующем
её главному максимуму.
, соответствующем
её главному максимуму.
На рисунке 8 приведён подробный процесс
необходимых вычислений, выполненных с помощью пакета программ Mathcad 14.
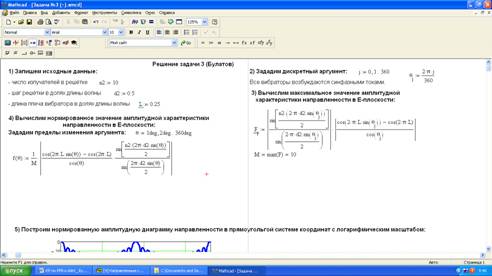
Рисунок 8
Результат расчёта приведён на рисунке 9.
Рисунок 9
Излучающие поверхности - Задача 4
Прямоугольная излучающая поверхность,
изображённая на рисунке 10, возбуждённая синфазно и равномерно, находится в
центре системы координат и имеет размер 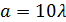 ,
,
 .
Рассчитать нормированную амплитудную характеристику направленности в плоскости
.
Рассчитать нормированную амплитудную характеристику направленности в плоскости 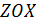 и
построить её диаграмму направленности в прямоугольной системе координат с
линейным масштабом по оси ординат. Рассчитать коэффициент направленного
действия излучающей поверхности
и
построить её диаграмму направленности в прямоугольной системе координат с
линейным масштабом по оси ординат. Рассчитать коэффициент направленного
действия излучающей поверхности 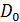 в направлении
максимального излучения. Результат расчёта
в направлении
максимального излучения. Результат расчёта 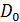 представить
в децибелах.
представить
в децибелах.
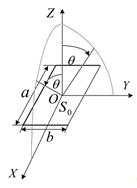
Рисунок 10
Решение. Представим возбужденную поверхность и
систему координат, как это показано на рисунке 10. Для расчета нормированной
амплитудной характеристики направленности в плоскости 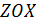 воспользуемся
формулой (1.14) из [4], которую запишем в следующем виде:
воспользуемся
формулой (1.14) из [4], которую запишем в следующем виде:
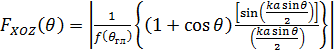 (9),
(9),
где 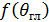 -
значение функции
-
значение функции 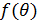 , являющейся
произведением множителей в фигурных скобках, в направлении
, являющейся
произведением множителей в фигурных скобках, в направлении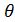 =
=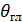 .
.
На рисунке 11 показана последовательность
необходимых вычислений с применением пакета программ Mathcad 14.
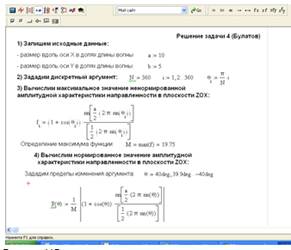
Рисунок 11
На рисунке 12 представлен результат расчета в
виде требуемой амплитудной диаграммы направленности.
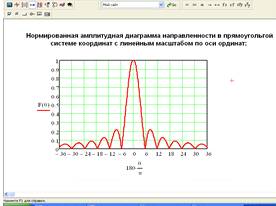
Рисунок 12
Расчет коэффициента направленного действия
идеальной излучающей
поверхности
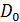 в
направлении максимального излучения можно определить
в
направлении максимального излучения можно определить
по
формуле (1.31) из [4], которая имеет вид:
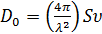 (10),
(10),
где 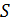 -
геометрическая площадь возбуждённой поверхности;
-
геометрическая площадь возбуждённой поверхности;
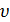 - коэффициент
использования поверхности.
- коэффициент
использования поверхности.
Значение коэффициента использования поверхности
для идеальной поверхности равно единице, т.е. 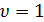 .
С учетом этого формула (10) приобретает вид:
.
С учетом этого формула (10) приобретает вид:
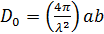 (11).
(11).
По условиям задачи 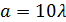 ,
,
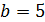 .
Подставив эти величины в (11), получим, что
.
Подставив эти величины в (11), получим, что 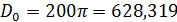 .
Величина
.
Величина 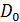 не
имеет размерности.
не
имеет размерности.
Перейдём к децибельной мере: 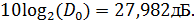
Получили, что 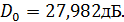
Распространение радиоволн - Задача 5
антенна направленность сигнал
радиоволна
Для линии радиосвязи Земля/космический аппарат
определить предельное расстояние, на котором земная станция будет принимать
сигналы космического аппарата, основные потери передачи в свободном
пространстве и полные потери передачи на трассе. Исходные условия: частота
передатчика земной станции 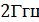 ; коэффициент
усиления передающей и приёмной антенн земной станции
; коэффициент
усиления передающей и приёмной антенн земной станции 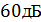 ;
мощность передатчика на земной станции
;
мощность передатчика на земной станции 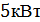 ;
минимальная мощность, которая регистрируется приёмником земной станции
;
минимальная мощность, которая регистрируется приёмником земной станции 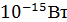 ;
космический аппарат выполняет роль пассивного ретранслятора, его эффективная
площадь рассеяния в направлении на приёмную антенну равна
;
космический аппарат выполняет роль пассивного ретранслятора, его эффективная
площадь рассеяния в направлении на приёмную антенну равна 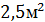 .
.
Решение. Из [5] для радиолинии 2-го рода имеем:
 (12),
(12),
где:
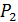 - мощность на
входе РПУ;
- мощность на
входе РПУ;
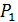 - мощность на
выходе РПД;
- мощность на
выходе РПД;
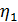 - кпд передающего
фидера;
- кпд передающего
фидера;
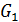 - коэффициент
усиления передающей антенны;
- коэффициент
усиления передающей антенны;
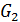 - коэффициент
усиления приёмной антенны;
- коэффициент
усиления приёмной антенны;
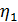 - кпд приёмного
фидера;
- кпд приёмного
фидера;
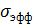 - эффективная
площадь рассеяния в направлении на приёмную антенну;
- эффективная
площадь рассеяния в направлении на приёмную антенну;
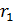 - расстояние от
земной станции до космического аппарата;
- расстояние от
земной станции до космического аппарата;
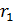 - расстояние от
космического аппарата до земной станции.
- расстояние от
космического аппарата до земной станции.
Мы знаем, что 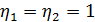 и
и
 .
Выразим из (12)
.
Выразим из (12) 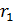 :
:
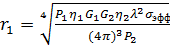 ( 13).
( 13).
Определим длину волны: 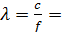
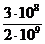
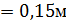 . Переведём в разы коэффициенты
усиления передающей и приёмной антенн земной станции:
. Переведём в разы коэффициенты
усиления передающей и приёмной антенн земной станции: 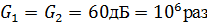 . Теперь,
зная чему численно равна каждая величина из (13), определим предельное
расстояние, на котором земная станция будет принимать сигналы космического
аппарата:
. Теперь,
зная чему численно равна каждая величина из (13), определим предельное
расстояние, на котором земная станция будет принимать сигналы космического
аппарата:

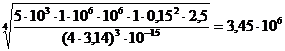
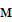 (14).
(14).
Получили, что 
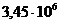
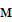 .
.
Формула для вычисления основных
потерь передачи в свободном пространстве, согласно [5], имеет вид:
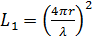 (15).
(15).
Подставив в (15) численные значения,
получим:
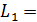
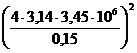
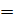
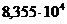 (16).
(16).
Представим 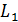 в
децибелах:
в
децибелах: 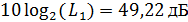 .
.
Получили, что 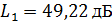 .
.
Формула для вычисления полных потерь
передачи на трассе, согласно [5] будет выглядеть:
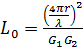 (18).
(18).
Подставив в (18) численные значения,
получим:
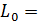
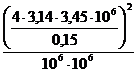
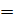
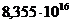 (19).
(19).
Представим 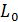 в
децибелах:
в
децибелах: 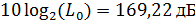 .
.
Получили, что 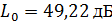 .
.
Использованные ресурсы
1.
Кубанов В.П. Антенны и фидеры - назначение и параметры. -
Самара,
ПГУТИ, 2012. -60 с.: ил.
.
Кубанов В.П. Линейные симметричные электрические вибраторы в свободном
пространстве. Учебное пособие для вузов. - Самара, ПГУТИ, 2011. - 52 с.: ил.
.
Кубанов В.П. Направленные свойства антенных решеток. Учебное
пособие
для вузов. - Самара, ПГУТИ, 2011. - 56 с.: ил.
.
Кубанов В.П. Излучение возбужденных поверхностей. Учебное
пособие
для вузов. - Самара, ПГУТИ, 2011. - 56 с.: ил.
.
Слайды к лекциям профессора Кубанова В.П. по дисциплине «Антенно-фидерные
устройства и распространение радиоволн»