Термодинамический анализ молекулярно-лучевой эпитаксии InGaPAs
Министерство
образования и науки Российской Федерации
Новосибирский
государственный технический университет
Кафедра
ПП и МЭ
Курсовая
работа по дисциплине: «Физико-химические основы процессов микро- и
нанотехнологии»
Термодинамический
анализ молекулярно-лучевой эпитаксии InGaPAs
Выполнил Котовщиков
И. О.
Факультет РЭФ
Группа:РНТ1-11
Проверил Илюшин В.
А.
Новосибирск
2014
Введение
В настоящее время метод молекулярно-пучковой
эпитаксии (МПЭ) - наиболее эффективная эпитаксиальная технология, позволяющая
получать полупроводниковые гетероструктуры тройных соединений AIIIBV с одним
элементом V группы, отличающаяся высокой точностью профилей состава. В то же
время при МПЭ тройных соединений с двумя элементами V группы и, в особенности,
четверных соединений управление составом растущего слоя становится весьма
сложной задачей и требует большого количества ростовых экспериментов в
сочетании с послеростовыми исследованиями. В связи с этим создание адекватной
теоретической модели процесса роста многокомпонентных соединений при МПЭ до
настоящего времени является весьма актуальной задачей. В 1985 г. Хекингботтом
показал, что процесс МПЭ можно рассматривать как квазинеравновесный и описывать
в рамках термодинамической модели [1]. Данный подход получил развитие в работе
[2], в которой приводятся методика расчета условий, контролирующих процесс
роста, и результаты термодинамического анализа в случае выращивания бинарных и
тройных соединений AIIIBV.
Термодинамическая модель роста четверного
соединения GaхIn1-хPуAs1-у
Термодинамическое рассмотрение процесса роста
четверных растворов при МПЭ основано на следующих основных приближениях. МПЭ
рассматривается как квазиравновесный процесс, где равновесие между газовой и
твердой фазами устанавливается на поверхности растущего слоя [1]. За
температуру системы берется температура подложки. За равновесные парциальные
давления приняты давления, соответствующие потокам атомов и молекул от
поверхности подложки. Термодинамические свойства четверных систем аппроксимируются
моделью регулярного раствора [3].
Полагая для определенности, что элементы III
группы поступают на поверхность роста в атомарном виде, а элементы V группы - в
виде димеров, рассмотрим реакцию между основными компонентами при МПЭ
четверного соединения GaхIn1-хPуAs1-у:
хGa(g) + (1 -
x)In(g) + 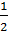 yP2(g) +
yP2(g) + 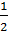 (1
- y)As2 (g) <=> GaхIn1-хPуAs1-у
(s), (1)
(1
- y)As2 (g) <=> GaхIn1-хPуAs1-у
(s), (1)
где символом g отмечены вещества в газовой фазе,
а символом s - в твердой.
Твердый раствор GaхIn1-хPуAs1-у рассматривается
как гомогенная смесь четырех бинарных соединений с соответствующими
коэффициентами активности. Коэффициенты активности характеризуют степень
отклонения свойств рассматриваемого бинарного компонента в реальном растворе от
его свойств в идеальном растворе. Тогда, согласно закону действующих масс, для
указанной реакции будет справедлива система уравнений
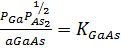 ,
, 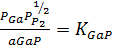
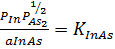 ,
, 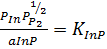 ,
(2)
,
(2)
Активности бинарных соединений в четверном твердом
растворе могут быть выражены через параметры взаимодействия бинарных соединений
в тройных твердых растворах [3] и определяются следующими выражениями:
kT ln aInAs = kT ln[(1 - x)(1 - y)]
+ [ya1 + (1 - y)a2]x2 + [xa3 + (1 - x)a4]y2
[ac - (1 - x)(a2 -a1) - (1-y)(
a4-a3)]xy, (3.1)
lnaGaP = kT ln xy[ya1 + (1 - y)a2](1
- x)2 + [xa3 + (1 - x)a4](1 - y)2 -[ac + x(a2 - a1) + y(a4 - a3)](1 - x)(1 -
y), (3.2)
ln aInP = kT ln[(1 - x)y]+ [ya1 + (1
- y)a2]x2 + [xa3 + (1 - x)a4](1 - y)2 + [ac - (1 - x)(a2 - a1) + y(a4 - a3)]x(1
- y), (3.3) ln aGaAs = kT ln[x(1 - y)] + [ya1 + (1 - y)a2](1 - x)2 + [xa3 + (1
- x)a4]y2 + [ac + x(a2 - a1) - (1 - y)(a4 - a3)](1 - x)y, (3.4)
где a1 - параметр взаимодействия между GaP и InP
в тройном растворе GaAsP; a2, a3, a4 - то же самое в GaAs-InAs, GaAs-GaP,
InAs-InP соответственно. Из 4-х уравнений (3.1-3.4) лишь 3 являются линейно
независимыми, поскольку на систему уравнений накладывается ограничение в виде
взаимосвязи между химическими потенциалами μ
бинарных компонентов в твердой фазе
μGaAs + μInP = μGaP + μInAs,
(4)
которое определяет параметр ac. Уравнение (4)
фактически представляет собой условие равновесия твердофазной реакции обмена
+ InP <=> GaP + InAs. (5)
Тогда, используя системы уравнений (2) и (3), мы
можем выразить ac через константы равновесия реакций образования бинарных
соединений
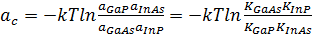 , (6)
, (6)
В случае роста стехиометрического соединения
потоки атомов III и V групп, идущие на рост, равны. Согласно закону сохранения
масс, можно записать следующее выражение:
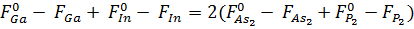 , (7)
, (7)
где F0 - падающие потоки атомов или молекул на
поверхность роста (внешние потоки), Fi - переиспаренные потоки, создающие
равновесные парциальные давления элементов над поверхностью роста.
Соотношение мольных долей компонентов четверного
раствора x и y также определяется соотношением потоков, идущих на рост:
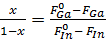 , (8)
, (8)
 , (9)
, (9)
Используя (8) и (9), мы можем записать (7)
только через потоки In и P
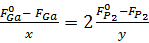 , (10)
, (10)
Выражая поток через давление по формуле
Где Рi - соответствующее потоку давление, mi -
молекулярная масса, и используя (2), получаем
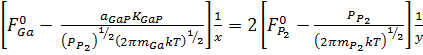 . (12)
. (12)
Теперь, задавая падающие потоки Ga и P: 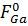 ,
,
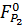 ,
а также состав четверного соединения, т. е. значения x и y, можно найти решение
этого уравнения относительно
,
а также состав четверного соединения, т. е. значения x и y, можно найти решение
этого уравнения относительно 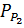 . Подставляя
найденные значения
. Подставляя
найденные значения 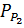 в систему
уравнений (2), мы находим все давления, соответствующие переиспаренным потокам,
- PGa, PIn, PAs2, а затем, воспользовавшись (11), найдем и сами переиспаренные
потоки. Далее используя уравнения (8) и (9), находим необходимые падающие
потоки In и As:
в систему
уравнений (2), мы находим все давления, соответствующие переиспаренным потокам,
- PGa, PIn, PAs2, а затем, воспользовавшись (11), найдем и сами переиспаренные
потоки. Далее используя уравнения (8) и (9), находим необходимые падающие
потоки In и As: 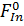 и
и 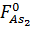 .
.
Таким образом, установлены все внешние потоки
элементов III и V групп, необходимые для получения четверного твердого раствора
GaxIn1-xPyAs1-y определенного состава, а также переиспаренные потоки элементов.
Расчеты, основанные на построенной
термодинамической модели
Константы равновесия реакций образования
бинарных соединений, используемые при расчетах, брались из работы [4], а
параметры взаимодействия бинарных соединений в тройных твердых растворах - из
работы [5].
Результаты расчетов в случае выращивания
раствора GaPyAs1-y на подложке GaAs представлены на рис. 1 и 2. Расчеты были
выполнены в предположении, что на поверхности GaAs образуется упругонапряженный
слой GaPyAs1-y, постоянная кристаллической решетки которого в плоскости роста
определяется постоянной решетки GaAs. При данных расчетах учитывалось влияние
изменения свободной энергии Гиббса образования бинарных соединений в случае
упругонапряженного роста на константы равновесия реакций согласно [7].
На рис. 1 показано соотношение между долей
внешнего потока P в суммарном потоке элементов V группы и мольной долей P в
выращиваемом соединении тройного раствора при фиксированных внешних потоках As2
и Ga и различных температурах выращивания. На рисунке для сравнения приведены
экспериментальные данные, взятые из работы [6], и результаты расчета из работы
[2], в которой не учитывалось влияние упругих напряжений на свободную энергию
Гиббса образования бинарных соединений. Из рисунка видно, что учет влияния
упругих напряжений приводит к лучшему согласию теоретических и
экспериментальных данных.
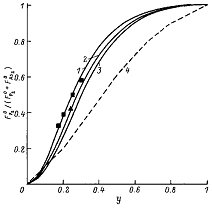
Рис. 1. Соотношение между долей внешнего потока
фосфора в суммарном внешнем потоке элементов V группы и составом растущего
соединения GaPyAs1-y [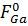 = 1014 (см2 ∙
с)-1,
= 1014 (см2 ∙
с)-1, 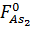 =
3 ∙ 1014 (см2 ∙ с)-1 ] при температурах подложки T, °C: 1 - 400, 2
- 500, 3 - 600. Штриховой линией показаны результаты расчета из работы [2].
Символами отмечены экспериментальные данные [6].
=
3 ∙ 1014 (см2 ∙ с)-1 ] при температурах подложки T, °C: 1 - 400, 2
- 500, 3 - 600. Штриховой линией показаны результаты расчета из работы [2].
Символами отмечены экспериментальные данные [6].
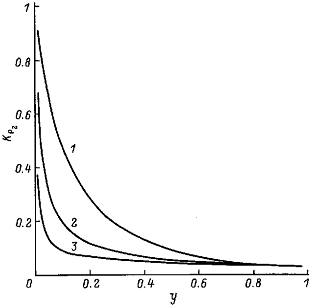
Рис. 2. Зависимость коэффициента встраивания
фосфора от состава растущего соединения GaPyAs1-y [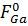 = 1014 (см2 ∙ с)-1, T = 520°C] при внешних потоках мышьяка
= 1014 (см2 ∙ с)-1, T = 520°C] при внешних потоках мышьяка 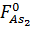 ,
(см2 ∙ с)-1: 1 - 1014, 2 - 3 ∙ 1014, 3 - 1015.
,
(см2 ∙ с)-1: 1 - 1014, 2 - 3 ∙ 1014, 3 - 1015.
На рис. 2 приведены зависимости коэффициента
встраивания фосфора KP2, определенного как отношение части падающего потока P,
встраивающейся в растущий слой, к полному падающему потоку P, от состава
выращиваемого слоя при фиксированном потоке 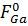 =
1014 (см2 ∙ с)-1 для различных значений
=
1014 (см2 ∙ с)-1 для различных значений 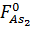 при
условии обогащения по элементам V группы
при
условии обогащения по элементам V группы
(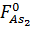 +
+ 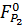 )
>
)
> 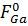 .
.
Коэффициент встраивания фосфора определяется
следующим выражением при T < 620°C:
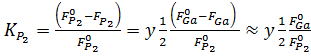 (15)
(15)
В области составов с малой мольной долей P при
приближении величины 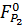 к величине y
к величине y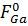 /2
коэффициент встраивания оказывается близким к 1, т. е. практически весь
падающий P встраивается. Уменьшение коэффициента встраивания с увеличением
мольной доли P связано, как видно из рис. 1, с увеличением необходимого
внешнего потока P2 для получения соединения определенного состава при
фиксированном падающем потоке As2, в то время как поток Ga при этом остается
неизменным. Аналогичные рассуждения объясняют также уменьшение KP2 с
увеличением падающего потока
/2
коэффициент встраивания оказывается близким к 1, т. е. практически весь
падающий P встраивается. Уменьшение коэффициента встраивания с увеличением
мольной доли P связано, как видно из рис. 1, с увеличением необходимого
внешнего потока P2 для получения соединения определенного состава при
фиксированном падающем потоке As2, в то время как поток Ga при этом остается
неизменным. Аналогичные рассуждения объясняют также уменьшение KP2 с
увеличением падающего потока 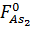 .
.
Диаграммы отношения потоков элементов III и V
групп в зависимости от мольных долей компонентов (x и у) четверного твердого
раствора в случае выращивания GaxIni_xPyAsi_y, согласованного по параметру
решетки с GaAs для различных температур роста в диапазоне 500^600° C при
выращивании в условиях обогащения по элементам V группы, показаны на рис. 3 и
4.

Рис. 3. Соотношение между долей внешнего потока
фосфора в суммарном внешнем потоке элементов V группы и мольной долей фосфора в
выращиваемом соединении GaхIn1-хPуAs1-у при росте в условиях обогащения по
элементам V группы [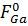 = 1014 (см2∙с)-1],
при температурах подложки в диапазоне 500-600° C и внешних потоках мышьяка
= 1014 (см2∙с)-1],
при температурах подложки в диапазоне 500-600° C и внешних потоках мышьяка 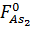 ,
(см2∙с)-1: 1 - 2 ∙ 1014, 2 - 2 ∙ 1015.
,
(см2∙с)-1: 1 - 2 ∙ 1014, 2 - 2 ∙ 1015.
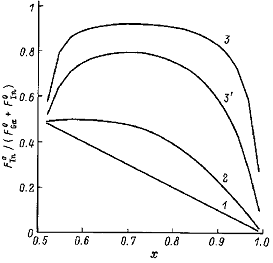
Рис. 4. Соотношение между долей внешнего потока
In в суммарном внешнем потоке элементов III группы и мольной долей Ga [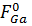 =
1014 (см2 ∙ с)-1] в выращиваемом соединении GaxIn1-xPyAs1-y при росте в
условиях обогащения по элементам V группы, при температурах подложки T, °C и
внешних потоках мышьяка
=
1014 (см2 ∙ с)-1] в выращиваемом соединении GaxIn1-xPyAs1-y при росте в
условиях обогащения по элементам V группы, при температурах подложки T, °C и
внешних потоках мышьяка 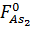 , (см2 ∙
с)-1: 1 - 500 и 2 ∙ 1014, 2 - 550 и 2 ∙ 1014, 3 - 600 и 2 ∙
1014, 3' - 600 и 2 ∙ 1015.
, (см2 ∙
с)-1: 1 - 500 и 2 ∙ 1014, 2 - 550 и 2 ∙ 1014, 3 - 600 и 2 ∙
1014, 3' - 600 и 2 ∙ 1015.
На рис. 4 приведено соотношение между долей
внешнего потока индия 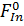 в суммарном
внешнем потоке элементов III группы
в суммарном
внешнем потоке элементов III группы 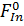 +
+
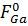 и
мольной доли Ga в выращиваемом соединении. Из рисунка видно, что при
температуре выращивания 500°C отношение внешнего потока индия к суммарному
внешнему потоку элементов III группы
и
мольной доли Ga в выращиваемом соединении. Из рисунка видно, что при
температуре выращивания 500°C отношение внешнего потока индия к суммарному
внешнему потоку элементов III группы 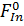 /(
/(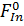 +
+ 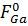 )
является линейной функцией от мольной доли Ga. Указанный результат является
следствием того, что при данной температуре выращивания переиспаренные потоки
In и Ga пренебрежимо малы по сравнению с внешними потоками соответствующих
элементов, т. е. коэффициенты прилипания Ga и In близки к 1. Однако при
увеличении температуры выращивания переиспаренный поток In существенно
возрастает, что отражено на рис. 5, где показана зависимость переиспаренного
потока In от состава растущего слоя для 3 различных температур выращивания. В
то же время переиспаренный поток Ga остается пренебрежимо малым и не превышает
величины 2 ∙ 1011 (см2 ∙ с)-1 для температуры 600°C. В результате
этого для высоких температур выращивания (500-600)°C зависимость отношения
)
является линейной функцией от мольной доли Ga. Указанный результат является
следствием того, что при данной температуре выращивания переиспаренные потоки
In и Ga пренебрежимо малы по сравнению с внешними потоками соответствующих
элементов, т. е. коэффициенты прилипания Ga и In близки к 1. Однако при
увеличении температуры выращивания переиспаренный поток In существенно
возрастает, что отражено на рис. 5, где показана зависимость переиспаренного
потока In от состава растущего слоя для 3 различных температур выращивания. В
то же время переиспаренный поток Ga остается пренебрежимо малым и не превышает
величины 2 ∙ 1011 (см2 ∙ с)-1 для температуры 600°C. В результате
этого для высоких температур выращивания (500-600)°C зависимость отношения 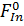 /(
/(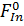 +
+ 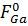 )
становится нелинейной. Увеличение суммарного потока элементов V группы
)
становится нелинейной. Увеличение суммарного потока элементов V группы 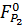 +
+
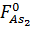 приводит
к уменьшению переиспаренного потока In (рис. 5, кривая 3'), вследствие чего для
выращивания соединения одинакового состава при высоких температурах подложки
требуется меньший внешний поток In. Зависимость отношения
приводит
к уменьшению переиспаренного потока In (рис. 5, кривая 3'), вследствие чего для
выращивания соединения одинакового состава при высоких температурах подложки
требуется меньший внешний поток In. Зависимость отношения 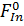 /(
/(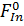 +
+ 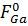 )
при увеличенном потоке
)
при увеличенном потоке 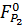 +
+ 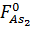 показана
на рис. 4. Расчеты выполнены для внешнего потока Ga
показана
на рис. 4. Расчеты выполнены для внешнего потока Ga 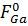 =1014(см2
∙ с)-1, что соответствует скорости роста арсенида галлия VGaAs = 1 Å/с.
Зависимость скорости роста соединения от его состава в случае выращивания
четверного твердого раствора для зависимостей, приведенных на рисунке,
определяется выражением VGaAs/(1 - x).
=1014(см2
∙ с)-1, что соответствует скорости роста арсенида галлия VGaAs = 1 Å/с.
Зависимость скорости роста соединения от его состава в случае выращивания
четверного твердого раствора для зависимостей, приведенных на рисунке,
определяется выражением VGaAs/(1 - x).
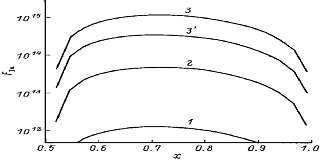
Рис. 5. Поток In, переиспаренный с поверхности
роста соединения GaxIn1-xPyAs1-y, в зависимости от мольной доли Ga [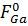 = 1014 (см2 ∙ с)-1] в соединении при температурах подложки T, °C и внешних
потоках мышьяка
= 1014 (см2 ∙ с)-1] в соединении при температурах подложки T, °C и внешних
потоках мышьяка 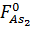 , (см2 ∙
с)-1: 1 - 500 и 2 ∙ 1014, 2 - 550 и 2 ∙ 1014, 3 - 600 и 2 ∙
1014, 3' - 600 и 2 ∙ 1015.
, (см2 ∙
с)-1: 1 - 500 и 2 ∙ 1014, 2 - 550 и 2 ∙ 1014, 3 - 600 и 2 ∙
1014, 3' - 600 и 2 ∙ 1015.
Заключение
Проведён термодинамический анализ четверного
соединения GaxIn1-xPyAs1-y и рассмотрены тонкости технических проблем при МПЭ.
Рассмотрено влияние переиспаренных потоков элементов на стехиометрический
состав. Используя существующие измерения, показано, что учёт упругих
напряжений, при расчётах, приближает значения к экспериментальным.
лучевая эпитаксия термодинамическая
Список использованной литературы
Р.
Хекингботом. В кн.: Молекулярно-лучевая эпитаксия и гетероструктуры, под ред.
Л. Ченга и К. Плога (М., Мир, 1989) с. 65.. Seki, A. Koukitu. J.
Cryst. Growth, 78, 342 (1986)..S. Jordan, M. Ilegems. J. Phys. Chem. Sol., 36,
329 (1975).
П.С.
Копьев,
Н.Н.
Леденцов.
ФТП,
22, 1729 (1988)..B. Panish, M. Ilegems. Prog. Sol. St. Chem., 7, 39 (1972)..W.
Liang, C.W. Tu. J. Appl. Phys., 74, 255 (1993)..V. Ivanov, P.D. Altukhov, T.S.
Argunova, A.A. Bakun, A.A. Budza, V.V. Chaldyshev, YuA. Kovalenko, P.S. Kop'ev,
R.N. Kutt, B.Ya. Meltser, S.S. Ruvimov, S.V. Shaposhnikov, L.M. Sorokin, V.M.
Ustinov. Semicond. Sci. Technol., 8, 347 (1993).
А.Ю.
Егоров, А.Р. Ковш, А.Е. Жуков, В.М. Устинов, П.С. Копьев, «Термодинамический
анализ процесса роста четверных соединений AIIIBV при молекулярно-пучковой
эпитаксии на примере соединений GaхIn1-хPуAs1-у
Данилова
Т.И., Смирнова К.И., Илюшин В.А., Величко А.А., «Процессы микро- и
нанотехнологии»,Томск,2005.
Курносов
А.И. , Юдин В.В. , Технология производства полупроводниковых приборов и
интегральных схем М: «Высшая школа» , 1986.
Жуков
А.Е., Семенова Е.С., Устинов В.М., Вебер Е.Р., «Молекулярно-пучковая эпитаксия
GaAsN на GaAs с использованием плазменного источника, возбуждаемого постоянным
током»; Журнал технической физики, 2001, том 71, вып.10.