Теория спиновых волн в ферромагнетике с периодической доменной структурой
КУРСОВАЯ
РАБОТА
на
тему: «Теория спиновых волн в ферромагнетике с периодической доменной
структурой»
Содержание
Введение
. Постановка задачи
2. Приведение квадратичной формы 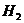 к диагональному виду
к диагональному виду
. Нахождение элементарных возбуждений и их энергетического спектра
Выводы
Список литературы
Введение
В настоящее время одной из
актуальных проблем физики твердого тела является изучение различных дефектов в
кристаллических структурах и влияние их на свойства веществ. Магнитные дефекты,
как и кристаллографические, могут быть точечными или протяженными.
Цель данной работы - создание общей
схемы применения метода вторичного квантования для нахождения спектра
элементарных возбуждении в ферромагнетиках с простейшей доменной структурой при
учете дипольной энергии. Предлагаемая схема позволяет с единой точки зрения
рассматривать некоторые кинетические, релаксационные и другие явления в
ферромагнетиках с доменной структурой. Кроме того, такое рассмотрение облегчает
изучение влияния других, более сложных, протяженных дефектов в
ферро-антиферромагнетиках на их физические свойства.
1. Постановка задачи
Будем рассматривать
неограниченный ферромагнетик. Допустим, что спины лежат в плоскости 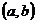 параллельно
оси
параллельно
оси 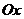 ,
ось
,
ось 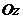 направим
вдоль оси
направим
вдоль оси 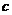 .
Феноменологический гамильтониан для таких ферромагнетиков можно записать так:
.
Феноменологический гамильтониан для таких ферромагнетиков можно записать так:
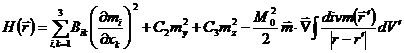 , (1.1)
, (1.1)
где  ;
;
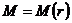 -
локальная намагниченность;
-
локальная намагниченность; 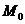 - намагниченность
насыщения;
- намагниченность
насыщения; 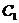 и
и
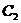 -
произвольные постоянные. В уравнении (1.1) первое слагаемое является энергией
обмена, второе - энергия анизотропии, третье - магнитодипольной энергией.
-
произвольные постоянные. В уравнении (1.1) первое слагаемое является энергией
обмена, второе - энергия анизотропии, третье - магнитодипольной энергией.
Для решения данного
уравнения требуется найти все три слагаемых.
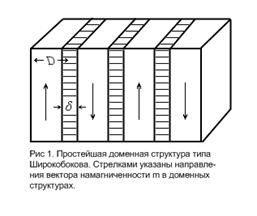
Для простоты ограничимся
рассмотрение случая, когда образец состоит из плоскопараллельных доменов,
разделенных переходными слоями (рис. 1), в состоянии равновесия все домены
имеют одинаковую толщину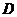 (доменная структура типа Широбокова), в переходном слое
(доменная структура типа Широбокова), в переходном слое 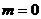 .
.
Для определения
равновесной намагниченности 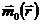 минимизирует
минимизирует 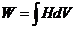 .
В блоховском приближении
.
В блоховском приближении 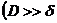 ,
,
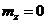 ,
,
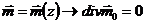 ;
;
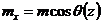 ;
;
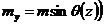 получаем:
получаем:
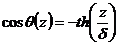 ,
, 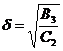 -
толщина доменной границы (1.2)
-
толщина доменной границы (1.2)
Согласно общей схеме, в
гамильтониане (1.1) перейдем от классических величин к операторам 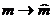 ,
которые удовлетворяют соотношениям коммутации
,
которые удовлетворяют соотношениям коммутации
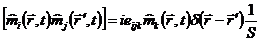 ,
, 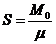 - величина спина, (1.3)
- величина спина, (1.3)
где 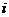 ,
,
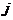 ,
,
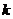 принимают
значения 1, 2, 3 в циклическом порядке;
принимают
значения 1, 2, 3 в циклическом порядке; 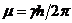 (
(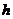 - постоянная Планка,
- постоянная Планка, 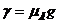 ,
,
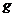 -
фактор Ланде);
-
фактор Ланде); 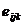 -
единичный антисимметричный тензор третьего ранга.
-
единичный антисимметричный тензор третьего ранга.
В исходной системе
координат  ось
квантования не фиксирована. Так как распределение намагниченности получилось
неоднородным, а с другой стороны имеется представление
ось
квантования не фиксирована. Так как распределение намагниченности получилось
неоднородным, а с другой стороны имеется представление 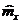 ,
,
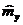 ,
,
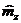 ,
то необходимо перейти в систему отсчета в которой каждый спин поляризован вдоль
оси
,
то необходимо перейти в систему отсчета в которой каждый спин поляризован вдоль
оси 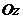 .
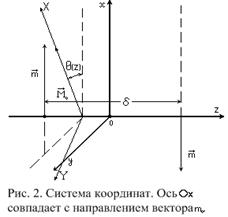
Поэтому в неоднородном случае удобно перейти к локальной системе координат, в
которой ось
.
Поэтому в неоднородном случае удобно перейти к локальной системе координат, в
которой ось 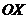 -
направлена вдоль равновесного вектора
-
направлена вдоль равновесного вектора 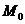 , ось
, ось 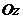 остается
без изменения (рис. 2). Такая система координат поворачивается вокруг оси
остается
без изменения (рис. 2). Такая система координат поворачивается вокруг оси 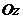 вместе
с
вместе
с 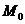 .
Тогда ось
.
Тогда ось 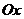 можно
принять за ось квантования. Следовательно необходимо в каждой точке повернуть
систему на соответствующий угол зависящий от
можно
принять за ось квантования. Следовательно необходимо в каждой точке повернуть
систему на соответствующий угол зависящий от 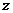 .
.
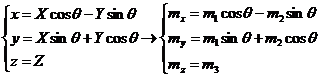 (1.4)
(1.4)
где 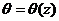 .
Легко проверить, что при таких преобразованиях соотношения (1.3) сохраняются.
Дальнейшие вычисления оказываются более простыми, если считать величины
.
Легко проверить, что при таких преобразованиях соотношения (1.3) сохраняются.
Дальнейшие вычисления оказываются более простыми, если считать величины 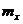 ,
,
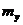 и
и
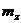 функциями
координат
функциями
координат 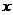 ,
,
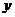 ,
,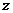 .
.
Доменные границы могут
совершать малые колебания около их положения равновесия. Устойчивость доменных
границ по отношению к смещению будем учитывать путем добавления к гамильтониану
(1.1) квазиупругой энергии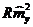 .
Строго говоря, добавление такого члена в гамильтониане оправдывается только в
пределах переходного слоя. Однако в модели Широкобокова нет резкой границы
между переходным слоем и доменами. Кроме того, ввиду малости члена
.
Строго говоря, добавление такого члена в гамильтониане оправдывается только в
пределах переходного слоя. Однако в модели Широкобокова нет резкой границы
между переходным слоем и доменами. Кроме того, ввиду малости члена 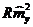 по
сравнению с энергией анизотропии наличие его в гамильтониане не может оказать
существенного влияния на определение движения спинов в пределах доменов. В
общем случае аналогичный член в гамильтониане обуславливается магнитоупругими
силами в образце. При более точном описании движения спинов следует взять в
гамильтониане главные члены магнитоупругой энергии.
по
сравнению с энергией анизотропии наличие его в гамильтониане не может оказать
существенного влияния на определение движения спинов в пределах доменов. В
общем случае аналогичный член в гамильтониане обуславливается магнитоупругими
силами в образце. При более точном описании движения спинов следует взять в
гамильтониане главные члены магнитоупругой энергии.
Подставляем в (1.1)
вместо 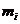 его
проекции в движущейся системе координат
его
проекции в движущейся системе координат 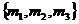 :
:
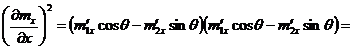
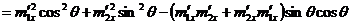 ,
,
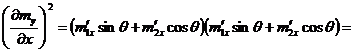
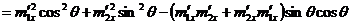 ,
,
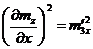 .
.
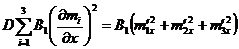 ;
; 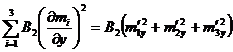 .
.
При вычислении
слагаемого с 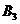 заметим,
что
заметим,
что  .
.
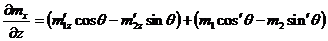 ,
,
тогда
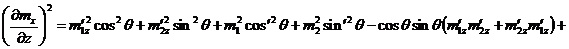
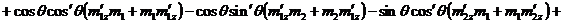
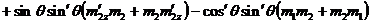 .
.
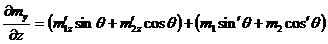 ,
,
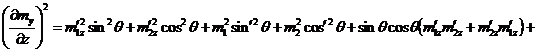
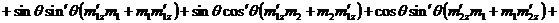
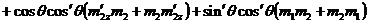
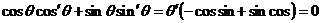 ;
; 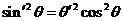 ;
;
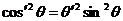
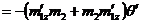 ;
; 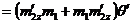
Исходя из того что:
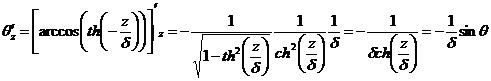 ,
,
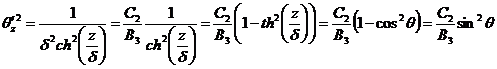 .
.
Таким образом энергия
обмена … в общем виде
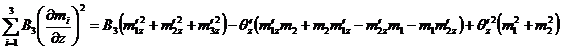 ,
,
но для нашего случая 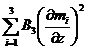 примет
вид
примет
вид
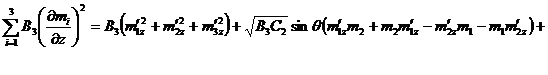
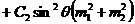 .
.
Проведем также учет
магнитодипольного взаимодействия.
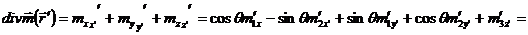
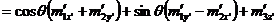 ;
;
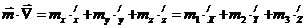 ;
;
учитывая что
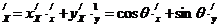 ,
, 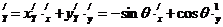 ,
,
пересчитываем 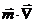 согласно
формуле, получаем
согласно
формуле, получаем
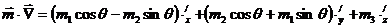 .
.
Следовательно
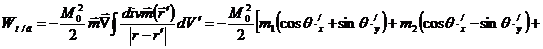
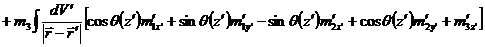 .
.
Но такой вид
магнотодипольной энергии неудобен для дальнейших вычислений. Рассмотрим
винтеровское приближение (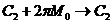 ).
В нулевом приближении магнитодипольная энергия равна нулю. Перераспределив
).
В нулевом приближении магнитодипольная энергия равна нулю. Перераспределив 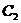 ,
мы можем записать энергию анизотропии:
,
мы можем записать энергию анизотропии:
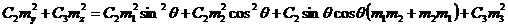 .
.
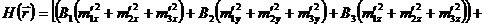
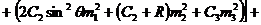
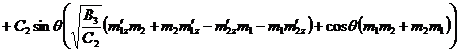 . (1.5)
. (1.5)
. Приведение
квадратичной формы 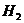 к
диагональному виду
к
диагональному виду
В общем случае
квадратичная форма 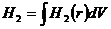 имеет
весьма сложное выражение, диагонализация ее с учетом
имеет
весьма сложное выражение, диагонализация ее с учетом 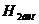 представляет
очень трудную задачу. Для системы в состоянии равновесия, отвечающей минимуму
энергии в соответствии с (1.5) равновесное распределение дается (1.2). Если же
систему выводят из этого состояния, то возникают колебания намагниченности в
каждой точке ферромагнетика. Представим энергию возбуждения в виде энергии
магнонов и вычислим спектр возбуждений. Вводим бозе-операторы рождения -
представляет
очень трудную задачу. Для системы в состоянии равновесия, отвечающей минимуму
энергии в соответствии с (1.5) равновесное распределение дается (1.2). Если же
систему выводят из этого состояния, то возникают колебания намагниченности в
каждой точке ферромагнетика. Представим энергию возбуждения в виде энергии
магнонов и вычислим спектр возбуждений. Вводим бозе-операторы рождения - 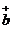 и
уничтожения
и
уничтожения 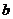 ,
подчиняя их коммутативным соотношениям:
,
подчиняя их коммутативным соотношениям:
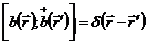 ;
;
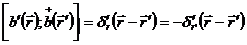 ;
;
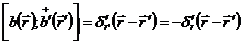 ;
;
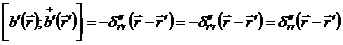 . (2.1)
. (2.1)
Для операторов  ,
,
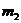 ,
,
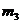 используем
представление Хольштейна-Примакова:
используем
представление Хольштейна-Примакова:
 ;
; 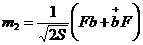 ;
;
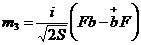 .
.
В данном случае
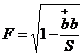 .
.
Но так как в нулевом
приближении 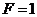 ,
то имеем
,
то имеем
 ;
;  ;
;
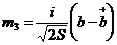 (2.2)
(2.2)
При учете последующих
слагаемых в разложении по степеням 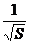 (что справедливо вообще
говоря, для больших значений
(что справедливо вообще
говоря, для больших значений 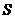 ) возникают более
высокие степени операторов. Для их правильной записи в
) возникают более
высокие степени операторов. Для их правильной записи в 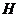 необходимо
ввести упорядочение
необходимо
ввести упорядочение 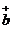 левее
в это делается с помощью коммутационных соотношений:
левее
в это делается с помощью коммутационных соотношений:
. 1. 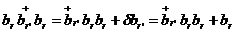
. 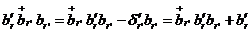
В выражениях 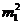 ,
,
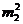 ,
,
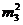 отбросим
слагаемые степени
отбросим
слагаемые степени 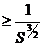 :
:
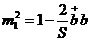 ;
;
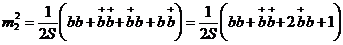 ;
;
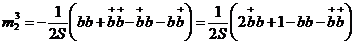 .
.
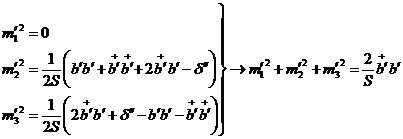 -
-
обменное взаимодействие
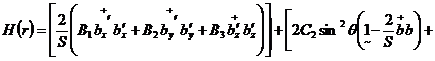
Перегруппируем слагаемые
и представим  в
виде:
в
виде:
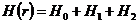 ,
,
где
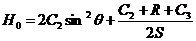 ,
,
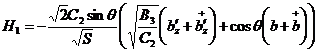 .
.
Положим 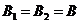 .
Перегруппировав слагаемые в
.
Перегруппировав слагаемые в 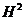 , получаем:
, получаем:
спиновой волна
ферромагнетик доменный
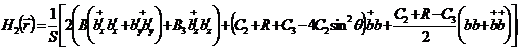 .
.
Перейдем к безразмерным
переменным 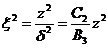 ,
,
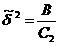 .
Используем:
.
Используем:
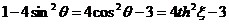 ,
,
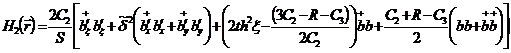 .
.
Представить 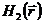 на
данном этапе нам мешают дополнительные слагаемые вида
на
данном этапе нам мешают дополнительные слагаемые вида 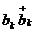 ,
которые не дают возможности назвать энергию магнонов. Поэтому нам следует
диагонализировать
,
которые не дают возможности назвать энергию магнонов. Поэтому нам следует
диагонализировать 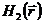 .
.
Переходим к
фурье-представлению в плоскости 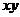 .
.
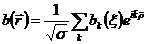 ,
,  (2.3)
(2.3)
Операторы 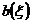 и
и
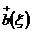 подчиняются
коммутативным соотношениям:
подчиняются
коммутативным соотношениям:
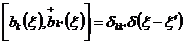 .
.
Подставляя (2.3) в 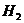 ,
находим:
,
находим:
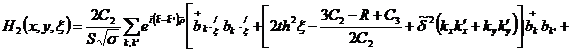
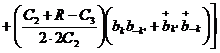 .
.
Проинтегрируем  по
по
 и
и
 .
Так как (
.
Так как ( )
ортогональны. То в сумме останутся слагаемые только с
)
ортогональны. То в сумме останутся слагаемые только с 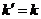 .
Обозначим
.
Обозначим 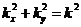 ,
получаем:
,
получаем:
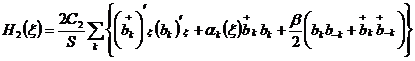 (2.4)
(2.4)
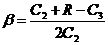 ;
; 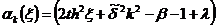 ;
;
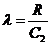 .
.
Необходимо
диагонализировать гамильтониан (2.4). Представив его в виде:
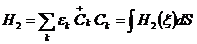 (2.5)
(2.5)
С новыми операторами 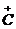 и
и
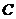 ,
которые подчиним коммутативным соотношениям:
,
которые подчиним коммутативным соотношениям:
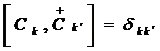 ;
; 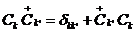 , (2.6)
, (2.6)
и не зависящими от 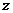 .
.
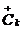
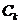 - оператор числа
магнонов с
- оператор числа
магнонов с 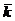 ;
;
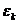 -
соответствующая энергия. В решении зависимость
-
соответствующая энергия. В решении зависимость 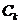 следует из уравнения
движения:
следует из уравнения
движения:
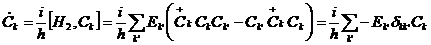 ,
,
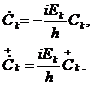 (2.7)
(2.7)
Причем
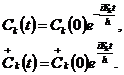
Введем уравнения
движения для операторов 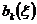 :
:
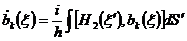 (2.8)
(2.8)
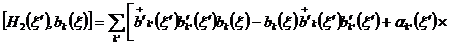
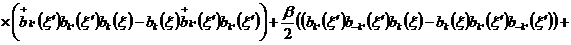
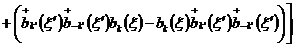 .
.
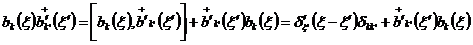 ,
,
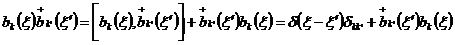 ,
,
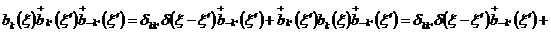
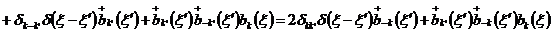 .
.
Тогда
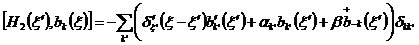 .
.
Интегрируя по 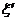 ,
находим
,
находим
 ;
;
Таким образом, уравнение
движения для  имеет
вид:
имеет
вид:
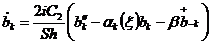 . (2.9)
. (2.9)
Для приведения (2.9) к
(2.7), а 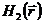 -
к диагональному виду (2.5), зададим каноническое преобразование:
-
к диагональному виду (2.5), зададим каноническое преобразование:
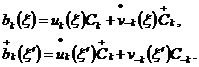 (2.10)
(2.10)
Из (2.5) и (2.6)
следует:
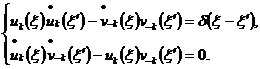 (2.11)
(2.11)
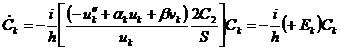
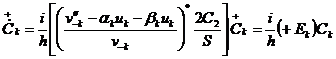
Следовательно, 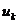 и
и
 подчиняются
уравнениям:
подчиняются
уравнениям:
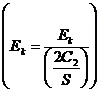
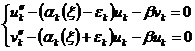 (2.12)
(2.12)
Представим их в виде:
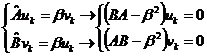 ,
,
если 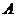 и
и
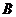 коммутируют,
то уравнения для
коммутируют,
то уравнения для 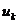 и
и
 имеют
одинаковый вид, то есть
имеют
одинаковый вид, то есть 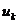 и
и
 отличаются
на некий множитель:
отличаются
на некий множитель:
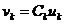 . (2.13)
. (2.13)
В нашем случае
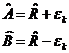
где 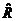 -
линейный оператор, такой что
-
линейный оператор, такой что 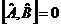 . Перепишем уравнения
(2.12) с учетом (2.13):
. Перепишем уравнения
(2.12) с учетом (2.13):
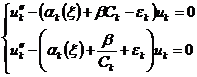 (2.14)
(2.14)
Так как эти уравнения
должны совпадать, то
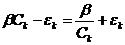 .
.
Отсюда
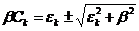 .
.
Подставляя в (2.15),
получаем:
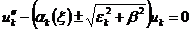
или
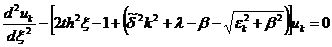 . (2.16)
. (2.16)
Это уравнение имеет
ограниченное на бесконечности решение при условии, когда скобка равна нулю, то
есть
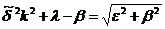

Так как
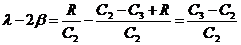 ,
,
то отсюда получаем для
энергии:
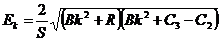 .
.
. Нахождение спектра
элементарных возбуждений
Решение уравнения (2.16)
аналогично решению уравнения Шредингера для потенциала
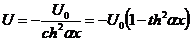
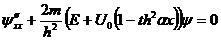
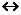
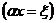 :
: 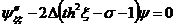
где
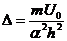 ,
, 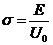 .
.
Возможны решения при
которых решение конечно
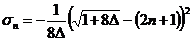 .
.
Причем выражение под
квадратом строго положительно.
В нашем случае 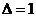 ,
так что
,
так что 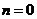 -
единственно возможный случай, из этого следует что
-
единственно возможный случай, из этого следует что 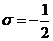 ,
чему соответствует уравнение:
,
чему соответствует уравнение:
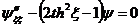 .
.
Запишем уравнение (2.9)
в, движущейся со скоростью 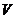 , системе отсчета. Это
эквивалентно замене производной по времени:
, системе отсчета. Это
эквивалентно замене производной по времени:
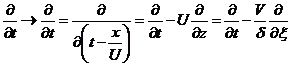 ,
,
следовательно вместо
(2.9) получаем уравнение:
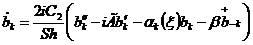 ,
,
где
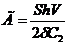 .
.
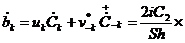
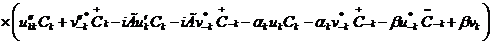 .
.
По аналогии с (2.12)
получаем:
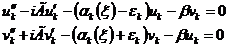 .
.
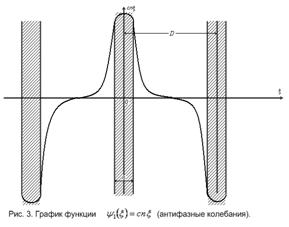
Таким образом,
ферромагнетикам с доменной структурой свойственны всего три типа элементарных
возбуждений. Из них два имеют форму плоских волн, распространяющихся
параллельно доменной границе. В направлении, нормальном к границе (вдоль оси 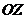 ),
возможны волны только определенной длины, равной удвоенной толщине домена
),
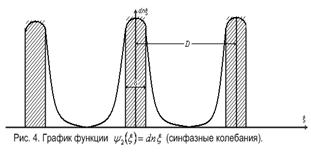
возможны волны только определенной длины, равной удвоенной толщине домена 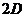 (рис.
3, 4) или толщине домена
(рис.
3, 4) или толщине домена 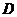 (рис.
5). В отличие от обычных волн они выражаются через эллиптические функции.
(рис.
5). В отличие от обычных волн они выражаются через эллиптические функции.
Эти волны можно
истолковать иначе: их можно рассматривать, как плоские, распространяющиеся в
плоскости, параллельной доменной границе, но с переменой амплитудой,
изменяющейся в зависимости от 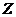 по закону эллиптических
функций. Амплитуды для этих возбуждений имеют максимальные значения в середине
переходного слоя, в доменах постепенно уменьшаются и в середине домена
обращаются в нуль. В случае 1 фазы волн в двух соседних границах противоположны
(антифазны), тогда как в случае 2 - одинаковы (синфазны). Поэтому возбуждения
типа 1 и 2 можно назвать характерными для переходного слоя. Появление этих двух
типов возбуждений можно объяснить связанными колебаниями доменных границ -
антифазными в одном случае (см. рис. 3) и синфазными в другом (см. рис. 4).
Когда нет взаимодействий между переходными слоями (при
по закону эллиптических
функций. Амплитуды для этих возбуждений имеют максимальные значения в середине
переходного слоя, в доменах постепенно уменьшаются и в середине домена
обращаются в нуль. В случае 1 фазы волн в двух соседних границах противоположны
(антифазны), тогда как в случае 2 - одинаковы (синфазны). Поэтому возбуждения
типа 1 и 2 можно назвать характерными для переходного слоя. Появление этих двух
типов возбуждений можно объяснить связанными колебаниями доменных границ -
антифазными в одном случае (см. рис. 3) и синфазными в другом (см. рис. 4).
Когда нет взаимодействий между переходными слоями (при  ),
энергия этих двух ветвей совпадает. При более точном учете дипольной энергии
возможны более сложные связанные колебания.
),
энергия этих двух ветвей совпадает. При более точном учете дипольной энергии
возможны более сложные связанные колебания.
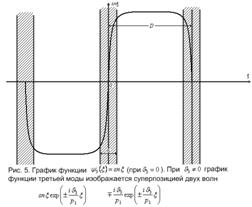
Для случая 3 характерны
сложные спиновые волны, аналогичные таковым для однодоменного ферромагнетика,
но сильно деформированные под влиянием доменной структуры. Эти волны можно
рассматривать как суперпозицию двух более простых волн 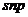 ,
,
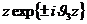 и
и
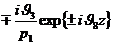 .
При
.
При 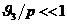 (для
длинноволновых возбуждений по
(для
длинноволновых возбуждений по 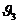 ) главную роль играет в
(3.16) первое слагаемое; наоборот, при
) главную роль играет в
(3.16) первое слагаемое; наоборот, при 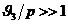 (при коротковолновых
возбуждениях по
(при коротковолновых
возбуждениях по 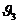 )
- второе. Таким образом, при коротковолновом возбуждении (по
)
- второе. Таким образом, при коротковолновом возбуждении (по 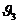 )
третий тип не «чувствует» доменную структуру.
)
третий тип не «чувствует» доменную структуру.
Выводы
В ферромагнитном образце
с периодической доменной структурой имеются всего три типа элементарных
возбуждений, различающихся энергетическим спектром. Первые два из них имеют
форму плоских волн, распространяющихся параллельно доменной границе. В
направлении, нормальном к границе, возможны волны только определенной длины,
равной толщине или удвоенной толщине домена. Появление этих двух типов
возбуждений объясняется связанными (антифазными и синфазными) колебаниями
доменных структур. Энергия синфазных колебаний несколько ниже, чем антифазных.
При энергетические щели для двух типов возбуждений мало отличаются друг от друга.
Тем не менее даже в этом случае возбуждения, которым всегда соответствуют
ортогональные собственные функции, необходимо рассматривать как два различных
типа. Следует отметить, что в модели Ландау-Лифшица возможен всего один
дополнительный тип специфических элементарных возбуждений, распространяющихся в
пределах переходного слоя, разделяющего два домена.
энергетические щели для двух типов возбуждений мало отличаются друг от друга.
Тем не менее даже в этом случае возбуждения, которым всегда соответствуют
ортогональные собственные функции, необходимо рассматривать как два различных
типа. Следует отметить, что в модели Ландау-Лифшица возможен всего один
дополнительный тип специфических элементарных возбуждений, распространяющихся в
пределах переходного слоя, разделяющего два домена.
Ввиду малости параметра 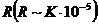 возможны
такие случаи, когда
возможны
такие случаи, когда 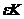 сравнимо
с
сравнимо
с 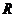 .
В винтеровском приближении для дипольной энергии закон дисперсии одинаков для
двух типов возбуждений, но при более точном учете дипольной энергии они
различаются и по этому закону. Третий тип возбуждений представляет собой
сложные спиновые волны, аналогичные однородному случаю, но сильно
деформированные под воздействием доменной структуры. Энергетический спектр для
этого типа возбуждений мало отличается от спектра спиновых волн в однородном
ферромагнетике.
.
В винтеровском приближении для дипольной энергии закон дисперсии одинаков для
двух типов возбуждений, но при более точном учете дипольной энергии они
различаются и по этому закону. Третий тип возбуждений представляет собой
сложные спиновые волны, аналогичные однородному случаю, но сильно
деформированные под воздействием доменной структуры. Энергетический спектр для
этого типа возбуждений мало отличается от спектра спиновых волн в однородном
ферромагнетике.
Амплитуды трех типов
возбуждений по порядку величин одинаковы, а соответствующие волновые функции
ортогональны. Энергетическая щель для двух типов возбуждений значительно
меньше, чем для третьего типа. В связи с этим изменяется энтропия,
теплоемкость, резонансные и релаксационные свойства образца, Учет
взаимодействий различных типов возбуждений приводит к существенному изменению
кинетических явлений.
Список литературы
1. М.М. Фарзтдинов, Е.А. Туров, ФММ, 2010, т. 29, вып. 2, с.
458-470
2. А.П. Танкеев, Ю.Г. Райдугин, ФММ, 2009, т. 56, вып. 1, с.
30-40
. Л.Д. Ландау, Е.М. Лифшиц «Квантовая механика», М., Н.,
2011, 768 с.