Методические особенности обучения учащихся методу моделирования через решения задач с параметрами
Федеральное
агентство по образованию РФ
ФГБОУ ВПО
«Ишимский государственный педагогический институт им. П.П. Ершова»
Кафедра
математики, информатики и методики их преподавания
Выпускная
квалификационная работа
Методические
особенности обучения учащихся методу моделирования через решения задач с
параметрами
Исполнитель:
Фадеев Виктор Александрович
студент 5 курса 192 группы
дневного отделения
физико-математического факультета
Научный руководитель:
к. ф-м. н., доцент
Столбов Виктор Николаевич
Ишим 2014
Содержание
Глава 1. Теоретические основы
развития у учащихся умений моделирования при решении задач с параметрами
.1 О развитии у учащихся умений
моделирования при обучении математике в школе
.1.1 Сущность деятельности учащихся
при обучении методу моделирования
.1.2 Формирование деятельности
учащихся при обучении методу моделирования
.1.3 Функции метода моделирования
.2. Решение задач с параметрами как
способ обучения методу моделирования
.2.1 Развивающие функции задач в
обучении
.2.2 Задачи как средство обучения
методу моделирования учащихся
.2.3 Методы решения задач с
параметрами
Выводы по первой главе
Глава 2. Развитие у учащихся умений
моделирования при решении задач с параметрами
.1. Система учебно-исследовательских
задач с параметрами
.1.1 Понятие параметра
.1.2 Употребление букв в математике
.1.3 Задачи с параметрами в V - VI
классах
.1.4 Задачи с параметрами в VII
классе
.1.5 Задачи с параметрами в VIII
классе
.1.6 Задачи с параметрами в IX
классе
.1.7 Задачи с параметрами в X-XI
классах
.2 Организация, проведение и
основные итоги педагогического эксперимента
Выводы по второй главе
Заключение
Библиографический список
использованной литературы
Введение
Значение математической подготовки в
образовании, развитии и воспитании человека предопределяет основные задачи
обучения математике в школе. Среди них выделяется задача формирования и
развития средствами математики интеллектуальных качеств личности: это и
определенный уровень психического и познавательного развития, и соответствующий
уровень математической культуры. Школа вносит большой вклад в развитие этих
качеств: на уроках математики формируются умения мыслить логически и
абстрактно, умения грамотно излагать и объяснять производимые действия,
заниматься теоретическими рассуждениями и самоанализом, проводить исследования
и т.д. Причем развитие умений моделирования значительно влияет на
интеллектуальное развитие личности учащихся.
Часто содержание подлежащего изучению в школе
математического материала содействует интеллектуальному развитию учащихся.
Причем в настоящее время различными авторскими коллективами разрабатываются
учебники и учебные пособия, в которых реализуется та или иная теория
развивающего обучения. Но не меньший эффект в развитии учащихся достигается при
использовании активных методов обучения и соответствующих систем математических
задач.
В историческом плане заметим, что в содержании
учебного материала школьных учебников по математике до 70-х годов для развития
умений и навыков моделирования включались специальные разделы: исследование
линейных и квадратных уравнений и неравенств, исследование систем линейных
уравнений и неравенств и др. А с переходом школы на новые программы по
математике для средней школы в 1972 году, основная нагрузка по развитию у
учащихся умений моделирования была переложена на задачный материал, а теория
являлась обоснованием различных методов решения математических задач.
В настоящее время, стремясь повысить качество
обучения математике, учителя поднимают требования к знаниям учащихся и уделяют
серьезное внимание подбору используемого на уроках задачного материала. А в
старших классах средней школы в целях развития математических способностей
учащихся используются задачи повышенной трудности, извлекаемые учителями из
различных сборников задач. Среди них в последние годы часто появляются задачи с
параметрами. В целом же решению задач с параметрами в средних школах уделяется
мало внимания - зачастую лишь в классах (школах) с углубленным изучением
математики. Однако в связи с потребностью подготовки учащихся к сдаче
вступительных и единых экзаменов задачи с параметрами начинают включать в
программу большинства подготовительных факультативов, а также ряда базовых
курсов алгебры и начал анализа. Значимость заданий этого типа не ограничивается
лишь их диагностической ценностью, так как деятельность по их решению
способствует повышению качества знаний и умений учащихся, интеллектуальному
развитию, а также позволяет формировать у них представления об особенностях
реальных умений моделирования математиков.
Таким образом, актуальность данной работы
обусловлена значимостью проблемы развития умений моделирования у учащихся
«через задачи», её малой разработанностью. Исходя из этого, мною была выбрана
тема «Методические особенности обучения учащихся методу моделирования через
решение задач с параметрами»,
К сожалению, в школьных учебниках задач с
параметрами недостаточно, поэтому цель данной работы состоит в том,
чтобы отчасти восполнить этот пробел, привлечь внимание к этим задачам,
«привить вкус» к их решению и способствовать формированию у учащихся умений
моделирования.
Объект исследования: процесс
обучения учащихся решению задач с параметрами.
Предмет исследования: методика
обучения методу моделирования учащихся при решении задач с параметрами.
Гипотеза исследования: если
в процессе обучения учащихся решению задач с параметрами использовать
специальный комплекс упражнений, то можно ожидать развития у учащихся умений
моделирования.
Исходя из объекта, предмета, цели и гипотезы
исследования были определены задачи исследования:
1. Изучить психолого-педагогические теории
развития у учащихся умений моделирования при обучении математике в школе.
. Установить развивающие функции задач в
обучении.
. Рассмотреть основные методы решения
задач с параметрами.
. Выполнить анализ содержания школьного
курса алгебры с точки зрения подготовки учащихся к решению задач с параметрами.
5....... Разработать комплекс задач с
параметрами обучающих методу моделирования.
6. Организовать и подвести основные итоги
педагогического эксперимента
Методы исследования: изучение
и систематизация математической, психолого-педагогической и научно-методической
литературы по проблеме исследования; изучение передового педагогического опыта;
педагогический эксперимент. В ходе работы использовался анализ педагогической,
методической и учебно-математической литературы по теме исследования.
Научная новизна выполненного
исследования заключается в разработке специального комплекса упражнений по
формированию у учащихся умений моделирования.
Практическая значимость: разработана методика
формирования у учащихся умений моделирования в процессе их обучения решению
задач с параметрами.
Данная выпускная работа состоит из введения,
двух глав, заключения и списка использованной литературы. В первой главе
рассказывается о том, как развивать у учащихся умения моделирования, т.е. при
каких условиях организации учебного процесса, при решении каких задач. Еще
рассматриваются образовательная значимость задач с параметрами, причины
сложности обучения этим задачам в школе и пути устранения этих сложностей, а
также разбираются методы решения уравнений с параметрами. Вторая глава
посвящена системе учебно-познавательных задач с параметрами, начиная с 5 и
заканчивая 11 классом. Здесь подробно рассказывается о том, как лучше знакомить
учащихся с понятием «параметр», а также приводятся конкретные примеры задач с
параметрами.
Глава
1. Теоретические основы развития у учащихся умений моделирования при решении
задач с параметрами
.1
О развитии у учащихся умений моделирования при обучении математике в школе
.1.1
Сущность деятельности учащихся при обучении методу моделирования
Теоретической предпосылкой метода моделирования
является то, что учебное моделирование, как и научное, является процессом
познания объективного мира, поэтому совпадают такие составляющие их элементы,
как усвоение уже известного по данной проблеме; выявление новых фактов и
явлений; установление непонятных явлений, подлежащих моделированию; изучение
фактов, связанных с непонятными явлениями; объяснение непонятного;
формулирование выводов из изученного; их применение к дальнейшему моделированию
и практике. Однако специфика учебного процесса накладывает отпечаток на данные
этапы, в связи с чем некоторые этапы научного познания могут отсутствовать.
Анализ взаимосвязи научного и учебного познания
позволяет заключить следующее:
·учебное
познание циклично, а новизна результата познания субъективна, что позволяет
ученику выполнять не весь цикл познания, а отдельные его элементы в различных
сочетаниях под руководством учителя, что позволяет управлять деятельностью
школьников при обучении методу моделирования;
·центральным
этапом учебного познания, интегрируемого на основе взаимосвязи его цикличности
и теории и практики формирования у учащихся научных понятий, является этап
учебного моделирования, в котором целесообразно отражается научное познание;
·для
осуществления учебного моделирования учащимся необходимы определенные знания и
практические умения и навыки, которыми к его началу они должны владеть;
·успешное
учебное познание школьников возможно, если возбуждаются и развиваются их
внутренние мотивы учения на всех этапах моделирования и обеспечена рефлексия
познавательной деятельности.
Таким образом, анализируя сущность научного и
учебного моделирований, можно сделать вывод, что основным их отличием является
то, что научное моделирование имеет одну цель - «открытие» нового, а учебное -
несколько целей, главной из которых является обучение учащихся методу
моделирования, методам научного познания, способам мыслительной деятельности,
развитию интуиции и творческих способностей.
Для раскрытия сущности понятия учебного
моделирования можно выделить его характерные признаки:
) учебное моделирование - это процесс поисковой
познавательной деятельности (изучение, выявление, установление чего-либо и
т.д.);
) учебное моделирование всегда направлено на
получение новых знаний, то есть моделирование всегда начинается с потребности
узнать что-либо новое;
) учебное моделирование предполагает
самостоятельность учащихся при выполнении задания;
) учебное моделирование должно быть направлено
на реализацию дидактических целей обучения.
Участвуя в учебном моделировании, учащиеся
обучаются математической деятельности, ибо непосредственно проделывают эту
деятельность. Учебные моделирования создают своего рода платформу для активной
мыслительной деятельности учащихся. В таком случае важна не только работа
учащихся, но и то, каким образом она делается.
Учебное моделирование как метод обучения
математике не только формирует, развивает мышление учащихся, но и способствует
формированию высшего типа мышления - творческого мышления, без которого
немыслима творческая деятельность.
.1.2 Формирование деятельности
учащихся при обучении методу моделирования
К факторам, способствующим обучению методу
моделирования учащихся, можно отнести следующие:
Ø личностно ориентированный подход к
обучению;
Ø ориентация на продуктивное
достижение результата;
Ø проблемное обучение как инструмент
развития опыта творческой деятельности;
Ø оптимальное сочетание логических и
эвристических методов решения задач;
Ø креативная организация учебного
процесса, максимальное насыщение его творческими ситуациями;
Ø создание ситуации совместной
поисковой деятельности;
Ø детализация учебного процесса;
Ø создание психологической атмосферы,
оптимальных условий для творческой деятельности.
Условиями, способствующими активизации
деятельности учащихся при обучении методу моделирования, являются:
·доброжелательная
атмосфера в коллективе;
·сочетание
индивидуальных и коллективных форм обучения;
·структурирование
учебного материала по принципу нарастания познавательной трудности учебной
работы;
·вооружение
учащихся рациональными приемами познавательной деятельности;
·формирование
внутренних стимулов к учению, самообразованию и др.
Тормозят же активную познавательную деятельность
учащихся следующие факторы: при опросе вопросы учители и ответы учащихся носят
репродуктивный характер; при изучении нового материала на абсолютном
большинстве уроков преобладает усвоение учащимися готовых знаний; закрепление и
применение знании проводятся в основном лишь по образцу и т.п.
К общим принципам организации учебного процесса,
обеспечивающим развитие у учащихся умений моделирования, можно отнести:
ü педагогическое руководство в
создании мотивов и стимулов к учению;
ü привитие интереса к изучаемому
объекту;
ü вооружение учащихся необходимыми
приемами познавательно-поисковой деятельности;
ü систематическое осуществление
принципа индивидуализации в обучении;
ü широкое использование технических и
наглядных средств обучения;
ü внедрение в практику работы и
систематическое использование компьютерных технологий;
ü разработка творческих заданий,
требующих нестандартных решений и самостоятельного поиска источников
информации;
ü сочетание и соединение дидактически
и методически обоснованных методов, способствующих развитию познавательной
деятельности и творческих способностей учащихся.
Предназначение умений моделирования у учащихся
состоит в том, что, будучи формой активности индивида, она является условием и
средством его психического развития. Психическое же развитие обеспечивает
школьнику усвоение теоретических знаний и способствует формированию у него
специфических способностей и качеств личности: любознательности,
целеустремленности, научной фантазии.
Приобщение обучающихся к методу моделирования
можно реализовать через решение специальных задач или через дополнительную
работу над задачей.
Привлечение школьников к учебным моделированиям
должно идти в двух направлениях содержательном и организационном.
Содержательная самостоятельность проявляется в том, чтобы ученик мог без помощи
со стороны поставить перед собой учебную задачу и представить ход ее решения.
Организационная самостоятельность выражается в
умении ученика организовать свою работу по решению постановленной задачи.
Таким образом, перед учителем встает проблема
поиска эффективных форм и способов учебной деятельности учащихся, которые бы не
просто вовлекали бы их в исследовательскую работу, но и способствовали обучению
самой этой деятельности. В конечном счете, необходимо так организовать познавательную
деятельность школьников, чтобы процедура учебного моделирования усваивалась ими
вместе с тем содержанием, на котором оно осуществляется.
В литературе предлагаются следующие рекомендации
для педагогов по выработке у детей умений моделирования:
§ не занимайтесь наставлениями; помогайте детям
действовать независимо; не давайте прямых инструкций относительно того, чем они
должны заниматься;
§ не делайте скоропалительных допущений, на основе
тщательного наблюдения и оценки определяйте сильные и слабые стороны детей, не
следует полагаться на то, что они уже обладают определенными базовыми навыками
и знаниями;
§ не сдерживайте инициативы детей и не делайте за
них то, что они могут сделать (или могут научиться делать) самостоятельно;
§ научитесь не торопиться с вынесением суждения;
научите детей прослеживать меж предметные связи;
§ используйте трудные ситуации, возникшие у детей
в школе или дома, как область приложения полученных навыков в решении задач;
§ помогайте детям научиться управлять процессом усвоения
знаний;
§ подходите ко всему творчески.
Итак, под учебным моделированием мы будем
понимать такой вид познавательной деятельности учащихся, который способствует
формированию следующих умений:
·добывать
новые предметные знания, приемы и способы действий;
·самостоятельно
организовывать поиск;
·достигать
поставленных целей обучения;
·формировать
мыслительные операции, такие как аналогия, классификация, обобщение и т.п.
1.1.3
Функции метода моделирования
В настоящее время учебное моделирование преимущественно
используются для достижения развивающих целей обучения, поскольку они являются
мощным инструментом формирования мышления, так как:
ü обладают большими потенциальными
возможностями для развития умственных операций;
ü формируют активность и целенаправленность
мышления;
ü развивают гибкость мышления;
ü формируют культуру логических
рассуждений.
Поскольку во всех работах, посвященных
привлечению учащихся к методу моделирования в процессе решения задач,
доказывается развитие умений и навыков моделирования (формируются умения
выдвигать гипотезу, выявлять существенные аспекты исследуемой ситуации и т.д.),
то развивающая функция моделирования очевидна.
Кроме того, учебное моделирование помогает
достижению познавательного отношения к действительности, в силу того, что оно
формируют широту кругозора и являются стимулом познавательного интереса,
способствуют воспитанию научного мировоззрения, выполняя, таким образом,
воспитывающую функцию.
Наконец, нельзя не принять во внимание и тот
факт, что именно с помощью учебного моделирования можно осуществлять контроль
знаний основных разделов школьной математики и владение определенными методами
решений, уровень логического мышления и т.п.
К основным дидактическим функциям метода
моделирования мы относим следующие:
· функцию открытия новых (неизвестных
ученику) знаний (т.е. установление существенных свойств понятий; выявление
математических закономерностей; отыскание доказательства математического
утверждения и т.п.);
· функцию углубления изучаемых знаний
(т.е. получение определений, эквивалентных исходному; обобщение изученных
теорем; нахождение различных доказательств изученных теорем и т.п.);
· функцию систематизации изученных
знаний (т.е. установление отношений между понятиями; выявление взаимосвязей
между теоремами; структурирование учебного материала и т.п.);
· функцию развития учащегося,
превращение его из объекта обучения в субъект управления, формирование у него
самостоятельности к самоуправлению (самообразованию, самовоспитанию,
самореализации );
· функцию обучения учащихся способам
деятельности.
Таким образом, анализ этапов моделирования,
выделяемого разными авторами, позволяет сделать вывод, что обязательными из них
являются четыре, которые и образуют основную структуру учебного моделирования:
. постановка проблемы;
. выдвижение гипотезы;
. проверка гипотезы;
. вывод.
При более детальном анализе структуры учебного
моделирования можно выделить и такие его этапы, как:
ü мотивация учебной деятельности;
ü постановка проблемы моделирования;
ü анализ имеющейся информации по
рассматриваемому вопросу;
ü экспериментирование (проведение
измерений, испытаний, проб и т.д.) с целью получения фактического материала;
ü систематизация и анализ полученного
фактического материала; выдвижение гипотезы;
ü подтверждение или опровержение
гипотез;
ü доказательство гипотез.
Очевидно, что различные виды моделирований имеют
свои особенности, поэтому для каждого из них характерно свое сочетание
названных этапов.
При отборе и составлении задач необходимо
принимать во внимание следующие требования:
· при отборе и составлении задач
учитывать, что в процессе их решения будут использоваться все возможные
обобщения;
· решение задач будет направлено на
нахождение определенных зависимостей между величинами, вывод определенных
формул, которые можно использовать в дальнейшем;
· в процессе решения «частных» задач
возможность нахождения рационального способа решения;
· в процессе решения задач можно
создать условия для формирования способностей (компонентов) творческого
мышления.
Обучение математике обладает уникальными
возможностями в плане интеллектуального развития учащихся, в формировании
компонентов и качеств мышления, необходимых не только для продолжения
образования и освоения новых областей знаний, но и обеспечивающих успешность
профессиональной деятельности и полноценность повседневной жизни в современном
обществе. В первую очередь это развитие абстрактного и логического мышления,
воспитание алгоритмической культуры, и в то же время - приобретение опыта
творческой деятельности.
Овладение учащимися в процессе обучения
математике математическими методами мышления, включающими в себя все
способы научного познания - дедукцию и индукцию, обобщение, сравнение, аналогию
и т.п., способствует выработке у них математического стиля мышления, характеризуемого,
прежде всего, доказательностью, критичностью, независимостью логической схемы
рассуждения от его содержания, структурированностью рассуждений. Эти качества
мышления необходимы каждому человеку независимо от сферы его деятельности, но
именно обучение математике способно внести наибольший вклад в их развитие.
Еще более трехсот лет назад английский философ
Д. Локк писал, что математику следует изучать не столько для того, чтобы
сделаться математиками, сколько для того, чтобы стать разумными людьми. Этому
тезису созвучна современная расстановка акцентов в определении целей и задач
школьного математического образования: «Обучение математике в школе должно быть
ориентировано не столько на собственно математическое образование в
узком смысле слова, сколько на образование с помощью математики» (Г.В.
Дорофеев).
Развивающая функция обучения требует от учителя
не простого изложения знаний в определенной системе, а предполагает также учить
школьников мыслить, искать и находить ответы на поставленные вопросы, добывать новые
знания, опираясь на уже известные. Уместно в связи с этим привести слова
французского философа М. Монтеня: «Мозг хорошо устроенный стоит больше, чем
мозг хорошо наполненный».
Учебная дисциплина должна рассматриваться не как
предмет с набором готовых знаний, а как специфическая интеллектуальная
деятельность человека. Обучение же должно в разумной мере проходить в форме
повторного открытия, а не простой передачи суммы знаний. Учебную дисциплину
надо изучать не столько ради лишних фактов, сколько ради процесса их получения,
и тогда, по словам Б. Рассела, предмет предстанет как могучее орудие познания и
преобразования природы, а не как формальная схема, в которой «неизвестно, о чем
говорится».
Сейчас в школе обучение в значительной степени
строится по формуле:
«Усвоение = Понимание + Запоминание».
Но если мы хотим действительно еще и развивать
молодежь, то должны руководствоваться следующей формулой:
«Овладение =
Усвоение + Применение знаний на практике».
Познавательные процессы эффективно развиваются лишь
при такой организации обучения, при которой школьники включаются в активную по
исковую деятельность. Поиск нового составляет основу для развития воли
внимания, памяти, воображения и мышления.
Опыт многих учителей показывает, что эффективным
средством обучения методу моделирования, цель которого состоит в том, чтобы
помочь учащимся самостоятельно открыть новые знания и способы деятельности,
углубить и систематизировать изученное.
1.2
Решение задач с параметрами как способ обучения методу моделирования
.2.1
Развивающие функции задач в обучении
Под развивающими функциями задач следует
понимать те, которые направлены на развитие мышления учащихся (в частности, на
формирование у них качеств научно-теоретического мышления), на овладение ими
эффективными приемами умственной деятельности.
Некоторые педагоги считают, что математическое
развитие это нечто производное, нечто автоматически сопутствующее процессу
усвоения фактов и навыков в области математической науки. Пройдет человек через
какое-то количество формул, определений, теорем, решит определенное число задач
- вот он и приобретает необходимое развитие. Стоит уменьшить эту сумму знаний и
навыков, и прежнее развитие обеспечить уже нельзя.
Эта позиция считается принципиально ошибочной.
Конечно, ознакомление с математическими фактами, разбор и усвоение
математических теорем, выведение формул, решение значительного количества
упражнений развивают способности человека и. оказывают известное влияние на
развитие математического мышления учащихся. Однако только этими средствами
(особенно средствами традиционными, к которым многие школы привыкли) задача
математического развития и воспитания в той мере, в какой это требуется в
современных условиях, не может быть обеспечена.
К числу общих развивающих относятся функции задач,
направленные на формирование у учащихся умений использовать известные методы
научного познания как методы изучения (наблюдение, сравнение, опыт, анализ и
синтез, обобщение и специализацию, абстрагирование и конкретизацию); проводить
умозаключения индуктивного и дедуктивного характера (в частности, правильно
пользоваться аналогией и интуицией); правильно ставить мысленный и практический
эксперимент, высказывать гипотезы и проверять их; осуществлять простейшее
моделирование учебных ситуаций и использовать имеющиеся (или сконструированные)
модели для изучения свойств объектов (построение и использование графиков,
диаграмм, рисунков, схем и т.д.); выделять существенное классифицировать
изучаемые объекты, систематизировать имеющиеся знания, устанавливать причинно-следственные
и структурные связи между ними; осуществлять выбор средств и методов для
достижения поставленной цели, учитывая конкретные условия; усматривать связь
изучаемого материала с окружающей жизнью, с практической деятельностью людей,
оценивать практическую значимость изучаемого материала; проявлять логическую
грамотность и качества, присущие научному мышлению, и т.д.
К специальным развивающим функциям учебных
математических задач могут быть отнесены, например, функции, направленные на
формирование у учащихся следующих умений: автоматизировать простейшие ситуации
жизненного характера, усматривать математические закономерности в окружающем
мире; предсказывать (предполагать) с достаточной степенью правдоподобия
существование того или иного математического факта, свойства или отношения;
дедуктивно доказывать или опровергать то или иное математическое положение;
планировать поиск решения задачи, исключать из ее условия ненужные данные,
дополнять недостающие; отбирать методы, средства и операции, необходимые для ее
решения; осуществлять проверку правильности решения; формулировать определения
математических понятий; соотносить то или иное понятие с данным определением,
распознавать его среди других понятий, правильно проводить вычисления с
привлечением простейших вычислительных средств (для облегчения вычисления на
соответствующем этапе); создавать (на основе теоретических знаний) удобную
вычислительную ситуацию; осуществлять проверку и прикидку правильности
результата вычислений; проводить моделирование в простейших учебных ситуациях;
эффективно пользоваться математической символикой при записи математических
положений и решении задач, читать и понимать предложения, записанные
символически; иметь четкое представление о логической структуре курса математики,
о том, что абстрактный характер математики обуславливает ее прикладной характер
(возможность разнообразных приложений в других науках, технике, народном
хозяйстве) и т.д.
Понятно, что перечень конкретных развивающих
функций учебных математических задач слишком велик, чтобы быть
охарактеризованным частичным перечислением.
Ограничимся одним иллюстрированным примером.
Использование задач с целью формирования у
учащихся умения обобщать изученное - их общая развивающая функция; формирование
умений обобщать то или иное геометрическое понятие - специальная развивающая
функция; помочь учащимся усмотреть возможность обобщения понятий симметрии,
вращения и параллельного переноса в понятии «перемещение» - конкретная
развивающая функция задач.
1.2.2
Задачи как средство обучения методу моделирования учащихся
Обучение ученика методу моделирования - сложный
и многогранный процесс. Проблема формирования обучения методу моделирования
учащихся имеет богатую историю, но с момента появления в педагогике метода
моделирования проведение учебных исследований приходилось в основном на
естественнонаучную и гуманитарную области. Выделялись основные черты метода:
соответствие научному методу (в основном методу научной индукции),
самостоятельность и активность обучающихся. Следует отметить, что
самостоятельность учащихся в методе моделирования понималась как относительная,
поскольку учащиеся открывали уже открытые истины и их «исследовательская»
работа должна была проходить под руководством и при помощи учителя.
На современном этапе развития педагогической и
методической науки непосредственно проблемой обучения методу моделирования и
формированием ее элементов в процессе обучения математике занимались И.И.
Баврин, В.А. Викол, В.А. Гусев, И.В. Дробышева, Ю.М. Колягин, В.И. Крупич, В.Л.
Матросов, Ф.Ф. Нагибин, Р.С. Черкасов, Г.Б. Лудина, Г.В. Токмазов, В.В.
Успенский, А.Я .Цукарь и др.
В научной литературе очень часто метод
моделирования рассматривается в широком смысле слова, как научный труд, что в
общеобразовательной школе не применимо из-за сложности процесса научного
поиска, необходимо адаптировать его к возрастным особенностям учащихся.
Безусловно, что в процессе обучения учащихся математике можно сформировать лишь
некоторые элементы научного поиска, например, проблемное видение и постановка
проблемы, построение или выдвижение гипотез и др. Для формирования обучения
методу моделирования лучше всего подходят учащиеся 7 - 9 классов, так как
именно в этом возрасте формируются все основные качества личности, а в смысле
умственного развития учащихся происходит основной пик развития интеллекта. Как
бы то ни было, но этот возраст действительно есть основа формирования мотивов
учения (интереса), период определения будущего пути, выявление интересов и
склонностей. Это заставляет особенно ответственно относиться к учащимся этого
возраста.
При этом обучение методу моделирования учащихся
должно осуществляться в разном объеме, в разных временных рамках, в сочетании с
другими видами деятельности, на разных уровнях и ступенях обучения.
Формирование опыта моделирования в процессе обучения математике у учащихся 7 -
9 классов включает в себя как формирование определенных специальных умений,
например, видение новой проблемы в знакомой ситуации, видение альтернативы
решения, так и овладение основными ее элементами.
Формирование опыта моделирования в процессе
обучения математике осуществляется посредством решения задач. В
психолого-педагогической литературе встречаются следующие термины: «поисковая
задача», «творческая задача», «исследовательская задача» и «познавательная
задача» (В.А. Гусев, Ю.М. Колягин, В.И. Крупич, А.А. Кирсанов, М.П. Пальянов,
В.В. Успенский и др.). Во всех рассмотренных определениях прослеживается
направленность исследовательских задач на самостоятельное формулирование
проблемы и ее разрешение. Систематическое включение исследовательских задач в
процесс обучения математике позволяет целенаправленно формировать опыт
моделирования у учащихся, при этом в большой степени следует использовать
потенциал школьных учебников и задачников по математике.
Основываясь на классификации математических
задач, данной в методической литературе, выделим два вида задач: задачи
исследовательского характера и исследовательские задачи и будем понимать под
ними задачи, направленные на формирование видов моделирования и соответствующих
им умений. К задачам исследовательского характера отнесем задачи на выявление и
формулировку определенных закономерностей, задачи, предполагающие
самостоятельную формулировку вопроса по данному условию, задачи на
существование того или иного математического объекта. К исследовательским
задачам отнесем задачи, предполагающие различные способы решения,
параметрические задачи, задачи на исследование геометрического объекта с целью
установления его характерных признаков. Таким образом, выделим шесть типов
задач:
1)задачи,
не содержащие требования;
2)задачи
на установление истинности высказывания;
3)задачи,
решаемые различными способами;
4)задачи
с измененными условиями;
5)задачи,
обратные данным;
6)задачи
с параметрами.
Нас, конечно, интересуют задачи шестого типа.
Они ставят учащихся на позицию исследователя, так как позволяют учащимся
рассмотреть проблему с разных точек зрения, дать полное и исчерпывающее ее
решение. Формировать такой подход к решению задач можно на примерах обобщенных
задач, которые позволяют рассмотреть все возможные дающие разные решения
случаи.
Таким образом, в математике включение учащихся в
определенный вид деятельности происходит посредством решения ими конкретного
класса задач. Средством формирования опыта моделирования могут служить и задачи
с параметрами. Овладение опытом такой деятельности как требует от учащихся, так
и формирует у них способности к самостоятельному осмыслению и поиску решения
задач. Как нетрудно заметить, эти два процесса взаимосвязаны.
1.2.3
Методы решения задач с параметрами
.2.3.1
Образовательная значимость задач с параметрами
Задачи с параметрами в настоящее время включены
в программу большинства подготовительных факультативов, а также ряда базовых
курсов алгебры и начал анализа в связи с потребностью подготовки учащихся к
сдаче вступительных и единых экзаменов.
Однако значимость заданий этого типа не
ограничивается лишь их диагностической ценностью, так как деятельность по их
решению способствует повышению качества знаний и умений учащихся,
интеллектуальному развитию, а также позволяет формировать у них представления
об особенностях метода моделирования математиков.
К постановке задач с параметрами приводят,
например, следующие исследовательские задачи:
· выявление условий разрешимости тех
или иных математических задач;
· вывод общей вычислительной формулы и
определение границ её применимости;
· изучение условий сохранения и
степени варьирования свойств математических объектов;
· установление границ влияния
характеристик реального объекта на тот или иной, с ним связанный, процесс,
изучаемый с помощью метода математического моделирования и т.д.
С многими из этих исследовательских задач
учащиеся сталкивались в процессе доказательства теорем школьного курса
математики. Так, например, вывод формулы корней уравнения cost=а представляет
собой типичную задачу на поиск решения уравнения в зависимости от значений
параметра а.
С задачами исследования решений относительно
параметра учащиеся встречаются и в процессе решения текстовых и геометрических
задач, содержащих буквенные данные. Приведем в качестве примера две из них.
Задача 1.
Выяснить, сколько решений может иметь задача на построение треугольника,
заданного углом а, прилежащей к нему стороной, имеющей длину 4 см, и разностью
двух других сторон - 2 см.
Задача 2.
Требуется получить переливанием 15% - й раствор кислоты. Для этого у нас есть
два сосуда с кислотой, каждый из которых имеет емкость три литра. В первом
сосуде находится два литра 5% -го раствора кислоты. Во втором сосуде находится
два литра r%-го раствора этой же кислоты. Необходимо выяснить, при каких
значениях г, переливая раствор из второго сосуда в первый, можно добиться
желаемого результата.
С задачами с параметром учащиеся встречаются и
при изучении курса физики. Например, им может быть предложена следующая
физическая задача.
Задача 3.
Какой силы броска «от груди» (высота ≈ 1,5м) необходимо добиться
баскетболисту, чтобы попасть мячом в корзину, расположенную на высоте 3,05 м с
расстояния 6,25 м (трехочковый бросок)?
Приведенные нами примеры доказывают, что
уравнения и неравенства с параметром вовсе не являются «хитроумной выдумкой
экзаменаторов», а имеют реальное внутри математическое и прикладное значения.
Таким образом, задачи с параметром являются ценнейшим средством развития способности
учащихся к осуществлению математической деятельности.
Доказав образовательную значимость этих задач,
остановимся теперь на причинах сложности обучения их решению в школе.
1.2.3.2
Причины сложности обучения решению задач с параметрами в школе и пути их
преодоления
Основными причинами здесь, конечно, являются
трудности, определяемые спецификой самой деятельности по решению этих задач: ее
не алгоритмичность, необходимость комплексного использования знаний и умений,
переноса их в новые условия. Значительную роль также играет недостаточная
разработанность методики введения относящихся к этим задачам теоретических
вопросов, и как следствие, апеллирование преподавателей к чувственной основе
действий, которое выражается, например, в предложениях: «представьте, что
параметр - это конкретное число, но не забывайте, что он является переменной»,
«иногда удобно посмотреть на уравнение с параметром как на функцию», «для
решения задачи надо выделить контрольные значения параметра такие, чтобы на
полученных промежутках решение уравнения (неравенства) подчинялось одному
алгоритму, однако найти их сразу нельзя» и т.п.
Еще одной причиной является низкая эффективность
методики обучения, основанной на группировке упражнений по видам выражений
(линейные, квадратные, целые, рациональные, дробно-рациональные,
иррациональные, тригонометрические, логарифмические, показательные ), так как в
данном случае стратегия решения слабо определяется видом выражения. Например,
изменяя лишь положение параметра в структуре линейного уравнения, мы приходим к
трем различным стратегиям его решения («последовательное преобразование»,
«исследование на промежутках», «разложение на множители»).
1. 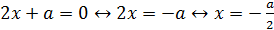
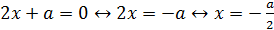 при любых
при любых 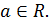
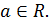
. 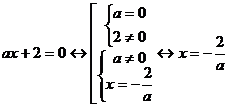
. 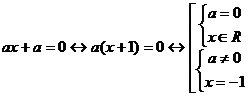
Предлагаемая методика предполагает другой способ
планирования содержания обучения, а именно по видам требований задач с параметром,
так как различие между переменными (неизвестным и параметром), а следовательно
и специфика задач проявляются лишь относительно заданной цели деятельности. Это
дает следующую последовательность изучения уравнений и неравенств с параметром.
Таблица №1
|
Тема
|
Основное
содержание
|
|
Уравнения
и неравенства с параметром: основные понятия
|
Уравнение
(неравенство) с двумя переменными, связь переменных, неизвестная и параметр,
уравнение (неравенство) с параметром, область допустимых значений, область
допустимых значений параметра, область возможных значений неизвестной,
решение (а;х), корень х(а), виды задач.
|
|
Задачи
на нахождение множества корней уравнения (неравенства) зависимости от
параметра
|
Критерии
успешности решения, формула зависимости x(a), контрольные
значения параметра, условия выделения контрольных значений параметра, их
связь с видом выражений
|
|
Задачи
на нахождение значений параметра, удовлетворяющих условиям, на множество
корней
|
Критерии
успешности решения, виды условий, накладываемых на корни уравнения
(неравенства), их роль в определении стратегии решения; приемы решения, их
связь с видом выражений
|
|
Задачи,
сводящиеся к решению уравнений и неравенств с параметром
|
Решение
сюжетных, прикладных геометрических задач, на исследование свойств функции,
сводящихся к уравнениям и неравенствам
|
Необходимо отметить, что традиционная схема
обучения состоит в информированности учащихся об особенностях решения задач и
организации деятельности по использованию этой информации. Однако в случае
задач с параметром специфической является лишь информация методологического
характера (о критериях успешности, приемах решения, условиях выделения
контрольных значений и т.п.), а теоретическая информация и терминология,
введенная для уравнений и неравенств с одной переменной, распространяется без
каких-либо существенных изменений. Поэтому здесь предпочтительней иной путь
организации обучения, основанный не на усвоении готовой информации, а на
рефлексивном анализе собственных затруднений и успехов в решении задач. Этот путь
определяется спецификой природы методологического знания, которое относится к
знанию рефлексивного типа (источником является не восприятие внешней
действительности, а осознание внутреннего «Я»).
К категории рефлексивной деятельности психологи
и педагоги обратились сравнительно недавно в связи с задачами гуманизации и
гуманитаризации образования, усиления его развивающей функции.
Психологами И.Н. Семеновым и С.Ю. Степановым
было доказано, что в мышлении можно выделить несколько иерархических уровней,
наивысшими из которых являются уровни интеллектуальной и личностной рефлексии.
Рефлексия выполняет регулирующую функцию в мышлении (планирует деятельность,
контролирует осуществление программы, производит диагностику затруднений,
корректировку образов и про грамм), а также интегрирующую функцию -
способствует выявлению и обобщению знаний, содержащихся в опыте. Именно вторая
функция рефлексии делает эту деятельность образовательно-значимой
Рефлексивные механизмы активизируются лишь в
случаях появления интеллектуальных затруднений, поэтому включение учащихся в
рефлексивную деятельность должно начинаться с подведения их к осознанию
проблемы. Реализацию этого положения предлагается осуществлять по следующей
схеме.
. Учитель ставит перед учащимися проблемную
ситуацию, связанную с анализом их деятельности или оценкой результатов
деятельности учителя.
. Учитель обсуждает с учащимися параметры
анализа, демонстрирует спектр возможных направлений осуществления действий,
критерии их
оценки.
. Учитель предоставляет учащимся возможность
самостоятельного принятия решений.
1.2.3.3
Основные понятия уравнений с параметрами, общая схема решения уравнений F(а;
х)=0
Начиная с шестидесятых годов в содержание
вступительных экзаменов в вузы включаются уравнения и неравенства с параметрами,
а ныне уже выдвигается идея внедрения линии параметров в содержание школьного
курса математики. Основанием для её реализации являются разработка системы
понятий и поиск методов решения уравнений и неравенств с параметрами данного
вида (линейных, рациональных и т.д.).
Для каждого вида уравнений школьного курса
математики установим общий метод решения соответствующих уравнений с
параметрами - единый как для одного, так и для двух параметров. Метод решения
всякого уравнения с параметрами данного вида, в свою очередь, выведем из
обобщенной схемы решения произвольных уравнений F(a;х)=0 или F(a;b;х)=0
соответственно с одним или двумя параметрами.
Основные понятия уравнений с
параметрами. В уравнении F(x;у)=0 с двумя переменными х и у
фиксированному значению х=ао соответствует частное уравнение F(ao;у)
=0 с переменной у. Если b1,
b2,
…, bk
-
все решения частного уравнения F(ao;у) = о, то (ао;b1),
(ао;b2),
...
, (ао;bk) - все решения уравнения F(x; у)=0 с первой координатой,
равной ао. Изменяя значения х=ai и решая соответствующие
частные уравнения F(ai;у)=0, получим другие решения исходного уравнения F(x;у)=0.
Поставим следующую задачу: для каждого значения х=а,
решить соответствующее частное уравнение F(ai;у)=0 с переменной у.
При такой постановке переменная х называется параметром, совокупность
всех частных уравнений представлена в общей форме F(a;у)=0, где а-произвольное
фиксированное значение переменной х.
Ясно, что переход от уравнения F(x;у)=0 к
уравнению F(a;у)=0 есть способ указания всех решений в зависимости от
значений первых координат. Аналогично поиск всех решений уравнения F(x;y)=0
в зависимости от фиксированных значений вторых координат у=bi приводит
к уравнению F(x;b)=0
с параметром b
и
переменной х. Например, уравнение с двумя переменными
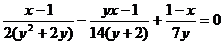
может рассматриваться: как линейное
уравнение
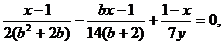
и как рациональное уравнение
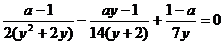
Подобным образом уравнение F(a;b;х)=0 называется
уравнением с параметрами а,b и переменной
х, если для каждой упорядоченной пары значений переменных а и b
необходимо решить соответствующее частное уравнение относительно переменой х.
Так, уравнение
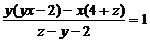
удобнее всего рассматривать как
линейное уравнение
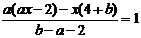
параметрами а и b и переменной
х, т.е. как совокупность частных уравнений первой степени для конкретных
значений а и b.
в уравнении Р(а;х)=0 частные
уравнения F(ai;х)=0 могут быть определены не для всех значений
параметра. Например, в уравнении 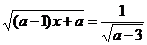 частные уравнения не определены для
частные уравнения не определены для
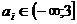 будем
записывать кратко:
будем
записывать кратко: 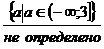 ). и
). и 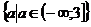 - область
допустимых значений параметра. В общем случае область допустимых значений
параметра уравнения Р(а ;х)=0 есть множество всех значений параметра,
для которых частные уравнения определены.
- область
допустимых значений параметра. В общем случае область допустимых значений
параметра уравнения Р(а ;х)=0 есть множество всех значений параметра,
для которых частные уравнения определены.
В уравнении с параметром возможны
ограничения как на множество значений параметра, так и на множество значений
переменной. В качестве примера опять приведем уравнение 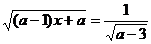 , где для
допустимого значения параметра
, где для
допустимого значения параметра 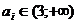 область определения частного
уравнения имеет вид
область определения частного
уравнения имеет вид 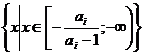 в связи с
этим имеет смысл говорить об области определения уравнения F(а;x)=0 как о
множестве всех упорядоченных пар (ai;х), где а=а, принадлежит
области допустимых значений параметра, a x принадлежит
области определения соответствующего частного уравнения F(ai;х)=0. В
данном случае область определения имеет вид
в связи с
этим имеет смысл говорить об области определения уравнения F(а;x)=0 как о
множестве всех упорядоченных пар (ai;х), где а=а, принадлежит
области допустимых значений параметра, a x принадлежит
области определения соответствующего частного уравнения F(ai;х)=0. В
данном случае область определения имеет вид 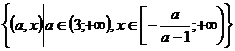 .
.
Итак, уравнение Р(а;х)=0 есть бесконечная
совокупность частных уравнений F(ai;х)=0 для допустимых значений
параметра а=ai.
Его
решение осуществляется в два этапа:
1. разбиение совокупности всех частных
уравнений на непересекающиеся типы;
. поиск общих решений частных уравнений
каждого типа. В процессе разбиения частных уравнений выделяются:
· совокупность особых частных
уравнений типа Ø - все
ложные числовые равенства;
· совокупность особых частных
уравнений типа ∞ - все истинные числовые равенства;
· тип не особых частных уравнений, не
имеющих решений;
· типы (один или несколько) частных
уравнений с одинаковыми общими решениями.
Пример 1. В
линейном уравнении 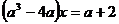 значению а=0
и а=2 соответствуют особые частные уравнения типа Ø, для а=-2
частное уравнение
значению а=0
и а=2 соответствуют особые частные уравнения типа Ø, для а=-2
частное уравнение 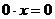 является
особым типа ∞. Значениям параметра из множества
является
особым типа ∞. Значениям параметра из множества 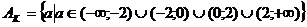 соответствует
тип не особых частных уравнений с общим решением
соответствует
тип не особых частных уравнений с общим решением 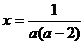 .
.
В результате получаем ответ, который
запишем компактно следующим образом:
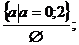
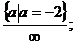
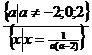
Пример 2. В
линейном уравнении 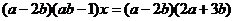 всем точкам
прямой
всем точкам
прямой 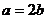 соответствуют
частные уравнения
соответствуют
частные уравнения 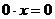 типа ∞,
точкам гиперболы
типа ∞,
точкам гиперболы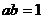 , отличным
то точек прямой
, отличным
то точек прямой 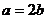 ,соответствует
тип Ø
особых
частных уравнений
,соответствует
тип Ø
особых
частных уравнений 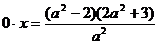 с отличной
от нуля правой частью (рис.1).
с отличной
от нуля правой частью (рис.1).
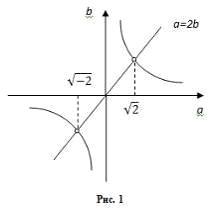
Для остальных точек плоскости Оаb соответствующие
частные уравнения имеют единственное решение, вычисляемое по формуле 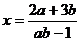 .
.
Итак:
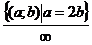 ;
; 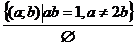 ;
; 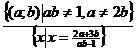
Пример 3. В
квадратном уравнении 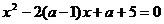 ни одно из
частных уравнений не является особым типа Ø или типа ∞.
Дискриминант
ни одно из
частных уравнений не является особым типа Ø или типа ∞.
Дискриминант 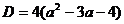 обращается в
нуль для значений а=-1 и а=4, причем D<0 для
обращается в
нуль для значений а=-1 и а=4, причем D<0 для 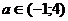 и D>0
для
и D>0
для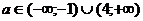 . Тогда
совокупность всех частных уравнений разбивается на три типа:
. Тогда
совокупность всех частных уравнений разбивается на три типа:
· тип J не особых частных уравнений, не имеющих
решений в множестве всех действительных чисел и соответствующих значениям
параметра 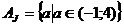 ;
;
· тип К не особых частных уравнений, имеющих
двукратные корни вида  и
соответствующих множеству
и
соответствующих множеству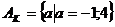 ;
;
· тип L не особых частных уравнений, имеющих
различные общие решения 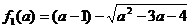 и
и 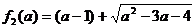 на
множестве
на
множестве 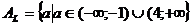
Ответ:  ;
; 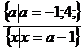 ;
; 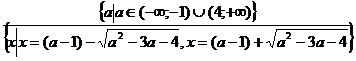
Обратим внимание на два факта:
разбиение частных уравнений на типы
осуществляется выделением областей однотипности во множестве допустимых
значений параметров. В уравнениях с одним параметром выделение областей
проводится некоторыми точками - контрольными значениями параметра (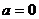 и
и 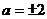 в первом
примере,
в первом
примере, 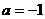 и
и 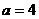 в третьем).
В уравнениях с двумя параметрами области однотипности выделяются линиями
контрольных значений параметров (
в третьем).
В уравнениях с двумя параметрами области однотипности выделяются линиями
контрольных значений параметров (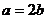 и
и 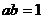 во втором
примере).
во втором
примере).
для типов не особых частных
уравнений находятся общие решения - определенные функции, зависящие от
параметров. При этом тип частных уравнений характеризуется либо одним общим
решением, либо несколькими.
Определение. В уравнении F(а;х)=0 с
параметром а и переменной х функция х=f(а) называется
общим решением на множестве Af значений
параметра, если для любого 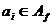 значение х = f(ai) является
решением частного уравнения F(ai;х)=0.
значение х = f(ai) является
решением частного уравнения F(ai;х)=0.
В определении важен не только вид
функции х = f(a), но и множество Af
соответствующих значений параметра. Для уравнения 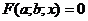 с двумя
параметрами в качестве общих решений выступают функции
с двумя
параметрами в качестве общих решений выступают функции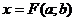 на множестве
на множестве
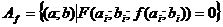 .
.
Рассмотрим способ классификации
частных уравнений с помощью модели общих решений.
Пример 4. В
рациональном уравнении 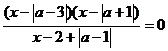
Функция 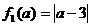 является
общим решением для тех значений параметра, для которых
является
общим решением для тех значений параметра, для которых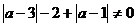 . Поскольку
. Поскольку
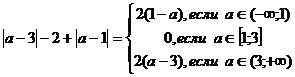
то 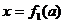 - общее решение уравнения на
- общее решение уравнения на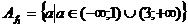 .
.
Функция 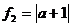 есть общее
решение уравнения на множестве на
есть общее
решение уравнения на множестве на 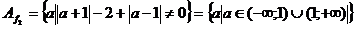 .
.
Построим модель общих решений в
следующем виде(Рис. №2):
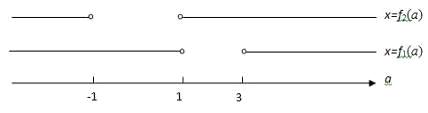
Рис. 2
На модели выделяем все типы частных
уравнений:
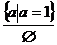 ;
; 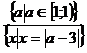 ;
; 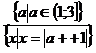 ;
; 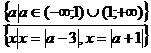
Итак, на простых примерах
рассмотрены основные понятия уравнений с параметрами: область допустимых
значений, область определения, общие решения, контрольные значения параметров,
типы частных уравнений. Способы их нахождения будут устанавливаться в каждом
виде уравнений отдельно.
На базе введенных понятий определим
общую схему решения всякого уравнения F(а;х)=0 с
параметром а (для случая двух параметров схема аналогична) :
· устанавливаются область допустимых
значений параметра и область определения;
· определяются контрольные значения
параметра, разбивающие область допустимых значений параметра на области
однотипности частных уравнений;
· для контрольных значений параметра
соответствующие частные уравнения исследуются отдельно;
· находятся общие решения 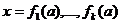 уравнения F(а; х) =0 на
соответствующих множествах
уравнения F(а; х) =0 на
соответствующих множествах 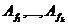 значений параметра:
значений параметра:
· составляется модель общих решений, контрольных
значений параметра в следующем виде (Рис. №3):
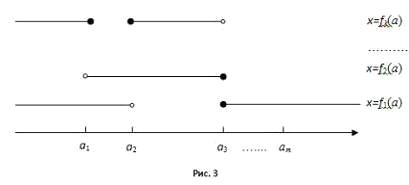
· на модели выделяются промежутки
значений параметра с одинаковыми общими решениями (области однотипности);
· для контрольных значений параметра и
выделенных областей
· однотипности записываются
характеристики всех типов частных уравнений.
1.2.3.4 Общая схема решения линейных
уравнений с параметром вида 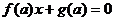
В линейном уравнении 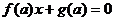 с параметром
а и переменной х всякое частное уравнение принадлежит одному из
следующих типов:
с параметром
а и переменной х всякое частное уравнение принадлежит одному из
следующих типов:
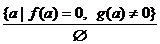 ;
; 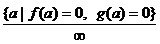 ;
; 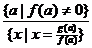 .
.
Приведенная классификация позволяет
определить общую схему решения.
. На числовой прямой отмечаются все
значения параметра, для которых соответствующие частные уравнения не
определены.
. На области допустимых значений
параметра исходное уравнение при
помощи равносильных преобразований приводится к виду 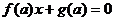 .
.
. Определяются контрольные значения
параметра, для которых 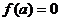 . В
множестве таких значений выделяются подмножества
. В
множестве таких значений выделяются подмножества 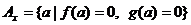 и
и  . Значениям параметра из
. Значениям параметра из 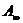 соответствуют
особые частные уравнения типа ∞. Значениям параметра из А0 соответствуют
особые частные уравнения типа
соответствуют
особые частные уравнения типа ∞. Значениям параметра из А0 соответствуют
особые частные уравнения типа 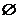 .
.
. Для значений параметра из
множества 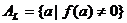 соответствующие
частные уравнения принадлежат типу L с общим решением
соответствующие
частные уравнения принадлежат типу L с общим решением 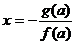 .
.
Заметим, что если уравнение 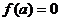 имеет
конечное множество решений
имеет
конечное множество решений 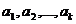 , то для каждого из найденных
контрольных значений параметра соответствующие частные уравнения решаются
отдельно. В случае, когда множеством решений уравнения
, то для каждого из найденных
контрольных значений параметра соответствующие частные уравнения решаются
отдельно. В случае, когда множеством решений уравнения 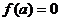 является числовой
промежуток, удобнее найти также множество решений уравнения
является числовой
промежуток, удобнее найти также множество решений уравнения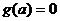 ,
пересечению найденных множеств решений соответствуют особые частные уравнения
типа ∞.
,
пересечению найденных множеств решений соответствуют особые частные уравнения
типа ∞.
1.2.3.5
Решение уравнений с параметрами не выше второй степени
Уравнения с параметрами не выше
второй степени являются самыми распространенными в практике итоговых и
конкурсных заданий. Их общий вид определяется многочленом 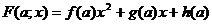 с параметром
а или многочленом
с параметром
а или многочленом 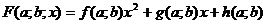 с
параметрами а и b не выше
второй степени.
с
параметрами а и b не выше
второй степени.
Отметим, что наиболее важными в
практике являются следующие задачи:
· решить уравнение (неравенство) с
параметрами;
· найти значение параметров, при
которых общее решение уравнения (неравенства) обладает некоторыми свойствами.
В уравнении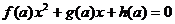 не выше
второй степени с параметром а и переменной x всякое
частное уравнение принадлежит одному из следующих типов:
не выше
второй степени с параметром а и переменной x всякое
частное уравнение принадлежит одному из следующих типов:
) 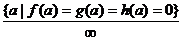 ;
;
) 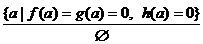 ;
;
) 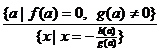 ;
;
) 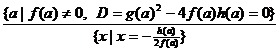 ;
;
) 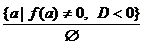 ;
;
) 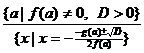
Контрольные значения параметра
определяются уравнением 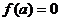 и уравнением
и уравнением
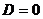 . На
выделенных контрольными значениями промежутках допустимых значений параметра
дискриминант D имеет определенный знак, соответствующие частные
уравнения принадлежат одному из двух последних типов.
. На
выделенных контрольными значениями промежутках допустимых значений параметра
дискриминант D имеет определенный знак, соответствующие частные
уравнения принадлежат одному из двух последних типов.
Тогда решение всякого уравнения с параметром не
выше второй степени осуществляется по следующим этапам.
. На числовой прямой отмечаются все
контрольные значения параметра, для которых соответствующие частные уравнения
не определены.
2. На области допустимых
значений параметра исходное уравнение при помощи равносильных преобразований
приводится к виду 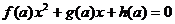
. Выделяется множество
контрольных значений параметра, для которых 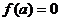 .
.
Если уравнение 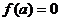 имеет
конечное множество решений, то для каждого найденного контрольного значения
параметра соответствующее частное уравнение решается отдельно. Проводится
классификация частных уравнений по первым трем типам.
имеет
конечное множество решений, то для каждого найденного контрольного значения
параметра соответствующее частное уравнение решается отдельно. Проводится
классификация частных уравнений по первым трем типам.
На бесконечном множестве решений
уравнения 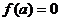 проводится
решение уравнения
проводится
решение уравнения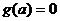 , выделяются
типы
, выделяются
типы 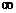 и
и 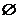 особых
частных уравнений. Множеству
особых
частных уравнений. Множеству 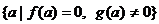 Соответствует тип 3) не особых
частных уравнений.
Соответствует тип 3) не особых
частных уравнений.
. Выделяются контрольные
значения параметра, для которых 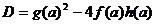 обращается в нуль. Соответствующие
не особые частные уравнения имеют двукратный корень
обращается в нуль. Соответствующие
не особые частные уравнения имеют двукратный корень 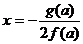 .
.
. Найденные контрольные
значения параметра разбивают область допустимых значений параметра на
промежутки. На каждом из промежутков определяется знак дискриминанта D.
Множеству 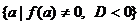 соответствует
тип не особых частных уравнений, не имеющих решений, для значений параметра
соответствует
тип не особых частных уравнений, не имеющих решений, для значений параметра 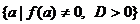 частные
уравнения имеют два различных действительных корня.
частные
уравнения имеют два различных действительных корня.
Рассмотрим пример: Решить
уравнение
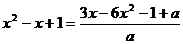 .
.
Решение. В уравнении значение 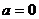 является
контрольным, для него соответствующее частное уравнение не определено.
является
контрольным, для него соответствующее частное уравнение не определено.
На множестве 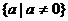 исходное
уравнение равносильно
исходное
уравнение равносильно 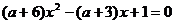
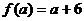 обращается в нуль для
обращается в нуль для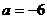 .
Соответствующее частное уравнение
.
Соответствующее частное уравнение 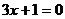 имеет единственное решение
имеет единственное решение 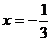 .
.
На множестве 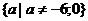 частные
уравнения являются квадратными с дискриминантом
частные
уравнения являются квадратными с дискриминантом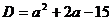 . Дискриминант
. Дискриминант 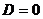 для
для 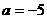 и
и 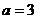
Пусть 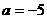 , соответствующее частное уравнение
, соответствующее частное уравнение 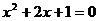 имеет
двукратный корень
имеет
двукратный корень 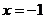 . Для
. Для 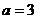 соответствующее
частное уравнение
соответствующее
частное уравнение 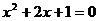 имеет
двукратный корень
имеет
двукратный корень 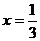 .
.
На числовой прямой отметим найденные
значения параметра и на каждом из полученных промежутков установим знак
дискриминанта(Рис. №4).

Рис. 4
моделирование обучение задача
параметр
Если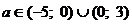 , то соответствующие частные
уравнения не имеют решений. Для значений параметров из
, то соответствующие частные
уравнения не имеют решений. Для значений параметров из 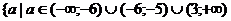 частные
уравнения имеют два различных корня, их общие решения
частные
уравнения имеют два различных корня, их общие решения 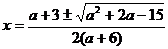 .
.
Ответ: 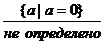 ;
; 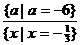 ;
;  ;
; 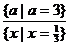 ;
; 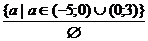 ;
; 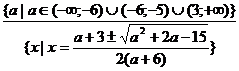 [28, с. 34-
35].
[28, с. 34-
35].
В уравнении 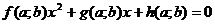 не выше
второй степени с параметрами
не выше
второй степени с параметрами 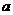 и
и 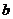 и переменной
и переменной 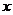 всякое
частное уравнение принадлежит одному из выше перечисленных типов с аналогичными
характеристиками. Контрольные значения параметров определяются уравнениями
всякое
частное уравнение принадлежит одному из выше перечисленных типов с аналогичными
характеристиками. Контрольные значения параметров определяются уравнениями 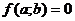 и
и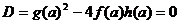 . В
плоскости
. В
плоскости 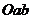 эти
уравнения выделяют области, на которых дискриминант D имеет определенный
знак. Тогда общая схема решения уравнений с двумя параметрами не меняется, лишь
вместо числовой прямой используется координатная плоскость
эти
уравнения выделяют области, на которых дискриминант D имеет определенный
знак. Тогда общая схема решения уравнений с двумя параметрами не меняется, лишь
вместо числовой прямой используется координатная плоскость 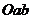 . Графическое
изображение линий контрольных значений параметров и выделенных ими областей
однотипности обеспечивает наглядность в выполнении каждого из этапов решения.
. Графическое
изображение линий контрольных значений параметров и выделенных ими областей
однотипности обеспечивает наглядность в выполнении каждого из этапов решения.
1.2.3.6
Интеграция алгебраического и геометрического методов при решении уравнений с
параметром
История математики свидетельствует о том, что
оба метода, алгебраический и геометрический, развивались в тесной взаимосвязи.
Первые элементы алгебры появились сразу в двух равноправно существующих
интерпретациях: геометрической и буквенно-символической. Именно благодаря взаимосвязи
алгебраического и геометрического методов были сделаны многие открытия в
математике.
В целом, как отмечал А.Д. Александров, «почти
всю математику можно рассматривать как развивающуюся из взаимодействия алгебры
(первоначально арифметики) и геометрии, а в смысле метода - из сочетания
выкладок и геометрических представлений». Именно эта взаимосвязь и должна
находить отражение в школьном курсе математики, показывая учащимся процесс
становления математического знания, делая их реальными участниками математических
«открытий».
Проиллюстрируем интеграцию алгебраического и
геометрического методов на примере решения уравнения с параметром.
Пример. При
каких значениях параметра а уравнение
Решение.
1. Алгебраический метод.
Разобьем всю числовую ось на три
участка (Рис. №5):
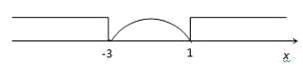
Рис. 5
Если 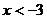 , то получаем:
, то получаем:
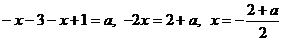 .
.
Уравнение будет иметь решения, если
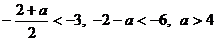 .
.
При 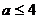 уравнение не будет иметь решений.
уравнение не будет иметь решений.
Если 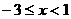 , то имеем:
, то имеем:
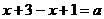 , откуда
, откуда 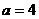 .
.
Уравнение имеет бесчисленное
множество решений при 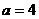 , в случае,
если
, в случае,
если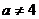 , не имеет
решений.
, не имеет
решений.
Если  , то имеем:
, то имеем:
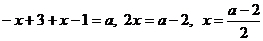 .
.
Уравнение имеет решения, если 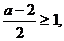 откуда
откуда 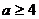 . При
. При 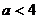 уравнение
не имеет решений.
уравнение
не имеет решений.
Ответ: при 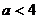 уравнение не
имеет решений; при
уравнение не
имеет решений; при 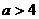 уравнение
имеет два решения; при
уравнение
имеет два решения; при 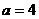 уравнение
имеет бесчисленное множество решений; одно решение уравнение не может иметь ни
при каком значении а.
уравнение
имеет бесчисленное множество решений; одно решение уравнение не может иметь ни
при каком значении а.
. Геометрический метод.
На геометрическом языке уравнение 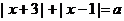 означает,
что надо найти такую точку
означает,
что надо найти такую точку 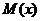 ,сумма расстояний от которой до
точек
,сумма расстояний от которой до
точек 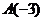 и
и 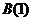 равна а.
На рис 1. Видно, что АВ=4, поэтому:
равна а.
На рис 1. Видно, что АВ=4, поэтому:
Если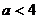 , то такой точки
, то такой точки 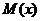 , сумма
расстояний от которой до точек
, сумма
расстояний от которой до точек 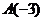 и
и 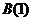 равна а, не существует, так
как для точек на отрезке АВ сумма расстояний до точек А и В равна 4, а для
точек, лежащих вне отрезка АВ, сумма расстояний больше 4. Значит, при
равна а, не существует, так
как для точек на отрезке АВ сумма расстояний до точек А и В равна 4, а для
точек, лежащих вне отрезка АВ, сумма расстояний больше 4. Значит, при 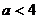 уравнение не
имеет решений.
уравнение не
имеет решений.

Рис. 6
Если 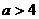 , то всегда существуют две точки
, то всегда существуют две точки 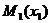 и
и 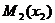 лежащие вне
отрезка АВ и симметричные относительно него, сумма расстояний от каждой из
которых до точек А и В равна а. И значит, уравнение имеет два решения.
лежащие вне
отрезка АВ и симметричные относительно него, сумма расстояний от каждой из
которых до точек А и В равна а. И значит, уравнение имеет два решения.
Если 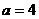 , то существует бесконечно много
точек
, то существует бесконечно много
точек 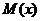 , сумма
расстояний от которых до точек А и В равна 4 (все они расположены на отрезке
АВ). Значит, в этом случае уравнение имеет бесчисленное множество решений.
, сумма
расстояний от которых до точек А и В равна 4 (все они расположены на отрезке
АВ). Значит, в этом случае уравнение имеет бесчисленное множество решений.
Кроме того, не существует одной
точки, сумма расстояний от которой до точек А и В равна а. Так как, если
есть одна точка, то найдется всегда и ей симметричная относительно отрезка АВ.
Следовательно, уравнение не может иметь одного решения ни при каком значении а.
В итоге ответ получаем такой же, как
и в случае алгебраического метода.
Выводы
по первой главе
Учебное моделирование, в отличие от научного,
имеет несколько целей, главной из которых является обучение учащихся самому
методу моделирования, методам научного познания, способам мыслительной
деятельности, развитию интуиции и творческих способностей.
Характерные признаки учебного моделирования:
) учебное моделирование - это процесс поисковой
познавательной деятельности (изучение, выявление, установление чего-либо и
т.д.);
) учебное моделирование всегда направлено на
получение новых знаний, то есть моделирование всегда начинается с потребности
узнать что-либо новое;
) учебное моделирование предполагает
самостоятельность учащихся при выполнении задания;
) учебное моделирование должно быть направлено
на реализацию дидактических целей обучения.
Под методом моделирования понимается учебная
деятельность по приобретению практических и теоретических знаний с
преимущественно самостоятельным применением научных методов познания, что
является условием и средством развития у обучающихся творческих умений
моделирования.
Структуру метода моделирования определяют
следующие компоненты: учебно-исследовательская задача, учебно-исследовательские
действия и операции, действия контроля и оценки.
Приобщение обучающихся к методу моделирования
можно реализовать через решение специальных исследовательских задач или через дополнительную
работу над задачей.
Исследовательская задача
- объект мысленной деятельности, в котором в диалектическом единстве
представлены составные элементы: предмет, условие и требование получения
некоторого познавательного результата при раскрытии отношений между известными
и неизвестными элементами задачи.
Таким образом, в математике включение учащихся в
определенный вид деятельности происходит посредством решения ими конкретного
класса задач. Средством формирования опыта метода моделирования могут служить и
задачи с параметрами. Овладение опытом такой деятельности как требует от
учащихся, так и формирует у них способности к самостоятельному осмыслению и
поиску решения задач.
В результате решены три первые задачи метода
моделирования:
1. Изучены психолого-педагогические теории
развития у учащихся умений моделирования при обучении математике в школе.
2.Установлены
развивающие функции задач в обучении.
3.Рассмотрены
основные методы решения задач с параметрами.
Глава 2. Развитие у учащихся умений
моделирования при решении задач с параметрами
.1 Система учебно-исследовательских
задач с параметрами
.1.1 Понятие параметра
Понятие параметра тесно связано с понятием переменной
величины. Переменная величина - величина, которая принимает различные
значения. Введение переменной величины в математику в XVII
в. является революционным скачком в развитии науки вообще. Оно означало новую
ступень познания явлений природы в их взаимной связи и движении. На основе
Декартовой переменной величины сформировалось понятие функции.
Итак, переменная - это общий термин для
обозначения различных меняющихся величин.
Параметр -
вспомогательная переменная, входящая в формулы и выражения. Обычно параметр
представляет собой скалярную величину или действительное число; параметр обозначается
буквой какого-либо алфавита. Часто параметр рассматривают и как постоянные
числа в условиях данной задачи, но в другой задаче они рассматриваются как
переменные.
Примеры.
1. В квадратном уравнении 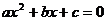 коэффициенты
коэффициенты
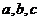 являются
параметрами, х переменная. При решении уравнения коэффициенты
являются
параметрами, х переменная. При решении уравнения коэффициенты 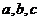 считаются
постоянными числами, но вообще они также могут быть приняты за переменные.
считаются
постоянными числами, но вообще они также могут быть приняты за переменные.
. Уравнение  в
прямоугольной декартовой системе координат представляет собой уравнение
множества окружностей единичного радиуса; числа
в
прямоугольной декартовой системе координат представляет собой уравнение
множества окружностей единичного радиуса; числа 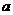 и
и 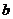 параметры
окружности в рассматриваемом множестве; если положить
параметры
окружности в рассматриваемом множестве; если положить  , то мы
получим вполне определенную окружность с центром в точке (1; 3) единичного
радиуса из множества окружностей того же радиуса.
, то мы
получим вполне определенную окружность с центром в точке (1; 3) единичного
радиуса из множества окружностей того же радиуса.
В задачах встречается 2 вида
символов: неизвестные переменные (обозначаются 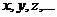 ) и параметры
) и параметры 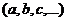 . Разница
между ними весьма условна, и можно считать, что параметр - это переменная,
значение которой считается фиксированным, и каждое значение параметра
определяет относительно неизвестного соответствующее уравнение (неравенство,
систему, функцию).
. Разница
между ними весьма условна, и можно считать, что параметр - это переменная,
значение которой считается фиксированным, и каждое значение параметра
определяет относительно неизвестного соответствующее уравнение (неравенство,
систему, функцию).
2.1.2 Употребление букв в математике
В связи с тем, что в математике широко
используют буквы, необходимо иметь в виду их различные функции.
Первая функция - обозначающая, когда
буква обозначает или любое число из данного множества, или даже какое-то
выражение, точку, прямую, фигуру и т.д.
При этом используются либо строчные
буквы  либо
заглавные буквы М, N, К, ....
либо
заглавные буквы М, N, К, ....
Например, с помощью букв
записывается переместительный закон: 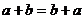 , где буквы в записи
обозначают любые числа. В записи а||b буквами
обозначаются прямые. MN прямая (луч, отрезок). М точка
(множество, фигура, выражение),
, где буквы в записи
обозначают любые числа. В записи а||b буквами
обозначаются прямые. MN прямая (луч, отрезок). М точка
(множество, фигура, выражение), 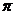 - обозначение конкретного числа.
- обозначение конкретного числа.
Вторая функция - обобщающая, когда
буква выступает в роли обобщения возможных значений какой-то величины,
коэффициента и т.д. В этом случае такую букву называют параметром.
Для записи параметров обычно
используются первые строчные буквы алфавита. Так, в записи уравнения ах +
b = с буквы а,
b и с являются
параметрами.
Третья функция - вопросительная, когда
требуется найти те значения этих букв, при которых выполняются указанные в
задаче условия. В этом случае эти буквы обозначают неизвестные (искомые)
значения задачи.
Для неизвестных используются
строчные буквы алфавита х, у, z, ... или
стандартные обозначения соответствующих величин: путь - s, S; время -
t, Т; скорость - 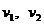 и т.д.
и т.д.
2.1.3 Задачи с параметрами в V - VI
классах
В V классе вместе с числовыми выражениями
изучаются буквенные выражения. Рассматривается серия задач с заменой некоторого
числа. Изменяющееся число обозначают буквой, получая новую задачу. Каждую из
задач решают, составляя выражение. Выражение для решения последней задачи
является буквенным.
Задача 1.
Поезд ехал двое суток. В первые сутки он проехал 980 км, а во вторые - на 50 км
больше. Сколько км проехал поезд за 2-е суток?
Решение.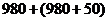 .
.
Задача 2. Поезд ехал
двое суток. В первые сутки он проехал 980 КМ, а во вторые - на 65 км больше.
Сколько км проехал поезд за 2-е суток?
Решение. 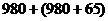
Обозначим буквой т число,
которое меняется от задачи к задаче. Получим новую задачу.
Задача 3. Поезд ехал
двое суток. В первые сутки он проехал 980 км, а во вторые - на т км
больше. Сколько км проехал поезд за 2-е суток?
Решение. Выражением
для решения этой задачи будет
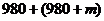
Выражение, содержащее буквы,
называют буквенным выражением. В этом выражении буквы могут
обозначать различные числа.
Рассматриваются упражнения на
запись, чтение буквенных выражений, определение компонентов операций, нахождение
значений выражений и сравнение этих значений, решают задачи, составляя
выражения.
Упражнения
1. Запишите выражение:
а) сумма 7 и 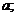
б) разность 16 и 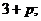
в) разность 45 и 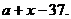
. Назовите слагаемы в сумме:
а) 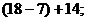
б) 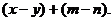
Назовите уменьшаемое и вычитаемое: 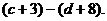
Прочитать выражение 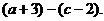
. Заполнить таблицу
Таблица №2
|
Значение
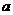 0 1 2 34 5 0 1 2 34 5
|
|
|
|
|
|
|
|
Значение
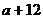
|
|
|
|
|
|
|
|
Значение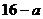
|
|
|
|
|
|
|
При каких значениях а:
а) 16 - а меньше, чем а + 12;
б) 16 - а больше, чем а + 12;
в) значения 16 - а и а + 12 равны?
. Пусть цена футболки а руб., а цена
трусов b
руб.
Какой смысл имеет выражение: а) а + b;
б)
а - b;
в)
250 - (а + b)?
Учащихся ориентируют на знание буквенной записи свойств
сложения и вычитания:
а + b
=
b
+
а;
а + (b
+
с) = (а + b)
+с;
a
+ о = о + a
=
а;
а - (b
+
с) = а - b
-
с, b
+
с ≤ а;
(а +
b) -
с = а +(b
-
с), с ≤ b;
(а +
b) -
с = (а - с) + b,
с
≤ а;
а - о = а,
а - а = О.
Аналогичная работа проводится при изучении
умножения и деления натуральных чисел. Определение умножения чисел дается с
помощью букв: Умножить число т на натуральное число n - значит
найти сумму n слагаемых, каждое из которых равно т:
т- n =
т + т + ... + т. (n штук)
Свойства умножения:
a*
в =
в * а;
а* (b*
с) = (а * b)
* с;
* n =
n. Исходя из переместительного свойства умножения условились n *1
= n
0*n=0.
Исходя из переместительного свойства умножения условились n*0 =0.
Появляются упражнения, при решении которых можно
ввести понятие параметр.
Упражнения
1. Существует ли такое число n, что
0*n = 6?
. При каких значениях т верно
равенство 0 * т= 0? Можно ли из этого равенства найти единственное
значение т? Можно ли разделить 0
на 0?
В VI
классе набор таких задач гораздо богаче. Среди них имеются и задачи с
неравенствами:
. При каких значениях а верно
неравенство: а) a
<
- а;
б) а > - а;
в)-а <
а;
г) - а > а?
Очевидно, наиболее удобным материалом для
введения понятия параметр являются уравнения и неравенства, в которые
входят вместе с неизвестной переменной буквы, обозначающие некоторые числа.
Обращается внимание на необычную форму ответов
при выполнении заданий с параметрами.
Например:
Решить уравнение х - а = 0.
Ответ: х =
а при любом значении а.
Решить уравнение Зх = а.
Ответ: х = -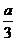 при любом
значении а.
при любом
значении а.
Решить уравнение ах = 8.
Ответ: х =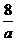 при a≠0;
нет решений при a=0
при a≠0;
нет решений при a=0
В V - VI классах не
ставится задача полного освоения параметра. Тем не менее, желательно методично
предлагать задачи с параметрами на уроках. Ими могут быть:
Задания:
1. Решить уравнения:
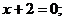
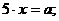
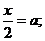
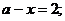
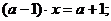
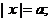
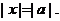
. Решить неравенства:
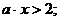
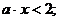
Сравнить: 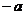 и
и 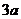 [21, с.14-
15].
[21, с.14-
15].
2.1.4 Задачи с параметрами в VII
классе
В VII классе круг задач, от которых
легко перейти к задачам с параметрами значительно шире. Да и теоретический
материал представляет богатые возможности. В VII классе,
например, учащиеся решают линейные уравнения и неравенства, причем уравнение 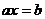 они должны
решать в общем виде и уметь выяснять знак корня при различных значениях
они должны
решать в общем виде и уметь выяснять знак корня при различных значениях 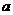 и
и 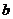 (то есть по
существу ими решается задача с двумя параметрами).
(то есть по
существу ими решается задача с двумя параметрами).
Покажем фрагмент урока на
тему «Линейные уравнения с параметром».
Решим уравнение 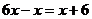 (1)
(1)
Получим: 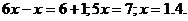
Если в уравнении (1) заменить
какое-либо число, например, 6, другим числом, то можно получать новые
уравнения:
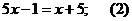
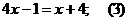
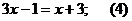
Каждое из этих уравнений решается
тем же способом, что и уравнение (1). Чтобы не решать несколько однотипных
уравнений одним и тем же способом, решим задачу в общем виде, заменив
изменяемое число (параметр) буквой:
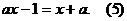
Действуя по тому же плану, что и при
решении уравнения (1), придем к уравнению 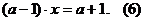
Только не будем торопиться с
делением на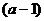 , ведь это
выражение при а = 1 обращается в 0, а на нуль делить нельзя. Случай а
= 1 надо рассматривать отдельно.
, ведь это
выражение при а = 1 обращается в 0, а на нуль делить нельзя. Случай а
= 1 надо рассматривать отдельно.
) Если а = 1, то уравнение
(6) имеет вид 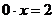 . Очевидно,
что уравнение (6) в этом случае не имеет корней.
. Очевидно,
что уравнение (6) в этом случае не имеет корней.
) Если же а ≠ 1, то
уравнение (6) имеет единственный корень 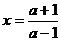
Нетрудно убедиться, что по формуле 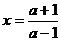 мы получим
корни уравнений (2) - (4), если в качестве a возьмем
числа 5, 4 и 3 соответственно.
мы получим
корни уравнений (2) - (4), если в качестве a возьмем
числа 5, 4 и 3 соответственно.
Задание, которое мы выполнили,
обычно формулируют так: для всех значений параметра а решите уравнение 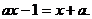
Ответ к этому заданию можно записать
так:
Ответ: 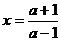 при
при 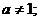 нет корней
при
нет корней
при 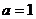 .
.
Замечание. Наши
рассуждения о параметре начались с уравнения (1), имевшего единственный корень,
но после замены числа 6 на букву а оказалось, что полученное уравнение
имеет единственный корень не при всех значениях а. При а=1 оно не
имеет корней.
Оформление решений задач с параметрами
1. Решите уравнение 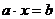
Ответ: при 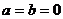 , х - любое
действительное число;
, х - любое
действительное число;
при 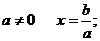
при 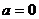 и
и 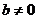 решений нет.
решений нет.
. Решите уравнение 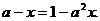
Решение. 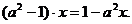
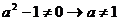 и
и 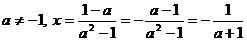
 или
или 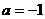
а) 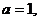 то
то 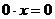 и
и 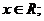 (или x - любое
число);
(или x - любое
число);
б) 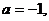 то
то 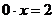 - уравнение не имеет решений.
- уравнение не имеет решений.
Ответ: 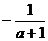 при
при 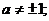 бесконечно
много корней при
бесконечно
много корней при 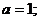 нет корней
при
нет корней
при 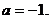
. Решите неравенство 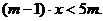
Определим множество допустимых значений
параметра: этим множеством является все множество чисел.
При 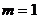 получаем
получаем 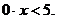 . Оно верно
при любых х.
. Оно верно
при любых х.
При 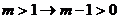 . Разделим на
. Разделим на 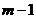 , получим
, получим 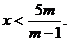
При . Разделим на
. Разделим на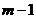 , получим
, получим 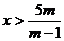 [ 15, с.
12].
[ 15, с.
12].
2.1.5 Задачи с параметрами в VIII
классе
В восьмом классе имеется много тем, где можно с
успехом использовать задачи с параметрами : при решении уравнений и неравенств
с одной переменной, при решении дробно-рациональных уравнений и, естественно,
при решении квадратных уравнений. Здесь основное внимание уделяется не только
вопросам теории, но и методам решения задач с параметрами . Например, можно ли
дать определение квадратного уравнения следующим образом:
«Уравнение вида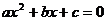 , где х- переменная(неизвестное),
а, b и с
параметры (или выражения, зависящие от параметров), причем,
, где х- переменная(неизвестное),
а, b и с
параметры (или выражения, зависящие от параметров), причем, 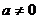 , называется квадратным».
, называется квадратным».
Особенно тщательно рассматривается
теоретический материал, позволяющий учащимся понять, когда квадратное уравнение
с параметрами не имеет корней, имеет один корень (или два равных) и имеет два
корня. Случай, когда корни квадратного уравнения должны быть или одного знака,
или разных, или обладать другими свойствами подкрепляться необходимыми
примерами. При решении неравенств особое внимание уделяется рассмотрению двух
методов: методу разложения на множители и методу введения новой переменной.
Рассмотрим пример: при каких
значениях параметра с уравнение 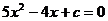
а) имеет различные действительные
корни;
б) имеет один (два равных) корень;
в) не имеет действительных корней;
г) имеет хотя бы один общий корень с
уравнением 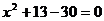 ?
?
Решение.
а) 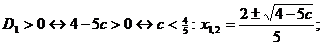
б) 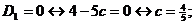
в) 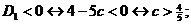
г) Уравнение 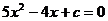 имеет корни
при
имеет корни
при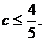 .
.
Рассмотрим уравнение 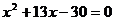
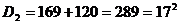
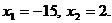
Пусть 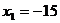 общий корень двух уравнений, тогда
общий корень двух уравнений, тогда 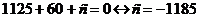
Пусть 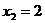 общий корень двух уравнений, тогда
общий корень двух уравнений, тогда 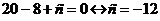
Если -15 и 2 являются корнями обоих уравнений,
то имеем систему 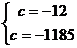 , которое не
имеет решении.
, которое не
имеет решении.
Ответ: а) 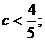 б)
б) 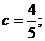 в)
в) 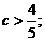 г)
г) 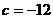 или
или 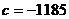 .
.
2.1.6 Задачи с параметрами в IX
классе
В девятом классе изучаются такие важные вопросы
как степень с рациональным показателем, квадратичная функция, решаются
уравнения и системы уравнений, неравенства. Поэтому включение в дидактический
материал задач с параметрами должно содействовать более качественному усвоению
учебного материала и одновременно создать условия и предоставить средства для
дальнейшего развития логического мышления и творческих способностей учащихся.
В связи с тем, что тема «Квадратичная функция»
изучается первой, с учащимися рассматривается следующий теоретический материал:
необходимые и достаточные условия для заданного расположения корней квадратного
трехчлена на числовой оси, свойства. функции в задачах с параметрами,
аналитические и графические приемы решения задач с параметрами.
На занятиях с ребятами теоретический материал
обобщается, рассматриваются соответствующие задачи с параметрами. Например, для
решения большинства задач с параметрами очень важно знать свойства квадратичной
функции и зависимость этих свойств от возможных соотношений между
коэффициентами. Причем исследование знака дискриминанта позволяет установить
наличие действительных корней, а теорема Виета знаки действительных корней.
Однако для целого ряда задач требуется еще
установить расположение действительных корней квадратного трехчлена на числовой
оси относительно каких-либо фиксированных точек числовой оси. Эти вопросы
рассматриваются более подробно, вводятся следующие обозначения:
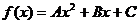 - квадратичная функция,
- квадратичная функция,
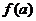 - значение функции в точке
- значение функции в точке 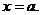
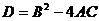 - дискриминант,
- дискриминант,
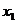 и
и 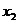 (причем
(причем 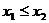 ) -
действительные корни уравнения
) -
действительные корни уравнения 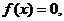
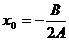 - абсцисса вершины параболы,
- абсцисса вершины параболы,
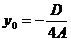 - ордината вершины параболы.
- ордината вершины параболы.
Ответом на поставленную задачу
служат следующие четыре
обобщающие теоремы:
Т1. 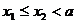 тогда и
только тогда, когда
тогда и
только тогда, когда 
Т2. 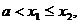 т.е.
т.е. 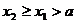 тогда и
только тогда, когда
тогда и
только тогда, когда 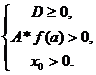
Т3. 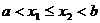 тогда и
только тогда, когда
тогда и
только тогда, когда 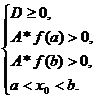
Т4. 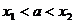 тогда и
только тогда, когда
тогда и
только тогда, когда 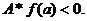 (В этом
случае
(В этом
случае 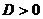 выполняется
автоматически).
выполняется
автоматически).
Эти теоремы часто применяются при
решении задач с параметрами и поэтому имеют большое значение. Однако лишь
немногие учащиеся знают их точные формулировки, поскольку они не входят в
школьную программу, а большинство учащихся даже не в состоянии запомнить их, не
говоря уже об аналитическом доказательстве теории, хотя оно и несложно
(используется теорема Виета и свойство квадратичных неравенств). Именно поэтому
с учащимися в школе предлагают рассматривать геометрическую интерпретацию
теорем:
)
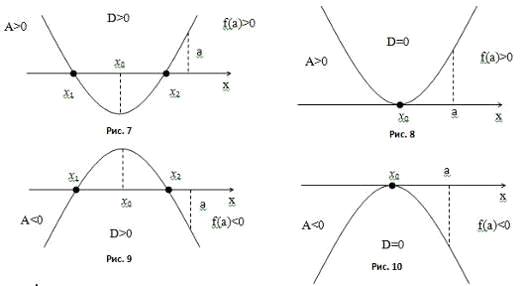
Объединяя все четыре случая, получим
систему Т1.
)
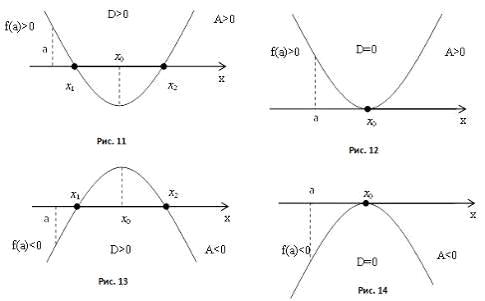
Объединяя эти условия, получим
систему Т2.
3)

Рис. 15
Рис. 16
В результате получим систему Т3.
)
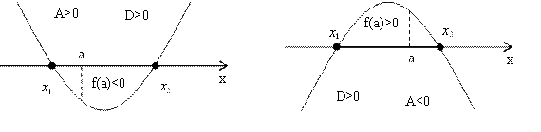
Рис. 17
Рис. 18
Оба случая объединяются в одно условие: Т4.
Приведенная графическая интерпретация
доказательства теории является не только более наглядной, но и избавляет
учеников от необходимости запоминания условий этих теорем.
Рассмотрим конкретную задачу:
Найти все значения параметра а, при которых
уравнение
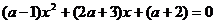 имеет корни одного знака.
имеет корни одного знака.
Решение.
Здесь возможны два случая:
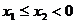 и 2)
и 2) 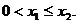
Разбираются эти варианты в
отдельности.
Случай 1. Искомыми
являются такие значения параметра а, при которых график квадратного
трехчлена из левой части уравнения занимает положение, схематично изображенное
на рисунке №19 сплошной линией, или положение, изображенное пунктирной линией:

Рис. 19
Это можно описать системой неравенств:
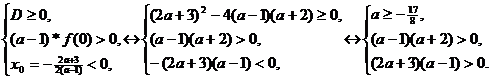
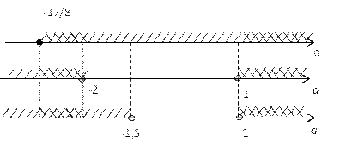
Рис. 20
Возьмем пересечение решений
неравенств системы и получим ответ: 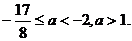
Случай 2. Он
описывается системой неравенств:
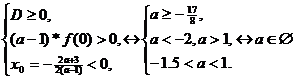
Таким образом, случай 2 не
реализуется ни при каких значениях параметра.
Ответ: 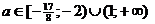 [10, с. 19-
20].
[10, с. 19-
20].
2.1.7 Задачи с параметрами в X-XI классах
в старших классах рассматриваются более сложные
уравнения с параметрами: иррациональные, тригонометрические, показательные и
логарифмические.
При решении параметрических
иррациональных уравнений полезно пользоваться общими формулами. Пусть 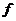 и
и 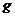 -некоторые
функции,
-некоторые
функции, 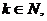 тогда:
тогда:
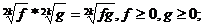
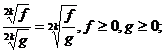
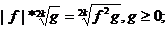

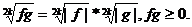
При этом следует иметь в виду, что
ОДЗ левой и правой частей могут быть различными, то есть ОДЗ правой её части
может быть шире ОДЗ левой. Например, выражение 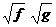 определено при
определено при 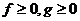 , а
выражение
, а
выражение 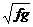 - как при
- как при 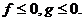
В то же время преобразования
уравнений с формальным использованием формул 1) - 5) «справа налево» не
допустимы, так как возможно сужение ОДЗ исходного уравнения, а, следовательно,
и потеря корней.
Уравнение вида 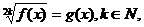 равносильно
системе
равносильно
системе 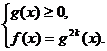
Проиллюстрируем все вышесказанное на
примере.
Решите уравнение 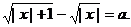
Решение.
Функция 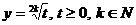 монотонно
возрастающая:
монотонно
возрастающая: 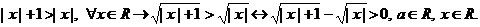
Если 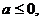 то
то 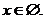
Если 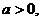 то сделаем замену:
то сделаем замену: 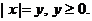
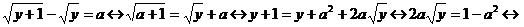
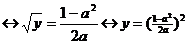 и
и 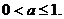
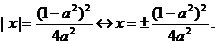
Ответ: 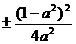 при
при 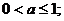 нет корней
при
нет корней
при 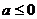 или
или 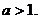
При решении показательных и
логарифмических уравнений с параметром важным является использование свойства
монотонности этих функций. Именно эту мысль необходимо довести учителю до
сведения учащихся. Покажем это на следующем уравнении:
При каждом а решите уравнение 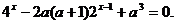
Решение.
Пусть 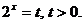
Тогда исходное уравнение примет вид:
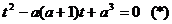
Если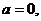 то
то  Т.е.
Т.е. 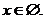
Если 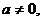 то
то 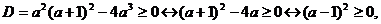
т.е. 
Корни уравнения (*) могут быть
только положительными.
Рассмотрим два случая:
. Оба корня положительные: 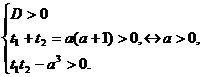
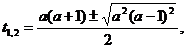 откуда
откуда 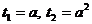
. Корни разных знаков 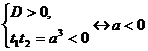
Получим 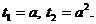 Так как
Так как 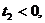 поэтому он
не может быть корнем уравнения (*). Остается один корень
поэтому он
не может быть корнем уравнения (*). Остается один корень 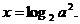
Ответ: 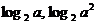 при
при 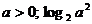 при
при 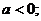 нет корней
при
нет корней
при 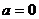 .
.
Что касается тригонометрических
уравнений, то их хорошо использовать в качестве повторения темы «
Тригонометрические уравнения ». Ибо, с одной стороны, учащиеся вспоминают
методы решения тригонометрических уравнений, с другой стороны, закрепляются
навыки решения линейных и квадратных уравнений с параметром.
Исследуйте уравнение 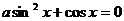
Решение.
Рассмотрим два случая:
) 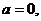 тогда имеем
частный случай простейшего тригонометрического уравнения
тогда имеем
частный случай простейшего тригонометрического уравнения 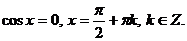
) 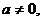 тогда
исходное уравнение приводим к виду:
тогда
исходное уравнение приводим к виду:
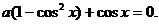
Пусть 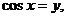 где
где 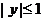 , тогда уравнение перепишем в виде:
, тогда уравнение перепишем в виде:
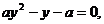 решение которого не вызывает
затруднений:
решение которого не вызывает
затруднений:
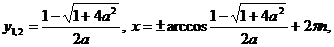 где
где 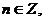 при условии
при условии
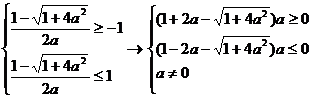
Рассмотрим совокупность двух систем:
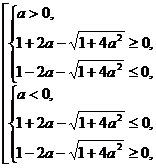
Решив которую, получаем ответ.
Ответ: 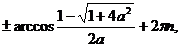 где
где 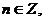 при
при 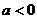 или
или 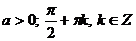
2.2 Организация, проведение и
основные итоги педагогического эксперимента
В ходе педагогической практики (Ишимская средняя
школа №31) нами проводился педагогический эксперимент. Он осуществлялся поэтапно:
констатирующий, поисковый, обучающий и контрольный. В ходе его проведения нам
было необходимо получить подтверждение эффективности разработанной методики
моделирования в процессе обучения учащихся решению задач с параметрами.
Эксперимент проводился на факультативных занятиях.
. Констатирующий эксперимент.
На данном этапе происходило выявление
исследуемой проблемы (развитие у учащихся умений моделирования при решении
уравнений с параметрами) в теории и практике обучения, изучалась и
анализировалась психолого-педагогическая литература, опыт учителей по
интересующей нас проблеме (параграфы 1.1 и 1.2 главы 1).
Были отобраны 10 учащихся для проведения с ними
самостоятельной работы с целью выявления их знаний по теме «Уравнения с
параметрами». Работа состояла из 10 заданий, из которых последние три были
более сложными. Для каждого задания предлагалось три ответа, один из которых
правильный, а два другие - неверные. Учащиеся должны были не просто указывать
букву правильного ответа, но и оформить подробное решение задания. Уравнения
были новыми, необычными для учащихся, вызывали у них интерес, побуждали к
активным поискам решения.
Критерии оценок:
оценка «5» - за 9 - 10 верных ответов; оценка «4» - за 7 - 8 верных ответов;
оценка «3» - за 5 - 7 верных ответов; оценка «2» - за 0 - 4 верных ответов.
Итоги тестирования были занесены в специальную таблицу, в которой рядом с
каждой фамилией ученика знаком «+» отмечались верные ответы, знаком «-» -
неверные, указывалось количество верных ответов и оценка.
Таблица №3
|
№
задания
|
|
|
№
|
Ф.И
ученика
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Кол-во
верных ответов
|
Оценка
|
|
1
|
Белова
Екатерина
|
+
|
+
|
+
|
-
|
-
|
+
|
+
|
-
|
-
|
-
|
5
|
«3»
|
|
2
|
Бучинская
Михайлина
|
+
|
-
|
-
|
-
|
+
|
-
|
-
|
-
|
-
|
2
|
«2»
|
|
3
|
Герасимов
Алексей
|
+
|
+
|
+
|
-
|
+
|
-
|
+
|
+
|
-
|
-
|
6
|
«3»
|
|
4
|
Иванова
Дарина
|
+
|
+
|
-
|
+
|
-
|
-
|
-
|
-
|
-
|
-
|
3
|
«2»
|
|
5
|
Королева
Алина
|
+
|
-
|
+
|
-
|
+
|
+
|
+
|
+
|
-
|
-
|
6
|
«3»
|
|
6
|
Осябрик
Полина
|
+
|
-
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
-
|
8
|
«4»
|
|
7
|
Павлов
Алексей
|
+
|
+
|
-
|
+
|
-
|
+
|
+
|
-
|
-
|
-
|
5
|
«3»
|
|
8
|
Рагозина
Валерия
|
+
|
+
|
-
|
-
|
-
|
+
|
-
|
-
|
-
|
-
|
3
|
«2»
|
|
9
|
Ширшова
Полина
|
+
|
-
|
+
|
+
|
-
|
+
|
+
|
-
|
+
|
-
|
6
|
«3»
|
|
10
|
Ярославцева
Валерия
|
+
|
+
|
-
|
+
|
+
|
-
|
+
|
+
|
-
|
+
|
7
|
«4»
|
С целью иллюстрации итогов констатирующего этапа
эксперимента приведем сравнительную диаграмму (рис. №21).
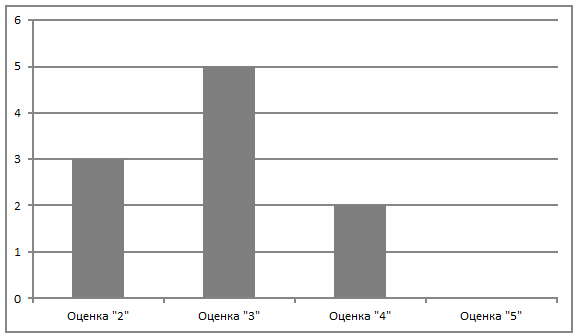
Рис. 21
Анализ проведенной самостоятельной работы
показал, что учащихся испытывают затруднения при решении уравнений с
параметрами. Это означает, что этот материал изучался ими формально. У учащихся
плохо развиты умения моделирования, значит предыдущее преподавание мало
способствовало их формированию у учеников, поэтому целесообразно уделить больше
внимания развитию данного вида умений, с помощью решения уравнений с
параметрами.
. Поисковый эксперимент.
На данном этапе проводилась разработка комплекса
учебных занятий, направленных на развитие у учащихся умений моделирования в
процессе решения уравнений с параметрами. Для этого было продумано поэтапное
повторение и отработка знаний, с использованием специального комплекса заданий.
Для разнообразия и возбуждения интереса учащихся были включены нестандартные
задания(параграф 2.1 главы 2). После анализа первой самостоятельной работы
каждый из учащихся выполнял дома работу над ошибками. В этой работе ученик
должен был представить подробное решение задачи, по которой был дан неверный
ответ, с теоретическим обоснованием допущенной ошибки.
Комплекс занятий:
Таблица №4
|
№
|
Тема
|
Количество
часов
|
|
1
|
Уравнения
с параметром: основные понятия
|
1
|
|
2
|
Решение
простейших уравнений с параметрами
|
1
|
|
3
|
Решение
задач на нахождение множества корней уравнения в зависимости от параметра
|
1
|
|
4
|
Решение
задач на нахождение значений параметра, удовлетворяющих условиям,
накладываемым на множество корней
|
1
|
|
5
|
Анализ
самостоятельной работы
|
2
|
|
6
|
Итоговое
занятие по проделанной работе
|
1
|
. Обучающий и контрольный эксперимент.
Здесь с учащимися был проведен разработанный на
втором этапе эксперимента комплекс заданий и проверка эффективности
разработанной методики - проведение письменной самостоятельной работы.
На выходе мы получили следующие результаты:
Таблица №5
|
№
задания
|
|
|
№
|
Ф.И
ученика
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Кол-во
верных ответов
|
Оценка
|
|
1
|
Белова
Екатерина
|
+
|
+
|
+
|
+
|
+
|
+
|
-
|
+
|
-
|
-
|
7
|
«4»
|
|
2
|
Бучинская
Михайлина
|
+
|
+
|
-
|
+
|
+
|
+
|
-
|
-
|
-
|
-
|
5
|
«3»
|
|
3
|
Герасимов
Алексей
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
-
|
-
|
-
|
7
|
«4»
|
|
4
|
Иванова
Дарина
|
+
|
+
|
-
|
+
|
-
|
+
|
+
|
-
|
-
|
-
|
5
|
«3»
|
|
5
|
Королева
Алина
|
+
|
+
|
+
|
+
|
+
|
-
|
+
|
-
|
+
|
+
|
8
|
«4»
|
|
6
|
Осябрик
Полина
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
-
|
9
|
«5»
|
|
7
|
Павлов
Алексей
|
+
|
+
|
+
|
+
|
-
|
+
|
+
|
-
|
+
|
-
|
7
|
«4»
|
|
8
|
Рагозина
Валерия
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
-
|
9
|
«5»
|
|
9
|
Ширшова
Полина
|
+
|
+
|
-
|
+
|
+
|
+
|
+
|
+
|
-
|
-
|
7
|
«4»
|
|
10
|
Ярославцева
Валерия
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
10
|
«5»
|
В таблице №6 более наглядно представим
результаты проведенной работы до эксперимента и после.
Таблица №6
|
Количество
полученных оценок
|
|
«5»
|
«4»
|
«3»
|
«2»
|
|
До
эксперимента
|
0
|
2
|
5
|
3
|
|
После
эксперимента
|
3
|
5
|
2
|
0
|
Ниже с целью иллюстрации эффективности внедрения
разработанного комплекса заданий приведем сравнительную диаграмму (рис. №22)
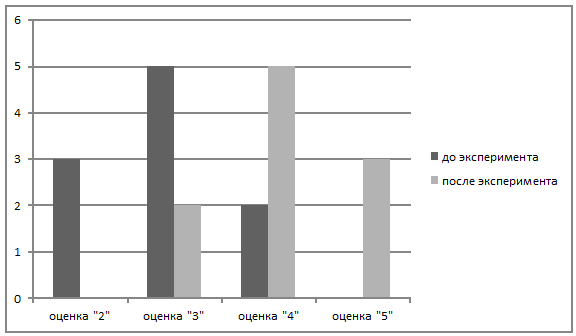
Рис. 22
Из таблицы видно, что уровень развития у
учащихся умений моделирования после проведения эксперимента значительно
повысился. Таким образом, мы экспериментально подтвердили гипотезу нашего
исследования - если в процессе обучения учащихся решению задач с параметрами,
использовать специальный комплекс упражнений, то можно ожидать развития у
учащихся умений моделирования.
Выводы по второй главе
в V - VI
классах не ставится задача полного освоения параметра. Тем не менее, желательно
методично предлагать задачи с параметрами на уроках. В VII
классе круг задач, От которых легко перейти к задачам с параметрами значительно
шире. Да и теоритически материал представляет богатые возможности. В VIII
классе имеется много тем, где можно с успехом использовать задачи с
параметрами: при решении уравнений и неравенств с одной переменной, при решении
дробно-рациональных уравнений и, естественно, при решении квадратных уравнений.
Здесь основное внимание уделяется не только вопросам теории, но и методам
решения задач с параметрами. В IX классе изучаются такие важные вопросы как
степень с рациональным показателем, квадратичная функция, решаются уравнения и
системы уравнений, неравенства. Поэтому включение в дидактический материал
задач с параметрами должно содействовать более качественному усвоению учебного
материала и одновременно создать условия и предоставить средства для
дальнейшего развития логического мышления и творческих способностей учащихся. В
старших классах рассматриваются более сложные уравнения с параметрами:
иррациональные, тригонометрические, показательные и логарифмические.
В результате решены три последние задачи
исследования:
. Выполнен анализ содержания школьного
курса алгебры с точки зрения
подготовки учащихся к решению задач с параметрами.
. Разработан комплекс
учебно-исследовательских задач с параметрами.
. Организован педагогический эксперимент
и подведены его основные итоги.
Заключение
В ходе исследования были получены следующие
результаты:
. Выявлено, что проблема развития у
учащихся умений моделирования «через задачи» действительно мало разработана и поэтому
очень важна и актуальна.
. Обоснована необходимость привлечения
внимания к задачам с параметрами, так как их решение способствует формированию
умений моделирования у учащихся.
. Разработана методика формирования
умений моделирования у учащихся в процессе их обучения решению задач с
параметрами.
. Экспериментально подтверждена гипотеза
исследования: если в процессе обучения учащихся решению задач с параметрами,
использовать специальный комплекс упражнений, то можно ожидать развития умений
моделирования у учащихся.
Совершенно ясно, что в школьном обучении конечно
должны быть представлены такие задачи и упражнения, решение которых
способствует глубокому пониманию и прочному усвоению школьниками той системы
математических знаний и умений, которые предусмотрены программой. Однако, кроме
того, в школьном курсе математики должны быть в достаточном объеме представлены
и задания по развитию умений моделирования. К числу таких заданий относятся
задачи с параметрами, которые позволяют формировать у учащихся представления об
особенностях метода моделирования математиков.
Библиографический
список использованной литературы
1. Виленкин, Н.Я. Математика
[Текст]: учеб. для 5 кл. средней школы / Н.Я. Виленкин, А.С. Чесноков, В.И.
Жохов.- М.: Просвещение, 2013.- 154с.
. Виноградова, Л.В. Методика
преподавания математики в средней школе [Текст] / Л.В. Виноградова- Ростов н/д:
Феникс, 2005.- 252с.
. Голубев, В.И. О параметрах
- с самого начала [Текст] / В.И. Голубев, А.М. Гольдман, Г.В. Дорофеев //
Репетитор. - 2007. - №2 - с. 3-13.
. Горбачев, В.И. Общие методы
решения уравнений и неравенств с параметрами [Текст] // Мат. в шк. г: 1999. -
№6.- С. 60-68.
. Горбачев, В.И. Общие методы
решения уравнений и неравенств с параметрами [Текст] // Мат. в шк. - 2000. -
№2.- С. 61-68.
. Горнштейн, П.И. Задачи с
параметрами [Текст] / П.И. Горнштейн, В.Б. Полонский. - М.: Просвещение, 1992.-
182с.
. Дубич, С.Л. Линейные и
квадратные уравнения с параметрами [Текст] / / Математика. - 2001. - №3.- С. 28
- 31.
. Егерман, Е.В. Задачи с
параметрами. 7 - 11 классы [Текст] // Математика. - 2003. - №1. - С. 18 - 20.
. Капкаева, Л.С.
Алгебраические и геометрические методы в обучении математике [Текст] // Мат. в
шк. - 2004. ·-№7. - С. 27-33.
. Котухов, С.К. Различные
способы решения задач с параметрами [Текст] // Мат. в шк.- 1998.-№6.- С. 9-12.
. Колягин, Ю.М. Методика
преподавания математики в средней школе: общая методика [Текст]: учеб. пособие
для студентов физико- математических факультетов пед. институтов.- М.:
Просвещение, 1975.- 462с.
. Леонтович, А.В.
Исследовательская деятельность школьников [Текст] / / Школьные технологии.-
2006.-№6.- С. 89- 98.
. Мишин, В.В. Решение задач с
параметрами. Теория и практика. [Текст]/ В.В. Мишин.- М.: Экзамен, 2009.- 176с.
. Моденов, В.П. Задачи с
параметрами [Текст]/ В.П. Моденов.-М: Экзамен, 2007.- 86с.
. Мордкович, А. Уравнения и
неравенства с параметрами [Текст] // Математика. - 2010. -№38.- С. 2 - 3.
. Пескова, Т.А. Первое
знакомство с параметрами в уравнениях. 7 класс [Текст] // Математика. - 1999.
-№36.- С. 29.
. Пронина, Е.С. Линейные
уравнения с параметрами: методические рекомендации [Текст] // Мат. в шк.- 2000.
-№12.- С.3-5.
. Романов, П.Ю. Решение задач
с параметрами [Текст] // Математика. - 2001. -№12. - С. 13-15.
. Савенков, А.И.
Исследовательская деятельность учащихся [Текст] // Школьные технологии.- 2008.-
№1.- С. 11- 20.
21. Цыпкин, А.Г. Справочник по
методам решения задач по математике для средней школы [Текст]
/ А.Г. Цыпкин, А.И. Пинский. - 2-е издание, перераб. и доп. - М.: Наука, 2009.
- 576 с.
. Шабанова, М.В. Уравнения и
неравенства с параметрами [Текст] // Математика. - 2002.-№38.- С. 27 - 31.
23. Шарыгин, И.Ф. Факультативный
курс по математике. Решение задач: Учеб. пособие для
10-х классов средней школы [Текст] / И.Ф. Шарыгин. - М.: Просвещение, 2008. -
384 с.
. Шарыгин, И.Ф.
Факультативный курс по математике. Решение задач: Учеб. пособие для 11 класса
средней школы [Текст] / И.Ф. Шарыгин, В.И. Голубев. - М.: Просвещение, 2007. -
384 с.
. Шахмейстер, А.Х. Уравнения
и неравенства с параметрами [Текст]/ А.Х. Шахмейстер.-М.: Виктория плюс,
2010,-136с.
. Шерстаков, С.В. Уравнения с
параметром [Текст] / С.В. Шерстаков, Е.Н. Юрченко.- М.: Слог,1993.- 107с.
. Шихалиев, Х.Ш. Уравнения и
неравенства с параметрами [Текст] // Мат. в шк.- 1980.-№21.- С. 34- 35.
. Ястребинецкий, Г.А. Задачи
с параметрами [Текст] / Г.А. Ястребинецкий.- М.: Просвещение, 2006.- 128с.