Исследование многолинейных СМО с отказами и их применение
Министерство
образования Республики Беларусь
Учреждение
образования «Гродненский государственный университет имени Янки Купалы»
Факультет
математики и информатики
Кафедра
стохастического анализа и эконометрии
ИССЛЕДОВАНИЕ
МНОГОЛИНЕЙНЫХ СМО С ОТКАЗАМИ И ИХ ПРИМЕНЕНИЕ
Курсовая работа студента 3 курса
стационара
Сабастынович Сергей Генрихович
Гродно 2008
Содержание
Введение. Постановка задачи
Глава 1. Анализ многолинейных СМО с
отказами
.1 Многолинейная СМО с отказами
.2 Многолинейная СМО с отказами и
“равномерной” взаимопомощью между каналами
.3 Многолинейная СМО с отказами и
взаимопомощью между линиями типа “все как один”
Глава 2. Сравнение основных
показателей многолинейных СМО с отказами
.1 Сравнение многолинейных СМО с
взаимопомощью между каналами типа ''все как'' один и с ''равномерной''
взаимопомощью между каналами
.1.1 Сравнение пропускной
способности системы
.1.2 Сравнение среднего времени
пребывания заявки в системе
.1.3 Сравнение среднего числа заявок
в системе
.2 Сравнение многолинейных СМО с
отказами без взаимопомощи с и взаимопомощью типа ''все как один''
.2.1 Сравнение пропускной
способности системы
.2.2 Сравнение среднего числа заявок
в систем
2.2.3 Сравнение
среднего пребывания заявки в системе
.3 Сравнение
многолинейных СМО с отказами без взаимопомощи и с ''равномерной'' взаимопомощью
между каналами
2.3.1 Сравнение пропускной
способности системы
.3.2 Сравнение среднего времени
пребывания заявки и среднего числа заявок в системе
Глава 3. Практическое применение СМО
с отказами
.1 Решение задач оптимизации.
Нахождение оптимального числа линий обслуживания
3.2
Оценка ожидаемого дохода и дисперсии дохода систем массового обслуживания
Заключение
Список
использованных источников
Приложение
Текст
программы, реализующей задачу оптимизации СМО
Введение. Постановка задачи
Теория массового обслуживания - область
прикладной математики, занимающаяся анализом процессов в системах производства,
обслуживания, управления, в которых однородные события повторяются многократно,
например, на предприятиях бытового обслуживания; в системах приема, переработки
и передачи информации; автоматических линиях производства и др.
Задача теории массового обслуживания -
установить зависимость результирующих показателей работы системы массового
обслуживания (вероятности того, что заявка будет обслужена; математического
ожидания числа обслуженных заявок и т.д.) от входных показателей (количества
каналов в системе, параметров входящего потока заявок и т.д.). Результирующими
показателями или интересующими нас характеристиками СМО являются - показатели
эффективности СМО, которые описывают способна ли данная система справляться с
потоком заявок.
Задачи теории массового обслуживания носят
оптимизационный характер и в конечном итоге включают экономический аспект по
определению такого варианта системы, при котором будет обеспечен минимум
суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на
обслуживание и простоев каналов обслуживания.
В качестве примеров СМО в
финансово-экономической сфере можно привести системы, представляющие собой
банки различных типов (коммерческие, инвестиционные, ипотечные, инновационные,
сберегательные), страховые организации (государственные, акционерные общества,
компании, фирмы, ассоциации, кооперативы), налоговые инспекции, аудиторские
службы, различные системы связи (в том числе телефонные станции),
погрузочно-разгрузочные комплексы (порты, товарные станции), автозаправочные
станции, различные предприятия и организации сферы обслуживания (магазины,
парикмахерские, больницы).
В теории СМО обслуживаемый объект называют
заявкой. В общем случае под заявкой обычно понимают запрос на удовлетворение
некоторой потребности, например, разговор с абонентом, посадка самолета,
покупка билета.
Каждая СМО включает в свою
структуру некоторое число обслуживающих устройств, которые называют линиями
(каналами) обслуживания. Роль каналов могут играть различные приборы, лица,
выполняющие тс или иные операции (кассиры, операторы, парикмахеры, продавцы),
линии связи, автомашины, краны, ремонтные бригады, железнодорожные пути,
бензоколонки и т.д.
Системы массового обслуживания
могут быть одноканальными или многоканальными.
Каждая СМО предназначена для
обслуживания (выполнения) некоторого потока заявок (требований), поступающих на
вход системы большей частью не регулярно, а в случайные моменты времени.
Обслуживание заявок, в общем случае, также длится не постоянное, заранее
известное время, а случайное время, которое зависит от многих случайных, порой
неизвестных нам, причин. После обслуживания заявки канал освобождается и готов
к приему следующей заявки. Случайный характер потока заявок и времени их
обслуживания приводит к неравномерной загруженности СМО: в некоторые промежутки
времени на входе СМО могут скапливаться не обслуженные заявки, что приводит к
перегрузке СМО, в некоторые же другие интервалы времени при свободных каналах
на входе СМО заявок не будет, что приводит к недогрузке СМО, т.е. к
простаиванию се каналов. Заявки, скапливающиеся на входе СМО, либо
"становятся" в очередь, либо по какой-то причине невозможности
дальнейшего пребывания в очереди покидают СМО не обслуженными.
Таким образом, во всякой СМО
можно выделить следующие основные элементы:
1)
«входящий
поток заявок;
2)
очередь
;
3)
каналы
обслуживания;
4)
выходящий
поток обслуженных заявок.
Каждая СМО в зависимости от
своих параметров: характера потока заявок, числа линий обслуживания и их
производительности, а так же от правил организации работы обладает определенной
эффективностью функционирования(пропускной способностью), позволяющей ей более
или менее успешно справляться с потоком заявок.
В данной работе будет
рассматриваться многолинейная СМО(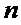 -канальная,
-канальная, 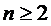 ), с
отказами(нулевым ожиданием или явными потерями), в которых заявка, поступившая
на вход СМО в момент, когда все каналы заняты, получает отказ и покидает СМО.
Чтобы эта заявка все же была обслужена, она должна снова поступить на вход СМО
и рассматриваться при как заявка поступившая впервые. Примером СМО с отказами
может служить АТС.
), с
отказами(нулевым ожиданием или явными потерями), в которых заявка, поступившая
на вход СМО в момент, когда все каналы заняты, получает отказ и покидает СМО.
Чтобы эта заявка все же была обслужена, она должна снова поступить на вход СМО
и рассматриваться при как заявка поступившая впервые. Примером СМО с отказами
может служить АТС.
Цель курсовой работы -
проанализировать многолинейные СМО с отказами без взаимопомощи, с взаимопомощью
между линиями типа ''все как один'' и с ''равномерной'' взаимопомощью и
сравнить предельные характеристики эффективности функционирования этих систем.
Задачи
1) Найти характеристики
многолинейной СМО с отказами без взаимопомощи, с взаимопомощью между линиями
типа ''все как один'' и с ''равномерной'' взаимопомощью между каналами;
2) Провести сравнительный
анализ характеристик эффективности функционирования многолинейных СМО с
отказами по пропускной способности, по среднему числу заявок и по среднему
времени пребывания заявки в системе;
) Решить задачу
оптимизации.
4) Оценить ожидаемый доход и дисперсию дохода
для СМО с отказами.
Глава 1. Анализ многолинейных
СМО с отказами
.1 Многолинейная СМО с отказами
Изучим работу n-линейной СМО с
отказами 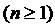 , на вход
которой поступает простейший поток заявок
, на вход
которой поступает простейший поток заявок  с интенсивностью
с интенсивностью 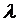 , а время
, а время 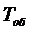 обслуживания
каждым каналом одной заявки распределено по показательному закону
обслуживания
каждым каналом одной заявки распределено по показательному закону 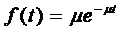
 . Тогда
поток обслуживаний каждым каналом будет простейшим с интенсивностью
. Тогда
поток обслуживаний каждым каналом будет простейшим с интенсивностью 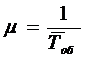 где
где 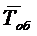 -среднее
время обслуживания одной заявки одним каналом.
-среднее
время обслуживания одной заявки одним каналом.
Задача исследования таких СМО
впервые возникла в области телефонии и была решена в 1909 г. А.К. Эрлангом.
Состояния системы занумеруем по
числу занятых каналов. Для СМО с отказами это означает, что мы нумеруем
состояния по числу заявок, находящихся в системе, т.е. под обслуживанием,
поскольку каждый канал в любой момент времени либо свободен, либо обслуживает
только одну заявку. Таким образом, СМО может находиться только в одном из следующих
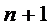 состояний:
состояний:
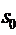 -все n каналов свободны,
-все n каналов свободны,
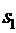 -занят только один канал, остальные
-занят только один канал, остальные 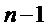 каналов
свободны
каналов
свободны
…
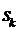 -заняты
-заняты 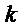 каналов,
остальные
каналов,
остальные 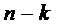 каналов
свободны
каналов
свободны
…
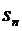 -заняты все
-заняты все 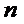 каналов.
каналов.
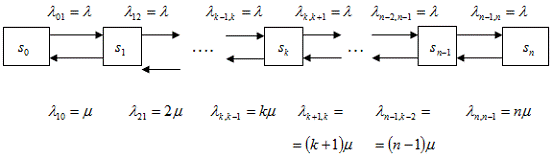
Рис. 1.1 Граф состояний СМО с
отказами.
Если СМО находится в состоянии  , т.е. когда
, т.е. когда
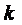 , каналов
заняты обслуживанием заявок, а остальные
, каналов
заняты обслуживанием заявок, а остальные 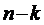 каналов свободны, то перескок се в
состояние
каналов свободны, то перескок се в
состояние 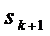 происходит
при поступлении на вход новой заявки. Таким образом, по стрелкам слева направо
из любого состояния в соседнее состояние справа систему переводит один и тот же
входящий поток заявок
происходит
при поступлении на вход новой заявки. Таким образом, по стрелкам слева направо
из любого состояния в соседнее состояние справа систему переводит один и тот же
входящий поток заявок 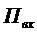 с
интенсивностью
с
интенсивностью 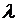 .
Следовательно, плотность вероятности перехода
.
Следовательно, плотность вероятности перехода 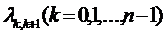 из любого
из любого 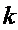 -го
состояния в
-го
состояния в 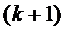 -е состояние
равна
-е состояние
равна 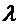 :
:
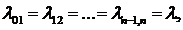
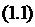
что и проставлено над стрелками
слева направо.
Так как по предположению входящий
поток 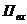 простейший,
то он является ординарным, т.е. заявки поступают по одной. Поэтому СМО, меняя
свои состояния слева направо, не может перескочить через состояние, а переходит
только в соседнее справа состояние. По этой причине на графе (см. рис.1.1)
отсутствуют стрелки, перескакивающие через состояния слева направо.
простейший,
то он является ординарным, т.е. заявки поступают по одной. Поэтому СМО, меняя
свои состояния слева направо, не может перескочить через состояние, а переходит
только в соседнее справа состояние. По этой причине на графе (см. рис.1.1)
отсутствуют стрелки, перескакивающие через состояния слева направо.
Вероятность того, что одновременно,
точно в один и тот же момент, освободятся более одного канала, пренебрежимо
мала, т.е. такие события практически невозможны. Поэтому на графе нет стрелок,
"перескакивающих" через состояния справа налево.
Выясним, каковы интенсивности
потоков событий, переводящих СМО по стрелкам справа налево.
На переход занятого канала в
состояние свободного действует простейший поток обслуживания 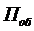 с
интенсивностью
с
интенсивностью 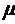 . Но тогда
переход СМО в целом из состояния
. Но тогда
переход СМО в целом из состояния 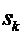 (в котором к каналов заняты, а
(в котором к каналов заняты, а 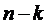 свободны) в
состояние
свободны) в
состояние 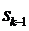 (в котором
по сравнению с предыдущим освободился один из
(в котором
по сравнению с предыдущим освободился один из 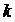 занятых каналов) происходит под
воздействием суммарного потока обслуживании
занятых каналов) происходит под
воздействием суммарного потока обслуживании 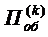 , представляющего собой результат
наложения k потоков обслуживании
, представляющего собой результат
наложения k потоков обслуживании 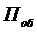 , действующих на каждый из
, действующих на каждый из 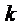 занятых
каналов. При этом интенсивность суммарного потока равна сумме интенсивностей
слагаемых потоков:
занятых
каналов. При этом интенсивность суммарного потока равна сумме интенсивностей
слагаемых потоков:
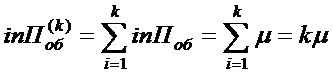
Таким образом,
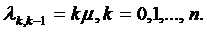
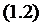
Итак, мы получили размеченный граф
состояний 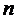 -канальной
СМО с отказами, из которого видно, что математической моделью процесса,
протекающего в этой СМО, является процесс гибели и размножения. Причем, под
размножением можно понимать процесс увеличения числа занятых каналов, т.е.
переходы СМО из состояния в состояние по стрелкам слева направо, а гибель
интерпретировать, как уменьшение числа занятых каналов, т.е. переходы системы
по стрелкам справа налево.
-канальной
СМО с отказами, из которого видно, что математической моделью процесса,
протекающего в этой СМО, является процесс гибели и размножения. Причем, под
размножением можно понимать процесс увеличения числа занятых каналов, т.е.
переходы СМО из состояния в состояние по стрелкам слева направо, а гибель
интерпретировать, как уменьшение числа занятых каналов, т.е. переходы системы
по стрелкам справа налево.
Пользуясь общим правилом составления
дифференциальных уравнений Колмогорова, можно для вероятностей состояний 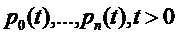 , составить
по графу на рис. 1.1 следующую систему дифференциальных уравнений:
, составить
по графу на рис. 1.1 следующую систему дифференциальных уравнений:
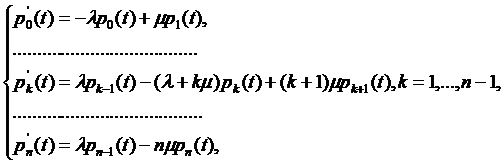
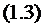
которая в случае рассматриваемой СМО
называется системой дифференциальных уравнений Эрланга.
Вероятности состояний в любой момент
времени 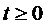 удовлетворяют
нормировочному условию
удовлетворяют
нормировочному условию
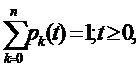
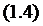
В начальный момент времени t=0
наблюдения за СМО естественно считать, что она находится в состоянии 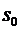 , т.е. все
каналы были свободны. Поэтому начальные условия для решения системы (1.3)
выглядят следующим образом:
, т.е. все
каналы были свободны. Поэтому начальные условия для решения системы (1.3)
выглядят следующим образом:
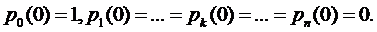
Решение общих систем
дифференциальных уравнений Эрланга в аналитическом виде представляет
значительные трудности. На практике такие системы решаются обычно в численном
виде на ЭВМ.
При достаточно длительном протекании
процесса  в
рассматриваемой СМО устанавливается стационарный режим, характеризующийся
предельными вероятностями состояний СМО:
в
рассматриваемой СМО устанавливается стационарный режим, характеризующийся
предельными вероятностями состояний СМО:
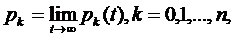
которые, как это. следует из
нормировочного условия (1.4), удовлетворяют нормировочному условию
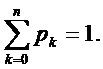 (1.5)
(1.5)
Для вычисления предельных
вероятностей состояний 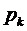 ,
, 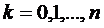 можно
предварительно, решив систему дифференциальных уравнений Эрланга (1.3), найти
вероятности состояний
можно
предварительно, решив систему дифференциальных уравнений Эрланга (1.3), найти
вероятности состояний 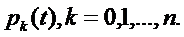 , а затем
подсчитать их пределы при
, а затем
подсчитать их пределы при 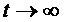 .
.
Можно поступить и иначе. Сначала в
каждом из дифференциальных уравнений системы Эрланга (1.3) перейти к пределу
при 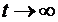 . В
результате из системы дифференциальных уравнений (1.3) можно получить
однородную систему линейных алгебраических уравнений, неизвестными в которой
как раз и будут предельные вероятности
. В
результате из системы дифференциальных уравнений (1.3) можно получить
однородную систему линейных алгебраических уравнений, неизвестными в которой
как раз и будут предельные вероятности 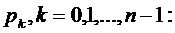
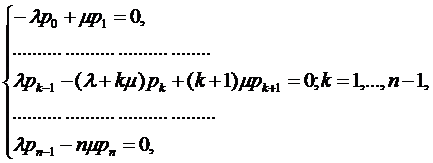
Решив эту систему, получим значения 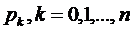 .
.
Но мы найдем предельные вероятности
из общих формул (3.19)-(3.21), выведенных для процесса гибели и размножения,
подставляя в них значения плотностей вероятностей переходов по формулам (1.1) и
(1.2).
Таким образом, получаем следующие
формулы для вычисления предельных вероятностей, выраженные через 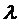 и
и 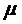 :
:
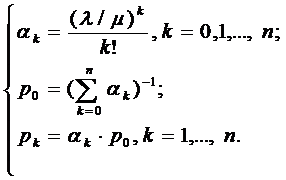 (1.6)
(1.6)
Из формул (1.6) видно, что
предельные вероятности 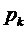 ,
, 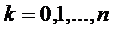 , зависят от
интенсивности входящего потока
, зависят от
интенсивности входящего потока  и интенсивности потока обслуживании
и интенсивности потока обслуживании
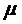 не по
отдельности, а от их отношения
не по
отдельности, а от их отношения 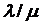 . Обозначим это отношение через
. Обозначим это отношение через 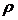 :
:
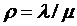
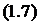
Величину 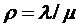 называют
приведенной интенсивностью входящего потока
называют
приведенной интенсивностью входящего потока  или показателем нагрузки СМО, или
трафиком. Так как
или показателем нагрузки СМО, или
трафиком. Так как 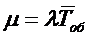 ,то
,то
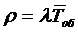
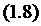
и таким образом приведенная
интенсивность входящего потока 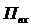 представляет собой среднее число
заявок, поступивших на вход СМО за среднее время
представляет собой среднее число
заявок, поступивших на вход СМО за среднее время 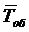 обслуживания одной заявки одним
каналом, и является показателем нагрузки системы. Единица измерения этого
показателя- эрланг.
обслуживания одной заявки одним
каналом, и является показателем нагрузки системы. Единица измерения этого
показателя- эрланг.
Подставив выражение (1.7) в систему
(1.6), получим
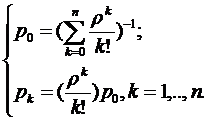 (1.9)
(1.9)
Формулы (1.9) называются формулами
Эрланга. Они выражают предельные вероятности состояний СМО через число каналов 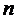 и
показатель нагрузки
и
показатель нагрузки 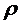 . Предельные
вероятности состояний можно выразить также и через средний интервал времени
. Предельные
вероятности состояний можно выразить также и через средний интервал времени  между двумя
соседними заявками но входящем потоке
между двумя
соседними заявками но входящем потоке 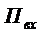 и среднее время
и среднее время 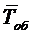 обслуживания
одной заявки одним каналом. Для этого достаточно выразить через эти средние
времена приведенную интенсивность. Подставим в равенство (1.8) величину
обслуживания
одной заявки одним каналом. Для этого достаточно выразить через эти средние
времена приведенную интенсивность. Подставим в равенство (1.8) величину
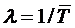 :
: 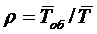 . (1.10)
. (1.10)
А теперь, подставив равенство (1.10)
в формулы Эрланга (1.9), получим требуемые формулы:
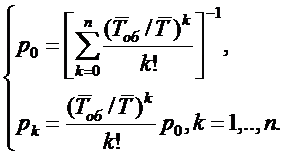
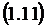
Зная все предельные вероятности
состояний 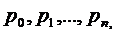
можно найти предельные
характеристики эффективности СМО.
Далее для краткости в названии
"предельные характеристики" будем опускать прилагательное
"предельные". Вместо "предельная вероятность отказа", и
т.д. будем говорить соответственно "вероятность отказа", и т.д.
По определению СМО с отказами,
заявка получает отказ, если поступает на вход в момент, когда вес каналы
заняты, т.е. когда СМО находится в состоянии 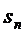 . Поэтому вероятность отказа
. Поэтому вероятность отказа 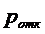 равна
вероятности
равна
вероятности 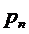 того, что
СМО находится в состоянии
того, что
СМО находится в состоянии 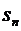 . Из второй
формулы системы (1.9) при
. Из второй
формулы системы (1.9) при 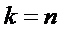 получаем
получаем
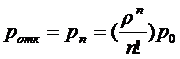
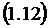
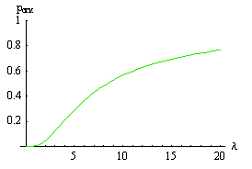
Рис 1.2. График зависимости
вероятности отказа 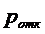 от
интенсивности входящего потока
от
интенсивности входящего потока  при n=5 и
при n=5 и 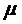 =1.
=1.
Так как событие, состоящее в том,
что пришедшая заявка получит отказ, и событие, состоящее и том, что пришедшая
заявка будет принята к обслуживанию, являются противоположными, то их
вероятности в сумме дают единицу. А потому вероятность того, что заявка будет
обслужена, можно подсчитать по формуле:
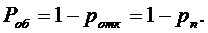
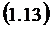
Относительная пропускная способность
равна вероятности обслуживания:
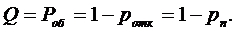
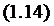
Абсолютная пропускная
способность
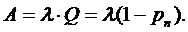
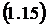
Интенсивность выходящего потока
обслуженных заявок
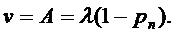
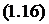
Для многоканальной СМО с отказами
одной из важных характеристик се эффективности является среднее число занятых
каналов 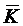 , или что то
же, среднее число заявок под обслуживанием
, или что то
же, среднее число заявок под обслуживанием 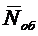 , которое для СМО с отказами
совпадает со средним числом заявок, находящихся в системе
, которое для СМО с отказами
совпадает со средним числом заявок, находящихся в системе 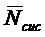 . Величину
. Величину 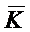 можно
подсчитать следующим образом: так как абсолютная пропускная способность А есть
среднее число заявок, обслуживаемых СМО в единицу времени, а один занятый канал
обслуживает в среднем за единицу времени
можно
подсчитать следующим образом: так как абсолютная пропускная способность А есть
среднее число заявок, обслуживаемых СМО в единицу времени, а один занятый канал
обслуживает в среднем за единицу времени 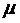 заявок, то среднее число
заявок, то среднее число 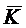 занятых
каналов будет равно отношению
занятых
каналов будет равно отношению 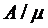 или, применяя (1.15) и (1.7),
получим
или, применяя (1.15) и (1.7),
получим
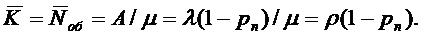
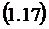
К формуле (1.17) можно было прийти и
другим путем, а именно, подсчитать величину 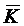 как математическое ожидание
как математическое ожидание 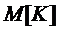 дискретной
случайной величины
дискретной
случайной величины 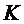 ,
представляющей собой число занятых каналов. Случайная величина
,
представляющей собой число занятых каналов. Случайная величина 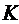 может
принимать значения
может
принимать значения 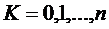 с
вероятностями соответственно
с
вероятностями соответственно 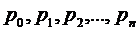 . Тогда, используя известную из
теории вероятностей (формулу для математического ожидания дискретной случайной
величины, формулы предельных вероятностей (1.9) и нормировочное условие (1.5),
получим:
. Тогда, используя известную из
теории вероятностей (формулу для математического ожидания дискретной случайной
величины, формулы предельных вероятностей (1.9) и нормировочное условие (1.5),
получим:
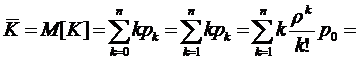
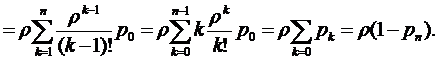
Наконец, выведем формулу для
вычисления среднего времени обслуживания заявки  , относящегося ко всем заявкам - как
к обслуженным, так и получившим отказ. Среднее время
, относящегося ко всем заявкам - как
к обслуженным, так и получившим отказ. Среднее время  не следует
путать со средним временем обслуживания заявки
не следует
путать со средним временем обслуживания заявки 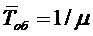 , которое относится только к
обслуженным заявкам. Для рассматриваемых СМО с отказами среднее время
, которое относится только к
обслуженным заявкам. Для рассматриваемых СМО с отказами среднее время 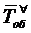 совпадает
со средним временем пребывания заявки в системе
совпадает
со средним временем пребывания заявки в системе 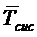 .
.
Рассмотрим 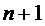 гипотез
гипотез 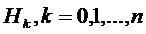 состоящих в
том, что система находится в состояниях
состоящих в
том, что система находится в состояниях 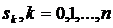 соответственно. Вероятности
соответственно. Вероятности 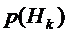 этих
гипотез равны
этих
гипотез равны 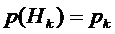 ,
, 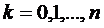 . Если
заявка поступает в СМО при гипотезе
. Если
заявка поступает в СМО при гипотезе 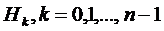 , т.е. когда СМО находится в
состоянии
, т.е. когда СМО находится в
состоянии 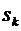 ,
, 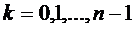 , то заявка
немедленно попадает под обслуживание, и потому условное математическое ожидание
, то заявка
немедленно попадает под обслуживание, и потому условное математическое ожидание
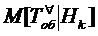 непрерывной
случайной величины
непрерывной
случайной величины 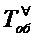 времени
обслуживания при гипотезе
времени
обслуживания при гипотезе 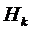 равно
среднему времени обслуживания
равно
среднему времени обслуживания  . Если же заявка приходит в СМО при
гипотезе
. Если же заявка приходит в СМО при
гипотезе 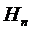 , т.е. когда
система находится в состоянии
, т.е. когда
система находится в состоянии 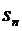 , в котором все
, в котором все 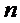 каналов
заняты, то заявка получает отказ, и потому
каналов
заняты, то заявка получает отказ, и потому 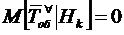 . Следовательно, по формуле полного
математического ожидания (см. [9], с. 77):
. Следовательно, по формуле полного
математического ожидания (см. [9], с. 77):
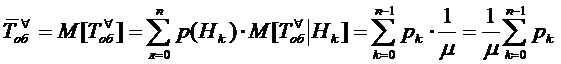 .
.
Но в силу нормировочного условия 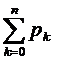 , имеем
, имеем
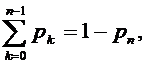
и следовательно,
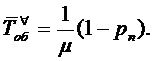
Отсюда, используя формулы (1.7) и
(1.17), получаем формулу Литтла:
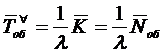 или
или 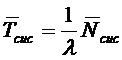
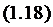
Формула Литтла показывает, что
среднее время 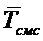 пребывания
заявки в СМО равно среднему числу заявок в системе
пребывания
заявки в СМО равно среднему числу заявок в системе 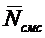 , деленному
на интенсивность
, деленному
на интенсивность 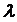 входящего
потока заявок, или, другими словами, среднее время
входящего
потока заявок, или, другими словами, среднее время 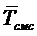 пребывания
заявки в СМО прямо пропорционально среднему числу заявок в системе
пребывания
заявки в СМО прямо пропорционально среднему числу заявок в системе 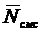 с
коэффициентом прямой пропорциональности, равным обратной величине интенсивности
с
коэффициентом прямой пропорциональности, равным обратной величине интенсивности
 входящего
потока заявок.
входящего
потока заявок.
1.2 Многолинейная СМО с отказами и взаимопомощью
между каналами «Все как один»
Во всех предыдущих разделах
рассмотренные СМО обладали общим свойством: каждая заявка могла обслуживаться
только одним каналом. На практике это условие не всегда выполняется. Существуют
такие СМО, в которых одна и та же заявка может одновременно обслуживаться
несколькими каналами.
Рассмотрим 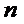 -канальную
СМО с отказами, на которую поступает простейший поток заявок
-канальную
СМО с отказами, на которую поступает простейший поток заявок 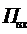 интенсивностью
интенсивностью
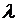 . Каналы
работают "'с взаимопомощью" типа "все как один", т.е. При
появлении первой заявки се начинают обслуживать все
. Каналы
работают "'с взаимопомощью" типа "все как один", т.е. При
появлении первой заявки се начинают обслуживать все 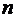 каналов,
которые будут занятыми до тех пор, пока заявка не будет обслужена. Если во
время занятости (всех) каналов поступает заявка, то она получает отказ и покидает
систему. После завершения обслуживания все
каналов,
которые будут занятыми до тех пор, пока заявка не будет обслужена. Если во
время занятости (всех) каналов поступает заявка, то она получает отказ и покидает
систему. После завершения обслуживания все 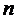 каналов оказываются свободными пока
не поступит следующая заявка, на обслуживание которой переключаются опять же
все
каналов оказываются свободными пока
не поступит следующая заявка, на обслуживание которой переключаются опять же
все 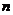 каналов, и
т.д. Таким образом, все
каналов, и
т.д. Таким образом, все 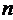 каналов
работают как один. Поэтому такую дисциплину взаимопомощи называют "все как
один". При такой дисциплине взаимопомощи каналов
каналов
работают как один. Поэтому такую дисциплину взаимопомощи называют "все как
один". При такой дисциплине взаимопомощи каналов 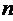 -канальная
СМО работает как одноканальная, но с более высокой интенсивностью обслуживания.
-канальная
СМО работает как одноканальная, но с более высокой интенсивностью обслуживания.
Каким образом ускорение обслуживания
зависит от числа каналов, является одним из важных вопросов при изучении
многоканальных СМО с взаимопомощью.
Будем полагать, что интенсивность
простейшего потока обслуживании есть некоторая функция 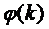 числа
числа 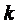 каналов,
одновременно обслуживающих заявку. Естественно предположить, что функция
каналов,
одновременно обслуживающих заявку. Естественно предположить, что функция 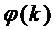 является
неубывающей, т.е. с увеличением числа
является
неубывающей, т.е. с увеличением числа 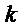 обслуживающих каналов интенсивность
обслуживающих каналов интенсивность
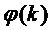 не будут
падать.
не будут
падать.
Как показывает практика,
неограниченное увеличение числа одновременно обслуживающих каналов не всегда
ведет к пропорциональному увеличению интенсивности обслуживания, естественнее
предположить, что начиная с некоторого критического числа каналов 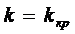 дальнейшее
увеличение числа обслуживающих каналов не повышает интенсивности потока
обслуживания.
дальнейшее
увеличение числа обслуживающих каналов не повышает интенсивности потока
обслуживания.
Простейшим случаем функции 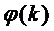 является
функция
является
функция
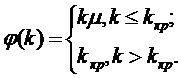
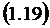
Здесь 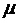 - интенсивность потока обслуживании
одним каналом, заранее известный коэффициент прямой пропорциональной
зависимости интенсивности
- интенсивность потока обслуживании
одним каналом, заранее известный коэффициент прямой пропорциональной
зависимости интенсивности 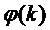 от числа
одновременно обслуживающих каналов
от числа
одновременно обслуживающих каналов 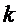 при
при 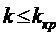 .
.
Если общее число каналов 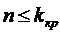 , то
, то 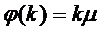 ,
, 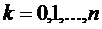 .
.
Если охарактеризовать состояния СМО
по числу занятых каналов, то очевидно, что она может пребывать только в одном
из двух состояний :
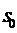 -все
-все 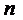 каналов свободны;
каналов свободны;
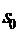 - все
- все 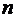 каналов заняты.
каналов заняты.
В системе, находящейся в состоянии 
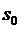 , заявок нет, а в состоянии
, заявок нет, а в состоянии 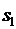 в системе
находится одна заявка, обслуживаемая одновременно всеми
в системе
находится одна заявка, обслуживаемая одновременно всеми 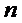 каналами.
каналами.
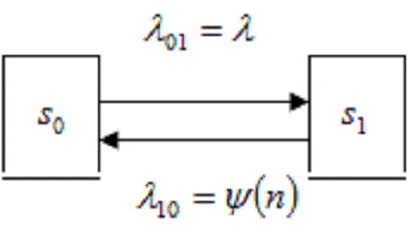
Рис. 1.3
Размеченный граф состояний будет
иметь вид, указанный на рис. 1.2.
Для предельных характеристик СМО с
взаимопомощью будем применять те же обозначения, что и в предыдущих параграфах,
добавляя в нижнем индексе знак "+".
Так как данная система работает как
одноканальная с отказами, то предельные характеристики ее функционирования
можно получить из уже выведенных в разделе 3 формул, заменяя в них 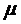 на
на 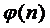 .
.
Из формул (1.17) и (1.18) получим
предельные вероятности состояний:
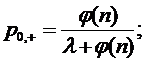
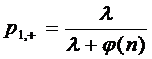

Вероятность того, что поступившая
заявка будет принята к обслуживанию или получит отказ, будут равны
соответственно:
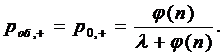 и
и 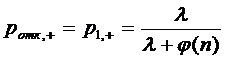
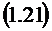
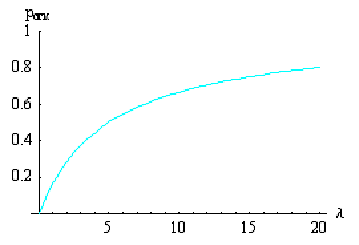
Рис 1.4. График зависимости
вероятности отказа 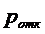 от
интенсивности входящего потока
от
интенсивности входящего потока  при n=5 и
при n=5 и 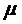 =1.
=1.
Относительную пропускную способность
получим из формулы (3.25):
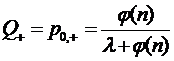 и
и 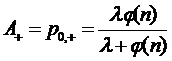
Среднее число 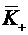 занятых
каналов получим как математическое ожидание
занятых
каналов получим как математическое ожидание 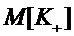 дискретной случайной величины
дискретной случайной величины 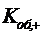 - числа
занятых каналов с законом распределения:
- числа
занятых каналов с законом распределения:
Таблица 1
В данном случае среднее число 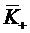 занятых
каналов отличается от среднего числа
занятых
каналов отличается от среднего числа 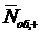 заявок, находящихся под
обслуживанием, которое можно определить как математическое ожидание
заявок, находящихся под
обслуживанием, которое можно определить как математическое ожидание 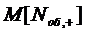 дискретной
случайной величины
дискретной
случайной величины 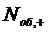 - числа
заявок под обслуживанием, принимающей значение 0 с вероятностью
- числа
заявок под обслуживанием, принимающей значение 0 с вероятностью 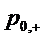 и значение
1 с вероятностью
и значение
1 с вероятностью 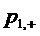 .
.
Таким образом, используя (1.20),
будем иметь
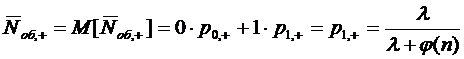 .
. 
Так как рассматриваемая СМО -
система с отказами, то среднее число 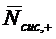 заявок в системе совпадает со
средним числом
заявок в системе совпадает со
средним числом 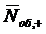 заявок
под обслуживанием:
заявок
под обслуживанием:
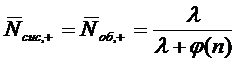 .
. 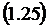
Среднее время обслуживания заявки,
относящееся только к обслуженным заявкам,
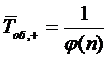 .
. 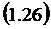
Для вычисления среднего времени 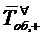 обслуживания
заявки, относящегося ко всем заявкам, как обслуженным, так и получившим отказ,
рассмотрим случайную величину
обслуживания
заявки, относящегося ко всем заявкам, как обслуженным, так и получившим отказ,
рассмотрим случайную величину 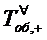 время обслуживания (любой) заявки и
две несовместные гипотезы
время обслуживания (любой) заявки и
две несовместные гипотезы 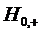 и
и 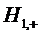 , состоящие
в том, что СМО находится соответственно в состояниях
, состоящие
в том, что СМО находится соответственно в состояниях 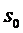 и
и 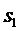 Вероятности
этих гипотез очевидно равны
Вероятности
этих гипотез очевидно равны 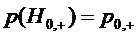 и
и 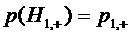 Если заявка поступила в СМО при
гипотезе
Если заявка поступила в СМО при
гипотезе 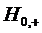 , т.е. когда
СМО находилась в состоянии
, т.е. когда
СМО находилась в состоянии 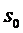 , в котором все каналы свободны, то
она немедленно начинает обслуживаться всеми
, в котором все каналы свободны, то
она немедленно начинает обслуживаться всеми 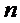 каналами и среднее время ее
обслуживания будет равно
каналами и среднее время ее
обслуживания будет равно 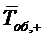 . Таким
образом, условное математическое ожидание случайной величины
. Таким
образом, условное математическое ожидание случайной величины 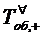 при
гипотезе
при
гипотезе 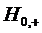 будет равно
будет равно
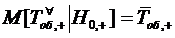 . Если же
заявка поступила в систему при гипотезе
. Если же
заявка поступила в систему при гипотезе 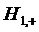 , т.е. когда СМО находилась в
состоянии
, т.е. когда СМО находилась в
состоянии 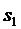 , в котором
все
, в котором
все 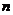 каналов
заняты, то она получает отказ и потому условное математическое ожидание
случайной величины
каналов
заняты, то она получает отказ и потому условное математическое ожидание
случайной величины 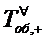 при
гипотезе
при
гипотезе 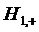 будет равно
будет равно
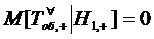 .
.
Применяя формулу полного
математического ожидания и используя (1.20), (1.24) и (1.26), , получим для 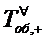 формулу
Литтла:
формулу
Литтла:
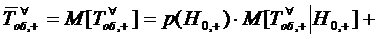
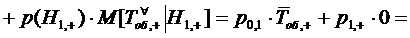
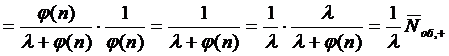 .
. 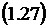
Опять же в силу того, что данная СМО
является системой с отказами, среднее время пребывания заявки в системе 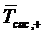 . совпадает
со средним временем нахождения заявки под обслуживанием
. совпадает
со средним временем нахождения заявки под обслуживанием 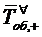 . Поэтому из
формул (1.25) и (1.27) получаем формулу Литтла для
. Поэтому из
формул (1.25) и (1.27) получаем формулу Литтла для 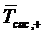 :
:
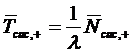 .
. 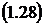
При 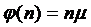 из формул соответственно получаем:
из формул соответственно получаем:
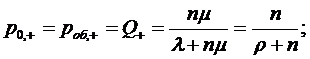
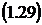
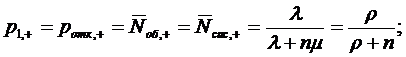
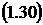
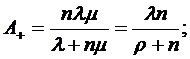
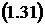
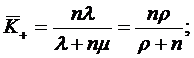
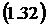
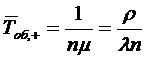
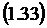
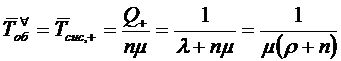
1.3 Многолинейная СМО с отказами и
«равномерной» взаимопомощью между каналами
Рассмотрим n -канальную СМО,
на вход которой подастся простейший поток заявок 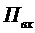 с интенсивностью
с интенсивностью  . Поток
обслуживании одним каналом также простейший с интенсивностью
. Поток
обслуживании одним каналом также простейший с интенсивностью 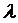 .
.
Если заявка поступает в СМО, когда
все n каналов свободны, то все n каналов приступают к се
обслуживанию. Если следующая заявка приходит в момент, когда все n
каналов заняты (обслуживанием предыдущей заявки), то часть каналов
переключается на ее обслуживание. Если во время обслуживания этих двух заявок
поступает третья, то часть каналов переключается на обслуживание третьей заявки
и т.д. до тех пор, пока каждая заявка, находящаяся в СМО, не окажется под
обслуживанием только одного канала. При этом, очевидно, все каналы будут
заняты, а заявка, пришедшая в этот момент, получает отказ и покидает СМО
необслуженной.
Таким образом, если в СМО находится
хотя бы одна заявка, то все n каналов заняты. Освободившиеся каналы
немедленно приступают к обслуживанию находящихся в СМО заявок.
Взаимопомощь между каналами
описанного типа называют равномерной.
Если интенсивность потока
обслуживания системой функционально зависит от числа каналов k следующим
образом:
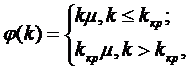
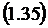
где 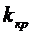 - некоторое критическое число каналов
системы (см график функции
- некоторое критическое число каналов
системы (см график функции 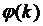 на рис. 12.1) и
на рис. 12.1) и 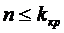 , то
для суммарно, интенсивности обслуживании, которая равна
, то
для суммарно, интенсивности обслуживании, которая равна 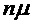 ,
безразлично какое принято количественное распределение каналов по обслуживаемым
заявкам, лишь бы в системе присутствовала хотя бы одна заявка, поскольку при
любом распределении все
,
безразлично какое принято количественное распределение каналов по обслуживаемым
заявкам, лишь бы в системе присутствовала хотя бы одна заявка, поскольку при
любом распределении все 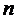 каналов
будут заняты.
каналов
будут заняты.
Припишем каждому состоянию системы
номер, равным числу заявок в системе, который, в силу того, что данная система
- система с отказами, совпадает с числом заявок, находящихся в состоянии
обслуживания.
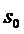 - в СМО нет заявок, нее n
каналов свободны;
- в СМО нет заявок, нее n
каналов свободны;
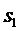 - в СМО одна заявка под
обслуживанием всеми
- в СМО одна заявка под
обслуживанием всеми 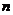 каналами;
каналами;
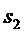 - в СМО две заявки под
обслуживанием, все каналы заняты
- в СМО две заявки под
обслуживанием, все каналы заняты
……..
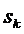 - в СМО
- в СМО 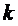 заявок под
обслуживанием, все каналы заняты;
заявок под
обслуживанием, все каналы заняты;
….
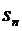 - в СМО n заявок, каждая из
которых обслуживается только одним каналом, все каналы заняты.
- в СМО n заявок, каждая из
которых обслуживается только одним каналом, все каналы заняты.
Рис. 1.5. Граф состояний СМО с отказами и
''равномерной'' взаимопомощью между каналами.
Таким образом, граф на рис 1.3
представляет собой граф состояний одноканальной СМО с ожиданием, ограничением
на длину очереди с максимальным числом мест в очереди  и с
интенсивностью потока обслуживаний
и с
интенсивностью потока обслуживаний  . Поэтому характеристики
рассматриваемой системы можно получить из соответствующих характеристик
однолинейной СМО с ожиданием и ограничением на длину очереди, заменяя в
последних
. Поэтому характеристики
рассматриваемой системы можно получить из соответствующих характеристик
однолинейной СМО с ожиданием и ограничением на длину очереди, заменяя в
последних 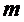 на
на 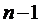 и
и 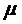 на
на 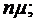 следовательно,
следовательно,
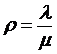 на
на 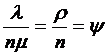 .
.
Вероятности состояний получим
равным:
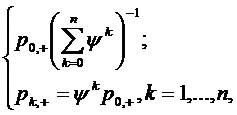
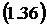
или:
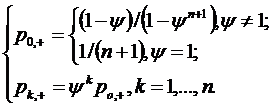
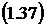
Вероятность отказа:
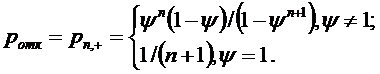
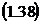
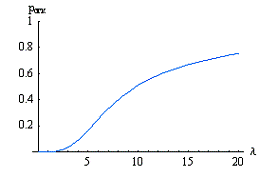
Рис 1.6. График зависимости
вероятности отказа 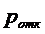 от
интенсивности входящего потока
от
интенсивности входящего потока  при n=5 и
при n=5 и 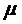 =1 ,
=1 ,  .
.
Вероятность того, что заявка будет
принята в систему 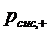 , равная
в данном случае вероятности того, что заявка будет обслужена
, равная
в данном случае вероятности того, что заявка будет обслужена 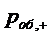 , выводим в
виде:
, выводим в
виде:
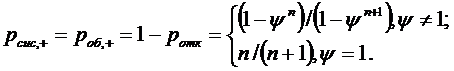
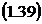
Относительная пропускная способность
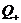 , которая
также совпадает с
, которая
также совпадает с 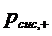 :
:
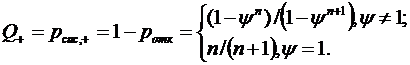
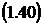
Тогда абсолютная пропускная
способность СМО
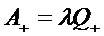 .
. 
Выражение для среднего числа 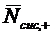 заявок и
системе, которое равно среднему числу
заявок и
системе, которое равно среднему числу 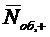 заявок, находящихся под обслуживанием:
заявок, находящихся под обслуживанием:
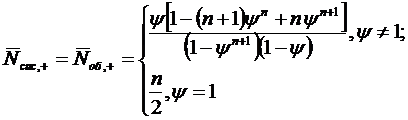
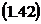
Для 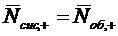 можно получить другое выражение.
Дли этого введем дискретную случайную величину
можно получить другое выражение.
Дли этого введем дискретную случайную величину 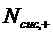 , представляющую собой число заявок
в СМО.
, представляющую собой число заявок
в СМО.
Закон распределения этой случайной
величины будет имен, следующий вид:
Таблица 2
Среднее число 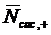 заявок в
СМО будет представлять с бой математическое ожидание случайной величины
заявок в
СМО будет представлять с бой математическое ожидание случайной величины 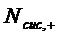 :
:
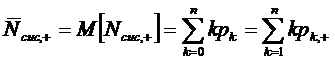
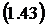
или, применяя (1.36),
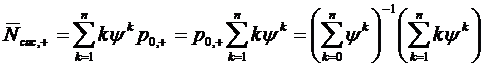

Если в правой части равенства (1.44)
сумму 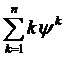 записать в
виде
записать в
виде  и , заменив
в ней
и , заменив
в ней 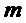 на
на 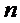 и
и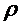 на
на  , а
, а 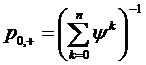 выразить по
формуле (1.37) то для
выразить по
формуле (1.37) то для 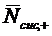 получим
формулу (1.42).
получим
формулу (1.42).
Поскольку заявка может обслуживаться
сразу несколькими каналами, то среднее число 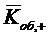 занятых каналов не совпадает со
средним числом
занятых каналов не совпадает со
средним числом 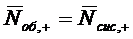 заявок под
обслуживанием
заявок под
обслуживанием
Среднее число 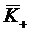 занятых
каналов можно рассчитать как математическое ожидание
занятых
каналов можно рассчитать как математическое ожидание 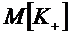 дискретной
случайной величины
дискретной
случайной величины 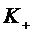 , представляющей
собой число занятых каналов и распределенной, очевидно, по следующему закону:
, представляющей
собой число занятых каналов и распределенной, очевидно, по следующему закону:
Таблица 3
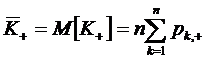
откуда, применяя (1.36),
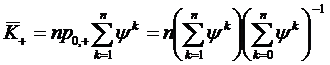
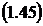
Если 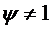 , то применяя в правой части формулы
(1.45) формулу суммы конечного числа членов геометрической прогрессии, будем
иметь:
, то применяя в правой части формулы
(1.45) формулу суммы конечного числа членов геометрической прогрессии, будем
иметь:
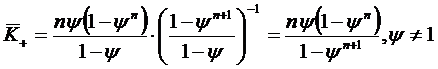 .
. 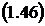
Если же 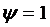 , то из
равенства (1.45):
, то из
равенства (1.45):
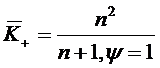
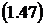
Запишем формулы (1.46) и (1.47) в
объединенной форме:
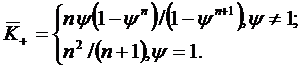
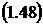
Из формул (1.46) и (1.47) получаем
неравенство
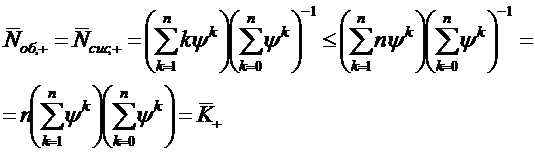
говорящее о том, что среднее число
заявок, находящихся под обслуживанием, не превышает среднего числа занятых
каналов, что является следствием взаимопомощи между каналами.
Нетрудно догадаться, что из формул
(1.41), (1.40) и (1.48) вытекает равенство:
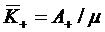 .
. 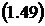
Среднее время пребывания заявки в
системе или что то же среднее время пребывания заявки в состоянии обслуживания
получим из формулы Литтла (5.27):
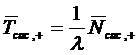
Глава 2. Сравнение основных
показателей многолинейных СМО с отказами
.1 Сравнение многолинейной СМО с
взаимопомощью между каналами типа ''все как'' один и с ''равномерной''
взаимопомощью между каналами
.1.1 Сравнение пропускной
способности системы
Проведем сравнительный анализ СМО с
взаимопомощью между каналами типа ''все как один'' и с ''равномерной''
взаимопомощью между каналами.
Так как обозначения характеристик
данных систем аналогичны, то для их различия для системы с взаимопомощью между
каналами типа ''все как один'' будем добавлять верхний индекс ''в'', а для
''равномерной'' взаимопомощи - верхний индекс ''р''. Например, 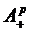 - абсолютная
пропускная способность в системе при ''равномерной'' взаимопомощи между
каналами, а
- абсолютная
пропускная способность в системе при ''равномерной'' взаимопомощи между
каналами, а 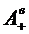 - при
взаимопомощи между каналами типа ''все как один''.
- при
взаимопомощи между каналами типа ''все как один''.
Из предыдущих пунктов следует, что 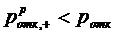 и
и 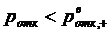 . Из этих
неравенств следует, что
. Из этих
неравенств следует, что
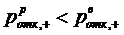 .
.
Следовательно, вероятность отказа
при ''равномерной'' взаимопомощи меньше, чем при взаимопомощи между каналами
типа ''все как один''.
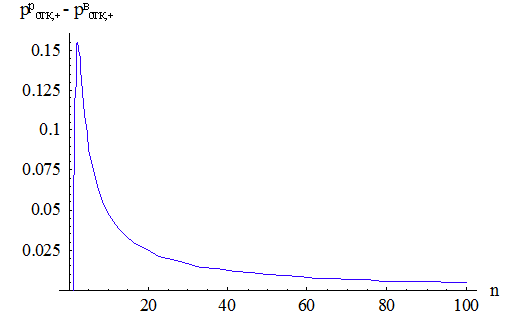
Рис. 2.1. График зависимости 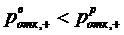 от числа
каналов обслуживания
от числа
каналов обслуживания 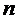 .
.
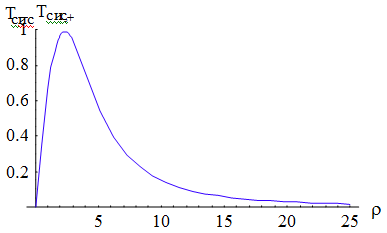
Рис. 2.2. График зависимости 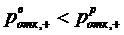 от
коэффициента нагрузки системы
от
коэффициента нагрузки системы 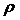 .
.
Как видно на рис. 2.2, что при 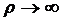 вероятность
отказа
вероятность
отказа 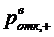 в
многоканальной СМО с взаимопомощью между каналами типа ''все как один'' будет
стремиться к вероятности отказа
в
многоканальной СМО с взаимопомощью между каналами типа ''все как один'' будет
стремиться к вероятности отказа 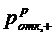 СМО с ''равномерной'' взаимопомощью
между каналами, то есть из (1.30) и (1.38) следует, что
СМО с ''равномерной'' взаимопомощью
между каналами, то есть из (1.30) и (1.38) следует, что
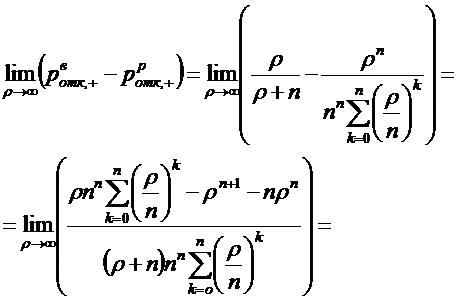
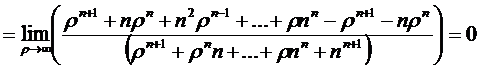 .
.
Аналогично для относительной и
абсолютной пропускной способности:
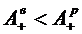 и
и 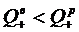 .
.
Таким образом, при ''равномерной''
взаимопомощи между каналами можно улучшить пропускную способность
многоканальной СМО с отказами по сравнению с взаимопомощью между каналами типа
''все как один''.
.1.2 Сравнение среднего времени
пребывания заявки в системе
Сравним пропускную способность 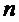 - канальной
СМО с отказами и ''равномерной'' взаимопомощью между каналами с такой же СМО,
но с взаимопомощью между каналами типа ''все как один'' при
- канальной
СМО с отказами и ''равномерной'' взаимопомощью между каналами с такой же СМО,
но с взаимопомощью между каналами типа ''все как один'' при 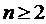 ,
, 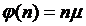 .
.
При 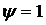 , то есть
, то есть  и
и 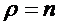 , получаем
из (1.50), (1.43), (1.37) и (1.34):
, получаем
из (1.50), (1.43), (1.37) и (1.34):
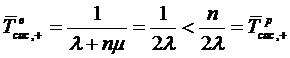 .
.
Таким образом, при 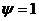 среднее
время пребывания заявки в системе при взаимопомощи ''все как один'' меньше, чем
при ''равномерной взаимопомощи''.
среднее
время пребывания заявки в системе при взаимопомощи ''все как один'' меньше, чем
при ''равномерной взаимопомощи''.
Случай 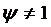 можно
пронаблюдать на рис. 2.1, из которого видно, что так же
можно
пронаблюдать на рис. 2.1, из которого видно, что так же  .
.
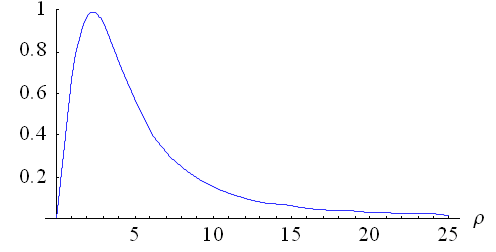
Рис. 2.3 График зависимости  от
коэффициента нагрузки системы
от
коэффициента нагрузки системы  .
.
Из рис. 2.3видно, что разность  , для любых
значений
, для любых
значений  .
Следовательно, среднее время пребывания заявки в системе при ''равномерной''
взаимопомощи больше, чем в случае взаимопомощи тира ''все как один'', т.е.
.
Следовательно, среднее время пребывания заявки в системе при ''равномерной''
взаимопомощи больше, чем в случае взаимопомощи тира ''все как один'', т.е.  .
.
Значит  при любом
значении показателя нагрузки системы.
при любом
значении показателя нагрузки системы.
Это связано с тем, что в
многоканальной СМО с ''равномерной'' взаимопомощью при приходе второй и
последующих заявок, как было сказано в пункте 1.3, то часть линий переключается
на их обслуживание.
.1.3 Сравнение среднего числа заявок
в системе
Теперь сравним многоканальные СМО с
''равномерной'' взаимопомощью и с взаимопомощью между каналами типа ''все как
один'' с точки зрения среднего числа заявок в системе при  ,
,  .
.
Из (1.30) и (1.42), следует, что:
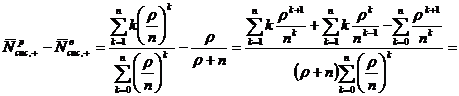
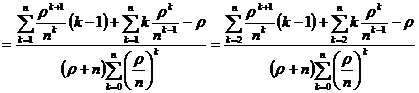 . (2.1)
. (2.1)
Но так как коэффициент нагрузки 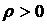 и данные
системы являются многоканальными, то есть
и данные
системы являются многоканальными, то есть 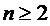 , то правая часть равенства (2.1)
является положительной. Следовательно,
, то правая часть равенства (2.1)
является положительной. Следовательно, 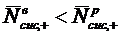
Аналогично можно наблюдать на рис.
2.4
Как видно на рис. 2.4 что при 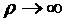 разность
разность  устремляется
к определенному значению. Покажем это,
устремляется
к определенному значению. Покажем это,
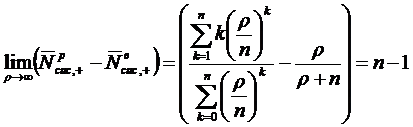
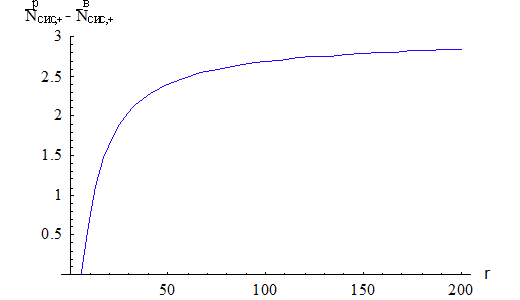
Рис. 2.4 График зависимости  от
коэффициента нагрузки системы
от
коэффициента нагрузки системы  .
.
.2 Сравнение многолинейной СМО с
отказами без взаимопомощи и с взаимопомощью типа ''все как один''
.2.1 Сравнение пропускной
способности системы
Проведем аналитическое и
компьютерное сравнение многоканальной СМО с отказами с точки зрения пропускной
способности 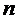 -канальную
систему с отказами без взаимопомощи между каналами и
-канальную
систему с отказами без взаимопомощи между каналами и 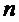 - канальную
систему с отказами с взаимопомощью между каналами типа '''все как один' при
- канальную
систему с отказами с взаимопомощью между каналами типа '''все как один' при 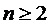 и
и  .
.
Используя формулы (1.6), (1.12), (1.30),
рассмотрим разность между  и
и  :
:
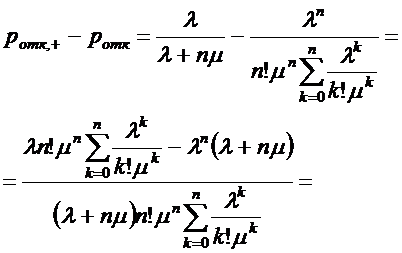
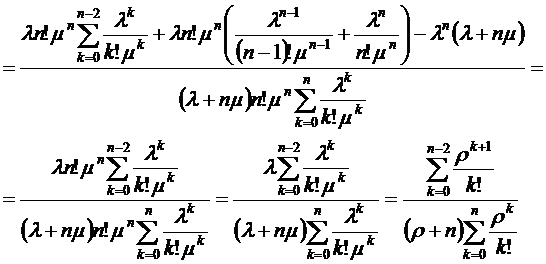
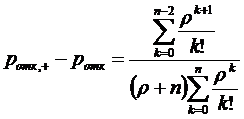 (2.2)
(2.2)
Так как коэффициент нагрузки системы
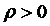 и данные
системы многоканальные(
и данные
системы многоканальные(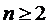 ), то правая
часть равенства (2.2) положительная. Значит
), то правая
часть равенства (2.2) положительная. Значит 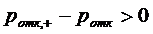 , следовательно
, следовательно  т.е.
вероятность отказа в
т.е.
вероятность отказа в  - канальной
системе с взаимопомощью между каналами типа ''все как один’' больше чем в
- канальной
системе с взаимопомощью между каналами типа ''все как один’' больше чем в  - канальной
системе без взаимопомощи.
- канальной
системе без взаимопомощи.
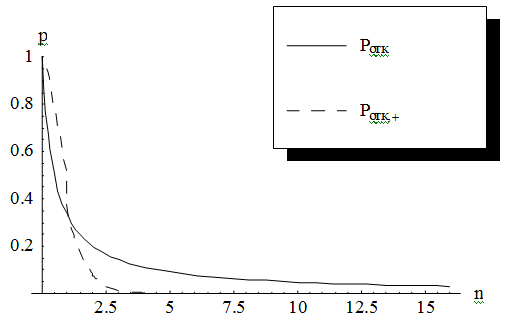
Рис 2.5 Графики вероятности отказа 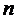 - канальной
СМО с взаимопомощью между каналами типа ''все как один'' и
- канальной
СМО с взаимопомощью между каналами типа ''все как один'' и 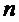 -канальной
СМО с отказами без взаимопомощи между каналами(
-канальной
СМО с отказами без взаимопомощи между каналами( 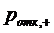 -пунктиром,
-пунктиром, 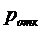 - сплошной
линией).
- сплошной
линией).
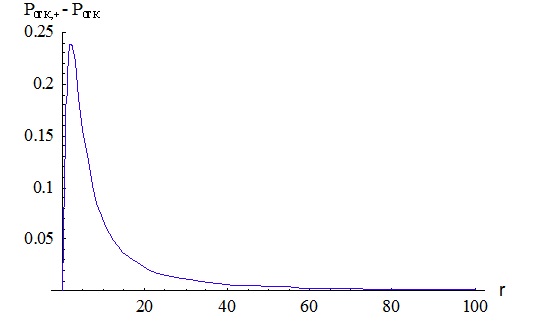
Рис. 2.6 график зависимости 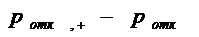 от
коэффициента нагрузки системы
от
коэффициента нагрузки системы 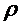 .
.
На рис. 2.6 видно, что вероятность
отказа 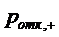 при
при 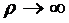 в
многоканальной СМО с взаимопомощью между каналами, будет стремиться к
вероятности отказа СМО без взаимопомощи, т.е.
в
многоканальной СМО с взаимопомощью между каналами, будет стремиться к
вероятности отказа СМО без взаимопомощи, т.е.
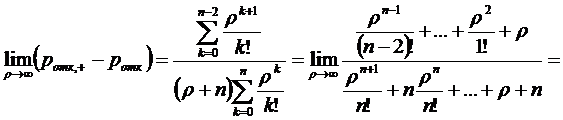
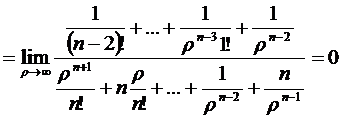
От сюда следует, что вероятность
отказа при наличии взаимопомощи типа ''все как один'' увеличивается. Это
происходит потому, что за время пока все 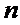 каналов заняты обслуживанием одной
заявки, в СМО могут поступать новые заявки, которые получают отказ.
каналов заняты обслуживанием одной
заявки, в СМО могут поступать новые заявки, которые получают отказ.
Так как в обоих случаях СМО без
взаимопомощи и с взаимопомощью относительная пропускная способность 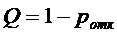 и
и 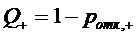 , то у СМО с
взаимопомощью типа '''все как один'' относительная пропускная способность
уменьшается, следовательно
, то у СМО с
взаимопомощью типа '''все как один'' относительная пропускная способность
уменьшается, следовательно 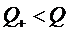 . Значит, уменьшается и абсолютная
пропускная способность
. Значит, уменьшается и абсолютная
пропускная способность
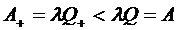 (2.3)
(2.3)
Из проведенных выше исследований,
можно сделать вывод, что взаимопомощь типа '' все как один '', по сравнению с
СМО без взаимопомощи, с точки зрения вероятности отказа и пропускной
способности, как относительной, так и абсолютной, оказывается невыгодной.
.2.2 Сравнение среднего числа заявок
в системе
Сравним многоканальные СМО с
взаимопомощью и без нее с точки зрения среднего числа заявок в системе при 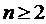 ,
, 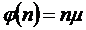 .
.
В (2.3) было показано, что
абсолютная пропускная способность СМО с взаимопомощью меньше, чем относительная
пропускная способность СМО без взаимопомощи, т.е. сеть 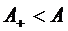 . Так как
интенсивность простейшего потока обслуживания каждого канала
. Так как
интенсивность простейшего потока обслуживания каждого канала 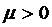 , то
следовательно:
, то
следовательно:
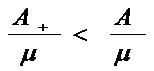 (2.4)
(2.4)
Так как в многоканальных системах 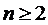 , то
получаем
, то
получаем 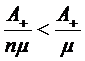 . С учетом
(2.4) получаем
. С учетом
(2.4) получаем
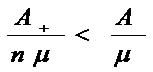 ,
,
это неравенство равносильно
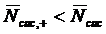 .
.
Согласно формул (1.17),(1.18),(1.22)
и (1.25),
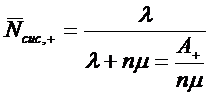 и
и 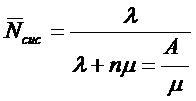
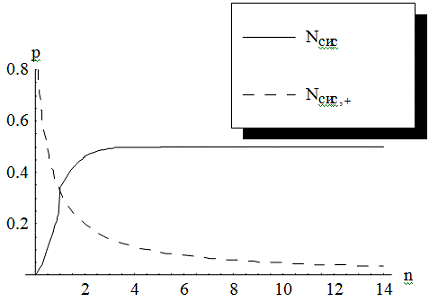
Рис. 2.7. Графики зависимости
среднего числа заявок в системе от числа каналов обслуживания в многоканальной
СМО с взаимопомощью типа ''все как один'' и без нее( -пунктиром,
-пунктиром,  - сплошной
линией).
- сплошной
линией).
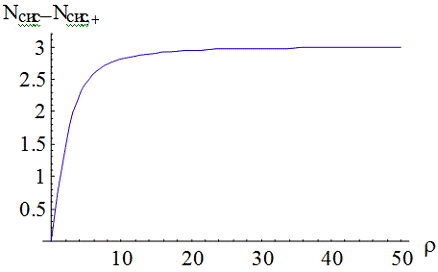
Рис. 2.8 График зависимости  от
коэффициента нагрузки системы
от
коэффициента нагрузки системы 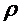 .
.
Из рис. 2.8. видно, что при 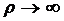 разность
между
разность
между 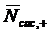 и
и 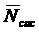 устремляется
в определенному значению. Покажем это:
устремляется
в определенному значению. Покажем это:

Среднее число заявок в системе с
взаимопомощью типа ''все как один'' уменьшилось, по сравнению с системой без
взаимопомощи. Следовательно, по среднему числу заявок СМО с взаимопомощью между
каналами типа ''все как один'' так же является невыгодной.
2.2.3 Сравнение среднего пребывания
заявки в системе
Проведем аналитическое и
компьютерное сравнение многоканальной СМО с взаимопомощью и без нее с точки
зрения среднего времени пребывания в системе при 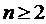 ,
,  .
.
Среднее время пребывания заявки в
системе, для системы без взаимопомощи из (1.18) и (1.17):
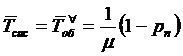
Среднее время пребывания заявки в
системе, для системы с взаимопомощью типа ''все как один'' из (1.34):
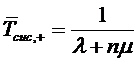 .
.
Рассмотрим разность 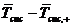 :
:

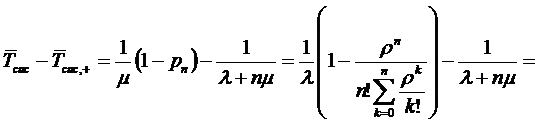
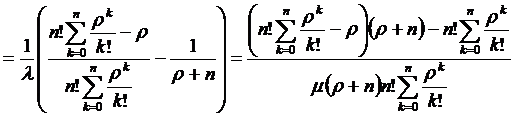 (2.5)
(2.5)
Так как коэффициент нагрузки системы
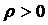 и
интенсивность простейшего потока обслуживания каждого канала
и
интенсивность простейшего потока обслуживания каждого канала 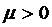 , данные
системы являются многоканальными(
, данные
системы являются многоканальными(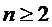 ), то знаменатель дроби в правой
части выражения (2.4) является положительным. Определим знак числителя:
), то знаменатель дроби в правой
части выражения (2.4) является положительным. Определим знак числителя:
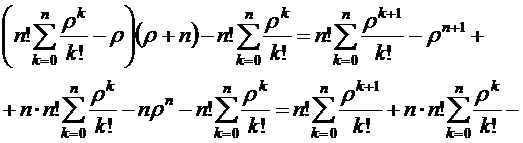
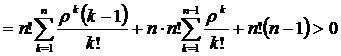 (2.6)
(2.6)
Из (2.6) и (2.5) следует, что
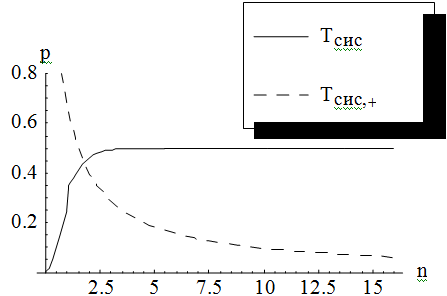
Рис. 2.9 Графики зависимости
среднего времени пребывания заявки в системе от числа каналов обслуживания в
многоканальной СМО с взаимопомощью типа ''все как один'' и без нее.
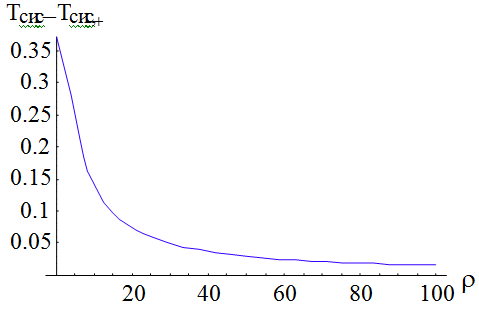
Рис. 2.10 График зависимости 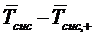 от
коэффициентов нагрузки системы
от
коэффициентов нагрузки системы 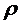 .
.
На рис. 2.10. видно, что при 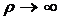 разность
разность 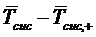 будет
стремиться к нулю, т.е. согласно (2.5) и (2.6):
будет
стремиться к нулю, т.е. согласно (2.5) и (2.6):
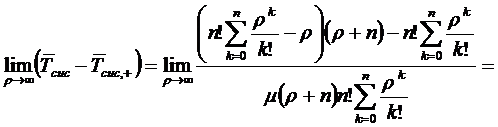
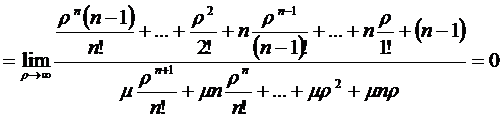
Следовательно, среднее время
пребывания заявки в системе с взаимопомощью типа ''все как один'' уменьшилось,
по сравнению с системой без взаимопомощи. Можно сделать вывод, что если имеются
причины, по которым желательно своротить время нахождения заявки в СМО(например
если пребывание в системе опасно для заявки), то, несмотря на уменьшение
пропускной способности, все же будет лучше ввести взаимопомощь каналов типа
''все как один''.
.3 Сравнение многолинейной СМО с
отказами без взаимопомощи и с ''равномерной'' взаимопомощью между каналами
.3.1 Сравнение пропускной
способности системы
Сравним пропускную способность 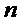 - канальной
СМО с отказами и ''равномерной'' взаимопомощью между каналами с такой же СМО,
но без взаимопомощи.
- канальной
СМО с отказами и ''равномерной'' взаимопомощью между каналами с такой же СМО,
но без взаимопомощи.
Сравним вероятности отказа этих двух
систем. Воспользуемся формулами (1.6), (1.7), (1.12), (1.36) и (1.37), и
рассмотрим разность 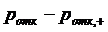 :
:
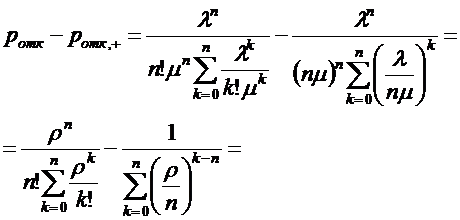
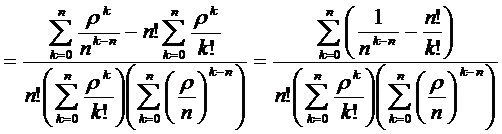
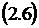
Рассмотрим 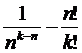 при
условии, что
при
условии, что 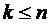 :
:
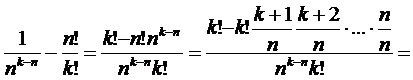
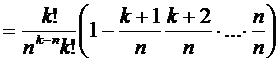 (2.7)
(2.7)
Так как 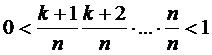 , то
значение (2.8) является положительным и, следовательно, (2.7) положительно,
т.е.
, то
значение (2.8) является положительным и, следовательно, (2.7) положительно,
т.е. 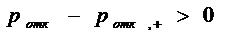 или
или 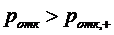 , то есть
вероятность отказа в
, то есть
вероятность отказа в  -канальной
системе с ''равномерной'' взаимопомощью между каналами меньше, чем в
-канальной
системе с ''равномерной'' взаимопомощью между каналами меньше, чем в  -канальной
системе без взаимопомощи.
-канальной
системе без взаимопомощи.
Аналогичное можно наблюдать на рис.
2.11 и рис. 2.12:

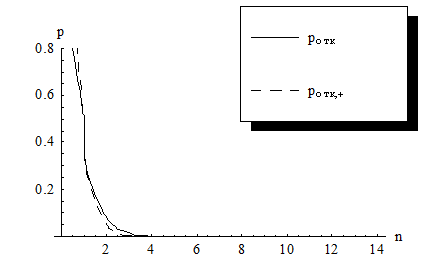
Рис. 2.11. Графики вероятностей
отказа  - канальной
СМО с ''равномерной'' взаимопомощью между каналами и
- канальной
СМО с ''равномерной'' взаимопомощью между каналами и  -канальной
СМО без взаимопомощи.
-канальной
СМО без взаимопомощи.
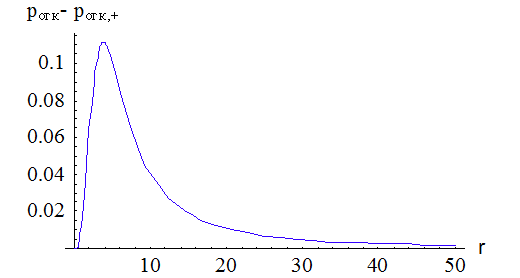
Рис. 2.12. Графики зависимости  от
коэффициента нагрузки системы
от
коэффициента нагрузки системы 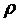 .
.
Как видно на рис. 2.12, что при 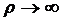 вероятность
отказа
вероятность
отказа 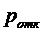 в
многоканальной СМО без взаимопомощи между каналами будет стремиться к
вероятности отказа
в
многоканальной СМО без взаимопомощи между каналами будет стремиться к
вероятности отказа 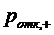 СМО с
''равномерной'' взаимопомощью между каналами, т.е. есть из (2.7) следует, что
СМО с
''равномерной'' взаимопомощью между каналами, т.е. есть из (2.7) следует, что
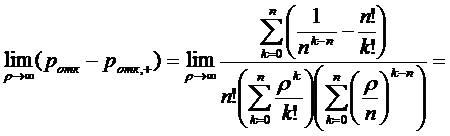
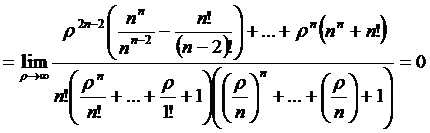
Таким образом, при ''равномерной''
взаимопомощи между каналами вероятность отказа меньше.
Так как 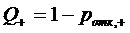 и
и 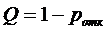 , то
, то 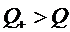 и,
следовательно,
и,
следовательно,
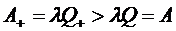 .
.
Полученные неравенства показывают,
что с введением ''равномерной взаимопомощи'' относительная и абсолютная
пропускная способности многоканальной СМО возрастают.
.3.2 Сравнение среднего времени
пребывания заявки и среднего числа заявок в системе
В данном пункте проведем графическое
сравнение многоканальной СМО с отказами с точки зрения среднего времени
пребывания заявки в 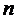 -канальную
систему с отказом, но с ''равномерной'' взаимопомощью между каналами.
-канальную
систему с отказом, но с ''равномерной'' взаимопомощью между каналами.
При ''равномерной'' взаимопомощи
уменьшиться среднее время 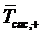 пребывания
заявки в системе, то есть
пребывания
заявки в системе, то есть
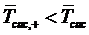 ,
,
Где 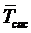 - среднее время пребывания заявки в
- среднее время пребывания заявки в 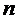 -канальной
СМО с отказами без взаимопомощи между каналами.
-канальной
СМО с отказами без взаимопомощи между каналами.
Это можно пронаблюдать на рис. 2.9:
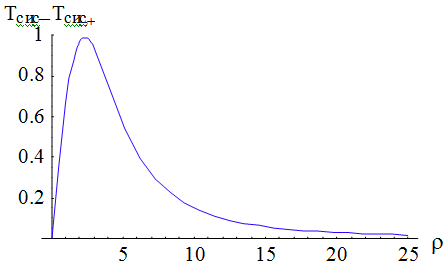
Рис. 2.13. Графики зависимости 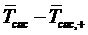 от
коэффициента нагрузки системы
от
коэффициента нагрузки системы 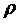 .
.
Из данного рис. 2.13 видно, что
разность 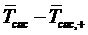 принимает положительные
значения, и согласно (1.9), (1.17),(1.18),(1.43),(1.50) и (1.36) данная
разность стремиться к нулю при
принимает положительные
значения, и согласно (1.9), (1.17),(1.18),(1.43),(1.50) и (1.36) данная
разность стремиться к нулю при 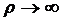 .
.
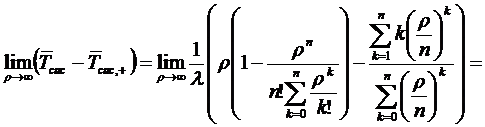
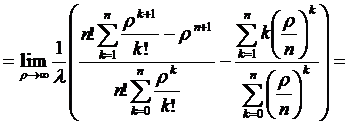
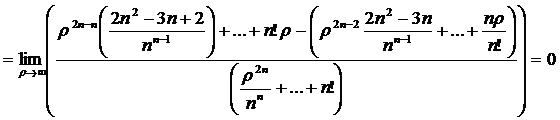
И так как 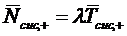 и
и 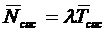 , а
интенсивностью простейшего входящего потока
, а
интенсивностью простейшего входящего потока 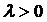 , то, значит, среднее число заявок в
системе так же уменьшиться:
, то, значит, среднее число заявок в
системе так же уменьшиться:
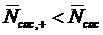 .
.
Следовательно, в многолинейной СМО с
отказами и с ''равномерной'' взаимопомощью между каналами уменьшится как
среднее время пребывания заявки в системе, так и среднее число заявок в
системе.
Глава 3. Практическое применение СМО
с отказами
.1 Решение задач оптимизации.
Нахождение оптимального числа линий обслуживания
Рассмотрим влияние предельных
характеристик на эффективность функционирования СМО.
Почти все рассмотренные выше
предельные характеристики эффективности функционирования СМО зависят от числа
линий обслуживания, следователь будет целесообразно рассмотреть задачу
оптимизации многолинейной СМО с отказами по числу линий обслуживания.
Рассмотрим многолинейную СМО 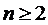 .
.
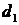 - затраты на содержание одной линии
обслуживания,
- затраты на содержание одной линии
обслуживания,
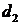 -потери от отказа заявки
-потери от отказа заявки
Тогда общие затраты можно описать
функцией вида:
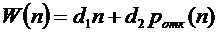
Нам необходимо подобрать число
каналов обслуживания 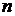 таким
образом, чтобы затраты оказались минимальными, т.е. решить следующую задачу
оптимизации:
таким
образом, чтобы затраты оказались минимальными, т.е. решить следующую задачу
оптимизации:
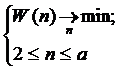 ,
,
где 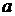 - некоторая константа,
характеризующая ограничение на число каналов.
- некоторая константа,
характеризующая ограничение на число каналов.
Для каждого вида СМО рассмотрим вид
функции 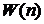 :
:
1. СМО без взаимопомощи:
Общие затраты
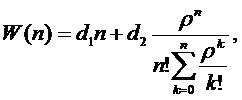
Задача оптимизации
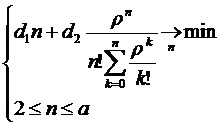
2. СМО с взаимопомощью между каналами типа ''все
как один''
Общие затраты
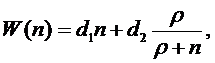
Задача оптимизации
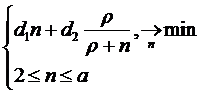
3. СМО с '' равномерной ''
взаимопомощью
Общие затраты
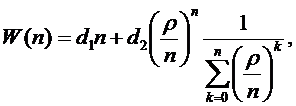
Задача оптимизации
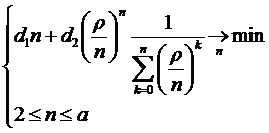
Решением данной задачи оптимизации
является программа, написанная на Delphi 7. Текст программы приведен в
приложении.
В Таблице 3.1 приведены примеры
работы данной программы. Легко заметить, что аналитические формулы, полученные
в Главе 1, имеют место и на практике.
Таблица 3.1 Оптимальное число линий
обслуживания для СМО с отказами
|
л
|
м
|
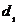 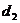 aСмо с отказамиВсе как
одинРавномерная взаимопомощь aСмо с отказамиВсе как
одинРавномерная взаимопомощь
|
|
|
|
|
|
|
1
|
3
|
150
|
10000
|
100
|
4
|
4
|
3
|
|
2
|
3
|
150
|
10000
|
100
|
6
|
6
|
4
|
|
2
|
5
|
1500
|
10000
|
100
|
2
|
2
|
2
|
|
2
|
9
|
150
|
10000
|
100
|
3
|
4
|
3
|
|
8
|
9
|
150
|
10000
|
100
|
7
|
7
|
4
|
|
21
|
22
|
150
|
10000
|
100
|
7
|
7
|
4
|
|
1
|
2
|
150
|
100
|
100
|
2
|
2
|
2
|
|
1
|
3
|
150
|
1000
|
100
|
2
|
2
|
2
|
|
1
|
3
|
15
|
10000
|
100
|
6
|
15
|
4
|
|
1
|
4
|
15
|
10000
|
100
|
5
|
13
|
4
|
|
1
|
4
|
15
|
10000
|
100
|
5
|
10
|
4
|
|
3
|
4
|
15
|
10000
|
100
|
14
|
22
|
5
|
3.2 Оценка ожидаемого дохода и дисперсии дохода
систем массового обслуживания
Рассмотрим СМО S Под ее состоянием
будем понимать вектор 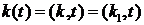 , где
, где 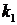 - число
заявок в системе S в момент времени
- число
заявок в системе S в момент времени 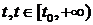 . Введем также систему
. Введем также систему 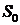 (внешнюю
среду), из которой в систему поступает простейший поток заявок с интенсивностью
(внешнюю
среду), из которой в систему поступает простейший поток заявок с интенсивностью
 .
.
Рассмотрим случай, когда
интенсивность обслуживания заявок в системе S 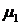 не зависит от числа заявок в ней.
Пусть
не зависит от числа заявок в ней.
Пусть  -
вероятность поступления заявки из системы
-
вероятность поступления заявки из системы 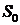 в систему S. Очевидно, что
в систему S. Очевидно, что 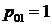 . Требуется
найти ожидаемы (средние) доходы систем за время
. Требуется
найти ожидаемы (средние) доходы систем за время 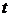 при условии, что известно ее
состояние в начальный момент
при условии, что известно ее
состояние в начальный момент 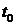 . При этом вначале будем,
предполагать, что сеть функционирует в условиях высокой нагрузки, т.е.
. При этом вначале будем,
предполагать, что сеть функционирует в условиях высокой нагрузки, т.е. 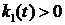 ,
, 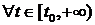 .
.
Рассмотрим динамику изменения
доходов системы S. Обозначим через  ее доход в момент времени
ее доход в момент времени 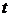 . Пусть в
некоторый момент
. Пусть в
некоторый момент 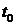 доход этой
системы был равен
доход этой
системы был равен 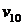 . Необходимо
найти доход системы
. Необходимо
найти доход системы 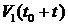 в момент
времени
в момент
времени 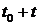 . Разобьем
отрезок
. Разобьем
отрезок 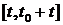 на
на  равных
частей длиной
равных
частей длиной 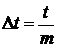 , считая
, считая  большим.
Для нахождения дохода системы выпишем вероятности тех событий, которые могут
произойти на
большим.
Для нахождения дохода системы выпишем вероятности тех событий, которые могут
произойти на  -ом отрезке
времени. При этом возможны следующие ситуации: а) с вероятностью
-ом отрезке
времени. При этом возможны следующие ситуации: а) с вероятностью 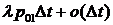 в систему S1
поступит заявка из внешней среды, которая принесет ей доход в размере
в систему S1
поступит заявка из внешней среды, которая принесет ей доход в размере 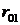 , где
, где 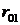 - СВ с
функцией распределения (ф.р.)
- СВ с
функцией распределения (ф.р.) 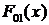 ; б) с вероятностью
; б) с вероятностью 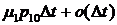 заявка из
системы S перейдет во внешнюю среду, при этом ее доход уменьшится на величину
заявка из
системы S перейдет во внешнюю среду, при этом ее доход уменьшится на величину 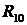 , где
, где 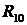 - СВ с ф.р.
- СВ с ф.р.
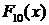 ; в) с
вероятностью
; в) с
вероятностью 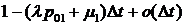 на отрезке
времени
на отрезке
времени 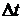 изменение
состояния системы S не произойдет.
изменение
состояния системы S не произойдет.
За каждый малый промежуток времени 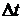 система S
увеличивает свой доход на величину
система S
увеличивает свой доход на величину 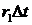 за счет процентов на денежные
средства, находящиеся в ней. Будем считать, что
за счет процентов на денежные
средства, находящиеся в ней. Будем считать, что 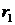 является СВ с ф.р.
является СВ с ф.р. 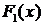 , а СВ
, а СВ 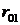 ,
, 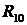 ,
, 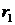 попарно
независимы.
попарно
независимы.
Пусть 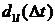 - изменение дохода СМО на
- изменение дохода СМО на  -ом отрезке
времени величиной
-ом отрезке
времени величиной 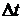 . Тогда из
вышеуказанного следует
. Тогда из
вышеуказанного следует
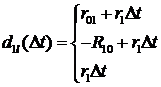 с вероятностью
с вероятностью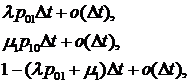 (3.1)
(3.1)
Доход системы S равен
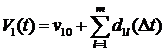 . (3.2)
. (3.2)
Введем обозначения для
соответствующих математических ожиданий (м.о.):
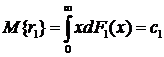 ,
, 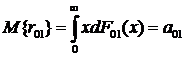 ,
,
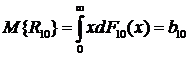 . (3.3)
. (3.3)
Выведем соотношение для м.о. системы
SВ в момент времени 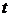 . По формуле для м.о. дискретной СВ,
. По формуле для м.о. дискретной СВ,
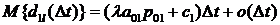 . (3.4)
. (3.4)
И, как следует из (3.2) с учетом 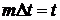 , при
, при 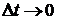
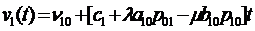 (3.5)
(3.5)
Для ожидаемого дохода в системе в
целом имеем:
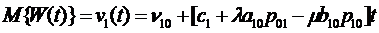 (3.6)
(3.6)
Таким образом, можно вывести формулу
для расчета дохода для различных СМО. Воспользовавшись соотношениями (1.7) и
(1.9), для СМО с отказами без взаимопомощи, получим, что
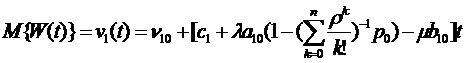
где 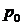 определяется соотношением (1.9).
определяется соотношением (1.9).
Для СМО с отказами и взаимопомощью
типа «все как один», воспользовавшись (1.21), получим
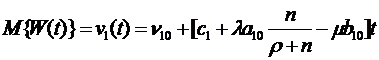

Применяя соотношения (1.39), получим
оценку дохода систем с «равномерной» взаимопомощью 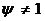
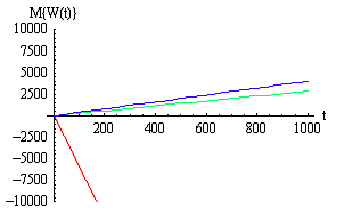
Рис 3.1 Графики доходов СМО с
отказами,с разнотипными дисциплинами и параметрами 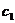 =1 ,
=1 , 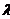 =4,
=4,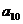 =1 ,
=1 , 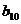 =1,
=1, =1,n=10,где
красный - СМО с отказами ,синий- с «равномерной» взаимопомощью
=1,n=10,где
красный - СМО с отказами ,синий- с «равномерной» взаимопомощью  ,зеленый - с
взаимопомощью типа «все как один».
,зеленый - с
взаимопомощью типа «все как один».
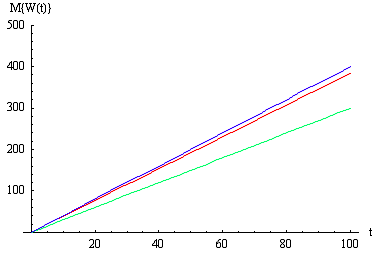
Рис 3.2 Графики доходов СМО с
отказами,с разнотипными дисциплинами и параметрами  =1 ,
=1 , 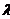 =5,
=5,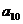 =1 ,
=1 , 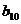 =1,
=1,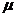 =2,n=10
=2,n=10
Выведем формулу получения дисперсий
доходов систем. Из соотношений (3.1), (3.2) следует, что
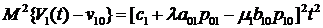 .
.
Введем обозначения:
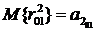 ,
, 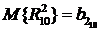 . (3.7)
. (3.7)
Рассмотрим выражение

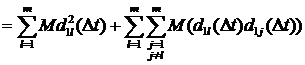 . (3.8)
. (3.8)
Учитывая (3.1)-(3.7), имеем:
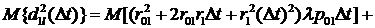
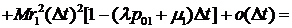
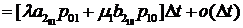 . (3.9)
. (3.9)
Кроме того, из независимости 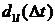 и
и 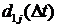 ,
, 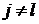 , с учетом
(3.1) вытекает, что
, с учетом
(3.1) вытекает, что 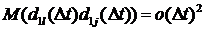 . Поэтому,
как следует из (3.8), (3.9) и
. Поэтому,
как следует из (3.8), (3.9) и 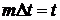 , для дисперсии дохода СМО при
, для дисперсии дохода СМО при 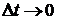 получаем
следующее выражение
получаем
следующее выражение
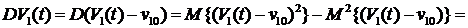
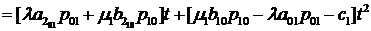 . (3.10)
. (3.10)
Оценка дисперсии для систем без
взаимопомощи будет иметь вид:
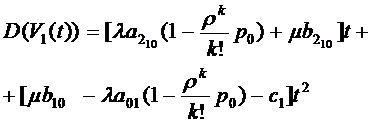
где 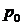 определяется соотношением (1.9).
определяется соотношением (1.9).
Для систем с взаимопомощью типа «все
как один» данное соотношение примет вид:
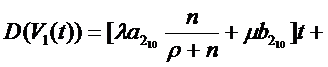
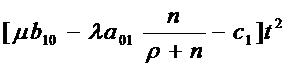
Для систем с «равномерной»
взаимопомощью получим
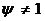
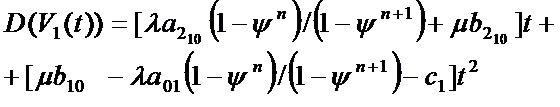
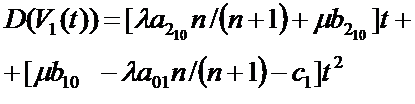
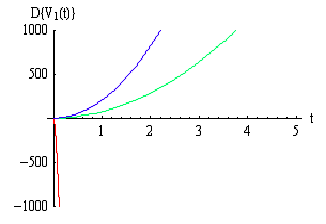
Рис 3.3 Графики дисперсии доходов
СМО с отказами с разнотипными дисциплинами и параметрами 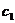 =0 ,
=0 , 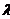 =10,
=10,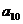 =1 ,
=1 , 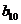 =1,
=1,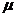 =2,n=10,
=2,n=10,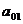 =10,
=10,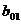 =1, где
красный - СМО с отказами, синий - с «равномерной» взаимопомощью
=1, где
красный - СМО с отказами, синий - с «равномерной» взаимопомощью 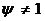 , зеленый -
с взаимопомощью типа «все как один».
, зеленый -
с взаимопомощью типа «все как один».
многолинейный заявка дисперсия доход
Заключение
В курсовой работе были исследованы многолинейные
СМО с отказами без взаимопомощи, с взаимопомощью между каналами типа ''все как
один'' и с ''равномерной'' взаимопомощью между каналами. Было сделано сравнение
основных показателей многолинейных СМО с отказами.
В ходе работы было показано, что среднее время
обслуживания одной заявки в СМО с ''равномерной'' взаимопомощью больше, чем при
взаимопомощи типа ''все как один'' при любом значении показателя нагрузки
системы. Отсюда можно сделать вывод, что если имеются причины, по которым нужно
уменьшить время нахождения заявки в СМО, то, не смотря на уменьшение пропускной
способности, следует ввести взаимопомощь между каналами типа ''все как один''.
Так как в многолинейных СМО с ''равномерной''
взаимопомощью при входе второй и последующей заявок часть каналов переключается
на их обслуживание, то тем самым если необходимо, можно увеличить среднее число
заявок в системе.
Было показано, что за время, пока
все 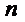 - каналов
заняты обслуживанием одной заявки, в СМО с взаимопомощью ''все как один'' могут
поступать другие заявки. Это объясняет то, что при введении ''равномерной''
взаимопомощи относительная и пропускные способности многолинейных СМО
возрастают, а при взаимопомощи ''все как один'' наоборот убывают.
Соответственно вероятность отказа при наличии взаимопомощи ''все как один''
увеличивается, а при ''равномерной'' взаимопомощи уменьшается.
- каналов
заняты обслуживанием одной заявки, в СМО с взаимопомощью ''все как один'' могут
поступать другие заявки. Это объясняет то, что при введении ''равномерной''
взаимопомощи относительная и пропускные способности многолинейных СМО
возрастают, а при взаимопомощи ''все как один'' наоборот убывают.
Соответственно вероятность отказа при наличии взаимопомощи ''все как один''
увеличивается, а при ''равномерной'' взаимопомощи уменьшается.
Таким образом, организуя
равномерную взаимопомощь между каналами, можно улучшить все характеристики
функционирования СМО.
Проведена оценка ожидаемых доходов и дисперсии
доходов СМО и получены формулы их расчета для случаев, когда интенсивность
обслуживания заявок не зависит от числа заявок в системе.
Выяснили, что на рост доходов
влияет: дисциплина обслуживания, количество линий обслуживания n, интенсивности
входящего потока  ,
интенсивности потока обслуживании
,
интенсивности потока обслуживании 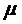 .
.
На скорость роста доходов влияют
коэффициенты при предельных вероятности состояний СМО с отказами.
Также была рассмотрена задача
оптимизации. Было показано, что на оптимизацию числа каналов обслуживания
существенно влияют такие показатели как, величина затрат на содержание одного
канала, коэффициент убытка, показатель нагрузки системы и ограничение на число
каналов.
Список использованных источников
1. Лабскер Л.Г., Бабешко Л.О.
Теория массового обслуживания в экономической сфере.- М.. Банки и Биржи, ЮНИТИ,
1988. - 319 с.
2. Лабскер Л.Г., Михайлова
В.П., Серегин Р.А. Математическое моделирование финансово-экономических
ситуаций с приложением компьютера(на основе Марковских случайных процессов).
Ф.: Фин. акад. при Правительстве РФ, 1997.- 273с.
. Вентцель Е.С., Овчаров
Л.А. Прикладные задачи теории вероятностей.- М.: радио и связь, 1983.- 414 с..
. Маталыцкий М.А. Элементы
теории случайных процессов: Учеб. пособие. - Гродно: ГрГУ, 2004. - 326 с.
. Гнеденко Б.В., Коваленко
И.Н. Введение в теорию массового обслуживания: Учеб. Пособие. - М.: Наука,
1966. - 441с.
. Саати Т. Элементы теории
массового обслуживания и ее приложения. - Москва: Советское радио, 1965. - 510
с.
Приложение
Текст программы для нахождения оптимального
числа каналов обслуживания
Программа написана на в среде Delphi 7.
Программа находит оптимальное число каналов обслуживания для СМО с отказами без
взаимопомощи, СМО с взаимопомощью между каналами ''все как один'' и СМО с
''равномерной'' взаимопомощью между каналами.
var: TForm1;Math;
{$R *.dfm}step_r(x: real;
n:integer):real;:integer;:real;:=1;i:=1 to n do
s:=s*x;_r:=s;;step_i(x,n:integer):integer;,s:integer;:=1;i:=1 to n do s:=s*x;_i:=s;;faktor(n:integer):integer;n=0
then faktor:=1 else faktor:=n*faktor(n-1);;TForm1.Button1Click(Sender:
TObject);.Close;;p0(n,Nn: integer;
l,m:real):extended;:integer;:real;:=0;(l/(m*n)=1) then begin
for k:=0 to n do
p:=p+step_i(n,k)/faktor(k);
p:=p+step_i(n,n)*Nn/faktor(n);
endbegin
for k:=0 to n do
p:=p+step_r(l/m,k)/faktor(k);
p:=p+step_r(l,n+1)*(step_r(m*n,Nn)-step_r(l,Nn))/(faktor(n)*(m*n-l)*step_i(n,Nn)*step_r(m,n+Nn));
end;:=1/p;;W_v(ro,d1,d2:real;n:integer):real;_v
:= d1*n+d2*ro/(ro+n);factorial(n:integer):int64;:int64;:=1;((n<>0)and(n<>1))then:=fact*factorial(n-1);:=fact;;w_a(ro,d1,d2:real;n:integer):real;:real;:integer;:=0;k:=0
to n
do:=p0+power(ro,k)/factorial(n);_a:=d1*n+d2*Power(ro,n)/factorial(n)/p0;;w_r(ro,d1,d2:real;n:integer):real;:real;:integer;:=0;k:=0
to n do
p0:=p0+Power(ro/n,k);_r:=d1*n+d2*n*power(ro/n,n)/p0;;TForm1.Button2Click(Sender:
TObject);
var max_n,i,min,N,min_n: integer;
l,m,d1,d2,min_w,w:real;:
real;:=StrToFloat(Edit1.Text);:=StrToFloat(Edit2.Text);_n:=StrToInt(Edit3.Text);:=StrToInt(Edit9.Text);:=StrToFloat(Edit7.text)/StrToFloat(Edit8.Text);
{-----1----- }_n:=2;max_n<>2
thenn := 3 to max_n dow_a(ro,d1,d2,n)<w_a(ro,d1,d2,min_n) then
min_n:=n;.Text:=IntToStr(min_n);
{-----2-----}_n:=2;max_n<>2
thenn:=3 to max_n doW_v(ro,d1,d2,n)<w_v(ro,d1,d2,min_n)then_n:=n;.Text:=IntToStr(min_n);
{-----3-----}_n:=2;max_n<>2
thenn:=3 to max_n
dow_r(ro,d1,d2,n)<w_r(ro,d1,d2,min_n)then_n:=n;.Text:=IntToStr(min_n);
{-----------};TForm1.Edit8KeyPress(Sender:
TObject; var Key: Char);(key<>#8) then(Key <>',') then(Key <'0')
or (Key >'9') then
Key:=#0;.Text:='';.Text:='';.Text:='';;TForm1.Edit3KeyPress(Sender: TObject;
var Key: Char);(key<>#8) then(Key <'0') or (Key >'9') then
Key:=#0;.Text:='';.Text:='';.Text:='';;TForm1.Edit4Change(Sender: TObject);;end;end.