Интерполяция по Эрмиту
Курсовая
работа
Интерполяция
по Эрмиту
Содержание
1. Введение
. Теория
.1 Полиномы Эрмита
.2 Интерполирование с кратными
узлами
.3 Представление полинома Эрмита
.4 Оценка погрешности
интерполирования
. Листинг программы
. Вывод программы
. Заключение
. Список используемых источников
. Приложение
Введение
Теория приближений изучает вопрос о возможности
приближенного представления одних математических объектов другими, как правило,
более простой природы, а так же вопросы об оценках вносимой при этом
погрешности. Значительная часть теории приближения относится к приближению
одних функций другими, однако есть и результаты, относящиеся к абстрактным
векторным или топологическим пространствам.
В процессе решения какой-то
конкретной задачи довольно часто бывает необходимо использовать значения f(x) для
промежуточных значений аргумента. В этом случае строят некоторую функцию j(x),
достаточно простую для вычисления, которая в заданных точках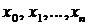 
принимает
значения 
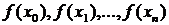, а в
остальных точках отрезка [a,b],
принадлежащего области определения f(x),
приближенно представляет функцию f(x) с той или
иной степенью точности, и при решении задачи вместо функции f(x) оперируют
с функцией j(x). Задача
построения такой функции j(x) называется
задачей интерполирования. Интерполяционный процесс- процесс получения
последовательности интерполирующих функций {fn(z)} при
неограниченном возрастании числа n условий интерполирования. Большой
вклад в теорию приближений внес Шарль Эрмит. В данной работе я рассматриваю
интерполяцию по Эрмиту.
теория
приближений интерполяции функция полином
2.
Теория
2.1
Полиномы Эрмита
Полиномы Эрмита образуют ортогональную систему
веса
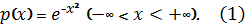
Теорема 1.
Полиномы Эрмита определяются формулой
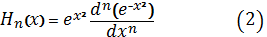
В самом деле, если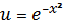 
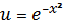, то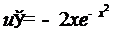 
, 
,
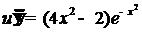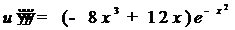
и вообще
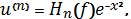
где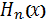 
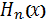есть полином степени n со старшим
коэффициентом, равным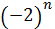 
.
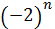Это легко проверяется методом полной
индукции. Значит, функция 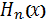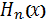, определённая формулой (2),
действительно есть полином степени n.
Так как
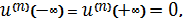
то из формулы
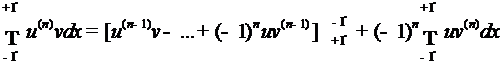
следует, что для любого полинома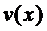 
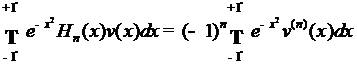(3)
В частности, если степень 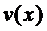ниже n, то
последний интеграл равен нулю, откуда и следует, что полиномы (1) образуют
ортогональную систему веса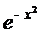 
.
Если в (3) положить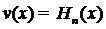 
и учесть,
что старший коэффициент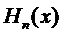 
есть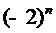 
, то мы
найдём, что
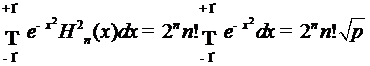. (4)
Таким образом
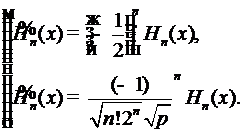(5)
Рекуррентная формула для полиномов Эрмита
такова:
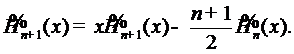(6)
В самом деле, из (2) методом полной
индукции легко убедиться, что в состав 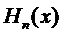входят только те степени 
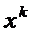, показатели
которых имеют одинаковую чётность с n, откуда
ясно, что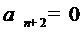 
. Кроме
того, из (4) и (5) вытекает, что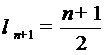 
.
Производящая функция полиномов
Эрмита есть
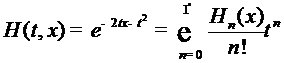. (7)
Действительно, если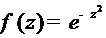 
, то по
формуле Тейлора
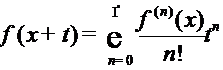. (8)
Но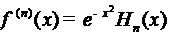 
, откуда и следует (6).
Нетрудно вывести дифференциальное
уравнение, которому удовлетворяет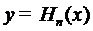 
. Именно, если 
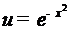, то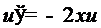 
. Беря
отсюда производные порядка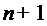 
, находим
,
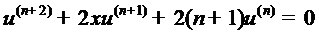но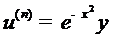 
, и потому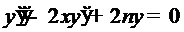 
В заключении докажем полноту системы полиномов
Эрмита.
Теорема 2.
При весе Эрмита
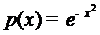
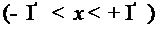
полиномы образуют множество всюду
плотное в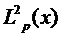 
.
Так как непрерывные функции, равные
нулю при достаточно больших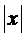 
, лежат в 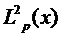всюду
плотно, то и достаточно показать, что именно эти функции можно приблизить
полиномами с любой степенью точности.
Более того, не ограничивая общности,
можно допустить, что рассматриваемые функции обращаются в нуль в некоторых
малых интервалах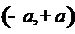 
, так как и
такие функции лежат в 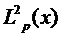всюду
плотно.
Итак, пусть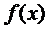 
-
непрерывная функция, отличная от нуля только при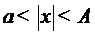 
. Предполагая её чётной, будем иметь
.
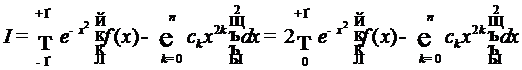С помощью подстановки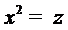 
, получаем
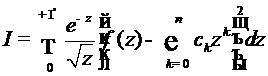
Функция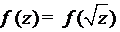 
, будучи
непрерывной и ограниченной, входит в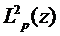 
при лагерровом весе 
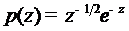. Но в этом
пространстве полиномы лежат всюду плотно, и за счёт выбора коэффициентов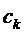 
интеграл 
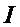можно
сделать сколь угодно малым.
Если же 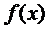- функция
нечётная, то та же подстановка даёт
,
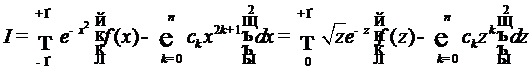где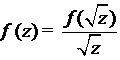 
непрерывна и ограничена. Значит,
опираясь на плотность полиномов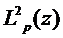 
при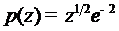 
, мы снова можем сделать 
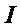сколь
угодно малым. Остаётся заметить, что всякая функция может быть представлена в
виде
,
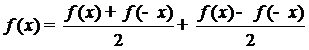причём первое слагаемое есть функция чётная, а
второе - нечётная.
2.2
Интерполирование с кратными узлами
Определение 1.
Алгебраический полином
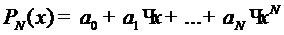
называется интерполяционным
полиномом Эрмита для функции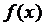 
, заданной на отрезке 
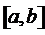, по её
значениям 
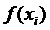, значениям
её первых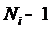 
производных
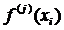в 
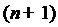-ой попарно
различных точках (узлах)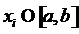 
, 
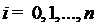, если
,
; 
.
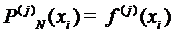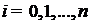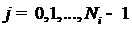Точки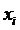 
называются узлами интерполяции
кратности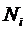 
.
Для определения полинома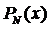 
(
неизвестное: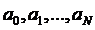 
) мы имеем 
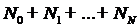условий
(уравнения(2)). Единственность решения математических конечномерных задач
обычно обеспечивается равенством числа неизвестных количеству накладываемых на
них условий, поэтому теперь будем считать, что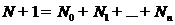 
.
Теорема 1. Задача
алгебраической интерполяции (2) при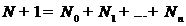 
имеет единственное решение.
Доказательство. Очевидно,
что система уравнений (2) относительно неизвестных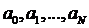 
является
линейной алгебраической системой порядка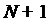 
. Следовательно, она имеет
единственное решение в том и только том случае, когда однородная система имеет
только нулевое решение (определитель матрицы этой системы отличен от нуля).
Предположим, что теорема неверна:
система уравнений (2) либо не имеет решения, либо имеет несколько решений.
Значит, однородная система имеет ненулевое решение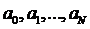 
,
определяющее ненулевой полином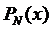 
степени 
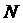и
удовлетворяющий условиям
, 
; 
.
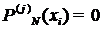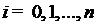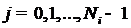Отсюда следует, что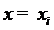 
является
его корнем кратности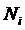 
, а, так как
интерполяционные узлы 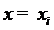попарно
различны, то
,
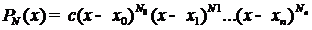т.е.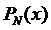 
является полиномом степени не
менее, чем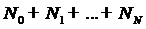 
,
следовательно, наше предположение ложно и теорема верна.
2.3
Представление полинома Эрмита
Форму Лагранжа представления интерполяционного
полинома для случая простых интерполяционных узлов можно обобщить и на случай
кратных узлов в следующем виде
,
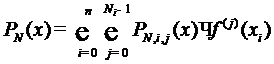где полином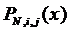 
степени 
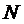определяется
условиями
,
; 
,
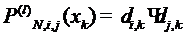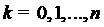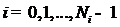где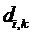 
- символ Кронекера. Пример.
Построим полином Эрмита при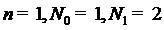 
. Введём дополнительный узел 
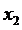, отличный
от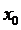 
и 
, и построим
интерполяционный полином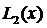 
в форме
Лагранжа на узлах 
.
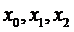
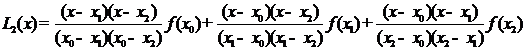Предельным переходом при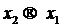 
получим
полином Эрмита
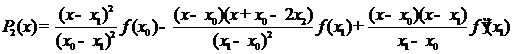
Интерполяционный полином Эрмита
можно построить и с помощью предельного перехода в интерполяционном полиноме в
форме Ньютона. Построим интерполяционный полином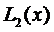 
в форме Ньютона на узлах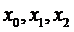
,
,
,
.
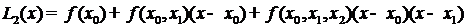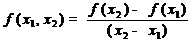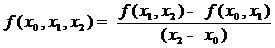Предельным переходом при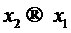 
получим
полином Эрмита
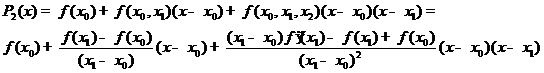
Легко заметить, что в этом случае находить
предел значительно проще, чем при использовании полинома в форме Лагранжа.
Установим законность последнего приёма для
построения интерполяционного полинома Эрмита.
Предположим, что каждый узел
интерполяции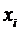 
кратности 
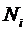заменён
набором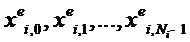 
, зависящим
от параметра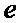 
, при
стремлении которого к нулю каждый узел набора сходиться к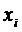 
.
Будем считать, что узлы набора
, 
,
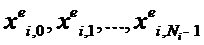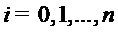попарно различны (построить такую
систему узлов можно, выбирая дополнительные узлы в достаточно малых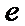 
-
окрестностях исходных интерполяционных узлов).
Представим интерполяционный полином
на этой системе узлов в форме Ньютона
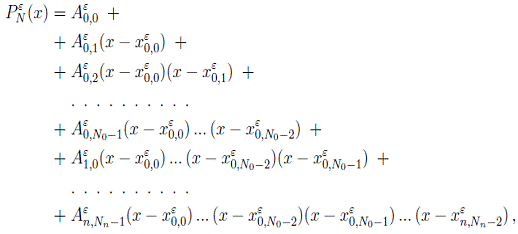
где
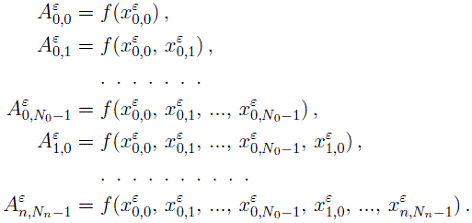
Лемма 1. На системе
узлов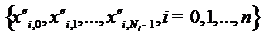 
существует
и конечен предел разделённых разностей:
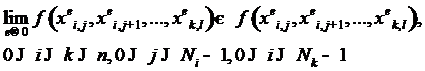
где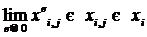 
.
Доказательство. Очевидно,
что пределы разделённых разностей нулевого порядка существуют и конечны:
,
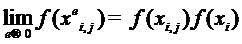
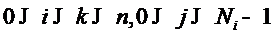Предположим, что существуют и
конечны пределы разделённых разностей до порядк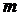а 
включительно и рассмотрим
разделённую разность порядка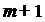 
:
,
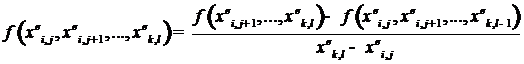где числитель является разностью
разделённых разностей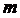 
-го порядка,
а значит по предположению имеет конечный предел.
Если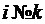 
, то знаменатель стремиться к
разности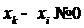 
и нужный
предел существует. Осталось рассмотреть случай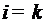 
, когда знаменатель стремиться к
нулю. Но в этом случае следует, что
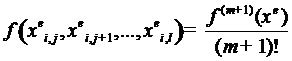
и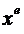 
лежит между узлами, по которым
строиться разделённая разность. Значит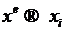 
, а разделённая разность стремиться
к (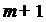
)-ой
производной функции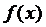 
в точке 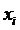, что и
требовалось доказать.
Теорема 2.
Интерполяционный полином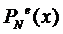 
на системе
узлов
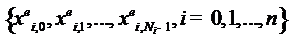
сходиться к полиному Эрмита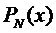 
из (2) при 
.
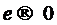Доказательство. Из леммы
(1) и её доказательства следует, что предел интерполяционного полинома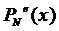 
можно
представить в следующем виде:
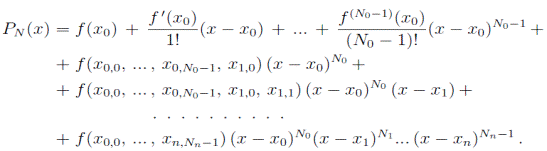
Непосредственной проверкой легко
установить, что этот предельный полином удовлетворяет всем условиям
интерполяции функции 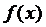в
интерполяционном узле 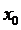в кратности
:
.
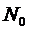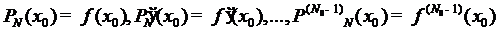Предельный полином 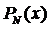удовлетворяет
условиям интерполяции функции 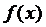и в любом другом интерполяционном
узле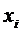 
кратности .
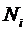Действительно, поменяв узлы 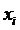и 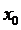местами, учитывая, что
интерполяционный полином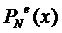 
единственен,
т.е. не зависит от нумерации узлов, получим, что его предел представим в виде
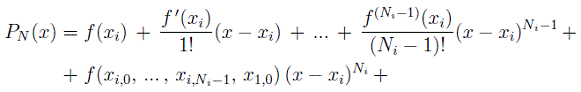
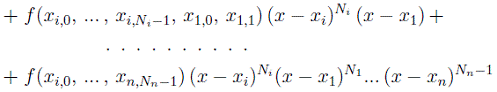
и удовлетворяет условиям
интерполяции
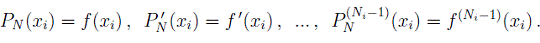
2.4
Оценка погрешности интерполирования
Погрешность интерполирования функции
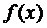, заданной
на отрезке 
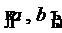, по её
значениям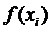 
, значениям
её первых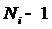 
производных
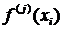в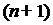 
-ой попарно
различных точках (узлах) 
, 
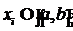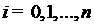, полиномом
Эрмита 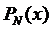из (2)
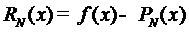(4)
можно оценить с помощью предельного перехода в
оценке
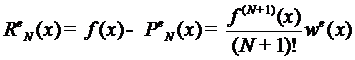, (5)
где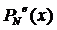 
- интерполяционный многочлен на
попарно различных узлах кратности один,
Так как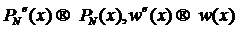 
при 
:
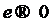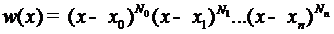(6)
- полином степени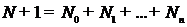 
, то из
представления (5) следует
.
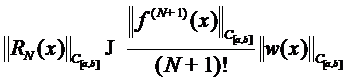Эта оценка вытекает также и из следующей
теоремы.
Теорема 3. Погрешность
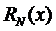интерполирования
функции 
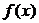, заданной
на отрезке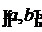 
, по её
значениям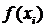 
, значениям
её первых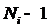 
производных
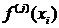в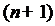 
-ой попарно
различных точках (узлах) 
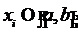
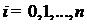, полиномом
Эрмита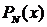 
из (2)
можно представить в виде
,
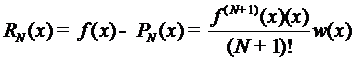где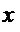 
некоторая точка из интервала 
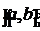(зависящая
от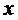 
), а полином
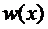определён в
(6).
3.
Листинг
программы
#include <conio.h>
#include <stdio.h>
#include <iostream>
#include <math.h>
#include <locale.h>namespace
std;function (double x)
{1/(x*x);
}l_k (double x, int k,double X[],
int n)// фундаментальный полином
{p=1.0;(int i=0; i<n+1;
i++)(i!=k) p=(double)(p*((x-X[i])/(X[k]-X[i])));p;
}Termit(double x, int n)//Полином
Эрмита
{P_0=1, P_1=2*x, P_2;(int i=1;
i<n+1; i++)
{_2=(double)(2*x*P_1-2*i*P_0);_0=P_1;_1=P_2;
}P_2;
}Del(double a, double b, int n,
double R)//функция половинного деления
{c1,a1,b1;=a; b1=b;((b1-a1)>R)
{=(b1+a1)/2.0;((Termit(a1,
n)*Termit(c1, n))<0) b1=c1;a1=c1;
}c1;
}main ()
{(LC_ALL,"Russian");double
pi=3.1415926535897932384626433832795; s=0.06, a=0, b=1, sum=0, *X, *T, *E, *Y,
*Ch, *N;n, i, j, k, c;int m=15; <<"Введите начало
участка:"<<a<<endl;<<"Введите конец
участка:"<<b<<endl;<<"Введите отступ от
начала:"<<s<<endl;=a+s;<<"Начало участка с
отступом:"<<a<<endl;<<"Конец участка с отступом:"<<b<<endl;<<"Введите
число узлов:";>>n;<<"Выберите 1 для равномерной сетки, 2
для Чебышевской сетки: ";>>c;=new double[n+1];//узлы=new
double[m+1];//текущие точки=new double[m+1];//полином Эрмита=new
double[m+1];//погрешность интерполяции=new double[n+1];//узлы Чебышева=new
double[m+1];//порядковый номер(c)
{1://разбиение, равномерная сетка
{(i=0;
i<n+1;i++)[i]=a+((b-a)/n)*i;;
}2://Чебышевская сетка
{(i=0; i<n+1; i++)
{[i]=cos((double)(pi*(1+2*i)/(2*n+2)));[i]=(double)(Ch[i]*(b-a)+b+a)/2.0;
};
}
}(i=0; i<m+1;
i++)[i]=(double)((a+0.01)+((b-a-0.02)/n)*i);<<'N'<<'\t'<<'x'<<'\t'<<'y'<<'\t'<<'f'<<'\t'<<'T'<<'\t'<<'E'<<endl;(j=0;
j<m+1; j++)
{sum=0;(i=0; i<n+1;
i++)=(double)(sum+(function(X[i])*l_k(Y[j],i, X,
n)));[j]=sum;[j]=abs(T[j]-function(Y[j]));
}(i=0; i<m+1;i++)
{N[i]=i;<<N[i]<<'\t'<<X[i]<<'\t'<<Y[i]<<'\t'<<function(Y[i])<<'\t'<<T[i]<<'\t'<<E[i]<<endl;
}[]X;[]Y;[]T;[]E;[]N;();
}
4.
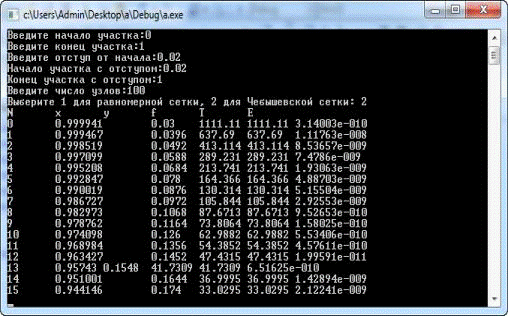
Вывод программы
Произведено построение интерполяционного
полинома Эрмита для функции на 2-х сетках узлов.
На точность построения влияют: количество узлов
интерполяции, особые точки и выбор сетки.
У функции особой точкой является число, равное
0.
Равномерная сетка.
Оптимальное количество равностоящих узлов около
35 - 40, а отступ от особой точки - 0,05-0,07. При увеличении отступа и
уменьшении количество узлов, погрешность становится минимальной.
Узлы Чебышева.
Оптимальное количество точек разбиения при таком
выборе сетки - 100, а отступ - 0,02. Если отступ увеличить, то точность
повысится.
Из результатов работы программы, делаем вывод,
что самой оптимальной сеткой узлов является Чебышевская. Можно достаточно
хорошо приблизиться к особой точке, и точность вычисления при этом не сильно
изменится.
5.
Заключение
В результате выполнения данной
работы был разработан алгоритм и программа на языке С/С++. Программа была
отлажена на задаче, которая представляет собой функцию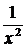 
, имеющую
особую точку 0 на отрезке интерполирования[0;1].
Стоит заметить, что погрешность аппроксимации
имеет большее значение в крайних точках. В середине области она минимальна.
Также стоит заметить тенденцию уменьшения
погрешности до определенных порядков. При дальнейшем увеличении порядка
аппроксимации погрешность практически не меняется. Выяснилось, что от выбора узлов
интерполируемой функции напрямую зависит, насколько точно многочлен будет
являться её приближением.
6.
Список используемых источников
1. И.П. Натансон «Конструктивная
теория функции», 1949г.
. Мацокин А.М. Численный анализ
(конспект лекций).
.[Электронный ресурс]
#"783790.files/image187.gif">
Чебышевская сетка узлов
