Понятие энтропии и информации
ВВЕДЕНИЕ
Предмет работы: энтропия и информация.
Цель работы: изучение энтропии и информации, а
так же: какое применение имеют данные понятия к рискам.
В ходе данной работы предстоит решить несколько
задач: рассмотрение понятия энтропии и информации, статистического и
термодинамического смысла энтропии, так же определение данного понятия, как
меры степени неопределенности, теоремы Шеннона о кодировании при наличии помех,
использования энтропии в прогнозировании и применения энтропии к рискам.
Данная тема является злободневной, так как
широко пользуются в физике, химии, биологии и теории информации. Клаузиузус
первым же в 1865 году положил начало применению понятия энтропия на основе
анализа тепловых машин. Трудно найти определения более общие для всех наук (не
только естественных), чем энтропия и информация. Возможно, это связано с самими
названиями. С тех пор энтропия многократно фигурировала в знаменитых спорах.
Например, в исторической науке энтропия имеет не малое значение для объяснения
экспликации феномена вариативности истории.
Существующему давно понятию “информация”, был
придан математически точный смысл К.Шенноном. Это как приводило, так и приводит
ко многим недоразумениям, поэтому очень важно уделить данному понятию должное
внимание. Никакая информация, никакое знание не появляется сразу - этому
предшествует этап накопления, осмысления, систематизации опытных данных,
взглядов. Информация является общим компонентом для всех наук, она связывает
между собой различные по характеру и содержанию науки, поэтому информационные
процессы, которые изучаются информатикой, имеют место во многих предметных
областях.
Нельзя ограничивать информационные процессы
рамками вычислений и пассивного получения или преобразования информации. Эти
процессы сложны и многообразны. Важно научить новое поколение это понимать.
Информация не всегда связана с компьютером. Чаще всего именно человек активно
ее обрабатывает. Умение в процессе обработки не только анализировать, но и
синтезировать из отдельных крупинок информации целое - весьма ценное качество
человека будущего.
Я согласна с необходимостью изучения понятия
энтропии, синергетики, социальной информатики, эволюции и т.п.
1.
Понятие энтропии
1.1. Статистический
смысл понятия энтропии
Вероятностное толкование понятия энтропии было
дано в статистической физике Людвигом Больцманом. Введем для начала понятие
термодинамической вероятности (W). Термодинамическая вероятность означает число
возможных неотличимых микроскопических состояний системы реализующих
определенное макроскопическое состояние этой системы.
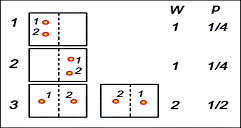
Рисунок 1
Будем рассматривать простую систему всего из
двух неотличимых молекул, которые находятся в некотором объеме. Мысленно
разделим этот объем на две части, и, пронумеровав молекулы, найдем число
способов, которым можно разместить их в этих двух частях.
Мы можем увидеть, что всего 4 способа, но два
нижних неотличимы, так как молекулы 1 и 2 совершенно одинаковы, и соответствуют
одному и тому же макроскопическому состоянию системы. Таким образом, мы имеем
три различных макроскопических состояния системы, два из которых (верхних) ,
реализуемых только одним способом, а третье, нижнее двумя. Число
способов-термодинамическая вероятность W. Все четыре способа равновероятны,
поэтому большую часть времени система будет находиться в третьем состоянии.
Мы рассматривали только 2 молекулы. Число
способов размещения n молекул в двух частях объема равно 2n, а число способов
размещения всех молекул в одной половине объема равно 1. Энтропия
термодинамического состояния системы определяется через термодинамическую
вероятность:
= k·lnW
где k - постоянная Больцмана. Данное выражение
называется принципом Больцмана [2].
В статистической термодинамике энтропия так же
характеризует меру беспорядка и хаоса.
1.2. Энтропия как
мера степени неопределенности
Существование неопределённости связано с
участием вероятностей в осуществлении событий. Устранение неопределённости есть
увеличение вероятности наступления того, что задано как цель. Поэтому
вероятности должны участвовать в математической формулировке величины
устранённой неопределённости.
Первая удачная попытка реализовать определение
информации на такой основе осуществлена в 1928 г. Л. Хартли. Пусть возможно в
данных условиях n вариантов некоторого результата. Целью является один из них.
Хартли предложил характеризовать неопределённость логарифмом числа n.
Количественная мера s полученной информации
(устранённой неопределённости)выражается логарифмом отношения вероятностей:
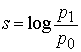
Есть один недостаток-это определение справедливо
только в приближении равновероятности всех исходов. Это выполняется далеко не
всегда. В пределе в этом определении невероятному исходу приравнивается
неизбежный. В 1948 г. это исправил К. Шеннон.
В качестве меры априорной неопределенности
системы (или прерывной случайной величины 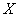 )
в теории информации применяется специальная характеристика, называемая
энтропией. Понятие об энтропии является в теории информации основным. Энтропией
системы называется сумма произведений вероятностей различных состояний системы
на логарифмы этих вероятностей, взятая с обратным знаком:
)
в теории информации применяется специальная характеристика, называемая
энтропией. Понятие об энтропии является в теории информации основным. Энтропией
системы называется сумма произведений вероятностей различных состояний системы
на логарифмы этих вероятностей, взятая с обратным знаком:
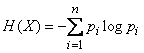
Энтропия 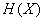 обладает
рядом свойств, которые оправдывают выбор данного понятия в качестве
характеристики степени неопределенности. Во-первых, обращение энтропии в нуль
объясняется достоверностью состояния системы при других-невозможных. Во-вторых,
энтропия обращается в максимум при равновероятности состояний, а при увеличении
числа состояний - увеличивается. Главное: свойство аддитивности.
обладает
рядом свойств, которые оправдывают выбор данного понятия в качестве
характеристики степени неопределенности. Во-первых, обращение энтропии в нуль
объясняется достоверностью состояния системы при других-невозможных. Во-вторых,
энтропия обращается в максимум при равновероятности состояний, а при увеличении
числа состояний - увеличивается. Главное: свойство аддитивности.
Энтропию дискретного опыта удобно находить как
вес следующего графа:

Рисунок 2.
Реальная ценность понятия энтропии определяется
в первую очередь тем, что выражаемая им «степень неопределенности» опытов
оказывается во многих случаях именно той характеристикой, которая играет роль в
разнообразных процессах, встречающихся в природе, обществе и технике и так или
иначе связанных с передачей и хранением каких-либо сообщений.
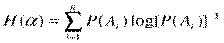
2.
Понятие об информации
Понятие информации (informatio - разъяснение,
осведомление, изложение) - это основное понятие не только в информатике (в
информологии - области знаний, изучающей проявление информации, её
представление, измерение и т.д.),но и в математике, в физике и др., плохо
формализуется и структурируется. Из-за его объёмности, расплывчатости оно часто
понимается неточно и неполно не только обучаемыми.
2.1. Формы
информации
Информация может существовать в
пассивной (не актуализированной) и активной (актуализированной) форме.
Информация по отношению к
окружающей среде (или к использующей ее среде) бывает трех типов: входная,
выходная и внутренняя.
Информация по отношению к
конечному результату проблемы бывает: исходная (на начало актуализации этой
информации); промежуточная (от начала до завершения актуализации информации);
результирующая (после завершения её актуализации).
Информация по изменчивости при
её актуализации бывает: постоянная (не изменяемая никогда при её актуализации);
переменная (изменяемая при актуализации); смешанная - условно - постоянная (или
условно-переменная).
2.2. Негативное
влияние информации
Информация может оказаться и вредной, влияющей
негативно на сознание, например, воспитывающей восприятие мира от безразличного
или же некритического - до негативного, "обозлённого", неадекватного.
Информационный поток -достаточно сильный раздражитель.
Пример. Негативной информацией - раздражителем может
быть информация о крахе коммерческого банка, о резком росте (спаде) валютного
курса, об изменении налоговой политики и др. [5].
2.3. Измерение
информации
2.3.1. Мера Р. Хартли
Пусть имеется N состояний системы S или N опытов
с различными, равновозможными, последовательными состояниями системы.
Наименьшее число, при котором это возможно, называется мерой разнообразия
множества состояний системы и задается формулой Р. Хартли:
H=klogаN
где k - коэффициент пропорциональности
(масштабирования, в зависимости от выбранной единицы измерения меры), а -
основание системы меры. Если измерение ведется в экспоненциальной системе, то
k=1, H=lnN (нат); если измерение было произведено в двоичной системе, то
k=1/ln2, H=log2N (бит); если измерение было произведено в десятичной системе,
то k=1/ln10, H=lgN (дит).
Пример. Чтобы узнать положение точки в системе
из двух клеток т.е. получить некоторую информацию, необходимо задать 1 вопрос:
("Левая или правая клетка?").
Узнав положение точки, мы увеличиваем суммарную
информацию о системе на 1 бит (I=log22). Для системы из четырех клеток
необходимо задать 2 аналогичных вопроса, а информация равна 2 битам (I=log24).
Если же система имеет n различных состояний, то максимальное количество
информации будет определяться по формуле: I=log2n.
Справедливо утверждение Хартли: если в некотором
множестве X={x1, x2, ..., xn} необходимо выделить произвольный элемент xi X, то
для того, чтобы выделить (найти) его, необходимо получить не менее logan
(единиц) информации [4].
.3.2. Мера К. Шеннона
Шеннон вывел это определение
энтропии из следующих предположений: мера должна быть непрерывной; т. е.
изменение значения величины вероятности на малую величину должно вызывать малое
результирующее изменение энтропии.
Шеннон показал, что любое
определение энтропии, удовлетворяющее этим предположениям, должно быть в форме:
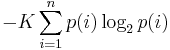
где K - константа (и в
действительности нужна только для выбора единиц измерения) [3].
Шеннон определил, что измерение
энтропии (H = − p1 log2 p1 − … − pn log2 pn), применяемое к
источнику информации, может определить требования к минимальной пропускной
способности канала, требуемой для надежной передачи информации в виде
закодированных двоичных чисел.
2.3.3. Термодинамическая
мера
Информационно-термодинамический подход связывает
величину энтропии системы с недостатком информации о внутренней структуре
системы (не восполняемым принципиально, а не просто нерегистрируемым). При этом
число состояний определяет, по существу, степень неполноты наших сведений о
системе.
Поставим некоторый вопрос о состоянии
термодинамической системы.
Пример. Предположим, что имеется
термодинамическая система - газ в объеме V , который расширяется до объема 2V.

Рисунок 3. Газ объема V (a) расширяемый до 2V
(б)
Нас интересует вопрос о координате молекулы m
газа. В начале (а) мы знали ответ на вопрос и поэтому p1=1 (lnp1=0). Изменение
(убыль) информации о состоянии системы будет равно ΔI
= -k ln(2V /V) = -k ln 2 (нат). Мы получили известное в термодинамике выражение
для прироста энтропии в расчете на одну молекулу, и оно подтверждает второе
начало термодинамики. Энтропия - мера недостатка информации о микросостоянии
статической системы.
Термодинамическая мера (энтропия) применима к
системам, находящимся в тепловом равновесии. Для систем, далеких от теплового
равновесия, например, живых биологических систем, мера-энтропия - менее
подходящая [6].
2.3.4. Энергоинформационная
(квантово-механическая) мера
Энергия (ресурс) и информация(структура) - две
фундаментальные характеристики систем реального мира, связывающие их
вещественные, пространственные, временные характеристики. Сейчас актуально
говорить о биоэнергоинформационных мерах, отражающих механизм взаимосвязей
биофизикоинформационных и вещественно-энергетических процессов в системе, в
ноосфере [7].
3.
Теорема Шеннона о кодировании при
наличии помех
Теорема Шеннона - Хартли в теории
информации <#"773090.files/image010.gif"> окиси
этилена при 400, 500 и 600 К. Энтропия 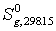 окиси
этилена составляет 242,4 Дж/(моль×К), значения
теплоемкостей C0p,T при 400, 500 и 600 К приведены в табл. 2.
окиси
этилена составляет 242,4 Дж/(моль×К), значения
теплоемкостей C0p,T при 400, 500 и 600 К приведены в табл. 2.
Решение: Вычислим энтропию окиси этилена при
интересующих температурах. При этом средние величины теплоемкостей окиси
этилена считаются величинами постоянными для каждого из температурных
диапазонов (от 300 до 400, от 400 до 500 и от 500 до 600 К) по условию создания
таблиц, допускающему линейную интерполяцию соседних значений в них.
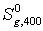 =
242,74+(48,53+62,55)/2·(ln400 - ln300) = 258,72 Дж/(моль×К);
=
242,74+(48,53+62,55)/2·(ln400 - ln300) = 258,72 Дж/(моль×К);
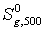 = 258,72+(62,55+75,44)/2·(ln500
- ln400) = 274,12 Дж/(моль×К);
= 258,72+(62,55+75,44)/2·(ln500
- ln400) = 274,12 Дж/(моль×К);
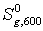 = 274,12
+(75,44+86,27)/2·(ln600 - ln500) = 288,86 Дж/(моль×К).
= 274,12
+(75,44+86,27)/2·(ln600 - ln500) = 288,86 Дж/(моль×К).
Температурная зависимость 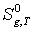 иллюстрируется
рисунком 4.
иллюстрируется
рисунком 4.
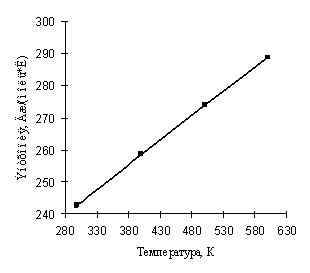
Рисунок 4. Зависимость идеально-газовой энтропии
Таблица 2.
|
Т,
К
|
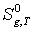 [1],
Дж/(моль·К) [1],
Дж/(моль·К)
|
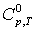 [1],
Дж/(моль·К) [1],
Дж/(моль·К)
|
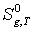 (расчет),
Дж/(моль·К) (расчет),
Дж/(моль·К)
|
Погрешность,
% отн.
|
|
298
|
242,42
|
48,28
|
|
|
|
300
|
242,76
|
48,53
|
242,74
|
0,00
|
|
400
|
258,65
|
62,55
|
258,72
|
0,03
|
|
500
|
274,01
|
75,44
|
274,12
|
0,04
|
|
600
|
288,78
|
86,27
|
288,86
|
0,03
|
4.2. Применение к рискам
Проведение классификации рисков, поставка
задачи, оценивание конкретного риска, проведение структуризации риска - важные
пункты при рассмотрении некоторых задач. Риски необходимо учитывать при
прогнозировании экономических последствий принимаемых решений, поведения
потребителей и конкурентного окружения, внешнеэкономических условий и
макроэкономического развития России, экологического состояния окружающей среды,
безопасности технологий, экологической опасности промышленных и иных объектов.
Большое число рисков связано с природными явлениями. Риски, которые связанны с
недостаточными знаниями о природе, экологических бедствиях, играют большую роль
(например,неизвестен точный объем полезных ископаемых в том или ином
месторождении, а потому нельзя точно предсказать развитие добывающей
промышленности и объем налоговых поступлений от ее предприятий). Метод энтропии
часто используют для описания неопределенностей во время компьютерного и
математического. Некоторые виды неопределенностей связаны с безразличными к
организации силами -природными (погодные условия) или общественными (смена
правительства). Разнообразные формальные методы оценки рисков и управления ими
во многих случаях (реально во всех нетривиальных ситуациях) не могут дать
однозначных рекомендаций. Поэтому процедуры энтропии естественно применять не
только на конечном, но и на всех остальных этапах анализа рассматриваемого
организацией проекта, используя при этом весь арсенал теории и практики
энтропии.
энергоинформационный шеннон неопределенность статистический
ЗАКЛЮЧЕНИЕ
Физическая переменная энтропия первично возникла
из задач описания тепловых процессов и затем широко использовалась во всех
областях науки. Информация - знание, используемое для развития и
совершенствования взаимодействия системы с окружающей средой. За развитием
системы следом развивается информация. Существование новых форм, принципов,
подсистем вызывает изменения в содержании информации, формах получения,
переработки, передачи и использования. Система, осуществляемая целесообразное
взаимодействие с окружающей средой, управляет или управляема из-за потоков
информации.
Стабилизирование, адаптирование и восстановление
системы может обеспечить оперативная информация, при нарушениях структуры и/или
подсистем. На устойчивость и развитие системы влияет: на сколько информирована
система ,процесс ее взаимодействие со средой. В наше время прогнозирование
играет большую роль. Любое предприятие в процессе организации сталкивается с
различными рисками, влияющими на ее состояние.
Существует достаточно примеров ситуаций, которые
связаны с рисками: социальными, технологическими, экономическими,
политическими, экологическими и другими, что подтверждает необходимость
прогнозирования. Известны различные виды критериев, используемых в теории
принятия решений в условиях неопределенности (риска). Возникает много
противоречий по результатам критериев, следовательно необходимо применять
энтропию в данной ситуации.
БИБЛИОГРАФИЯ
1. Колмогоров
А.Н. Теория информации и теория алгоритмов.
2. Хартли
Р. Передача информации// Теория информации и ее приложения.
. Дмитриев
В.Н.Прикладная теория информации.