Эконометрическое моделирование уровня рождаемости

Эконометрическое моделирование уровня рождаемости

Содержание

Введение

. Теоретические основы эконометрического анализа рождаемости в России

1.1 Эконометрика и эконометрическое моделирование

.2 Парная регрессия и корреляция

.3 Рождаемость в России

2. Многомерный эконометрический анализ уровня рождаемости в России

.1 Анализ уровня рождаемости в России с помощью множественной регрессии

.2 Анализ уровня рождаемости в России с помощью парной регрессии

. Прогнозирование уровня рождаемости в России

Заключение

Список используемой литературы

Введение

Для любого государства изучение рождаемости своего населения имеет огромное значение, так как рождаемость играет большую роль для определения демографической ситуации. Уровень демографии, в свою очередь, определяет социальное развитие государства, что является немаловажным показателем в современном мире, поэтому явление такого рода вызывает особый интерес к изучению. Все явления во времени, в том числе и рождаемость населения, изучаются методами эконометрики, а в частности, методами регрессионного анализа, который представляет собой исследования влияния одной или нескольких независимых переменных <#"771489.files/image001.gif">

Из графика видно, что с увеличением брачности рождаемость возрастает.

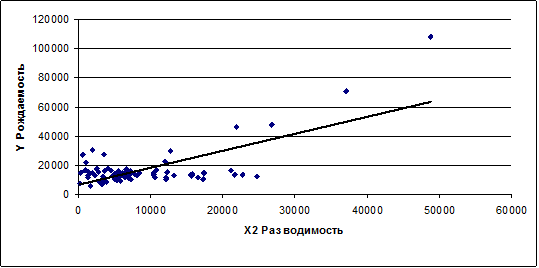
Из графика видно, что с увеличением разводимости рождаемость возрастает.

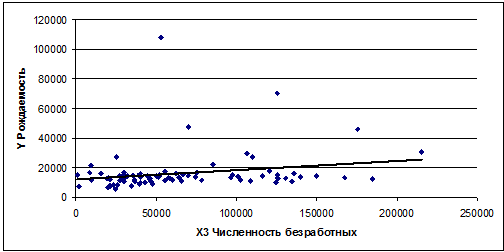
Из графика видно, что с увеличением численности безработных рождаемость возрастает.

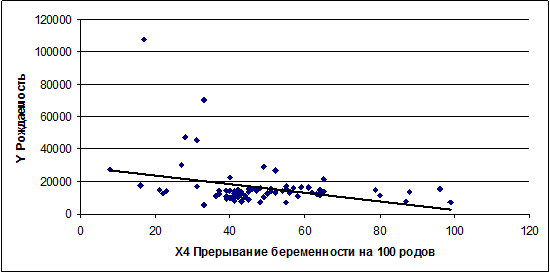
Из графика видно, что с увеличением прерывания беременности рождаемость сокращается.

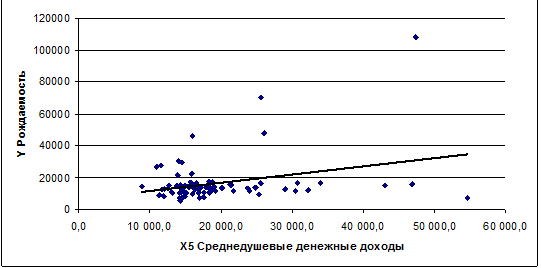
Из графика видно, что с увеличением среднедушевых денежных доходов рождаемость возрастает.

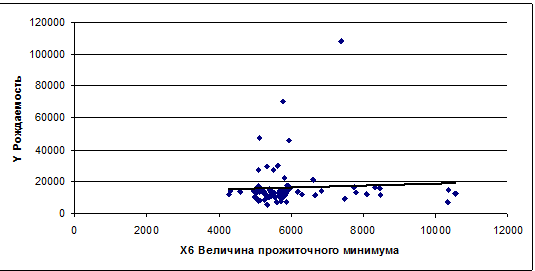
Из графика видно, что с увеличением величины прожиточного минимума рождаемость возрастает.

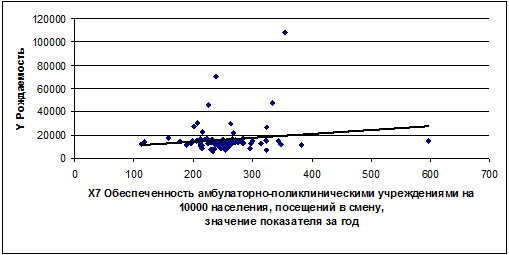
Из графика видно, что с увеличением обеспеченности амбулаторно-поликлиническими учреждениями на 10000 населения, посещений в смену, значение показателя за год рождаемость возрастает.

Построим уравнение множественной регрессии в линейной форме с полным набором факторов

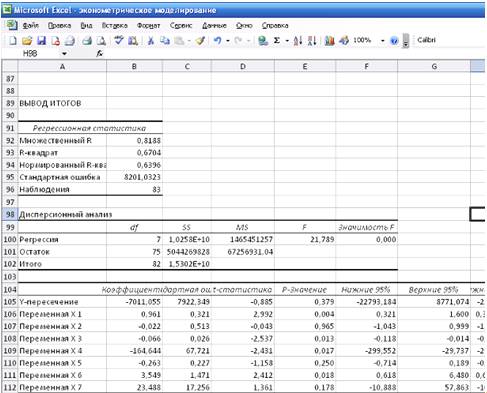
Уравнение регрессии имеет вид:

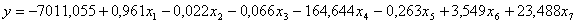
С увеличением брачности на 1 рождаемость возрастает в среднем на 0,961 при условии постоянства всех остальных факторов. С увеличением разводимости на 1 рождаемость сокращается в среднем на 0,022 при условии постоянства всех остальных факторов. С увеличением численности безработных на 1 рождаемость сокращается в среднем на 0,066 при условии постоянства всех остальных факторов. С увеличением прерывания беременности на 100 родов на 1 рождаемость сокращается в среднем на 164,644 при условии постоянства всех остальных факторов. С увеличением среднедушевых денежные доходов на 1 рождаемость сокращается в среднем на 0,263 при условии постоянства всех остальных факторов. С увеличением величины прожиточного минимума на 1 рождаемость возрастает в среднем на 3,549 при условии постоянства всех остальных факторов. С увеличением обеспеченности амбулаторно-поликлиническими учреждениями на 10000 населения, посещений в смену, значение показателя за год на 1 рождаемость возрастает в среднем на 23,488 при условии постоянства всех остальных факторов.

Рассчитаем интервальные оценки коэффициентов уравнения регрессии.

С увеличением брачности на 1 рождаемость увеличивается минимум на 0,321б. или увеличивается как максимум на 1,6. С увеличением разводимост рождаемость уменьшается максимум на 1,043 или увеличится как максимум на 0,999. С увеличением численности безработных на 1 рождаемость уменьшается максимум на 0,118 руб. или уменьшается как минимум на 0,014руб. С увеличением прерывания беременности на 100 родов на 1 рождаемость уменьшается максимум на 299,552 руб. или уменьшается как минимум на 29,737руб. С увеличением среднедушевых денежные доходов рождаемость уменьшается максимум на 0,714 или увеличится как максимум на 0,189. С увеличением среднедушевых денежные доходов рождаемость увеличивается минимум на 0,618 или увеличивается как максимум на 6,48. С увеличением обеспеченности амбулаторно-поликлиническими учреждениями на 10000 населения, посещений в смену, значение показателя за год на 1 рождаемость уменьшается максимум на 10,888 или увеличится как максимум на 57,863.

В границы доверительных интервалов переменных х1, х3, х4, х6 не попадает 0, это свидетельствует о статистической значимости и надежности рассматриваемых коэффициентов.

Дадим сравнительную оценку силы связи факторов с результатом с помощью средних коэффициентов эластичности

Вычислим коэффициент эластичности:

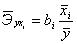
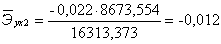
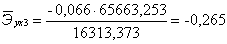
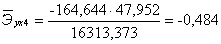
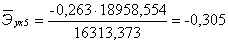
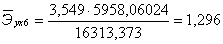
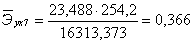
То есть с увеличением брачности на 1% от своего среднего уровня, средняя рождаемость увеличивается на 0,834% от своего среднего уровня, а с уменьшением брачности на 1% от своего среднего уровня, средняя рождаемость уменьшается на 0,834% от своего среднего уровня. С увеличением разводимости на 1% от своего среднего уровня, средняя рождаемость уменьшается на 0,012% от своего среднего уровня, а с уменьшением разводимости на 1% от своего среднего уровня, средняя рождаемость увеличивается на 0,012% от своего среднего уровня. С увеличением численности безработных на 1% от своего среднего уровня, средняя рождаемость уменьшается на 0,265% от своего среднего уровня, а с уменьшением численности безработных на 1% от своего среднего уровня, средняя рождаемость увеличивается на 0,265% от своего среднего уровня. С увеличением прерывания беременности на 100 родов на 1% от своего среднего уровня, средняя рождаемость уменьшается на 0,484% от своего среднего уровня, а с уменьшением прерывания беременности на 100 родов на 1% от своего среднего уровня, средняя рождаемость увеличивается на 0,484% от своего среднего уровня. С увеличением среднедушевых денежных доходов на 1% от своего среднего уровня, средняя рождаемость уменьшается на 0,305% от своего среднего уровня, а с уменьшением среднедушевых денежных доходов на 1% от своего среднего уровня, средняя рождаемость увеличивается на 0,305% от своего среднего уровня. С увеличением величины прожиточного минимума на 1% от своего среднего уровня, средняя рождаемость увеличивается на 1,296% от своего среднего уровня, а с уменьшением среднедушевых денежных доходов на 1% от своего среднего уровня, средняя рождаемость уменьшается на 1,296% от своего среднего уровня. С увеличением обеспеченности амбулаторно-поликлиническими учреждениями на 10000 населения, посещений в смену на 1% от своего среднего уровня, средняя рождаемость увеличивается на 0,366% от своего среднего уровня, а с уменьшением обеспеченности амбулаторно-поликлиническими учреждениями на 10000 населения, посещений в смену на 1% от своего среднего уровня, средняя рождаемость уменьшается на 0,366% от своего среднего уровня.

Наиболее сильное влияние на объем продаж оказывает цена товара Б, наименьшее доход потребителя.

Оценим статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента, сопоставим результаты t-статистик с интервальными оценками коэффициентов регрессии.

Находим наблюдаемое и фактическое значение критерия Фишера_табл(α=0,05)=2,21_факт = 21,789_табл<F_набл то уравнение в целом статистически значимо и надежно

Проверим значимость параметров с помощью критерия Стьюдента

Найдем t_крит(α=0,05; f=83)= 2,21_крит<t_набл для переменной х1, х3, х4, х6 значит эти коэффициенты регрессии значимы и надежны._крит>t_набл для переменной х2, х5, х7 значит эти коэффициенты регрессии не значимы и не надежны.

Вычислим среднюю ошибку аппроксимации:

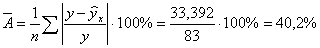
В среднем расчётные значения отличаются от фактических на 40,2%, что превышает допустимые пределы 8%-10%, следовательно, с этой точки зрения можно считать выбор уравнения не удачным.

Построим матрицу парных коэффициентов корреляции.

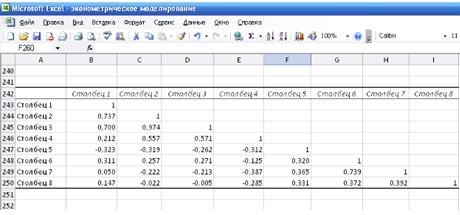
Из матрицы можно заметить, что факторы х1 и х2, х5 и х6 мультиколлинеарны, т.к. коэффициенты корреляции превышают 0,75. Таким образом, можно сказать, что они дублируют друг друга.

При отборе факторов в модель предпочтение отдается фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В нашем примере получаем, информативными факторами являются: х1 (брачность).

Проверим значимость коэффициентов корреляции на уровне значимости α=0,05.

Рассчитаем фактические значения критериев по формуле:

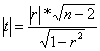
Табличное (критическое) значение статистики Стьюдента, определенное на уровне значимости α=0,05 при числе степеней свободы f=22 равно:

Найдем t_крит(α=0,05; f=20)= 2,09

По критерию t все коэффициенты х1, х2, х4, х5 значимы.

По матрице коэффициентов видим, что наибольшее влияние на рождаемость оказывает брачность.

Множественный коэффициент корреляции равен R=0,819, то есть связь между спросом (у) и включенными в модель факторами (х) очень сильная.

Коэффициент детерминации 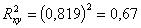 значит вариация рождаемости на 67% объясняется вариацией включенных в модель факторов и на 33% зависит от других факторов

Выберем лучшую факторную переменную из рассмотренных и обоснуем свой выбор.

Рассчитаем значения коэффициентов детерминации R² объясняющих переменных по всем остальным переменным, то есть в качестве зависимой переменной выбираем последовательно все переменные: х1, х2, х3, х4, х5, х6, х7 все остальные объясняющие переменные в качестве независимых.

Анализ оценок детерминации показал наличие тесной связи между объясняющей переменной х1 и всеми остальными признаками.

Лучшая факторная переменная х1 так как от нее в большей степени зависит изменение у.

Исходя из результатов исследования можно сузито количество независимых переменных до4-х при чем оставить только х1, х3, х4, х6. Не взяли переменную х2 т.к. она мультиколлинеарна с х1, следовательно достаточно выбрать любую из них, выбрали х1 потому, что она была значима по критерию Стьюдента. Х6 выбрали по той же причине, что и х1. х3,х4 были значимы по критерию Стьюдента.

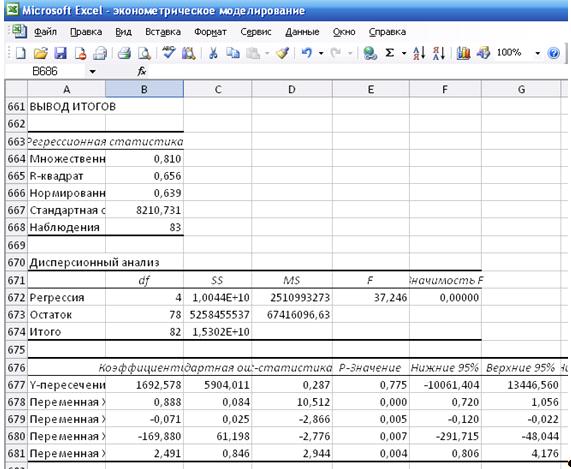
Уравнение регрессии имеет вид:

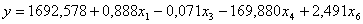
С увеличением брачности на 1 рождаемость возрастает в среднем на 0,888 при условии постоянства всех остальных факторов. С увеличением численности безработных на 1 рождаемость сокращается в среднем на 0,071 при условии постоянства всех остальных факторов. С увеличением прерывания беременности на 100 родов на 1 рождаемость сокращается в среднем на 169,88 при условии постоянства всех остальных факторов. С увеличением величины прожиточного минимума на 1 рождаемость возрастает в среднем на 2,491 при условии постоянства всех остальных факторов.

В границы доверительных интервалов переменных х1, х3, х4, х6 не попадает 0, это свидетельствует о статистической значимости и надежности рассматриваемых коэффициентов.

Коэффициент детерминации 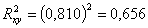 значит вариация рождаемости на 65,6% объясняется вариацией включенных в модель факторов и на 34,4% зависит от других факторов

По проведенному исследованию можно сказать, что рождаемость в большей степени зависит от брачности, поэтому в следующем разделе практической части проанализируем зависимость рождаемости от брачности.

.2 Анализ уровня рождаемости в России с помощью парной регрессии

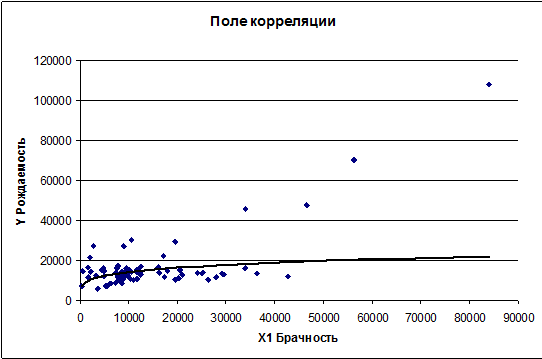
Примем за результативную переменную - переменную у (рождаемость),, а за факторную переменную - лучшую факторную переменную, выбранную в предыдущей главе брачность (х1). В данном разделе построим поле корреляции и сформулируйте гипотезу о форме связи. Рассчитаем параметры уравнения линейной регрессии и нанесем его на поле корреляции. Оценим тесноту связи с помощью показателей корреляции и детерминации. Дадим с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом. Оценим с помощью средней ошибки аппроксимации качество уравнения. С помощью t-критерия Стьюдента оцените статистическую надёжность показателей регрессионного моделирования. С помощью F-критерия Фишера оценим статистическую надёжность результатов регрессионного моделирования.

Рассчитаем параметры уравнений:

линейной регрессии

степенной регрессии;

экспоненциальной (показательной) регрессии;

полулогарифмической регрессии;

Каждое из построенных уравнений нанесем на поле корреляции.

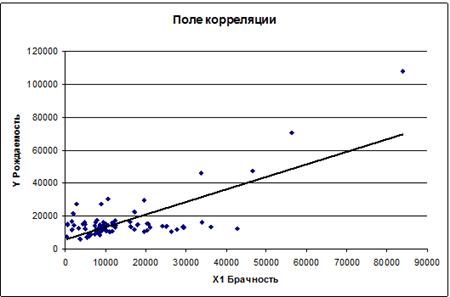
Строим поле корреляции:

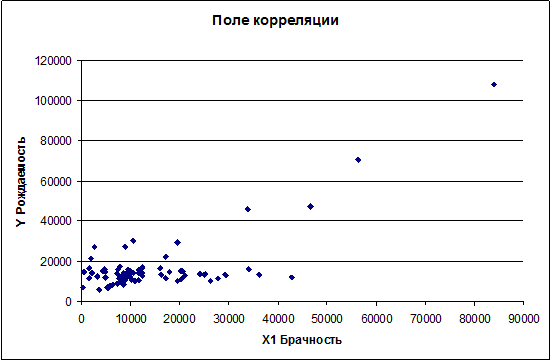
Предположим, что между х и у связь линейная, тогда уравнение регрессии имеет вид: ŷ_х=а+bx. Найдем параметры данного уравнения с помощью функций EXEL Сервис, Анализ данных.

Вообще данные параметры можно вычислить и по формулам:

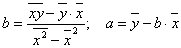
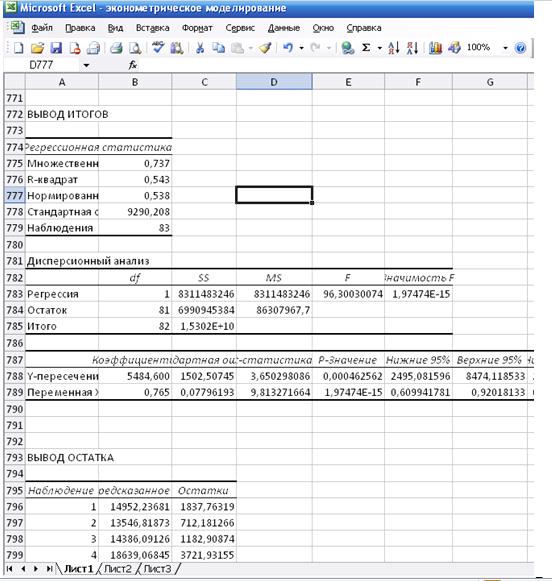
ŷ_х = 5484,600 + 0,765х - уравнение линейной регрессии.

Итак, с увеличением брачности на 1 рождаемость увеличивается в среднем на 0,765.

Коэффициент парной корреляции равнее 0,737, то есть связь между рождаемостью (у) и брачностью (х) сильная.

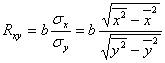
формула для вычисления коэффициента парной корреляции

Определим коэффициент детерминации:

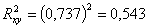
Итак, 54,3% вариации рождаемости объясняется вариацией брачности и на 45,7% зависит от других факторов.

Вычислим среднюю ошибку аппроксимации:

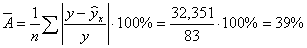
В среднем расчётные значения отличаются от фактических на 39%, что превышает допустимые пределы 8%-10%, следовательно, с этой точки зрения можно считать выбор уравнения не удачным.

Вычислим коэффициент эластичности:

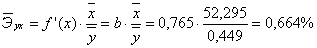
То есть с увеличением брачности на 1% от своего среднего уровня, рождаемость увеличивается на 0,664% от своего среднего уровня, а с уменьшением брачности на 1% от своего среднего уровня, рождаемость уменьшается на 0,664% от своего среднего уровня.

Проверим значимость уравнения регрессии с помощью F-критерия Фишера.

Выдвигаем гипотезы:

Н₀: уравнение регрессии в целом незначимо; Н₁: уравнение регрессии в целом значимо;

Находим наблюдаемое значение критерия:

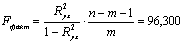
По таблице приложения находим критическое значение критерия: F_табл=3,96где

F(a; m; n-m-1)=F(0,05; 1; 83)=3,96. Так как F_факт>F_табл (96,3>3,96), то гипотеза Н₀ о случайной природе оцениваемых характеристик отклоняется (или не принимается) и признается их статистическая значимость и надёжность.

Нанесём полученное уравнение на поле корреляции:

Предположим, что между х и у связь степенная, тогда уравнение регрессии имеет вид: ŷ_х=а·x^b.

Построению степенной модели предшествует процедура линеаризации переменных. Линеаризация переменных производится путём логарифмирования обеих частей уравнения:

=lnа+b·lnx, тогда Y=А+b·X,

где Y=lny; X=lnx; А=lna.

По методу наименьших квадратов (МНК) из решения системы:

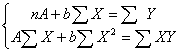
Найдем параметры данного уравнения с помощью функций EXEL Сервис, Анализ данных.

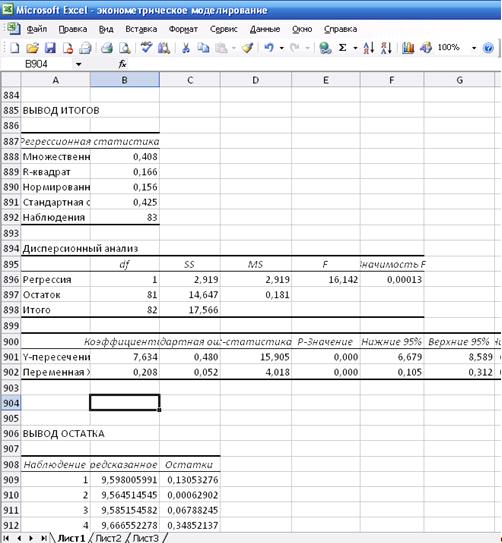
Уравнение парной линейной регрессии Y на X имеет вид:

Ŷ_X = 7,634 + 0,208X

Выполнив его потенцирование, получим: ŷ_х=е^7,634 · х ^0,208 или

ŷ_х= 1963,412 · х ^0,208

Рассчитаем индекс корреляции:

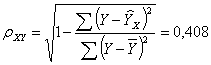
то есть связь между рождаемостью (у) и брачностью (х) ниже средней.

Определим индекс детерминации: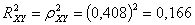

Итак, 16,6% вариации рождаемости объясняется вариацией брачности и на 83,4% зависит от других факторов.

Вычислим среднюю ошибку аппроксимации:

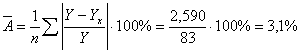
В среднем расчётные значения отличаются от фактических на 3,1%, что не превышает допустимые пределы 8%-10%, следовательно, с этой точки зрения можно считать выбор уравнения удачным.

Вычислим коэффициент эластичности: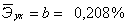

То есть с увеличением брачности на 1% от своего среднего уровня, рождаемость увеличивается на 0,208% от своего среднего уровня, а с уменьшением брачности на 1% от своего среднего уровня, рождаемость уменьшается на 0,208% от своего среднего уровня.

Проверим значимость уравнения регрессии с помощью F - критерия Фишера.

Выдвигаем гипотезы: Н₀: уравнение регрессии незначимо; Н₁: уравнение регрессии значимо; Находим наблюдаемое значение критерия:

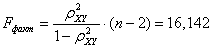
По таблице приложения находим критическое значение критерия: F_табл=3,96 где F(a; m; n-m-1)=F(0,05; 1; 83)=3,96. Так как F_факт>F_табл (16,142>3,96), то гипотеза Н₀ о случайной природе оцениваемых характеристик отклоняется (или не принимается) и признается их статистическая значимость и надёжность.

Предположим, что между х и у связь показательная, тогда уравнение регрессии имеет вид:

ŷ_х=а·b^x.

Построению показательной модели предшествует процедура линеаризации переменных. Линеаризация переменных производится путём логарифмирования обеих частей уравнения:

lny=lnа+x·lnb, тогда Y=А+B·x,

где Y=lny; B=lnb; А=lna.

по методу наименьших квадратов (МНК) из решения системы:

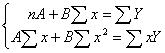
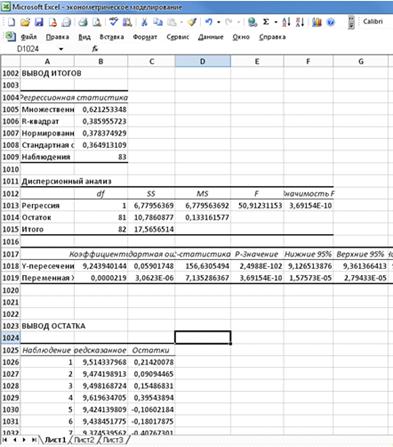
уравнение парной линейной регрессии Y на x имеет вид:

Ŷ_х= 9,244 + 0,0000219х

Выполнив его потенцирование, получим: ŷ_х=е^9,244 ·е^0,0000219х

или ŷ_х= 9716,298 · 1,0000217^х

Рассчитаем индекс корреляции:

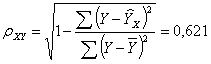
то есть связь между рождаемостью (у) и брачностью (х) выше средней.

Определим индекс детерминации:

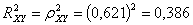
Итак, 38,6% вариации средних объемов продаж объясняется вариацией средней цены товара и 61,4% зависит от других факторов.

Вычислим среднюю ошибку аппроксимации:

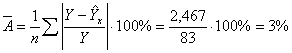
В среднем расчётные значения отличаются от фактических на 3%, что не превышает допустимые пределы 8%-10%, следовательно, с этой точки зрения можно считать выбор уравнения удачным.

Вычислим коэффициент эластичности:

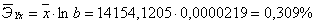
То есть с увеличением брачности на 1% от своего среднего уровня, рождаемость увеличивается на 0,309% от своего среднего уровня, а с уменьшением брачности на 1% от своего среднего уровня, рождаемость уменьшается на 0,309% от своего среднего уровня.

Проверим значимость уравнения регрессии с помощью F - критерия Фишера.

Выдвигаем гипотезы: Н₀: уравнение регрессии незначимо; Н₁: уравнение регрессии значимо; Находим наблюдаемое значение критерия:

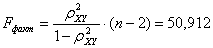
По таблице приложения находим критическое значение критерия: F_табл=3,96 где F(a; m; n-m-1)=F(0,05; 1; 83)=3,96. Так как F_факт>F_табл (50,912>3,96), то гипотеза Н₀ о случайной природе оцениваемых характеристик отклоняется (или не принимается) и признается их статистическая значимость и надёжность.

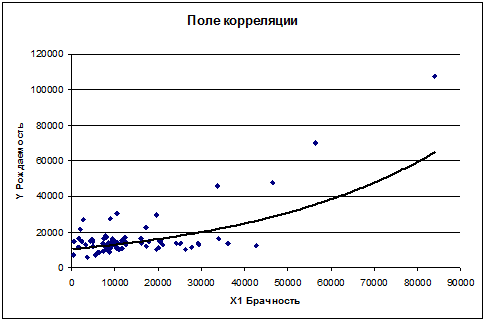
Нанесём полученное уравнение на поле корреляции:

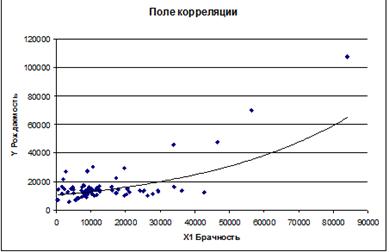
Предположим, что между х и у связь полулогарифмическая, тогда уравнение регрессии имеет вид:

ŷ_х=а+blnx, у=а+bХ,

где X=lnx;

по методу наименьших квадратов (МНК) из решения системы:

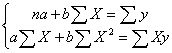
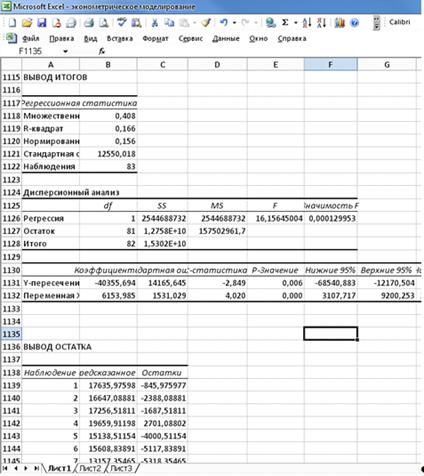
уравнение парной линейной регрессии y на X имеет вид:

ŷ_Х= -40355,694 + 6153,985Х или ŷ_х= -40355,694 + 6153,985lnх

Рассчитаем индекс корреляции:

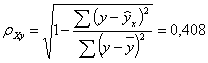
то есть связь между рождаемостью (у) и брачностью (х) ниже средней.

Определим индекс детерминации:

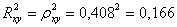
Итак, 16,6% вариации средних объемов продаж объясняется вариацией средней цены товара и 83,4% зависит от других факторов.

Вычислим среднюю ошибку аппроксимации:

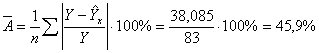
В среднем расчётные значения отличаются от фактических на 45,9%, что превышает допустимые пределы 8%-10%, следовательно, с этой точки зрения можно считать выбор уравнения не удачным.

Вычислим коэффициент эластичности:

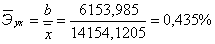
То есть с увеличением брачности на 1% от своего среднего уровня, рождаемость увеличивается на 0,435% от своего среднего уровня, а с уменьшением брачности на 1% от своего среднего уровня, рождаемость уменьшается на 0,435% от своего среднего уровня.

Проверим значимость уравнения регрессии с помощью F - критерия Фишера.

Выдвигаем гипотезы: Н₀: уравнение регрессии незначимо; Н₁: уравнение регрессии значимо; Находим наблюдаемое значение критерия:

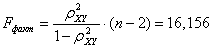
По таблице приложения находим критическое значение критерия: F_табл=3,96 где F(a; m; n-m-1)=F(0,05; 1; 83)=3,96. Так как F_факт>F_табл (16,156>3,96), то гипотеза Н₀ о случайной природе оцениваемых характеристик отклоняется (или не принимается) и признается их статистическая значимость и надёжность.

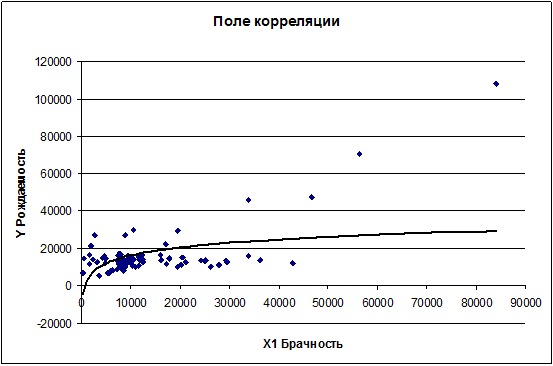
Нанесём полученное уравнение на поле корреляции:

3. Прогнозирование уровня рождаемости в России

Составим сравнительную таблицу полученных оценок в главе 2, пункта 2.2:

Уравнение показательной регрессии является лучшим т.к. средняя ошибка аппроксимации в нем меньше чем в других.

Рассчитаем прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от его среднего уровня по уравнению показательной регрессии:

ŷ_х= 9716,298 · 1,0000217^х

;

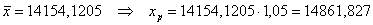ŷ_х= 9716,298 · 1,0000217^14861,827 = 13414,672

Если прогнозное значение брачности увеличится на 5% от среднего уровня, т.е. станет равным 14862 то рождаемость увеличится и станет составлять 13415.

Заключение

Таким образом, в данной курсовой работе рассмотрены теоретические основы эконометрического анализа, разработана модель множественной и парной регрессии зависимости рождаемости населения России от различных факторов. Изучены теоретические основы регрессионного анализа. Рассмотрены виды регрессионного анализа. Построены модели регрессии с включенными факторами.

На основе проведенного исследования можно сделать следующие выводы о рождаемости населения Российской федерации. С увеличением брачности на 1 рождаемость увеличивается минимум на 0,321б. или увеличивается как максимум на 1,6. С увеличением разводимости рождаемость уменьшается максимум на 1,043 или увеличится как максимум на 0,999. С увеличением численности безработных на 1 рождаемость уменьшается максимум на 0,118 руб. или уменьшается как минимум на 0,014руб. С увеличением прерывания беременности на 100 родов на 1 рождаемость уменьшается максимум на 299,552 руб. или уменьшается как минимум на 29,737руб.

С увеличением среднедушевых денежные доходов рождаемость уменьшается максимум на 0,714 или увеличится как максимум на 0,189. С увеличением среднедушевых денежные доходов рождаемость увеличивается минимум на 0,618 или увеличивается как максимум на 6,48. С увеличением обеспеченности амбулаторно-поликлиническими учреждениями на 10000 населения, посещений в смену, значение показателя за год на 1 рождаемость уменьшается максимум на 10,888 или увеличится как максимум на 57,863.

При чем вариация рождаемости на 67% объясняется вариацией включенных в модель факторов и на 33% зависит от других факторов и составленное уравнение значимо, также выяснено, что из факторных переменных лучшей является брачность и для дальнейших исследований зависимости рождаемости от брачности лучше использовать уравнение показательной регрессии

Список используемой литературы

1. Домбровский В.В. Эконометрика: Учебник / В. В. Домбровский. - М.: Новый учебник, 2009. - 342с.

. Колемаев В.А. Эконометрика: Учебник / В. А. Колемаев. - М.: ИНФРА-М, 2011. - 160с.

. Макарова Е.А. Моделирование и прогнозирование экономических процессов: Учебно-методическое пособие ( для студентов экономических специальностей ) / ВЗФЭИ. - Волгоград: ВолГУ, 2011. - 246с.

. Орлов А.Н. Эконометрика: Учебное пособие / А. Н. Орлов. - М.: Экзамен, 2010. - 576с.

. Орлова И.В. Экономико-математическое моделирование. Практическое пособие по решению задач / И. В. Орлова; ВЗФЭИ. - М.: Вузовский учебник, 2009. - 144с.

. Тихомиров Н.П. Эконометрика: Учебник / Н. П. Тихомиров, Е. Ю. Дорохина. - М.: Экзамен, 2009. - 512с.

. Эконометрика: Учебник / Под ред. Елисеевой И.И. - М.: Финансы и статистика, 2011. - 344с.

. Медков В.М. Демография: Учебник. - М.: ИНФРА-М, 2009. - 683с.

. Борисов В.А. Демография: Учебник для вузов. - М.: Изд. Дом «Нота бене», 2010. - 344с.

. Бутов В.И. Демография. - ИКЦ «МарТ», 2010. - 592с.

. Валентей Д.И., Кваша А.Я. Основы демографии: Учебник. - М.: Мысль, 2012.

. Симагин Ю.А. Территориальная организация населения: учеб. пособие / Ю.А. Симагин. - М.: Дашков и К, 2009. - 240с.

. Социальная статистика: Учебник. / Под ред. Елисеевой И.И. - М.: Финансы и статистика, 2009. - 280с.